Abstract
It has been shown that the photonic bandgap of one-dimensional (1D) dielectric periodic thin films can vanish at the first Bragg condition for TM modes. Here, we address the case of 1D photonic crystal slabs formed by a chain of high-index dielectric particles with transversal confinement and show that the Bragg bandgap can vanish for both TE- and TM-like modes. Calculations using plane-wave expansion and finite-difference time-domain methods confirm that the PBG vanishes. PBG closure is explained as being a result of the interplay between the electric and magnetic dipole resonances of the isolated nanoparticle with Bragg resonance, as confirmed by calculating the electric and magnetic dipoles of the isolated nanobricks. This can be considered as a manifestation of the metamaterial behavior of the 1D system when using silicon as an underlying material. Our finding may have important consequences for the fields of photonic crystals and all-dielectric metamaterials.
1. Introduction
The periodic modulation (period a) of the index of refraction of a dielectric medium gives rise to photonic band gaps (PBGs) where electromagnetic propagation along the direction of periodicity is forbidden [1]. If we consider a periodic medium formed by periodic layers of indices n1 and n2, a so-called 1D photonic crystal, the lowest-frequency PBG opens due to the splitting of the so-called dielectric and air bands at the Bragg wavelength, defined as , where . Interestingly, the width of the PBG is directly proportional to the index contrast, as . This essentially means that the PBG arises even for minute values of ∆n, as in the case of fiber Bragg gratings used as wavelength filters in telecom networks [2], and can become very large when high-index materials—such as silicon—are used. Indeed, the existence of full, three-dimensional (3D) PBGs in 3D photonic crystals can be explained as the overlapping of wide 1D-PBGs in every possible spatial direction, i.e., for every possible wave vector k [3,4].
The first PBG is remarkably important in integrated guided optics since it is usually the only one placed below the light cone [5,6]; therefore, it can give rise to localized modes with large Q factor when defect-like cavities are created. In the integrated optics arena, the confinement of light waves below the light line is achieved due to total internal reflection in the two dimensions perpendicular to the propagation direction, in which the system is periodic.
Recently, it has been shown theoretically [7] that the first (or Bragg) PBG can vanish in a 1D periodic thin film, though only for TM modes (with the electric field perpendicular to the film) and not for TE modes (with the electric field parallel to the film). This result is explained from the different boundary conditions to be satisfied by the electric and magnetic fields when propagating along the periodic film. However, this study was two-dimensional (2D) and did not include lateral confinement of the waves. From a practical perspective, it would be interesting to see whether the closure of the PBG is also maintained when transversal confinement via total internal reflection (TIR) is introduced, as in 1D photonic crystal slabs [8] built in high-index films.
Here, we study a 1D photonic crystal with full transversal confinement formed by a set of silicon nanobricks and show that the Bragg PBG for TE-like modes can vanish under proper conditions. We choose this system because it allows for an easy analysis of the unit cell and can be easily fabricated using standard silicon micro- and nanofabrication tools, as shown in recent experiments [9,10,11]. Notably, interchanging the thickness and the width of the nanobricks should also lead to the closure of the PBG for TM-like modes, in contrast to the case addressed in [7]. To explain the closure, and since we cannot describe the system analytically, we adopt a strategy different to [7] and consider the electric and magnetic Mie resonances of the isolated nanobricks. Our results suggest that the interplay between both Mie resonances and the Bragg resonance leads to PBG closure, resulting in a metamaterial-like behavior of the periodic structure.
2. Results
We consider a periodic structure made of high-index (n = 3.5) nanobricks with the dimensions of wx, wy and wz surrounded by air (see Figure 1a). The structure is periodic along the z axis (period a), whilst confinement of guided waves in the x and y direction is ensured by TIR. Figure 1b shows the photonic bands—calculated using the plane wave expansion method—of the TE-like (or x-even parity) modes for wx = 220 nm, wy = 450 nm, and a = 455 nm for three different values of wz. Notice that, due to the addition of the confinement along the y direction, we cannot classify the guided modes into TE or TM since the three components of the electric and magnetic fields are now present [12]. Nonetheless, the modes are usually termed either TE-like (the main component of transverse field is Ey) or TM-like (the main component of transverse field is Ex) in integrated optics due to their resemblance to the 2D picture. When wz = 200 nm (blue curves), a wide TE PBG opens between the dielectric and the air bands, as expected for high-contrast periodic systems [1]. The same happens for wz = 320 nm (red curves), though the PBG is redshifted because of the larger amount of dielectric material in the unit cell.
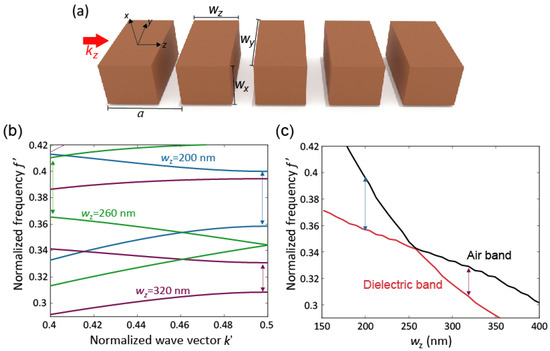
Figure 1.
(a) Sketch of the 1D periodic systems under study: a chain of high-index dielectric nanobricks. (b) Photonic bands for x-even parity (TE-like) modes for different values of wz. (c) Frequencies of the dielectric and air bands as a function of wz. Vertical arrows show the PBG for each value of wz (for wz = 260 nm a higher-order PBG is shown). The numerical simulations were performed for a 1D periodic chain of nanobricks with index n = 3.5 and dimensions wx = 220 nm, wy = 450 nm, a = 455 nm. The normalized frequency f’ is given in units of ωa/2πc, ω being the angular frequency and c the speed of light in vacuum. The normalized wave vector k’ is given in units of 2πk/a.
When, analyzing the intermediate case (wz = 260 nm, black curves) we observe that the PBG vanishes. This means that the PBG width is neither directly nor inversely proportional to the parameter wz. To know more about this relation, we calculate the frequencies of the dielectric and air bands at the boundary of the first Brillouin zone. Notice that these frequencies establish the boundaries of the Bragg bandgap. The results, depicted in Figure 1c, clearly show a crossing of the bands—or band flip [7]—delimiting the Bragg PBG at wz ≈ 258 nm. This means that, counterintuitively, the PBG vanishes even though we have a high-index contrast system. In general, an increase in wz results not only in a red-shift of the bands but also in a modification of the width of the Bragg PBG that eventually closes. To establish the effect of the period on PBG closure, we performed calculations for other values of a. We observed that the PBG was effectively closed at wz = 248 nm for a = 430 nm and at wz = 267 nm for a = 480 nm, meaning that the effect was also observed for other periods of the lattice.
In comparison to the results in [7], we may argue that we now have TIR confinement in the lateral direction, which resembles the TE case found there. Indeed, by interchanging wx and wy in our periodic system (or rotating the structure 90° around the z axis), we should find that the PBG closes for TM-like (or x-odd parity) modes, meaning that the first PBG can be closed irrespective of the type of mode.
We also tested the vanishing behaviour of the PBG using fully 3D finite-difference time-domain (FDTD) simulations. The normalized intensity (square of the electric field at the center of the waveguide) after transmission along a chain of 10 nanobricks using rectangular waveguides of width wx and thickness wy for different values of wz is shown in Figure 2. Normalization is performed with respect to the response of a single waveguide. Notice that intensities over 1 (0 dB) are because the electric field is monitored locally, so resonant effects (such as Fabry–Perot fringes close to the PBG regions) can lead to large local intensities, though the normalized transmitted power is always lower than 1. In agreement with Figure 1b, whilst broad dips appear for wz = 200 nm and wz = 320 nm at the expected frequency bands, there is not any observable dip for wz = 260 nm (the fall in transmission above f’ = 0.37 corresponds to higher-order PBGs, as shown in Figure 1b).
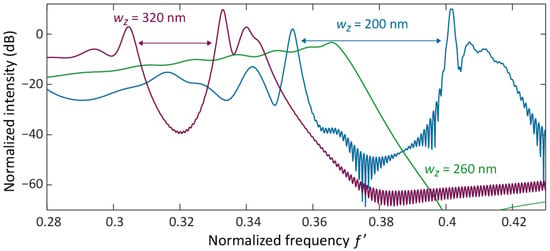
Figure 2.
FDTD-calculated normalized intensity after transmission along a chain of 10 nanobricks using waveguides as input and output ports for wz = 200 (blue), 260 (black) and 320 nm (red). The results are normalized with respect to the transmission along a perfect rectangular waveguide. The trend is as follows: the PBG (highlighted by the horizontal lines with arrows) shifts to lower frequencies when wz increases and disappears at wz ≈ 260 nm.
To obtain further insights about the closure of the Bragg PBG, we obtained the main components of the transverse electric field at k’ = 0.5 for the dielectric and air bands at different values of wz. The results are illustrated in Figure 3. For wz = 200 nm, the dielectric band is characterized by a z-even parity transverse electric field (Ey) closely resembling an electric dipole pointing along y. The air band shows an opposite behavior in terms of parity, and the electric field patterns corresponds to those of a magnetic dipole oriented along x (the magnetic field pattern is not shown here for the sake of simplicity). For wz = 320 nm, the situation completely reverses; now, the dielectric (air) band has a magnetic (electric) dipole character. Therefore, it is the transition from electric to magnetic Mie resonances of the isolated nanobricks that explains the closure of the Bragg PBG. Indeed, the bandgap is closed because, for certain dimensions of the system, the Mie electric and magnetic resonances of the isolated nanobrick become degenerate at a frequency within a Bragg PBG. The band flip can also be observed in the Supplementary Visualizations 1 to 12, which show the evolution of the Ey and Hx fields when propagating along a chain of ten nanobricks at frequencies corresponding to the dielectric band, the bandgap and the air band and for wz = 200 and 320 nm, respectively.
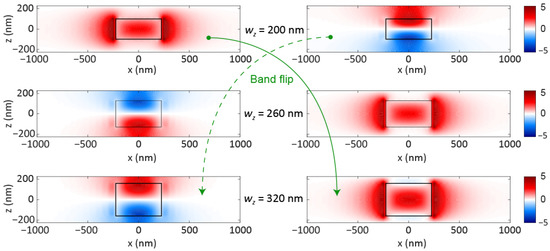
Figure 3.
Ey field maps at the boundary of the first Brillouin zone for the dielectric (left column) and air (right column) bands at different values of wz. For wz = 260 nm (middle panels) the frequency difference between the two bands is negligible, meaning that they are close to the degeneracy point.
To support this explanation, we calculated the frequencies of the electric and magnetic dipole responses of isolated nanobricks as a function of wz, following the approach in [13]. The results, depicted in Figure 4, show that, for small values of wz, the frequency of the electric dipole is smaller than that of the magnetic dipole, and this feature is inherited by the dielectric and air bands when the periodic system is formed. When wz increases, the frequency of the magnetic dipole decreases faster than that of the electric dipole, resulting in the crossing of the Mie resonances, which are related to the band flipping and PBG closure in the periodic system. Indeed, even though we have only studied the effects of the wz variation for simplicity, we can state that, for a given target frequency, there will be a triplet of (wx, wy, wz) values for which the electric and magnetic dipole resonances are degenerate. Therefore, it will be always possible to design a 1D periodic system with a closed bandgap at a certain wavelength. Moreover, if the degeneracy is achieved for a nanobrick with wx = wy, the Bragg PBG will be closed for both TE and TM modes simultaneously as a result of the symmetry of the system.
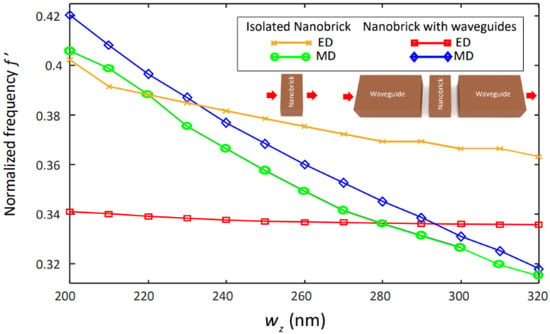
Figure 4.
Calculation of the electric (orange) and magnetic (green) dipole frequencies of an isolated nanobrick as a function of wz obtained from a multipole decomposition. The red and blue curves show the frequencies of the maximum Ey and Hx at the nanobrick center when the nanobrick is embedded in a waveguide gap (illumination and collection using the TE-like mode of the waveguide ports). Inset: scheme of the illumination of the silicon nanobrick for each result.
Notice that the crossing of the electric and magnetic dipole of the isolated nanobricks takes place for a wz value smaller than that obtained for the PBG closure. However, this can be explained because the isolated nanobrick is surrounded by a vacuum; when forming the chain part of the field, the electromagentic field penetrates the neighbouring nanobricks, resulting in a perturbation of the modes. To account for the additional presence of dielectric material, we calculated the frequencies of the electric and magnetic dipoles corresponding to the maximum of the electric field and the magnetic field at the center of the nanobrick, respectively; this occurred when a single nanobrick was embedded in a waveguide gap of a length equal to a (see Figure 4, inset). The results, also shown in Figure 4, indicate that, now, the flip frequency is red-shifted and the crossing point shifts to larger values of wz.
3. Discussion and Conclusions
Our results highlight the importance of the properties of the isolated unit cell when forming 1D lattices of high-index dielectric materials [14]. Noticeably, when the Mie resonances of the unit cell dominate over the periodic response, the structure could, in principle, be considered as an all-dielectric metamaterial [15]. However, looking at the classification proposed in [16], the PBG closure takes place just when the Bragg wavelength equals the electric and magnetic dipole wavelengths, meaning that we are just at the frontier separating the photonic crystal and metamaterial phases. Indeed, in the 2D periodic systems arranged in a square lattice studied in [16], which require very large indices to reach the metamaterial phase, the use of a hexagonal lattice [17] would allow one to obtain a “metamaterial” behavior in 2D silicon photonic crystals. Our results show that such metamaterial behavior naturally arises in a realistic 1D photonic crystal made of silicon nanobricks at bands placed below the light cone, which would ensure lossless performance. This behavior is manifested by the fact that the overlapping of the electric and magnetic dipolar Mie resonances closes the Bragg PBG, which is the fundamental feature of a photonic crystal.
In summary, we have shown that the interplay between the electric and magnetic dipole resonances of a single nanobrick can lead to the closure of the Bragg PBG for guided modes when forming a 1D photonic crystal. This result is somewhat counterintuitive since, in principle, any 1D periodic lattice should induce a forbidden band for waves propagating in the direction of the periodicity. Even though we have analyzed a very simple structure, the performance should be the same if the unit cell supports electric and magnetic resonances so that a band flip might arise under certain conditions. Noticeably, the PBG only vanishes for a perfect photonic crystal, so any tiny perturbation can open the PBG. This could be used to build active or tunable devices where the properties of a single nanobrick can be actively modified using electrical, optical or even mechanical means. Our finding could lead to advances in the design of subwavelength integrated photonic devices [18] for application in signal processing, communication systems or bio- and chemo-sensing. Notably, the resulting devices could be easily manufactured using mainstream silicon photonic technology.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/photonics9100691/s1. Visualizations S1 to S12 are animated movies of the propagation of the electric and magnetic field along a chain of 10 nanobricks for different frequencies and values of wz.
Author Contributions
Conceptualization, A.M. and J.G.-R.; methodology, A.M., L.M. and Á.I.B.; investigation, E.D.-E.; data curation, E.D.-E.; writing—original draft preparation, A.M.; writing—review and editing, all; visualization, E.D.-E.; supervision, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
A. M. acknowledges funding from Generalitat Valenciana (PROMETEO/2019/123). A. B. is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the International Research Training Group (IRTG) 2675 “Meta-ACTIVE”, project number 437527638. L. M. thanks financial support from the Next generation EU program, Ministerio de Universidades (Gobierno de España).
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Joannopoulos, J.D.; Villeneuve, P.R.; Fan, S. Photonic crystals: Putting a new twist on light. Nature 1997, 386, 143–149. [Google Scholar] [CrossRef]
- Oh, M.C.; Lee, H.J.; Lee, M.H.; Ahn, J.H.; Han, S.G.; Kim, H.G. Tunable wavelength filters with Bragg grating fiber in polymer waveguides. Appl. Phys. Lett. 1998, 73, 2543–2545. [Google Scholar] [CrossRef]
- Ho, K.M.; Chan, C.T.; Soukoulis, C.M. Existence of a photonic gap in periodic dielectric structures. Phys. Rev. Lett. 1990, 65, 3152–3155. [Google Scholar] [CrossRef] [PubMed]
- Blanco, A.; Chomski, E.; Grabtchak, S.; Ibisate, M.; Jhon, S.; Leonard, S.W.; Lopez, C.; Meseguer, F.; Miguez, H.; Mondia, J.P.; et al. Large-scale synthesis of a silicon photonic crystal with a complete three-dimensional bandgap near 1.5 micrometres. Nature 2000, 405, 437–440. [Google Scholar] [CrossRef] [PubMed]
- Martínez, A.; García, J.; Sanchis, P.; Cuesta-Soto, F.; Blasco, J.; Martí, J. Intrinsic losses of coupled-cavity waveguides in planar-photonic crystals. Opt. Lett. 2007, 32, 635–637. [Google Scholar] [CrossRef]
- Halir, R.; Bock, P.J.; Cheben, P.; Ortega-Moñux, A.; Alonso-Ramos, C.; Schmid, J.H.; Lapointe, J.; Xu, D.; Wangüemert-Pérez, J.G.; Molina-Fernández, Í.; et al. Waveguide sub-wavelength structures: A review of principles and applications. Laser Photonics Rev. 2015, 9, 25–49. [Google Scholar] [CrossRef]
- Lee, S.G.; Magnusson, R. Essential differences between TE and TM band gaps in periodic films at the first Bragg condition. Opt. Lett. 2019, 44, 4658–4661. [Google Scholar] [CrossRef] [PubMed]
- García, J.; Sanchis, P.; Martínez, A.; Martí, J. 1D periodic structures for slow-wave induced non-linearity enhancement. Opt. Express 2008, 16, 3146–3160. [Google Scholar] [CrossRef] [PubMed]
- Ding, L.; Morits, D.; Bakker, R.; Li, S.; Eschimese, D.; Zhu, S.; Yu, Y.F.; Paniagua-Dominguez, R.; Kuznetsov, A.I. All-Optical Modulation in Chains of Silicon Nanoantennas. ACS Photonics 2020, 7, 1001–1008. [Google Scholar] [CrossRef]
- Pereira-Martín, D.; Luque-González, J.M.; Wangüemert-Pérez, J.G.; Hadij-ElHouati, A.; Molina-Fernández, Í.; Cheben, P.; Schmid, J.H.; Wang, S.; Ye, W.N.; Čtyroký, J.; et al. Complex spectral filters in silicon waveguides based on cladding-modulated Bragg gratings. Opt. Express 2021, 29, 15867–15881. [Google Scholar] [CrossRef] [PubMed]
- Farnesi, D.; Pelli, S.; Soria, S.; Conti, G.N.; Le Roux, X.; Ballester, M.M.; Vivien, L.; Cheben, P.; Ramos, C.A. Metamaterial engineered silicon photonic coupler for whispering gallery mode microsphere and disk resonators. Optica 2021, 8, 1511–1514. [Google Scholar] [CrossRef]
- Espinosa-Soria, A.; Martínez, A. Transverse spin and spin-orbit coupling in silicon waveguides. IEEE Photonics Technol. Lett. 2016, 28, 1561–1564. [Google Scholar] [CrossRef]
- Díaz-Escobar, E.; Bauer, T.; Pinilla-Cienfuegos, E.; Barreda, A.I.; Griol, A.; Kuipers, L.; Martínez, A. Radiationless anapole states in on-chip photonics. Light. Sci. Appl. 2021, 10, 204. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically resonant dielectric nanostructures. Science 2016, 354, 2472. [Google Scholar] [CrossRef] [PubMed]
- Staude, I.; Schilling, J. Metamaterial-inspired silicon nanophotonics. Nat. Photonics 2017, 11, 274–284. [Google Scholar] [CrossRef]
- Rybin, M.V.; Filonov, D.; Samusev, K.B.; Belov, P.A.; Kivshar, Y.S.; Limonov, M.F. Phase diagram for the transition from photonic crystals to dielectric metamaterials. Nat. Commun. 2015, 6, 10102. [Google Scholar] [CrossRef] [PubMed]
- Li, S.V.; Kivshar, Y.S.; Rybin, M.V. Toward Silicon-Based Metamaterials. ACS Photonics 2018, 5, 4751–4757. [Google Scholar] [CrossRef]
- Cheben, P.; Halir, R.; Schmid, J.H.; Atwater, H.A.; Smith, D.R. Subwavelength integrated photonics. Nature 2018, 560, 565–572. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).