Average BER Performance Estimation of Relayed THz Links with Losses, Molecular Attenuation, Adverse Weather Conditions, Turbulence and Generalized Pointing Errors
Abstract
1. Introduction
2. System and Channel Model
2.1. Basic Principles of the Investigated THz System
2.2. Total Attenuation
2.3. Atmospheric Turbulence Model
2.4. Generalized Pointing Errors Model
2.5. Joint Impact of Attenuation, Turbulence and NZB Pointing Errors
3. Average BER Estimation
3.1. On-Off Keying Modulation
3.2. L-Symbol Pulse Amplitude Modulation Modulation
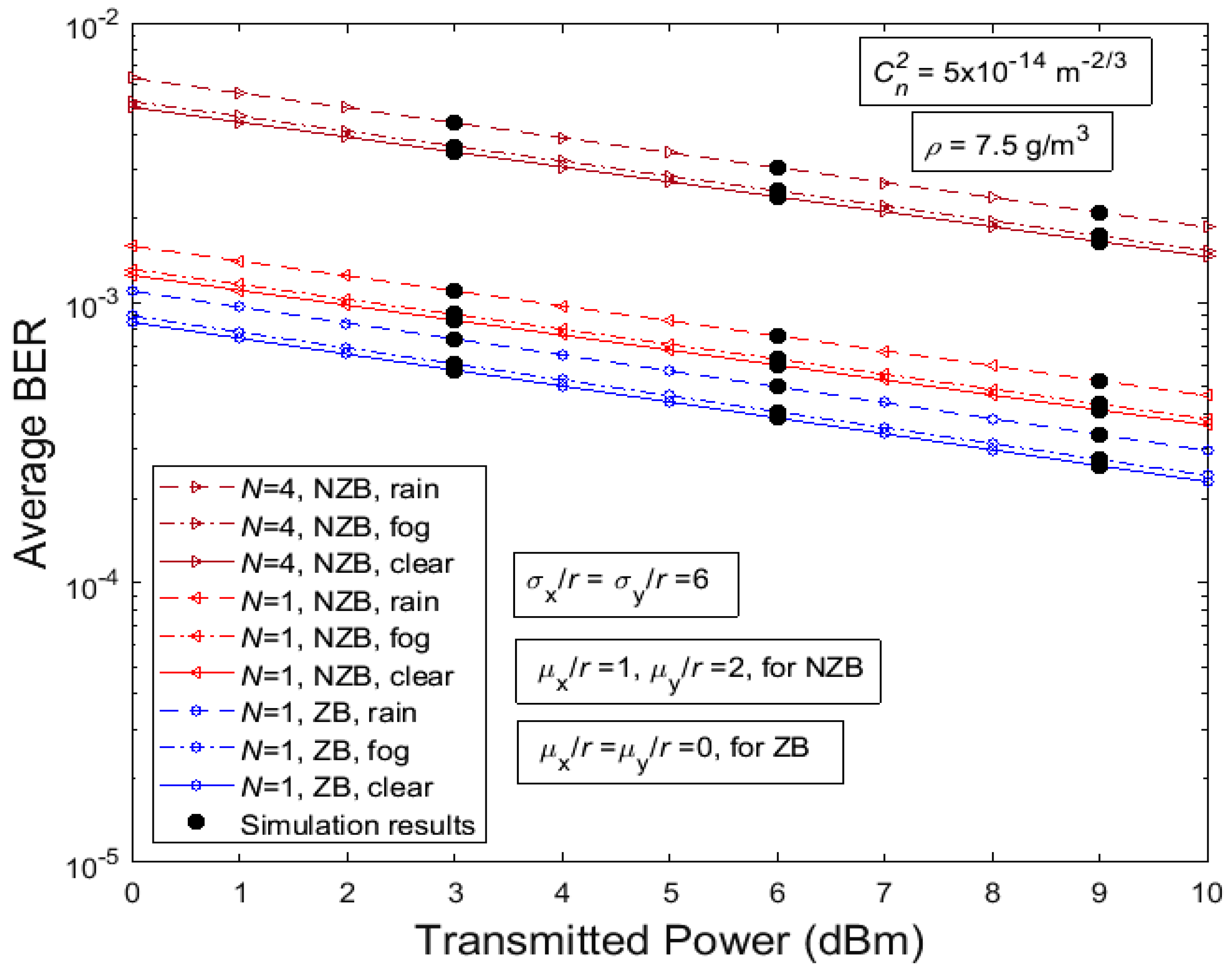
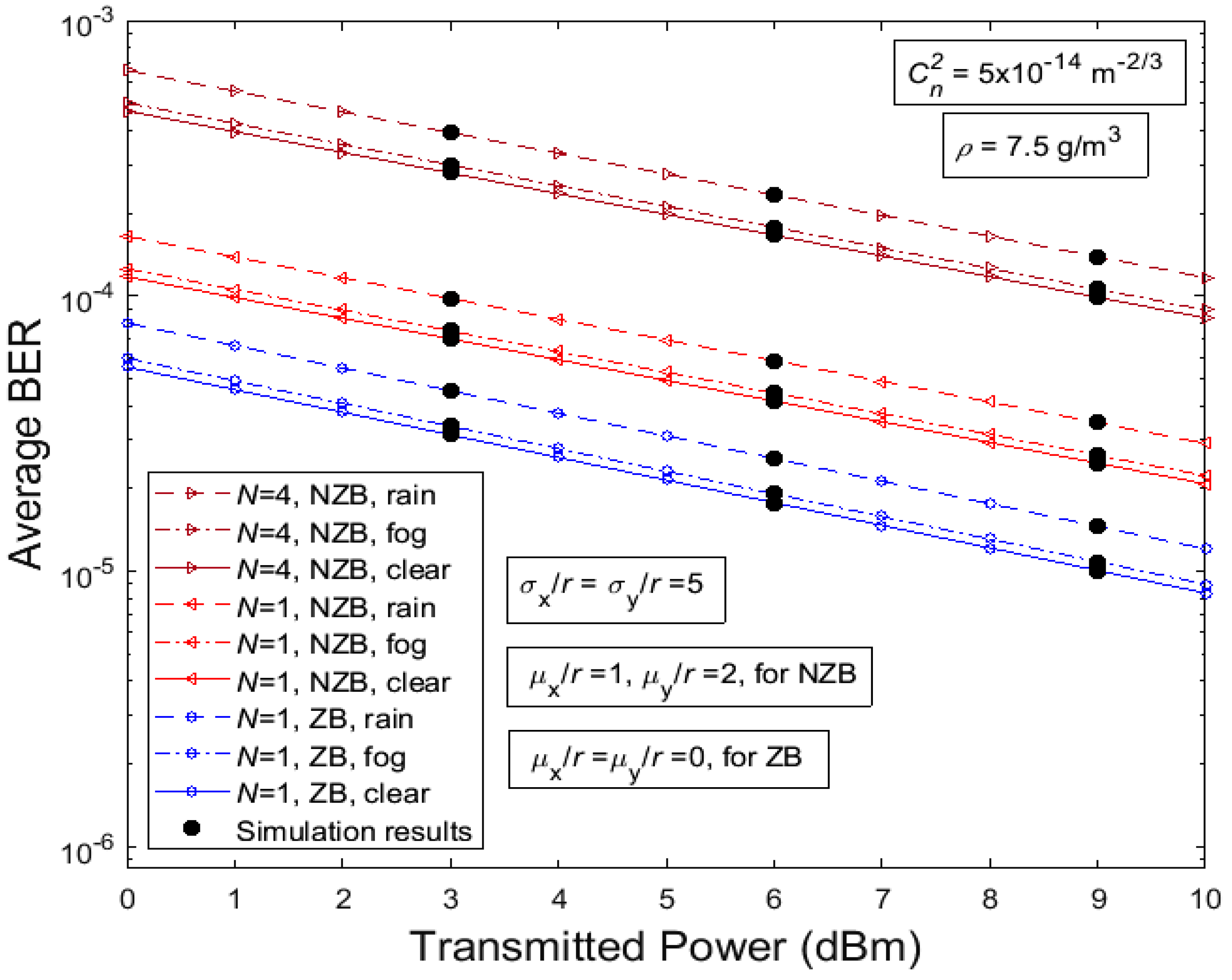
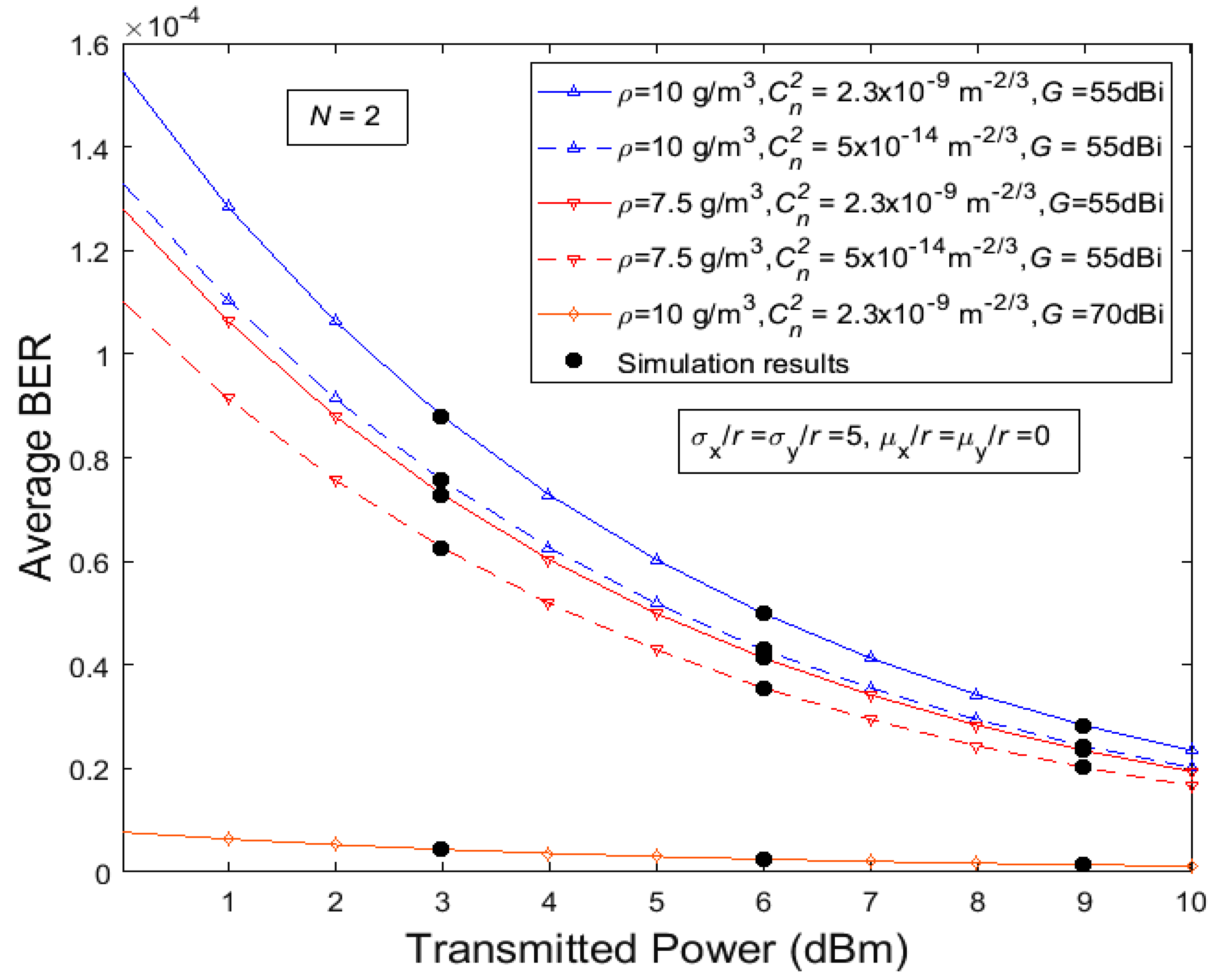
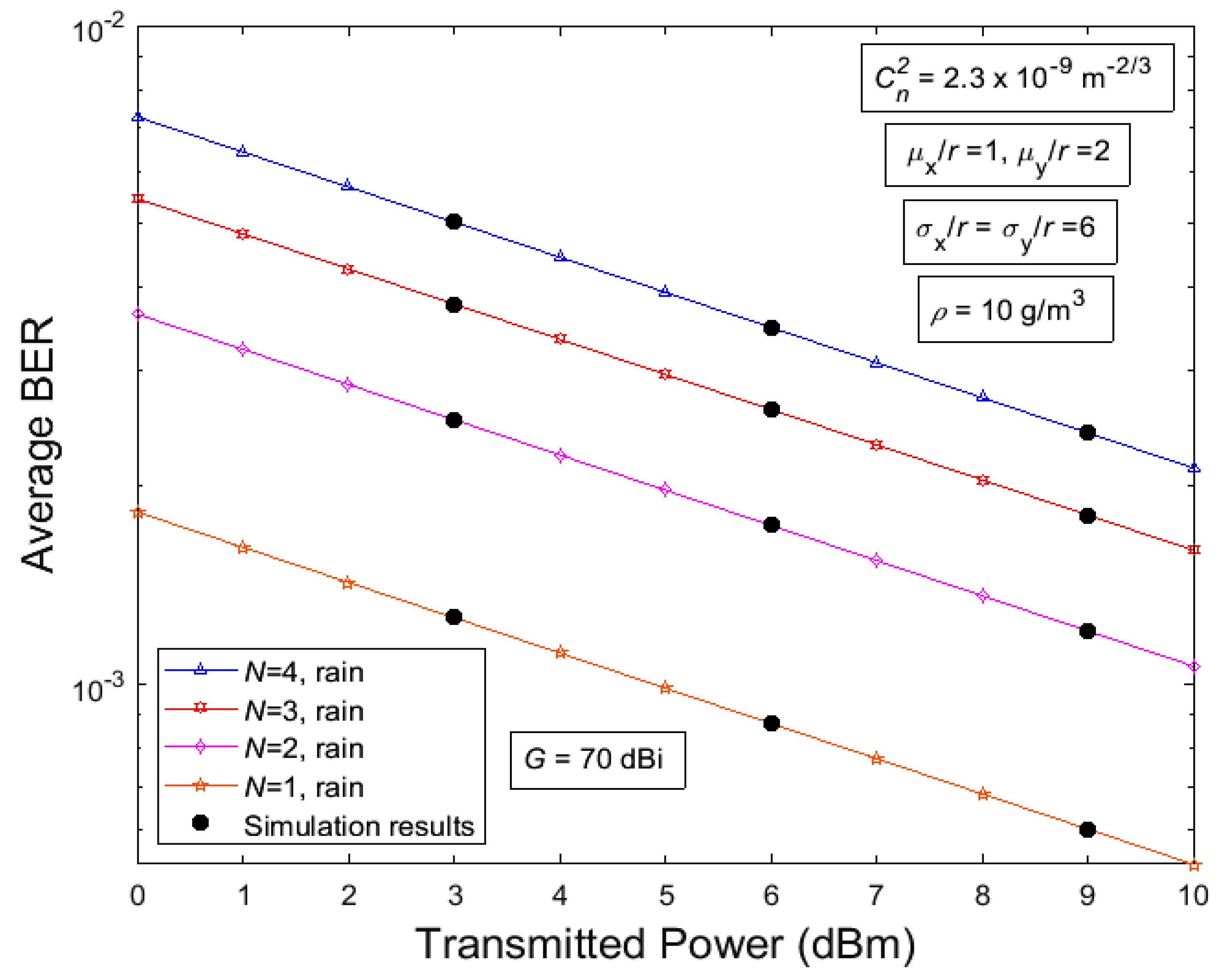
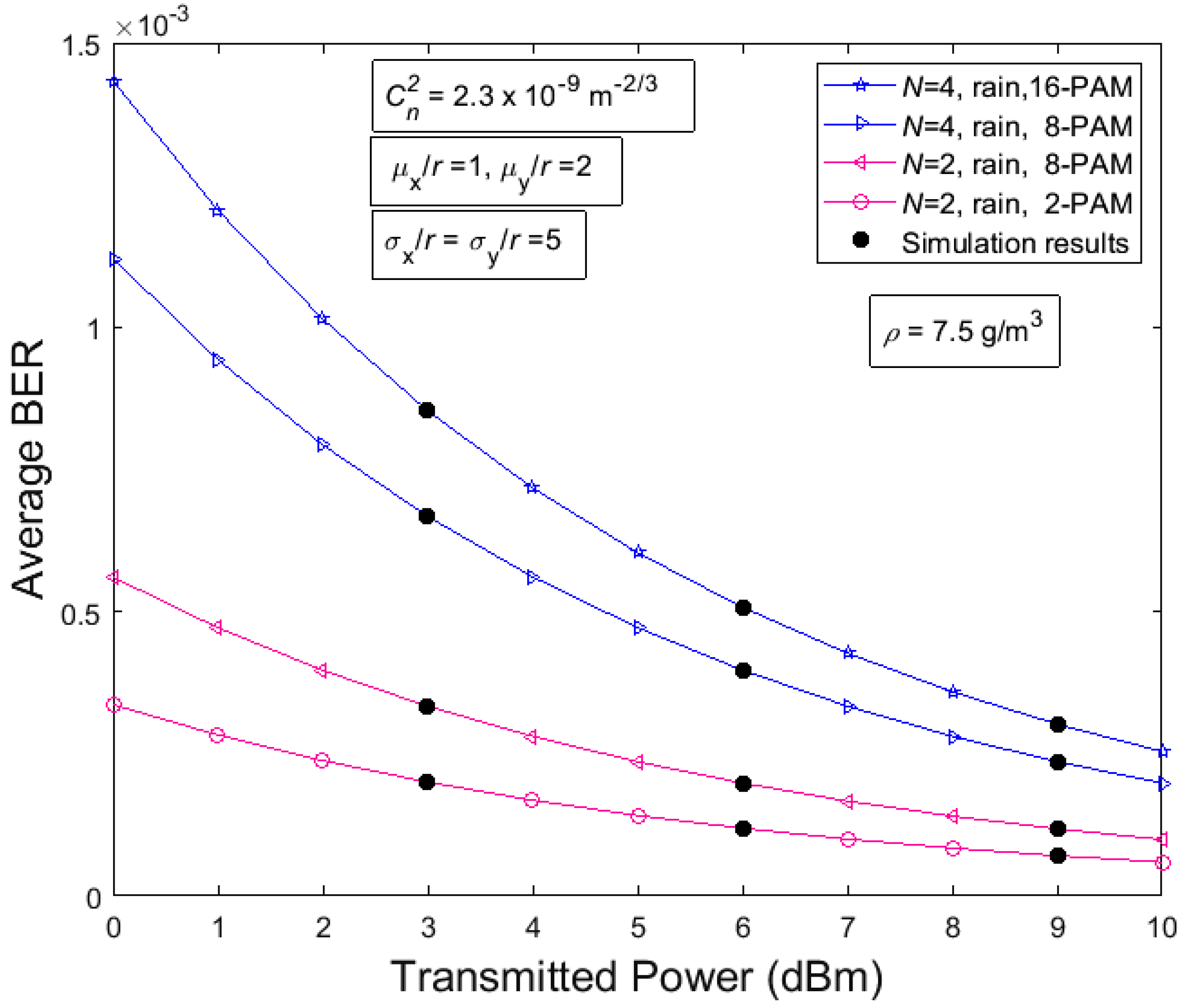
4. Analytical Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ghassemlooy, Z.; Arnon, S.; Uysal, M.; Xu, Z.; Cheng, J. Emerging optical wireless communications-advances and challenges. IEEE J. Sel. Areas Commun. 2015, 33, 1738–1749. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Petkovic, M.I.; Djordjevic, G.T.; Tombras, G.S. SIMO optical wireless links with nonzero boresight pointing errors over M modeled turbulence channels. Opt. Commun. 2017, 403, 391–400. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Aidinis, K.; Jaber, F.; Rahman, K.K. Transdermal Optical Wireless Links with Multiple Receivers in the Presence of Skin-Induced Attenuation and Pointing Errors. Computation 2019, 7, 33. [Google Scholar] [CrossRef]
- Wang, X.; Kong, L.; Kong, F.; Qiu, F.; Xia, M.; Arnon, S.; Chen, G. Millimeter wave communication: A comprehensive survey. IEEE Commun. Surv. Tutor. 2018, 20, 1616–1653. [Google Scholar] [CrossRef]
- Shawon, M.E.; Chowdhury, M.Z.; Hossen, M.B.; Ahmed, M.F.; Jang, Y.M. Rain Attenuation Characterization for 6G Terahertz Wireless Communication. In Proceedings of the 2021 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Jeju Island, Korea, 20–23 April 2021; pp. 3535–3538. [Google Scholar]
- Seeds, A.J.; Shams, H.; Fice, M.J.; Renaud, C.C. Terahertz photonics for wireless communications. J. Light. Technol. 2015, 33, 579–587. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Jornet, J.M.; Han, C. Terahertz band: Next frontier for wireless communications. Phys. Commun. 2014, 12, 16–32. [Google Scholar] [CrossRef]
- Federici, J.F.; Ma, J.; Moeller, L. Review of weather impact on outdoor terahertz wireless communication links. Nano Commun. Netw. 2016, 10, 13–26. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.; Shahjalal, M.; Ahmed, S.; Jang, Y.M. 6G wireless communication systems: Applications, requirements, technologies, challenges, and research directions. IEEE Open J. Commun. Soc. 2020, 1, 957–975. [Google Scholar] [CrossRef]
- Federici, J.; Moeller, L. Review of terahertz and subterahertz wireless communications. J. Appl. Phys. 2010, 107, 111101. [Google Scholar] [CrossRef]
- Su, K.; Moeller, L.; Barat, R.B.; Federici, J.F. Experimental comparison of terahertz and infrared data signal attenuation in dust clouds. JOSA A 2012, 29, 2360–2366. [Google Scholar] [CrossRef]
- Su, K.; Moeller, L.; Barat, R.B.; Federici, J.F. Experimental comparison of performance degradation from terahertz and infrared wireless links in fog. JOSA A 2012, 29, 179–184. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Mandehgar, M.; Grischkowsky, D.R. Broadband THz signals propagate through dense fog. IEEE Photon. Technol. Lett. 2014, 27, 383–386. [Google Scholar] [CrossRef]
- Ma, J.; Moeller, L.; Federici, J.F. Experimental comparison of terahertz and infrared signaling in controlled atmospheric turbulence. J. Infrared Millim. Terahertz Waves 2015, 36, 130–143. [Google Scholar] [CrossRef]
- Ma, J.; Vorrius, F.; Lamb, L.; Moeller, L.; Federici, J.F. Experimental comparison of terahertz and infrared signaling in laboratory-controlled rain. J. Infrared Millim. Terahertz Waves 2015, 36, 856–865. [Google Scholar] [CrossRef]
- Ma, J.; Vorrius, F.; Lamb, L.; Moeller, L.; Federici, J.F. Comparison of experimental and theoretical determined terahertz attenuation in controlled rain. J. Infrared Millim. Terahertz Waves 2015, 36, 1195–1202. [Google Scholar] [CrossRef]
- Ishii, S.; Sayama, S.; Kamei, T. Measurement of rain attenuation in terahertz wave range. Wirel. Eng. Technol. 2011, 2, 119–124. [Google Scholar] [CrossRef]
- Yang, Y.; Mandehgar, M.; Grischkowsky, D. Determination of the water vapor continuum absorption by THz-TDS and molecular response theory. Opt. Express 2014, 22, 4388–4403. [Google Scholar] [CrossRef]
- Taherkhani, M.; Kashani, Z.G.; Sadeghzadeh, R.A. On the performance of THz wireless LOS links through random turbulence channels. Nano Commun. Netw. 2020, 23, 100282. [Google Scholar] [CrossRef]
- Chatzidiamantis, N.D.; Sandalidis, H.G.; Karagiannidis, G.K.; Matthaiou, M. Inverse Gaussian modeling of turbulence-induced fading in free-space optical systems. J. Light. Technol. 2011, 29, 1590–1596. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Stassinakis, A.N.; Volos, C.K.; Christofilakis, V.; Tombras, G.S. Mixed Topology of DF Relayed Terrestrial Optical Wireless Links with Generalized Pointing Errors over Turbulence Channels. Technologies 2018, 6, 121. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Tombras, G.S. OFDM RoFSO Links with Relays Over Turbulence Channels and Nonzero Boresight Pointing Errors. J. Commun. 2017, 12, 644. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Gappmair, W.; Sandalidis, H.G.; Tombras, G.S. DF relayed subcarrier FSO links over Malaga turbulence channels with phase noise and non-zero boresight pointing errors. Appl. Sci. 2018, 8, 664. [Google Scholar] [CrossRef]
- Farid, A.A.; Hranilovic, S. Outage capacity optimization for free space optical links with pointing errors. IEEE/OSA J. Light. Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef]
- Tsiftsis, T.A.; Sandalidis, H.G.; Karagiannidis, G.K.; Uysal, M. Optical wireless links with spatial diversity over strong atmospheric turbulence channels. IEEE Trans.Wirel. Commun. 2009, 8, 951–957. [Google Scholar] [CrossRef]
- Gappmair, W.; Hranilovic, S.; Leitgeb, E. Performance of PPM on terrestrial FSO links with turbulence and pointing errors. IEEE Commun. Lett. 2010, 14, 468–470. [Google Scholar] [CrossRef]
- Boulogeorgos, A.A.A.; Papasotiriou, E.N.; Alexiou, A. Analytical performance assessment of THz wireless systems. IEEE Access 2019, 7, 11436–11453. [Google Scholar] [CrossRef]
- Yang, F.; Cheng, J.; Tsiftsis, T.A. Free-space optical communication with nonzero boresight pointing errors. IEEE Trans. Commun. 2014, 62, 713–725. [Google Scholar] [CrossRef]
- Yang, Y.; Shutler, A.; Grischkowsky, D.J.O.E. Measurement of the transmission of the atmosphere from 0.2 to 2 THz. Opt. Express 2011, 19, 8830–8838. [Google Scholar] [CrossRef]
- Nagatsuma, T.; Yoshimizu, Y.; Yasuda, Y.; Oogimoto, K.; Horiguchi, S.; Minamikata, Y.; Hisatake, S. 30-Gbit/s wireless transmission over 10 meters at 300 GHz. In Proceedings of the 2014 39th International Conference on Infrared, Millimeter, and Terahertz waves (IRMMW-THz), Tucson, AZ, USA, 14–19 September 2014; pp. 1–2. [Google Scholar]
- Kim, G.R.; Jeon, T.I.; Grischkowsky, D. 910-m propagation of THz ps pulses through the atmosphere. Opt. Express 2017, 25, 25422–25434. [Google Scholar] [CrossRef]
- Kokkoniemi, J.; Lehtomäki, J.; Juntti, M. Simplified molecular absorption loss model for 275–400 gigahertz frequency band. In Proceedings of the 12th European Conference on Antennas and Propagation (EuCAP 2018), London, UK, 9–13 April 2018; pp. 1–5. [Google Scholar]
- Boulogeorgos, A.A.A.; Papasotiriou, E.N.; Kokkoniemi, J.; Lehtomäki, J.; Alexiou, A.; Juntti, M. Performance evaluation of THz wireless systems operating in 275–400 GHz band. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–5. [Google Scholar]
- Fiorino, S.T.; Bartell, R.J.; Krizo, M.J.; Marek, S.L.; Bohn, M.J.; Randall, R.M.; Cusumano, S.J. A computational tool for evaluating THz imaging performance in brownout or whiteout conditions at land sites throughout the world. In Atmospheric Propagation VI; SPIE: Orlando, FL, USA, 2009; Volume 7324, pp. 308–319. [Google Scholar]
- Kokkonen, M.; Juttula, H.; Mäkynen, A.; Myllymäki, S.; Jantunen, H. The effect of drop shape, sensing volume and raindrop size statistics to the scattered field on 300 GHz. IEEE Access 2021, 9, 101381–101389. [Google Scholar] [CrossRef]
- Moon, E.B.; Jeon, T.I.; Grischkowsky, D.R. Long-path THz-TDS atmospheric measurements between buildings. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 742–750. [Google Scholar] [CrossRef]
- Castro, C.; Elschner, R.; Merkle, T.; Schubert, C.; Freund, R. Long-range high-speed THz-wireless transmission in the 300 GHz band. In Proceedings of the 2020 Third International Workshop on Mobile Terahertz Systems (IWMTS), Essen, Germany, 1–2 July 2020; pp. 1–4. [Google Scholar]
- Ma, J.; Moeller, L.; Federici, J. Terahertz performance in atmospheric turbulence. In Proceedings of the 2014 39th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Tucson, AZ, USA, 14–19 September 2014; pp. 1–4. [Google Scholar]
- Bao, L.; Zhao, H.; Zheng, G.; Ren, X. Scintillation of THz transmission by atmospheric turbulence near the ground. In Proceedings of the 2012 IEEE Fifth International Conference on Advanced Computational Intelligence (ICACI), Nanjing, China, 18–20 October 2012; pp. 932–936. [Google Scholar]
- Taherkhani, M.; Sadeghzadeh, R.A.; Kashani, Z.G. Attenuation analysis of THz/IR waves under different turbulence conditions using gamma-gamma model. In Proceedings of the Electrical Engineering (ICEE), Iranian Conference on, Sadjad University of Technology, Mashhad, Iran, 8–10 May 2018; pp. 424–428. [Google Scholar]
- Varotsos, G.K.; Chatzikontis, E.V.; Kapotis, E.; Nistazakis, H.E.; Aidinis, K.; Christofilakis, V. THz Links Performance Study for Gamma Turbulence Links with Path Loss and Pointing Errors. In Proceedings of the 2022 11th International Conference on Modern Circuits and Systems Technologies (MOCAST), Bremen, Germany, 8–10 June 2022; pp. 1–4. [Google Scholar]
- Priebe, S.; Jacob, M.; Kürner, T. The impact of antenna directivities on THz indoor channel characteristics. In Proceedings of the 2012 6th European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 2012; pp. 478–482. [Google Scholar]
- Ekti, A.R.; Boyaci, A.; Alparslan, A.; Ünal, İ.; Yarkan, S.; Görçin, A.; Arslan, H.; Uysal, M. Statistical modeling of propagation channels for terahertz band. In Proceedings of the 2017 IEEE Conference on Standards for Communications and Networking (CSCN), Helsinki, Finland, 18–20 September 2017; pp. 275–280. [Google Scholar]
- Han, C.; Akyildiz, I.F. Three-dimensional end-to-end modeling and analysis for graphene-enabled terahertz band communications. IEEE Trans. Veh. Technol. 2016, 66, 5626–5634. [Google Scholar] [CrossRef]
- Papasotiriou, E.N.; Boulogeorgos, A.A.A.; Alexiou, A. Performance analysis of THz wireless systems in the presence of antenna misalignment and phase noise. IEEE Commun. Lett. 2020, 24, 1211–1215. [Google Scholar] [CrossRef]
- Kokkoniemi, J.; Boulogeorgos, A.A.A.; Aminu, M.; Lehtomäki, J.; Alexiou, A.; Juntti, M. Impact of beam misalignment on THz wireless systems. Nano Commun. Netw. 2020, 24, 100302. [Google Scholar] [CrossRef]
- Rong, Z.; Leeson, M.S.; Higgins, M.D. Relay-assisted nanoscale communication in the THz band. Micro Nano Lett. 2017, 12, 373–376. [Google Scholar] [CrossRef]
- Abbasi, Q.H.; Nasir, A.A.; Yang, K.; Qaraqe, K.A.; Alomainy, A. Cooperative in-vivo nano-network communication at terahertz frequencies. IEEE Access 2017, 5, 8642–8647. [Google Scholar] [CrossRef]
- Samarasekera, A.C.J.; Shin, H. Outage probability for cooperative nano communication in the THz gap frequency range. KSII Trans. Internet Inf. Syst. 2017, 11, 102–122. [Google Scholar]
- Boulogeorgos, A.A.A.; Alexiou, A. Outage probability analysis of THz relaying systems. In Proceedings of the 2020 IEEE 31st Annual International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, 31 August–3 September 2020; pp. 1–7. [Google Scholar]
- Stratidakis, G.; Papasotiriou, E.N.; Konstantinis, H.; Boulogeorgos, A.A.A.; Alexiou, A. Relay-based blockage and antenna misalignment mitigation in THz wireless communications. In Proceedings of the 2020 2nd 6G Wireless Summit (6G SUMMIT), Levi, Finland, 17–20 March 2020; pp. 1–4. [Google Scholar]
- Xia, Q.; Jornet, J.M. Multi-hop Relaying Distribution Strategies for Terahertz-band Communication Networks: A Cross-layer Analysis. IEEE Trans. Wirel. Commun. 2021, 21, 5075–5089. [Google Scholar] [CrossRef]
- Li, S.; Yang, L. Performance analysis of dual-hop THz transmission systems over α-μ fading channels with pointing errors. IEEE Internet Things J. 2021, 9, 11772–11783. [Google Scholar] [CrossRef]
- Bhardwaj, P.; Zafaruddin, S.M. Performance of dual-hop relaying for THz-RF wireless link. In Proceedings of the 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Helsinki, Finland, 25–28 April 2021; pp. 1–5. [Google Scholar]
- Tsiftsis, T.A.; Sandalidis, H.G.; Karagiannidis, G.K.; Sagias, N.C. Multihop free-space optical communications over strong turbulence channels. In Proceedings of the 2006 IEEE International Conference on Communications, Istanbul, Turkey, 11–15 June 2006; Volume 6, pp. 2755–2759. [Google Scholar]
- Safari, M.; Uysal, M. Relay-assisted free-space optical communication. IEEE Trans. Wirel. Commun. 2008, 7, 5441–5449. [Google Scholar] [CrossRef]
- Sheng, M.; Jiang, P.; Hu, Q.; Su, Q.; Xie, X.X. End-to-end average BER analysis for multihop free-space optical communications with pointing errors. J. Opt. 2013, 15, 055408. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Z.; Xu, Z.; Ghassemlooy, Z. Multihop free-space optical communications over turbulence channels with pointing errors using heterodyne detection. J. Light. Technol. 2014, 32, 2597–2604. [Google Scholar] [CrossRef]
- Siles, G.A.; Riera, J.M.; Garcia-del-Pino, P. Atmospheric attenuation in wireless communication systems at millimeter and THz frequencies [wireless corner]. IEEE Antennas Propag. Mag. 2015, 57, 48–61. [Google Scholar] [CrossRef]
- Ippolito Jr, L.J. Attenuation by Atmospheric Gases. In Radiowave Propagation in Satellite Communications; Van Nostrand Reinhold Co.: New York, NY, USA, 1986; pp. 25–37. [Google Scholar]
- Ghassemlooy, Z.; Popoola, W.O. Terrestrial free-space optical communications. In Mobile and Wireless Communications; InTech: London, UK, 2010; pp. 355–392. [Google Scholar]
- Popoola, W.O.; Ghassemlooy, Z.; Ahmadi, V. Performance of sub-carrier modulated free-space optical communication link in negative exponential atmospheric turbulence environment. Int. J. Auton. Adapt. Commun. Syst. 2008, 1, 342–355. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Volos, C.K.; Tombras, G.S. FSO links with diversity pointing errors and temporal broadening of the pulses over weak to strong atmospheric turbulence channels. Optik 2016, 127, 3402–3409. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Popoola, W.O.; Leitgeb, E. Free-space optical communication using subcarrier modulation in gamma-gamma atmospheric turbulence. In Proceedings of the 2007 9th International Conference on Transparent Optical Networks, Rome, Italy, 1–5 July 2007; Volume 3, pp. 156–160. [Google Scholar]
- Al-Habash, A.; Andrews, L.C.; Phillips, R.L. Mathematical model for the irradiance probability density function of a laser beam propagating through turbulent media. Opt. Eng. 2001, 40, 1554–1562. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 6th ed.; Academic Press, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Varotsos, G.K.; Nistazakis, H.E.; Stassinakis, A.N.; Tombras, G.S.; Christofilakis, V.; Volos, C.K. Outage performance of mixed, parallel and serial DF relayed FSO links over weak turbulence channels with nonzero boresight pointing errors. In Proceedings of the 2018 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; pp. 1–4. [Google Scholar]
- Nistazakis, H.E.; Tombras, G.S. On the use of wavelength and time diversity in optical wireless communication systems over gamma–gamma turbulence channels. Opt. Laser Technol. 2012, 44, 2088–2094. [Google Scholar] [CrossRef]
- Boluda-Ruiz, R.; García-Zambrana, A.; Castillo-Vázquez, C.; Castillo-Vázquez, B. Novel approximation of misalignment fading modeled by Beckmann distribution on free-space optical links. Opt. Express 2016, 24, 22635–22649. [Google Scholar] [CrossRef]
- Abramovitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th ed.; Dover: New York, NY, USA, 1972. [Google Scholar]
- The Wolfram Functions Site. 2008. Available online: https://functions.wolfram.com (accessed on 13 July 2022).
- Adamchik, V.S.; Marichev, O.I. The algorithm for calculating integrals of hypergeometric type functions and its realization in REDUCE system. In Proceedings of the International Symposium on Symbolic and Algebraic Computation, Tokyo, Japan, 1 July 1990; pp. 212–224. [Google Scholar]
- Morgado, E.; Mora-Jimenez, I.; Vinagre, J.J.; Ramos, J.; Caamano, A.J. End-to-end average BER in multihop wireless networks over fading channels. IEEE Trans. Wirel. Commun. 2010, 9, 2478–2487. [Google Scholar] [CrossRef]
- Androutsos, N.A.; Nistazakis, H.E.; Petkovic, M.I.; Djordjevic, G.T.; Stassinakis, A.N.; Volos, C.K. Multi-hop DF relayed FSO links with various modulation formats emulated by a dual-hop scheme for strong turbulence conditions. Optik 2021, 227, 165972. [Google Scholar] [CrossRef]
- Elganimi, T.Y. Studying the BER performance, power-and bandwidth-efficiency for FSO communication systems under various modulation schemes. In Proceeding of the 2013 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies (AEECT), Amman, Jordan, 3–5 December 2013; pp. 1–6. [Google Scholar]
- Varotsos, G.K.; Nistazakis, H.E.; Aidinis, K.; Jaber, F.; Nasor, M.; Rahman, K.M. On the Utilization of L-PAM Technique in Transdermal Optical Wireless Links with Stochastic Pointing Errors for ABER Performance Estimation. In Proceedings of the 2021 10th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 5–7 July 2021; pp. 1–4. [Google Scholar]
- Wang, H.; Dong, X.; Yi, M.; Xue, F.; Liu, Y.; Liu, G. Terahertz high-gain offset reflector antennas using SiC and CFRP material. IEEE Trans. Antennas Propag. 2017, 65, 4443–4451. [Google Scholar] [CrossRef]
- Awan, M.S.; Capsoni, C.; Leitgeb, E.; Nebuloni, R.; Nadeem, F.; Khan, M.S. FSO-relevant new measurement results under moderate continental fog conditions at graz and milan. In Proceedings of the 2008 4th Advanced Satellite Mobile Systems, Bologna, Italy, 26–28 August 2008; pp. 116–121. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varotsos, G.K.; Aidinis, K.; Nistazakis, H.E. Average BER Performance Estimation of Relayed THz Links with Losses, Molecular Attenuation, Adverse Weather Conditions, Turbulence and Generalized Pointing Errors. Photonics 2022, 9, 671. https://doi.org/10.3390/photonics9100671
Varotsos GK, Aidinis K, Nistazakis HE. Average BER Performance Estimation of Relayed THz Links with Losses, Molecular Attenuation, Adverse Weather Conditions, Turbulence and Generalized Pointing Errors. Photonics. 2022; 9(10):671. https://doi.org/10.3390/photonics9100671
Chicago/Turabian StyleVarotsos, George K., Konstantinos Aidinis, and Hector E. Nistazakis. 2022. "Average BER Performance Estimation of Relayed THz Links with Losses, Molecular Attenuation, Adverse Weather Conditions, Turbulence and Generalized Pointing Errors" Photonics 9, no. 10: 671. https://doi.org/10.3390/photonics9100671
APA StyleVarotsos, G. K., Aidinis, K., & Nistazakis, H. E. (2022). Average BER Performance Estimation of Relayed THz Links with Losses, Molecular Attenuation, Adverse Weather Conditions, Turbulence and Generalized Pointing Errors. Photonics, 9(10), 671. https://doi.org/10.3390/photonics9100671





