Pre-Chirp-Managed Adiabatic Soliton Compression in Pressure-Gradient Hollow-Core Fibers
Abstract
:1. Introduction
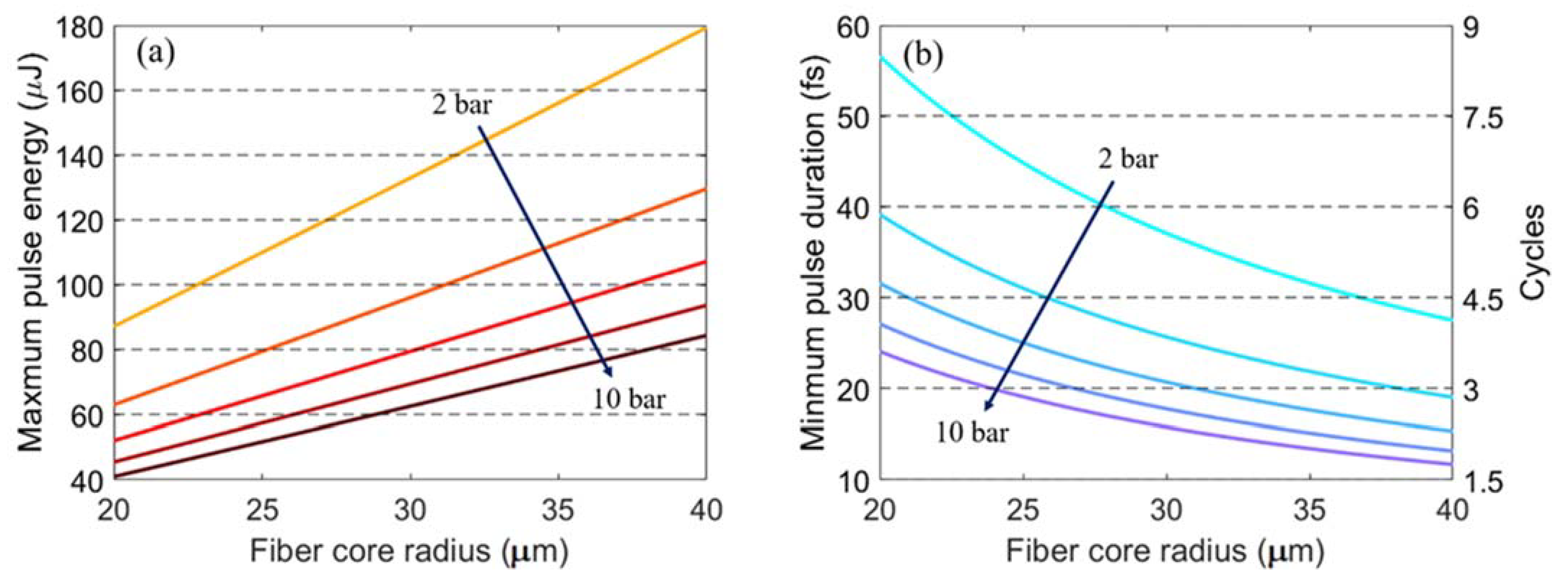
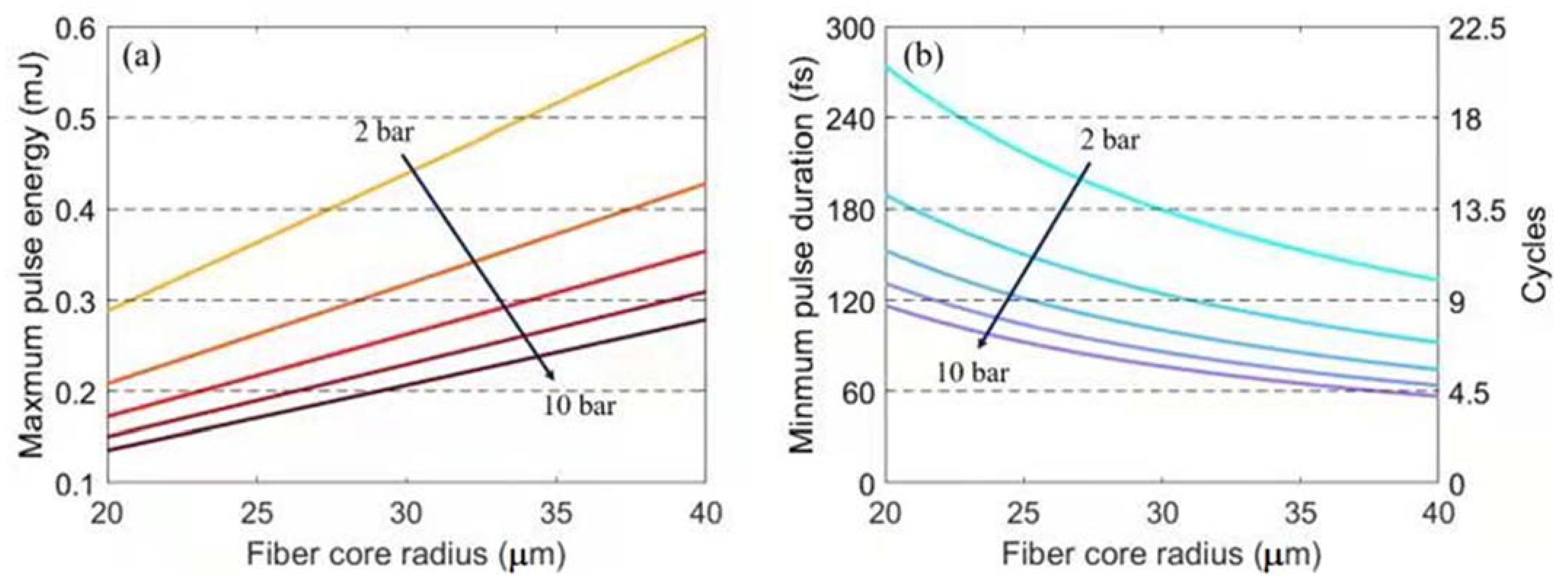
2. Simple Analysis of ASC in Pressure-Gradient HCFs Based on the Soliton Area Theorem
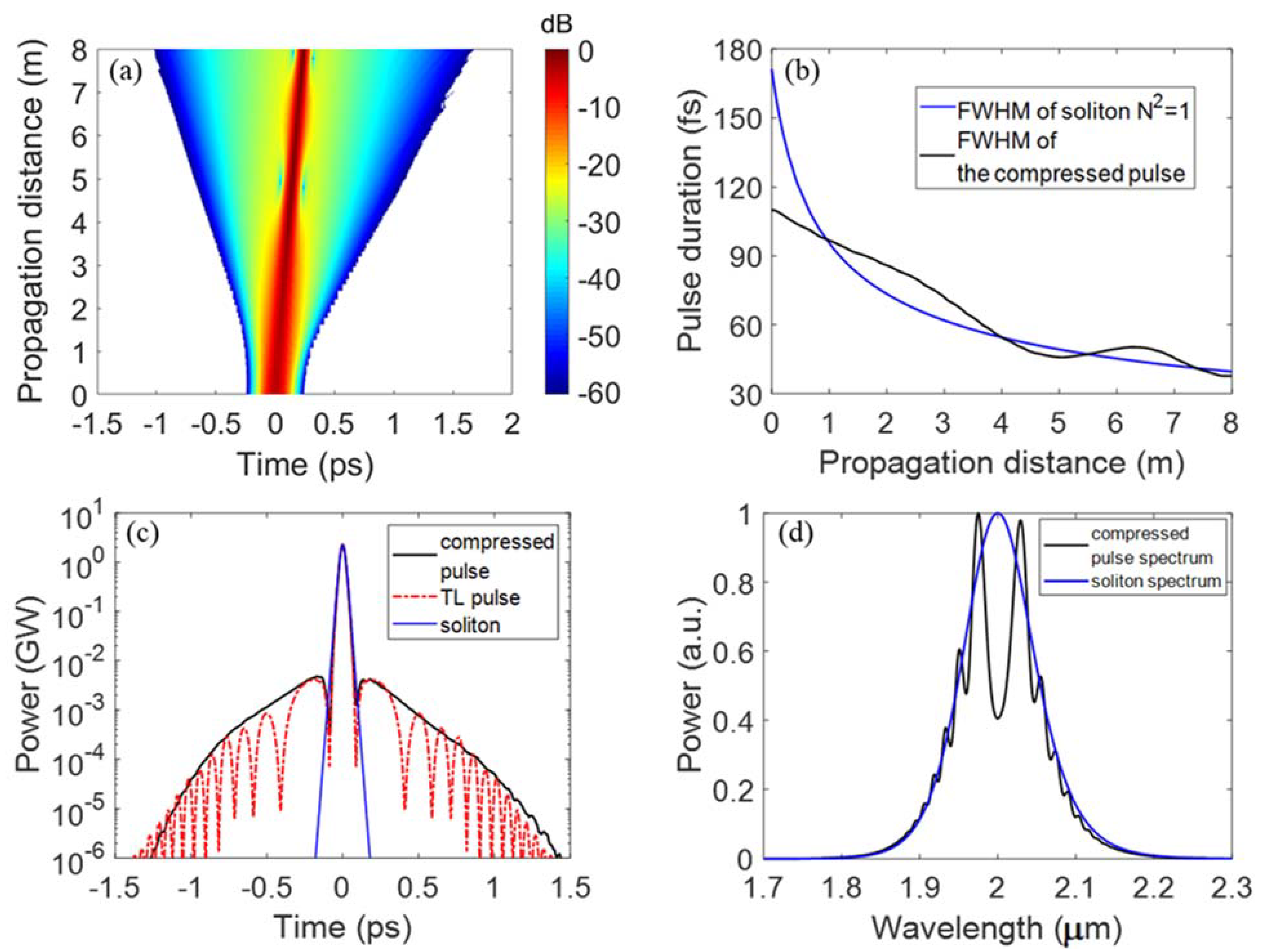
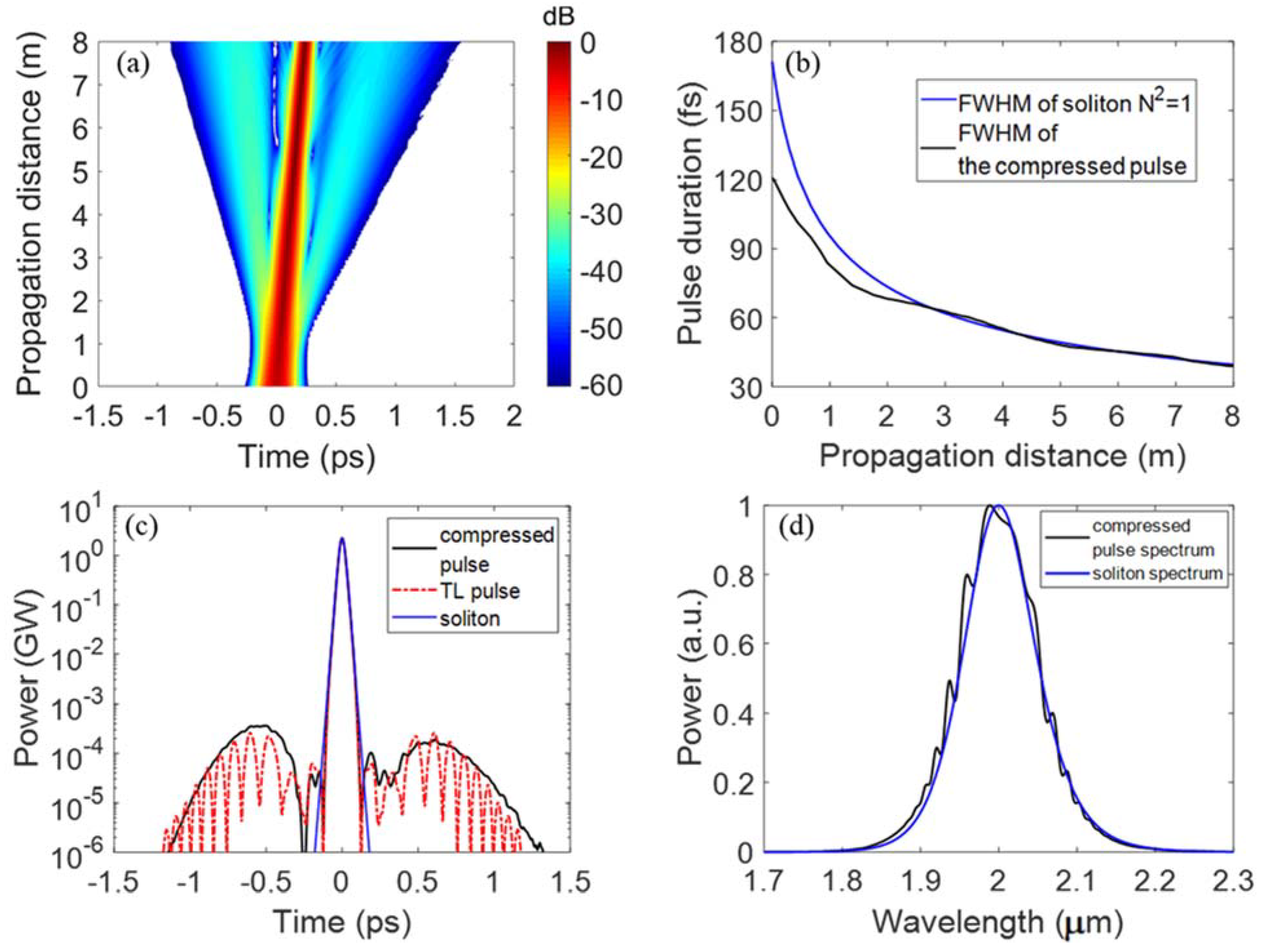
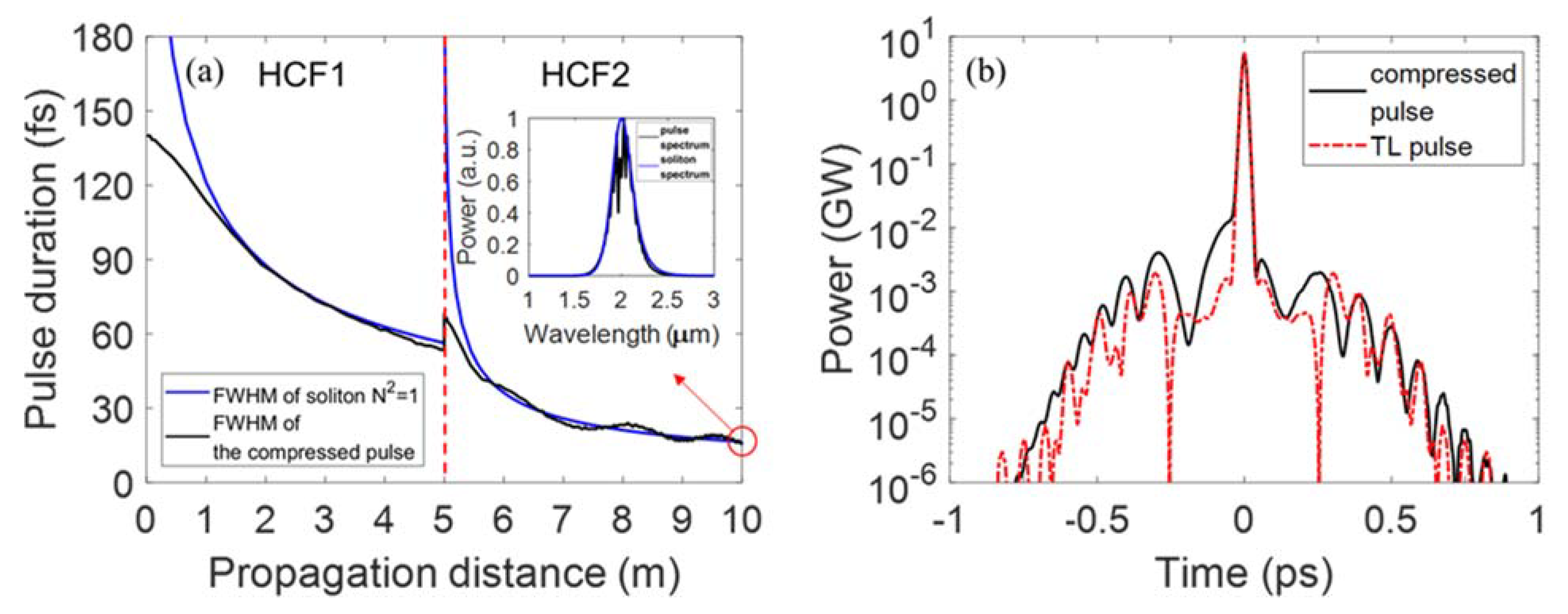
3. Simulation Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nagy, T.; Simon, P.; Veisz, L. High-energy few-cycle pulses: Post-compression techniques. Adv. Phys. X 2021, 6, 11845795. [Google Scholar]
- Kuehl, H.H. Solitons on an axially nonuniform optical fiber. J. Opt. Soc. Am. B 1988, 5, 709–713. [Google Scholar] [CrossRef]
- Smith, K.; Mollenauer, L.F. Experimental-Observation of Adiabatic-Compression and Expansion of Soliton Pulses over Long Fiber Paths. Opt. Lett. 1989, 14, 751–753. [Google Scholar] [CrossRef]
- Iwatsuki, K.; Suzuki, K.-I.; Nishi, S. Adiabatic soliton compression of gain-switched DFB-LD pulse by distributed fiber Raman amplification. IEEE Photonics Technol. Lett. 1991, 3, 1074–1076. [Google Scholar] [CrossRef]
- Quiroga-Teixeiro, M.L.; Anderson, D.; Andrekson, P.A.; Berntson, A.; Lisak, M. Efficient soliton compression by fast adiabatic amplification. J. Opt. Soc. Am. B 1996, 13, 687–692. [Google Scholar] [CrossRef]
- Chernikov, S.V.; Mamyshev, P.V. Femtosecond Soliton Propagation in Fibers with Slowly Decreasing Dispersion. J. Opt. Soc. Am. B 1991, 8, 1633–1641. [Google Scholar] [CrossRef]
- Suzuki, K.; Iwatsuki, K.; Nishi, S.; Saruwatari, M.; Kitoh, T. 160 Gbit/s sub-picosecond transform-limited pulse signal generation utilizing adiabatic soliton compression and optical time-division multiplexing. IEEE Photonics Technol. Lett. 1994, 6, 352–354. [Google Scholar] [CrossRef]
- Travers, J.C.; Stone, J.M.; Rulkov, A.B.; Cumberland, B.A.; George, A.K.; Popov, S.V.; Knight, J.C.; Taylor, J.R. Optical pulse compression in dispersion decreasing photonic crystal fiber. Opt. Express 2007, 15, 13203–13211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tse, M.L.V.; Horak, P.; Price, J.H.V.; Poletti, F.; He, F.; Richardson, D.J. Pulse compression at 1.06 μm in dispersion-decreasing holey fibers. Opt. Lett. 2006, 31, 3504–3506. [Google Scholar] [CrossRef] [PubMed]
- Lenz, G.; Eggleton, B.J. Adiabatic Bragg soliton compression in nonuniform grating structures. J. Opt. Soc. Am. B 1998, 15, 2979–2985. [Google Scholar] [CrossRef]
- Russell, P.S.J.; Hölzer, P.; Chang, W.; Abdolvand, A.; Travers, J.C. Hollow-core photonic crystal fibres for gasbased nonlinear optics. Nat. Photonics 2014, 8, 278–286. [Google Scholar] [CrossRef]
- Lægsgaard, J.; Roberts, P.J. Theory of adiabatic pressure-gradient soliton compression in hollow-core photonic bandgap fibers. Opt. Lett. 2009, 34, 3710–3712. [Google Scholar] [CrossRef]
- Huang, Z.Y.; Chen, Y.F.; Yu, F.; Wu, D.K.; Zhao, Y.; Wang, D.; Leng, Y.X. Ionization-induced adiabatic soliton compression in gas-filled hollow-core photonic crystal fibers. Opt. Lett. 2019, 44, 5562–5565. [Google Scholar] [CrossRef]
- Schade, D.; Köttig, F.; Koehler, J.R.; Frosz, M.H.; Russell, P.S.J.; Tani, F. Scaling rules for high quality soliton self-compression in hollow-core fibers. Opt. Express 2021, 29, 19147–19158. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.I.; Akhmediev, N.; Chang, W. Empirical Formulae for Dispersion and Effective Mode Area in Hollow-Core Antiresonant Fibers. J. Lightwave Technol. 2018, 36, 4060–4065. [Google Scholar] [CrossRef]
- Nurhuda, M.; Suda, A.; Kaku, M.; Midorikawa, K. Optimization of hollow fiber pulse compression using pressure gradients. Appl. Phys. B 2007, 89, 209–215. [Google Scholar] [CrossRef]
- Mak, K.F.; Travers, J.C.; Joly, N.Y.; Abdolvand, A.; Russell, P.S.J. Two techniques for temporal pulse compression in gas-filled hollow-core kagomé photonic crystal fiber. Opt. Lett. 2013, 38, 3592–3595. [Google Scholar] [CrossRef]
- Gebhardt, M.; Gaida, C.; Heuermann, T.; Stutzki, F.; Jauregui, C.; Antonio-Lopez, J.; Schulzgen, A.; Amezcua-Correa, R.; Limpert, J.; Tünnermann, A. Nonlinear pulse compression to 43 W GW-class few-cycle pulses at 2 μm wavelength. Opt. Lett. 2017, 42, 4179–4182. [Google Scholar] [CrossRef]
- Vozzi, C.; Nisoli, M.; Sansone, G.; Stagira, S.; Silvestri, S.D. Optimal spectral broadening in hollow-fiber compressor systems. Appl. Phys. B 2005, 80, 285–289. [Google Scholar] [CrossRef]
- Wang, P.; Li, Y.; Li, W.; Su, H.; Shao, B.; Li, S.; Wang, C.; Wang, D.; Zhao, R.; Peng, Y.; et al. 2.6 mJ/100 Hz CEP-stable near-single-cycle 4 μm laser based on OPCPA and hollow-core fiber compression. Opt. Lett. 2018, 43, 2197–2200. [Google Scholar] [CrossRef]
- Kanai, T.; Lee, Y.; Seo, M.; Kim, D.E. Supercontinuum-seeded, carrier-envelope phase-stable, 4. 5-W, 3.8-μm, 6-cycle, KTA optical parametric amplifier driven by a 1.4-ps Yb:YAG thin-disk amplifier for nonperturbative spectroscopy in solids. J. Opt. Soc. Am. B 2019, 36, 2407–2413. [Google Scholar]
- Saleh, M.; Chang, W.; Hölzer, P.; Nazarkin, A.; Travers, J.C.; Joly, N.; Russell, P.S.J.; Biancalana, F. Theory of photoionization-induced blueshift of ultrashort solitons in gas-filled hollow-core photonic crystal fibers. Phys. Rev. Lett. 2011, 107, 203902. [Google Scholar] [CrossRef] [PubMed]
- Sprangle, P.; Peñano, J.R.; Hafizi, B. Propagation of intense short laser pulses in the atmosphere. Phys. Rev. E 2002, 66, 046418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ammosov, M.V.; Delone, N.B.; Krainov, V.P. Tunnel ionization of complex atoms and of atomic ions in an alternating electromagnetic field. Int. Soc. Opt. Photonics 1986, 64, 1191–1194. [Google Scholar]
- Brabec, T.; Krausz, F. Nonlinear Optical Pulse Propagation in the Single-Cycle Regime. Phys. Rev. Lett. 1997, 78, 3282–3285. [Google Scholar] [CrossRef]
- Yu, F.; Knight, J. Negative curvature hollow core optical fiber. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 4400610. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Schimpf, D.N.; Eidam, T.; Limpert, J.; Tuennermann, A.; Kaertner, F.X.; Chang, G.Q. Pre-chirp managed nonlinear amplification in fibers delivering 100 W, 60 fs pulse. Opt. Lett. 2015, 40, 151. [Google Scholar] [CrossRef]
- Heuermann, T.; Gaida, C.; Gebhardt, M.; Limpert, J. Thulium-doped nonlinear fiber amplifier delivering 50 fs pulses at 20 W of average power. Opt. Lett. 2018, 43, 4441. [Google Scholar] [CrossRef]
- Le, T.; Tempea, G.; Cheng, Z.; Hofer, M.; Stingl, A. Routes to fiber delivery of ultra-short laser pulses in the 25 fs regime. Opt. Lett. 2009, 17, 1240. [Google Scholar] [CrossRef]
- Kalashyan, M.; Lefort, C.; -León, L.M.; Mansuryan, T.; Mouradian, L.; Louradour, F. Ultrashort pulse fiber delivery with optimized dispersion control by reflection grisms at 800 nm. Opt. Express 2012, 20, 25624. [Google Scholar] [CrossRef] [Green Version]
- Andreana, M.; Le, T.; Drexler, W.; Unterhuber, A. Ultrashort pulse Kagome hollow-core photonic crystal fiber delivery for nonlinear optical imaging. Opt. Lett. 2019, 44, 1588. [Google Scholar] [CrossRef]
- Várallyay, Z.; Fekete, J.; Bányász, Á.; Szipőcs, R. Optimizing input and output chirps up to the third-order for sub-nanojoule, ultra-short pulse compression in small core area PCF. Appl. Phys. B 2007, 86, 567. [Google Scholar] [CrossRef]
- Martial, I.; Papadopoulos, D.; Hanna, M.; Druon, F.; Georges, P. Nonlinear compression in a rod-type fiber for high energy ultrashort pulse generation. Opt. Express 2009, 17, 11155. [Google Scholar] [CrossRef] [PubMed]
- Ganz, T.; Pervak, V.; Apolonski, A.; Baum, P. 16 fs, 350 nJ pulses at 5 MHz repetition rate delivered by chirped pulse compression in fibers. Opt. Lett. 2011, 36, 1107. [Google Scholar] [CrossRef]
- Tauser, F.; Adler, F.; Leitenstorfer, A. Widely tunable sub-30-fs pulses from a compact erbium-doped fiber source. Opt. Lett. 2004, 29, 516–518. [Google Scholar] [CrossRef]
- Rosenberg, Y.; Drori, J.; Bermudez, D.; Leonhardt, U. Boosting few-cycle soliton self-frequency shift using negative prechirp. Opt. Express 2020, 28, 3107. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Chang, G. Pre-chirp managed self-phase modulation for efficient generation of wavelength-tunable energetic femtosecond pulses. J. Opt. Soc. Am. B 2020, 37, 2388–2397. [Google Scholar] [CrossRef]
- Anderson, D.; Lisak, M.; Malomed, B.; Quiroga-Teixeiro, M. Tunneling of an optical soliton through a fiber junction. J. Opt. Soc. Am. B 1994, 11, 2380–2384. [Google Scholar] [CrossRef]
- Bertilsson, K.; Aakjer, T.; Quiroga-Teixeiro, M.L.; Andrekson, P.A.; Hedekvist, P. Investigation of soliton compression by propagation through fiber junctions. Opt. Fiber Technol. 1995, 1, 117–124. [Google Scholar] [CrossRef]
- Balciunas, T.; Fourcade-Dutin, C.; Fan, G.; Witting, T.; Voronin, A.A.; Zheltikov, A.M.; Gerome, F.; Paulus, G.G.; Baltuska, A.; Benabid, F. A strong-field driver in the single-cycle regime based on self-compression in a Kagome fibre. Nat. Commun. 2015, 6, 6117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nagy, T.; Hädrich, S.; Simon, P.; Blumenstein, A.; Walther, N.; Klas, R.; Buldt, J.; Stark, H.; Breitkopf, S.; Jójárt, P.; et al. Generation of three-cycle multi-millijoule laser pulses at 318 W average power. Optica 2019, 6, 1423–1424. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Shi, Z.; Chang, G. Pre-Chirp-Managed Adiabatic Soliton Compression in Pressure-Gradient Hollow-Core Fibers. Photonics 2021, 8, 357. https://doi.org/10.3390/photonics8090357
Chen R, Shi Z, Chang G. Pre-Chirp-Managed Adiabatic Soliton Compression in Pressure-Gradient Hollow-Core Fibers. Photonics. 2021; 8(9):357. https://doi.org/10.3390/photonics8090357
Chicago/Turabian StyleChen, Runzhi, Zhuo Shi, and Guoqing Chang. 2021. "Pre-Chirp-Managed Adiabatic Soliton Compression in Pressure-Gradient Hollow-Core Fibers" Photonics 8, no. 9: 357. https://doi.org/10.3390/photonics8090357
APA StyleChen, R., Shi, Z., & Chang, G. (2021). Pre-Chirp-Managed Adiabatic Soliton Compression in Pressure-Gradient Hollow-Core Fibers. Photonics, 8(9), 357. https://doi.org/10.3390/photonics8090357




