Band-Gap Solitons in Nonlinear Photonic Crystal Waveguides and Their Application for Functional All-Optical Logic Gating
Abstract
:1. Introduction
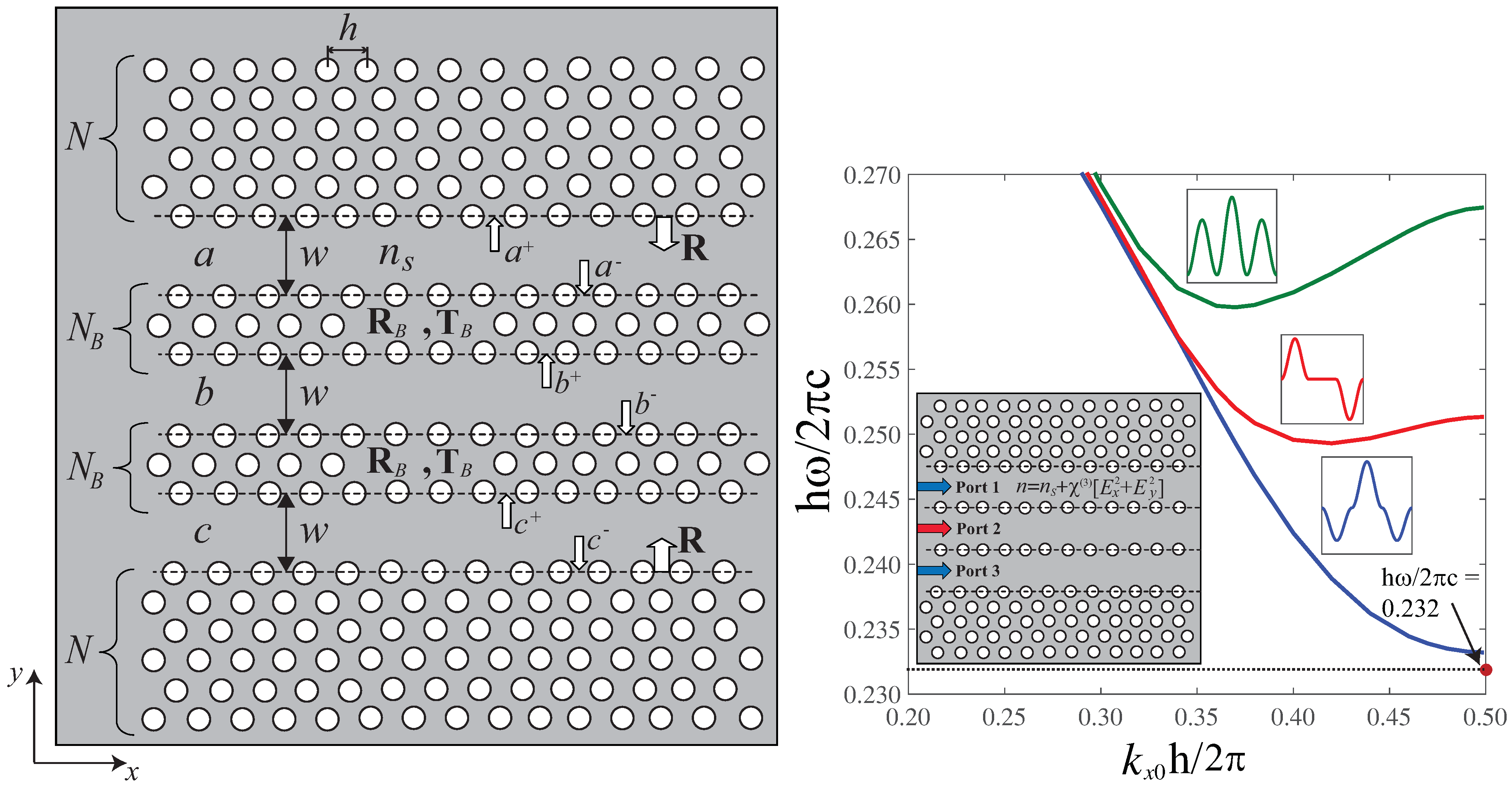
2. Formulation of the Problem
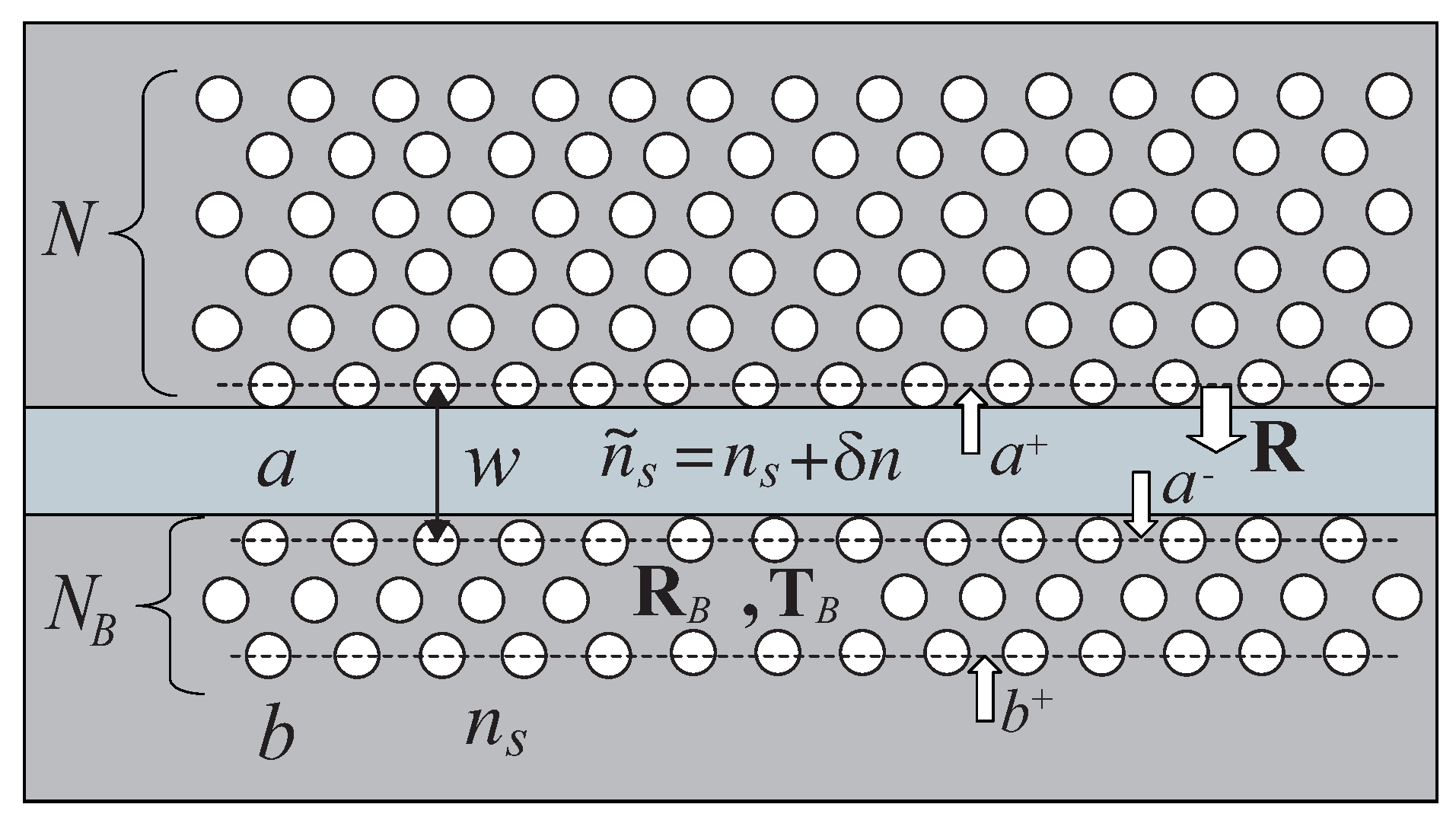
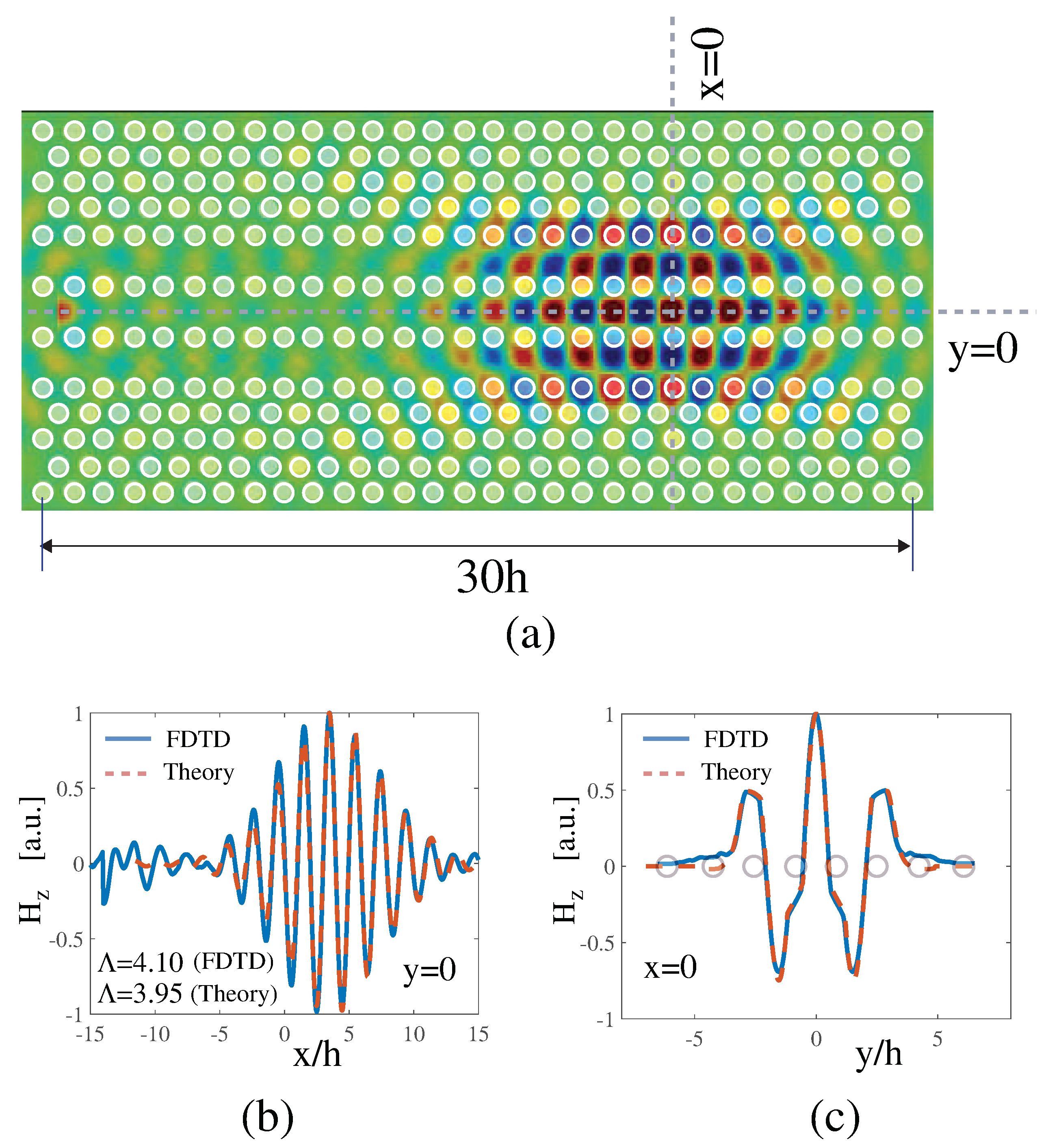
3. Soliton Solution for Coupled Nonlinear Photonic Crystal Waveguides
4. Numerical Simulations on Functional All-optical Logic Gates and Discussions
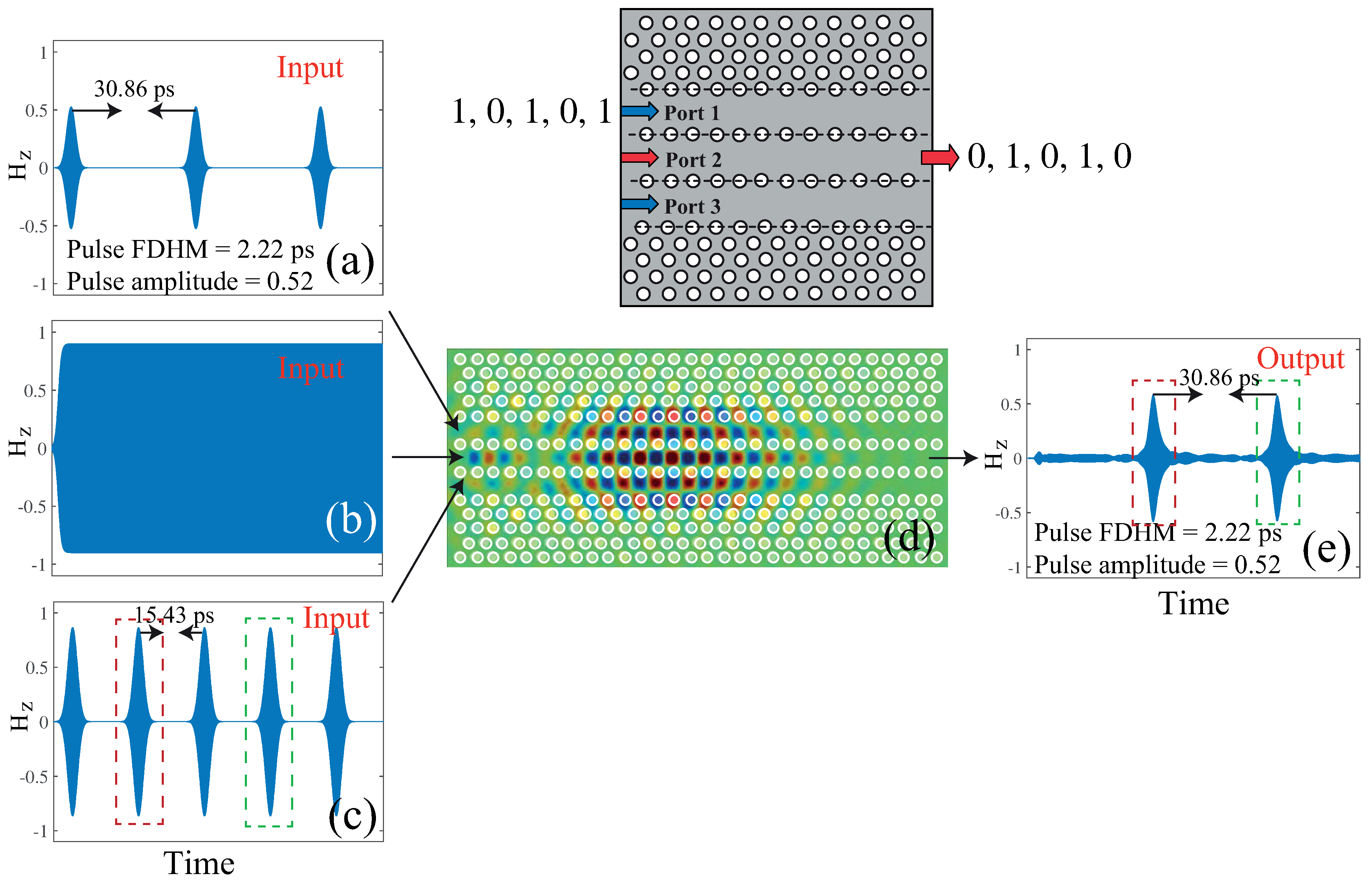
4.1. All-Optical NOT Logic Gate
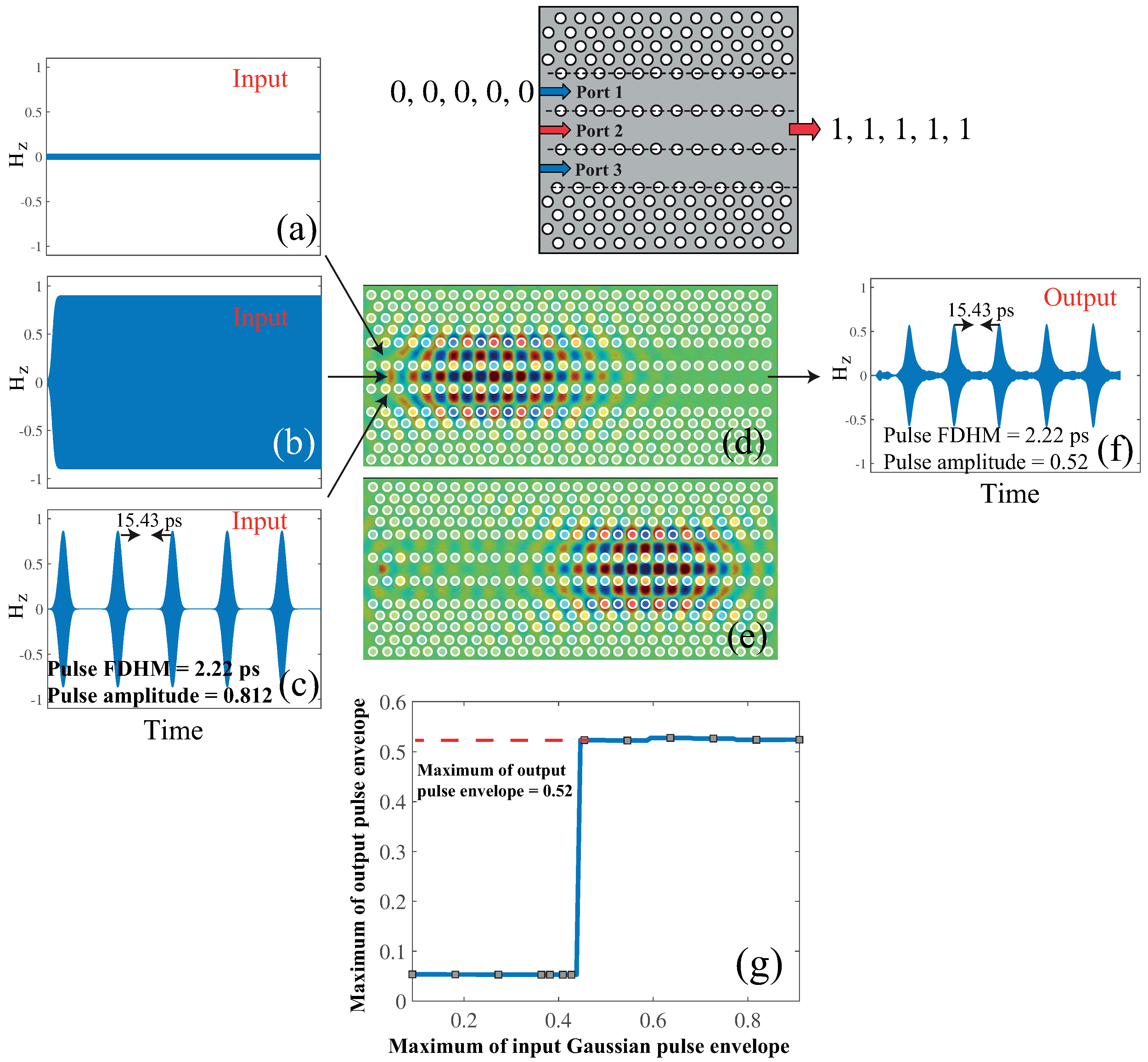
4.2. All-Optical AND Logic Gate
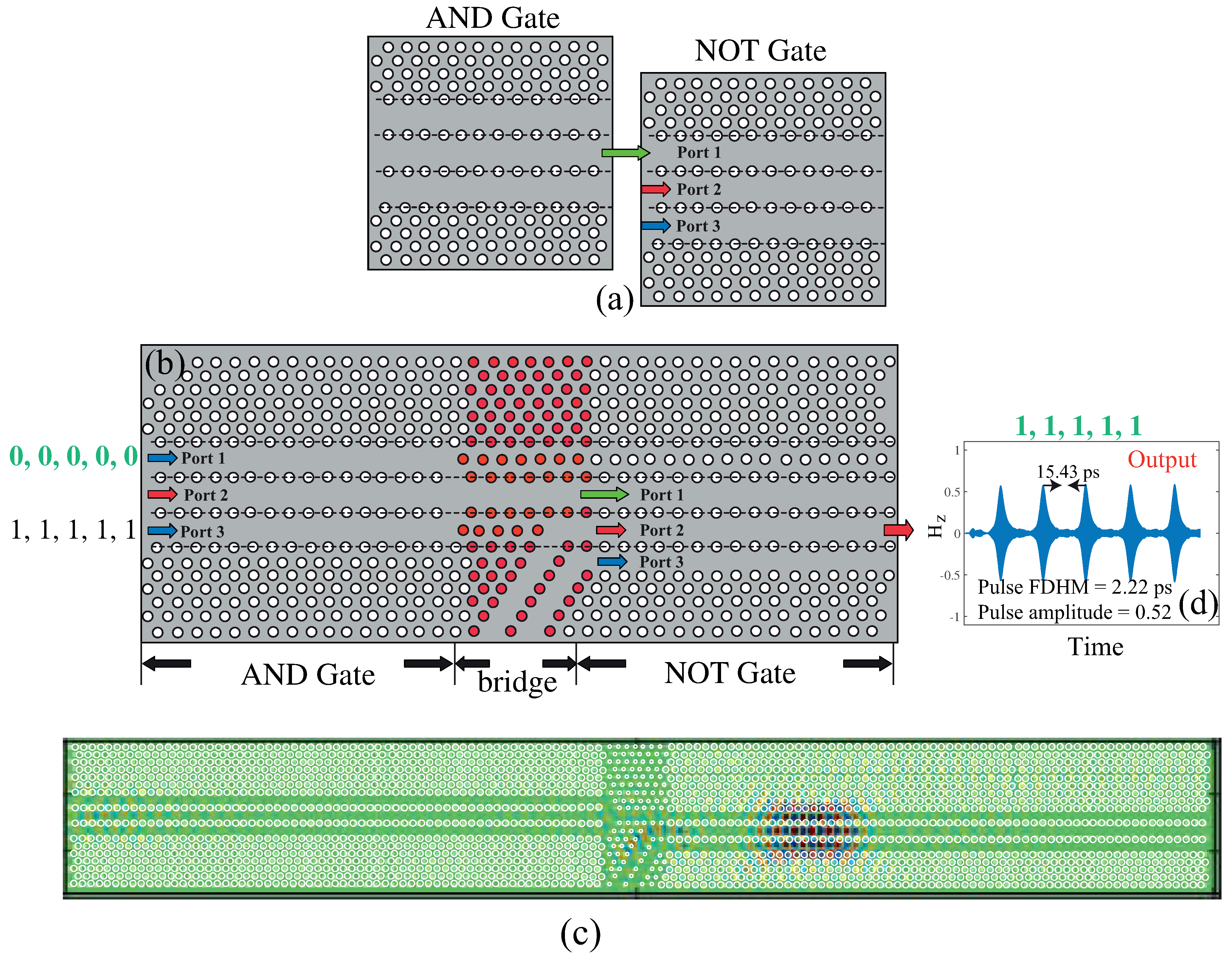
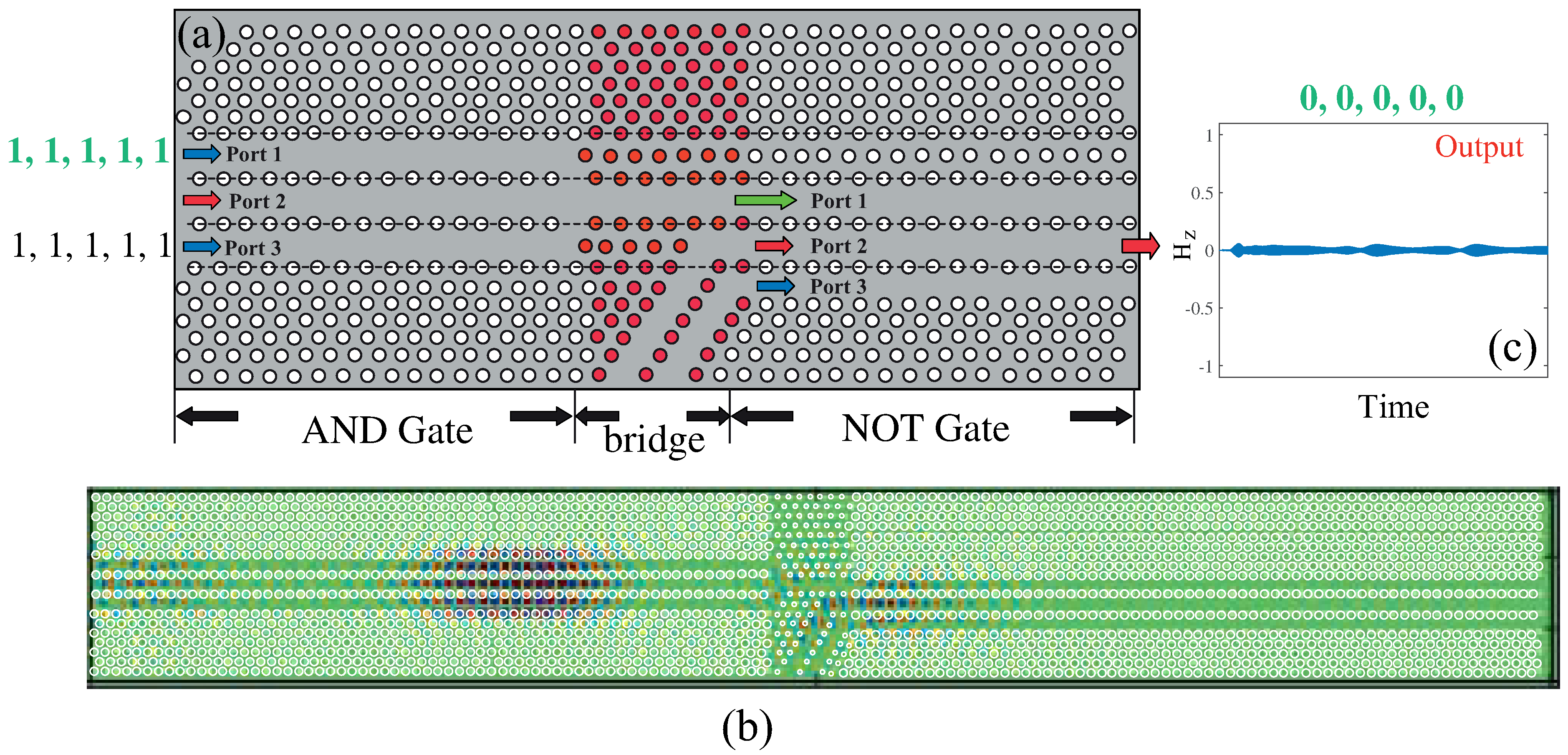
4.3. All-Optical NAND Logic Gate
5. Conclusions
Funding
Conflicts of Interest
Abbreviations
| PhC | Photonic crystal |
| PCW | Photonic crystal waveguide |
| C-PCW | Coupled photonic crystal waveguide |
| CW | Continuous wave |
References
- Remoissenet, M. Waves Called Solitons: Concepts and Experiments; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Dauxois, T.; Peyrard, M. Physics of Solitons; Cambridge University: Cambridge, UK, 2010. [Google Scholar]
- Kivshar, Y.; Agrawal, G. Optical Solitons: From Fibers to Photonic Crystals; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Scott, A. Encyclopedia of Nonlinear Science; Taylor & Francis Group: Abingdon, UK, 2005. [Google Scholar]
- Hasegawa, A.; Kodama, Y. Guiding-center soliton in optical fibers. Optics Lett. 1990, 15, 1443–1445. [Google Scholar] [CrossRef]
- Russell, P.S.J. Photonic crystal fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef] [PubMed]
- Gersen, H.; Karle, T.J.; Engelen, R.J.P.; Bogaerts, W.; Korterik, J.P.; van Hulst, N.F.; Krauss, T.F.; Kuiper, L. Real-space observation of ultraslow light in photonic crystal waveguides. Phys. Rev. Lett. 2005, 94, 073903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mekis, A.; Fan, S.; Joannopoulos, J.D. Bound states in photonic crystal waveguides and waveguide bends. Phys. Rev. B 1998, 58, 4809–4817. [Google Scholar] [CrossRef] [Green Version]
- Qiu, M.; Azizi, K.; Karlsson, A.; Swillo, M.; Jaskorzynska, B. Numerical studies of mode gaps and coupling efficiency for line-defect waveguides in two-dimensional photonic crystals. Phys. Rev. B 2001, 64, 155113. [Google Scholar] [CrossRef]
- Adibi, A.; Xu, Y.; Lee, R.; Yariv, A.; Scherer, A. Properties of the slab modes in photonic crystal optical waveguides. J. Lightwave Technol. 2000, 18, 1554–1564. [Google Scholar] [CrossRef] [Green Version]
- Enoch, S.; Tayeb, G.; Maystre, D. Dispersion diagrams of Bloch modes applied to the design of directive sources. Progr. Electromagn. Res. 2003, 41, 61–81. [Google Scholar] [CrossRef] [Green Version]
- Weily, A.R.; Horvath, L.; Esselle, K.P.; Sanders, B.C.; Bird, T.S. A planar resonator antenna based on a woodpile EBG material. IEEE Trans. Antennas Propag. 2005, 53, 216–223. [Google Scholar] [CrossRef]
- Ceccuzzi, S.; Pajewski, L.; Ponti, C.; Schettini, G. Directive EBG antennas: A comparison between two different radiating mechanisms. IEEE Trans. Antennas Propag. 2014, 62, 5420–5424. [Google Scholar] [CrossRef]
- Jandieri, V.; Yasumoto, K.; Gupta, B. Directivity of radiation from a localized source coupled to electromagnetic crystals. J. Infrared Millim. Terahertz Waves 2009, 30, 1102–1112. [Google Scholar] [CrossRef]
- Vlasov, Y.A.; O’Boyle, M.; Hamann, H.F.; McNab, S.J. Active control of slow light on a chip with photonic crystal waveguides. Nature 2005, 438, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Notomi, M.; Yamada, K.; Shinya, A.; Takahashi, J.; Takahashi, C.; Yokohama, I. Extremely large group-velocity dispersion of line-defect waveguides in photonic crystal slabs. Phys. Rev. Lett. 2001, 87, 253902. [Google Scholar] [CrossRef] [Green Version]
- Krauss, T. Slow light in photonic crystal waveguides. J. Phys. D Appl. Phys. 2007, 40, 2666–2670. [Google Scholar] [CrossRef] [Green Version]
- Monat, C.; Corcoran, B.; Pudo, D.; Ebnali-Heidari, M.; Grillet, C.; Pelusi, M.; Moss, D.; Eggleton, B.; White, T.; Krauss, T. Slow light enhanced nonlinear optics in silicon photonic crystal waveguides. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 344–356. [Google Scholar] [CrossRef]
- Blanco-Redondo, A.; Husko, C.; Eades, D.; Zhang, Y.; Li, J.; Krauss, T.F.; Eggleton, B.J. Observation of soliton compression in silicon photonic crystals. Nat. Commun. 2014, 5, 3160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yariv, A. Quantum Electronics, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1988. [Google Scholar]
- Jandieri, V.; Khomeriki, R.; Erni, D.; Chew, W.C. Realization of all-optical digital amplification in coupled nonlinear photonic crystal waveguides. Prog. Electromagn. Res. 2017, 158, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Jandieri, V.; Khomeriki, R.; Erni, D. Realization of true all-optical AND logic gate based on the nonlinear coupled air-hole type photonic crystal waveguide. Opt. Express 2018, 26, 19845–19853. [Google Scholar] [CrossRef] [Green Version]
- Jandieri, V.; Onoprishvili, T.; Khomeriki, R.; Erni, D.; Pistora, J. Digital signal processing in coupled photonic crystal waveguides and its application to an all-optical AND logic gate. Opt. Quantum Electron. 2019, 51, 1–15. [Google Scholar] [CrossRef]
- Jandieri, V.; Khomeriki, R.; Berakdar, J.; Erni, D. Theory of soliton propagation in nonlinear photonic crystal waveguides. Opt. Express 2019, 27, 29558–29566. [Google Scholar] [CrossRef]
- Jandieri, V.; Khomeriki, R.; Onoprishvili, T.; Werner, D.H.; Berakdar, J.; Erni, D. Functional all-optical logic gates for true time-domain signal processing in nonlinear photonic crystal waveguides. Opt. Express 2020, 28, 18317. [Google Scholar] [CrossRef]
- Malaguti, S.; Bellanca, G.; Combrie, S.; de Rossi, A.; Trillo, S. Temporal gap solitons and all-optical control of group delay in line-defect waveguides. Phys. Rev. Lett. 2012, 109, 163902. [Google Scholar] [CrossRef] [PubMed]
- Ablowitz, M.J.; Musslimani, Z.H. Discrete spatial solitons in a diffraction-managed nonlinear waveguide array: A unified approach. Phys. D 2003, 184, 276–303. [Google Scholar] [CrossRef]
- Tanaka, Y.; Nakamura, H.; Sugimoto, Y.; Ikeda, N.; Asakawa, K.; Inoue, K. Coupling properties in a 2-D photonic crystal slab directional coupler with a triangular lattice of air holes. IEEE J. Quantum Electron. 2005, 41, 76–84. [Google Scholar] [CrossRef]
- Strasser, P.; Flückiger, R.; Wüest, R.; Robin, F.; Jäckel, H. InP-based compact photonic crystal directional coupler with large operation range. Opt. Express 2007, 15, 8472–8478. [Google Scholar] [CrossRef] [PubMed]
- Slusher, R.E.; Eggleton, B.J. Nonlinear Photonic Crystals; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Rani, P.; Fatima, S.; Kalra, Y.; Sinha, R.K. Realization of all optical logic gates using universal NAND gates on photonic crystal platform. Superlattice Microst. 2017, 109, 619–625. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, F.; Meng, Z.; Zhou, F.; Mao, Q.; Li, Z. All-optical logic gates based on two-dimensional low-refractive-index nonlinear photonic crystal slabs. Opt. Express 2011, 19, 1945–1953. [Google Scholar] [CrossRef]
- Andalib, P.; Granpayeh, N. All-optical ultracompact photonic crystal AND gate based on nonlinear ring resonators. J. Opt. Soc. Am. B 2009, 26, 10–16. [Google Scholar] [CrossRef]
- Husko, C.; Vo, T.D.; Corcoran, B.; Li, J.; Krauss, T.; Eggleton, B. Ultracompact all-optical XOR logic gate in a slow-light silicon photonic crystal waveguide. Opt. Express 2011, 19, 20681–20690. [Google Scholar] [CrossRef] [Green Version]
- Ishizaka, Y.; Kawaguchi, Y.; Saitoh, K.; Koshiba, M. Design of ultracompact all-optical XOR and ANG logic gates with low power consumption. Opt. Commun. 2011, 284, 3528–3533. [Google Scholar] [CrossRef]
- He, L.; Zhang, W.X.; Zhang, X.D. Topological all-optical logic gates based on two-dimensional photonic crystals. Opt. Express 2019, 27, 25841–25860. [Google Scholar] [CrossRef]
- Geniet, F.; Leon, J. Energy transmission in the forbidden band gap of a nonlinear chain. Phys. Rev. Lett. 2002, 89, 134102. [Google Scholar] [CrossRef] [Green Version]
- Khomeriki, R. Nonlinear band-gap transmission in optical waveguide arrays. Phys. Rev. Lett. 2004, 92, 063905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, W.; Mills, D.L. Gap solitons and the nonlinear optical response of superlattices. Phys. Rev. Lett. 1987, 58, 160–163. [Google Scholar] [CrossRef] [PubMed]
- De Sterke, C.M.; Sipe, J.E. Envelope-function approach for the electrodynamics of nonlinear periodic structures. Phys. Rev. A 1988, 38, 5149–5165. [Google Scholar] [CrossRef] [PubMed]
- De Sterke, C.M.; Sipe, J.E. Coupled modes and the nonlinear Schrödinger equation. Phys. Rev. A 1990, 42, 550–555. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic Press: New York, NY, USA, 1989. [Google Scholar]
- Kim, J.-Y.; Kang, J.-M.; Kim, T.-Y.; Han, S.-K. All-optical multiple logic gates with XOR, NOR, OR, and NAND functions using parallel SOA-MZI structures: Theory and experiment. J. Light. Technol. 2006, 24, 3392–3399. [Google Scholar]
- Jandieri, V.; Baccarelli, P.; Valerio, G.; Schettini, G. 1-D periodic lattice sums for complex and leaky waves in 2-D structures using higher-order Ewald formulation. IEEE Trans. Antennas Propag. 2019, 67, 2364–2378. [Google Scholar] [CrossRef]
- Yasumoto, K.; Toyama, H.; Kushta, R. Accurate analysis of two-dimensional electromagnetic scattering from multilayered periodic arrays of circular cylinders using lattice sums technique. IEEE Trans. Antennas Propag. 2004, 52, 2603–2611. [Google Scholar] [CrossRef]
- Jandieri, V.; Baccarelli, P.; Valerio, G.; Yasumoto, K.; Schettini, G. Modal propagation in periodic chains of circular rods: Real and complex solutions. IEEE Photon. Technol. Lett. 2020, 32, 1053–1056. [Google Scholar] [CrossRef]
- Taflove, A. Computational Electrodynamics: The Finite-Difference Time-Domain Method; Artech House: Norwood, MA, USA, 1995. [Google Scholar]
- Baizakov, B.B.; Malomed, B.A.; Salerno, M. Multidimensional solitons in periodic potentials. EPL 2003, 63, 642–648. [Google Scholar] [CrossRef] [Green Version]
- Trombettoni, A.; Smerzi, A. Discrete solitons and breathers with dilute Bose-Einstein condensates. Phys. Rev. Lett. 2001, 86, 2353. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leuthold, J.; Koos, C.; Freude, W. Nonlinear silicon photonics. Nat. Photonics 2010, 4, 535–544. [Google Scholar] [CrossRef]
- Taniuti, T.; Yajima, N. Perturbation method for a nonlinear wave modulation. J. Math. Phys. 1969, 10, 1369–1372. [Google Scholar] [CrossRef]
- Malishava, M.; Khomeriki, R. All-phononic digital transistor on the basis of gap-soliton dynamics in an anharmonic oscillator ladder. Phys. Rev. Lett. 2015, 115, 104301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boyle, J.W.; Nikitov, S.A.; Boardman, A.D.; Booth, J.G.; Booth, K. Nonlinear self-channeling and beam shaping of magnetostatic waves in ferromagnetic films. Phys. Rev. B 1996, 53, 12173–12181. [Google Scholar] [CrossRef]
- Hasegawa, A.; Tappert, F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl. Phys. Lett. 1973, 23, 142–144. [Google Scholar] [CrossRef]
- Smajic, J.; Hafner, C.; Erni, D. Design and optimization of an achromatic photonic crystal bands. Opt. Express 2003, 11, 1378–1384. [Google Scholar] [CrossRef]
- Wang, F.; Gong, Z.; Hu, X.; Yang, X.; Yang, H.; Gong, Q. Nanoscale on-chip all-optical logic parity checker in integrated plasmonic circuits in optical communication range. Sci. Rep. 2016, 6, 24433. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jandieri, V.; Khomeriki, R.; Onoprishvili, T.; Erni, D.; Chotorlishvili, L.; Werner, D.H.; Berakdar, J. Band-Gap Solitons in Nonlinear Photonic Crystal Waveguides and Their Application for Functional All-Optical Logic Gating. Photonics 2021, 8, 250. https://doi.org/10.3390/photonics8070250
Jandieri V, Khomeriki R, Onoprishvili T, Erni D, Chotorlishvili L, Werner DH, Berakdar J. Band-Gap Solitons in Nonlinear Photonic Crystal Waveguides and Their Application for Functional All-Optical Logic Gating. Photonics. 2021; 8(7):250. https://doi.org/10.3390/photonics8070250
Chicago/Turabian StyleJandieri, Vakhtang, Ramaz Khomeriki, Tornike Onoprishvili, Daniel Erni, Levan Chotorlishvili, Douglas H. Werner, and Jamal Berakdar. 2021. "Band-Gap Solitons in Nonlinear Photonic Crystal Waveguides and Their Application for Functional All-Optical Logic Gating" Photonics 8, no. 7: 250. https://doi.org/10.3390/photonics8070250
APA StyleJandieri, V., Khomeriki, R., Onoprishvili, T., Erni, D., Chotorlishvili, L., Werner, D. H., & Berakdar, J. (2021). Band-Gap Solitons in Nonlinear Photonic Crystal Waveguides and Their Application for Functional All-Optical Logic Gating. Photonics, 8(7), 250. https://doi.org/10.3390/photonics8070250





