Abstract
Industrial processes involving thermal plasma such as cutting, welding, laser machining with ultra-short laser pulses (nonequilibrium conditions), high temperature melting using electrical discharge or ion-beams, etc., generate non-repeatable fast transient events which can reveal valuable information about the processes. In such industrial environments containing high temperature and radiation, it is often difficult to install conventional lens-based imaging windows and components to observe such events. In this study, we compare imaging requirements and performances with invasive and non-invasive modes when a fast transient event is occluded by a metal window consisting of numerous holes punched through it. Simulation studies were carried out for metal windows with different types of patterns, reconstructed for both invasive and non-invasive modes and compared. Sparks were generated by rapid electrical discharge behind a metal window consisting of thousands of punched through-holes and the time sequence was recorded using a high-speed camera. The time sequence was reconstructed with and without the spatio-spectral point spread functions and compared. Commented MATLAB codes are provided for both invasive and non-invasive modes of reconstruction.
1. Introduction
Imaging through occlusion such as mist, fog, or a scattering medium is a challenging task [1,2,3]. There are many techniques developed which allows reconstruction of the object information from the deformed images [3,4,5,6]. Techniques which utilize the information of the imaging configuration such as the point spread function (PSF), scattering matrix, and distances are categorized as invasive since additional information related to the scattering media is needed [4]. The techniques which do not require any of the information as described above are classified as non-invasive [5,6].
The two modes: invasive and non-invasive have their own advantages and disadvantages. The requirement of additional information about the imaging components and configuration in invasive mode is the disadvantage but the method can reconstruct up to 5D information in space, spectrum, and time [7,8]. In non-invasive approaches, the capability is often limited to 2D [6]. In the recent years, there has been numerous research works on non-invasive approaches and the method has been successfully extended to obtain an additional dimension—depth [9,10,11]. Another major difference between invasive and non-invasive approaches is that with invasive methods, it is possible to reconstruct the object information as close as possible to reality, with higher signal to noise ratio (SNR), optimal resolution and field of view. In the non-invasive approaches, the demonstration is often carried out with much smaller objects and the quality of reconstructions are much lower than direct and invasive approaches. Furthermore, the non-invasive approach relies on an initial guess (random matrix) which controls the degree of convergence, necessitating several initial guess cases in [6], that were tried until an optimal reconstruction was obtained.
In this tutorial, a comprehensive comparison of different types of correlation based invasive reconstruction methods and non-invasive type reconstruction using phase-retrieval algorithm is studied. The manuscript consists of five sections. In the next section, the methodology of the study is described. The simulative studies are presented in third section. The computational reconstruction with MATLAB code is described in the fourth section. In the fifth section, the experimental results are presented and discussed. The conclusion and summary are presented in the final section. Supplementary files consisting of original MATLAB code with comments are provided for a freshman in this area of research.
2. Methodology
The optical configuration of light collection from an isolated fast transient industrial process through an occlusion (metal window with holes) by a ultra-high-speed camera is shown in Figure 1. Many industrial processes produce intense temperature, light intensity, and pressure so are generally isolated from their surroundings. This makes it difficult to image or monitor using conventional lens-based imaging systems. A metal occlusion consisting of few holes is better than a glass window as it can substantially cut down the light intensity. Additionally, an electrical bias of such “metallic-optics” can be used to mitigate material (re)deposition for a close placement of them near high-temperature event. Furthermore, if the holes have sizes of the order of the wavelength of interest then the light will undergo diffraction and generate intensities within recordable range of values. Let us consider that the fast transient event generates light that is spatially as well as temporally incoherent (Figure 1).
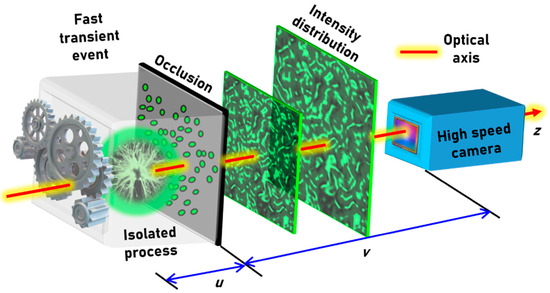
Figure 1.
Optical configuration of light collection from an isolated fast transient industrial process through an occlusion (metal window with punched holes) by a high-speed camera.
As it is seen in Figure 1, what is recorded by the high-speed camera is not the image of the object or the event but a scattered intensity distribution. Therefore, the recorded intensity distribution needs to be processed to reconstruct the event as close as possible to reality. This reconstruction can be achieved using two modes: invasive and non-invasive. In the invasive approach, as the name suggests it is necessary to carry out some measurements in the region invasively where the event occurs to extract additional information about the system. This invasion can be either in the form of recording the image of the occlusion and generating the transmission matrix or mounting a point object such as a pinhole at different axial locations and recording the PSF library. The above invasion is possible in some cases and may be safe where the space beyond the occlusion is accessible or the occlusion itself is detachable. In such cases, a PSF library can be recorded for different wavelengths or the occlusion can be imaged. By processing the PSF library with the recorded scattered intensity distribution, the event can be completely reconstructed in depth and wavelength up to five dimensions. However, in many industrial processors, the above is not possible where the occlusion is welded on to the system and the space beyond the occlusion is not accessible. Besides, this invasive procedure is especially not safe in biomedical applications where the surface of an organ or tissue is occluded by the skin. In such cases, the only information that is available is the scattered intensity distribution and the reconstruction mechanisms which use only this scattered intensity distribution are called as non-invasive imaging methods. Phase-retrieval based image reconstruction techniques that can reconstruct the event or the image of the object just by processing only the scattered intensity distribution without any other information of the system were developed. However, is the phase retrieval-based reconstruction universal? i.e., does this approach work in all types of occlusions? In the next sections, the mathematical formulations are presented and simulative studies on different types of occlusions are investigated.
2.1. Invasive
Let Io(λ) be the intensity of a point object emitting light with a wavelength λ, located in the (xo, yo) plane at a distance of u from the occluding object. The complex amplitude at the occlusion is given by
where , and are the linear and quadratic phase factors respectively, C1 is a complex constant and oxx and oyy are the projections along the x and y directions. Considering the occlusion as a metal consisting of many holes of the order of wavelength, the following design can be made. The occlusion at a plane m consisting of N micro-holes that are randomly located can be expressed as
where is a Delta function, R is the radius of the pinhole and ‘’ is a two dimensional (2D) convolutional operator, , and , U is a uniform random variable distributed on [0, C2] and circ(R) is the circle function. The above convolution operation creates holes in the locations of the Delta functions. The complex amplitude after the mask is given as
The sensor located at a distance of v from the occlusion records an intensity distribution given by
where is the location vector in the sensor plane. The above equation can be modified as
which indicates that a point in the object plane located not along the optical axis will generate the same intensity pattern but shifted in the sensor plane by . So, the location vector is modified by including this shift. A 2D object consisting of multiple points can be represented as
where ai is the intensity at the object plane (at the point i). The object intensity pattern at the sensor plane is given as
The image of the object is reconstructed by a cross-correlation between O and IPSF
where M is the magnification of the system given by v/u and Λ is a Delta-like function which samples the object and K is a function indicating background noise arising due to cross-correlating two positive functions. If the conditions of either the object or the point object in u or λ are different from one another, then the width of Λ increases with the minimal width corresponding to ~2.44λ/NA when there is a perfect match in wavelength and distance. The above correlation can be accomplished through different filters such as matched filter [12], phase-only filter [13], non-linear filter (NLR) [14], Weiner filter (WF) [15] and other algorithms such as Lucy–Richardson algorithm (LRA) [16,17], maximum likelihood algorithm (MLA) [18], regularized filter algorithm (RFA) [19]. The previous studies [20] have proven that the NLR has better performance than different filters and iterative methods due to the high level of adaptability and versatility [20].
2.2. Non-Invasive
In non-invasive approach, the reconstruction is not by a cross-correlation with the PSF but by a phase-retrieval algorithm which uses the magnitude of the autocorrelation of the object intensity distribution given as IA = O∗O, where ‘∗’ is a 2D correlation operator. Rewriting the above expression by expanding the object intensity distribution O, we get IA = (o⊗IPSF)∗(o⊗IPSF). The terms can be rearranged by convolution theorem such that IA = (o∗o)⊗(IPSF∗IPSF) [21]. The autocorrelation of IPSF gives rise to a Delta-like function Λ with a background given by K and so IA = (o∗o)⊗(Λ + K). The function of K is given by the nature of the occlusion as described in [22]. So, the above expression can be written as IA = (o∗o + K1). For simplicity, the occlusion is considered as highly scattering and so K1 is nearly constant which can be suppressed by subtraction of the average minimum value. The autocorrelation of the object intensity distribution can be expressed in terms of Fourier transforms as [23]. A Fourier transform operation followed by a square root on IA will result in As the magnitude of Fourier transform of the object information is available, the object information can be obtained using Fienup type phase retrieval algorithm [24].
The block diagram for the phase-retrieval algorithm is shown in Figure 2. In the first step, the autocorrelation of the object intensity distribution is calculated, followed by a Fourier transform and square root operation yielding the magnitude of the Fourier transform of the object. There are two planes of interest with complex amplitudes A1(x, y) and exp[jΦ(kx, ky)] as shown in Figure 2. The size of A1(x, y) is predicted as approximately half of the extend of IA as the autocorrelation of the intensity is equivalent to the autocorrelation of the object if the autocorrelation of the PSF generates a Delta-like function. The algorithm begins with an initial guess object function A1(x, y) with a size about half of the width of IA and a value of zero for all other pixels of the matrix. This matrix is Fourier transformed and the resulting complex amplitude’s real part is replaced by while the phase Φ(kx, ky) was carried on. The resulting matrix is inverse Fourier transformed and the constraints of non-negativity and real are applied and this process is iterated until the matrix A1(x, y) converges and reaches non-changing values. Thus, the object function is reconstructed. Previous studies have indicated that convergence of the algorithm is highly dependent upon the initial guess matrices and so it was repeated many numbers of times with different initial guess matrices mostly with a random profile [6].
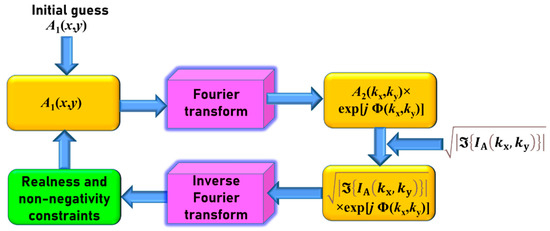
Figure 2.
Block diagram of the phase-retrieval algorithm.
3. Simulative Studies
In this section, the invasive and non-invasive approaches were studied for different types of occlusion as shown in Figure 3a–d and for an object consisting of two circular objects as shown in Figure 3e. The previous studies have shown that the non-invasive approaches work well only for simpler objects with a smaller field of view [6]. The main difference between Figure 3a–d is that the first three are periodic structures while the final one is chaotic [7]. Even though the inversion images of Figure 3a,b are typically used, the current images were used for decreasing the light throughput. The simulation studies were carried out and the PSFs are shown in Figure 4. As is seen, the periodic structures generate PSFs that have periodic intensity patterns. Consequently, the autocorrelation of the periodic patterns give rise to multiple peaks other than a single peak as described in Section 2. For this reason, the generated function cannot be considered as a Delta-like function for the periodic cases. The object intensity distributions for different cases are simulated by convolving the respective PSFs with the object function shown in Figure 3e. As expected, the object intensity distribution appears periodic except for the case with randomly punched holes. The phase retrieval method has been applied to reconstruct the object information without the PSF and the results for different types of occlusion are shown in Figure 4. As expected, the reconstruction for periodic intensity cases have lower quality than the case with randomly punched holes. The invasive approach was implemented with NLR given as and the parameters α and β are tuned between −1 and 1 until a minimum entropy given as is obtained where , (m,n) are the indexes of the correlation matrix, and C(m,n) is the correlation distribution. The reconstruction results are better for the case with random intensity distribution than other cases of occlusion with periodic mesh patterns. The results shown in the rows 4 and 5 (from top) of Figure 4 are magnified versions of the reconstructed images with the central part filling up the window. Every reconstructed pixel information of the reconstructed image is approximately twice the size of the diffraction limited spot as the object function o is sampled by the autocorrelation function of the imaging system. The image reconstruction by NLR can be given as IO = O∗IPSF = (o⊗IPSF)∗IPSF. Rearranging the terms of the equation we get o⊗(IPSF∗IPSF) = o⊗Λ, where Λ is twice the diffraction limited spot size for matched filter [13] and can be equal to the size of the diffraction limited spot size at the optimal case of the NLR [14].
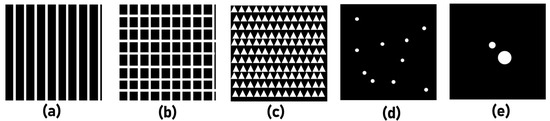
Figure 3.
Intensity images of different types of occlusion (a) 1-D mesh, (b) 2D mesh, (c) triangular mesh and (d) block with randomly arranged holes. (e) Image of the object. The white regions indicate the opening, and the dark regions indicate the metal block.
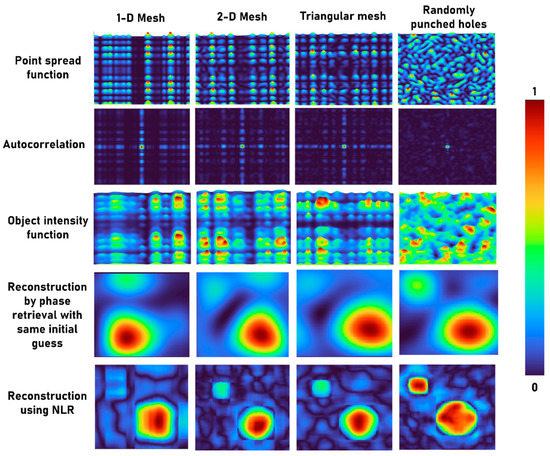
Figure 4.
Simulated PSF, autocorrelation of PSF, object intensity function, reconstruction using phase retrieval and NLR Figure 1. D mesh, 2-D mesh, triangular mesh and randomly arranged holes in a metal plate. All the images are normalized to a range of values between 0 and 1.
4. Software
The computational reconstruction has been carried out using the software MATLAB. The step-by-step approach is provided using pseudo code for invasive and non-invasive cases in Table 1 and Table 2 respectively. In invasive mode, there are two inputs namely the object intensity pattern and the PSF and in non-invasive mode, there is only a single input which is the object intensity distribution. In invasive mode, the reconstruction is direct where the matrices of object intensity pattern and PSF are cross correlated by NLR filter. By setting different values to α and β, different filters such as matched filter, phase-only filter and Weiner or inverse filter cases can be obtained. Other iterative reconstruction methods such as LRA and MLA and noise removal method RFA are available as one line syntax in MATLAB software. The pre-processing of the recorded intensity distributions is similar in both cases.

Table 1.
Pseudocode for the reconstruction of the image for invasive mode of imaging through occlusion.

Table 2.
Pseudocode for the reconstruction of the image for non-invasive mode of imaging through occlusion.
5. Experiments
The schematic of the experimental set up is exactly same as the optical configuration shown in Figure 1. A spark is generated behind an occlusion and the scattered intensity pattern was recorded using an ultra-high-speed camera. The spark generation circuit is shown in Figure 5a and the photograph of the experimental set up is shown in Figure 5b. The occlusion for the experiment was fabricated on a 4-inch chromium coated glass plate with a thin layer of resist. A design consisting of 12,000 holes grouped into sets of 2000, 1500 and 1000 holes each with a diameter of about 100 μm was made for the experiment. The design was transferred to the resist layer using Intelligent micropatterning SF100 XPRESS on a standard non-contact photo-lithography mask-blank. A standard chrome etchant was used to transfer the pattern to the chromium layer. Only a small area (~64 mm2) consisting of about 2000 holes of the mask was unblocked while the rest of the areas were blocked by a black tape. An ultra-high-speed camera (Phantom v2512, monochrome, 800 × 1280, Δ = 28 μm) was mounted at a distance of about 15 cm from the occlusion.
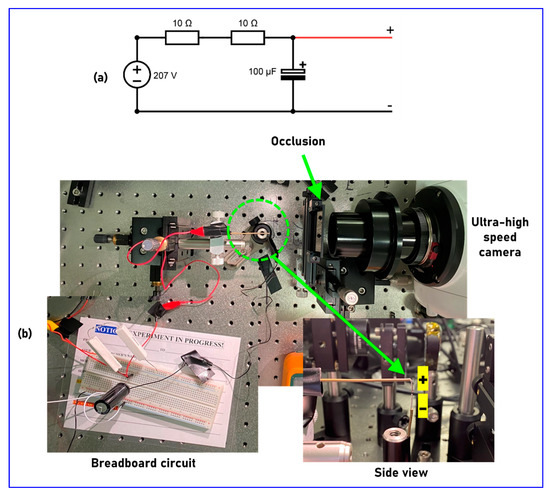
Figure 5.
(a) Circuit diagram for generating a spark. (b) Photograph of the experimental set up. A spark event was generated using (a) at a distance of 5 cm from the occlusion and an ultra-high-speed camera was mounted at a distance of 15 cm from the occlusion.
For this tutorial study, a spark was generated by capacitor discharge using a simple circuit, as shown in Figure 5a. The circuit consisted of two 10 W, 10 Ω resistors connected in series with a capacitor 100 μF, 400 V [25]. The capacitor was charged to about 207 V and discharged by touching the wires that were connected parallel to the terminals of the capacitor resulting in a sudden discharge causing a spark. This spark event was located approximately 5 cm from the occlusion. The photograph of the experimental set up is shown in Figure 5b. The camera was configured to record the 2 s preceding that start of the fast transient event and triggered manually and saved as a cine file. The Phantom Camera Control software was used to export the cine file into a 12-bit TIFF file for processing in MATLAB. In order to have reliable comparison between invasive and non-invasive approaches, a PSF was recorded using a pinhole with a size of 20 μm at the location of the event. The image of the recorded green PSF (λ = 530 nm, Δλ = 33 nm) and the object intensity distribution of the spark event with a time lapse of 40 μs between successive frames are shown in Figure 6a–g.
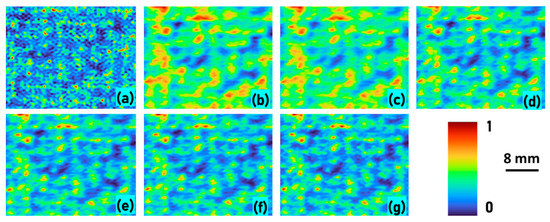
Figure 6.
Experimentally recorded green PSF (a), object intensity distributions at t = 0 μs (b), 40 μs (c), 80 μs (d), 120 μs (e), 160 μs (f) and 200 μs (g).
The reconstructed intensity distributions from invasive and non-invasive approaches are shown in Figure 7. It is seen that the reconstructed intensity distributions from NLR (α = 0, β = 0.7) matched with that of RFA, LRA (50 iterations) and MLA (50 iterations) and the non-invasive method yielded the reconstructions with additional information. The reconstructed intensity distributions for invasive methods enhance the information corresponding to the green wavelength and the corresponding depth which may not happen with the non-invasive approach leading to additional information. The results for non-invasive approach matched with that of the invasive methods for a set of values of the parameters in the phase retrieval algorithm such as spatial frequency range of low-pass filter, computational space and initial guess matrix. However, it was found that the pattern of the initial guess matrix was not crucial if the computational space and filter were optimized. The results obtained did not vary much even when the initial guess matrix consisted of only constant values such as 0 or 1. Furthermore, the number of iterations needed was only about 20 and only mild variations were seen after that indicating a faster convergence which is different from the earlier studies which required hundreds or thousands of iterations [6].
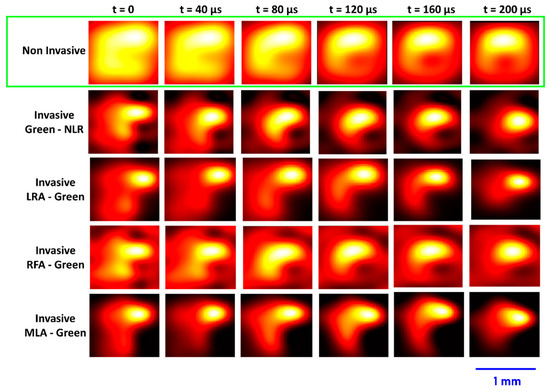
Figure 7.
Reconstructed intensity distributions for the spark event separated by t = 40 μs non-invasive and invasive methods NLR, LRA, RFA and MLA for green PSF.
6. Summary and Conclusions
In the recent years, there have been a shift in interest from developing invasive imaging methods towards non-invasive ones. Bypassing the need to record or generate PSFs means that in environments where the target area cannot be accessed, imaging through a scattering or occluding window can still be achieved. Even in situations where conventional imaging is used, the optical window can degrade over time, leading to increased scattering or occlusion and creating an environment highly suitable for this method. This tutorial summarises the invasive and non-invasive methods of image reconstruction and goes through the mathematical operations required to accomplish both. A simple simulation is shown to demonstrate the effects of the occluding medium on the resultant reconstruction, which shows a better result when the occluder is not periodic. Finally, a model system consisting of an electrical spark is used to compare the invasive and non-invasive methods and to show the effects of different filters in the invasive approach. We believe that this tutorial along with commented code provides good starting point and background for users that want to begin implementing these methods by facilitating quick learning of the fundamentals of invasive and non-invasive approaches for freshman in this area of research. This non-invasive imaging is directly amenable to artificial intelligence analysis of images. The recently developed edge and contrast enhancement studies can be directly applied to the methods discussed here [26].
Supplementary Materials
The following are available online at https://doi.org/10.5281/zenodo.4882872, Supplementary files Supplementary_Code_1 and Supplementary_Code_2.
Author Contributions
Conceptualization, V.A.; methodology, V.A.; software, V.A.; validation, V.A. and S.H.N.; Experiments, S.H.N., V.A. and T.K.; resources, S.J.; data curation, V.A. and S.H.N.; writing—original draft preparation, V.A.; writing—review and editing, S.H.N. and S.J.; visualization, S.J.; supervision, S.J.; project administration, S.J.; funding acquisition, S.H.N. and S.J. All authors have read and agreed to the published version of the manuscript.
Funding
Australian Research Council (LP190100505).
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Acknowledgments
The Nano Lab fabrication facility at Swinburne University of Technology is acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fade, J.; Panigrahi, S.; Carré, A.; Frein, L.; Hamel, C.; Bretenaker, F.; Ramachandran, H.; Alouini, M. Long-range polarimetric imaging through fog. Appl. Opt. 2014, 53, 3854–3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jaruwatanadilok, S.; Ishimaru, A.; Kuga, Y. Optical imaging through clouds and fog. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1834–1843. [Google Scholar] [CrossRef]
- Paciaroni, M.; Linne, M. Single-shot, two-dimensional ballistic imaging through scattering media. Appl. Opt. 2004, 43, 5100–5109. [Google Scholar] [CrossRef]
- Mukherjee, S.; Vijayakumar, A.; Kumar, M.; Rosen, J. 3D imaging through scatterers with interferenceless optical system. Sci. Rep. 2018, 8, 1134. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Xie, X.; Thendiyammal, A.; Zhuang, H.; Xie, J.; Liu, Y.; Zhou, J.; Mosk, A.P. Imaging of objects through a thin scattering layer using a spectrally and spatially separated reference. Opt. Express 2018, 26, 15073–15083. [Google Scholar] [CrossRef] [Green Version]
- Katz, O.; Small, E.; Guan, Y.; Silberberg, Y. Noninvasive nonlinear focusing and imaging through strongly scattering turbid layers. Optica 2014, 1, 170–174. [Google Scholar] [CrossRef] [Green Version]
- Anand, V.; Ng, S.H.; Maksimovic, J.; Linklater, D.; Katkus, T.; Ivanova, E.P.; Juodkazis, S. Single shot multispectral multidimensional imaging using chaotic waves. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Rosen, J. Spectrum and space resolved 4D imaging by coded aperture correlation holography (COACH) with diffractive objective lens. Opt. Lett. 2017, 42, 947–950. [Google Scholar] [CrossRef]
- Horisaki, R.; Okamoto, Y.; Tanida, J. Single-shot noninvasive three-dimensional imaging through scattering media. Opt. Lett. 2019, 44, 4032–4035. [Google Scholar] [CrossRef] [Green Version]
- Takasaki, K.T.; Fleischer, J.W. Phase-space measurement for depth-resolved memory-effect imaging. Opt. Express 2014, 22, 31426–31433. [Google Scholar] [CrossRef]
- Singh, A.K.; Naik, D.N.; Pedrini, G.; Takeda, M.; Osten, W. Exploiting scattering media for exploring 3D objects. Light Sci. Appl. 2017, 6, e16219. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography–A new type of incoherent digital holograms. Opt. Express 2016, 24, 12430–12441. [Google Scholar] [CrossRef]
- Horner, J.L.; Gianino, P.D. Phase-only matched filtering. Appl. Opt. 1984, 23, 812–816. [Google Scholar] [CrossRef]
- Rai, M.R.; Vijayakumar, A.; Rosen, J. Non-linear adaptive three-dimensional imaging with interferenceless coded aperture correlation holography (I-COACH). Opt. Express 2018, 26, 18143–18154. [Google Scholar] [CrossRef]
- Hardie, R.C.; Barnard, K.J.; Ordonez, R. Fast super-resolution with affine motion using an adaptive Wiener filter and its application to airborne imaging. Opt. Express 2011, 19, 26208–26231. [Google Scholar] [CrossRef] [Green Version]
- Richardson, W.H. Bayesian-based iterative method of image restoration. J. Opt. Soc. Am. 1972, 62, 55–59. [Google Scholar] [CrossRef]
- Lucy, L.B. An iterative technique for the rectification of observed distributions. Astron. J. 1974, 79, 745–754. [Google Scholar] [CrossRef] [Green Version]
- Biggs, D.S.C.; Andrews, M. Acceleration of iterative image restoration algorithms. Appl. Opt. 1997, 36, 1766–1775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Addison-Wesley Publishing Company, Inc.: Boston, MA, USA, 1992. [Google Scholar]
- Anand, V.; Katkus, T.; Lundgaard, S.; Linklater, D.P.; Ivanova, E.P.; Ng, S.H.; Juodkazis, S. Fresnel incoherent correlation holography with single camera shot. Opto-Electron. Adv. 2020, 3, 200004. [Google Scholar]
- Bertolotti, J.; van Putten, E.G.; Blum, C.; Lagendijk, A.; Vos, W.L.; Mosk, A.P. Non-invasive imaging through opaque scattering layers. Nature 2012, 491, 232–234. [Google Scholar] [CrossRef]
- Mukherjee, S.; Vijayakumar, A.; Rosen, J. Spatial light modulator aided noninvasive imaging through scattering layers. Sci. Rep. 2019, 9, 17670. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Greenwood Village, CO, USA, 2005. [Google Scholar]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vijayakumar, A.; Ng, S.H.; Katkus, T.; Juodkazis, S. Spatio-spectral-temporal imaging of fast transient phenomena using a random array of pinholes. Adv. Photo Res. 2021, 2, 2000032. [Google Scholar]
- Anand, V.; Rosen, J.; Ng, S.H.; Katkus, T.; Linklater, D.P.; Ivanova, E.P.; Juodkazis, S. Edge and Contrast Enhancement Using Spatially Incoherent Correlation Holography Techniques. Photonics 2021, 8, 224. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).