Theoretical Considerations of Photonic Crystal Fiber with All Uniform-Sized Air Holes for Liquid Sensing
Abstract
1. Introduction
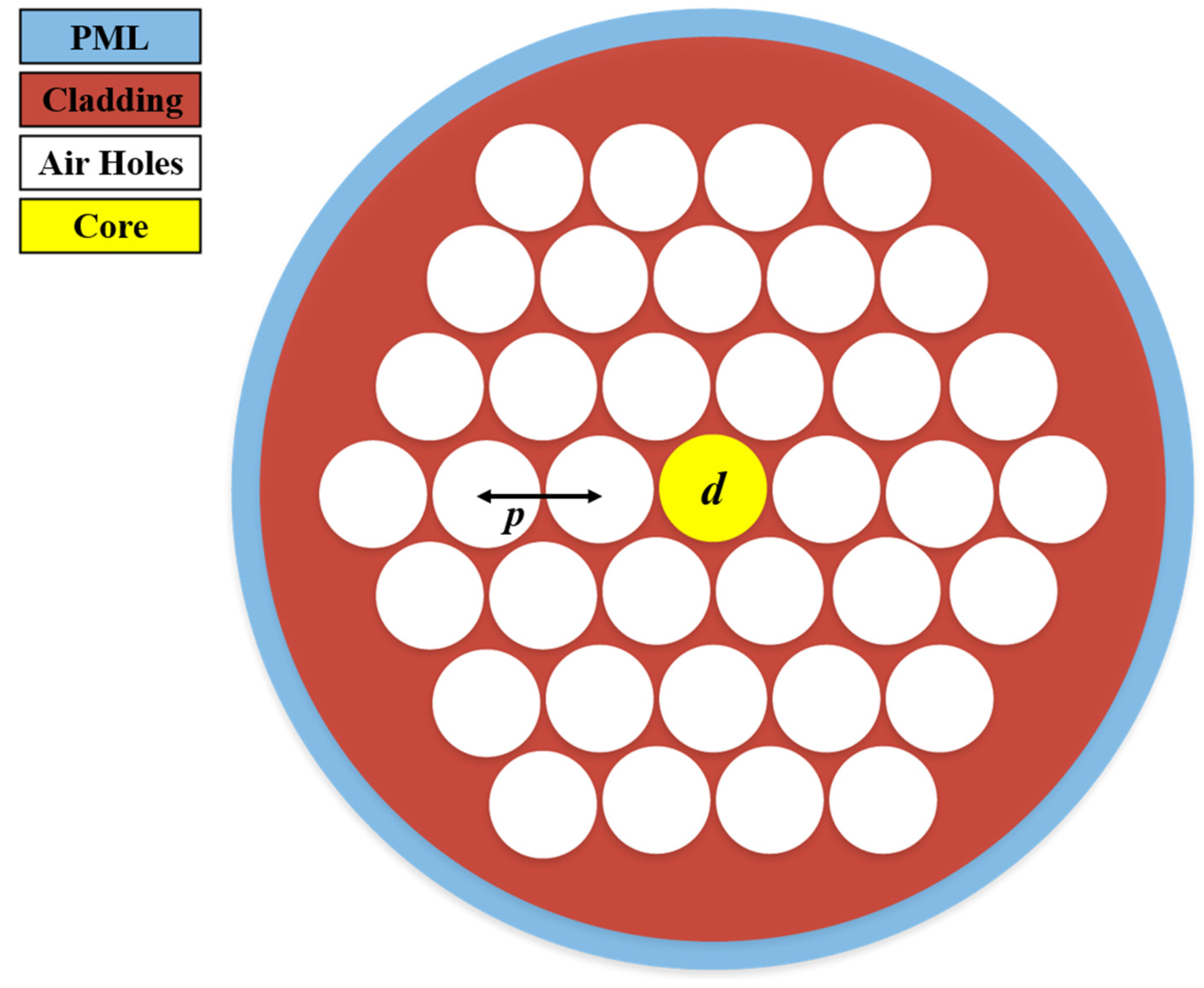
2. Design
3. Methodology
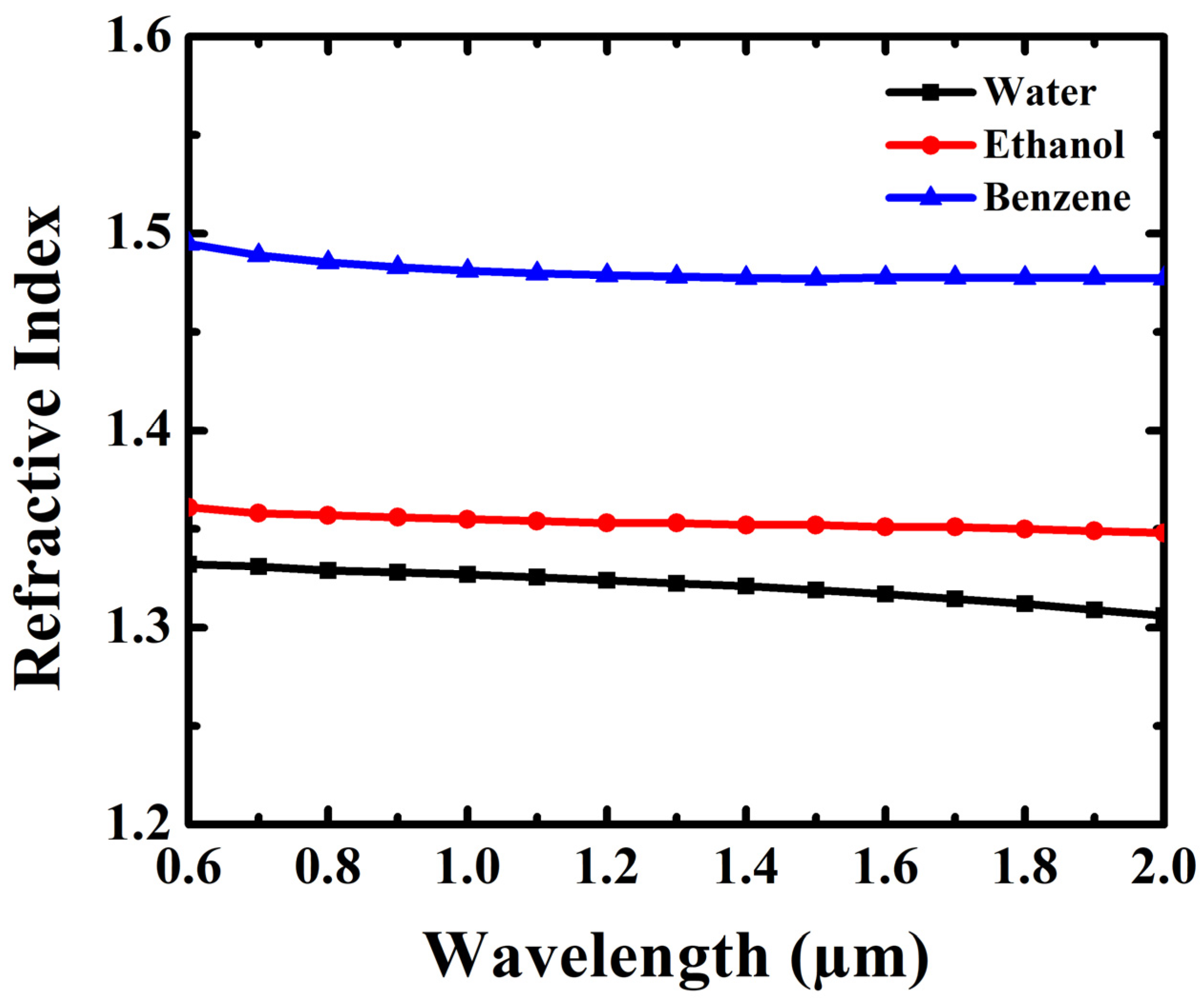
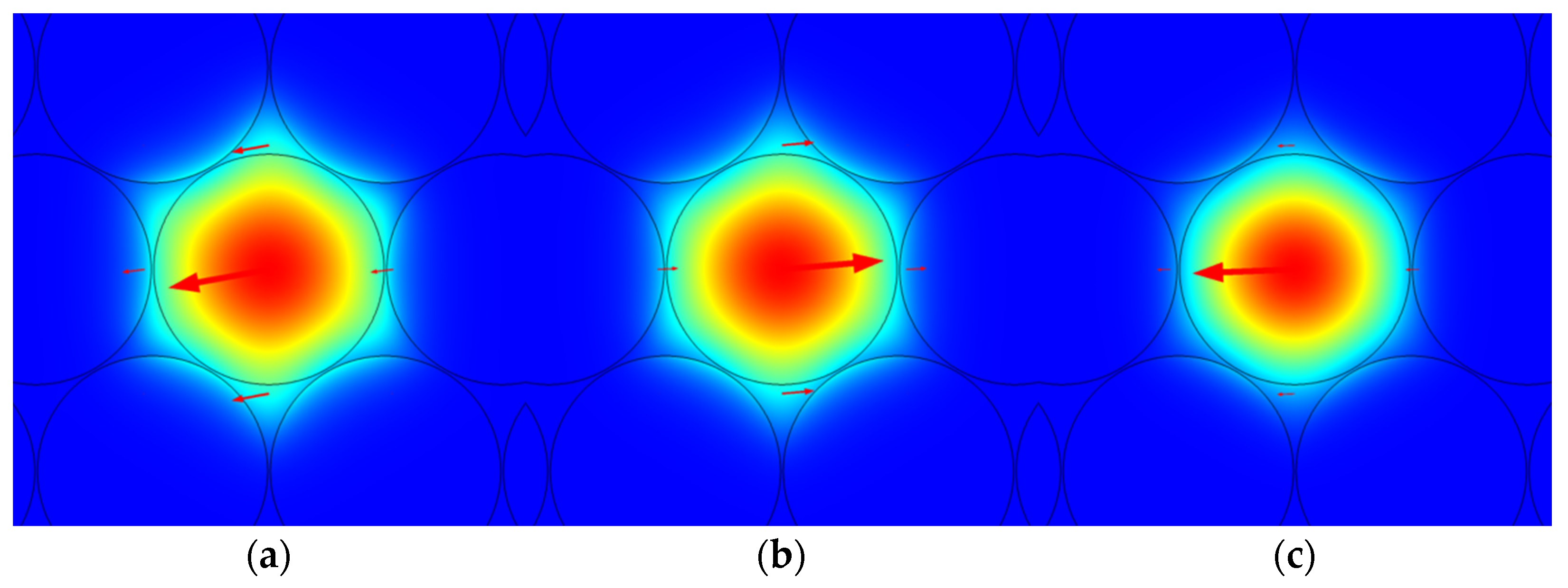
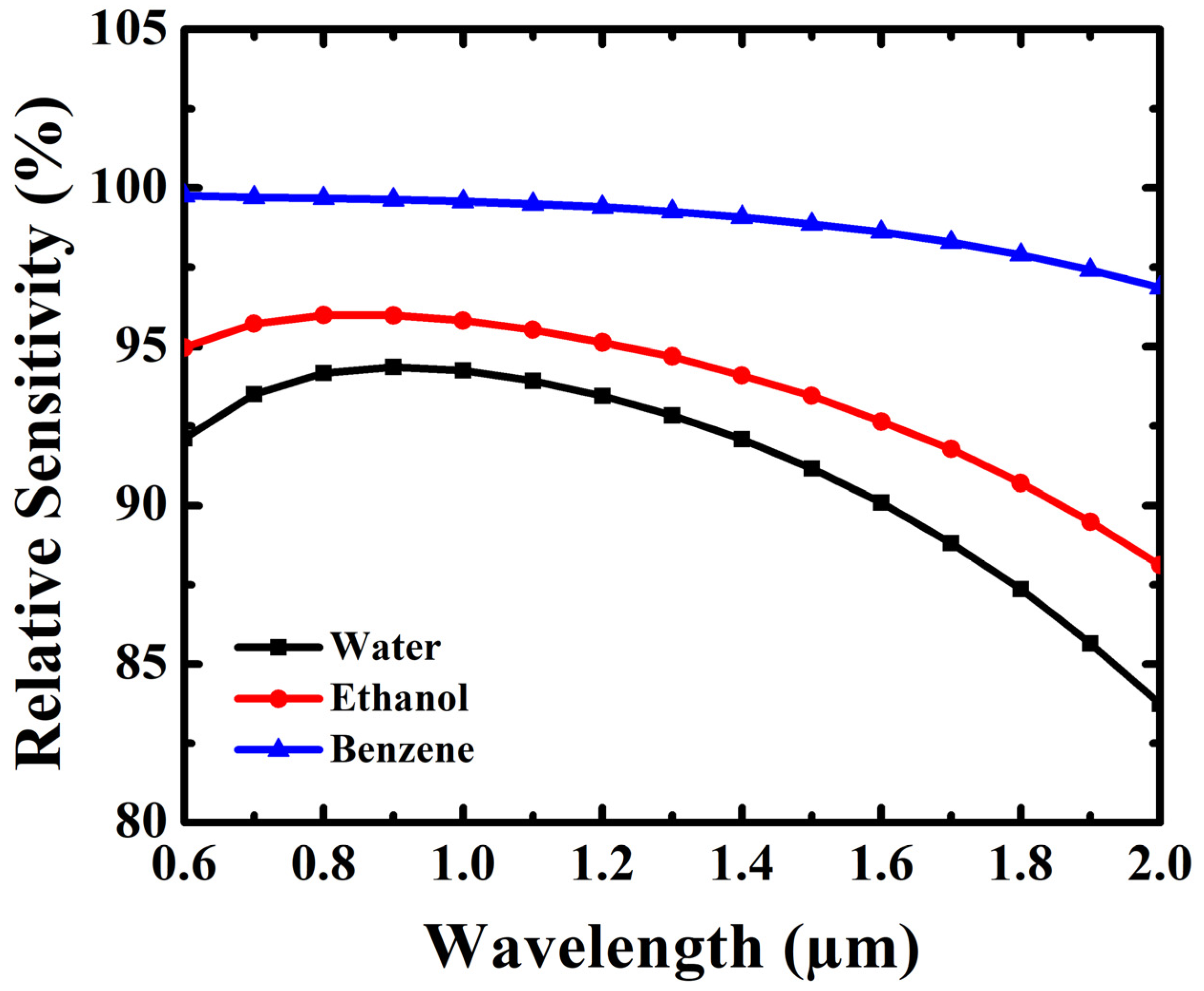
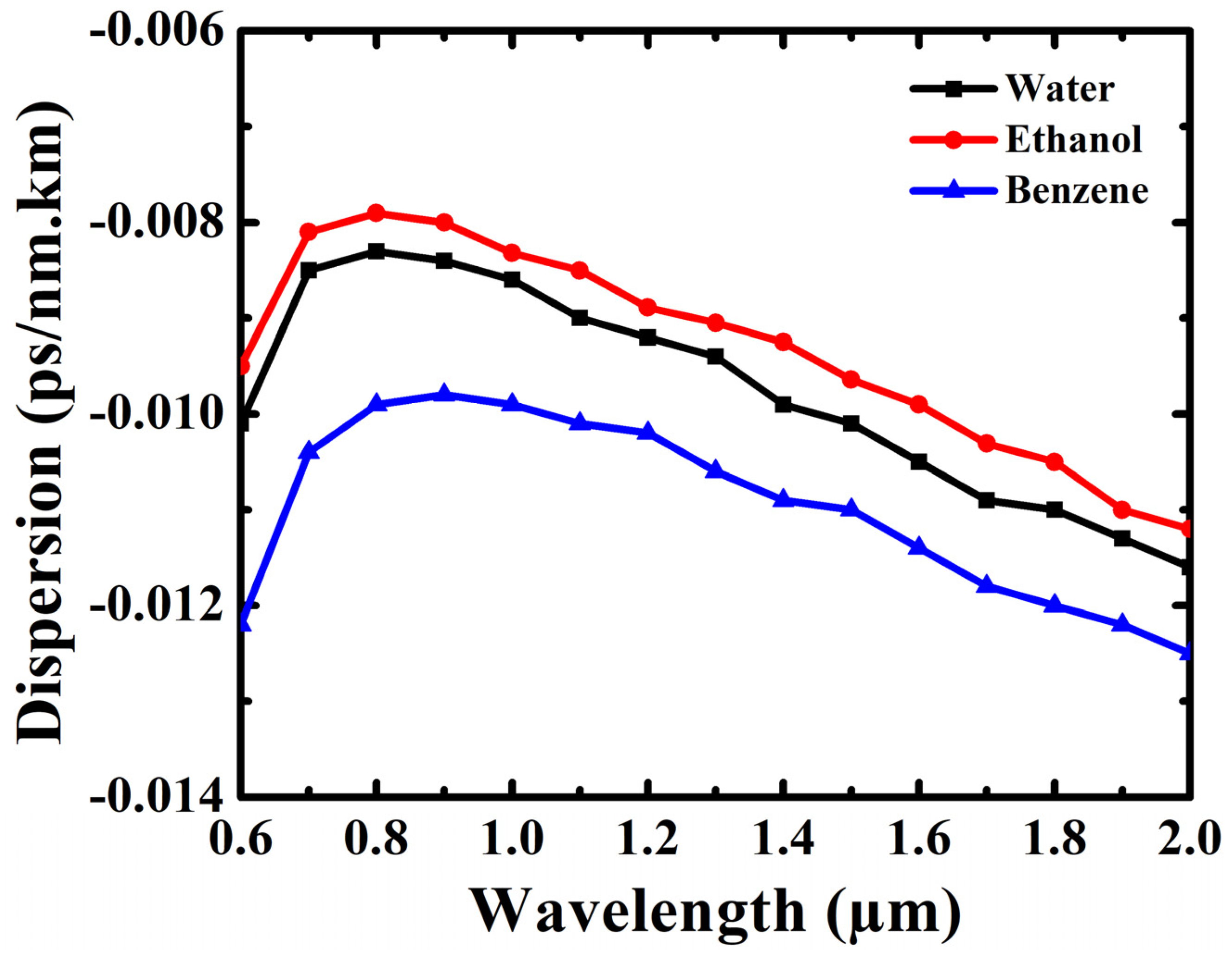
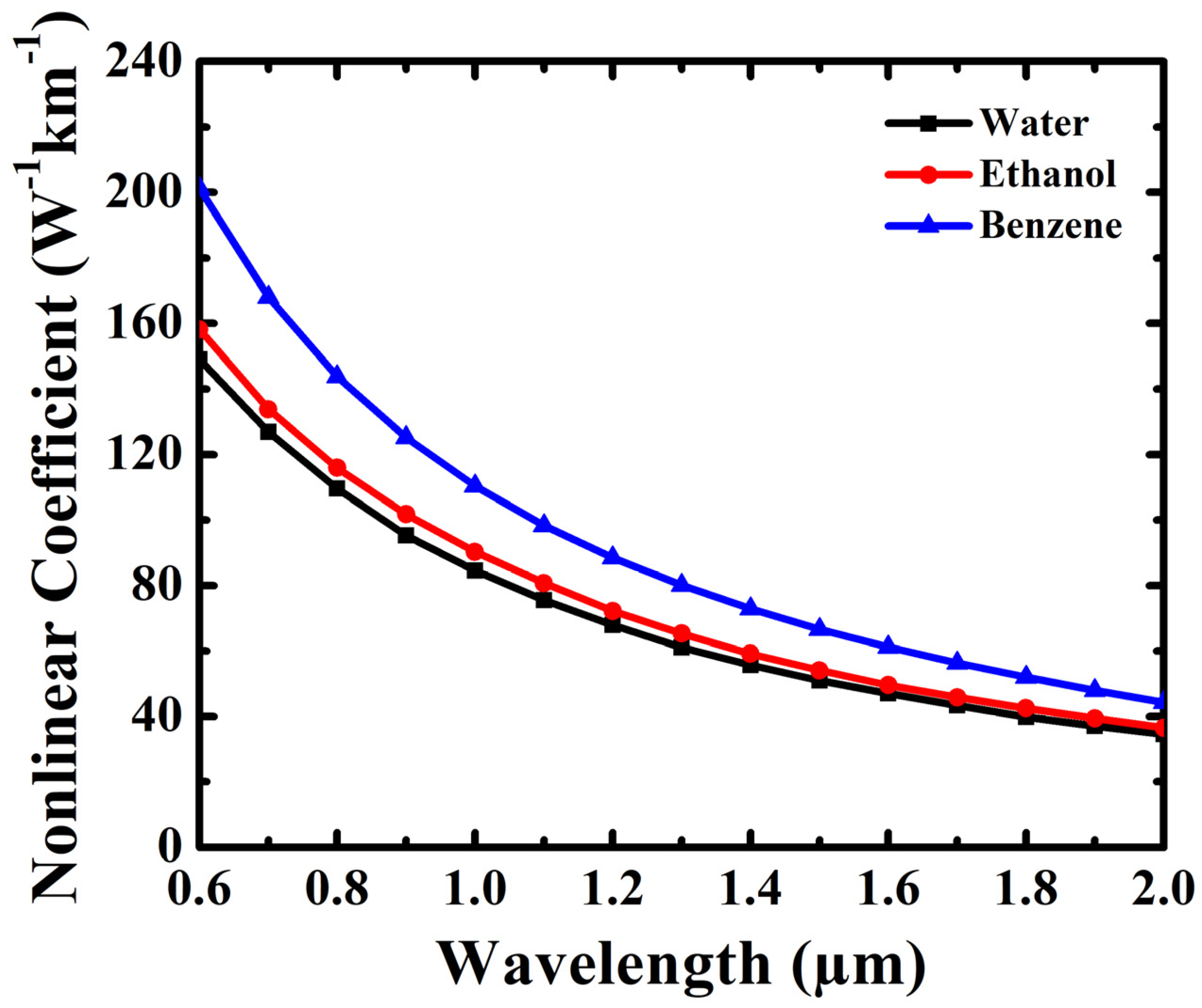
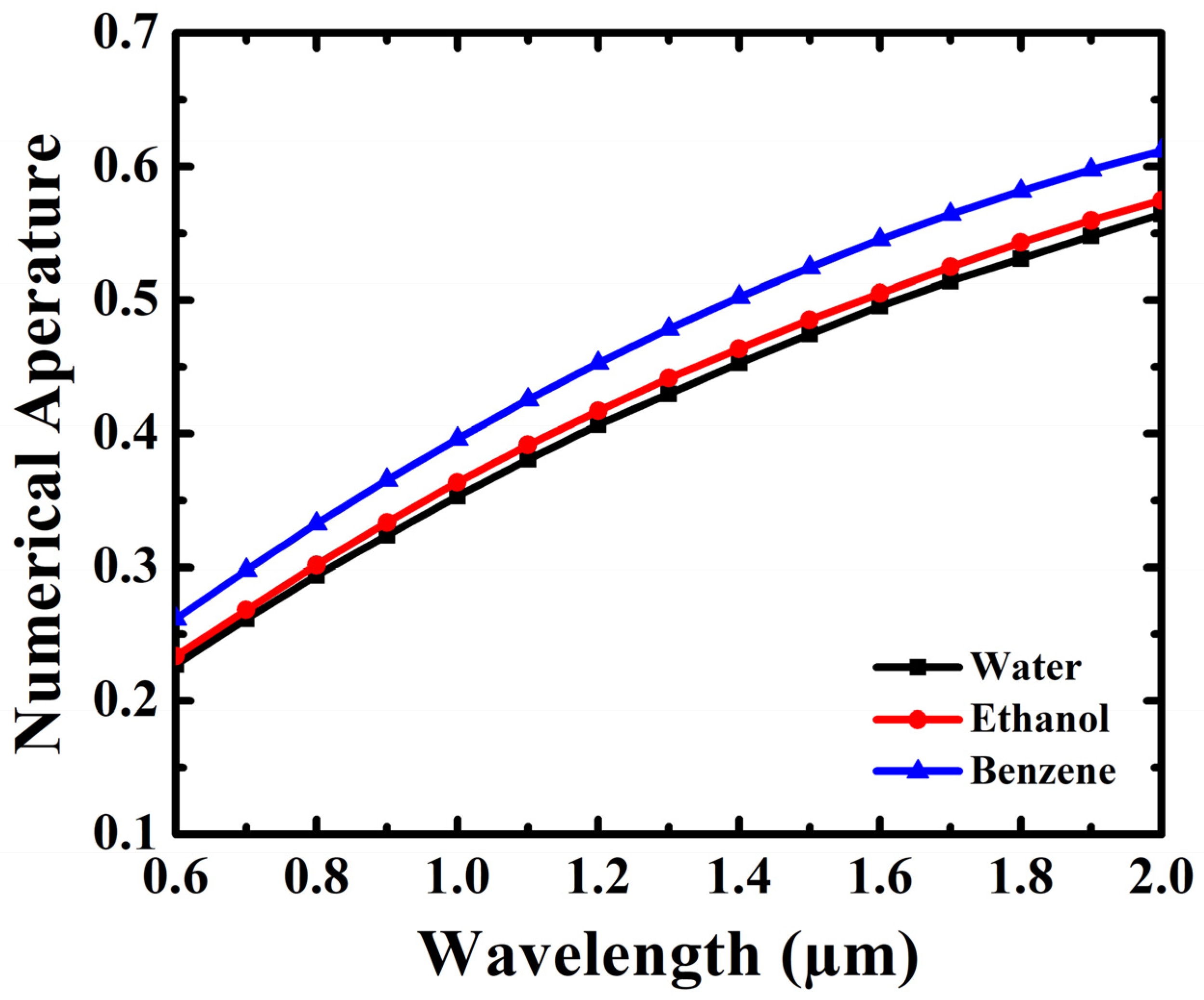
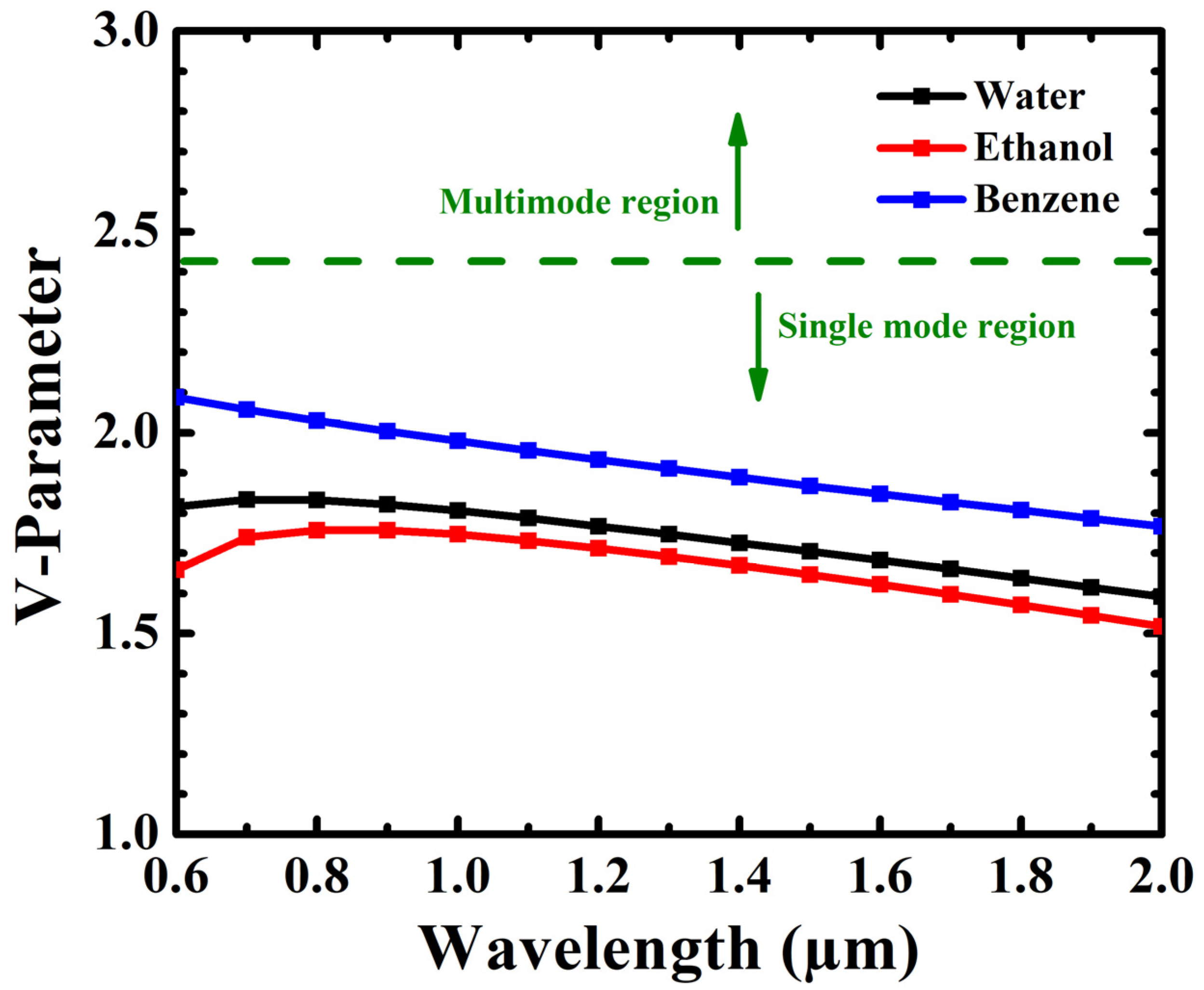
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Atkin, D.M. All-silica single-mode optical fiber with photonic crystal cladding: Errata. Opt. Lett. 1997, 22, 484. [Google Scholar] [CrossRef]
- Cordeiro, C.M.B.; Franco, M.A.R.; Chesini, G.; Barretto, E.C.S.; Lwin, R.; Brito Cruz, C.H.; Large, M.C.J. Microstructured-core optical fibre for evanescent sensing applications. Opt. Express 2006, 14, 13056. [Google Scholar] [CrossRef] [PubMed]
- Leon, M.J.B.M.; Kabir, M.A. Design of a liquid sensing photonic crystal fiber with high sensitivity, bireferingence & low confinement loss. Sens. Bio-Sens. Res. 2020, 28, 100335. [Google Scholar] [CrossRef]
- Buczynski, R. Photonic crystal fibers. Acta Phys. Pol. A 2004, 106, 141–167. [Google Scholar] [CrossRef]
- Lucki, M. Photonic Crystal Fibers with Optimized Dispersion for Telecommunication Systems. Recent Prog. Opt. Fiber Res. 2012. [Google Scholar] [CrossRef]
- Kumar, S.; Bisht, A.; Bisht, A.; Singh, G.; Amphawan, A. Design of photonics crystal fiber sensors for bio-medical applications. Opt. Meas. Syst. Ind. Insp. IX 2015, 9525, 95252B. [Google Scholar] [CrossRef]
- Pinto, A.M.R.; Lopez-Amo, M. Photonic crystal fibers for sensing applications. J. Sens. 2012, 2012. [Google Scholar] [CrossRef]
- Sharma, M.; Mishra, S.K.; Ung, B. Ultra-sensitive and large dynamic range refractive index sensor utilizing annular core photonic crystal fiber. SPIE 2019, 5, 1112305. [Google Scholar] [CrossRef]
- Paul, A.K. Design and analysis of photonic crystal fiber plasmonic refractive Index sensor for condition monitoring of transformer oil. OSA Contin. 2020, 3, 2253. [Google Scholar] [CrossRef]
- Maidi, A.M.; Yakasai, I.; Abas, P.E.; Nauman, M.M.; Apong, R.A.; Kaijage, S.; Begum, F. Design and Simulation of Photonic Crystal Fiber for Liquid Sensing. Photonics 2021, 8, 16. [Google Scholar] [CrossRef]
- Ahmed, K.; Morshed, M. Design and numerical analysis of microstructured-core octagonal photonic crystal fiber for sensing applications. Sens. Bio-Sens. Res. 2016, 7, 1–6. [Google Scholar] [CrossRef]
- Asaduzzaman, S.; Ahmed, K.; Bhuiyan, T.; Farah, T. Hybrid photonic crystal fiber in chemical sensing. Springerplus 2016, 5. [Google Scholar] [CrossRef]
- Islam, M.S.; Paul, B.K.; Ahmed, K.; Asaduzzaman, S.; Islam, M.I.; Chowdhury, S.; Sen, S.; Bahar, A.N. Liquid-infiltrated photonic crystal fiber for sensing purpose: Design and analysis. Alex. Eng. J. 2018, 57, 1459–1466. [Google Scholar] [CrossRef]
- Ahmed, K.; Morshed, M.; Asaduzzaman, S.; Arif, M.F.H. Optimization and enhancement of liquid analyte sensing performance based on square-cored octagonal photonic crystal fiber. Optik 2017, 131, 687–696. [Google Scholar] [CrossRef]
- Sen, S.; Chowdhury, S.; Ahmed, K.; Asaduzzaman, S. Design of a porous cored hexagonal photonic crystal fiber based optical sensor with high relative sensitivity for lower operating wavelength. Photonic Sens. 2017, 7, 55–65. [Google Scholar] [CrossRef]
- Eid, M.M.A.; Habib, M.A.; Anower, M.S.; Rashed, A.N.Z. Highly sensitive nonlinear photonic crystal fiber based sensor for chemical sensing applications. Microsyst. Technol. 2020. [Google Scholar] [CrossRef]
- Arif, M.F.H.; Asaduzzaman, S.; Ahmed, K.; Morshed, M. High sensitive PCF based chemical sensor for ethanol detection. In Proceedings of the 5th International Conference on Informatics, Electronics & Vision (ICIEV), Dhaka, Bangladesh, 13–14 May 2016; pp. 6–9. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 1965, 55, 1205. [Google Scholar] [CrossRef]
- Hale, G.M.; Querry, M.R. Bladder cancers respond to EGFR inhibitors. Cancer Discov. 2014, 4, 980–981. [Google Scholar] [CrossRef][Green Version]
- Moutzouris, K.; Papamichael, M.; Betsis, S.C.; Stavrakas, I.; Hloupis, G.; Triantis, D. Refractive, dispersive and thermo-optic properties of twelve organic solvents in the visible and near-infrared. Appl. Phys. B Lasers Opt. 2014, 116, 617–622. [Google Scholar] [CrossRef]
- Akowuah, E.K.; Gorman, T.; Ademgil, H.; Haxha, S.; Robinson, G.K.; Oliver, J.V. Numerical analysis of a photonic crystal fiber for biosensing applications. IEEE J. Quantum Electron. 2012, 48, 1403–1410. [Google Scholar] [CrossRef]
- Yakasai, I.K.; Abas, P.E.; Ali, S.; Begum, F. Modelling and simulation of a porous core photonic crystal fibre for terahertz wave propagation. Opt. Quantum Electron. 2019, 51. [Google Scholar] [CrossRef]
- Yakasai, I.; Abas, P.E.; Kaijage, S.F.; Caesarendra, W.; Begum, F. Proposal for a quad-elliptical photonic crystal fiber for terahertz wave guidance and sensing chemical warfare liquids. Photonics 2019, 6, 78. [Google Scholar] [CrossRef]
- Begum, F.; Namihira, Y.; Kinjo, T.; Kaijage, S. Supercontinuum generation in photonic crystal fibres at 1.06, 1.31, and 1.55 m wavelengths. Electron. Lett. 2010, 46, 1518–1520. [Google Scholar] [CrossRef]
- Begum, F.; Abas, P.E. Near infrared supercontinuum generation in silica based photonic crystal fiber. Prog. Electromagn. Res. C 2019, 89, 149–159. [Google Scholar] [CrossRef]
- Arif, M.F.H.; Hossain, M.M.; Islam, N.; Khaled, S.M. A nonlinear photonic crystal fiber for liquid sensing application with high birefringence and low confinement loss. Sens. Bio-Sens. Res. 2019, 22, 100252. [Google Scholar] [CrossRef]
- Begum, F.; Namihira, Y.; Razzak, S.M.A.; Kaijage, S.F.; Hai, N.H.; Miyagi, K.; Higa, H.; Zou, N. Flattened chromatic dispersion in square photonic crystal fibers with low confinement losses. Opt. Rev. 2009, 16, 54–58. [Google Scholar] [CrossRef]
- Hossain, M.; Podder, E.; Adhikary, A.; Al-Mamun, A. Optimized Hexagonal Photonic Crystal Fibre Sensor for Glucose Sensing. Adv. Res. 2018, 13, 1–7. [Google Scholar] [CrossRef]
- Islam, M.S.; Sultana, J.; Ahmed, K.; Islam, M.R.; Dinovitser, A.; Ng, B.W.-H.; Abbott, D. A Novel Approach for Spectroscopic Chemical Identification Using Photonic Crystal Fiber in the Terahertz Regime. IEEE Sens. J. 2018, 18, 575–582. [Google Scholar] [CrossRef]
- Chowdhury, S.; Sen, S.; Ahmed, K.; Asaduzzaman, S. Design of highly sensible porous shaped photonic crystal fiber with strong confinement field for optical sensing. Optik 2017, 142, 541–549. [Google Scholar] [CrossRef]
- Habib, A.; Anower, S.; Haque, I. Highly sensitive hollow core spiral fiber for chemical spectroscopic applications. Sens. Int. 2020, 1, 100011. [Google Scholar] [CrossRef]
- Rana, S.; Saiful Islam, M.; Faisal, M.; Roy, K.C.; Islam, R.; Kaijage, S.F. Single-mode porous fiber for low-loss polarization maintaining terahertz transmission. Opt. Eng. 2016, 55, 076114. [Google Scholar] [CrossRef]
- Yu, C.-P.; Liou, J. Selectively liquid-filled photonic crystal fibers for optical devices. Opt. Express 2009, 17, 8729. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Xu, Y.; Yariv, A. Fabrication of functional microstructured optical fibers through a selective-filling technique. Appl. Phys. Lett. 2004, 85, 5182–5184. [Google Scholar] [CrossRef]
- Xiao, L.; Jin, W.; Demokan, M.S.; Ho, H.L.; Hoo, Y.L.; Zhao, C. Fabrication of selective injection microstructured optical fibers with a conventional fusion splicer. Opt. Express 2005, 13, 9014. [Google Scholar] [CrossRef] [PubMed]
- Cordeiro, C.M.B.; dos Santos, E.M.; Brito Cruz, C.H.; de Matos, C.J.; Ferreiira, D.S. Lateral access to the holes of photonic crystal fibers—Selective filling and sensing applications. Opt. Express 2006, 14, 8403. [Google Scholar] [CrossRef] [PubMed]




| Change in Global Parameters | Relative Sensitivity (%) | Confinement Loss (dB/m) | ||||
|---|---|---|---|---|---|---|
| Water | Ethanol | Benzene | Water | Ethanol | Benzene | |
| +2% | 94.29 | 95.86 | 99.59 | 1.73 × 10−11 | 1.41 × 10−12 | 5.82 × 10−16 |
| +1% | 94.27 | 95.84 | 99.58 | 1.61 × 10−11 | 1.35 × 10−12 | 5.95 × 10−16 |
| Optimum | 94.26 | 95.82 | 99.58 | 1.52 × 10−11 | 1.21 × 10−12 | 6.01 × 10−16 |
| −1% | 94.23 | 95.80 | 99.57 | 1.41 × 10−11 | 1.11 × 10−12 | 6.39 × 10−16 |
| −2% | 94.21 | 95.77 | 99.57 | 1.32 × 10−11 | 1.04 × 10−12 | 6.51 × 10−16 |
| No. of Rings | Structure | Relative Sensitivity (%) | Confinement Loss (dB/m) | Dispersion (ps/nm·km) | Nonlinear Coefficient (W−1km−1) | Numerical Aperture | ||
|---|---|---|---|---|---|---|---|---|
| Core | Cladding | |||||||
| Ref. [10] | 3 | 3 core holes | Circular holes in hexagonal | 59.9 (W) 62.7 (E) 78.8 (B) | ~10−7 (W) ~10−8 (E) ~10−11 (B) | −0.0104 (W) −0.0101 (E) −0.0115 (B) | 99 (W) 109 (E) 138 (B) | - |
| Ref. [11] | 5 | 9 core holes | Circular holes in hexagonal | 43.3(W) 44.31 (E) 47.2 (B) | ~10−13 (W) ~10−14 (E) ~10−15 (B) | - | - | - |
| Ref. [12] | 3 | 16 core holes | Circular holes in circle | 46.3 (W) 46.5 (E) 46.9 (B) | ~10−9 (W) ~10−9 (E) ~10−10 (B) | - | - | - |
| Ref. [13] | 3 | 7 core holes | Circular holes in hexagonal | 47.5(W) 51.6 (E) 54.2 (B) | - | - | 56.1 (W) 56.2 (E) 56.5 (B) | - |
| Ref. [14] | 5 | 9 core holes | Circular holes in octagonal | 44.2 (W) 47.3(E) 52.5 (B) | ~10−13 (W) ~10−13 (E) ~10−13 (B) | - | 4.2 (W) 4.4 (E) 4.9 (B) | - |
| Ref. [15] | 5 | Porous core | Circular holes in hexagonal | 57.3 (W) 57.7 (E) 57.9 (B) | ~10−8 (W) ~10−9 (E) ~10−9 (B) | - | 9.80(W) 10.4(E) 11.9(B) | - |
| Ref. [16] | 5 | 1 core hole | Circular holes in circle | 91.2 (W) 94.0 (E) 97.5 (B) | ~10−11 (W) ~10−13 (E) ~10−10 (B) | - | 53.1 (W) 52.5 (E) 58.9 (B) | 0.284 (W) 0.291 (E) 0.312 (B) |
| Proposed PCF | 3 | 1 core hole | Circular holes in hexagonal | 94.26 (W) 95.82(E) 99.58 (B) | ~10−11 (W) ~10−12 (E) ~10−16 (B) | −0.0086 (W) −0.00832 (E) −0.0099 (B) | 84.55 (W) 90.26 (E) 110.39 (B) | 0.3534 (W) 0.3636 (E) 0.3963 (B) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maidi, A.M.; Abas, P.E.; Petra, P.I.; Kaijage, S.; Zou, N.; Begum, F. Theoretical Considerations of Photonic Crystal Fiber with All Uniform-Sized Air Holes for Liquid Sensing. Photonics 2021, 8, 249. https://doi.org/10.3390/photonics8070249
Maidi AM, Abas PE, Petra PI, Kaijage S, Zou N, Begum F. Theoretical Considerations of Photonic Crystal Fiber with All Uniform-Sized Air Holes for Liquid Sensing. Photonics. 2021; 8(7):249. https://doi.org/10.3390/photonics8070249
Chicago/Turabian StyleMaidi, Abdul Mu’iz, Pg Emeroylarffion Abas, Pg Iskandar Petra, Shubi Kaijage, Nianyu Zou, and Feroza Begum. 2021. "Theoretical Considerations of Photonic Crystal Fiber with All Uniform-Sized Air Holes for Liquid Sensing" Photonics 8, no. 7: 249. https://doi.org/10.3390/photonics8070249
APA StyleMaidi, A. M., Abas, P. E., Petra, P. I., Kaijage, S., Zou, N., & Begum, F. (2021). Theoretical Considerations of Photonic Crystal Fiber with All Uniform-Sized Air Holes for Liquid Sensing. Photonics, 8(7), 249. https://doi.org/10.3390/photonics8070249







