Comparison of THz-QCL Designs Supporting Clean N-Level Systems
Abstract
:1. Introduction
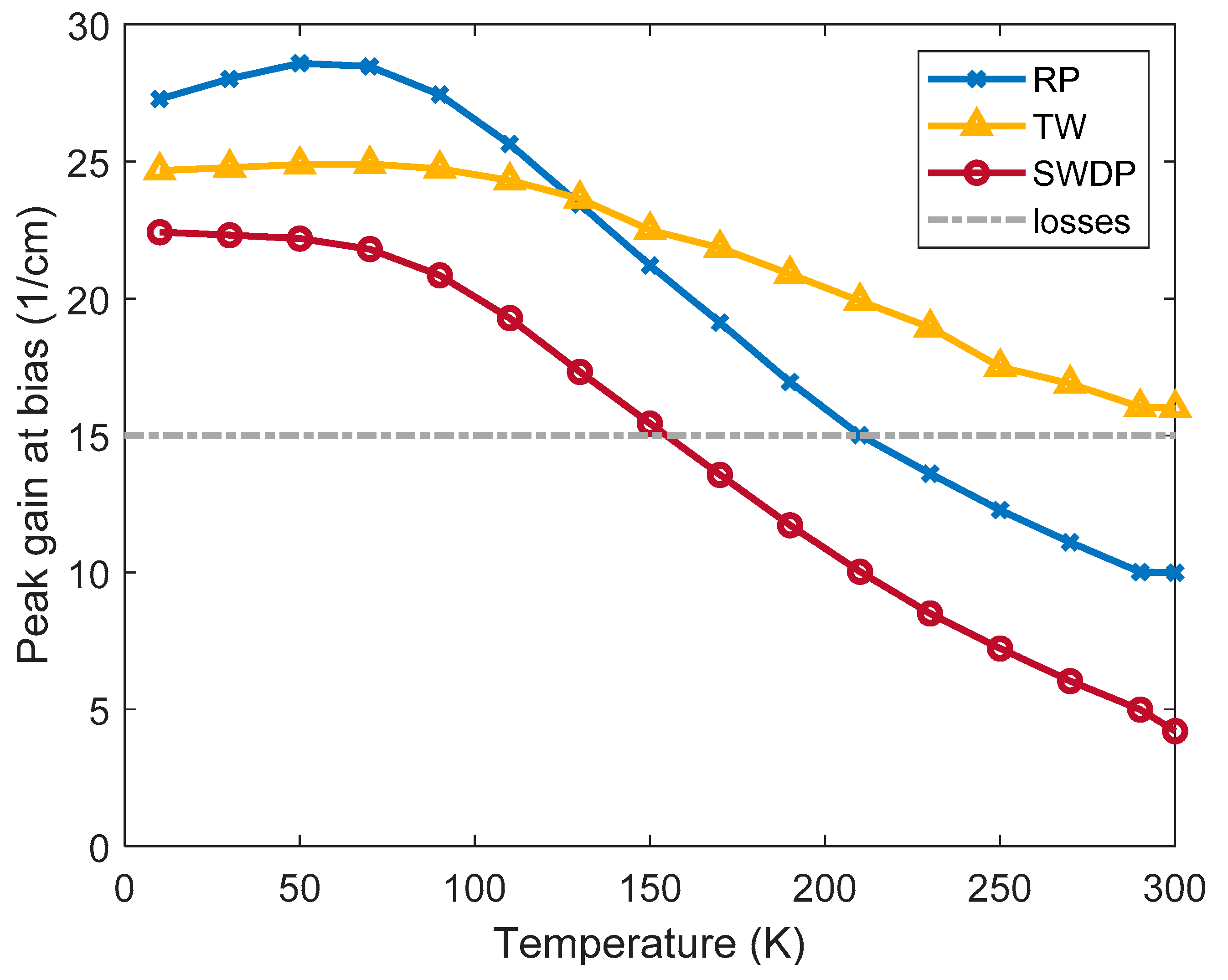
2. Results
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kohler, R.; Tredicucci, A.; Beltram, F.; Beere, H.E.; Linfield, E.H.; Davies, A.G.; Ritchie, D.A.; Iotti, R.C.; Rossi, F. Terahertz semiconductor-heterostructure laser. Nature 2002, 417, 156–159. [Google Scholar] [CrossRef]
- Darmo, J.; Tamosiunas, V.; Fasching, G.; Kroll, J.; Unterrainer, K.; Beck, M.; Giovannini, M.; Faist, J.; Kremser, C.; Debbage, P. Imaging with a Terahertz quantum cascade laser. Opt. Express 2004, 12, 1879–1884. [Google Scholar] [CrossRef]
- Hubers, H.-W.; Pavlov, S.G.; Richter, H.; Semenov, A.D.; Mahler, L.; Tredicucci, A.; Beere, H.E.; Ritchie, D.A. High-resolution gas phase spectroscopy with a distributed feedback terahertz quantum cascade laser. Appl. Phys. Lett. 2006, 89, 061115. [Google Scholar] [CrossRef]
- Williams, B.S. Terahertz quantum-cascade lasers. Nat. Photonics 2007, 1, 517–525. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.; Wanke, M.C. Searching for a solid-state terahertz technology. Science 2007, 316, 64–65. [Google Scholar] [CrossRef] [PubMed]
- Kidd Walker, C.; Kulesa, C.; Goldsmith, P.; Groppi, C.; Helmich, F.; Hollenbach, D.; Kawamura, J.; Langer, W.; Melnick, G.; Neufeld, D.; et al. GUSTO: Gal/Xgal U/LDB Spectroscopic-Stratospheric Terahertz Observatory; American Astronomical Society: Washington, DC, USA, 2018. [Google Scholar]
- Mittleman, D.M. Twenty years of terahertz imaging. Opt. Express 2018, 26, 9417–9431. [Google Scholar] [CrossRef] [PubMed]
- Rahman, A.; Rahman, A.K.; Rao, B. Early detection of skin cancer via terahertz spectral profiling and 3D imaging. Biosens. Bioelectron. 2016, 82, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Federici, J.F.; Schulkin, B.; Huang, F.; Gary, D.; Barat, R.B.; Oliveira, F.; Zimdars, D.A. THz imaging and sensing for security applications—Explosives, weapons and drugs. Sci. Technol. 2005, 20, 266–280. [Google Scholar] [CrossRef]
- Korter, T.; Plusquellic, D.F. Continuous-wave terahertz spectroscopy of biotin: Vibrational anharmonicity in the far-infrared. Chem. Phys. Lett. 2004, 385, 45–51. [Google Scholar] [CrossRef]
- Ogawa, Y.; Hayashi, S.; Oikawa, M.; Otani, C.; Kawase, K. Interference terahertz label-free imaging for protein detection on a membrane. Opt. Express 2008, 16, 22083–22089. [Google Scholar] [CrossRef]
- Bosco, L.; Franckie, M.; Scalari, G.; Beck, M.; Wacker, A.; Faist, J. Thermoelectrically cooled THz quantum cascade laser operating up to 210 K. Appl. Phys. Lett. 2019, 115, 010601. [Google Scholar] [CrossRef]
- Khalatpour, A.; Paulsen, A.K.; Deimert, C.; Wasilewski, Z.R.; Hu, Q. High-power portable terahertz laser systems. Nat. Photonics 2020, 15, 16–20. [Google Scholar] [CrossRef]
- Franckié, M.; Bosco, L.; Beck, M.; Bonzon, C.; Mavrona, E.; Scalari, G.; Wacker, A.; Faist, J. Two-well quantum cascade laser optimization by non-equilibrium Green’s function modelling. Appl. Phys. Lett. 2018, 112, 021104. [Google Scholar] [CrossRef] [Green Version]
- Albo, A.; Flores, Y.V.; Hu, Q.; Reno, J.L. Two-well terahertz quantum cascade lasers with suppressed carrier leakage. Appl. Phys. Lett. 2017, 111, 111107. [Google Scholar] [CrossRef]
- Albo, A.; Hu, Q. Investigating temperature degradation in THz quantum cascade lasers by examination of temperature dependence of output power. Appl. Phys. Lett. 2015, 106, 131108. [Google Scholar] [CrossRef]
- Albo, A.; Hu, Q. Carrier leakage into the continuum in diagonal GaAs/Al0.15GaAs terahertz quantum cascade lasers. Appl. Phys. Lett. 2015, 107, 241101. [Google Scholar] [CrossRef]
- Kumar, S.; Hu, Q.; Reno, J.L. 186 K operation of terahertz quantum-cascade lasers based on a diagonal design. Appl. Phys. Lett. 2009, 94, 131105. [Google Scholar] [CrossRef]
- Albo, A.; Hu, Q.; Reno, J.L. Room temperature negative differential resistance in terahertz quantum cascade laser structures. Appl. Phys. Lett. 2016, 109, 081102. [Google Scholar] [CrossRef]
- Albo, A.; Flores, Y.V.; Hu, Q.; Reno, J.L. Split-well direct-phonon terahertz quantum cascade lasers. Appl. Phys. Lett. 2019, 114, 191102. [Google Scholar] [CrossRef] [Green Version]
- Lander Gower, N.; Piperno, S.; Albo, A. The significance of carrier leakage for stable lasing in split-well direct phonon terahertz quantum cascade lasers. Photonics 2020, 7, 59. [Google Scholar] [CrossRef]
- Lander Gower, N.; Piperno, S.; Albo, A. Self-consistent gain calculations and carrier transport analysis for split-well direct-phonon terahertz quantum cascade lasers. AIP Adv. 2020, 10, 115319. [Google Scholar] [CrossRef]
- Grange, T. Electron transport in quantum wire superlattices. Phys. Rev. B 2014, 89, 165310. [Google Scholar] [CrossRef] [Green Version]
- Grange, T. Nanowire terahertz quantum cascade lasers. Appl. Phys. Lett. 2014, 105, 141105. [Google Scholar] [CrossRef] [Green Version]
- Grange, T. Contrasting influence of charged impurities on transport and gain in terahertz quantum cascade lasers. Phys. Rev. B 2015, 92, 241306(R). [Google Scholar] [CrossRef] [Green Version]
- Majer, N.; Lüdge, K.; Schöll, E. Cascading enables ultrafast gain recovery dynamics of quantum dot semiconductor optical amplifiers. Phys. Rev. B 2010, 82, 235301. [Google Scholar] [CrossRef]
- Wacker, A.; Lindskog, M.; Winge, D.O. Nonequilibrium Green’s function formulation of intersubband absorption for nonparabolic single-band effective mass Hamiltonian. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1200611. [Google Scholar] [CrossRef]
- Wang, K.; Grange, T.; Lin, T.-T.; Wang, L.; Jéhn, Z.; Birner, S.; Yun, J.; Terashima, W.; Hirayama, H. Broadening mechanisms and self-consistent gain calculations for GaN quantum cascade laser structures. Appl. Phys. Lett. 2018, 113, 061109. [Google Scholar] [CrossRef]
- Yasuda, H.; Kubis, T.; Hosako, I.; Hirakawa, K. Non-equilibrium Green’s function calculation for GaN-based terahertz-quantum cascade laser structures. J. Appl. Phys. 2012, 111, 083105. [Google Scholar] [CrossRef]
- Lee, S.-C.; Wacker, A. Nonequilibrium Green’s function theory for transport and gain properties of quantum cascade structures. Phys. Rev. B 2012, 66, 245314. [Google Scholar] [CrossRef] [Green Version]
- Wacker, A. Gain in quantum cascade lasers and superlattices: A quantum transport theory. Phys. Rev. B 2002, 66, 085326. [Google Scholar] [CrossRef] [Green Version]
- Kubis, T.; Yeh, C.; Vogl, P.; Benz, A.; Fasching, G.; Deutsch, C. Theory of nonequilibrium quantum transport and energy dissipation in terahertz quantum cascade lasers. Phys. Rev. B 2009, 79, 195323. [Google Scholar] [CrossRef] [Green Version]
- Schmielau, T.; Pereira, M.F., Jr. Nonequilibrium many body theory for quantum transport in terahertz quantum cascade lasers. Appl. Phys. Lett. 2009, 95, 231111. [Google Scholar] [CrossRef]
- Yasuda, H.; Kubis, T.; Vogl, P.; Sekine, N.; Hosako, I.; Hirakawa, K. A phonon scattering assisted injection and extraction based terahertz quantum cascade laser. Appl. Phys. Lett. 2009, 94, 151109. [Google Scholar] [CrossRef]
- Kostadinova, E.G.; Padgett, J.L.; Liaw, C.D.; Matthews, L.S.; Hyde, T.W. Numerical study of anomalous diffusion of light in semicrystalline polymer structures. Phys. Rev. Res. 2020, 2, 043375. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. A self-consistent quantum field theory for random lasing. Appl. Sci. 2019, 9, 2477. [Google Scholar] [CrossRef] [Green Version]
- Lubatsch, A.; Frank, R. Evolution of Floquet topological quantum states in driven semiconductors. Eur. Phys. J. B 2019, 92, 215. [Google Scholar] [CrossRef] [Green Version]
- Morozov, V.; Ignatyuk, V. Energy conservation and the correlation quasi-temperature in open quantum dynamics. Particles 2018, 1, 285–295. [Google Scholar] [CrossRef] [Green Version]
- Banit, F.; Lee, S.-C.; Knorr, A.; Wacker, A. Self-consistent theory of the gain linewidth for quantum-cascade lasers. Appl. Phys. Lett. 2005, 86, 041108. [Google Scholar] [CrossRef] [Green Version]
- Boyle, C.; Oresick, K.M.; Kirch, J.D.; Flores, Y.V.; Mawst, L.J.; Botez, D. Carrier leakage via interface-roughness scattering bridges gap between theoretical and experimental internal efficiencies of quantum cascade lasers. Appl. Phys. Lett. 2020, 117, 051101. [Google Scholar] [CrossRef]
- Almqvist, T.; Winge, D.O.; Dupont, E.; Wacker, A. Domain formation and self-sustained oscillations in quantum cascade lasers. Eur. Phys. J. B 2019, 92, 72. [Google Scholar] [CrossRef]
- Flores, Y.V.; Albo, A. Impact of interface roughness scattering on the performance of GaAs/AlxGa1–x as terahertz quantum cascade lasers. IEEE J. Quantum Electron. 2017, 53, 1–8. [Google Scholar] [CrossRef]
- Grange, T.; Mukherjee, S.; Capellini, G.; Montanari, M.; Persichetti, L.; Di Gaspare, L.; Birner, S.; Attiaoui, A.; Moutanabbir, O.; Virgilio, M.; et al. Atomic-scale insights into semiconductor heterostructures: From experimental three-dimensional analysis of the interface to a generalized theory of interfacial roughness scattering. Phys. Rev. Appl. 2020, 13, 044062. [Google Scholar] [CrossRef]
- Witzigmann, B.; Römer, F.; Martens, M.; Kuhn, C.; Wernicke, T.; Kneissl, M. Calculation of optical gain in AlGaN quantum wells for ultraviolet emission. AIP Adv. 2020, 10, 095307. [Google Scholar] [CrossRef]
- Shin, J.C.; D’Souza, M.; Liu, Z.; Kirch, J.; Mawst, L.J.; Botez, D.; Vurgaftman, I.; Meyer, J.R. Highly temperature insensitive, deep-well 4.8 μm emitting quantum cascade semiconductor lasers. Appl. Phys. Lett. 2009, 94, 201103. [Google Scholar] [CrossRef]
- Chan, C.W.I.; Albo, A.; Hu, Q.; Reno, J.L. Tradeoffs between oscillator strength and lifetime in terahertz quantum cascade lasers. Appl. Phys. Lett. 2016, 109, 201104. [Google Scholar] [CrossRef]
- Lander Gower, N.; Piperno, S.; Albo, A. The effect of doping in split-well direct phonon terahertz quantum cascade laser structures. Photonics 2021, 8, 195. [Google Scholar] [CrossRef]
- Chen, H.; Gao, S.; Zhang, M.; Zhang, J.; Qiao, L.; Wang, T.; Gao, F.; Hu, X.; Li, S.; Zhu, Y. Advances in random fiber lasers and their sensing application. Sensors 2020, 20, 6122. [Google Scholar] [CrossRef]
- Meinzer, N.; König, M.; Ruther, M.; Linden, S.; Khitrova, G.; Gibbs, H.M.; Busch, K.; Wegener, M. Distance-dependence of the coupling between split-ring resonators and single-quantum-well gain. Appl. Phys. Lett. 2011, 99, 111104. [Google Scholar] [CrossRef]
- Kazarinov, R.F.; Suris, R.A. Possible amplification of electromagnetic waves in a semiconductor with a superlattice. Sov. Phys. Semicond. 1971, 5, 707. [Google Scholar]
- Bhattacharya, I.; Chan, C.W.I.; Hu, Q. Effects of stimulated emission on transport in terahertz quantum cascade lasers based on diagonal designs. Appl. Phys. Lett. 2012, 100, 011108. [Google Scholar] [CrossRef]
- Sirtori, C.; Capasso, F.; Faist, J.; Hutchinson, A.L.; Sivco, D.L.; Cho, A.Y. Resonant tunneling in quantum cascade lasers. IEEE J. Quantum Electron. 1998, 34, 1722. [Google Scholar] [CrossRef]





| Design | Wafer Number | E21 [meV] | Lasing Energy (meV) | Oscillator Strength | Layer Sequence [#ML *] Barrier Composition and Doping Level |
|---|---|---|---|---|---|
| RP | VB0676 | 25 | 25 | 0.2 | 10.3/37.2/6.4/38.6/8.2/65.9 213 periods GaAs/Al0.3Ga0.7As 1.24 × 1017 cm−3 in the center 17 ML of the 65.9 ML well. (6.0 × 1010 cm−2) |
| TW | VB0747 | 56 | 13 | 0.18 | 13.5/25.5/11.0/50.2 354 periods GaAs/Al0.3Ga0.7As 1.26 × 1017 cm−3 in the centered 17 ML of the 50.2 ML well (6.0 × 1010 cm−2) |
| SWDP | VB0837 | 26 | 11 | 0.26 | 9.0/24.8/3.5/24.8/17.3/24.8 353 periods total thickness 10 μm GaAs/mixed barriers Al0.55Ga0.45As (Inj.) and Al0.15Ga0.85As (Rad., Intraw.) 2.13 × 1016 cm−3 in the 24.8 ML wells (2.98 × 1010 cm−2) |
| Design | Peak Gain at 10 K (1/cm) | Photon Energy at Peak Gain (meV) | Full Width at Half Maximum (meV) |
|---|---|---|---|
| RP | 27.28 | 25 | 6.64 |
| TW | 24.67 | 14 | 6.43 |
| SWDP | 22.42 | 11 | 6.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lander Gower, N.; Piperno, S.; Albo, A. Comparison of THz-QCL Designs Supporting Clean N-Level Systems. Photonics 2021, 8, 248. https://doi.org/10.3390/photonics8070248
Lander Gower N, Piperno S, Albo A. Comparison of THz-QCL Designs Supporting Clean N-Level Systems. Photonics. 2021; 8(7):248. https://doi.org/10.3390/photonics8070248
Chicago/Turabian StyleLander Gower, Nathalie, Silvia Piperno, and Asaf Albo. 2021. "Comparison of THz-QCL Designs Supporting Clean N-Level Systems" Photonics 8, no. 7: 248. https://doi.org/10.3390/photonics8070248
APA StyleLander Gower, N., Piperno, S., & Albo, A. (2021). Comparison of THz-QCL Designs Supporting Clean N-Level Systems. Photonics, 8(7), 248. https://doi.org/10.3390/photonics8070248





