Plasmonic Narrowband Filter Based on an Equilateral Triangular Resonator with a Silver Bar
Abstract
1. Introduction
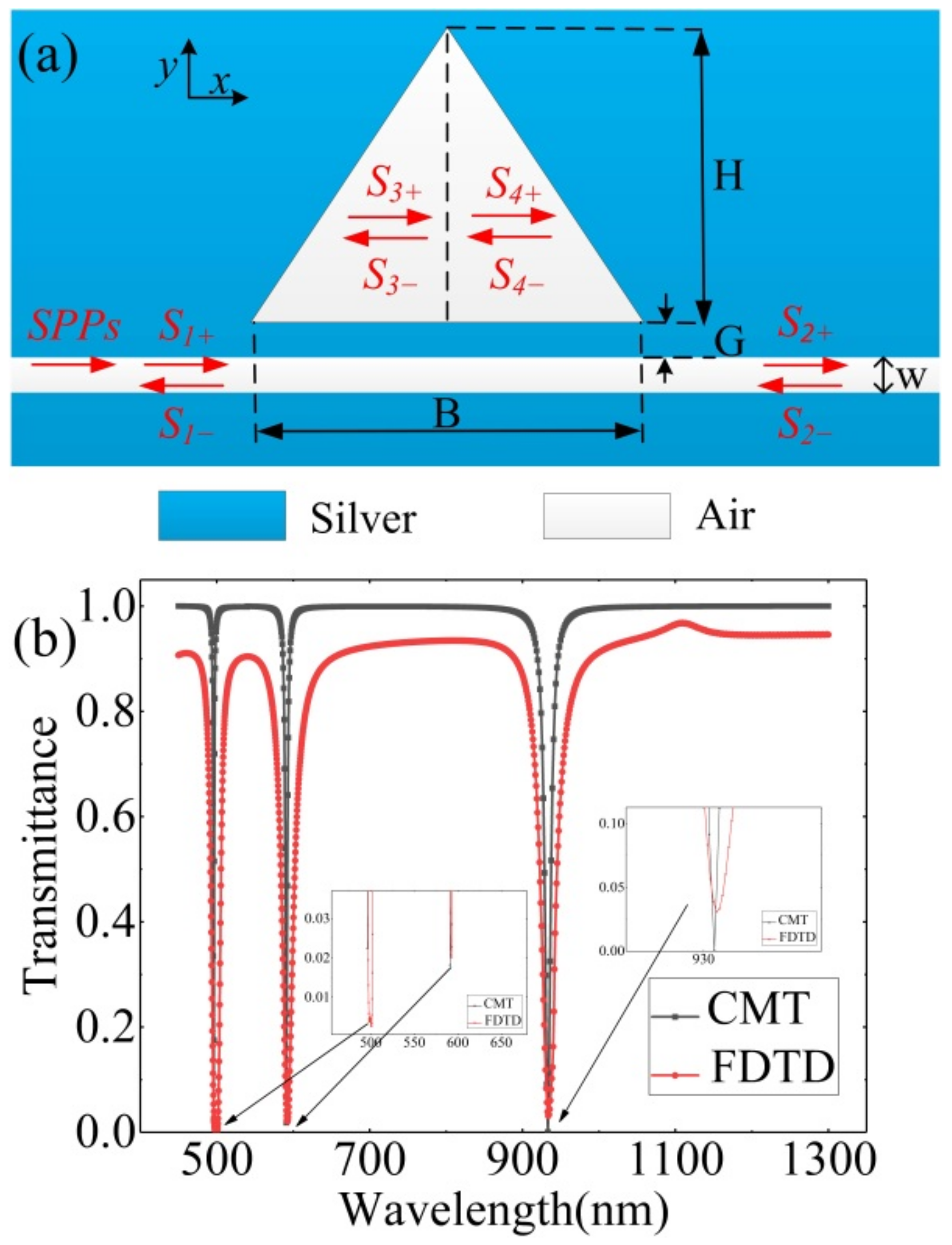
2. Materials and Methods
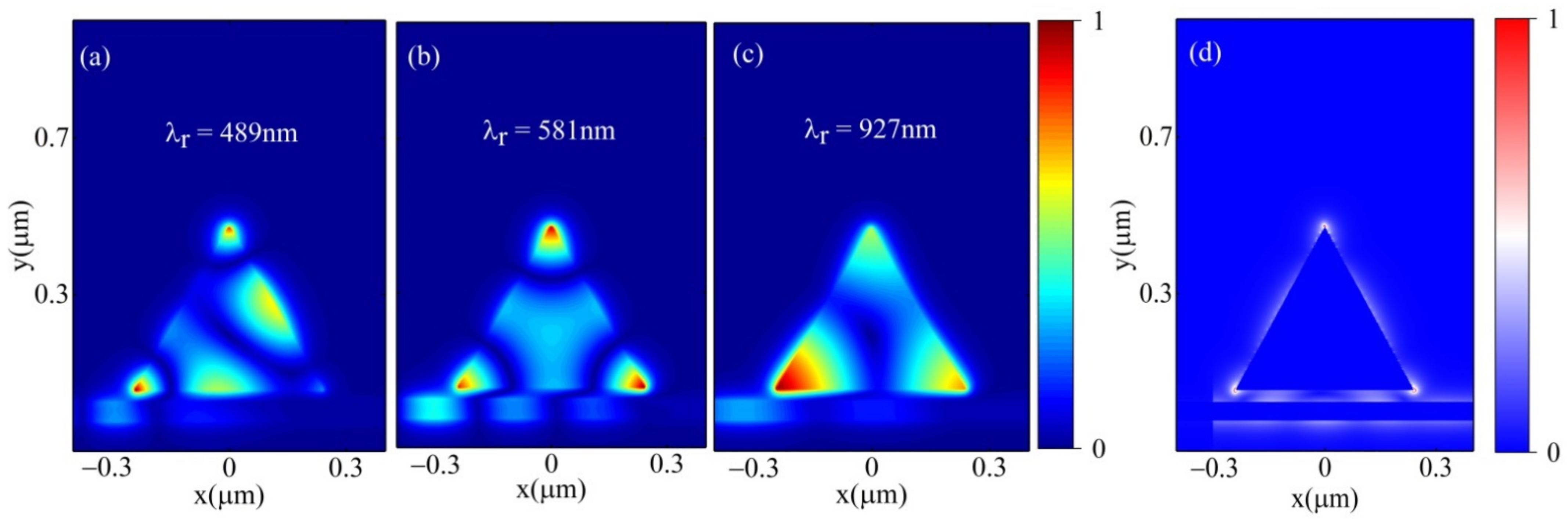
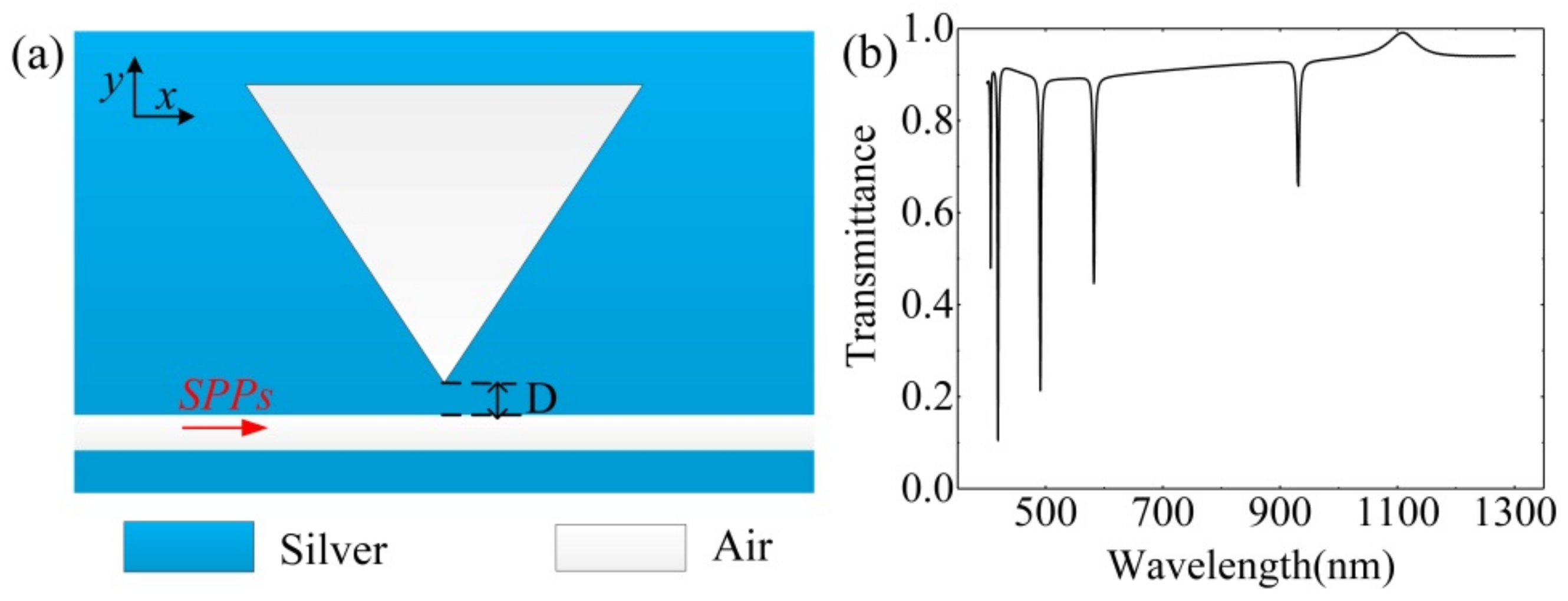
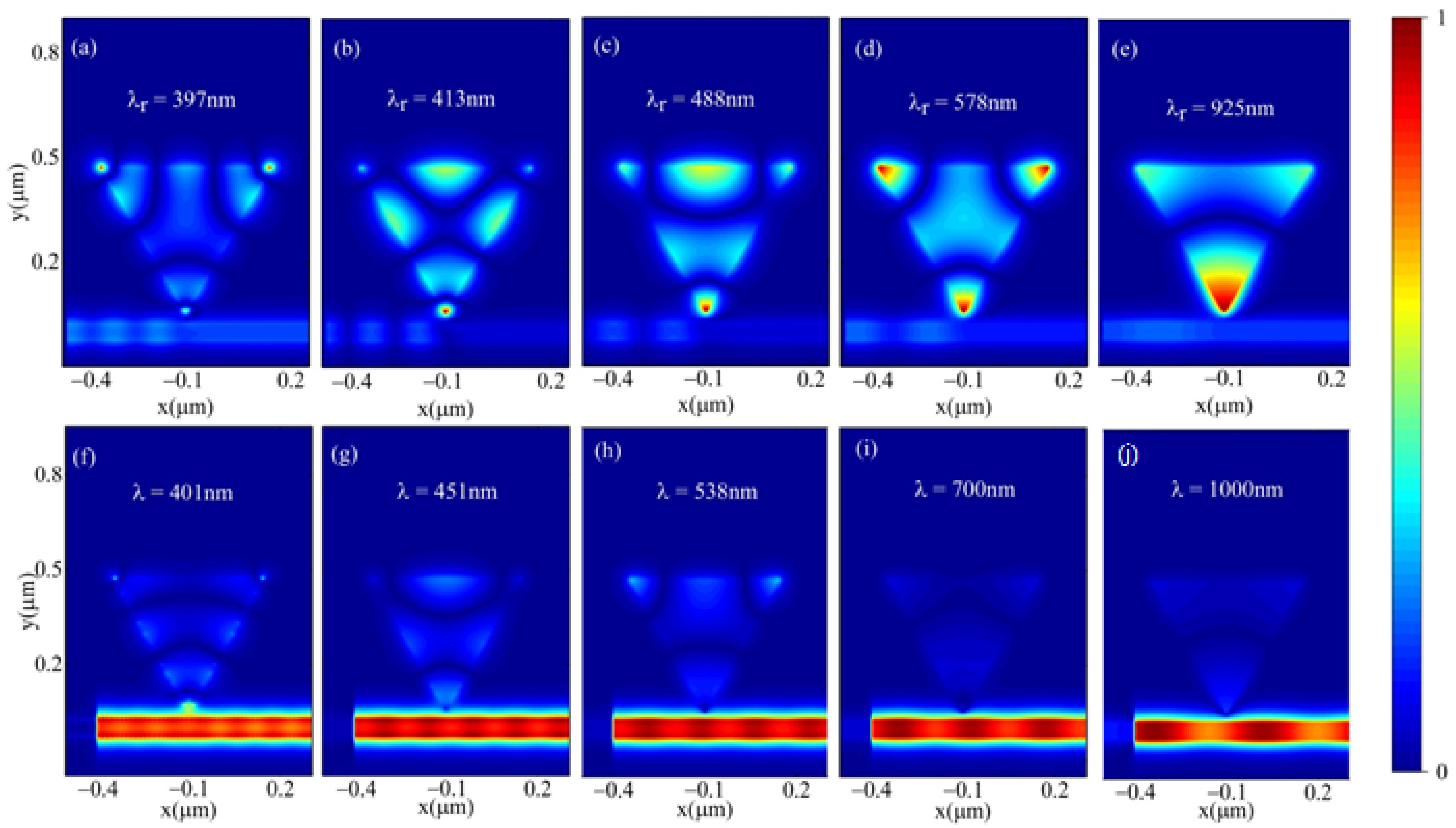
3. Results
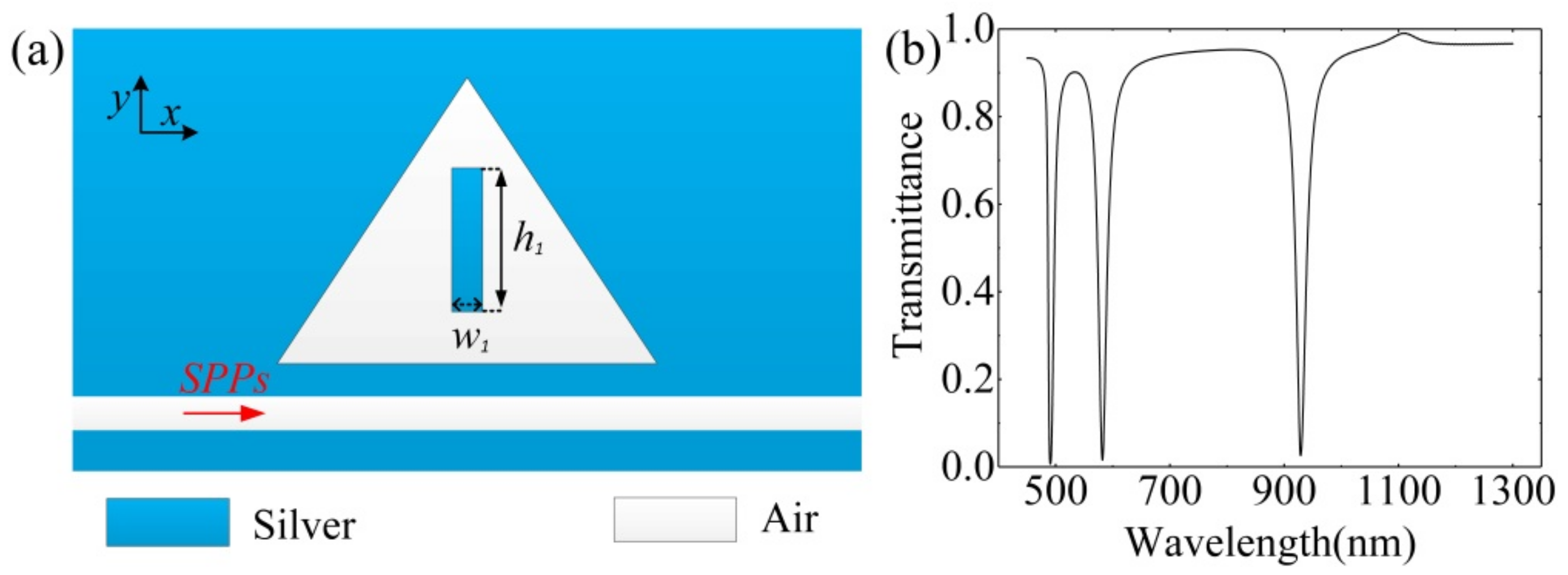
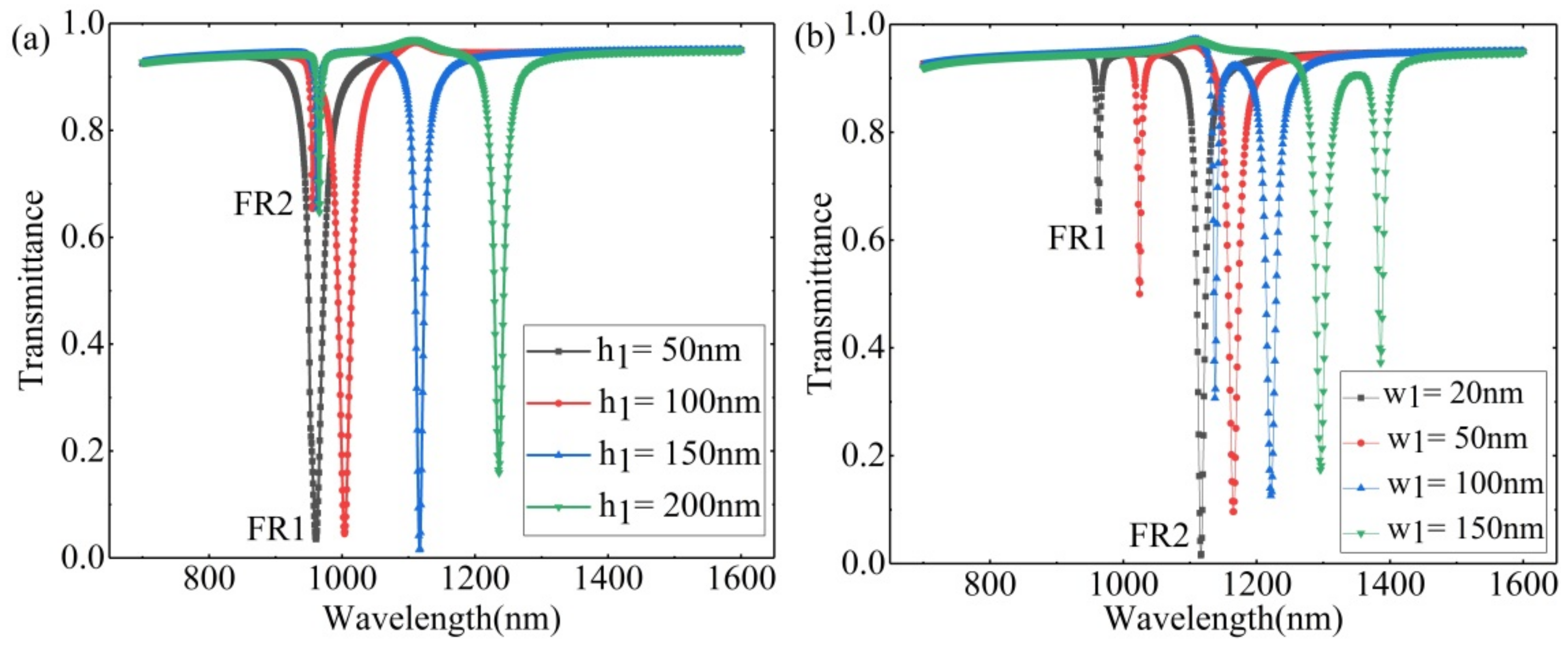
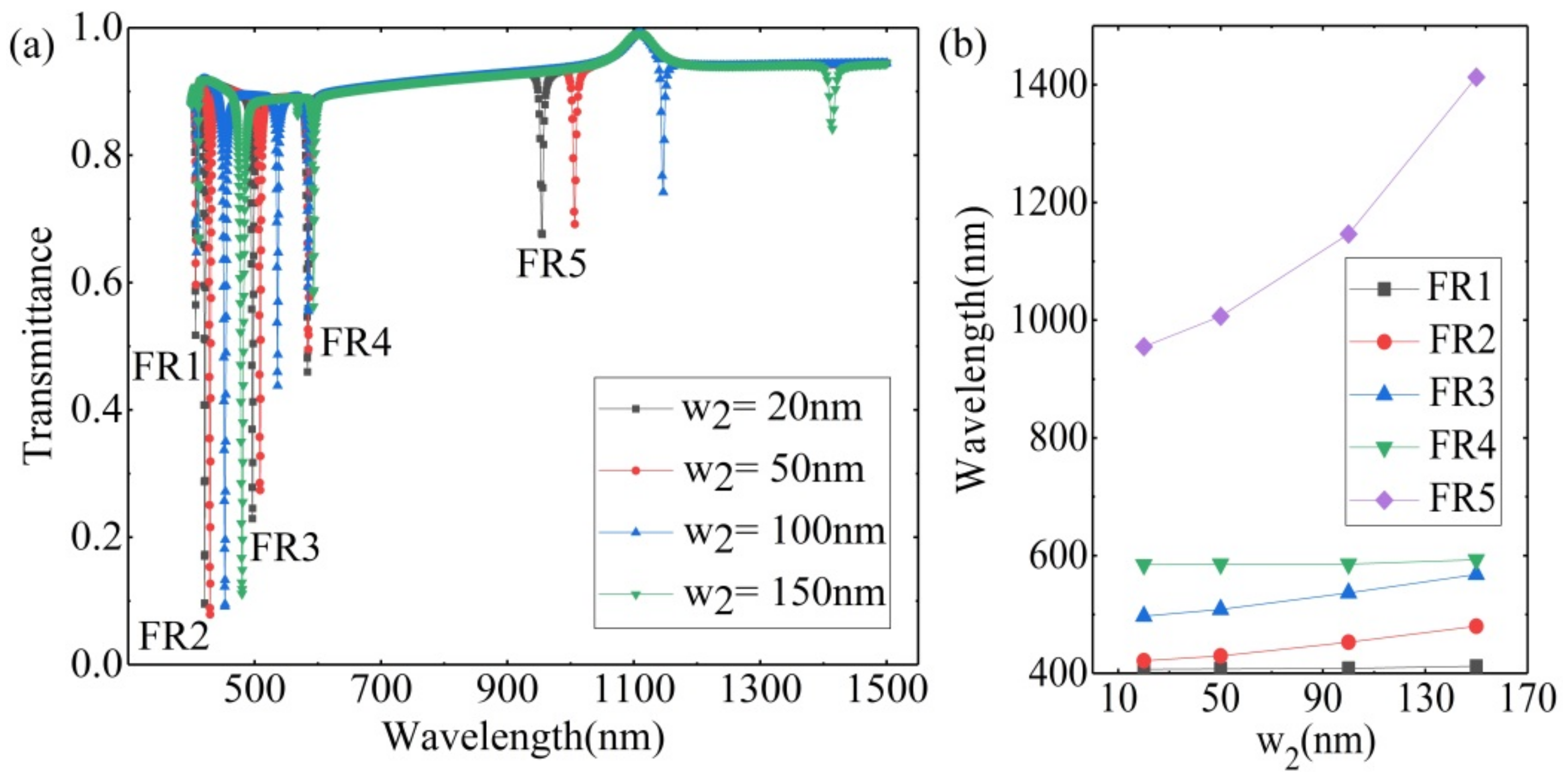
3.1. Bar Embedded ETSC Configuration
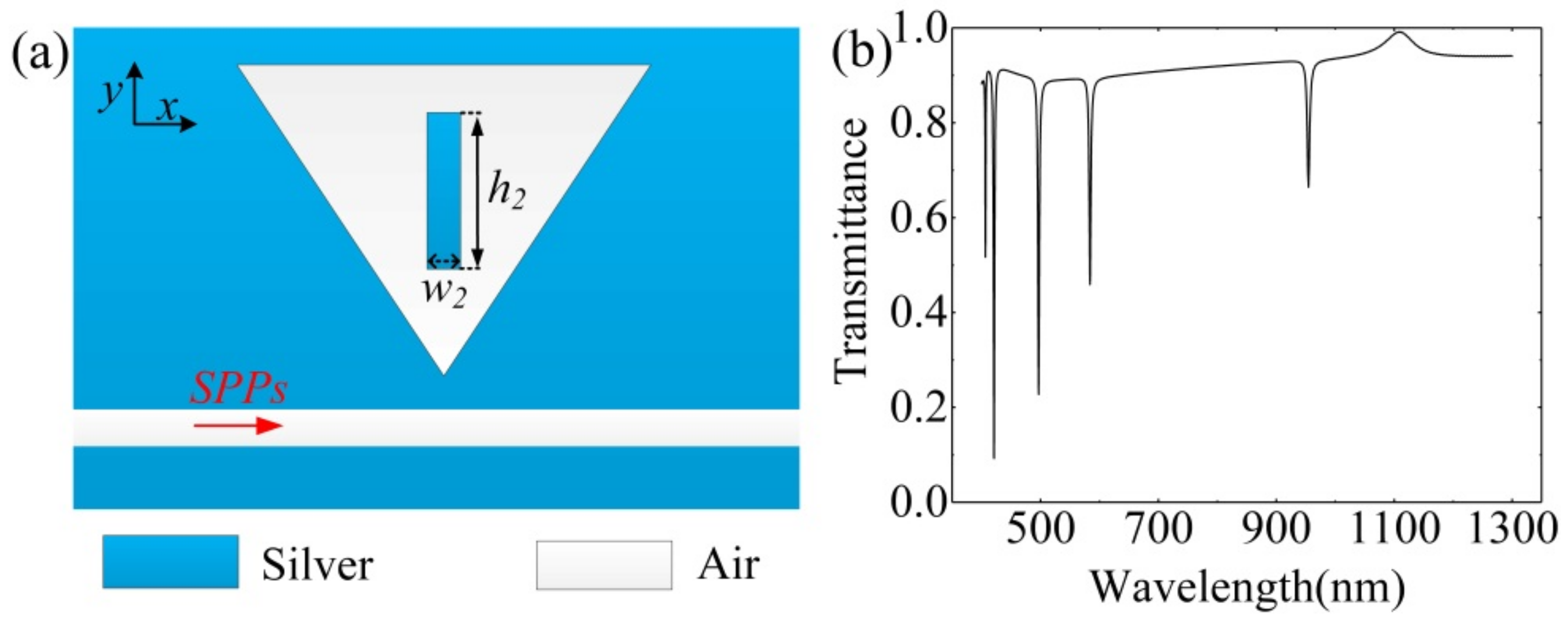
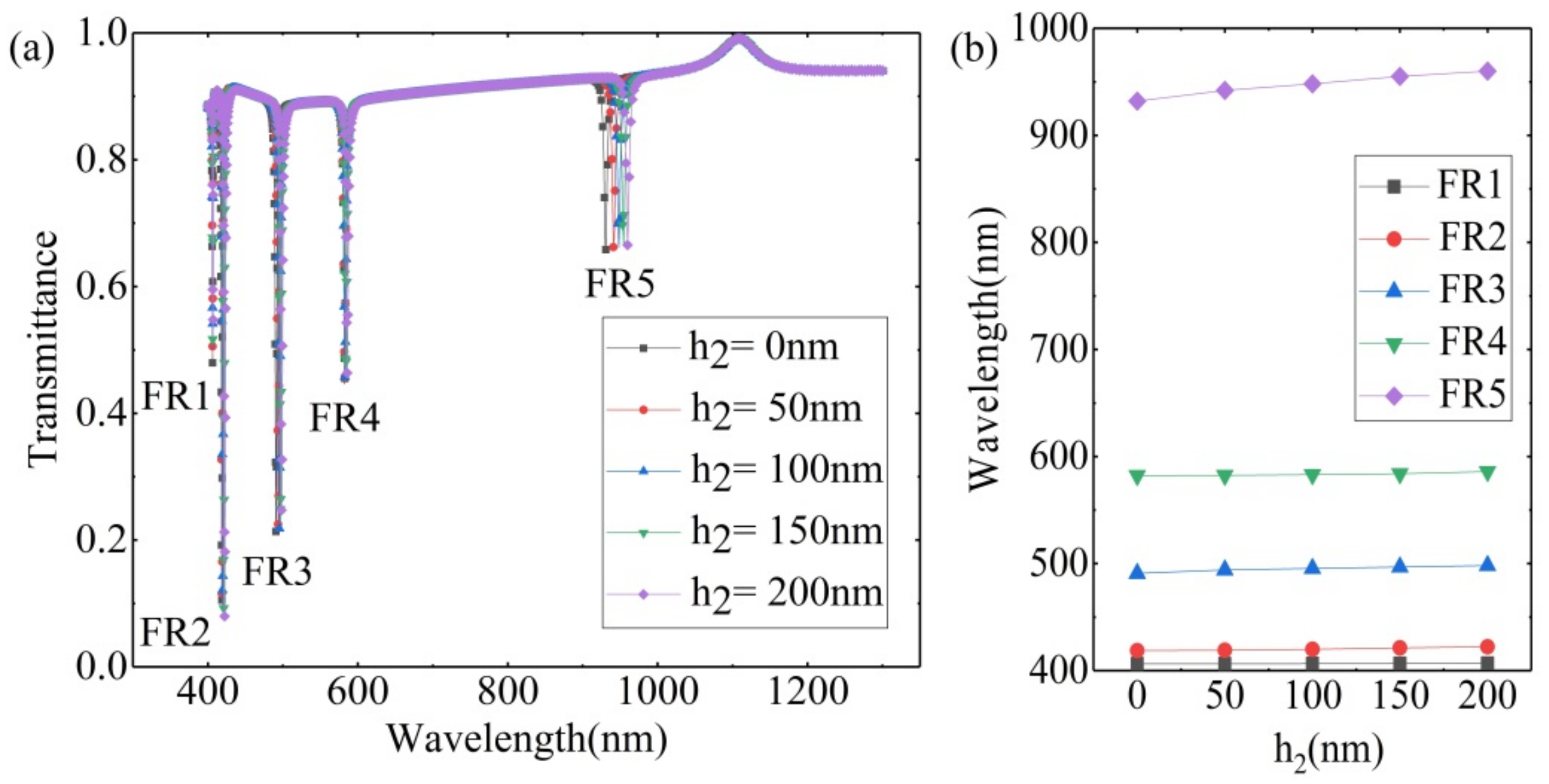
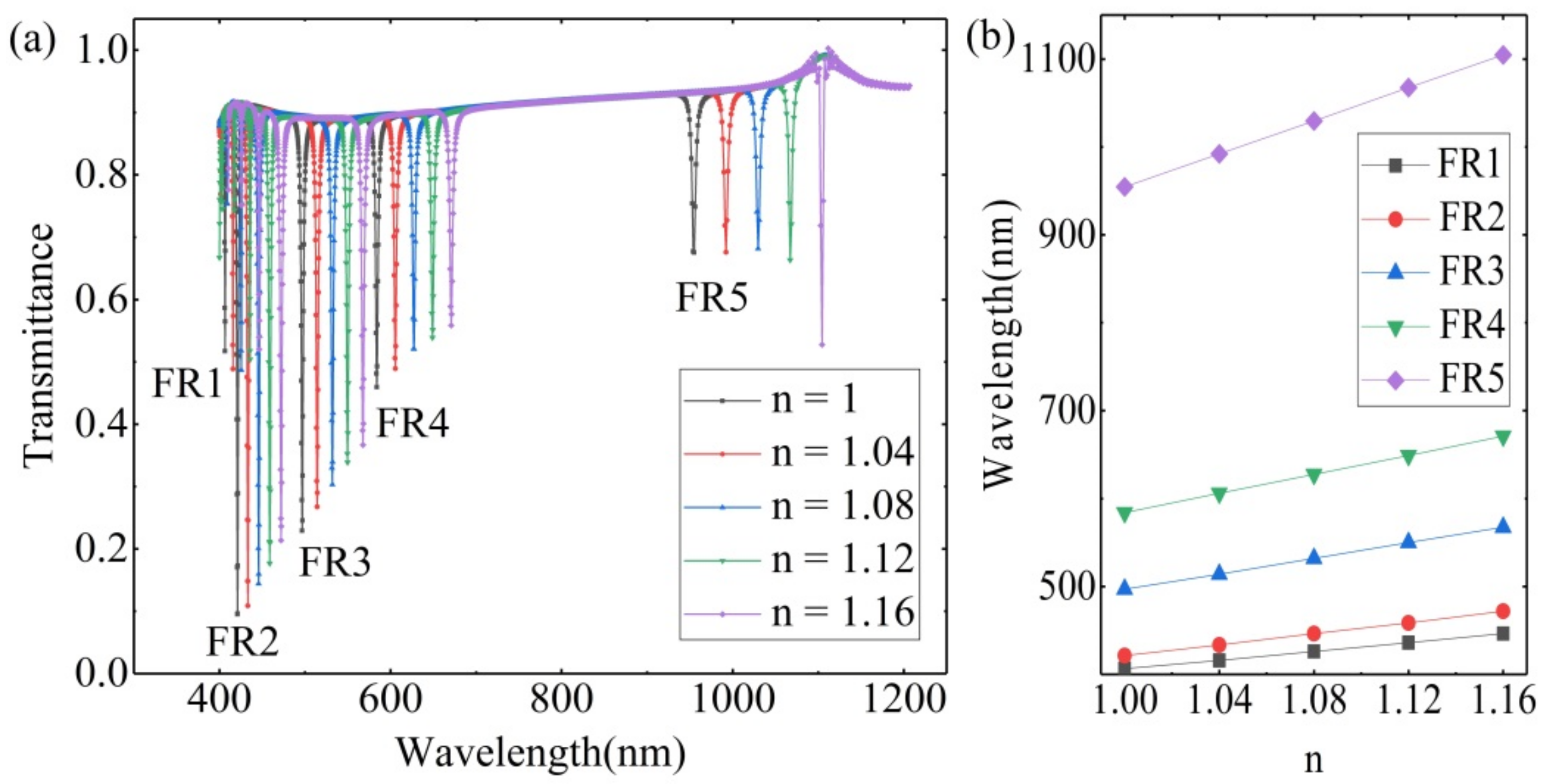
3.2. Bar Embedded the Inverted ETSC Configuration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Sun, C.; Gong, Q. Fano resonances in a single defect nanocavity coupled with a plasmonic waveguide. Opt. Lett. 2014, 39, 52–55. [Google Scholar] [CrossRef]
- Chou Chao, C.T.; Chou Chau, Y.F.; Huang, H.J.; Kumara, N.; Kooh, M.R.R.; Lim, C.M.; Chiang, H.P. Highly Sensitive and Tunable Plasmonic Sensor Based on a Nanoring Resonator with Silver Nanorods. Nanomaterials 2020, 10, 1399. [Google Scholar] [CrossRef]
- Farahani, M.; Granpayeh, N.; Rezvani, M. Improved plasmonic splitters and demultiplexers. Photonics Nanostruct. Fundam. Appl. 2013, 11, 157–165. [Google Scholar] [CrossRef]
- Lu, H.; Wang, G.; Liu, X. Manipulation of light in MIM plasmonic waveguide systems. Chin. Sci. Bull. 2013, 58, 3607–3616. [Google Scholar] [CrossRef][Green Version]
- Li, Z.; Wen, K.; Chen, L.; Lei, L.; Zhou, J.; Zhou, D.; Fang, Y.; Wu, B. Control of Multiple Fano Resonances Based on a Subwavelength MIM Coupled Cavities System. IEEE Access 2019, 7, 59369–59375. [Google Scholar] [CrossRef]
- Wen, K.; Yan, L.; Pan, W.; Luo, B.; Guo, Z.; Guo, Y.; Luo, X. Electromagnetically Induced Transparency-Like Transmission in a Compact Side-Coupled T-Shaped Resonator. J. Lightwave Technol. 2014, 32, 1701–1707. [Google Scholar] [CrossRef]
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic Surface Lattice Resonances: A Review of Properties and Applications. Chem. Rev. 2018, 118, 5912–5951. [Google Scholar] [CrossRef]
- Mejia-Salazar, J.R.; Oliveira, O.N., Jr. Plasmonic Biosensing. Chem. Rev. 2018, 118, 10617–10625. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Gerislioglu, B.; Ahuja, R.; Kumar Mishra, Y. Terahertz plasmonics: The rise of toroidal metadevices towards immunobiosensings. Mater. Today 2020, 32, 108–130. [Google Scholar] [CrossRef]
- Gutha, R.R.; Sadeghi, S.M.; Sharp, C.; Wing, W.J. Biological sensing using hybridization phase of plasmonic resonances with photonic lattice modes in arrays of gold nanoantennas. Nanotechnology 2017, 28, 355504. [Google Scholar] [CrossRef]
- Sadeghi, S.M.; Wing, W.J.; Campbell, Q. Tunable plasmonic-lattice mode sensors with ultrahigh sensitivities and figure-of-merits. J. Appl. Phys. 2016, 119, 244503. [Google Scholar] [CrossRef]
- Huang, L.; Ding, L.; Zhou, J.; Chen, S.; Chen, F.; Zhao, C.; Xu, J.; Hu, W.; Ji, J.; Xu, H.; et al. One-step rapid quantification of SARS-CoV-2 virus particles via low-cost nanoplasmonic sensors in generic microplate reader and point-of-care device. Biosens. Bioelectron. 2021, 171, 112685. [Google Scholar] [CrossRef]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Anderson, P.W. Localized Magnetic States in Metals. Phys. Rev. 1961, 124, 41–53. [Google Scholar] [CrossRef]
- Akhavan, A.; Ghafoorifard, H.; Abdolhosseini, S.; Habibiyan, H. Metal–insulator–metal waveguide-coupled asymmetric resonators for sensing and slow light applications. IET Optoelectron. 2018, 12, 220–227. [Google Scholar] [CrossRef]
- Chou Chau, Y.-F. Mid-infrared sensing properties of a plasmonic metal–insulator–metal waveguide with a single stub including defects. J. Phys. D Appl. Phys. 2020, 53, 115401. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N. Nanodots decorated asymmetric metal–insulator–metal waveguide resonator structure based on Fano resonances for refractive index sensing application. Laser Phys. 2020, 30, 076204. [Google Scholar] [CrossRef]
- Fang, Y.; Sun, M. Nanoplasmonic waveguides: Towards applications in integrated nanophotonic circuits. Light Sci. Appl. 2015, 4, e294. [Google Scholar] [CrossRef]
- Wang, S.; Yu, S.; Zhao, T.; Wang, Y.; Shi, X. A nanosensor with ultra-high FOM based on tunable malleable multiple Fano resonances in a waveguide coupled isosceles triangular resonator. Opt. Commun. 2020, 465, 125614. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Zhao, Y.; Lu, D.; Xiong, Z. Numerical Investigation of a Branch-Shaped Filter Based on Metal-Insulator-Metal Waveguide. Plasmonics 2011, 6, 773–778. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; He, X.; Han, Y.; Zhang, J.; Huang, J.; Chen, D. Plasmonic Filter and Demultiplexer Based on Square Ring Resonator. Appl. Sci. 2018, 8, 462. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N. Highly Sensitive Refractive Index Sensor Based on Plasmonic Bow Tie Configuration. Photonic Sens. 2020, 10, 223–232. [Google Scholar] [CrossRef]
- Yu, S.; Wang, S.; Zhao, T.; Yu, J. Tunable Plasmonic System Based on a Slotted Side-Coupled Disk Resonator and Its Multiple Applications on Chip-Scale Devices. Optik 2020, 212, 164748. [Google Scholar] [CrossRef]
- Yan, S.; Shi, H.; Yang, X.; Guo, J.; Wu, W.; Hua, E. Study on the Nanosensor Based on a MIM Waveguide with a Stub Coupled with a Horizontal B-Type Cavity. Photonics 2021, 8, 125. [Google Scholar] [CrossRef]
- Yang, X.; Hu, X.; Yang, H.; Gong, Q. Ultracompact all-optical logic gates based on nonlinear plasmonic nanocavities. Nanophotonics 2017, 6, 365–376. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, B.; Mao, J.; Lu, M. Plasmonic-induced transparency in a metallic stub with two cuts and transmission line model. J. Mod. Opt. 2018, 65, 2301–2307. [Google Scholar] [CrossRef]
- Le-Van, Q.; Zoethout, E.; Geluk, E.J.; Ramezani, M.; Berghuis, M.; Rivas, J.G. Enhanced Quality Factors of Surface Lattice Resonances in Plasmonic Arrays of Nanoparticles. Adv. Opt. Mater. 2019, 7, 8. [Google Scholar] [CrossRef]
- Bin-Alam, M.S.; Reshef, O.; Mamchur, Y.; Alam, M.Z.; Carlow, G.; Upham, J.; Sullivan, B.T.; Menard, J.M.; Huttunen, M.J.; Boyd, R.W.; et al. Ultra-high-Q resonances in plasmonic metasurfaces. Nat. Commun. 2021, 12, 974. [Google Scholar] [CrossRef]
- Jeong, P.A.; Goldflam, M.D.; Campione, S.; Briscoe, J.L.; Vabishchevich, P.P.; Nogan, J.; Sinclair, M.B.; Luk, T.S.; Brener, I. High Quality Factor Toroidal Resonances in Dielectric Metasurfaces. ACS Photonics 2020, 7, 1699–1707. [Google Scholar] [CrossRef]
- Ma, L.; Zheng, W.X.; Li, J.; Chen, D.X.; Wang, W.J.; Liu, Y.F.; Zhou, Y.D.; Yang, Y.J.; Huang, Y.J.; Wen, G.J. High-Q Hg-anapole resonator with microstrip line coupling for high-precision temperature sensing applications. Results Phys. 2021, 24, 5. [Google Scholar] [CrossRef]
- Dong, L.; Xu, X.; Sun, K.; Ding, Y.; Ouyang, P.; Wang, P. Sensing analysis based on fano resonance in arch bridge structure. J. Phys. Commun. 2018, 2, 105010. [Google Scholar] [CrossRef]
- Gupta, M.; Singh, R. Terahertz Sensing with Optimized Q /Veff Metasurface Cavities. Adv. Opt. Mater. 2020, 8, 1902025. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Gerislioglu, B.; Ramezani, Z. Gated graphene island-enabled tunable charge transfer plasmon terahertz metamodulator. Nanoscale 2019, 11, 8091–8095. [Google Scholar] [CrossRef]
- Min, B.; Ostby, E.; Sorger, V.; Ulin-Avila, E.; Yang, L.; Zhang, X.; Vahala, K. High-Q surface-plasmon-polariton whispering-gallery microcavity. Nature 2009, 457, 455–458. [Google Scholar] [CrossRef] [PubMed]
- Gierak, J.; Madouri, A.; Biance, A.L.; Bourhis, E.; Patriarche, G.; Ulysse, C.; Lucot, D.; Lafosse, X.; Auvray, L.; Bruchhaus, L.; et al. Sub-5nm FIB direct patterning of nanodevices. Microelectron. Eng. 2007, 84, 779–783. [Google Scholar] [CrossRef]
- Li, G.; Winick, K.A.; Griffin, H.C.; Joseph, S. Hayden Systematic modeling study of channel waveguide fabrication by thermal silver ion exchange. Appl. Opt. 2006, 45, 743–755. [Google Scholar] [CrossRef]
- Stewart, G.; Millar, C.A.; Laybourn, P.J.R.; Wilkinson, C.D.W.; Delarue, R.M. Planar Optical Waveguides Formed by Silver-Ion Migration in Glass. IEEE J. Quantum Electron. 1977, 13, 192–200. [Google Scholar] [CrossRef]
- Asgari, S.; Pooretemad, S.; Granpayeh, N. Plasmonic refractive index sensor based on a double concentric square ring resonator and stubs. Photonics Nanostruct. Fundam. Appl. 2020, 42, 100857. [Google Scholar] [CrossRef]
- Moradiani, F.; Farmani, A.; Mozaffari, M.H.; Seifouri, M.; Abedi, K. Systematic engineering of a nanostructure plasmonic sensing platform for ultrasensitive biomaterial detection. Opt. Commun. 2020, 474, 126178. [Google Scholar] [CrossRef]
- Rakhshani, M.R. Optical refractive index sensor with two plasmonic double-square resonators for simultaneous sensing of human blood groups. Photonics Nanostruct. Fundam. Appl. 2020, 39, 100768. [Google Scholar] [CrossRef]
- Rakhshani, M.R. Wide-angle perfect absorber using a 3D nanorod metasurface as a plasmonic sensor for detecting cancerous cells and its tuning with a graphene layer. Photonics Nanostruct. Fundam. Appl. 2021, 43, 100883. [Google Scholar] [CrossRef]
- Rakhshani, M.R.; Mansouri-Birjandi, M.A. A high-sensitivity sensor based on three-dimensional metal–insulator–metal racetrack resonator and application for hemoglobin detection. Photonics Nanostruct. Fundam. Appl. 2018, 32, 28–34. [Google Scholar] [CrossRef]
- To, N.; Juodkazis, S.; Nishijima, Y. Detailed Experiment-Theory Comparison of Mid-Infrared Metasurface Perfect Absorbers. Micromachines 2020, 11, 409. [Google Scholar] [CrossRef] [PubMed]
- Nishijima, Y.; Balčytis, A.; Naganuma, S.; Seniutinas, G.; Juodkazis, S. Kirchhoff’s metasurfaces towards efficient photo-thermal energy conversion. Sci. Rep. 2019, 9, 8284. [Google Scholar] [CrossRef]
- Nishijima, Y.; Balčytis, A.; Naganuma, S.; Seniutinas, G.; Juodkazis, S. Tailoring metal and insulator contributions in plasmonic perfect absorber metasurfaces. ACS Appl. Nano Mater. 2018, 1, 3557–3564. [Google Scholar] [CrossRef]

| References | Type | Q | S | FOM | td | Veff |
|---|---|---|---|---|---|---|
| [4] | Single | 29.67 | 2080 | 29.92 | N | N |
| [15] | Dual | Max 31.1 | Max 2300 | Max 31.5 | N | N |
| [16] | Dual | 106/123 | 900/1700 | Max 1.38 × 105 | N | N |
| This work | Quintuple | Max 322 | 923/542/427/301/250 | Max 710 | Min 5.4 × 10−3 fs | Min 0.02 × 105 μm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Feng, H.; Gao, Y. Plasmonic Narrowband Filter Based on an Equilateral Triangular Resonator with a Silver Bar. Photonics 2021, 8, 244. https://doi.org/10.3390/photonics8070244
Zhang J, Feng H, Gao Y. Plasmonic Narrowband Filter Based on an Equilateral Triangular Resonator with a Silver Bar. Photonics. 2021; 8(7):244. https://doi.org/10.3390/photonics8070244
Chicago/Turabian StyleZhang, Jingyu, Hengli Feng, and Yang Gao. 2021. "Plasmonic Narrowband Filter Based on an Equilateral Triangular Resonator with a Silver Bar" Photonics 8, no. 7: 244. https://doi.org/10.3390/photonics8070244
APA StyleZhang, J., Feng, H., & Gao, Y. (2021). Plasmonic Narrowband Filter Based on an Equilateral Triangular Resonator with a Silver Bar. Photonics, 8(7), 244. https://doi.org/10.3390/photonics8070244





