Second-Order Dispersion Sensor Based on Multi-Plasmonic Surface Resonances in D-Shaped Photonic Crystal Fibers
Abstract
1. Introduction
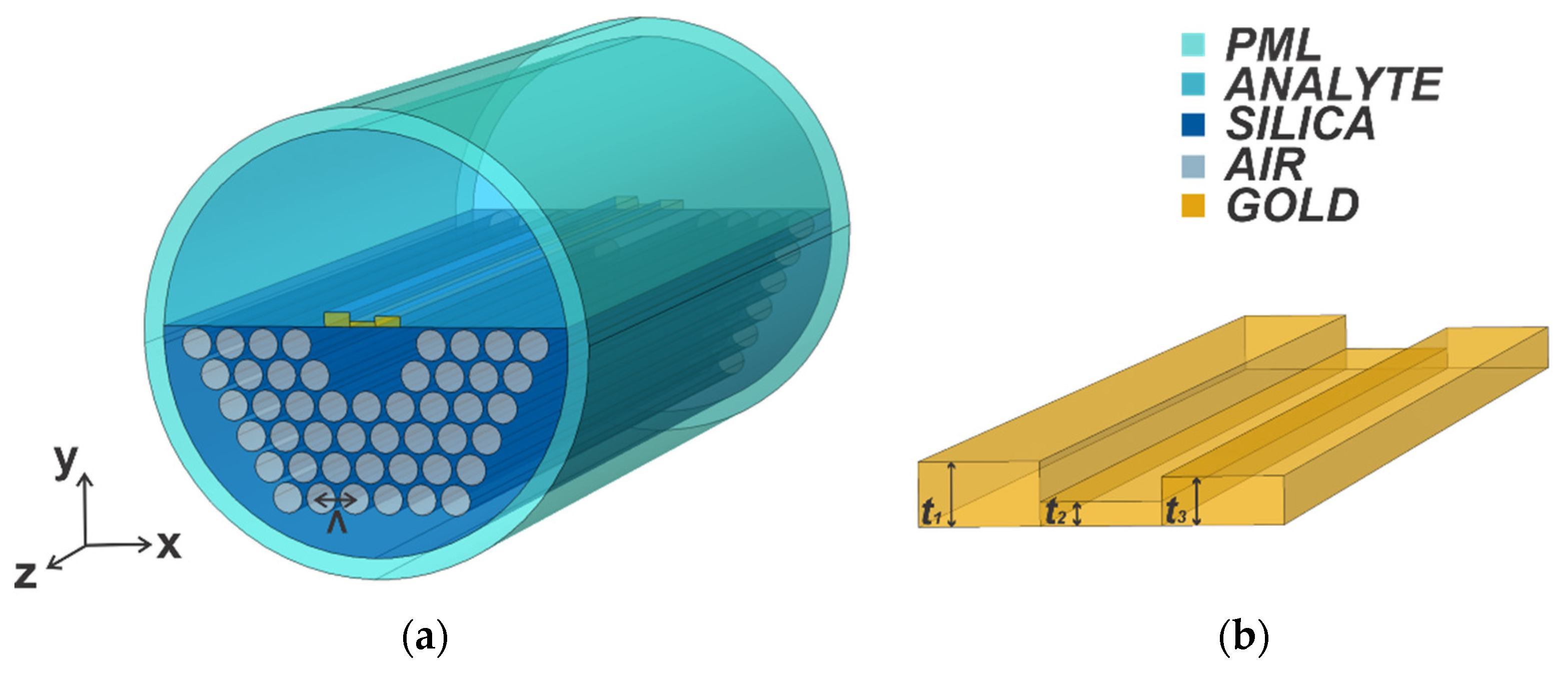
2. Designed Structure and Modeling
3. Results
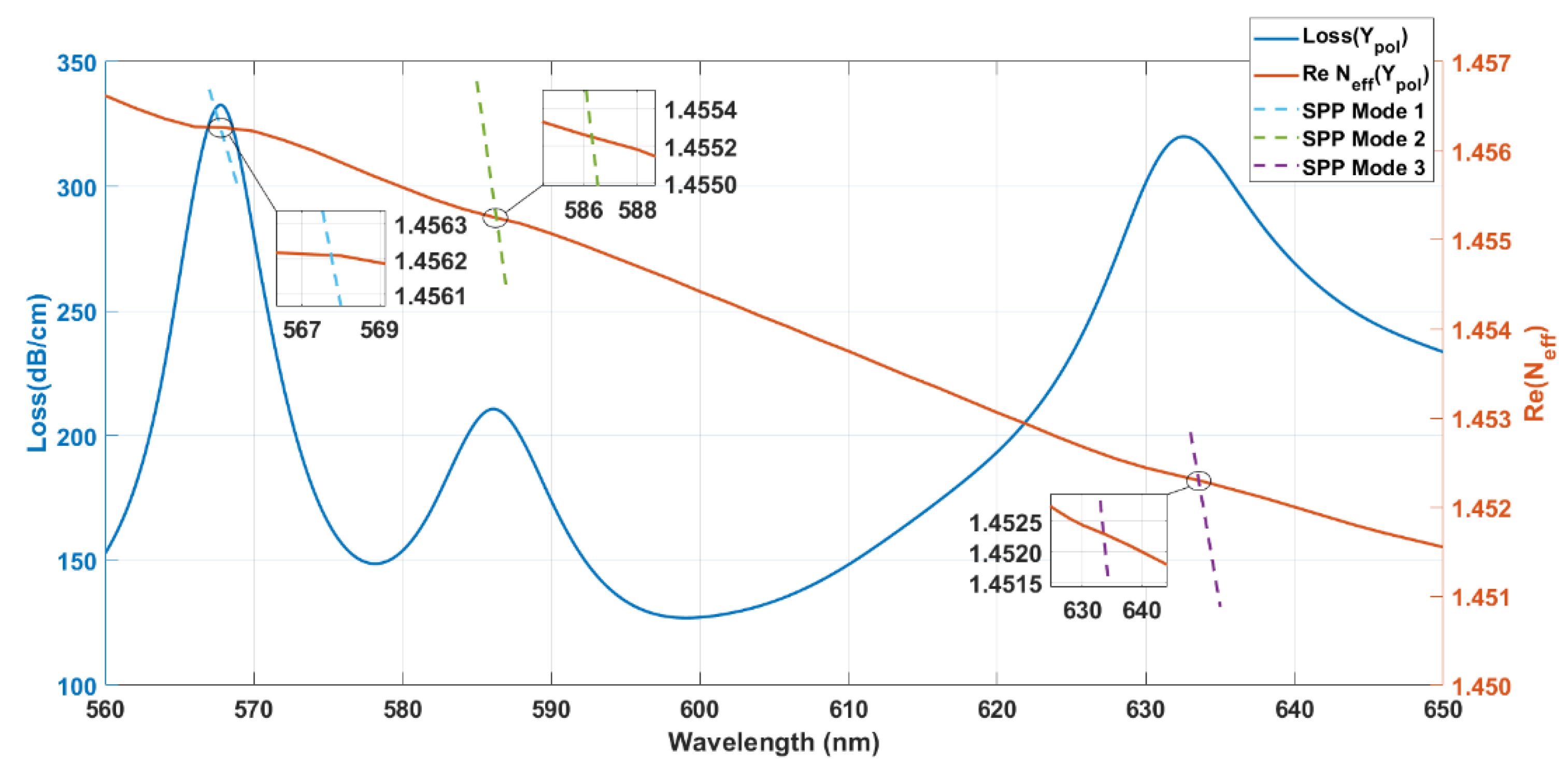
3.1. Sensitivity Performance Analysis
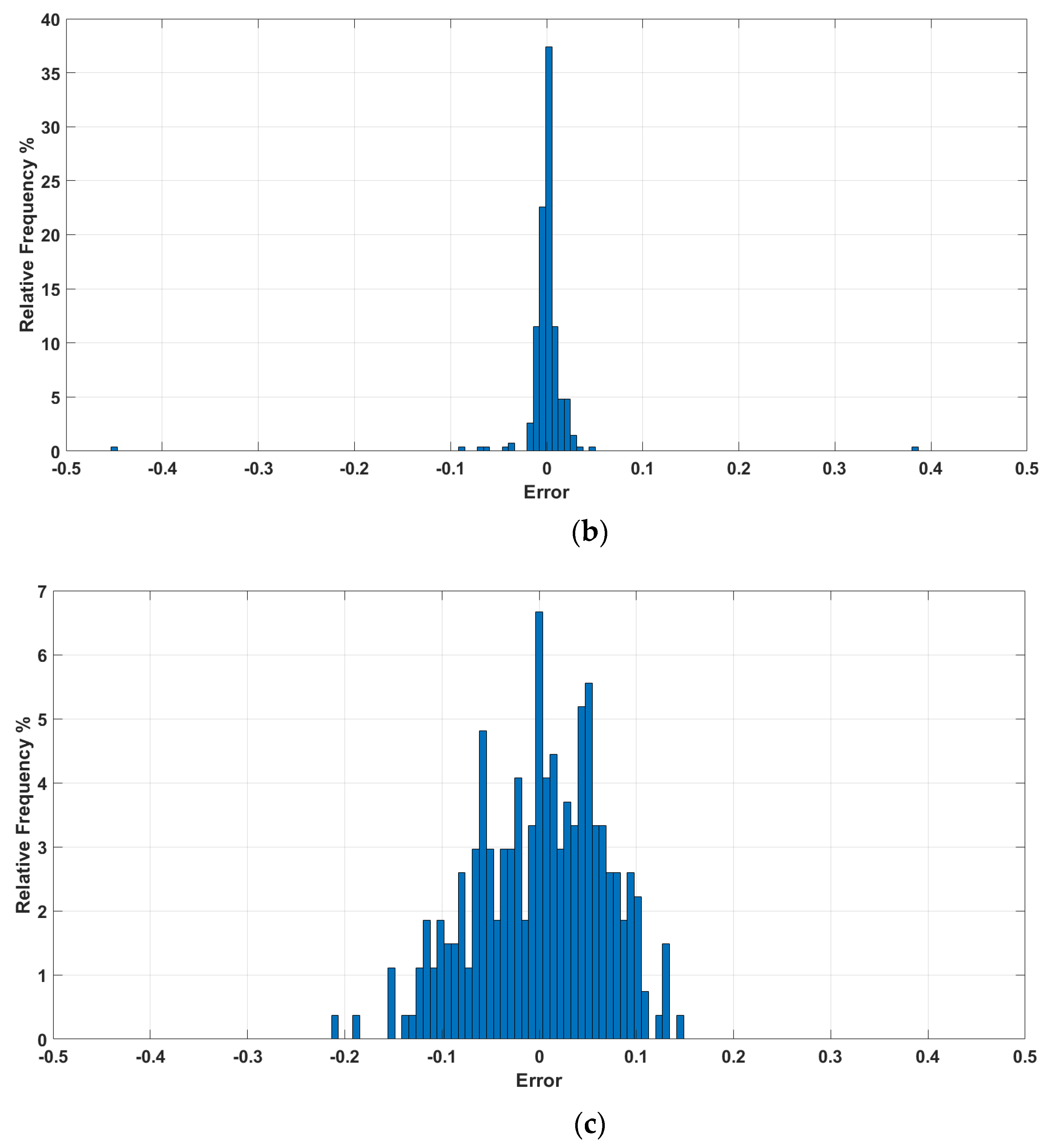
3.2. Sensing Response at Second-Order Dispersion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barnes, W.L. Surface plasmon–polariton length scales: A route to sub-wavelength optics. J. Opt. A Pure Appl. Opt. 2006, 8, S87–S93. [Google Scholar] [CrossRef]
- Homola, J. Surface Plasmons on Waveguides with a Perturbed Refractive Index Profile. In Surface Plasmon Polariton Based Sensors, 1st ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2018; Volume 4, pp. 19–26. [Google Scholar]
- Prabowo, B.A.; Purwidyantri, A.; Liu, K.C. Surface plasmon resonance optical sensor: A review on light source technology. Biosensors 2018, 8, 80. [Google Scholar] [CrossRef]
- Homola, J.; Koudela, I.; Yee, S.S. Surface plasmon resonance sensors based on diffraction gratings and prims couplers: Sensitivity comparison. Sens. Actuators B Chem. 1999, 54, 16–24. [Google Scholar] [CrossRef]
- Leong, H.-S.; Guo, J.; Lindquist, R.G.; Liu, Q.H. Surface plasmon resonance in nanostructured metal films under the Kretschmann configuration. J. Appl. Phys. 2009, 106, 124314. [Google Scholar] [CrossRef]
- Lin, H.-Y.; Huang, C.-H.; Cheng, G.-L.; Chen, N.K.; Chui, H.C. Tapered optical fiber sensor based on localized surface plasmon resonance. Opt. Express 2012, 20, 21693–21701. [Google Scholar] [CrossRef]
- Heidemann, B.R.; Chiamenti, I.; Oliveira, M.M.; Muller, M.; Fabris, J.L. Functionalized Long Period Grating—Plasmonic Fiber Sensor Applied to the Detection of Glyphosate in Water. J. Light. Technol. 2018, 36, 863–870. [Google Scholar] [CrossRef]
- Si, Y.; Lao, J.; Zhang, X.; Liu, Y.; Cai, S.; Gonzalez-Vila, A.; Li, K.; Huang, Y.; Yuan, Y.; Caucheteur, C.; et al. Electrochemical Plasmonic Fiber-optic Sensors for Ultra-Sensitive Heavy Metal Detection. J. Light. Technol. 2019, 37, 3495–3502. [Google Scholar] [CrossRef]
- Patnaik, A.; Senthilnathan, K.; Jha, R. Graphene-Based Conducting Metal Oxide Coated D-Shaped Optical Fiber SPR Sensor. IEEE Photonics Technol. Lett. 2015, 27, 2437–2440. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, Y.; Pan, S.; Shum, P.; Yan, M.; Leviatan, Y.; Li, C. A selectively coated photonic crystal fiber based surface plasmon resonance sensor. J. Opt. 2009, 12, 1–4. [Google Scholar] [CrossRef]
- Rifat, A.A.; Ahmed, R.; Yetisen, A.K.; Butt, H.; Sabouri, A.; Mahdiraji, G.A.; Yun, S.H.; Adikan, F.R. Photonic crystal fiber based plasmonic sensors. Sens. Actuators B Chem. 2017, 243, 311–325. [Google Scholar] [CrossRef]
- Rifat, A.A.; Haider, F.; Ahmed, R.; Mahdiraji, G.A.; Adikan, F.R.M.; Miroshnichenko, A.E. Highly sensitive selectively coated photonic crystal fiber-based plasmonic sensor. Opt. Lett. 2018, 43, 891–894. [Google Scholar] [CrossRef]
- Santos, D.F.; Guerreiro, A.; Baptista, J.M. SPR Microstructured D-Type Optical Fiber Sensor Configuration for Refractive Index Measurement. IEEE Sens. J. 2015, 15, 5472–5477. [Google Scholar] [CrossRef]
- Liu, Y.; Jing, X.; Li, S.; Zhang, S.; Zhang, Z.; Guo, Y.; Wang, J.; Wang, S. High sensitivity surface plasmon resonance sensor based on D-shaped photonic crystal fiber with circular layout. Opt. Fiber Technol. 2018, 46, 311–317. [Google Scholar] [CrossRef]
- Zhao, L.; Han, H.; Lian, Y.; Luan, N.; Liu, J. Theoretical analysis of all-solid D-type photonic crystal fiber based plasmonic sensor for refractive index and temperature sensing. Opt. Fiber Technol. 2019, 50, 165–171. [Google Scholar] [CrossRef]
- Cardoso, M.P.; Silva, A.O.; Romeiro, A.F.; Giraldi, M.T.R.; Costa, J.C.W.A.; Santos, J.L.; Baptista, J.M.; Guerreiro, A. Multi-plasmonic resonance based sensor for the characterization of optical dispersion using a D-shaped photonic crystal fiber. IEEE Instrum. Meas. Meg. accepted for publication.
- Sai, T.; Saba, M.; Dufresne, E.R.; Steiner, U.; Wilts, B.D. Designing refractive index fluids using the Kramers-Kroing relations. Faraday Discuss 2020, 223, 136–144. [Google Scholar] [CrossRef]
- Daimon, M.; Masumura, A. Measurement of the refractive index of distilled water from the near-infrared region to the ultraviolet region. Appl. Opt. 2007, 46, 3811–3820. [Google Scholar] [CrossRef]
- Mahdiraji, G.A.; Chow, D.M.; Sandoghchi, S.R.; Amirkhan, F.; Dermosesian, E.; Yeo, K.S.; Kakaei, Z.; Ghomeishi, M.; Poh, S.Y.; Gang, S.Y.; et al. Challenges and Solutions in Fabrication of Silica-Based Photonic Crystal Fibers: An Experimental Study. Fiber Integr. Opt. 2014, 33, 85–104. [Google Scholar] [CrossRef]
- Dash, J.N.; Jha, R. Highly sensitive D shaped PCF sensor based on SPR for near IR. Opt. Quantum Electron. 2016, 48, 1–7. [Google Scholar] [CrossRef]
- Sazio, P.J.A.; Amezcua-Correa, A.; Finlayson, C.E.; Hayes, J.R.; Scheidemantel, T.J.; Baril, N.F.; Jackson, B.R.; Won, D.-J.; Zhang, F.; Margine, E.R.; et al. Microstructured Optical Fibers as High-Pressure Microfluidic Reactors. Science 2006, 311, 1583–1586. [Google Scholar] [CrossRef]
- Comsol. Available online: www.br.comsol.com (accessed on 4 February 2021).
- Sharma, A.K.; Gupta, B.D. On the performance of different bimetallic combinations in surface plasmon resonance based fiber optic sensors. J. Appl. Phys. 2007, 101, 093111. [Google Scholar] [CrossRef]
- Vial, A.; Grimault, A.-S.; Macías, D.; Barchiesi, D.; De La Chapelle, M.L. Improved analytical fit of gold dispersion: Application to the modeling of extinction spectra with a finite-difference time-domain method. Phys. Rev. B 2005, 71, 085416. [Google Scholar] [CrossRef]
- Chapra, S.C. Multiple Linear Regression. In Applied Numerical Methods with Matlab for Engineers and Scientists, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2018; pp. 389–391. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cardoso, M.P.; Silva, A.O.; Romeiro, A.F.; Giraldi, M.T.R.; Costa, J.C.W.A.; Santos, J.L.; Baptista, J.M.; Guerreiro, A. Second-Order Dispersion Sensor Based on Multi-Plasmonic Surface Resonances in D-Shaped Photonic Crystal Fibers. Photonics 2021, 8, 181. https://doi.org/10.3390/photonics8060181
Cardoso MP, Silva AO, Romeiro AF, Giraldi MTR, Costa JCWA, Santos JL, Baptista JM, Guerreiro A. Second-Order Dispersion Sensor Based on Multi-Plasmonic Surface Resonances in D-Shaped Photonic Crystal Fibers. Photonics. 2021; 8(6):181. https://doi.org/10.3390/photonics8060181
Chicago/Turabian StyleCardoso, Markos P., Anderson O. Silva, Amanda F. Romeiro, M. Thereza R. Giraldi, João C. W. A. Costa, José L. Santos, José M. Baptista, and Ariel Guerreiro. 2021. "Second-Order Dispersion Sensor Based on Multi-Plasmonic Surface Resonances in D-Shaped Photonic Crystal Fibers" Photonics 8, no. 6: 181. https://doi.org/10.3390/photonics8060181
APA StyleCardoso, M. P., Silva, A. O., Romeiro, A. F., Giraldi, M. T. R., Costa, J. C. W. A., Santos, J. L., Baptista, J. M., & Guerreiro, A. (2021). Second-Order Dispersion Sensor Based on Multi-Plasmonic Surface Resonances in D-Shaped Photonic Crystal Fibers. Photonics, 8(6), 181. https://doi.org/10.3390/photonics8060181





