Compound Vector Light Generator Based on a Metasurface
Abstract
:1. Introduction
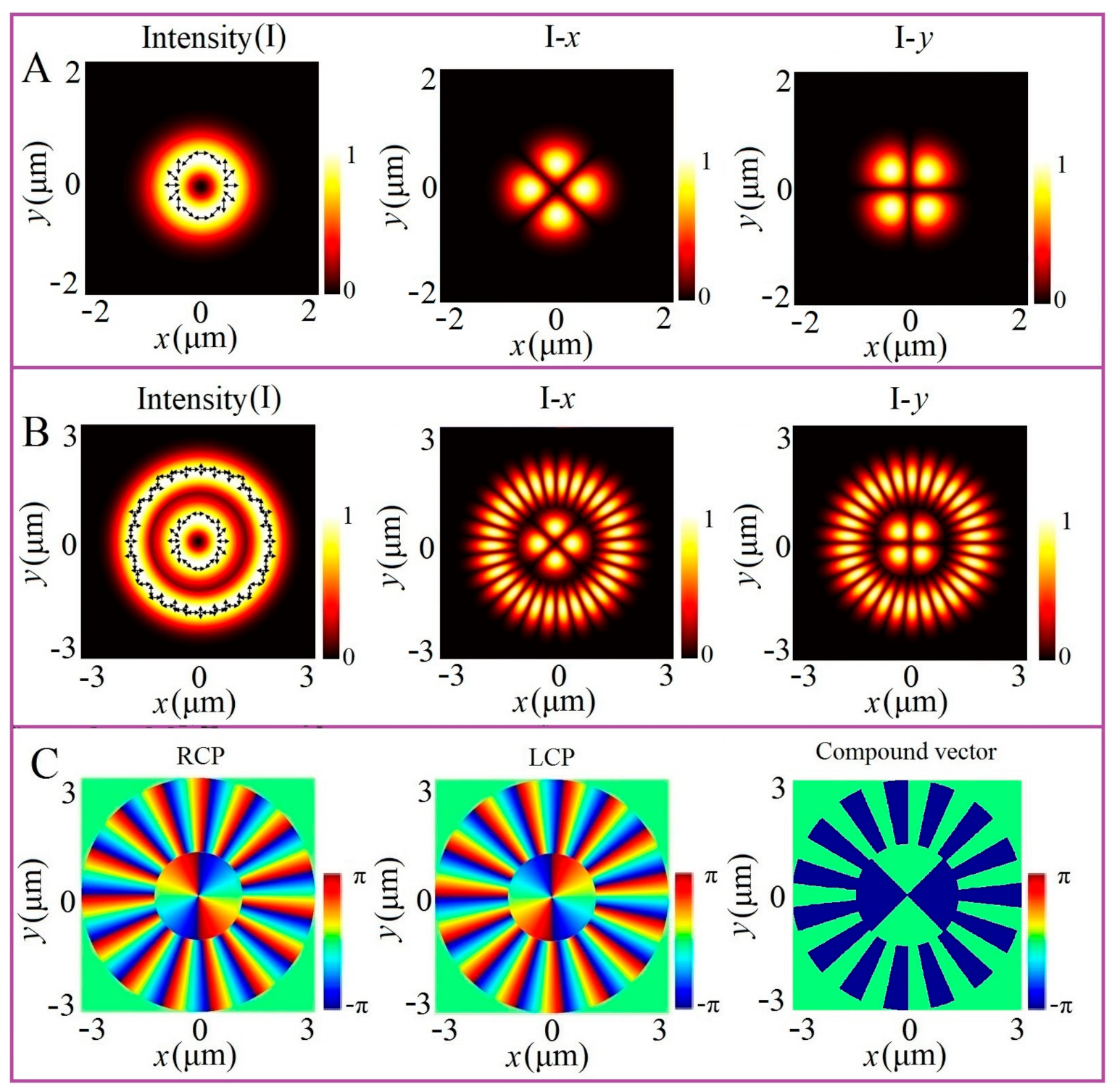
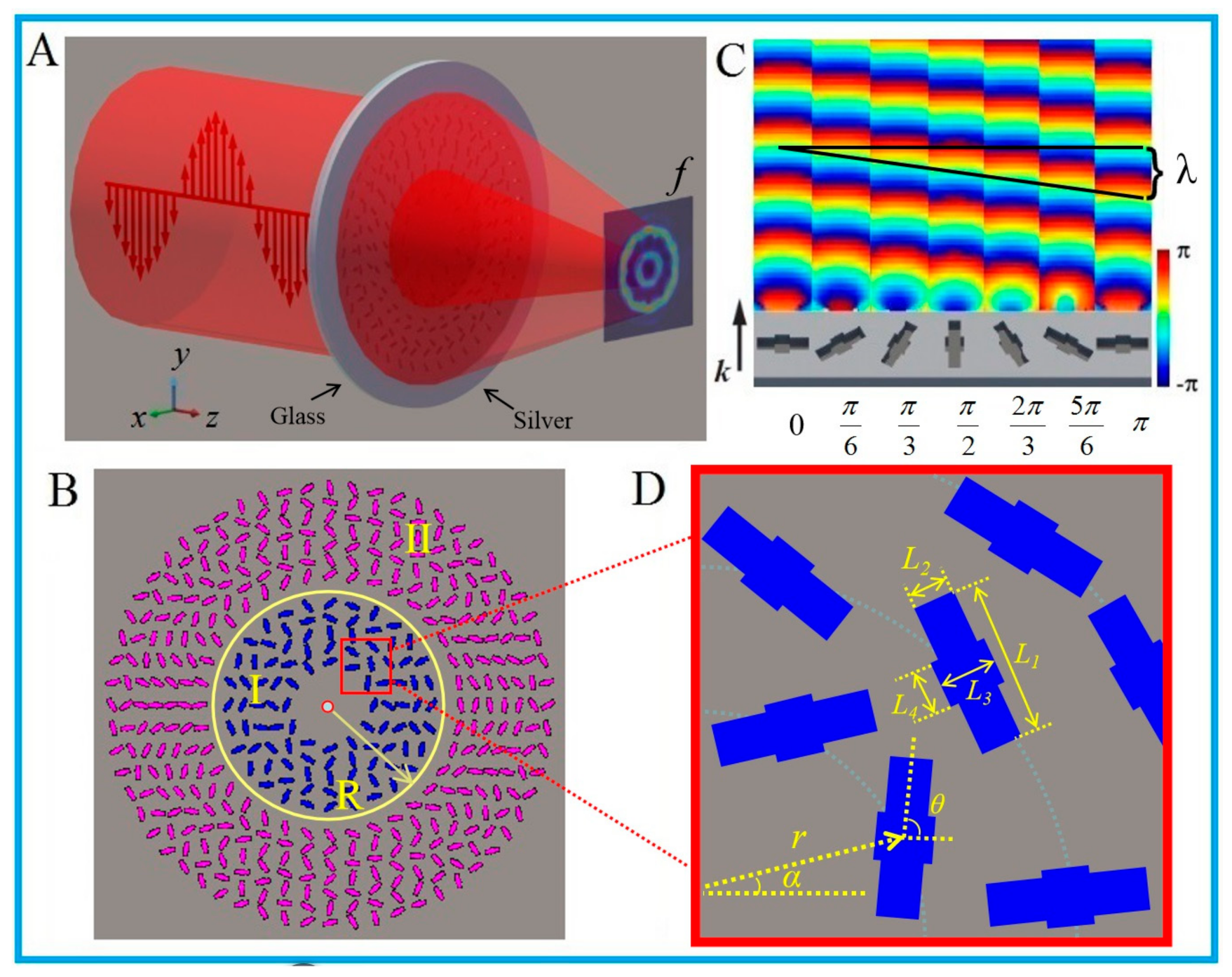
2. Design Principle
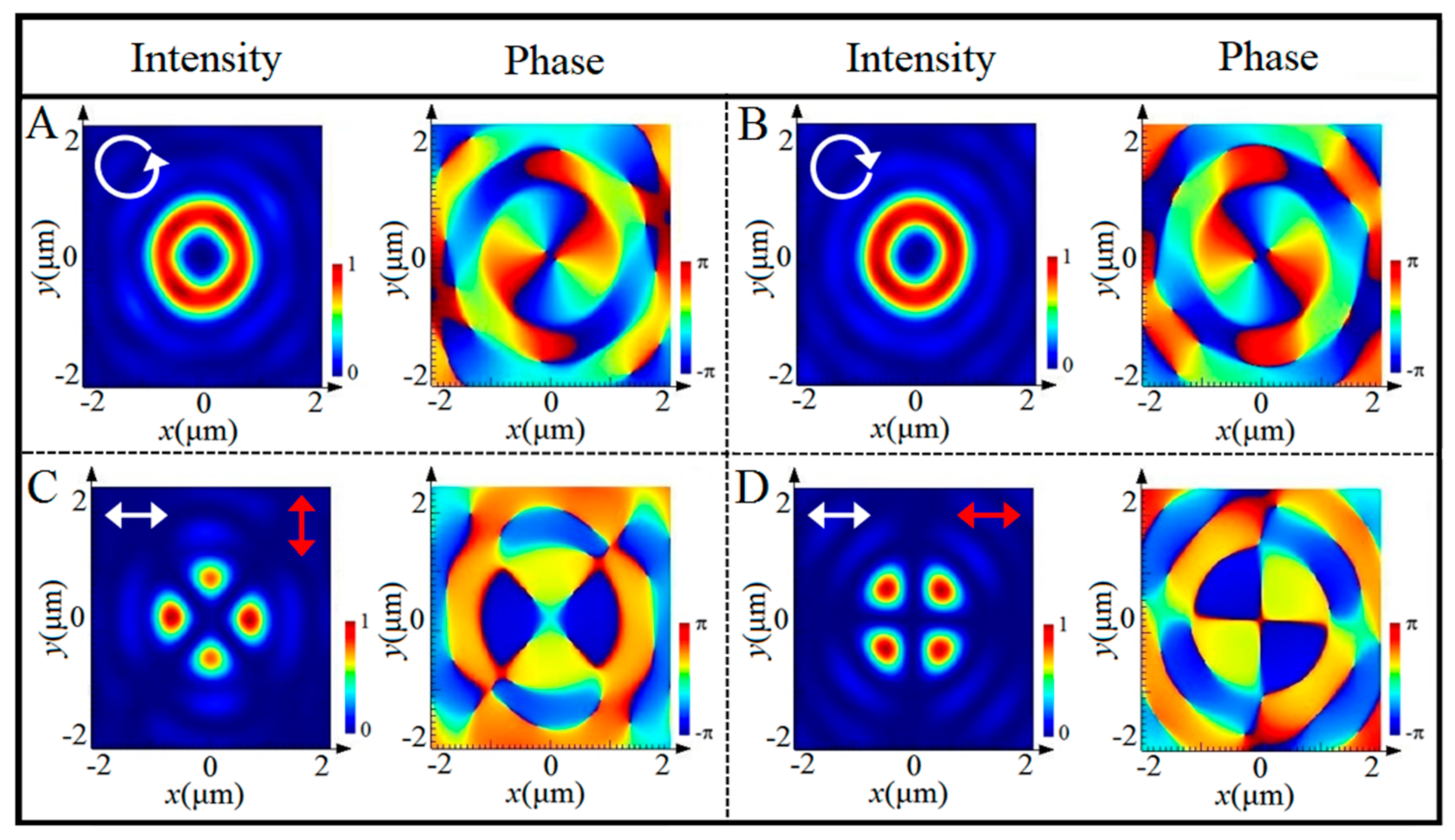
3. Simulation Verification for the CVL
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Wang, J. Advances in communications using optical vortices. Photon. Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Steinlechner, F.; Ecker, S.; Fink, M.; Liu, B.; Bavaresco, J.; Huber, M.; Scheidl, T.; Ursin, R. Distribution of high-dimensional entanglement via an intra-city free-space link. Nat. Commun. 2017, 8, 15971. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Huo, P.; Zhu, W.; Zhang, C.; Zhang, S.; Song, M.; Zhang, S.; Zhou, Q.; Chen, L.; Lezec, H.J.; et al. Broadband generation of perfect Poincaré beams via dielectric spin-multiplexed metasurface. Nat. Commun. 2021, 12, 2230. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Chen, Y.; Yang, K.; Zhou, J. Harnessing the Point-spread function for high-resolution far-field optical microscopy. Phy. Rev. Lett. 2014, 113, 263901. [Google Scholar] [CrossRef] [PubMed]
- Shvedov, V.G.; Hnatovsky, C.; Rode, A.V.; Krolikowski, W. Robust trapping and manipulation of airborne particles with a bottle beam. Opt. Express 2011, 19, 17350–17356. [Google Scholar] [CrossRef]
- Danilov, P.A.; Saraeva, I.N.; Kudryashov, S.I.; Porfirev, A.P.; Kuchmizhak, A.A.; Zhizhchenko, A.Y.; Rudenko, A.A.; Umanskaya, S.F.; Zayarny, D.A.; Ionin, A.A.; et al. Polarization-selective Excitation of Dye Luminescence on a Gold Film by Structured Ultrashort Laser Pulses. JETP Letters 2018, 107, 15–18. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Volotovsky, S.G. Shaping of spherical light intensity based on the interference of tightly focused beams with different polarizations. Opt. Las. Technol. 2014, 60, 99–106. [Google Scholar] [CrossRef]
- Padgett, M.J.; Allen, L. Orbital angular momentum exchange in cylindrical-lens mode converters. J. Opt. B Quantum Semiclass. Opt. 2002, 4, S17–S19. [Google Scholar] [CrossRef]
- Hirayama, T.; Kozawa, Y.; Nakamura, T.; Sato, S. Generation of a cylindrically symmetric, polarized laser beam with narrow linewidth and fine tunability. Opt. Exp. 2006, 14, 12839. [Google Scholar] [CrossRef]
- Zhou, H.; Fu, S.; Zhai, Y.; Yin, C.; Gao, C. Spatial light modulator-based programmable J-plate for the arbitrary spin-to-orbital angular momentum conversion of lights. Appl. Phys. B 2019, 125, 42. [Google Scholar] [CrossRef]
- Kozawa, Y.; Sato, S. Generation of a radially polarized laser beam by use of a conical Brewster prism. Opt. Lett. 2005, 30, 3063–3065. [Google Scholar] [CrossRef]
- Khonina, S.N.; Degtyarev, S.A.; Ustinov, A.V.; Porfirev, A.P. Metalenses for the generation of vector Lissajous beams with a complex Poynting vector density. Opt. Express 2021, 29, 18634–18645. [Google Scholar] [CrossRef]
- Zhang, L.; Mei, S.; Huang, K.; Qiu, C.-W. Advances in full control of electromagnetic waves with metasurfaces. Adv. Opt. Mater. 2016, 4, 818–833. [Google Scholar] [CrossRef]
- Chen, S.; Li, Z.; Zhang, Y.; Cheng, H.; Tian, J. Phase Manipulation of electromagnetic waves with metasurfaces and its applications in nanophotonics. Adv. Opt. Mater. 2018, 6, 1800104. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Liu, L.; Zhou, C.; Xu, J.; Zhang, M.; Teng, S.; Cai, Y. Vortex beam generation with variable topological charge based on a spiral slit. Nanophotonics 2019, 8, 317–324. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.; Cho, S.-W.; Lee, S.-Y.; Kang, M.; Lee, B. Synthesis and dynamic switching of surface plasmon vortices with Plasmonic Vortex Lens. Nano Lett. 2010, 10, 529–536. [Google Scholar] [CrossRef]
- Mou, Z.; Zhou, C.; Lv, H.; Bao, R.; Li, Z.; Teng, S. Uniform theory of plasmonic vortex generation based on nanoholes. Nanotechnology 2020, 31, 455301. [Google Scholar] [CrossRef]
- Sun, R.; Cheng, C.; Zhang, R.; Zeng, X.; Zhang, Y.; Gu, M.; Liu, C.; Ma, H.; Kong, Q.; Cheng, C. Spatially multiplexing of metasurface for manipulating the focused trefoil and cinquefoil vector light field. Nanomaterials 2021, 11, 858. [Google Scholar] [CrossRef]
- Asgari, S.; Fabritius, T. Equivalent circuit model of graphene chiral multi-band metadevice absorber composed of U-shaped resonator array. Opt. Express 2020, 28, 39850–39867. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.; Liu, L.; Teng, S. Generation of vector beams using spatial variation nanoslits with linearly polarized light illumination. Opt. Express 2018, 26, 24145–24153. [Google Scholar] [CrossRef]
- Yue, F.; Wen, D.; Zhang, C.; Gerardot, B.D.; Wang, W.; Zhang, S.; Chen, X. Multichannel polarization-controllable superpositions of orbital angular momentum states. Adv. Mater. 2017, 29, 1603838. [Google Scholar] [CrossRef]
- Lv, H.; Lu, X.; Han, Y.; Mou, Z.; Zhou, C.; Wang, S.; Teng, S. Metasurface cylindrical vector light generators based on nanometer holes. New J. Phys. 2019, 21, 123047. [Google Scholar] [CrossRef] [Green Version]
- Teng, S.; Zhang, Q.; Wang, H.; Liu, L.; Lv, H. Conversion between polarization states based on a metasurface. Photon. Res. 2019, 7, 246–250. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Liu, Z.; Liu, Y.; Zhou, J.; Ke, Y.; Luo, H.; Wen, S. Higher-order laser mode converters with dielectric metasurfaces. Opt. Lett. 2015, 40, 5506–5509. [Google Scholar] [CrossRef]
- Nie, Z.; Li, Z.; Shi, G.; Zhang, X.; Wang, Y.; Song, Y. Generation of a sub-wavelength focal spot with a long transversally polarized optical needle using a double-ring-shaped azimuthally polarized beam. Opt. Lasers Eng. 2014, 59, 93–97. [Google Scholar] [CrossRef]
- Wang, X.; Ding, J.; Ni, W.; Guo, C.; Wang, H. Generation of arbitrary vector beams with a spatial light modulator and a common path interferometric arrangement. Opt. Lett. 2007, 32, 3549–3551. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Liu, L.; Lu, X.; Lü, H.; Han, Y.; Wang, S.; Teng, S. Spatial multiplexing plasmonic metalenses based on nanometer cross holes. New J. Phys. 2018, 20, 123009. [Google Scholar] [CrossRef]
- Liu, L.; Wang, H.; Han, Y.; Lu, X.; Lv, H.; Teng, S. Color polarization multiplexing metalens based on cross nanoholes. Opt. Commun. 2019, 442, 27–30. [Google Scholar] [CrossRef]
- Zhou, C.; Mou, Z.; Bao, R.; Li, Z.; Teng, S. Compound plasmonic vortex generation based on spiral nanoslits. Front. Phys. 2021, 16, 33503. [Google Scholar] [CrossRef]
- Lu, X.; Han, Y.; Lv, H.; Mou, Z.; Teng, S. α spiral nanoslit and the higher order plasmonic vortex generation. Nanotechnology 2020, 31, 305201. [Google Scholar] [CrossRef]
- Han, Y.; Lu, X.; Lv, H.; Mou, Z.; Zhou, C.; Wang, S.; Teng, S. Multi-wavelength focusing based on nanoholes. New J. Phys. 2020, 22, 073021. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Mou, Z.; Lu, X.; Lv, H.; Han, S.; Yue, Q.; Wang, S.; Teng, S. Metasurface array illuminator based on Fresnel holography. Opt. Las. Engin. 2020, 131, 106146. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Mou, Z.; Lu, P.; Teng, S. Compound Vector Light Generator Based on a Metasurface. Photonics 2021, 8, 243. https://doi.org/10.3390/photonics8070243
Zhou C, Mou Z, Lu P, Teng S. Compound Vector Light Generator Based on a Metasurface. Photonics. 2021; 8(7):243. https://doi.org/10.3390/photonics8070243
Chicago/Turabian StyleZhou, Changda, Zhen Mou, Peiyao Lu, and Shuyun Teng. 2021. "Compound Vector Light Generator Based on a Metasurface" Photonics 8, no. 7: 243. https://doi.org/10.3390/photonics8070243
APA StyleZhou, C., Mou, Z., Lu, P., & Teng, S. (2021). Compound Vector Light Generator Based on a Metasurface. Photonics, 8(7), 243. https://doi.org/10.3390/photonics8070243





