Propagation-Invariant Off-Axis Elliptic Gaussian Beams with the Orbital Angular Momentum
Abstract
1. Introduction
2. Propagation-Invariant Off-Axis Gaussian Beams
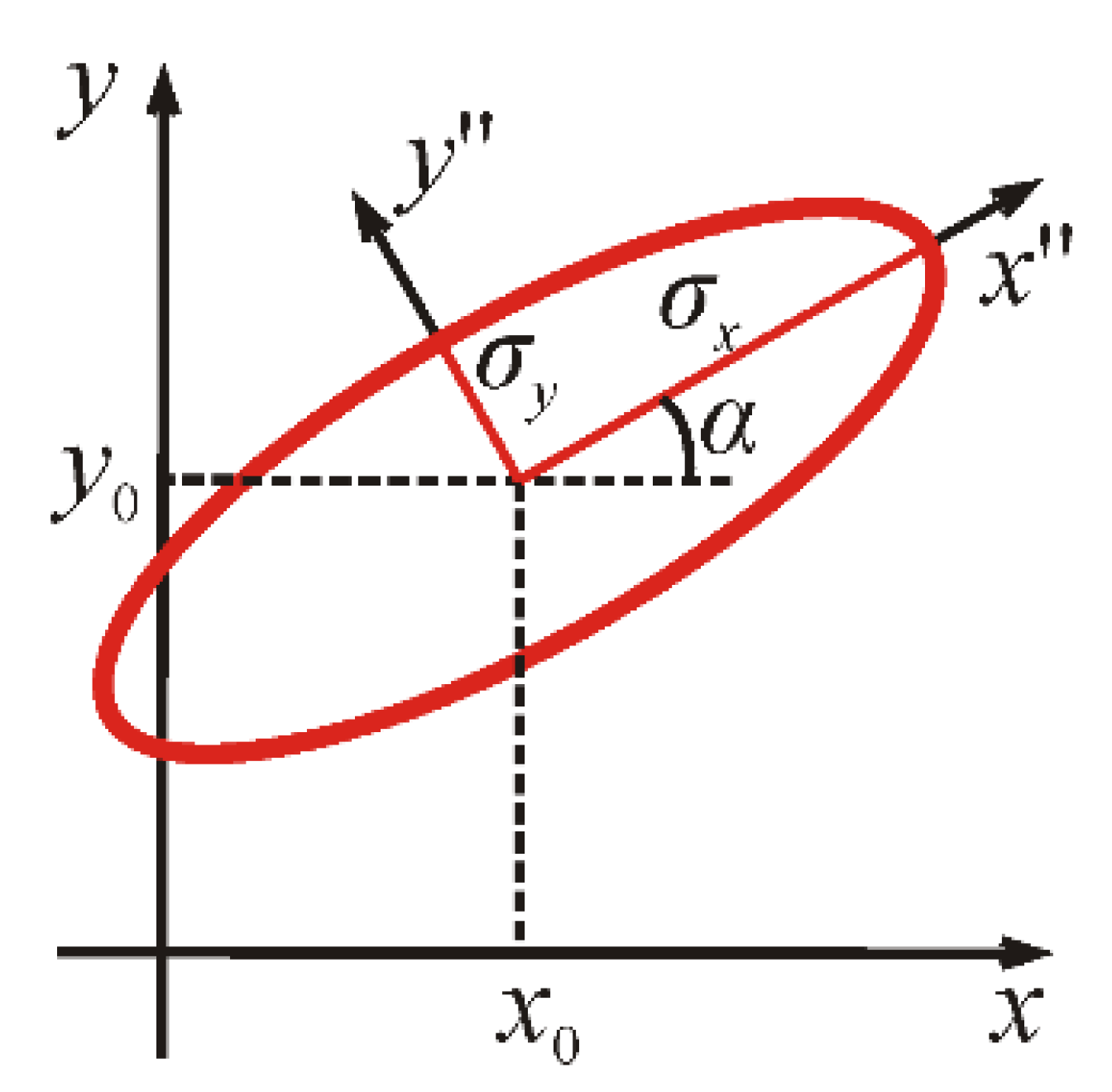
3. Propagation-Invariant Elliptic Gaussian Beams
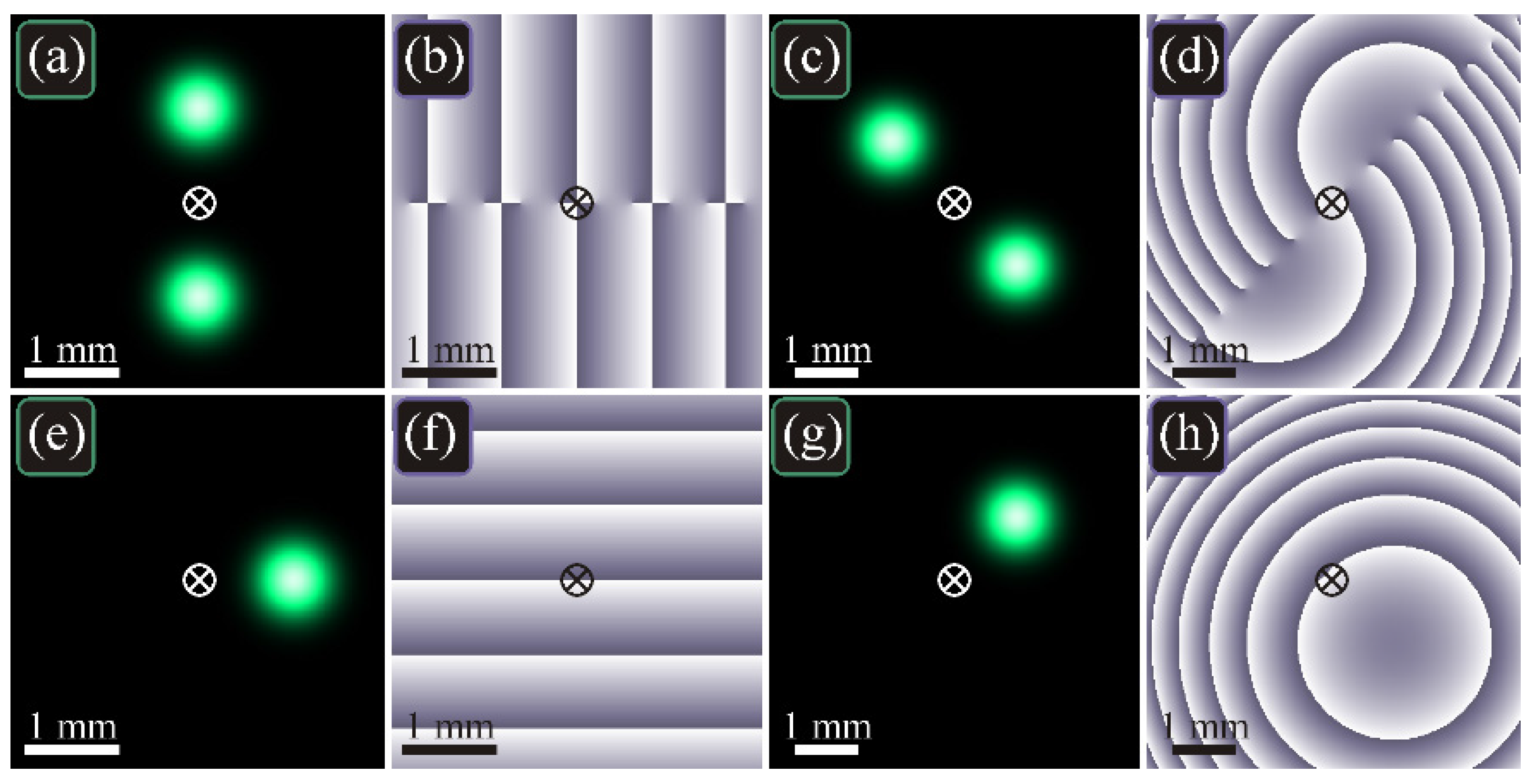
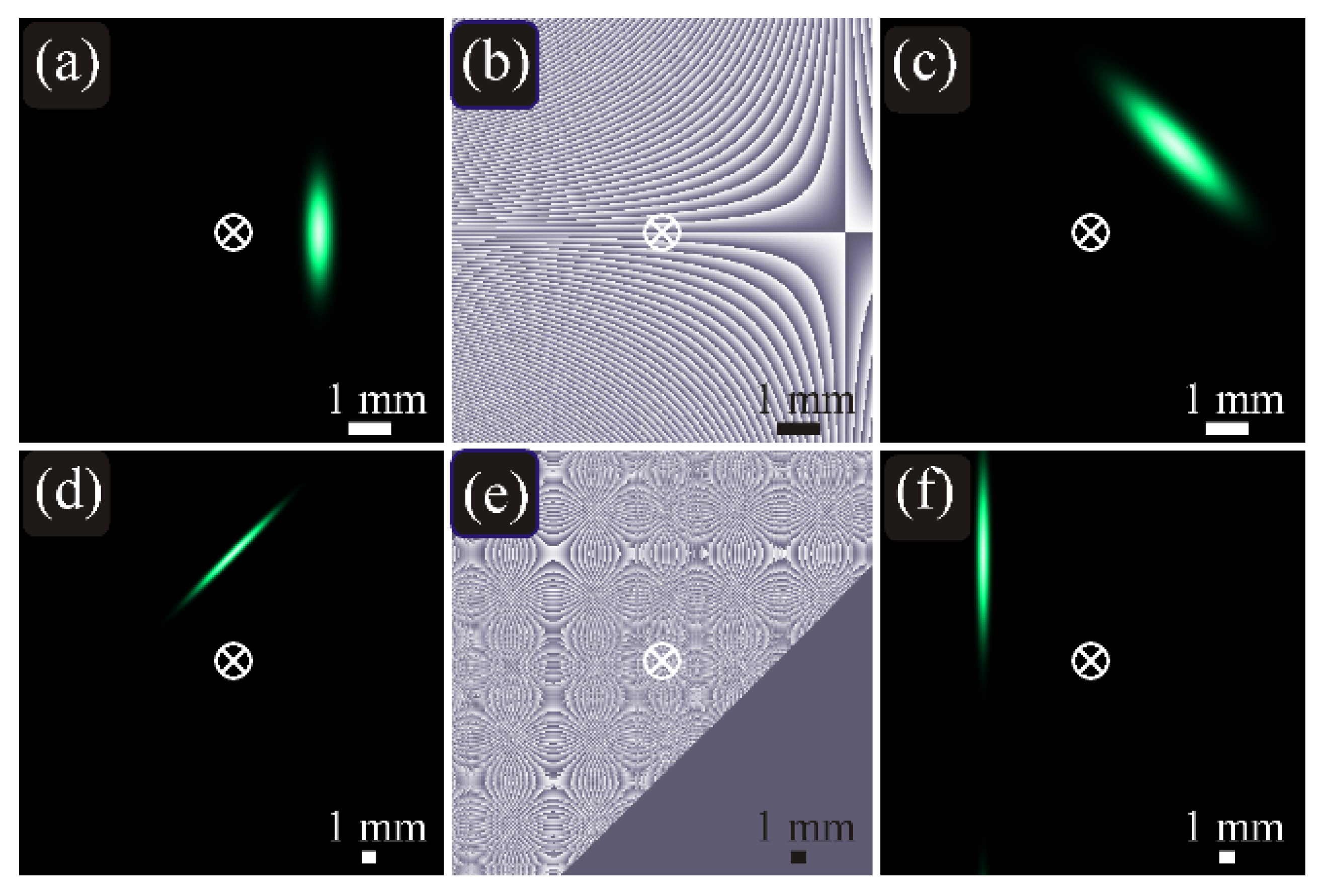
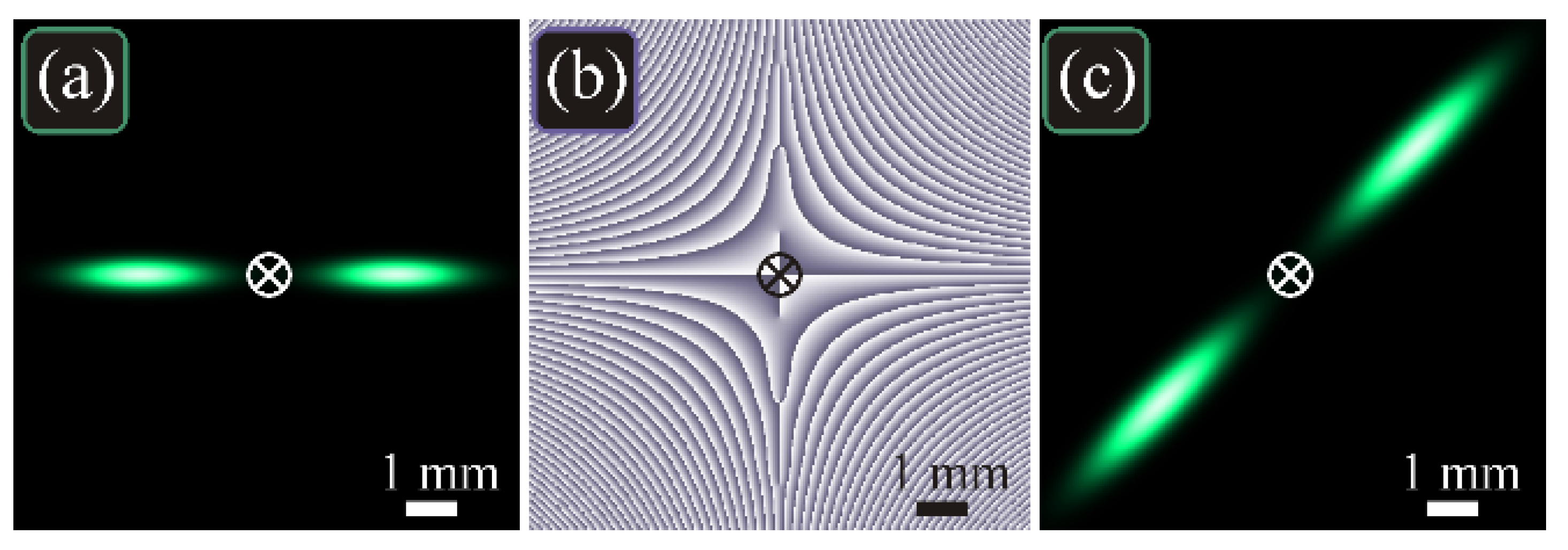
4. Numerical Modeling
5. Beam Power and the Orbital Angular Momentum
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Durnin, J.; Miceli, J.J., Jr.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Vega, J.; Iturbe-Castillo, M.; Chávez-Cerda, S. Alternative formulation for invariant optical fields: Mathieu beams. Opt. Lett. 2000, 25, 1493–1495. [Google Scholar] [CrossRef]
- Bandres, M.; Gutiérrez-Vega, J.; Chávez-Cerda, S. Parabolic nondiffracting optical wave fields. Opt. Lett. 2004, 29, 44–46. [Google Scholar] [CrossRef]
- Siegman, A.E. Lasers; University Science Books: Mill Valley, CA, USA, 1986. [Google Scholar]
- Indebetouw, G. Optical vortices and their propagation. J. Mod. Opt. 1993, 40, 73–87. [Google Scholar] [CrossRef]
- Abramochkin, E.G.; Volostnikov, V.G. Generalized Gaussian beams. J. Opt. A Pure Appl. Opt. 2004, 6, S157–S161. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Vortex Hermite–Gaussian laser beams. Opt. Lett. 2015, 40, 701–704. [Google Scholar] [CrossRef]
- Abramochkin, E.G.; Volostnikov, V.G. Modern Optics of Gaussian Beams; Fizmatlit: Moscow, Russia, 2010; ISBN 978-5-9221-1216-1. [Google Scholar]
- Bock, M.; Das, S.; Grunwald, R. Ultrashort highly localized wavepackets. Opt. Express 2012, 20, 12563–12578. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Pu, J. Investigation on the scintillation reduction of elliptical vortex beams propagating in atmospheric turbulence. Opt. Express 2011, 19, 26444–26450. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media; SPIE Press: Washington, DC, USA, 1998. [Google Scholar]
- Zhang, X.; Xia, T.; Cheng, S.; Tao, S. Free-space information transfer using the elliptic vortex beam with fractional topological charge. Opt. Commun. 2019, 431, 238–244. [Google Scholar] [CrossRef]
- Berry, M.V. Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A Pure Appl. Opt. 2004, 6, 259–268. [Google Scholar] [CrossRef]
- Wu, K.; Huai, Y.; Zhao, T.; Jin, Y. Propagation of partially coherent four-petal elliptic Gaussian vortex beams in atmospheric turbulence. Opt. Express 2018, 26, 30061–30075. [Google Scholar] [CrossRef]
- Skidanov, R.V.; Rykov, M.A. The modification of laser beam for optimization of optical trap force characteristics. Comput. Opt. 2013, 37, 431–435. [Google Scholar] [CrossRef]
- Belousov, D.A.; Dostovalov, A.V.; Korolkov, V.P.; Mikerin, S.L. A microscope image processing method for analyzing TLIPSS structures. Comput. Opt. 2019, 43, 936–945. [Google Scholar] [CrossRef]
- Dostovalov, A.V.; Okotrub, K.A.; Bronnikov, K.A.; Terentyev, V.S.; Korolkov, V.P.; Babin, S.A. Influence of femtosecond laser pulse repetition rate on thermochemical laser-induced periodic surface structures formation by focused astigmatic Gaussian beam. Laser Phys. Lett. 2019, 16, 026003. [Google Scholar] [CrossRef]
- Dostovalov, A.V.; Derrien, T.J.Y.; Lizunov, S.A.; Přeučil, F.; Okotrub, K.A.; Mocek, T.; Korolkov, V.P.; Babin, S.A.; Bulgakova, N.M. LIPSS on thin metallic films: New insights from multiplicity of laser-excited electromagnetic modes and efficiency of metal oxidation. Appl. Surf. Sci. 2019, 491, 650–658. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics, 2nd ed.; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Cai, Y.; Lin, Q. Decentered elliptical Gaussian beam. Appl. Opt. 2002, 41, 4336–4340. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Vortex astigmatic Fourier-invariant Gaussian beams. Opt. Express 2019, 27, 657–666. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Astigmatic laser beams with a large orbital angular momentum. Opt. Express 2018, 26, 141–156. [Google Scholar] [CrossRef]
- Kovalev, A.A.; Kotlyar, V.V. Optical vortex beams with the infinite topological charge. J. Opt. 2021, 23, 055601. [Google Scholar] [CrossRef]
- Bullen, P.S. The Power Means. In Handbook of Means and Their Inequalities; Kluwer: Dordrecht, The Netherlands, 2003; pp. 175–265. [Google Scholar]
- Backlund, M.P.; Lew, M.D.; Backer, A.S.; Sahl, S.J.; Grover, G.; Agrawal, A.; Piestun, R.; Moerner, W.E. The double-helix point spread function enables precise and accurate measurement of 3D single-molecule localization and orientation. Proc. SPIE 2013, 8590, 85900. [Google Scholar]
- Berry, M.V.; Jeffrey, M.R.; Mansuripur, M. Orbital and spin angular momentum in conical diffraction. J. Opt. A: Pure Appl. Opt. 2005, 7, 685–690. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O.; Zhao, D.; Mao, Y. Self-focusing vortex beams. Opt. Lett. 2021, 46, 2384–2387. [Google Scholar] [CrossRef] [PubMed]
- Goorden, S.; Bertolotti, J.; Mosk, A. Superpixel-based spatial amplitude and phase modulation using a digital micromirror device. Opt. Express 2014, 22, 17999–18009. [Google Scholar] [CrossRef]
- Mendoza-Yero, O.; Mínguez-Vega, G.; Lancis, J. Encoding complex fields by using a phase-only optical element. Opt. Lett. 2014, 39, 1740–1743. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovalev, A.A.; Kotlyar, V.V.; Kalinkina, D.S. Propagation-Invariant Off-Axis Elliptic Gaussian Beams with the Orbital Angular Momentum. Photonics 2021, 8, 190. https://doi.org/10.3390/photonics8060190
Kovalev AA, Kotlyar VV, Kalinkina DS. Propagation-Invariant Off-Axis Elliptic Gaussian Beams with the Orbital Angular Momentum. Photonics. 2021; 8(6):190. https://doi.org/10.3390/photonics8060190
Chicago/Turabian StyleKovalev, Alexey A., Victor V. Kotlyar, and Darya S. Kalinkina. 2021. "Propagation-Invariant Off-Axis Elliptic Gaussian Beams with the Orbital Angular Momentum" Photonics 8, no. 6: 190. https://doi.org/10.3390/photonics8060190
APA StyleKovalev, A. A., Kotlyar, V. V., & Kalinkina, D. S. (2021). Propagation-Invariant Off-Axis Elliptic Gaussian Beams with the Orbital Angular Momentum. Photonics, 8(6), 190. https://doi.org/10.3390/photonics8060190




