Simulation of Photonic-Crystal Surface-Emitting Lasers with Air-Hole and Air-Pillar Structures
Abstract
1. Introduction
2. Simulated Structures
3. Methods and Results
3.1. Vertical Mode Profile
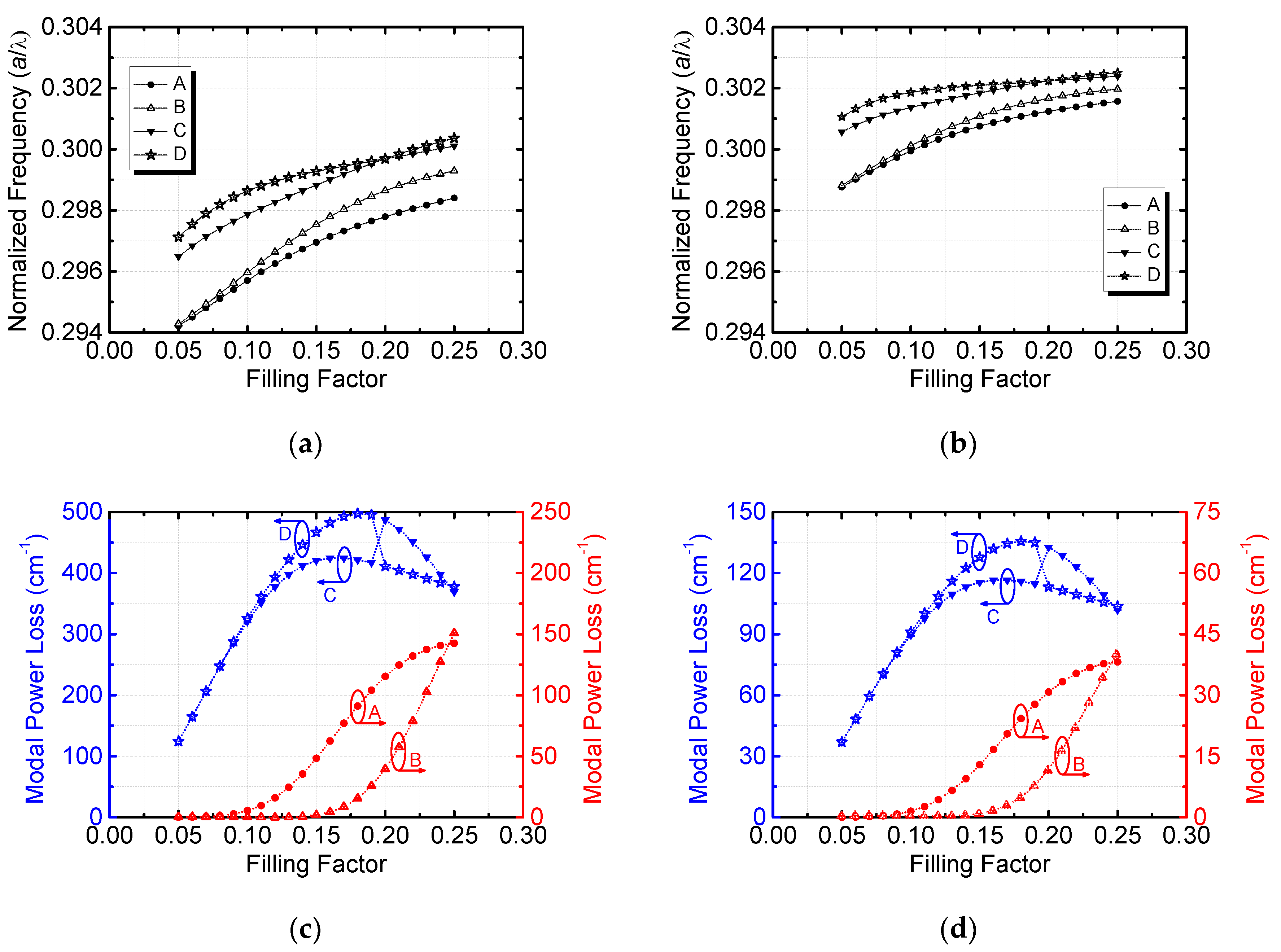
3.2. Threshold Behavior of Infinite Cavity
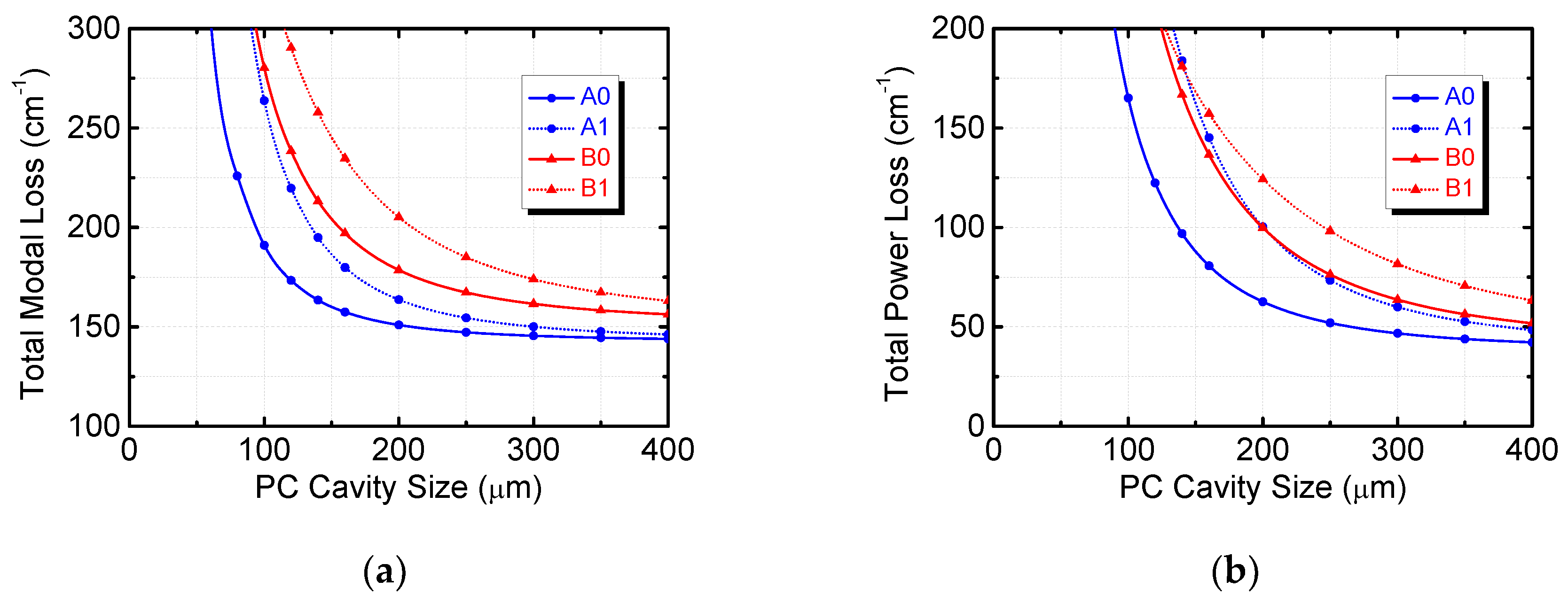
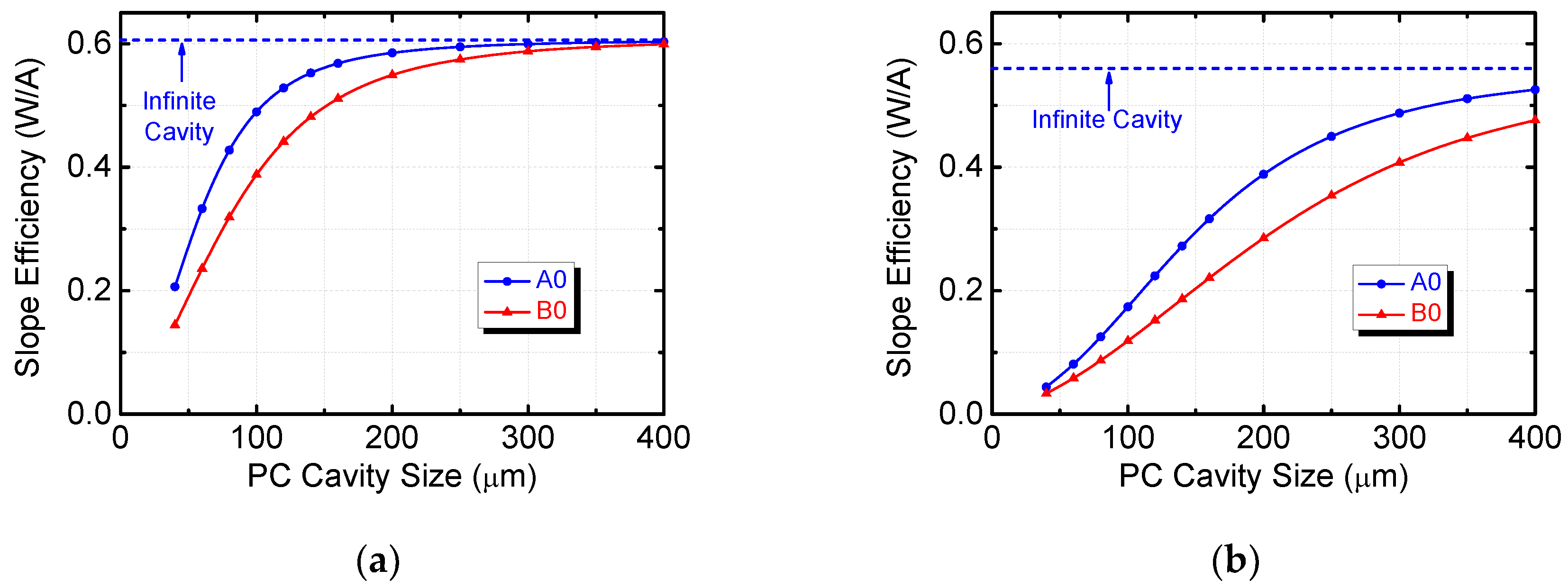
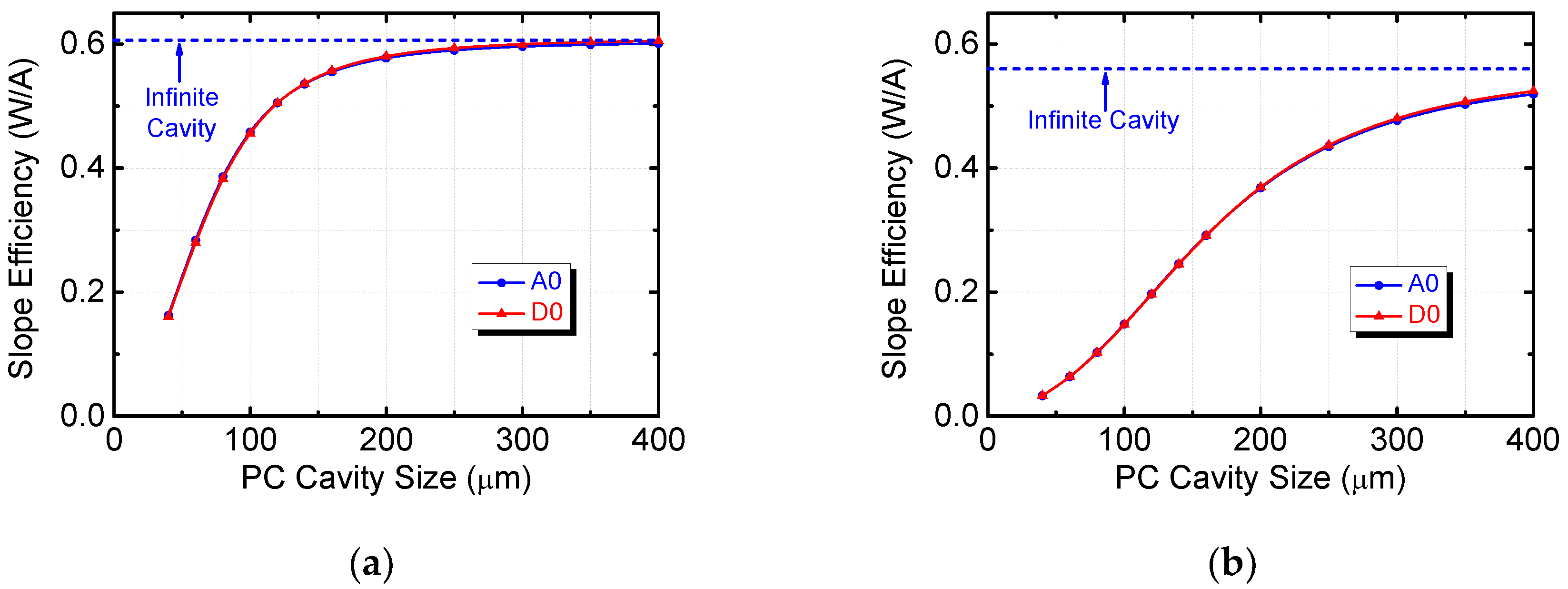
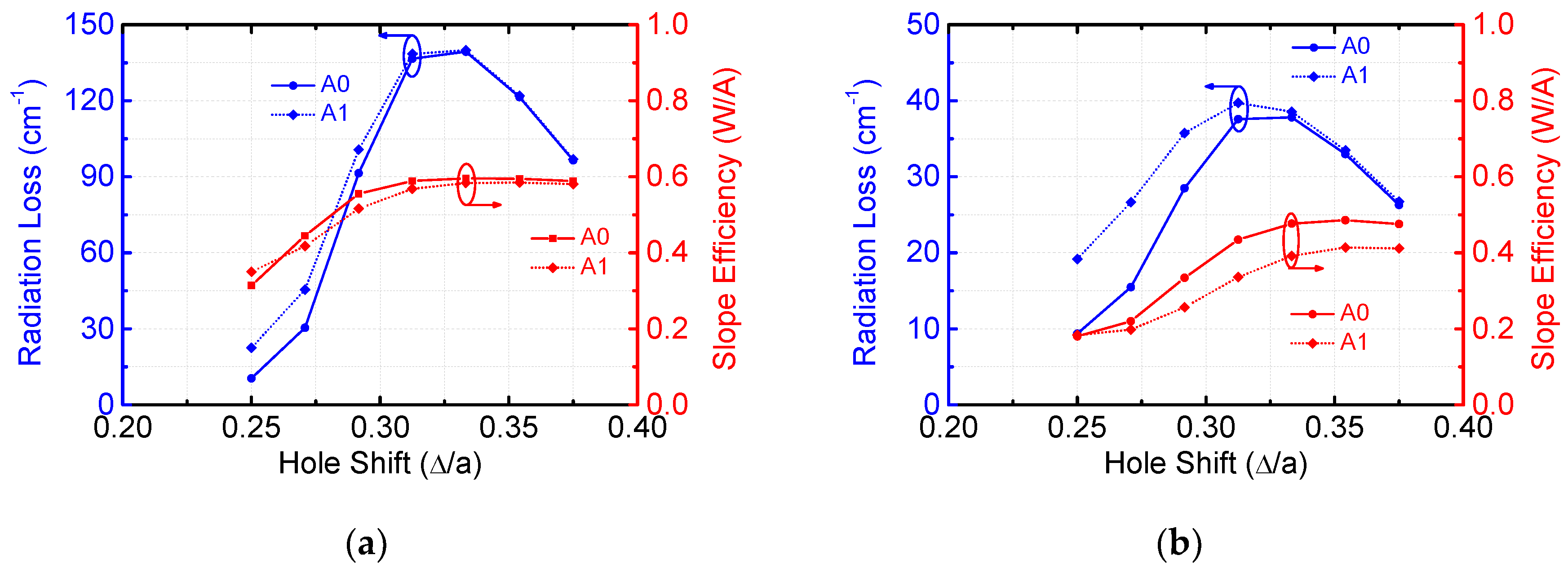
3.3. Finite Size Effect
3.4. Depth Effect
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meier, M.; Mekis, A.; Dodabalapur, A.; Timko, A.; Slusher, R.E.; Joannopoulos, J.D.; Nalamasu, O. Laser action from two-dimensional distributed feedback in photonic crystals. Appl. Phys. Lett. 1999, 74, 7–9. [Google Scholar] [CrossRef]
- Imada, M.; Noda, S.; Chutinan, A.; Tokuda, Y.; Murata, M.; Sasaki, G. Coherent two-dimensional lasing action in surface-emitting laser with triangular-lattice photonic crystal structure. Appl. Phys. Lett. 1999, 75, 316–318. [Google Scholar] [CrossRef]
- Riechel, S.; Kallinger, C.; Lemmer, U.; Feldmann, J.; Gombert, A.; Wittwer, V.; Scherf, U. A nearly diffraction limited surface emitting conjugated polymer laser utilizing a two-dimensional photonic band structure. Appl. Phys. Lett. 2000, 77, 2310–2312. [Google Scholar] [CrossRef]
- Hirose, K.; Liang, Y.; Kurosaka, Y.; Watanabe, A.; Sugiyama, T.; Noda, S. Watt-class high-power, high-beam-quality photonic-crystal lasers. Nat. Photonics 2014, 8, 406–411. [Google Scholar] [CrossRef]
- Yoshida, M.; De Zoysa, M.; Ishizaki, K.; Tanaka, Y.; Kawasaki, M.; Hatsuda, R.; Song, B.; Gelleta, J.; Noda, S. Double-lattice photonic-crystal resonators enabling high-brightness semiconductor lasers with symmetric narrow-divergence beams. Nat. Mater. 2019, 18, 121–128. [Google Scholar] [CrossRef] [PubMed]
- Noda, S.; Yokoyama, M.; Imada, M.; Chutinan, A.; Mochizuki, M. Polarization mode control of two-dimensional photonic crystal laser by unit cell structure design. Science 2001, 293, 1123–1125. [Google Scholar] [CrossRef] [PubMed]
- Mitsuru, Y.; Noda, S. Polarization mode control of two-dimensional photonic crystal laser having a square lattice structure. IEEE J. Quantum Electron. 2003, 39, 1074–1080. [Google Scholar]
- Miyai, E.; Sakai, K.; Okano, T.; Kunishi, W.; Ohnishi, D.; Noda, S. Lasers producing tailored beams. Nature 2006, 441, 946. [Google Scholar] [CrossRef] [PubMed]
- Kurosaka, Y.; Hirose, K.; Ito, A.; Hitaka, M.; Higuchi, A.; Sugiyama, T.; Takiguchi, Y.; Nomoto, Y.; Uenoyama, S.; Edamura, T. Beam pattern projecting on-chip lasers at visible wavelength. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO): Science and Innovation, San Jose, CA, USA, 5–10 May 2019; p. SM4N.2. [Google Scholar]
- Sakata, R.; Ishizaki, K.; De Zoysa, M.; Fukuhara, S.; Inoue, T.; Tanaka, Y.; Iwata, K.; Hatsuda, R.; Yoshida, M.; Gelleta, J.; et al. Dually modulated photonic crystals enabling high-power high-beam-quality two-dimensional beam scanning lasers. Nat. Commun. 2020, 11, 3487. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y.; Nishigo, A.; Kitamura, K.; Gelleta, J.; Noda, S. Modulated photonic-crystal surface-emitting laser with elliptical lattice points for two-dimensional coupling enhancement. AIP Adv. 2019, 9, 115204. [Google Scholar] [CrossRef]
- Noda, S. Progress of Photonic Crystal Surface-Emitting Lasers: Paradigm Shift for LiDAR Sensing and Laser Processing. In Proceedings of the SPIE 11672, Laser Resonators, Microresonators, and Beam Control XXIII, SPIE Photonics West, San Francisco, CA, USA, 6–11 March 2021. [Google Scholar]
- Noda, S.; Yoshida, M.; Kunishi, W.; Inoue, T.; Ishizaki, K.; De Zoysa, M.; Kitamura, K.; Shimaji, N.; Nishimura, K. Photonic crystal lasers: Fabrication with AI-assisted technology and application to LiDAR system. In Proceedings of the SPIE 11703, AI and Optical Data Sciences II, SPIE Photonics West, San Francisco, CA, USA, 6–11 March 2021. [Google Scholar]
- Kim, D.U.; Kim, S.; Lee, J.; Jeon, S.R.; Jeon, H. Free-standing GaN based photonic crystal band-edge laser. IEEE Photonics Technol. Lett. 2011, 23, 1454–1456. [Google Scholar] [CrossRef]
- Hsu, M.Y.; Lin, G.; Pan, C.H. Electrically injected 1.3-μm quantum-dot photonic-crystal surface- emitting lasers. Opt. Express 2018, 25, 32697–32704. [Google Scholar] [CrossRef]
- Hsu, M.Y.; Lin, G.; Li, Z.L.; Pan, P.C. Threshold current temperature dependence of quantum-dot photonic crystal surface-emitting lasers with respect to gain-cavity detuning. Opt. Express 2018, 26, 13483–13488. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Peng, C.; Sakai, K.; Iwahashi, S.; Noda, S. Three-dimensional coupled-wave model for square-lattice photonic crystal lasers with transverse electric polarization: A general approach. Phys. Rev. B 2011, 84, 195119. [Google Scholar] [CrossRef]
- Liang, Y.; Peng, C.; Sakai, K.; Iwahashi, S.; Noda, S. Three-dimensional coupled-wave analysis for square-lattice photonic crystal surface emitting lasers with transverse-electric polarization: Finite-size effects. Opt. Express 2012, 20, 15945–15961. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.; Liang, Y.; Sakai, K.; Iwahashi, S.; Noda, S. Coupled-wave analysis for photonic-crystal surface-emitting lasers on air holes with arbitrary sidewalls. Opt. Express 2011, 19, 24672–24686. [Google Scholar] [CrossRef] [PubMed]
- Sakai, K.; Miyai, E.; Noda, S. Coupled-wave theory for square-lattice photonic crystal lasers with TE polarization. IEEE J. Quantum Electron. 2010, 46, 788–795. [Google Scholar] [CrossRef]
- Iwahashi, S.; Sakai, K.; Kurosaka, Y.; Noda, S. Air-hole design in a vertical direction for high-power two-dimensional photonic-crystal surface-emitting lasers. J. Opt. Soc. Am. B 2010, 27, 1204–1207. [Google Scholar] [CrossRef]
- Hung, C.T.; Syu, Y.C.; Wu, T.T.; Lu, T.C. Design of Low-Threshold Photonic Crystal Surface-Emitting Lasers. IEEE Photonics Technol. Lett. 2012, 24, 866–868. [Google Scholar] [CrossRef]
- Inoue, T.; Yoshida, M.; De Zoysa, M.; Ishizaki, K.; Noda, S. Design of photonic-crystal surface-emitting lasers with enhanced in-plane optical feedback for high-speed operation. Opt. Express 2020, 28, 5050–5057. [Google Scholar] [CrossRef]
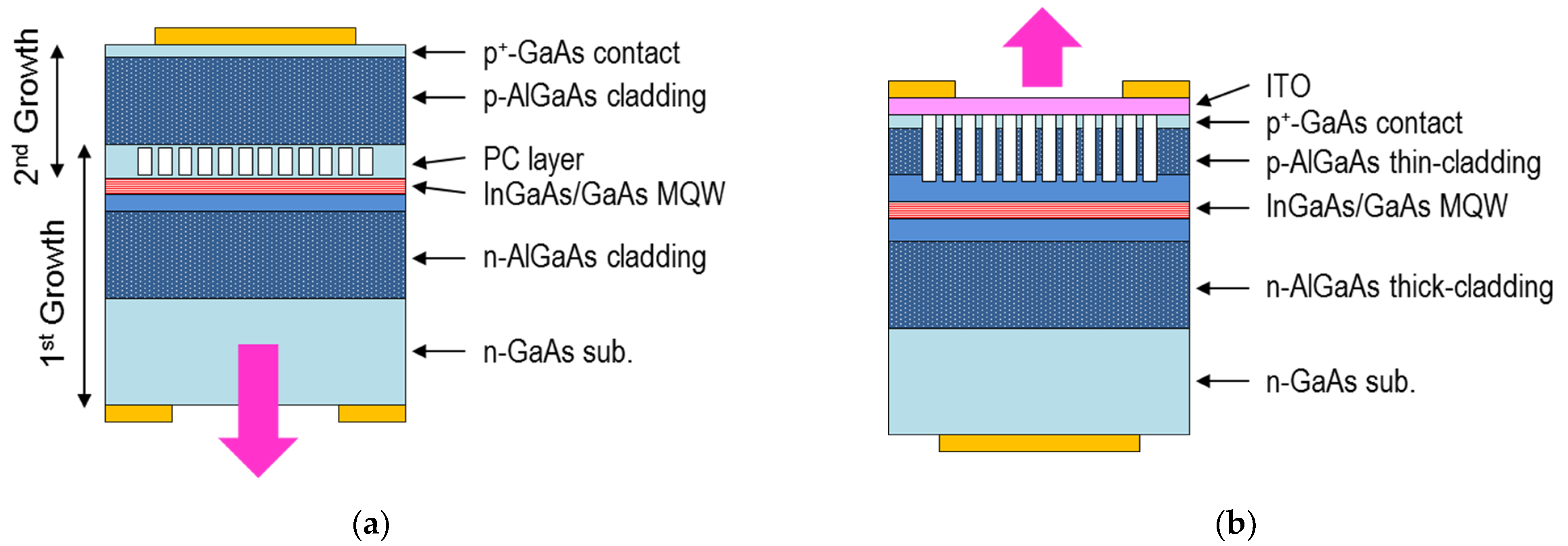
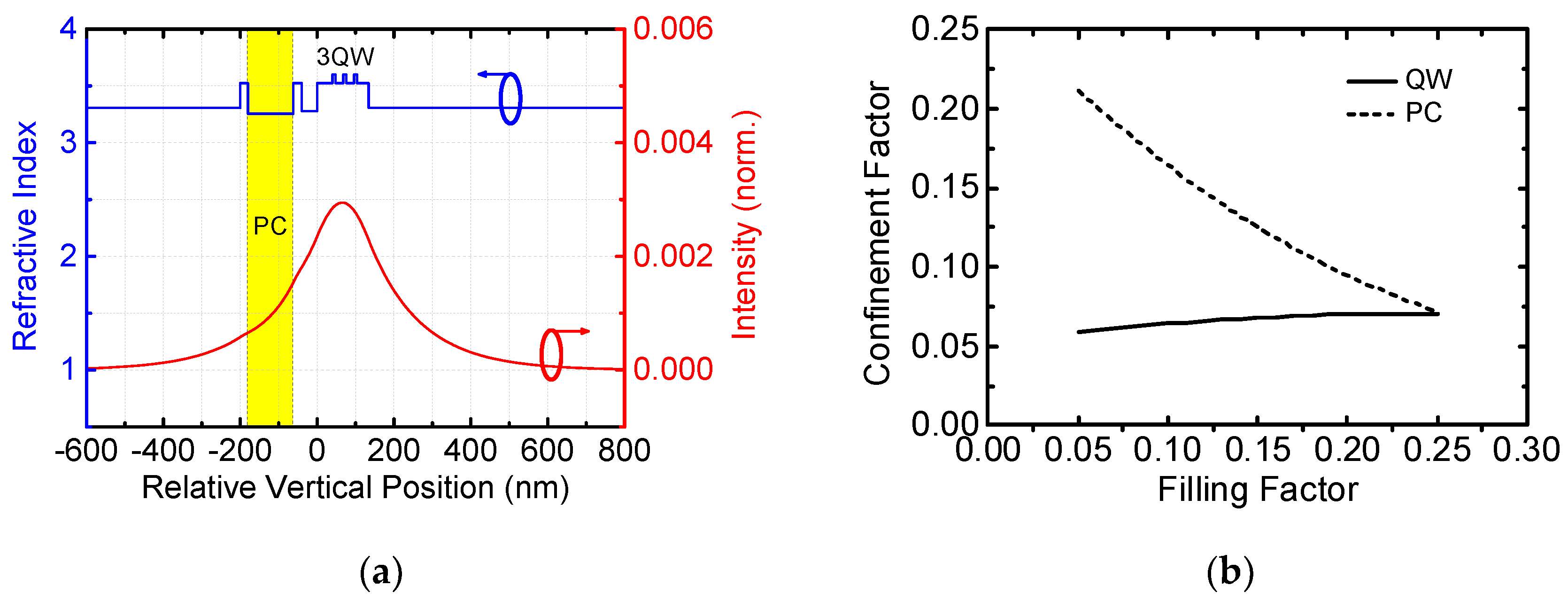
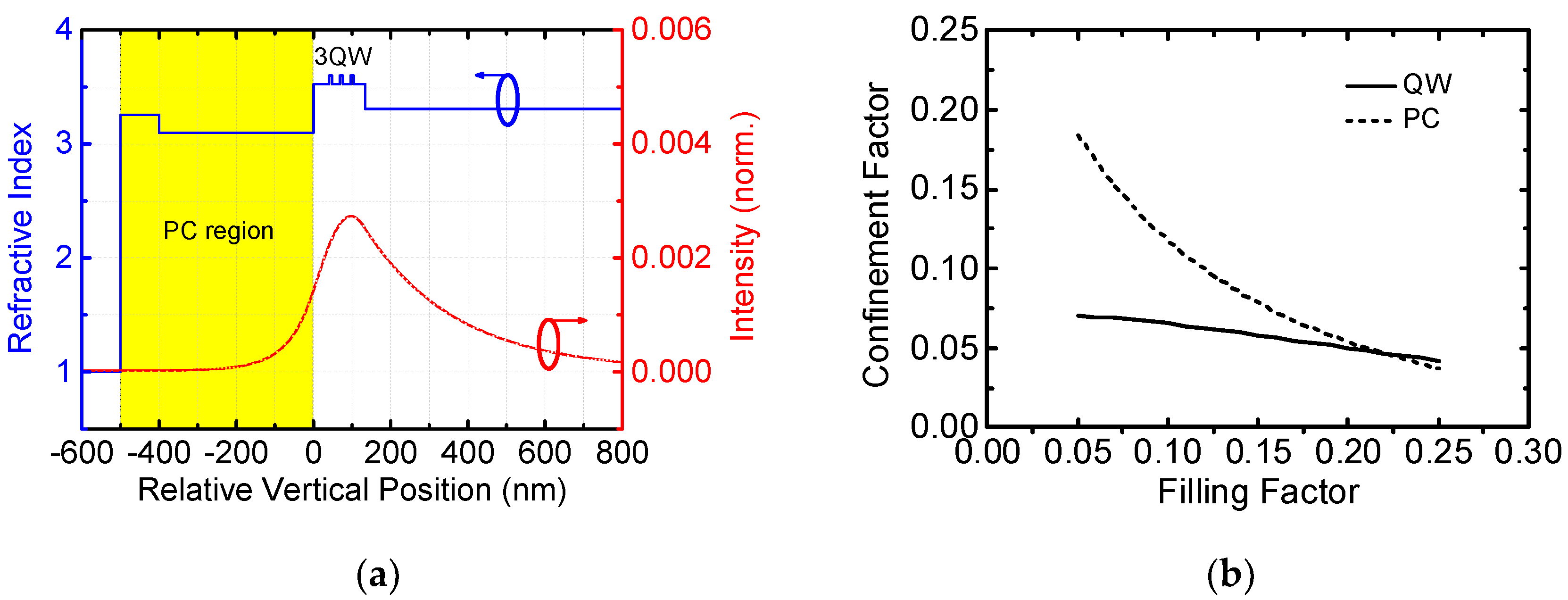
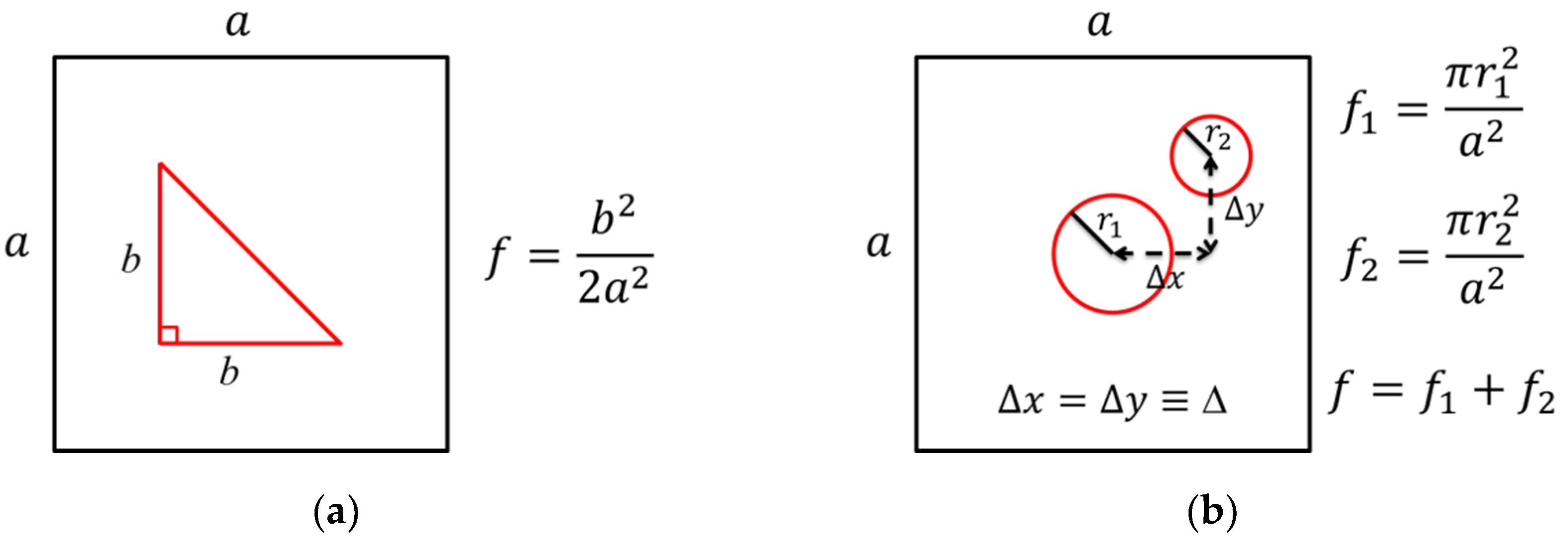



| Layer Description | Thickness (nm) | Refractive Index [18] |
|---|---|---|
| Dummy | - | 1.0 |
| p-contact (GaAs) | 100 | 3.524 |
| p-cladding (AlGaAs) | 1500 | 3.307 |
| GaAs | 20 | 3.524 |
| GaAs + PC (Air Hole) | 118 | nav (3.524 & 1.0) |
| GaAs | 22 | 3.524 |
| cladding (AlGaAs) | 40 | 3.279 |
| GaAs spacer | 40 | 3.524 |
| 3QW (InGaAs/GaAs) | 8 × 3/20 × 2 | 3.6/3.524 |
| GaAs spacer | 30 | 3.524 |
| n-cladding (AlGaAs) | 1500 | 3.307 |
| Layer Description | Thickness (nm) | Refractive Index |
|---|---|---|
| Dummy | - | 1.0 |
| p-contact (GaAs) + PC1 (Air Pillar) | 100 | nav1 (3.524 & 1.0) |
| p-cladding (AlGaAs) + PC2 (Air Pillar) | 400 | nav2 (3.307 & 1.0) |
| GaAs spacer | 40 | 3.524 |
| 3QW (InGaAs/GaAs) | 8 × 3/20 × 2 | 3.6/3.524 |
| GaAs spacer | 30 | 3.524 |
| n-cladding (AlGaAs) | 1500 | 3.307 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.-X.; Kuo, C.-Y.; Lin, G. Simulation of Photonic-Crystal Surface-Emitting Lasers with Air-Hole and Air-Pillar Structures. Photonics 2021, 8, 189. https://doi.org/10.3390/photonics8060189
Yang Z-X, Kuo C-Y, Lin G. Simulation of Photonic-Crystal Surface-Emitting Lasers with Air-Hole and Air-Pillar Structures. Photonics. 2021; 8(6):189. https://doi.org/10.3390/photonics8060189
Chicago/Turabian StyleYang, Zi-Xian, Chia-Yu Kuo, and Gray Lin. 2021. "Simulation of Photonic-Crystal Surface-Emitting Lasers with Air-Hole and Air-Pillar Structures" Photonics 8, no. 6: 189. https://doi.org/10.3390/photonics8060189
APA StyleYang, Z.-X., Kuo, C.-Y., & Lin, G. (2021). Simulation of Photonic-Crystal Surface-Emitting Lasers with Air-Hole and Air-Pillar Structures. Photonics, 8(6), 189. https://doi.org/10.3390/photonics8060189






