Single-Photon Emission by the Plasmon-Induced Transparency Effect in Coupled Plasmonic Resonators

Abstract

The plasmon-induced transparency (PIT) effect with unique spectrum transmission characteristics is a significant property of plasmonic structures. A resonant nanocavity with nanoscale dimensions around a single-photon emitter dramatically enhances the emission rate of the emitter. Thus, we propose detuned resonant nanocavities to manipulate the emission rate of the emitter inside, of which either cell consists of a rectangular resonator surrounded by a U-like resonator. An InGaAs quantum dot in a GaAs nanowire placed in the center of the detuned resonant nanocavity was employed as a single-photon emitter. The finite-difference time domain simulation revealed that the distribution of the electromagnetic field can be affected by changing the coupling intensity between the bright and dark states of the PIT. Consequently, the emission rate of the single-photon emitter was dramatically enhanced by more than 2000 times due to the Purcell effect induced by the PIT in the resonant cavity. With the achievement of an ultrafast single-photon emission rate, the proposed single-photon emitter could have diverse applications in quantum information and quantum communications.

1. Introduction

Due to the quantum interference between different excitation pathways in a multilevel atomic system, an optically opaque medium can be rendered transparent for coherent laser radiation, and a narrow spectral range appears in an absorption line, which is known as the electromagnetically induced transparency (EIT) [1]. As a distinct optical phenomenon, EIT has attracted tremendous attention and possesses a great deal of potential applications, including slow light, quantum correlation transfer and nonlinear optics [2]. However, the need for very low-temperature, stable gas lasers and high-intensity optical pumps makes the experimental realization rather challenging and consequently hinders the realization of the EIT. Recently, a number of configurations have been proposed to realize the EIT-like transmission under mild experimental conditions, such as coupled dielectric resonators [3,4], metamaterial-induced transparency [5,6], phase-coupled plasmon-induced transparency [7] and some other multi-layer structures [8,9,10,11]. Among them, plasmon-induced transparency (PIT) based on surface plasmon polaritons (SPPs) attracted significant attention due to its slight restrictions on the experimental realization [12,13,14,15,16]. SPPs are a distinctive form of electromagnetic wave trapped and propagated at the interface of the metal and insulator with a penetration depth of several nanometers to hundreds of nanometers into the metal. The high confinement of light gives SPPs the capability to break the classical optical diffraction limit and manipulate light within the sub-wavelength scale [17,18,19,20,21,22]. Among plasmonic waveguides, metal–insulator–metal (MIM) structures are of significance due to supporting lightwave propagation in the deep sub-wavelength scale. Thus, MIM-based PIT possesses the advantages of narrower linewidth, faster response time and less power consumption, and has been proved to minimize the limitations of the abovementioned harsh conditions [23,24,25,26].

Therefore, based on the remarkable properties of SPPs, a fast III-V heterostructured QDNW single-photon emitter was proposed to enhance the spontaneous emission rate. The enhancement is realized by the on-chip MIM-based PIT in integrated plasmonic components using detuned coupling resonators that are aperture side-coupled to a bus waveguide. As the single-photon emitter, the InGaAs QD inside the heterostructured InGaAs/GaAs QDNW provides efficient photon generation. The structure of detuned coupling resonators has been elaborately designed to maximally enhance the photoemission rate of the InGaAs QD. By using the FDTD method, the transmission characteristics of the proposed PIT nanostructure and the impact of the nanocavity on the emitting properties of the QD were investigated in detail.

2. Structure and Method

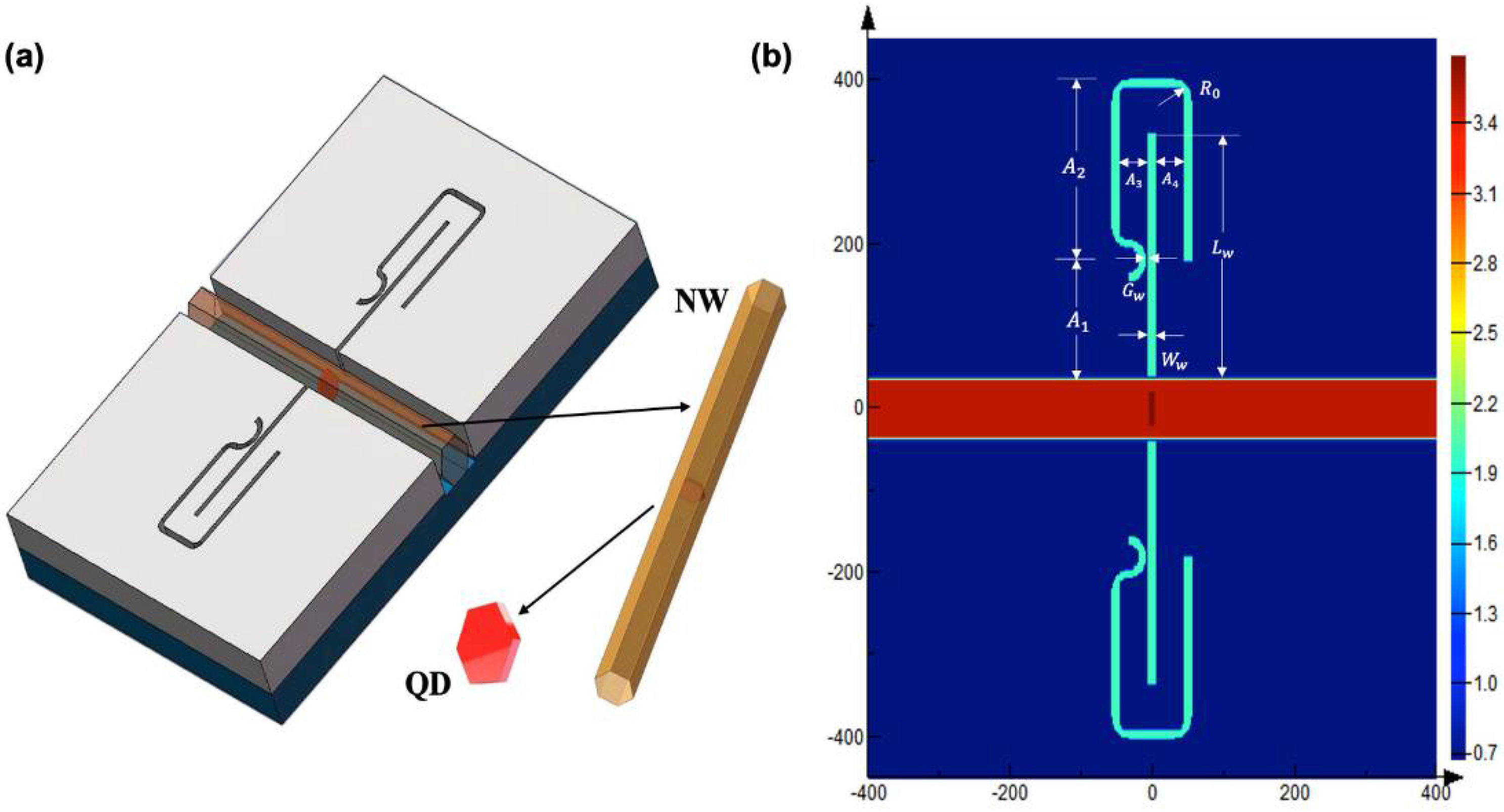
The three-dimensional schematic diagram of the proposed plasmonic nanostructure is depicted in Figure 1. The plasmonic nanostructure is based on the MIM waveguide, which consists of a bus waveguide, a rectangular resonator and a U-like resonator. In the proposed structure, the width of the resonator is denoted by W_w, the lengths of the rectangular resonator and the U-like resonators are denoted by L_w and A₁, A₂, respectively. The distances between the two resonators are denoted by A₃ and A₄.

The nanoscale MIM waveguide supports deep wavelength plasmonic mode propagation. The dispersive characteristic of the fundamental TM mode in the MIM waveguide is given by [27,28]:

$${\epsilon }_{in}{k}_{Z2}+{\epsilon }_m{k}_{Z1}\coth \left(-\frac{{ik}_{Z1}}{2}w\right)=0$$

(1)

where $k_{Z1}$ and $k_{Z2}$ are

$$k_{Z1}^2={\epsilon }_{in}{k}_0^2-{\beta }^2, k_{Z2}^2={\epsilon }_m{k}_0^2-{\beta }^2.$$

(2)

${\epsilon }_{in}$, ${\epsilon }_m$ are the dielectric constants of the insulator and the metal, $k_0=2\pi /\lambda$ is the free-space wave vector.

In the structure, the medium material of the waveguide is set to be Si₃N₄. The background metal is supposed to be silver, whose frequency-dependent relative permittivity can be characterized by the Drude model:

$${\epsilon }_{Ag}\left(\omega \right)={\epsilon }_{\infty }-{\omega }_p^2/[\omega \left(\omega +i\gamma \omega \right)$$

(3)

where ${\epsilon }_{\infty }=3.7,{\omega }_p=1.38\times {10}^{16}$ rad/s and $\gamma =2.73\times {10}^{13}$ rad/s [5,29,30].

At the opposite side of the bus waveguide are the two detuned aperture-coupled plasmonic resonators with a certain separation. SPPs generate when light with specific wavelength is injected into one port of the bus waveguide. In the condition of matched wave factors and resonance parameters, the propagating SPP wave confined at the metal–dielectric interface couples to the resonators. However, due to the separated position, the SPP wave inside the bus guide is only coupled to the rectangular resonator and cannot interact directly with the U-like resonator. Therefore, the rectangular resonator here serves as a bright resonator, while the U-like resonator behaves as the dark resonator. In order to achieve the nanoscale volume of the cavity, the rectangular and U-like resonators are set to be extremely narrow, with a width of 10 nm. The rectangular resonator is perpendicular to the QDNW and connected to the center of the bus waveguide. The InGaAs/GaAs QDNW is placed inside the MIM bus waveguide, and the InGaAs QD is embedded in the center of the GaAs NW. The diameter of the nanowire is 70 nm, the diameter and thickness of the QD are 40 nm and 8 nm, respectively. Considering the position deviation of the QDNW inside the bus waveguide, air gaps exist between the NW surface and channel walls. Thus, the width of the air gap is assumed to be 5 nm here. In our study, PIT effects are realized by constructing the coupling between bright and dark cavities, and the induced transparency peak value is controlled by adjusting the cavity length and coupling distance of the rectangular and U-like resonators. The proposed structure could be fabricated by the following steps: first, a metal film is deposited on a silica substrate; then the required pattern is fabricated by EBL and etching; lastly, the QDNW is placed inside the bus waveguide. This step needs fine micromanipulation.

3. Results and Discussion

To control the spontaneous emission rate of a single-photon emitter, cavity quantum electrodynamics (QED) was proposed by Weisskopf and Wigner [8,31,32]. In the cavity QED, optical cavities provide an intriguing way to alter the interaction of light with matter and have been employed in a wide range of fields. As the spontaneous emissivity of the emitter is proportional to the local density of the optical state, for an emitter placed in a homogeneous medium, its spontaneous emission rate is not constant depending on the transition dipole moment of the emitter and the dielectric constant of the surrounding medium. When the QDNW is placed in the channel of the bus waveguide, the electromagnetic energy is mainly confined inside the channel, allowing the propagation of the pumped and emitted photons inside the channel. As the two transmission dips show in Figure 2, the incident SPP wave from the bus waveguide excites the bright resonator directly, while the dark resonator is excited by the coupling with the bright resonator. Additionally, the magnetic fields Hz between the bus waveguide channel and bright resonator are always out of phase, consequently preventing the SPP wave passing through. At the transparency peak, the dark resonator is strongly excited, while its counterpart is suppressed. This is similar to the EIT effect of an atomic system, where cancellation of the bright resonator arises from the destructive interference of two pathways. As shown in Figure 3, the two pathways in the proposed device are as follows: bus waveguide → rectangular resonator and bus waveguide → rectangular resonator → U-like resonator → rectangular resonator. These two pathways destructively interfere with each other, creating a transparent spectral window. Thus, photons emitted from the QD at the specific transparent spectrum window transparently propagate through the bus waveguide.

To investigate the factors that produce PIT effects, the finite difference time domain method was adopted to calculate and simulate the proposed structure. This method allows us to use frequency-dependent dielectric constant of metals and dielectrics including both the real and imaginary parts to maximally approach the experimental data. Perfectly matched layer absorbing boundary conditions were used at all boundaries of the simulation domain. The parameters of the structure were set as $W_w=10 \mathrm{nm}$, $L_w=295 \mathrm{nm}$, $G_w=2 \mathrm{nm}$, $A_1=125 \mathrm{nm}$, $A_2=215 \mathrm{nm}$, $R_0=20 \mathrm{nm}$, $A_3=A_4=2\ast R_0+G_w+w_w$. The dielectric materials of the bus waveguide and resonator were regarded as air and Si₃N₄, respectively. As illustrated in Figure 2, the variation of the resonator parameters gives rise to the shift of the transmission spectrum. When the parameter of the U-like resonator is set to be zero, the detuning of wavelength disappears together with the absence of the PIT effect (the blue curve in Figure 2a). Figure 2b shows the distributions of the electric and magnetic amplitudes corresponding to the three characteristic frequencies represented by $f_A$, $f_B$ and $f_C$ in Figure 2a. The resonant characteristics of the bright and dark states can be clearly distinguished. At the frequencies of $f_A$ and $f_C$, when the rectangular cavity is coupled to the U-like cavity in the near field, the mode splitting in a single cavity results in in-phase and out-of-phase states. Each state corresponds to a minimum transmittance value at frequencies of $f_A$ and $f_C$, respectively. The electromagnetic wave enters the resonator through the coupling effect, and goes to the U-like resonator after being reflected by the end of the rectangular resonator. Inside the U-like resonator, plasmonic modes interfere and oscillate. Thus, most of the energy concentrates on both sides of the U-like cavity. Only a small part of the electromagnetic wave passes through the bus waveguide, yielding the minimum transmittance value in the transmission spectrum. Therefore, the transmission of the waveguide at frequencies $f_A$ and $f_C$ is low. At frequency $f_B$, due to the large difference between the incident wavelength and the resonance wavelength, a phase difference appears between the reflected waves on both sides of U-like resonator, leading to destructive interference. Therefore, the electromagnetic energy from the bus waveguide coupled into the cavity is suppressed. The coupling effect between the bright and dark resonators results in the strong resonance in the dark resonator. The oscillation of the bright resonator can be suppressed by the strong excitation of the dark resonator in a destructive way, meaning that the interaction between bright and dark resonators leads to an intense excitation in the dark resonator and a weak excitation in the bright resonator. Thus, a transmission peak appears at the frequency $f_B$.

The local electromagnetic field density has a great impact on the spontaneous emission rate. Therefore, the spontaneous emission rate can be modified by adjusting the spatial and spectral redistribution of the vacuum fluctuation. The eigen radiation life of a quantum emitter placed in an unconstrained dielectric is about 10 ns, which is not fast enough to satisfy the high repetition rate of single-photon emission for quantum communications. Here, QDNW is placed inside the channel and a resonator is connected on one side to realize the enhancement effect of the local field. The Purcell factor can be defined as the ratio of the spontaneous radiation rate of an artificial atom in a given mode (usually a cavity mode) of a structure to the spontaneous emission rate in a bulk material [29,33]. Thus, the Purcell factor can be used to quantify the enhancement level of the emission rate of quantum dots in the nanocavity. The specific expression is:

$$F_P=\frac{{\gamma }_{SE}}{{\gamma }_0}=\frac{3Q{\lambda }^3}{4{\pi }^{2}V}$$

(4)

where ${\gamma }_0$ and ${\gamma }_{SE}$ are the free space and modified spontaneous emission rates, respectively.

The quality factor Q indicates how long the stored energy remains in the cavity when inter-band transitions are absent, which is defined as:

$$\frac{1}{Q}=\frac{{\gamma }_{cav}}{\omega }=\frac{V_{g,z}\left(\omega \right)}{\omega }[{\alpha }_i+\frac{1}{L}In(\frac{1}{R})]$$

(5)

A high-quality factor indicates a low rate of energy loss relative to the stored energy of the cavity. In the weak coupling between the quantum system and the cavity, the Purcell factor F is proportional to Q/V. The SPPs are induced by the electron collective oscillation of the metal electrons, accompanied by the near-field enhancement. When quantum dots are placed in the near-field region of the plasmonic structure, the plasmonic structure acts as an optical cavity. The mode volume V can be shrunk to the sub-wavelength scale. However, due to the large intrinsic loss of this structure, the quality factor Q is relatively small. Here, to quantify the nanoscale confinement, the modal effective volume V is defined as the product of the modal effective area and nanocavity length. The modal effective area is defined as the ratio of a mode’s total energy density per unit length and its peak energy density [29]:

$$V=\frac{\int W_{\left(r\right)}}{\max \left\{W_{\left(r\right)}\right\}}$$

(6)

where $W_{\left(r\right)}$ is the energy density for dispersive and lossy materials.

$$W_{\left(r\right)}=\frac{1}{2}\left(\frac{d\left(\epsilon \left(r\right)\omega \right)}{d\omega }\left|E\left(r\right){|}^2+{\mu }_0\right|H\left(r\right){|}^2\right)$$

(7)

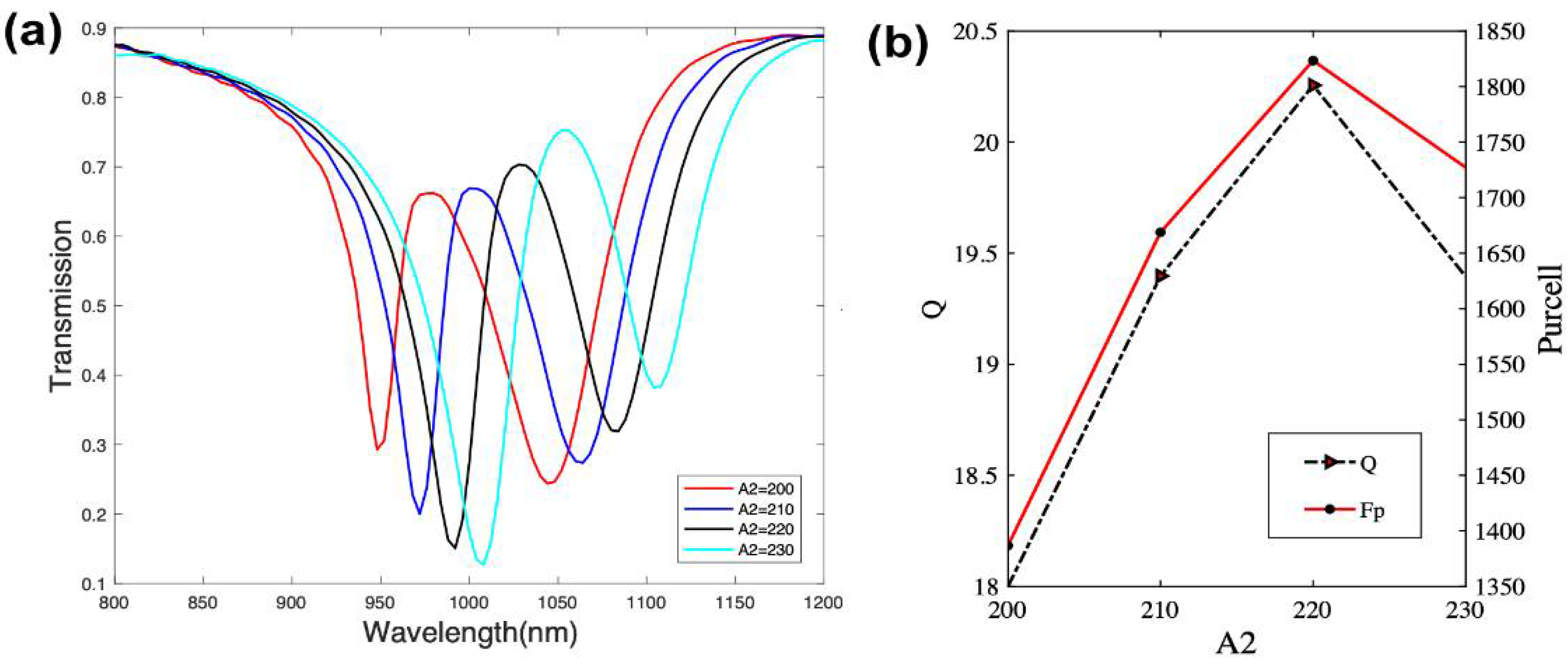
In order to reveal the physical mechanism and realization conditions of the PIT effect in a resonant structure in detail, structural parameters with different coupling distances and cavity lengths were calculated to observe the effects on the coupling resonance. Figure 4 demonstrates the transmission spectra corresponding to different $A_2$ when $L_w$ = 295 nm, $W_w$ = 10 nm and $A_1$ = 125 nm. From the simulation results, the transmittance curve moves towards the short wavelength as $A_2$ is reduced, and the resonance wavelength cavity shows red-shift behavior. This phenomenon can be explained by the Fabry–Perot cavity theory. With the increasing cavity length, the SPP wavelength satisfies the resonant conditions in the cavity and also increases. As for the dependences of the resonant wavelength ${\lambda }_R$ on the rectangular length depicted in Figure 5, the resonant wavelength moves towards shorter a wavelength with decreasing length, which remains consistent with the standing-wave condition in an oscillating cavity:

$${\lambda }_R\propto 2n_{eff}L$$

(8)

where $n_{eff}$ and L are effective refractive index and cavity length, respectively. From the equation, the resonant wavelength has positive proportional relationships with the effective refractive index and nanocavity length. When the material of structure is fixed, the nanocavity length is determined by the resonant wavelength. As the length $L_w$ of the rectangular cavity increases, the coupling between rectangular and U-like cavities gradually strengthens. Consequently, the full width at half maximum of the PIT transparent spectral window significantly increases. The penetration depth of SPPs in the metal decreases exponentially due to the ohmic loss of the metal. With the decreasing coupling spacing, more energy couples to the resonator. The larger coupling strength results in the increase in the effective refractive index of the resonator. Thus, a smaller width results in a red shift of the resonant wavelength, while a larger width results in a blue shift of the resonant wavelength. The nanocavity width is crucial to the modal effective index. The resonant wavelength decreases with the increase in $W_w$, and the effective refractive index of the MIM waveguide decreases with the increase in the resonant cavity width. Furthermore, by adjusting the parametric values of length and width of the nanocavity, the resonant wavelength could match the tuning composition of the QD single-photon emitter.

According to Formula (4), the Purcell factor is mainly determined by the Q factor and modal volume. The impacts of the Q factor and modal volume on the Purcell factor are contradictory. As it is known that plasmonic cavities are highly lossy with ultra-small dimensions, it is difficult to achieve large Q factors in plasmonic cavities. However, the modal effective volume in plasmonic cavities can be shrunk into dimensions beyond the optical diffraction limit. Under this circumstance, the modal effective volume dominated the Purcell factor of plasmonic cavities. Therefore, regardless of the relatively small Q factor, a very large Purcell factor could still be achieved due to the nanoscale structures and ultra-small modal effective volume. As shown in Figure 4, both the Q and Purcell factors increase with the increase in $A_2$. As the lengths of the nanocavities $A_2$ increase, the coupling between the U-like shaped resonator and QDNW becomes stronger, allowing more energy coupling in the cavity. As shown in Figure 6, when the length of the resonator remains unchanged, a larger width of the resonator results in more energy coupling in the cavity. Thus, the position, width and shape of the PIT transparent window can be controlled effectively by selecting appropriate structural parameters. The increase in resonator width W reduces the effective refractive index of the MIM waveguide and weakens the light field confinement. Although the Q factor becomes smaller accordingly, the modal volume increases with the increasing W_w, leading to a decreasing Purcell factor with the increase in W_w.

4. Conclusions

The MIM-based PIT effect has been numerically investigated in the MIM nanostructured plasmonic resonator consisting of a U-like resonator, a rectangular cavity and a bus waveguide. The QDNW placed inside the bus waveguide offers site controllability for the QD single-photon emitter with efficient photon generation. The nanocavity constructed by the wire slot perpendicular to quantum dots has a very narrow width of 10 nm. Hence, the dimensions are far beyond the optical diffraction limit and the nanoscale modal effective volume significantly modified the electromagnetic environment surrounding the QD. Bright and dark states were obtained by the coupling between the U-like resonator and rectangular cavities. The destructive interference between the bright and dark states led to a PIT transmission spectrum of the proposed structure. The induced transparency peak of the PIT can be manipulated by tuning the coupling distance between the bright and dark resonators. Due to the Purcell effect arising from the modified electromagnetic environment by the coupling of the bright and dark resonators, the spontaneous emission rate can be maximally enhanced by more than 2000 times. Thus, the proposed ultrafast plasmonic QDNW single-photon emitter is promising for quantum information areas.