Electron Dynamics and Thomson Scattering for Ultra-Intense Lasers: Elliptically Polarized and OAM Beams
Abstract
1. Introduction
2. General Formulation
2.1. Classical Equations of Motion for the Electron
2.2. Asymptotic Liénard–Wiechert Retarded Radiation Fields
2.3. Spectral Asymptotic Liénard–Wiechert Retarded Radiation Fields: Integral Representations
3. Elliptically Polarized Radiation: Parametric Representation of Dynamical Variables
3.1. Representation of an Arbitrary Non-Monochromatic Plane Wave through the Vector Potential
3.2. The Vector Potential and the Solution of the Electron Dynamics for Monochromatic Elliptically Polarized Radiation
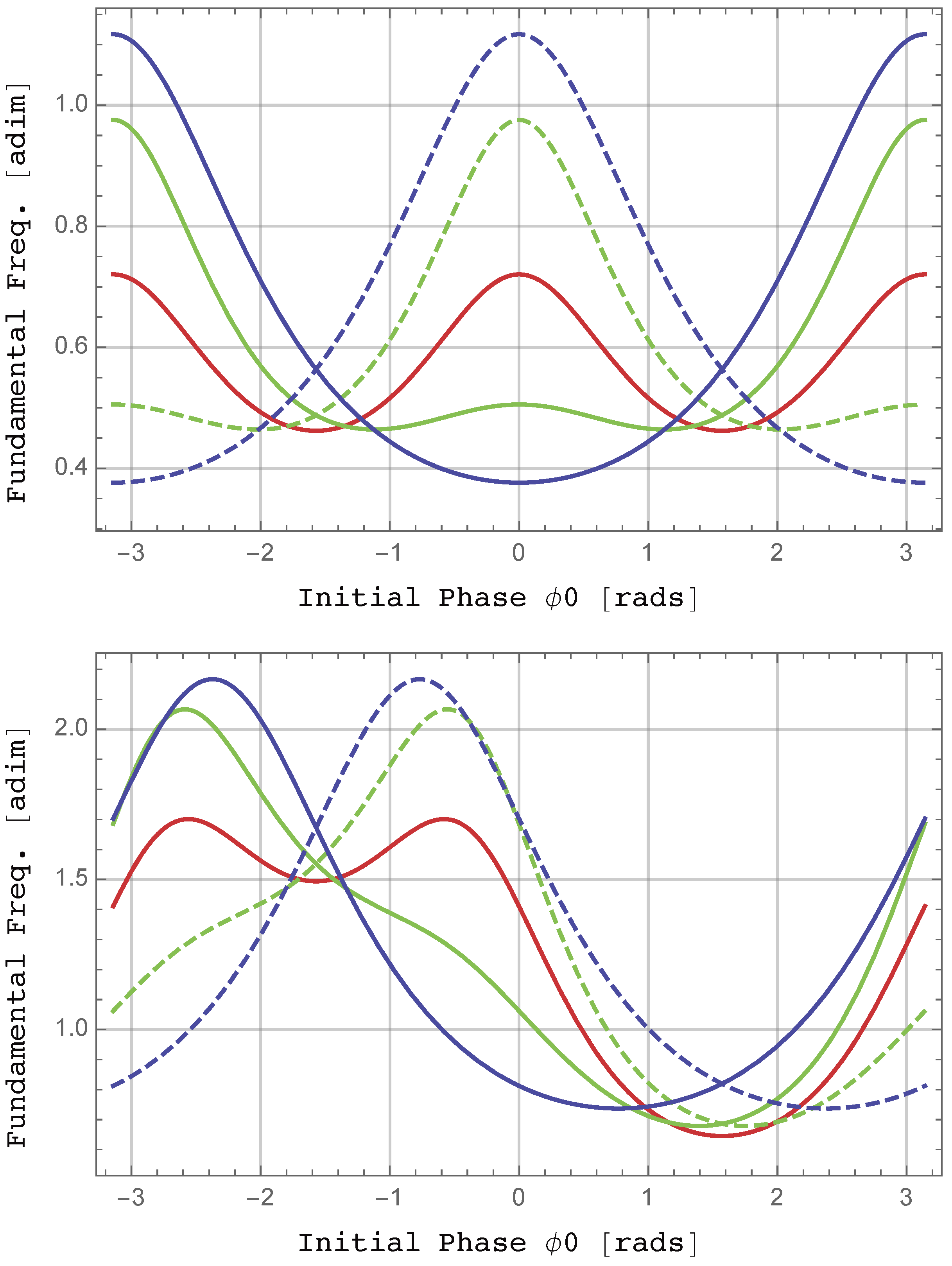
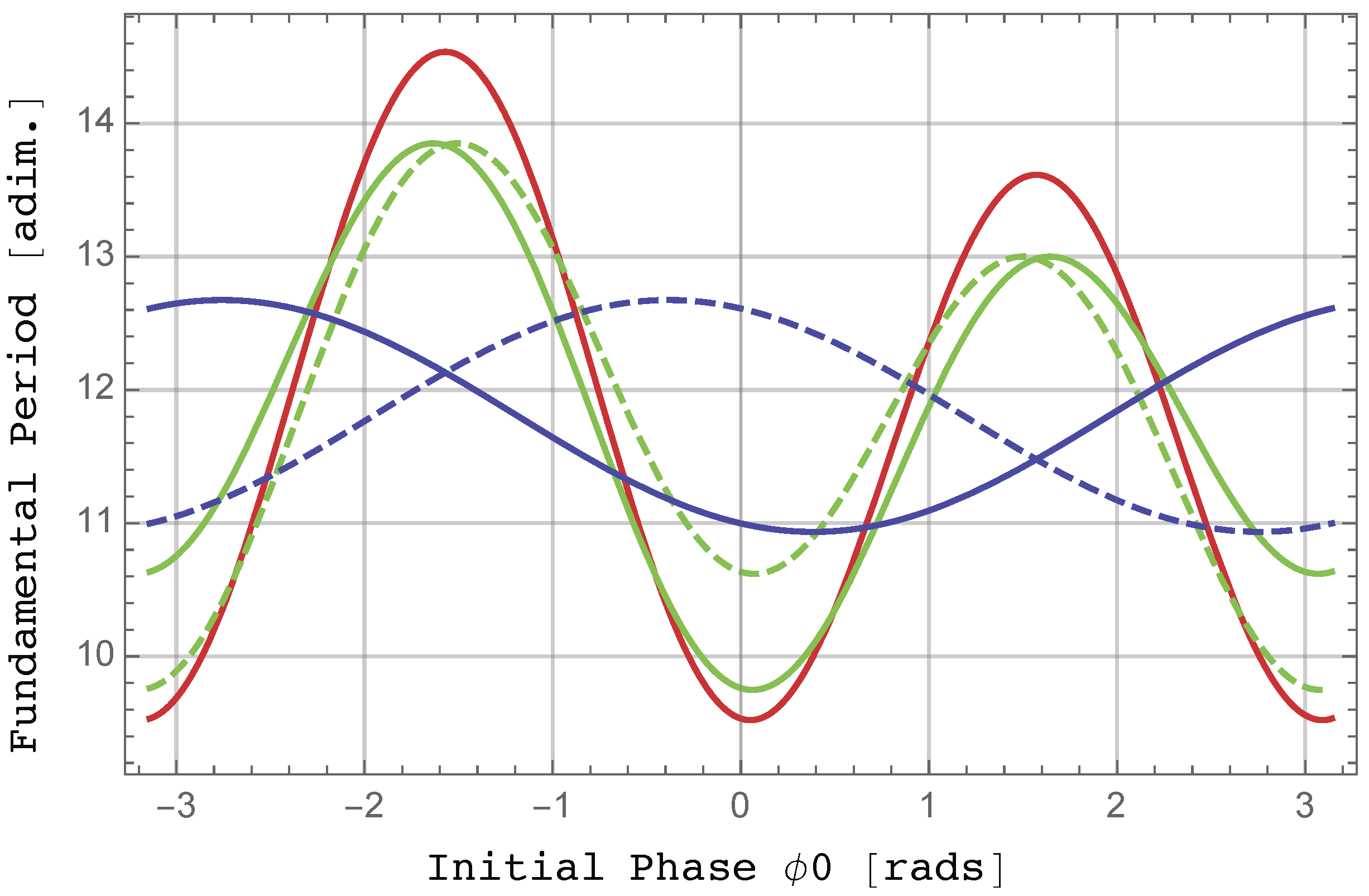
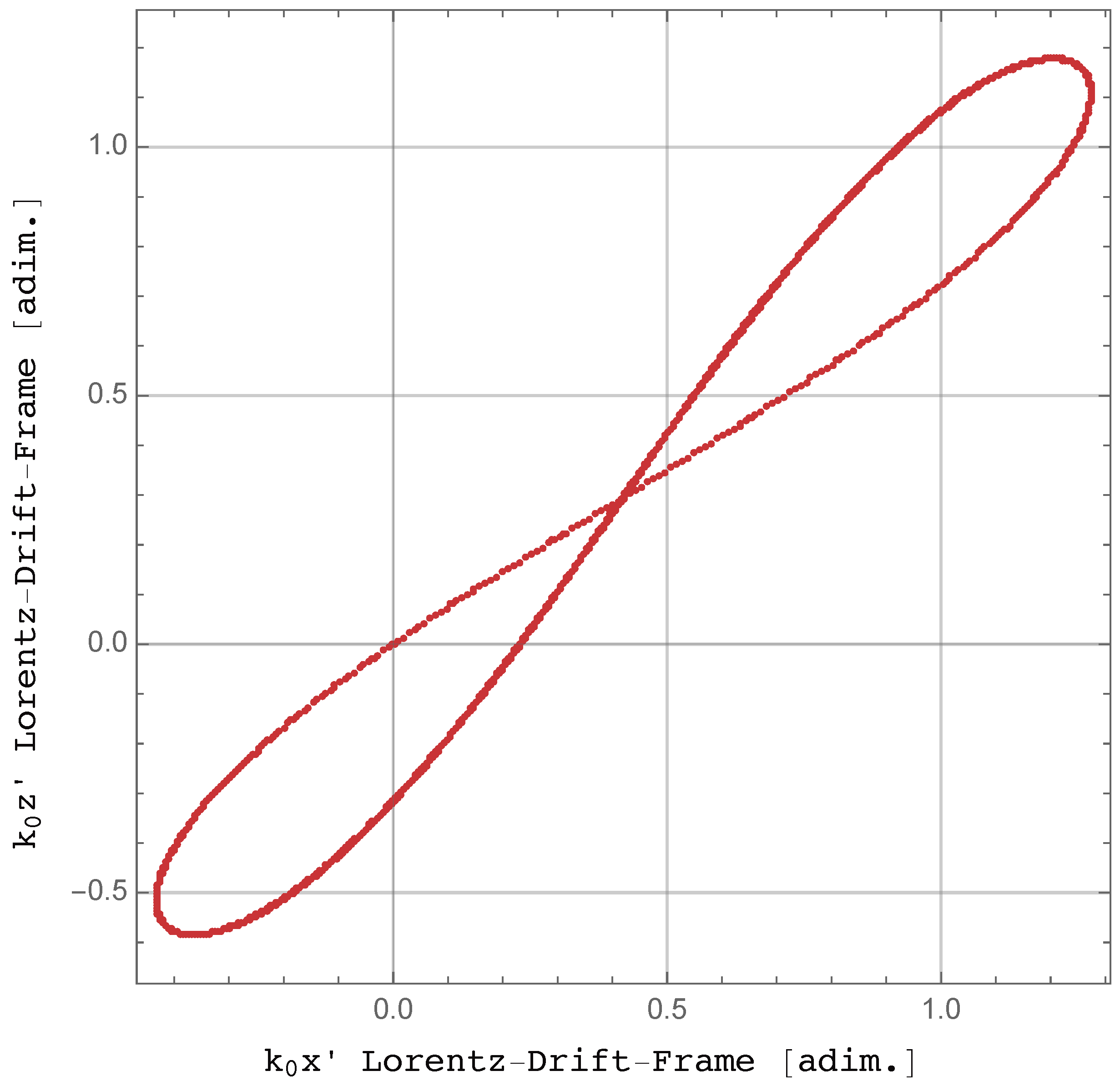
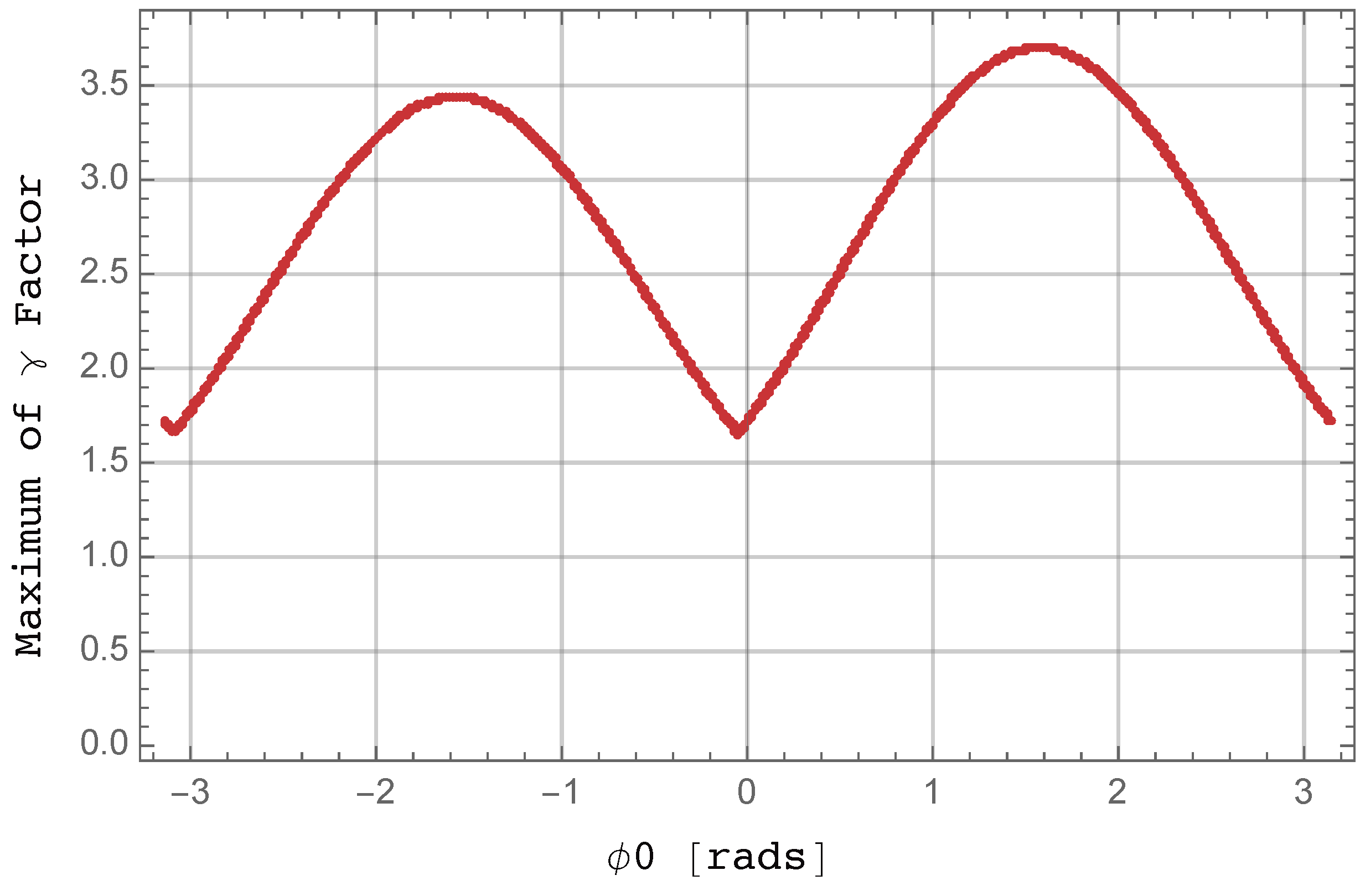
3.3. Magnitudes Derived from the Parametric Representation of Trajectories
4. Spectral Representation for Elliptically Polarized Incoming Radiation: The Integrand and Doppler Frequencies
5. TS for an Incoming Laser Beam with OAM
5.1. Incoming Laser Beam with OAM: Vector Potential and Electromagnetic Fields
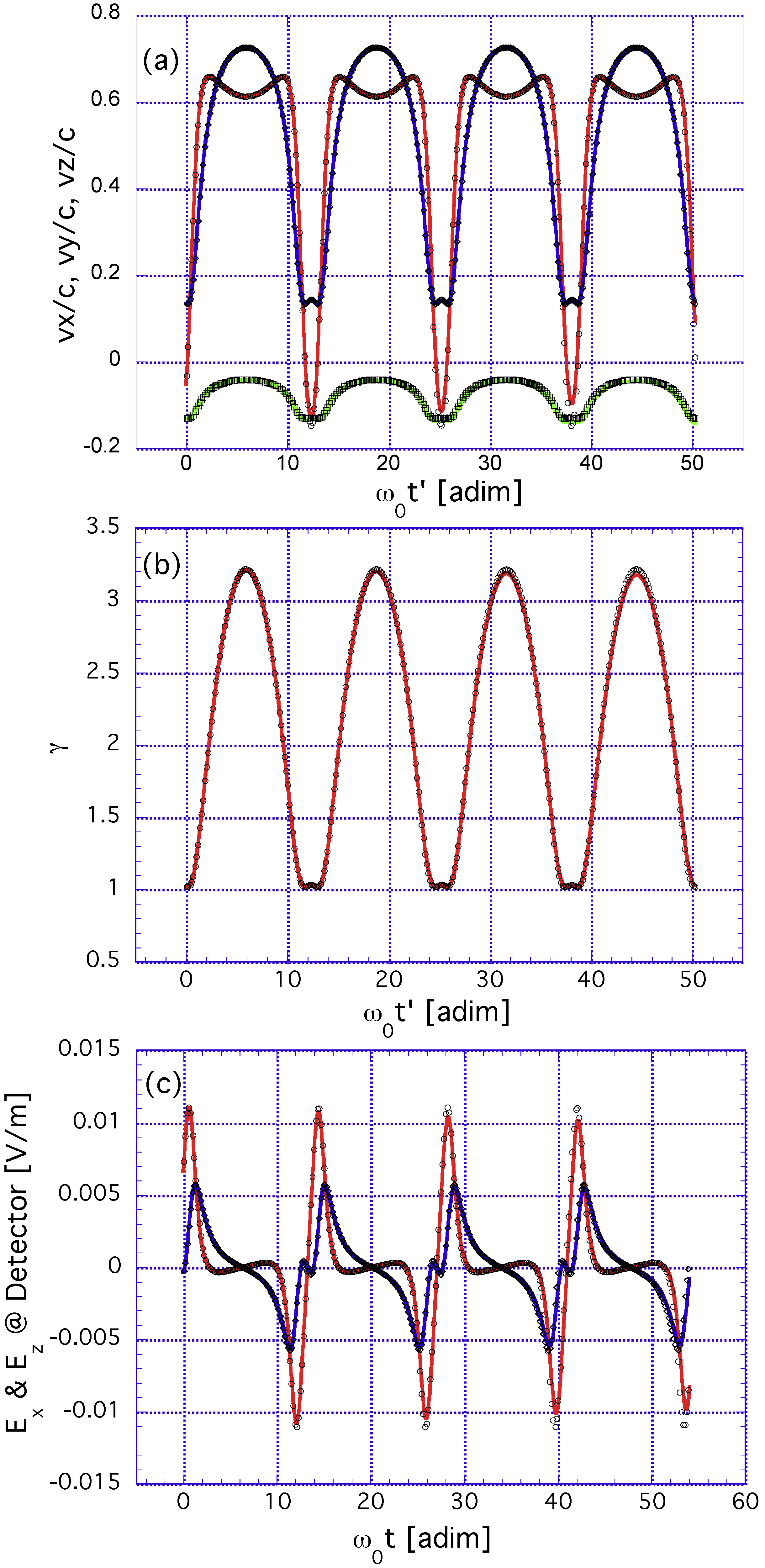
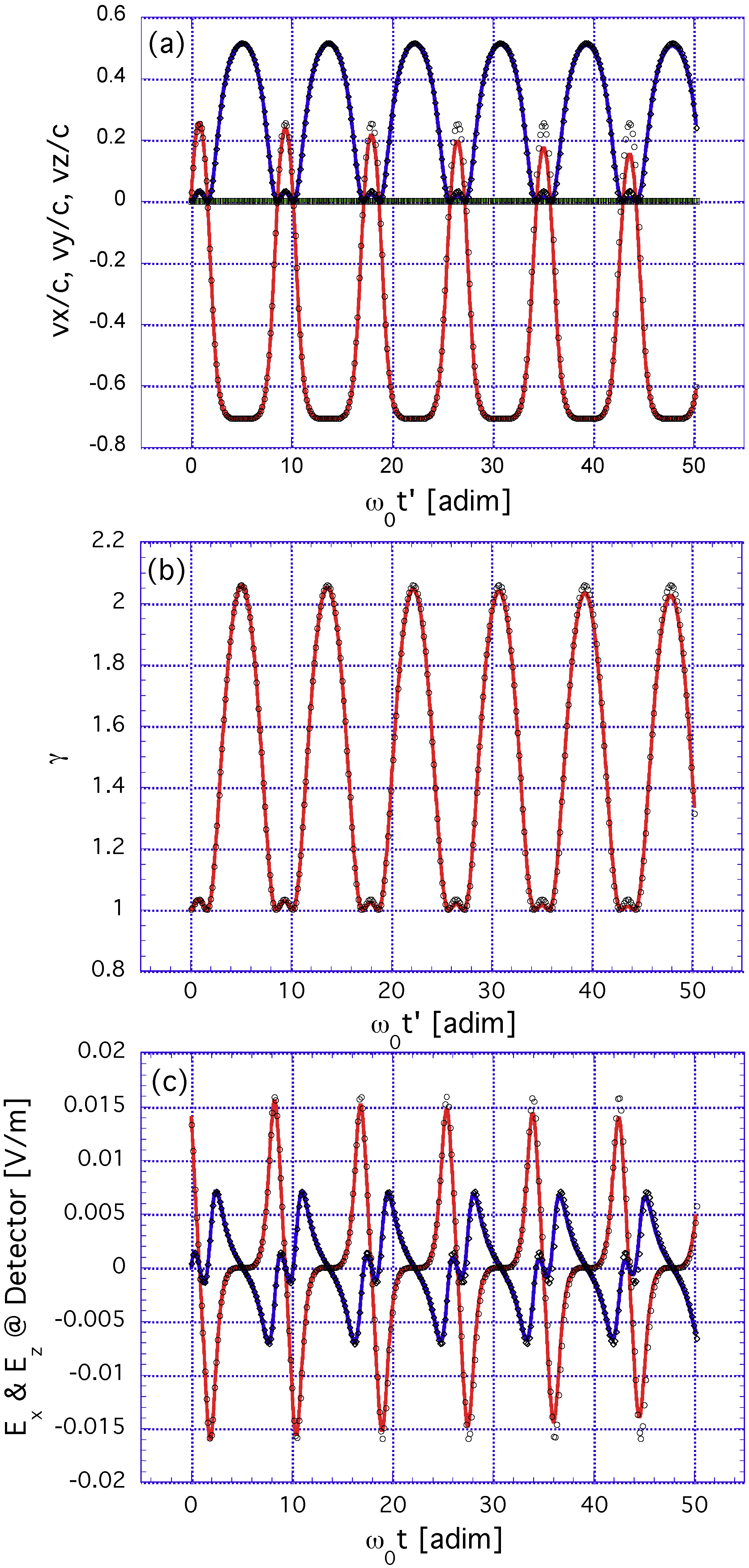
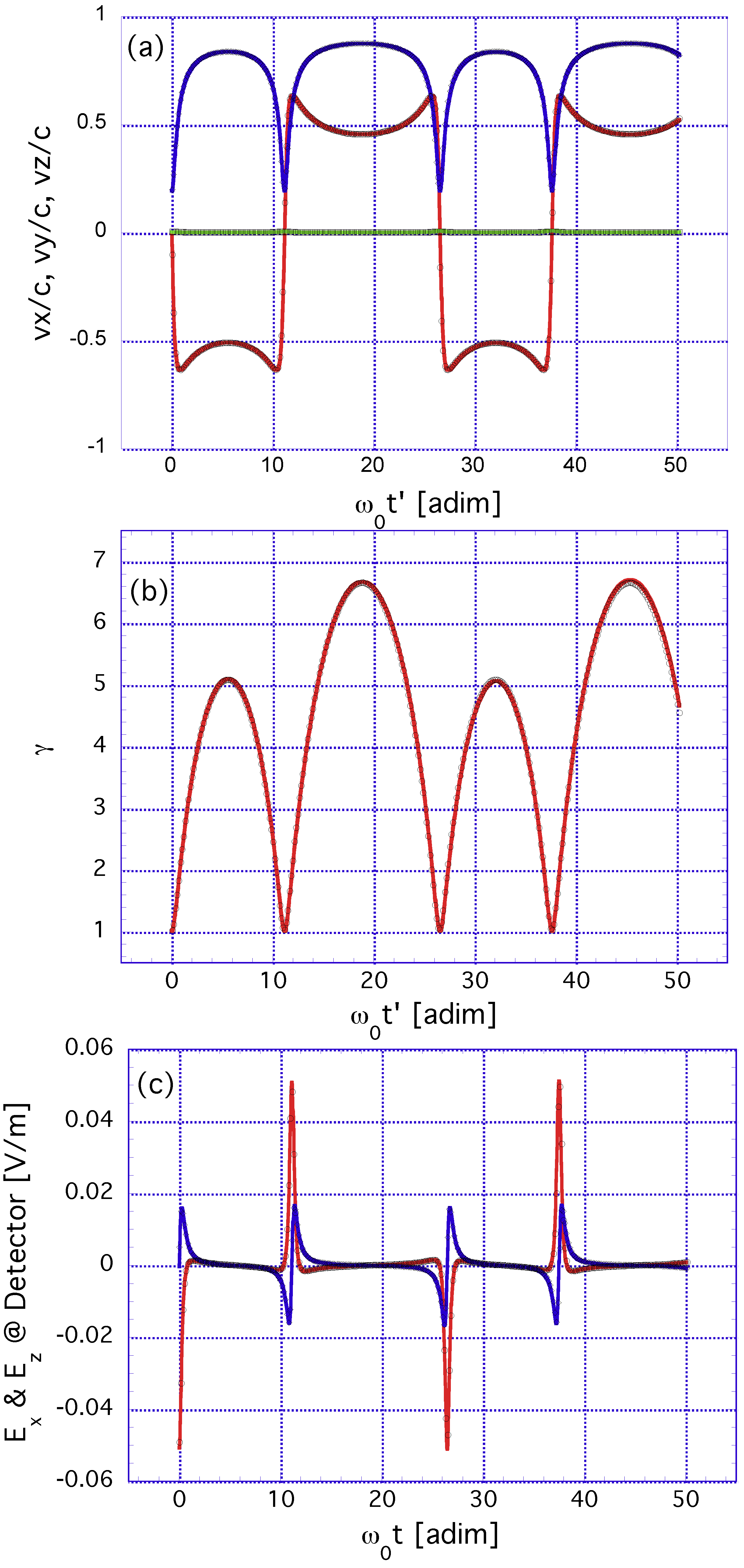
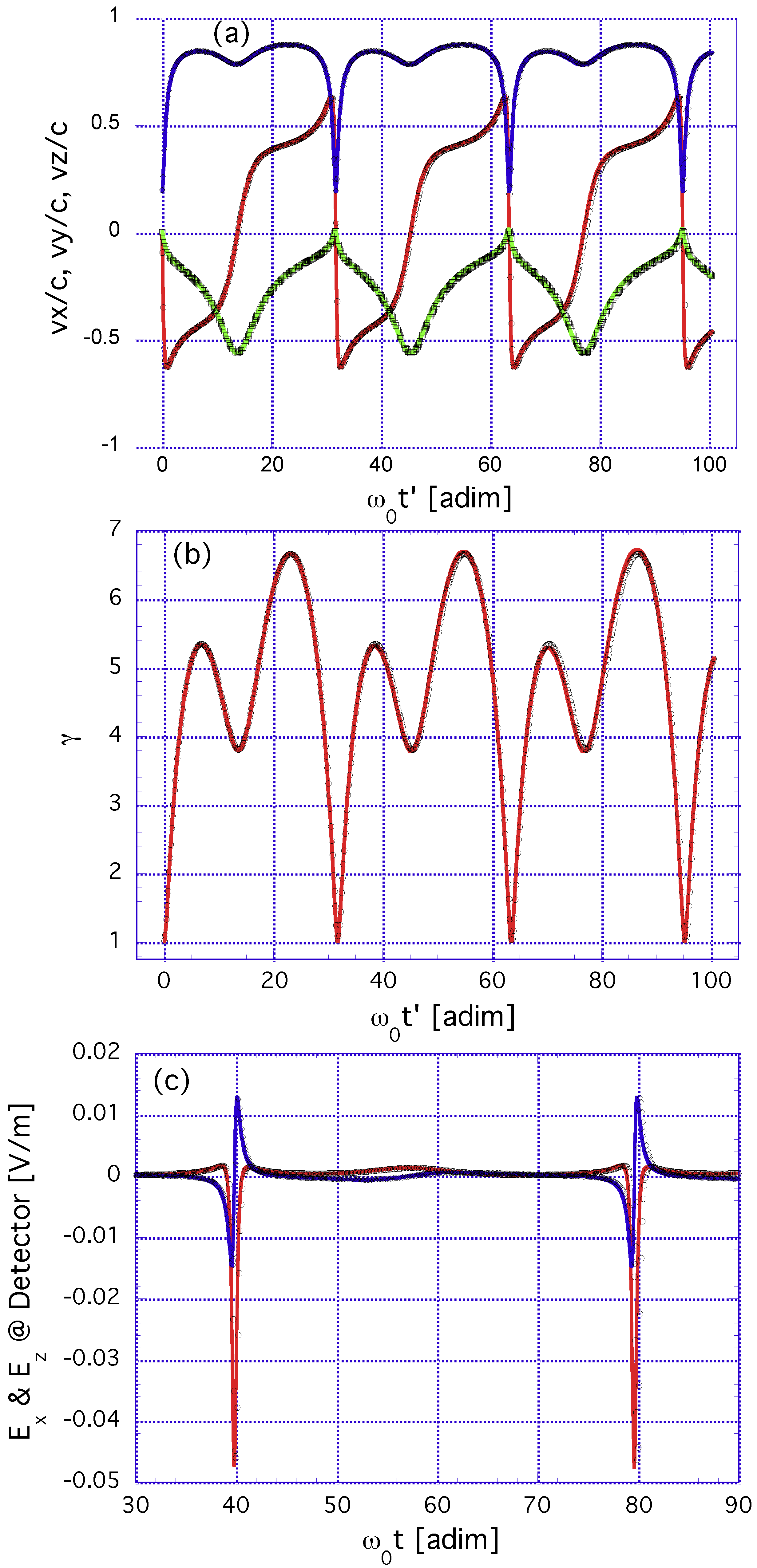
5.2. Approximating the Electron Dynamics in OAM Beams by the Plane-Wave Solution: Numerical Computations
6. Conclusions and Final Comments
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Miscellaneous Symbol Definitions and Formulas
Appendix B. The Function () and Some Properties
Appendix C. Monochromatic Polarized Radiation with φ0 ≠ 0: Linearly and Circularly
Appendix C.1. Linear Polarization
Appendix C.2. Circular Polarization
Appendix D. OAM
References
- Froula, D.H.; Glenzer, S.H.; Luhmann, N.C., Jr.; Sheffield, J. Plasma Scattering of Electromagnetic Radiation: Theory and Measurement Techniques; Academic Press, Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Hutchison, I. Principles of Plasma Diagnostics; Cambridge Univ. Press: Cambridge, UK, 2006. [Google Scholar]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Comm. 1985, 55, 447–449. [Google Scholar] [CrossRef]
- Danson, C.N.; Haefner, C.; Bromage, J.; Butcher, T.; Chanteloup, J.-C.F.; Chowdhury, E.A.; Galvanauskas, A.; Gizzi, L.A.; Hein, J.; Hillier, D.I.; et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci. Eng. 2019, 7, e54. [Google Scholar] [CrossRef]
- Rohrlich, F. Classical Charged Particles, 3rd ed.; World Scientific: Singapore, 2007. [Google Scholar]
- Allen, L.; Barnett, S.M.; Padgett, M.J. Optical Angular Momentum; IOP Publishing: London, UK, 2003. [Google Scholar]
- Torres, J.P.; Torner, L. (Eds.) Twisted Photons: Applications of Light with Orbital Angular Momentum; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Karimi, E.; Schulz, S.A.; De Leon, I.; Qassim, H.; Upham, J.; Boyd, R.W. Generating optical orbital angular momentum at visible wavelengths using a plasmonic metasurface. Light Sci. Appl. 2014, 3, e167. [Google Scholar] [CrossRef]
- Noyan, M.A.; Kikkawa, J.M. Time-resolved orbital angular momentum spectroscopy. Appl. Phys. Lett. 2015, 107, 032406. [Google Scholar] [CrossRef]
- Persuy, D.; Ziegler, M.; Crégut, O.; Kheng, K.; Gallart, M.; Honerlage, B.; Gilliot, P. Four-wave mixing in quantum wells using femtosecond pulses with Laguerre–Gauss modes. Phys. Rev. B 2015, 92, 115312. [Google Scholar] [CrossRef]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Schmidt-Kaler, F. Transfer of optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef]
- Seghilani, M.S.; Myara, M.; Sellahi, M.; Legratiet, L.; Sagnes, I.; Beaudoin, G.; Lalanne, P.; Garnache, A. Vortex Laser based on III-V semiconductor metasurface: Direct generation of coherent Laguerre–Gauss modes carrying controlled orbital angular momentum. Sci. Rep. 2016, 6, 38156. [Google Scholar] [CrossRef]
- Shigematsu, K.; Yamane, K.; Morita, R.; Toda, Y. Coherent dynamics of exciton orbital angular momentum transferred by optical vortex pulses. Phys. Rev. B 2016, 93, 045205. [Google Scholar] [CrossRef]
- Picón, A.; Benseny, A.; Mompart, J.; Vázquez de Aldana, J.R.; Plaja, L.; Calvo, G.F.; Roso, L. Transferring orbital and spin angular momenta of light to atoms. New J. Phys. 2010, 12, 083053. [Google Scholar] [CrossRef]
- Longman, A.; Salgado, C.; Zeraouli, G.; Apinariz, J.I.; Pérez-Hernández, J.A.; Eltahlawy, M.K.; Volpe, L.; Fedosejevs, R. Off axis spiral phase mirrors for generating high-intensity optical vortices. Opt. Lett. 2020, 45, 2187. [Google Scholar] [CrossRef] [PubMed]
- Pastor, I.; Alvarez-Estrada, R.F.; Roso, L.; Castejon, F.; Guasp, J. Nonlinear relativistic electron Thomson scattering for laserradiation with orbital angular momentum. J. Phys. Commun. 2020, 4, 065010. [Google Scholar] [CrossRef]
- He, F.; Lau, Y.Y.; Umstadter, D.P.; Strickler, T. Phase dependence of Thomson scattering in an ultraintense laser field. Phys. Plasmas 2002, 9, 4325. [Google Scholar] [CrossRef][Green Version]
- Evans, D.E.; Katzenstein, J. Laser light scattering in laboratory plasmas. Rep. Prog. Phys. 1969, 32, 207. [Google Scholar] [CrossRef]
- Mattioli, M. Incoherent Light Scattering from High Temperature Plasmas; Report DPh-PFC-SPP (EUR-CEA-FC) 752; EURATOM-CEA: Fontenay-aux-Roses, France, 1974. [Google Scholar]
- Matoba, T.; Itagaki, T.; Yamauchi, T.; Funahashi, A. Analytical Approximations in the Theory of Relativistic Thomson Scattering for High Temperature Fusion Plasma. Jpn. J. Appl. Phys. 1979, 18, 1127. [Google Scholar] [CrossRef]
- Weyssow, B. Motion of a single charged particle in electromagnetic fields with cyclotron resonances. J. Plasma Phys. 1990, 43, 119. [Google Scholar] [CrossRef]
- Naito, O.; Yoshida, H.; Matoba, T. Analytic formula for fully relativistic Thomson scattering spectrum. Phys. Fluids B Plasma Phys. 1993, 5, 4256. [Google Scholar] [CrossRef]
- Beausang, K.V.; Prunty, S.L. An analytic formula for the relativistic Thomson scattering spectrum for a Maxwellian velocity distribution. Plasma Phys. Control. Fusion 2008, 50, 095001. [Google Scholar] [CrossRef]
- Walsh, M.J.; Beurskens, M.; Carolan, P.G.; Gilbert, M.; Loughlin, M.; Morris, A.W.; Riccardo, V.; Xue, Y. Design challenges and analysis of the ITER core LIDAR Thomson scattering system. Rev. Sci. Instrum. 2006, 77, 10E525. [Google Scholar] [CrossRef]
- Ross, J.S.; Glenzer, S.H.; Palastro, J.P.; Pollock, B.B.; Price, D.; Divol, L.; Tynan, G.R.; Froula, D.H. Observation of Relativistic Effects in Collective Thomson Scattering. Phys. Rev. Lett. 2010, 104, 105001. [Google Scholar] [CrossRef]
- Palastro, J.P.; Ross, J.S.; Pollock, B.; Divol, L.; Froula, D.H.; Glenzer, S.H. Fully relativistic form factor for Thomson scattering. Phys. Rev. E 2010, 81, 036411. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifchitz, E.M. The Classical Theory of Fields, 4th ed.; Pergamon Press: New York, NY, USA, 1975. [Google Scholar]
- Sarachik, E.S.; Schappert, G.T. Classical Theory of the Scattering of Intense Laser Radiation by Free Electrons. Phys. Rev. D 1970, 1, 2738. [Google Scholar] [CrossRef]
- Esarey, E.; Ride, S.K.; Sprangle, P. Nonlinear Thomson scattering of intense laser pulses from beams and plasmas. Phys. Rev. E 1993, 48, 3003. [Google Scholar] [CrossRef]
- Ride, S.K.; Esarey, E.; Baine, M. Thomson scattering of intense lasers from electron beams at arbitrary interaction angles. Phys. Rev. E 1995, 52, 5425. [Google Scholar] [CrossRef] [PubMed]
- Brau, C.A. Modern Problems in Classical Electrodynamics; Oxford Univ. Press: Oxford, UK, 2004. [Google Scholar]
- Avetissian, H. Relativistic Nonlinear Electrodynamics; Springer Series in Optical Sciences; Springer: New York, NY, USA, 2006. [Google Scholar]
- Yang, J.H.; Craxton, R.S.; Haines, M.G. Explicit general solutions to relativistic electron dynamics in plane-wave electromagnetic fields and simulations of ponderomotive acceleration. Plasma Phys. Control. Fusion 2011, 53, 125006. [Google Scholar] [CrossRef]
- Panofsky, W.K.H.; Phillips, M. 1955 Classical Electricity and Magnetism; Addison-Wesley: Reading, MA, USA, 1965. [Google Scholar]
- Pastor, I.; Guasp, J.; Alvarez-Estrada, R.F.; Castejon, F. Monte Carlo approach to Thomson scattering in relativistic fusion plasmas with allowance for ultraintense laser radiation. Nucl. Fusion 2011, 51, 04011. [Google Scholar] [CrossRef]
- Alvarez-Estrada, R.F.; Pastor, I.; Guasp, J.; Castejon, F. Nonlinear relativistic single-electron Thomson scattering power spectrum for incoming laser of arbitrary intensity. Phys. Plasmas 2012, 19, 062302. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 2nd ed.; John Wiley and Sons: New York, NY, USA, 1974. [Google Scholar]
- Duke, P.J. Synchrotron Radiation: Production and Properties; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Loetstedt, E.; Jentschura, U.D. Recursive algorithm for arrays of generalized Bessel functions: Numerical access to Dirac-Volkov solutions. Phys. Rev. E 2009, 79, 026707. [Google Scholar] [CrossRef]
- Calvo, G.F.; Picón, A.; Bagan, E. Quantum field theory of photons with orbital angular momentum. Phys. Rev. A 2006, 73, 013805. [Google Scholar] [CrossRef]
- Olver, F.W.J. Bessel functions of integer order. In Handbook of Mathematical Functions; Abramowitz, M., Stegun, I.A., Eds.; Dover: New York, NY, USA, 1965. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pastor, I.; Álvarez-Estrada, R.F.; Roso, L.; Guasp, J.; Castejón, F. Electron Dynamics and Thomson Scattering for Ultra-Intense Lasers: Elliptically Polarized and OAM Beams. Photonics 2021, 8, 182. https://doi.org/10.3390/photonics8060182
Pastor I, Álvarez-Estrada RF, Roso L, Guasp J, Castejón F. Electron Dynamics and Thomson Scattering for Ultra-Intense Lasers: Elliptically Polarized and OAM Beams. Photonics. 2021; 8(6):182. https://doi.org/10.3390/photonics8060182
Chicago/Turabian StylePastor, Ignacio, Ramón F. Álvarez-Estrada, Luis Roso, José Guasp, and Francisco Castejón. 2021. "Electron Dynamics and Thomson Scattering for Ultra-Intense Lasers: Elliptically Polarized and OAM Beams" Photonics 8, no. 6: 182. https://doi.org/10.3390/photonics8060182
APA StylePastor, I., Álvarez-Estrada, R. F., Roso, L., Guasp, J., & Castejón, F. (2021). Electron Dynamics and Thomson Scattering for Ultra-Intense Lasers: Elliptically Polarized and OAM Beams. Photonics, 8(6), 182. https://doi.org/10.3390/photonics8060182




