Keen Investigation of the Electromagnetic Scattering Characteristics of Tiltrotor Aircraft Based on Dynamic Calculation Method
Abstract
1. Introduction
2. Dynamic Calculation Method
2.1. Dynamic Scattering Calculation
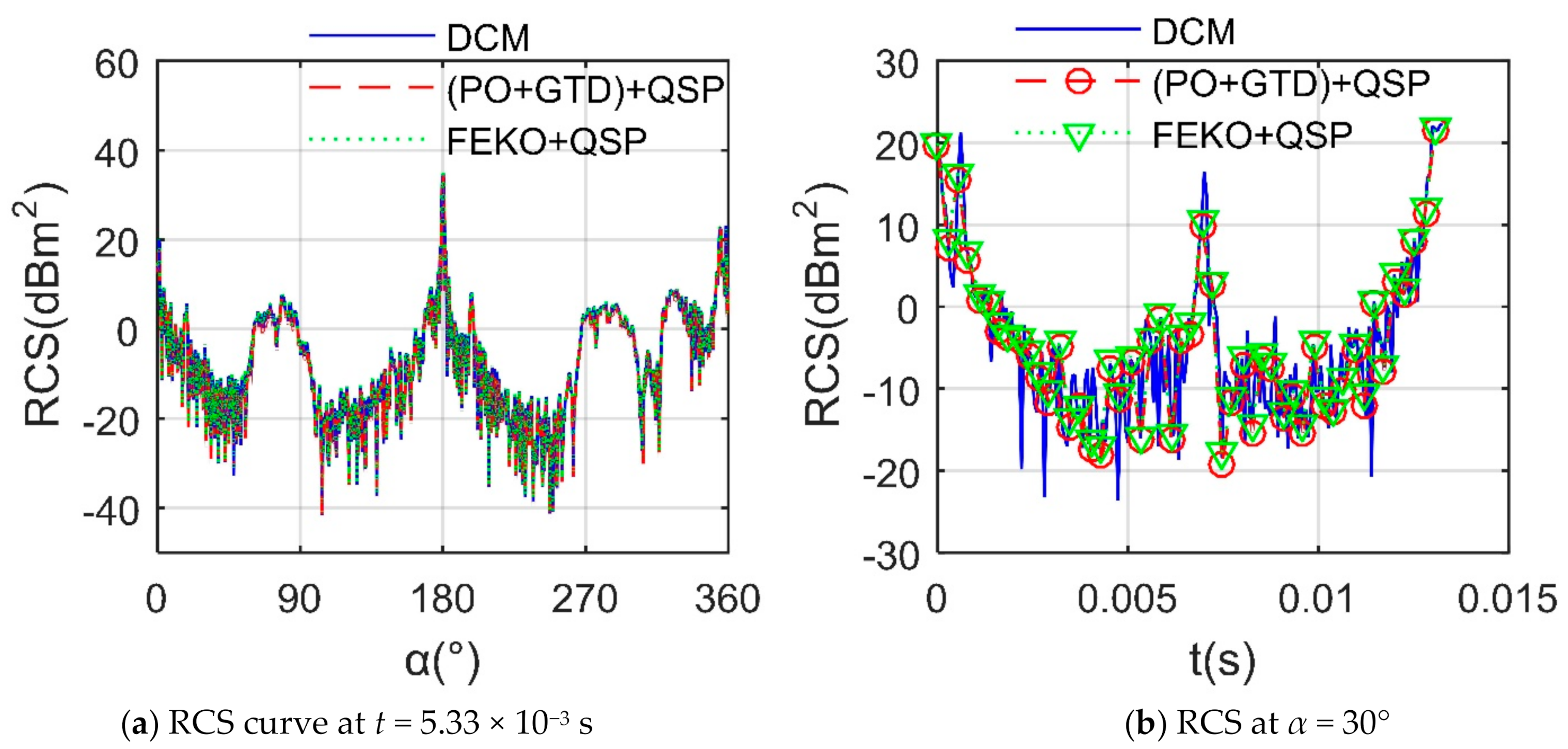
2.2. Method Validation
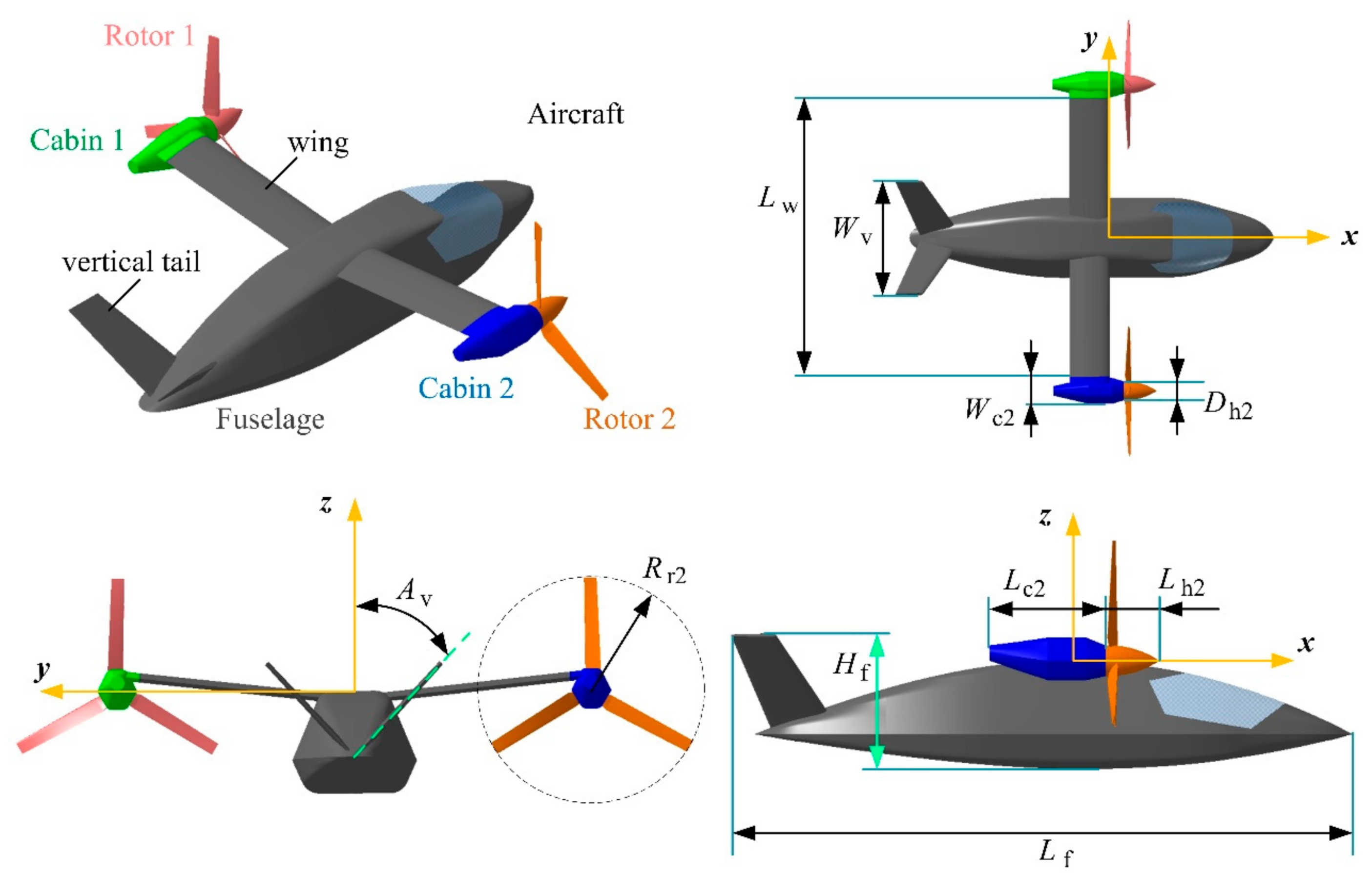
3. Models
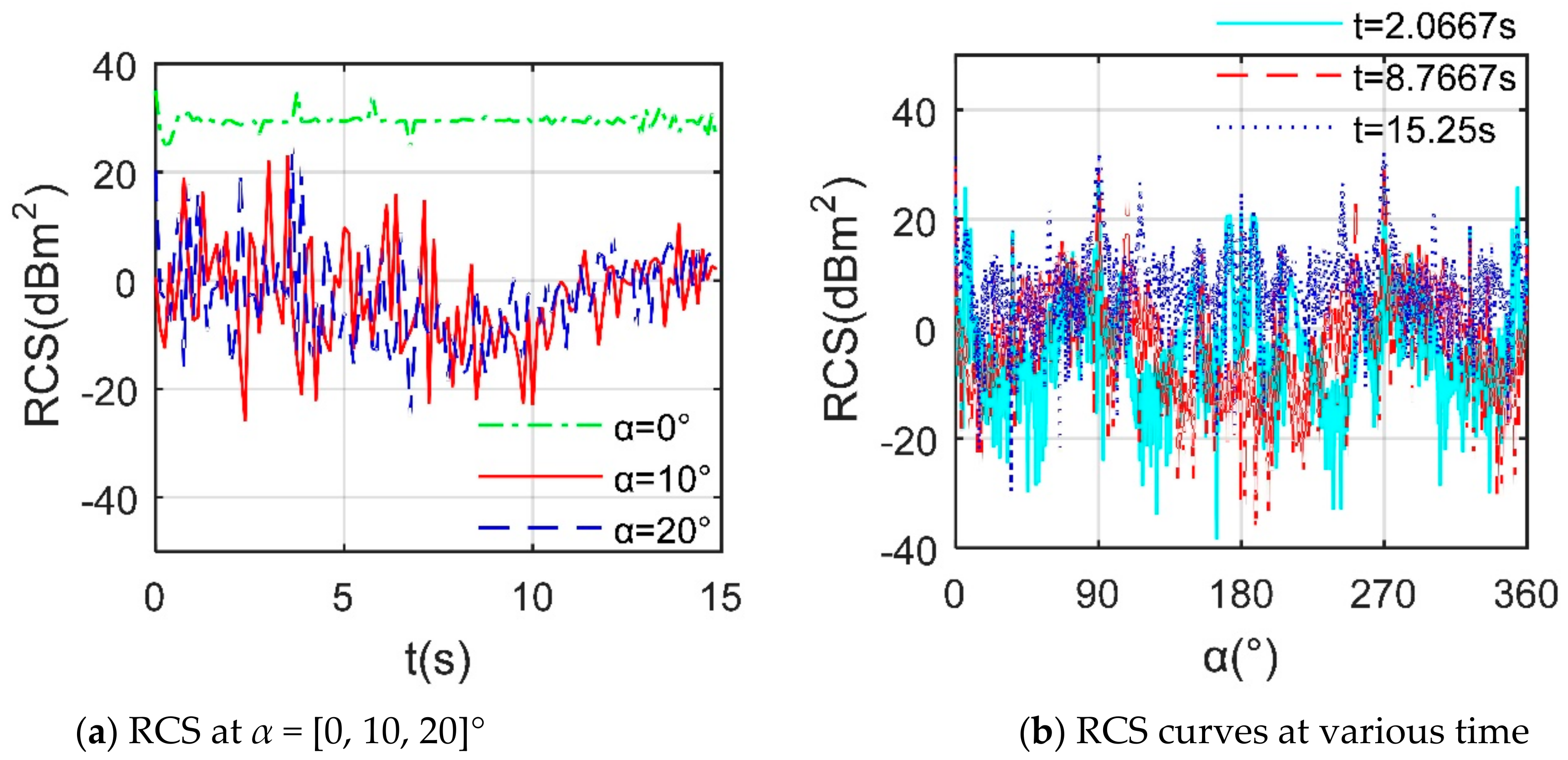
4. Results and Discussion
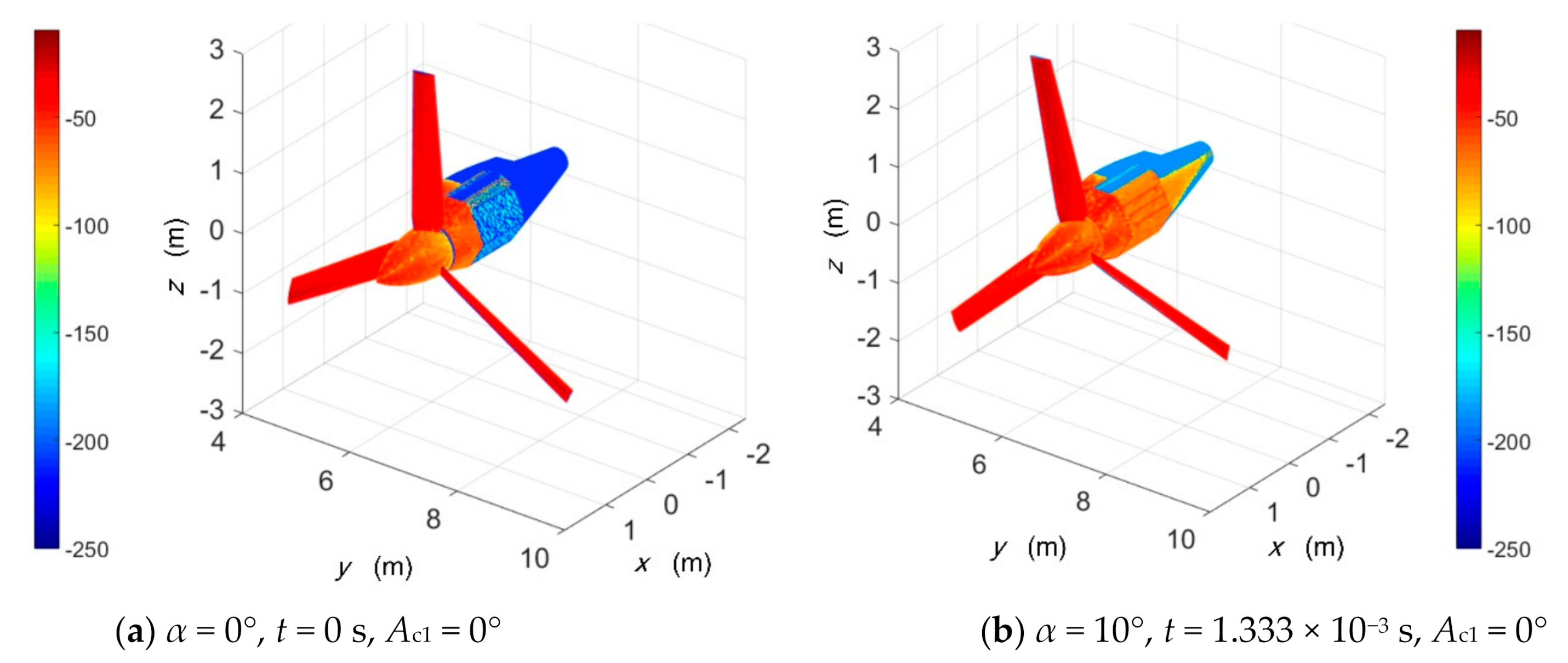
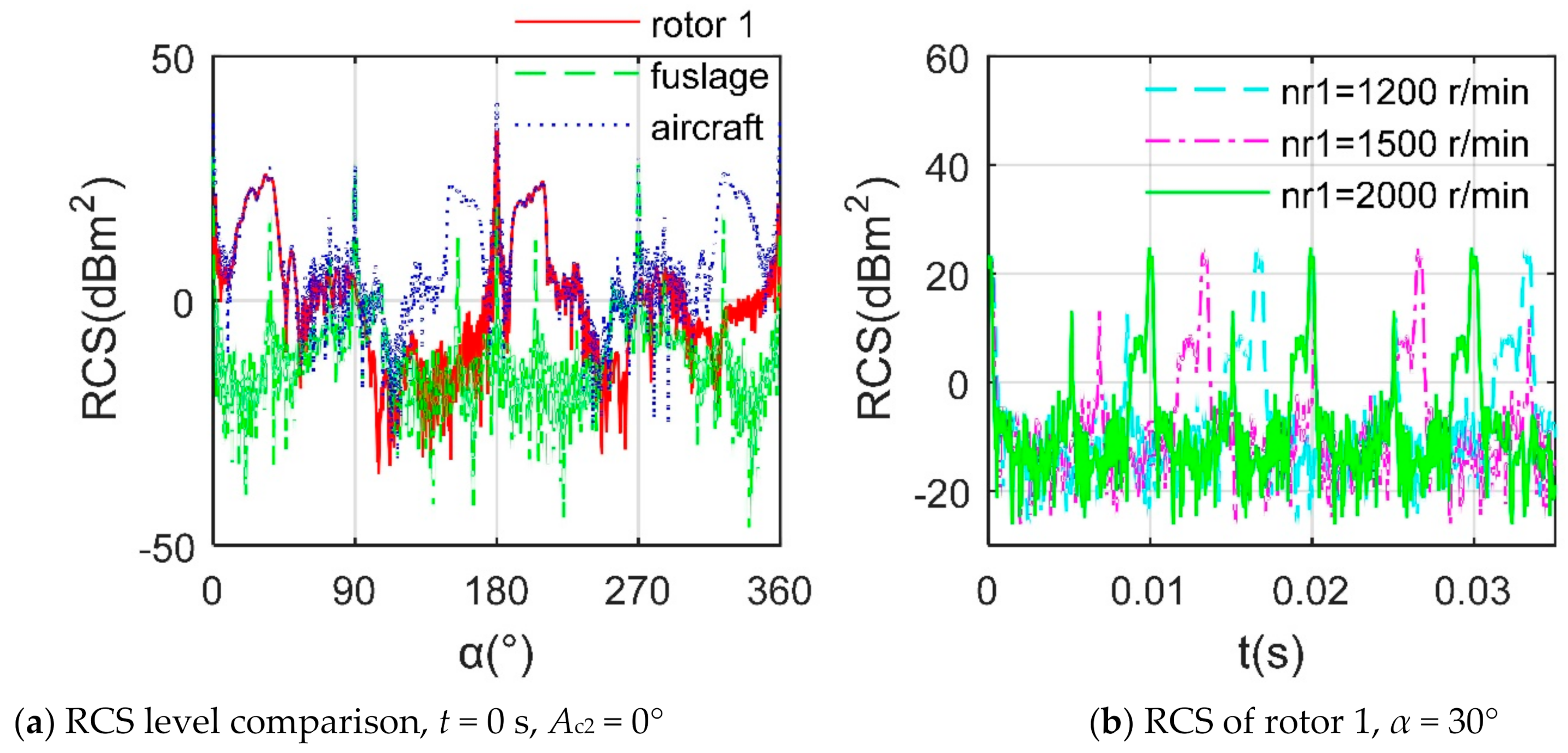
4.1. Analysis of Scattering Sources
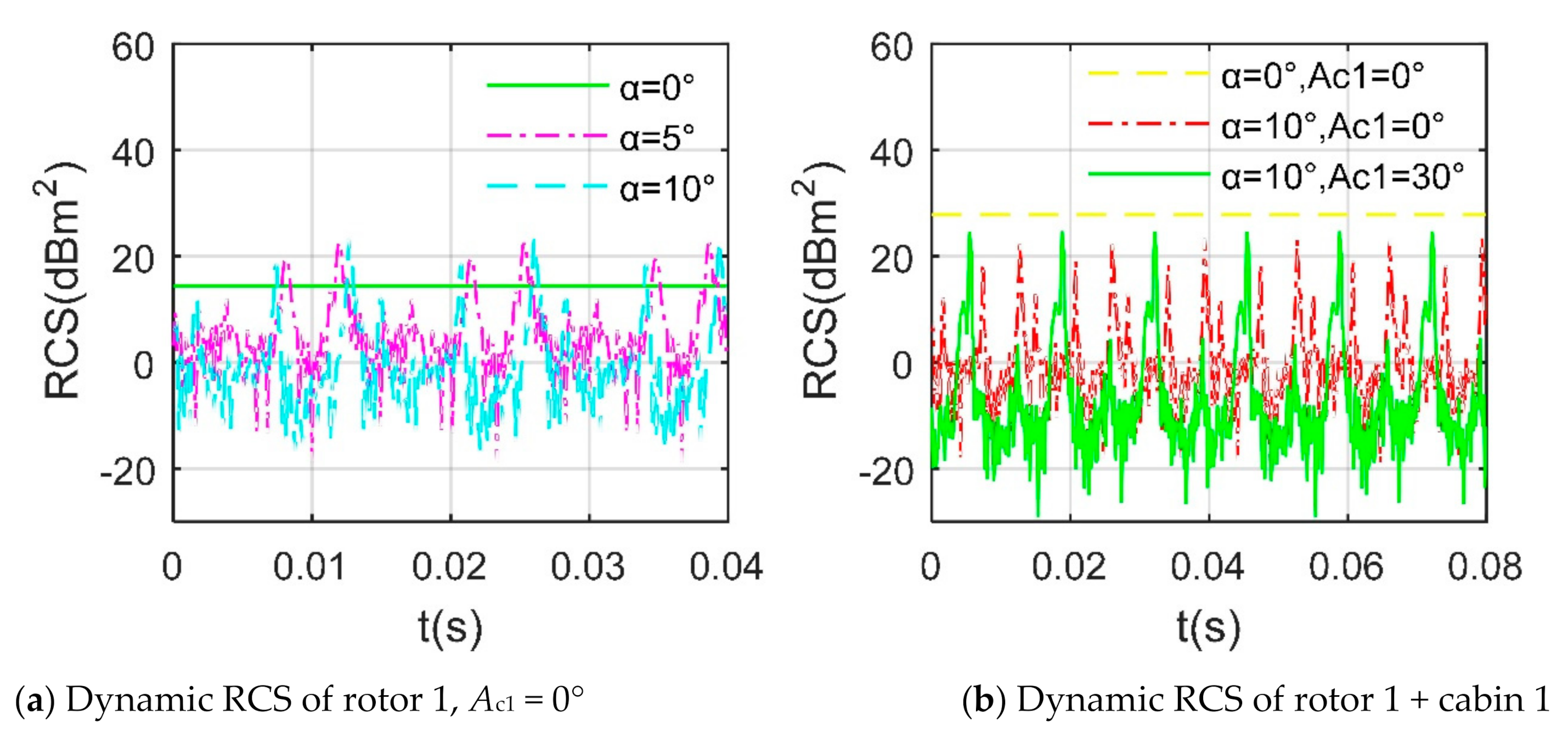
4.2. Influence of Different Components
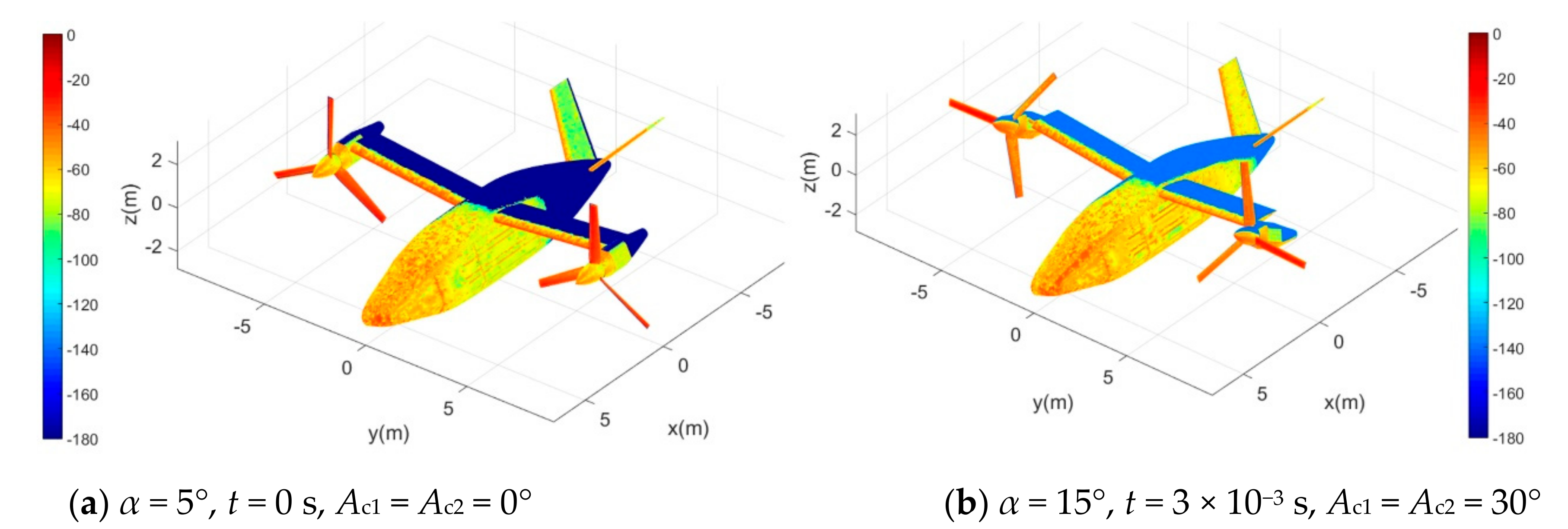
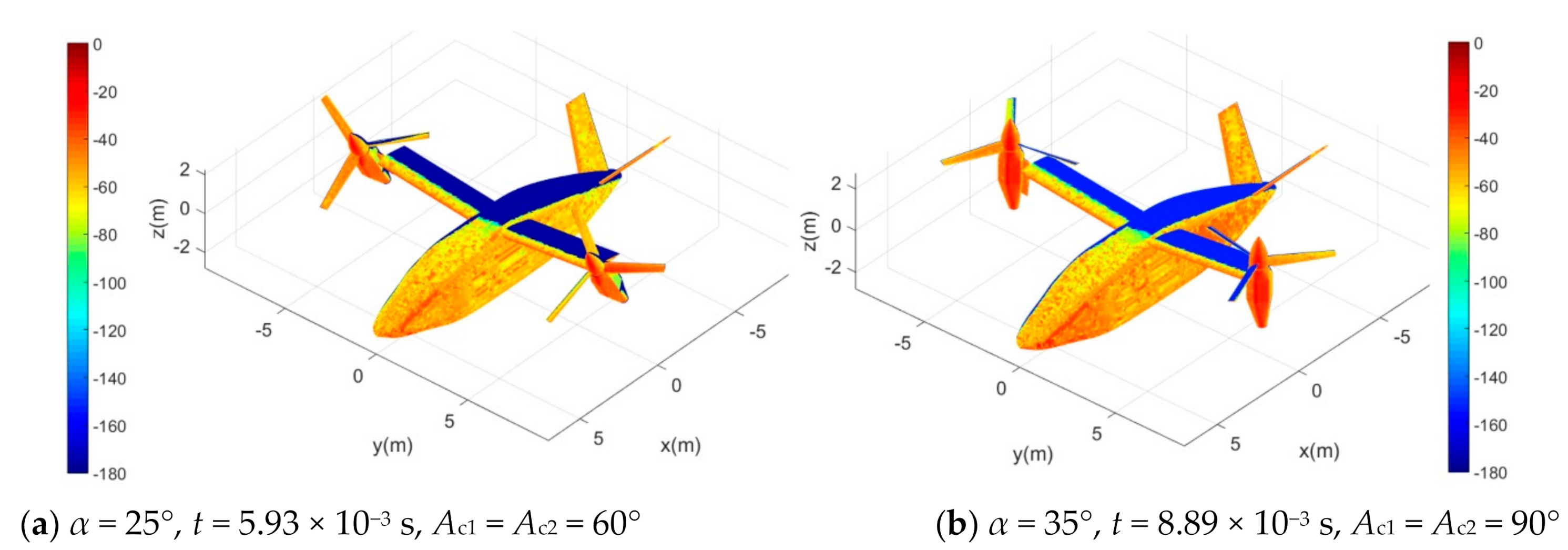
4.3. Investigation of Aircraft Surface Scattering
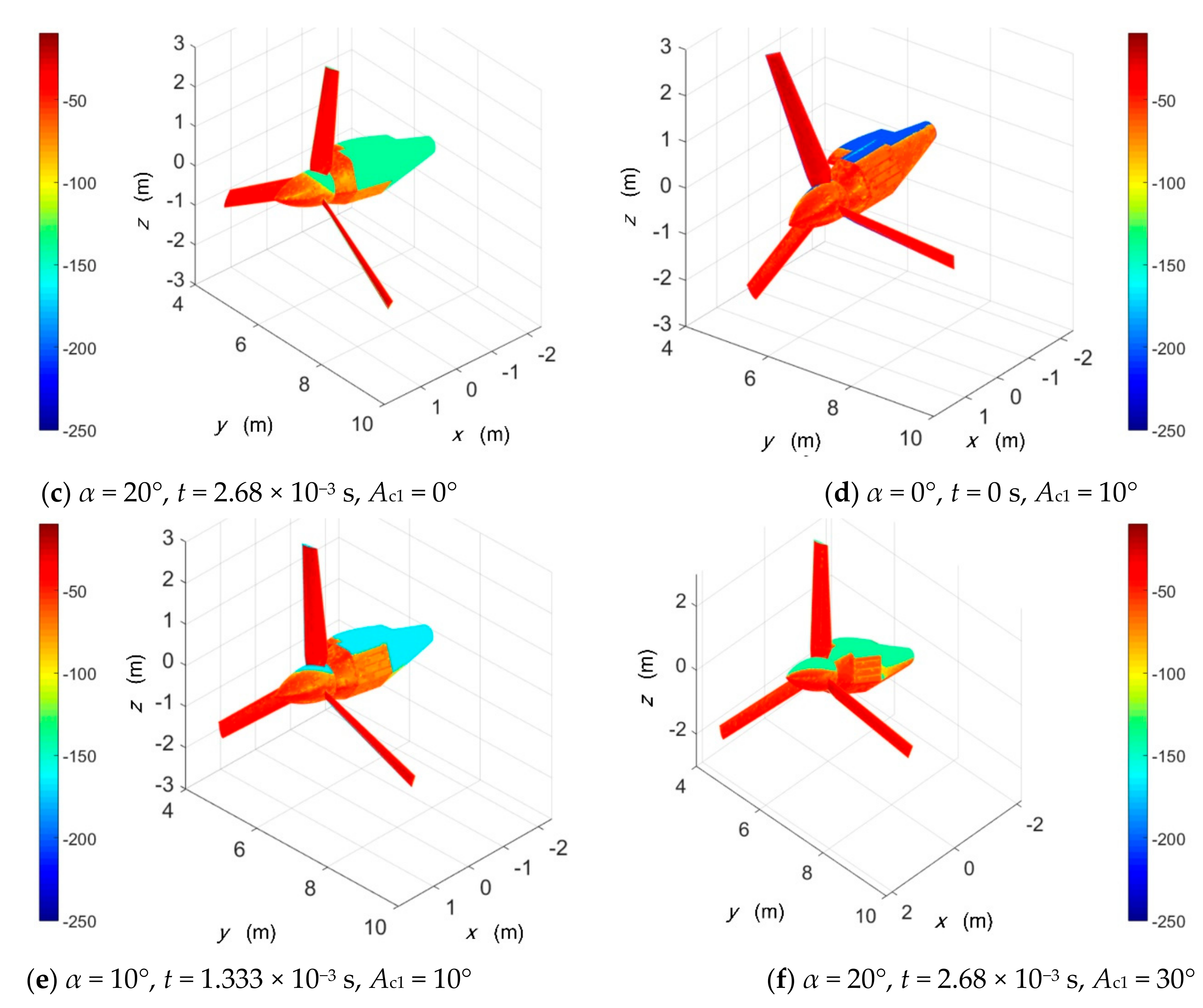
4.4. Effect of Tilting Action
5. Conclusions
- (1)
- After the initial stealth design of the fuselage was adopted, the electromagnetic scattering level of the entire aircraft was well improved. However, in the fixed-wing mode, the rotor blades can still become a strong scattering source when facing the incident radar wave in the horizontal plane.
- (2)
- The increase in speed can shorten the period of the rotor dynamic RCS, while the rotating rotor makes the aircraft’s RCS exhibit different dynamic characteristics in helicopter mode, fixed-wing mode and transition mode.
- (3)
- Increasing the tilt angle can significantly improve the RCS performance of the rotor, but it will make the engine cabin and the outer end of the wing become a new source of strong scattering, which can provide a reference for the stealth optimization design of the cabin in future work.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Aşırım, Ö.E.; Kuzuoğlu, M. Numerical study of resonant optical parametric amplification via gain factor optimization in dispersive microresonators. Photonics 2020, 7, 5. [Google Scholar] [CrossRef]
- Zhao, Q.; Jiang, S.; Li, P.; Wang, B.; Zhang, H. Aerodynamic optimization analyses of tiltrotor/propeller based on CFD method. Acta Aerodyn. Sin. 2017, 35, 544–553. [Google Scholar]
- Zhang, Y.; Zeng, F.; Dai, Q.; Wu, Z. Development status and trend of intelligent radar stealth technology. Tactical Missile Technol. 2019, 1, 56–63. [Google Scholar]
- Mirkovic, D.; Stepanian, P.M.; Kelly, J.F.; Chilson, P.B. Electromagnetic Model Reliably Predicts Radar Scattering Characteristics of Airborne Organisms. Sci. Rep. 2016, 6, 35637. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, J.; Yi, M. Comprehensive optimization of aerodynamic noise and radar stealth for helicopter rotor based on Pareto solution. Aerosp. Sci. Technol. 2018, 82, 607–619. [Google Scholar] [CrossRef]
- Bogatskaya, A.; Schegolev, A.; Klenov, N.; Popov, A. Generation of Coherent and Spatially Squeezed States of an Electromagnetic Beam in a Planar Inhomogeneous Dielectric Waveguide. Photonics 2019, 6, 84. [Google Scholar] [CrossRef]
- Ye, S.; Xiong, J. Dynamic RCS behavior of helicopter rotating blades. Acta Aeronaut. Astronaut. Sin. 2006, 27, 816–822. [Google Scholar]
- Jameson, A. Computational aerodynamics for aircraft design. Science 1989, 245, 361–371. [Google Scholar] [CrossRef]
- Konrad, T.G.; Hicks, J.J.; Dobson, E.B. Radar characteristics of birds in flight. Science 1968, 159, 274–280. [Google Scholar] [CrossRef]
- Li, P.; Zhao, Q. CFD calculations on the interaction flowfield and aerodynamic force of tiltrotor/wing in hover. Acta Aeronaut. Astronaut. Sin. 2014, 35, 362–372. [Google Scholar]
- Zhou, Z.; Huang, J. Influence of rotor dynamic scattering on helicopter radar cross-section. Sensors 2020, 20, 2097. [Google Scholar] [CrossRef]
- Komissarov, R.; Kozlov, V.; Filonov, D.; Ginzburg, P. Partially coherent radar unties range resolution from bandwidth limitations. Nat. Commun. 2019, 10, 1423. [Google Scholar] [CrossRef]
- Xiong, Y.; Ye, H.; Umeda, T.; Mizoguchi, S.; Morifuji, M.; Kajii, H.; Maruta, A.; Kondow, M. Photonic Crystal Circular Defect (CirD) Laser. Photonics 2019, 6, 54. [Google Scholar] [CrossRef]
- Chen, H.; Zuo, X.; Zhang, Y. Tiltrotor aircraft key technology developing research. Flight Dyn. 2007, 25, 6–9. [Google Scholar]
- Glover, K.M.; Hardy, K.R.; Konrad, T.G.; Sullivan, W.N.; Michaels, A.S. Radar observations of insects in free flight. Science 1966, 154, 967–972. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, J.; Wang, J. Electromagnetic scattering characteristics of coaxial helicopter based on dynamic transformation method. Chin. J. Aeronaut. 2020, 34, 516–528. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, J. Dynamic Scattering Approach for Solving the Radar Cross-Section of the Warship under Complex Motion Conditions. Photonics 2020, 7, 64. [Google Scholar] [CrossRef]
- Elachi, C. Spaceborne Imaging Radar Geologic and Oceanographic Applications. Science 1980, 209, 1073–1082. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Huang, Y.; Wang, X. Fault diagnosis for tiltrotor aircraft flight control system based on variable precision rough set-OMELM. Control Decis. 2015, 30, 434–441. [Google Scholar]
- Zhou, Z.; Huang, J.; Wang, J. Compound helicopter multi-rotor dynamic radar cross section response analysis. Aerosp. Sci. Technol. 2020, 105, 106047. [Google Scholar] [CrossRef]
- Schuck, M.; Steinert, D.; Nussbaumer, T.; Kolar, J.W. Ultrafast rotation of magnetically levitated macroscopic steel spheres. Sci. Adv. 2018, 4, e1701519. [Google Scholar] [CrossRef] [PubMed]
- Van Doren, B.M.; Horton, K.G. A continental system for forecasting bird migration. Science 2018, 361, 1115–1118. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; He, D. Areview of aircraft stealth and radar anti-stealth technology. Electron. Inf. Warf. Technol. 2016, 31, 41–44. [Google Scholar]
- Zhao, Y.; Liu, J. FDTD for hydrodynamic electron fluid Maxwell equations. Photonics 2015, 2, 459–467. [Google Scholar] [CrossRef]
- Gardner, A.D.; Wolf, C.C.; Raffel, M. Review of measurement techniques for unsteady helicopter rotor flows. Prog. Aerosp. Sci. 2019, 111, 100566. [Google Scholar] [CrossRef]
- Wang, R.; Hu, C.; Fu, X.; Long, T.; Zeng, T. Micro-Doppler measurement of insect wing-beat frequencies with W-band coherent radar. Sci. Rep. 2017, 7, 1396. [Google Scholar] [CrossRef] [PubMed]
- Carrer, L.; Bruzzone, L. Solving for ambiguities in radar geophysical exploration of planetary bodies by mimicking bats echolocation. Nat. Commun. 2017, 8, 1396. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Reno, J.L.; Kumar, S. Short barriers for lowering current-density in terahertz quantum cascade lasers. Photonics 2020, 7, 7. [Google Scholar] [CrossRef]
- Yan, X.; Chen, R. Control strategy optimization of dynamic conversion procedure of tilt-rotor aircraft. Acta Aeronaut. Astronaut. Sin. 2017, 25, 520865. [Google Scholar]
- Rahman, S.; Robertson, D.A. Radar micro-Doppler signatures of drones and birds at K-band and W-band. Sci. Rep. 2018, 8, 17396. [Google Scholar] [CrossRef]
- Sareh, P.; Chermprayong, P.; Emmanuelli, M.; Nadeem, H.; Kovac, M. Rotorigami: A rotary origami protective system for robotic rotorcraft. Sci. Robot. 2018, 3, eaah5228. [Google Scholar] [CrossRef]
- Makinson, J.C.; Woodgate, J.L.; Reynolds, A.; Capaldi, E.A.; Perry, C.J.; Chittka, L. Harmonic radar tracking reveals random dispersal pattern of bumblebee (Bombus terrestris) queens after hibernation. Sci. Rep. 2019, 9, 4651. [Google Scholar] [CrossRef]
- Brocklehurst, A.; Barakos, G.N. A review of helicopter rotor blade tip shapes. Prog. Aerosp. Sci. 2013, 56, 35–74. [Google Scholar] [CrossRef]
- Mittapalli, V.; Khan, H. Excitation Schemes of Plasmonic Angular Ring Resonator-Based Band-Pass Filters Using a MIM Waveguide. Photonics 2019, 6, 41. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Tian, Q.; Ji, J.; Yang, S. Analysis of influence of blade on electromagnetic scattering characteristics of heli-copter. Aeronaut. Comput. Tech. 2018, 48, 50–54. [Google Scholar]
- Tan, J.F.; Zhou, T.Y.; Sun, Y.M.; Barakos, G.N. Numerical investigation of the aerodynamic interaction between a tiltrotor and a tan-dem rotor during shipboard operations. Aerosp. Sci. Technol. 2019, 87, 62–72. [Google Scholar] [CrossRef]
- Chin, Y.W.; Kok, J.M.; Zhu, Y.Q.; Chan, W.L.; Chahl, J.S.; Khoo, B.C.; Lau, G.K. Efficient flapping wing drone arrests high speed flight using post-stall soaring. Sci. Robot. 2020, 5, eaba2386. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Pirandola, S.; Vitali, D.; Fink, J.M. Microwave quantum illumination using a digital receiver. Sci. Adv. 2020, 6, eabb0451. [Google Scholar] [CrossRef]





| Area | Max Size (mm) | Area | Max Size (mm) |
|---|---|---|---|
| Global minimum size | 1 | Trailing edge of rotor 1 | 2 |
| Trailing edge of rotor 2 | 2 | Leading edge of rotor 1 | 3 |
| Leading edge of rotor 2 | 3 | Blade tip | 5 |
| Hub edge | 10 | Blade surface | 25 |
| Hub surface | 30 | Cabin surface | 30 |
| Wing edge | 15 | Fuselage surface | 35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Huang, J.; Chen, C.; Zhang, J. Keen Investigation of the Electromagnetic Scattering Characteristics of Tiltrotor Aircraft Based on Dynamic Calculation Method. Photonics 2021, 8, 175. https://doi.org/10.3390/photonics8060175
Zhou Z, Huang J, Chen C, Zhang J. Keen Investigation of the Electromagnetic Scattering Characteristics of Tiltrotor Aircraft Based on Dynamic Calculation Method. Photonics. 2021; 8(6):175. https://doi.org/10.3390/photonics8060175
Chicago/Turabian StyleZhou, Zeyang, Jun Huang, Chen Chen, and Jiaren Zhang. 2021. "Keen Investigation of the Electromagnetic Scattering Characteristics of Tiltrotor Aircraft Based on Dynamic Calculation Method" Photonics 8, no. 6: 175. https://doi.org/10.3390/photonics8060175
APA StyleZhou, Z., Huang, J., Chen, C., & Zhang, J. (2021). Keen Investigation of the Electromagnetic Scattering Characteristics of Tiltrotor Aircraft Based on Dynamic Calculation Method. Photonics, 8(6), 175. https://doi.org/10.3390/photonics8060175







