Deep Learning-Assisted Index Estimator for Generalized LED Index Modulation OFDM in Visible Light Communication
Abstract
1. Introduction
- An IE-based DNN (IE-DNN) is introduced into the GLIM (multiple-input multiple-output) MIMO-VLC demodulator;
- Only a single IE-DNN module without the need to change the transmitter and the signal demodulation part in the receiver structure;
- Three different structures of the IE-DNN are proposed and compared to demonstrate that the CNN-based estimator delivers the best performance;
- In comparison with conventional detectors, a remarkable active LED index estimation accuracy significantly improves the BER performance at acceptable complexity costs.
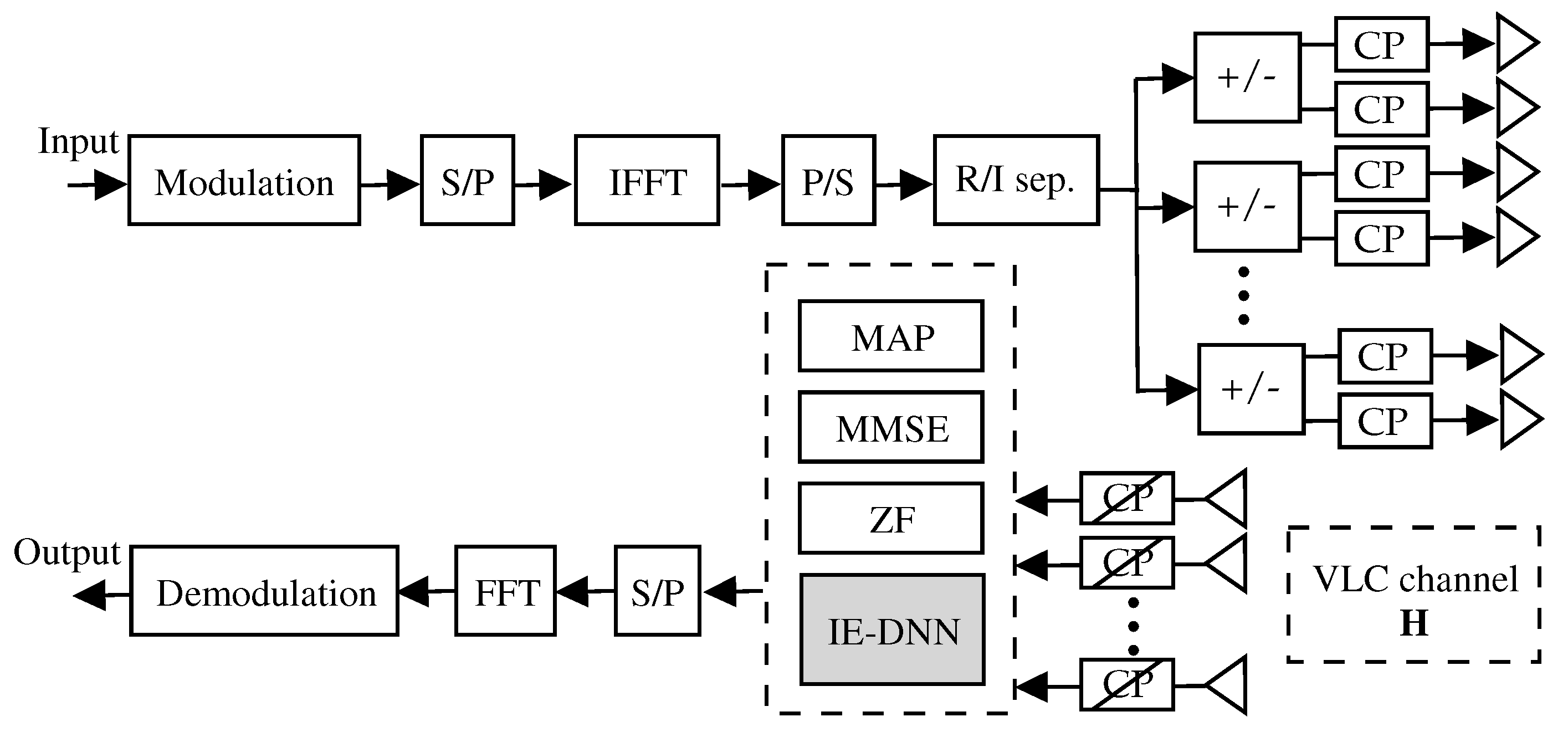
2. GLIM System Model
3. Structure and Operation of DL-Based Index Estimator
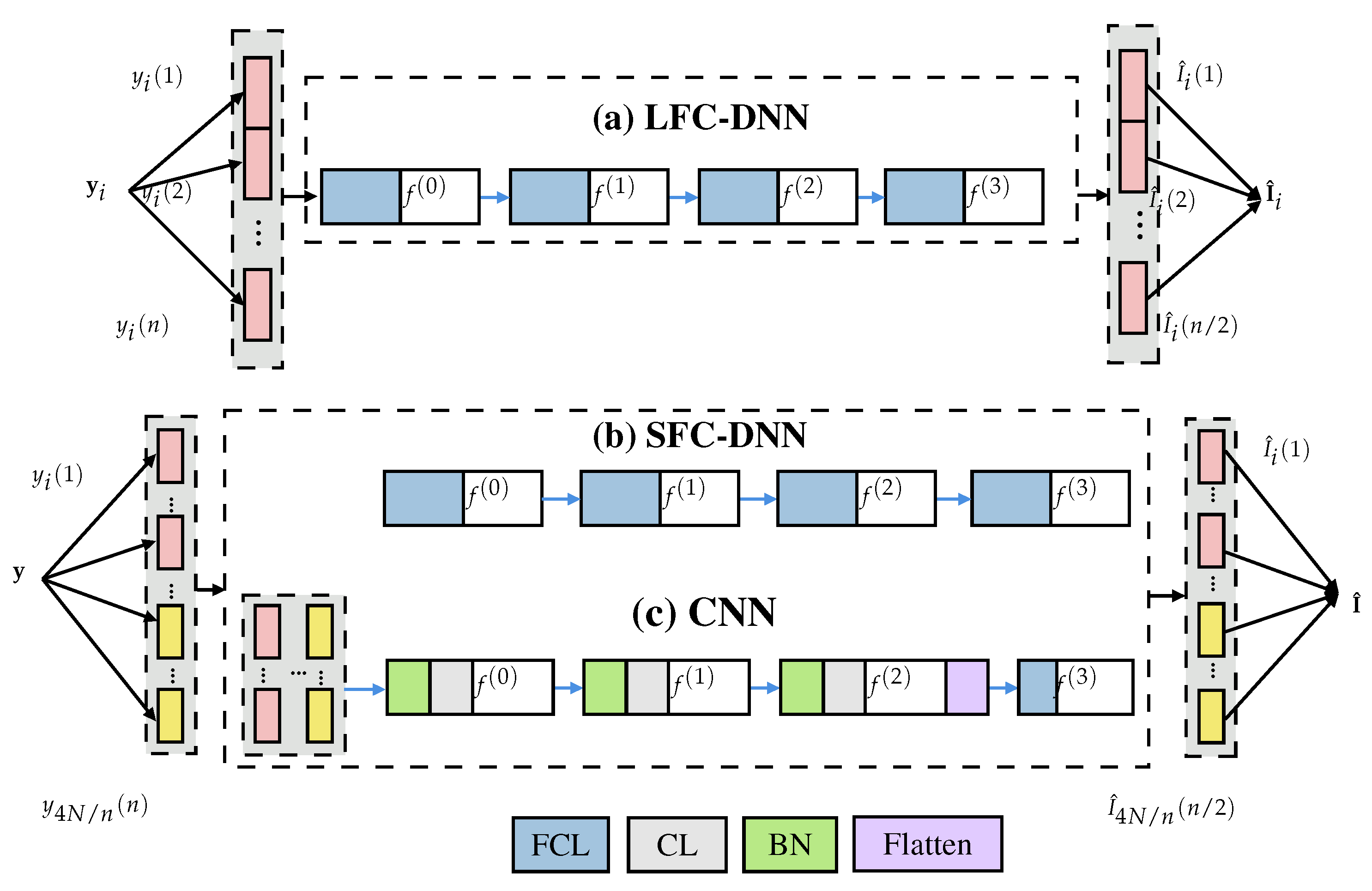
3.1. Proposed DL-Based Index Estimator
3.1.1. LFC-DNN
3.1.2. SFC-DNN
3.1.3. CNN
3.2. Sample Generation
3.3. Training Specification
3.4. Complexity Analysis
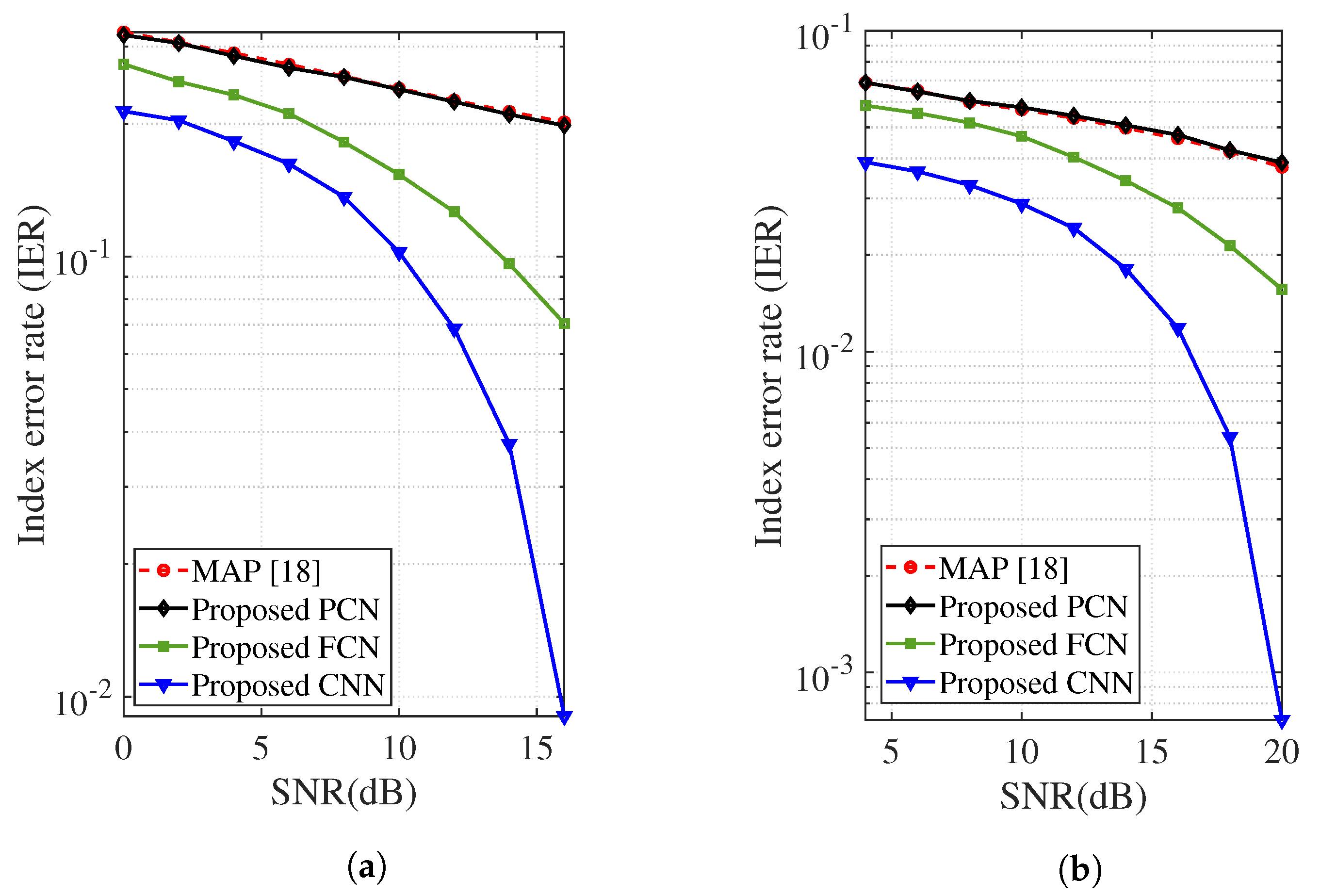
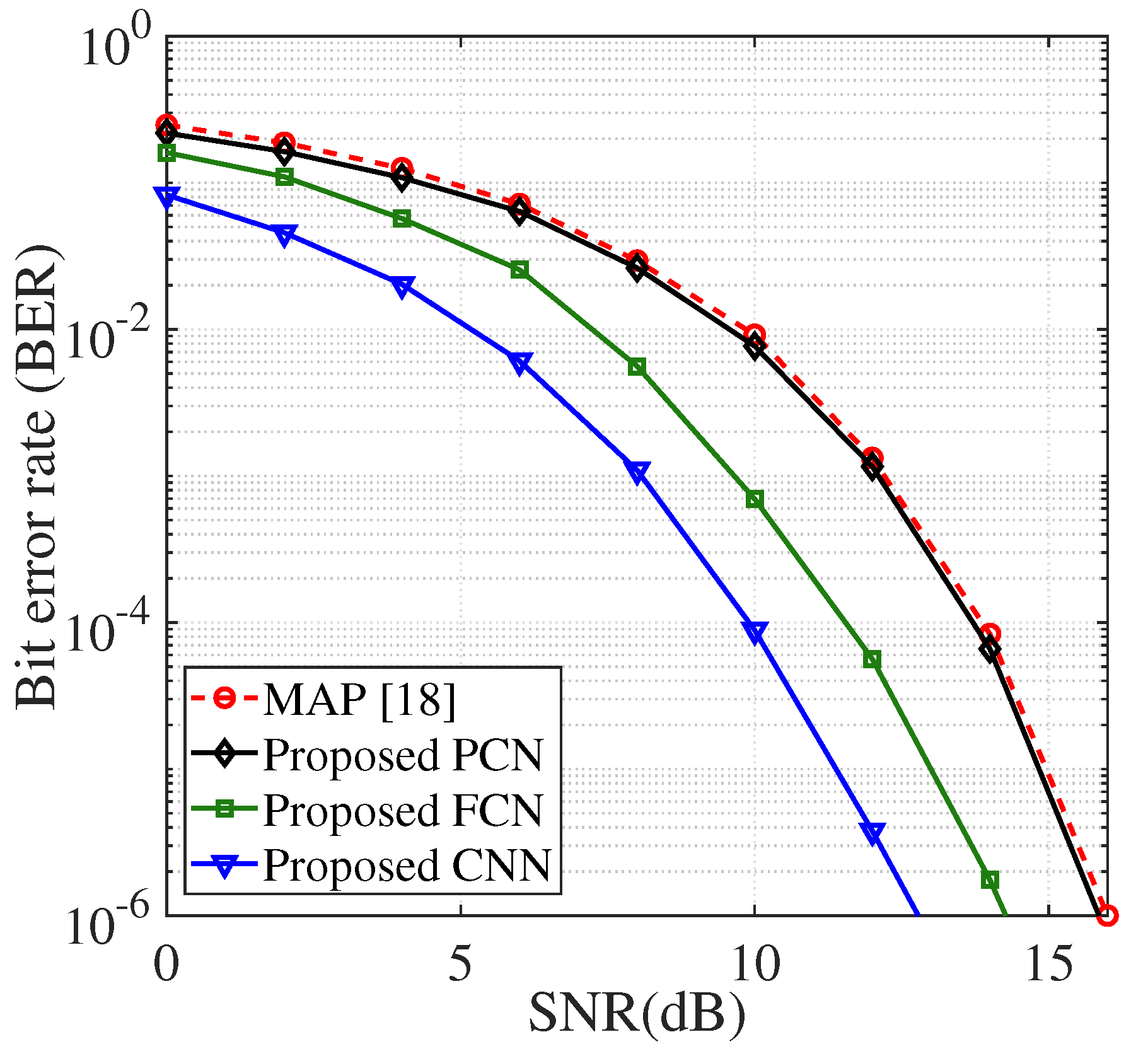
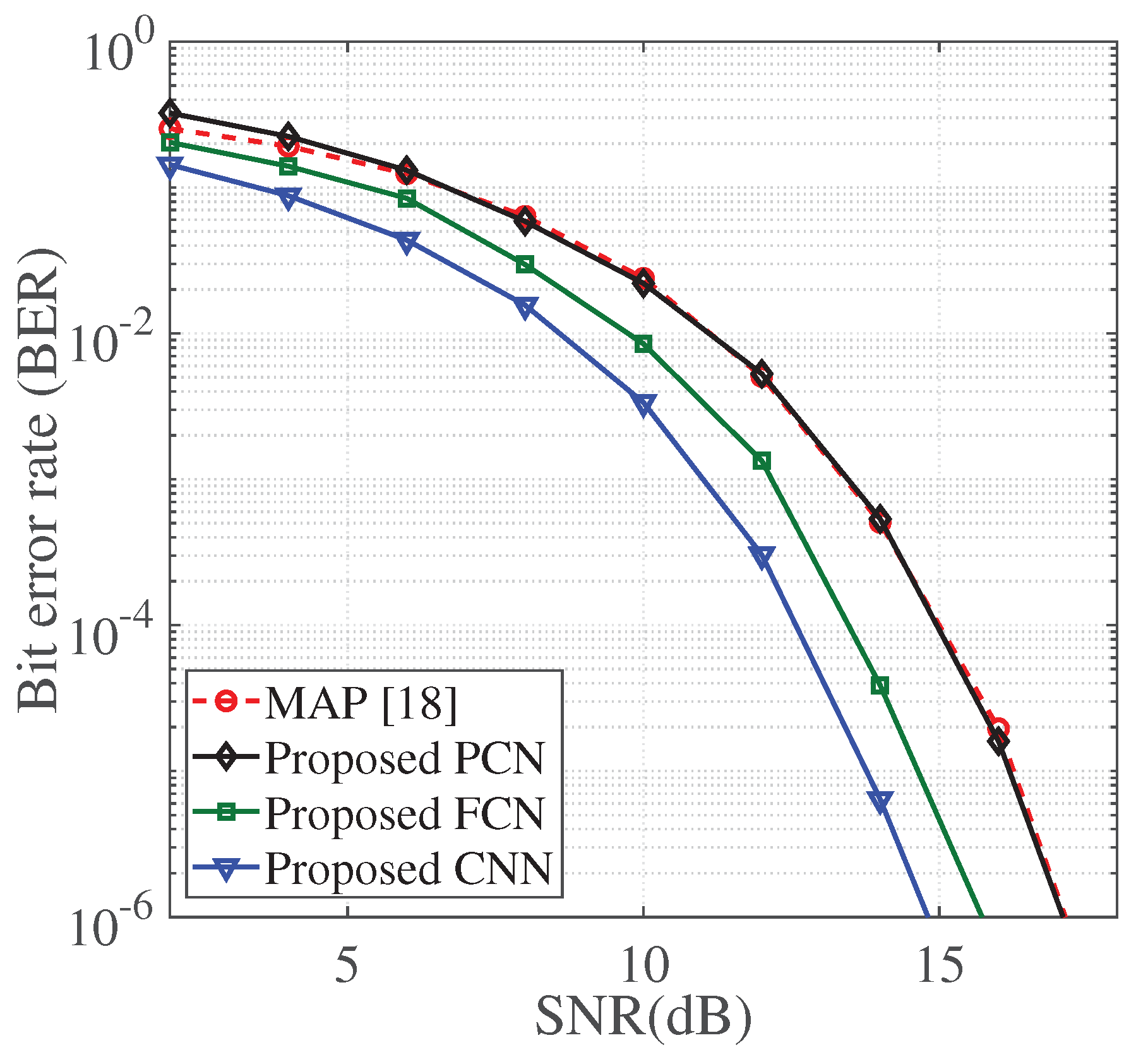
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AWGN | Additive white Gaussian noise |
| CL | Convolution layers |
| CNN | Convolutional neural network |
| DNN | Deep neural network |
| FCL | Fully connected layers |
| MIMO | Multiple-input multiple-output |
| LED | Light emitting diode |
| GLIM | Generalized LED index modulation optical orthogonal frequency-division multiplexing |
| PD | Photo detector |
| MAP | Maximum a posteriori |
| ZF | Zero-forcing |
| VLC | Visible light communication |
References
- Komine, T.; Nakagawa, M. Fundamental Analysis for Visible-Light Communication System Using LED Lights. IEEE Trans. Consum. Electron. 2004, 50, 100–107. [Google Scholar] [CrossRef]
- Matheus, L.E.M.; Vieira, A.B.; Vieira, L.F.M.; Vieira, M.A.M.; Gnawali, O. Visible Light Communication: Concepts, Applications and Challenges. IEEE Commun. Surv. Tutor. 2019, 21, 3204–3237. [Google Scholar] [CrossRef]
- Gong, C. Visible Light Communication and Positioning: Present and Future. Electronics 2019, 8, 788. [Google Scholar] [CrossRef]
- Le Tran, M.; Kim, S. Effective Receiver Design for MIMO Visible Light Communication with Quadrichromatic LEDs. Electronics 2019, 8, 1383. [Google Scholar] [CrossRef]
- Guo, J.N.; Zhang, J.; Xin, G.; Li, L. Constant Transmission Efficiency Dimming Control Scheme for VLC Systems. Photonics 2021, 8, 7. [Google Scholar] [CrossRef]
- Wang, Q.; Giustiniano, D.; Zuniga, M. In Light and in Darkness, in Motion and in Stillness: A Reliable and Adaptive Receiver for the Internet of Lights. IEEE J. Sel. Areas Commun. 2018, 36, 149–161. [Google Scholar] [CrossRef]
- Li, D.C.; Chen, C.C.; Liaw, S.K.; Afifah, S.; Sung, J.Y.; Yeh, C.H. Performance Evaluation of Underwater Wireless Optical Communication System by Varying the Environmental Parameters. Photonics 2021, 8, 74. [Google Scholar] [CrossRef]
- Armstrong, J. OFDM for Optical Communications. J. Light. Technol. 2009, 27, 189–204. [Google Scholar] [CrossRef]
- Pathak, P.H.; Feng, X.; Hu, P.; Mohapatra, P. Visible Light Communication, Networking, and Sensing: A Survey, Potential and Challenges. IEEE Commun. Surv. Tutor. 2015, 17, 2047–2077. [Google Scholar] [CrossRef]
- Basar, E.; Aygolu, U.; Panayirci, E.; Poor, H.V. Orthogonal Frequency Division Multiplexing With Index Modulation. IEEE Trans. Signal Process. 2013, 61, 5536–5549. [Google Scholar] [CrossRef]
- Basar, E. Reconfigurable Intelligent Surface-Based Index Modulation: A New Beyond MIMO Paradigm for 6G. IEEE Trans. Commun. 2020, 68, 3187–3196. [Google Scholar] [CrossRef]
- Mao, T.; Wang, Q.; Wang, Z.; Chen, S. Novel Index Modulation Techniques: A Survey. IEEE Commun. Surv. Tutor. 2018, 21, 1. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugiura, S.; Hanzo, L. 50 Years of Permutation, Spatial and Index Modulation: From Classic RF to Visible Light Communications and Data Storage. IEEE Commun. Surv. Tutor. 2018, 20, 1905–1938. [Google Scholar] [CrossRef]
- Fazeli, A.; Nguyen, H.H.; Hanif, M. Generalized OFDM-IM with Noncoherent Detection. IEEE Trans. Wirel. Commun. 2020, 4, 1323–1337. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, Q. Low-Complexity Soft-Decision Detection of Coded OFDM with Index Modulation. IEEE Trans. Veh. Technol. 2018, 67, 7759–7763. [Google Scholar] [CrossRef]
- Belaoura, W.; Althunibat, S.; Qaraqe, K.A.; Ghanem, K. Precoded Index Modulation Based Multiple Access Scheme. IEEE Trans. Veh. Technol. 2020, 69, 12912–12920. [Google Scholar] [CrossRef]
- Mesleh, R.; Elgala, H.; Haas, H. Optical Spatial Modulation. J. Opt. Commun. Netw. 2011, 3, 234. [Google Scholar] [CrossRef]
- Yesilkaya, A.; Basar, E.; Miramirkhani, F.; Panayirci, E.; Uysal, M.; Haas, H. Optical MIMO-OFDM with Generalized LED Index Modulation. IEEE Trans. Commun. 2017, 65, 3429–3441. [Google Scholar] [CrossRef]
- Le Tran, M.; Kim, S.; Ketseoglou, T.; Ayanoglu, E. LED Selection and MAP Detection for Generalized LED Index Modulation. IEEE Photon. Technol. Lett. 2018, 30, 1695–1698. [Google Scholar] [CrossRef]
- Chen, M.; Challita, U.; Saad, W.; Yin, C.; Debbah, M. Artificial Neural Networks-Based Machine Learning for Wireless Networks: A Tutorial. IEEE Commun. Surv. Tutor. 2019, 21, 3039–3071. [Google Scholar] [CrossRef]
- Luong, T.V.; Ko, Y.; Vien, N.A.; Nguyen, D.H.N.; Matthaiou, M. Deep Learning-Based Detector for OFDM-IM. IEEE Wireless Commun. Lett. 2019, 8, 1159–1162. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, C.; Zhang, H.; Ren, Y.; Chen, K.C.; Hanzo, L. Thirty Years of Machine Learning: The Road to Pareto-Optimal Wireless Networks. IEEE Commun. Surv. Tutor. 2020, 22, 1472–1514. [Google Scholar] [CrossRef]
- Le-Tran, M.; Kim, S. Deep Learning-Based Collaborative Constellation Design for Visible Light Communication. IEEE Commun. Lett. 2020, 24, 2522–2526. [Google Scholar] [CrossRef]
- Sun, L.; Wang, Y. CTBRNN: A Novel Deep-Learning Based Signal Sequence Detector for Communications Systems. IEEE Signal Process. Lett. 2019, 27, 21–25. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Ismail, M.; Serpedin, E.; Wang, J. Efficient Prediction of Link Outage in Mobile Optical Wireless Communications. IEEE Trans. Wirel. Commun. 2020, 20, 882–896. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning Adaptive Computation and Machine Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:cs/1412.6980. [Google Scholar]
- Golub, G.H.; Loan, C.F.V. Matrix Computations, 4th ed.; Johns Hopkins Studies in the Mathematical Sciences; Johns Hopkins University Press: Baltimore, MD, USA, 2012. [Google Scholar]
| Expression | Description | Multiplications | Summations | Total Flops |
|---|---|---|---|---|
| Vector Scaling | N | N | ||
| Matrix Scaling | ||||
| Ab | Matrix-Vector Prod. | |||
| AB | Matrix-Matrix Prod. | |||
| AD | Matrix-Diagonal Prod. | |||
| Inner Prod. | N | |||
| Outer Prod. | ||||
| Gram | ||||
| Euclidean norm | ||||
| Inverse of Pos. Definite | Including N roots |
| Detector | Numbers of Trainable Parameters | Estimation Time |
|---|---|---|
| (Case 1/Case 2) | (Case 1/Case 2) | |
| LFC-DNN | 994/994 | 13 ms/44 ms |
| SFC-DNN | 4736/9544 | 28 ms/78 ms |
| CNN | 3096/6328 | 22 ms/67 ms |
| MAP | -/- | 6 ms/23 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le-Tran, M.; Kim, S. Deep Learning-Assisted Index Estimator for Generalized LED Index Modulation OFDM in Visible Light Communication. Photonics 2021, 8, 168. https://doi.org/10.3390/photonics8050168
Le-Tran M, Kim S. Deep Learning-Assisted Index Estimator for Generalized LED Index Modulation OFDM in Visible Light Communication. Photonics. 2021; 8(5):168. https://doi.org/10.3390/photonics8050168
Chicago/Turabian StyleLe-Tran, Manh, and Sunghwan Kim. 2021. "Deep Learning-Assisted Index Estimator for Generalized LED Index Modulation OFDM in Visible Light Communication" Photonics 8, no. 5: 168. https://doi.org/10.3390/photonics8050168
APA StyleLe-Tran, M., & Kim, S. (2021). Deep Learning-Assisted Index Estimator for Generalized LED Index Modulation OFDM in Visible Light Communication. Photonics, 8(5), 168. https://doi.org/10.3390/photonics8050168





