Optimized Omnidirectional High-Reflectance Using Octonacci Photonic Crystal for Thermographic Sensing Applications
Abstract
1. Introduction
2. Theoretical Model
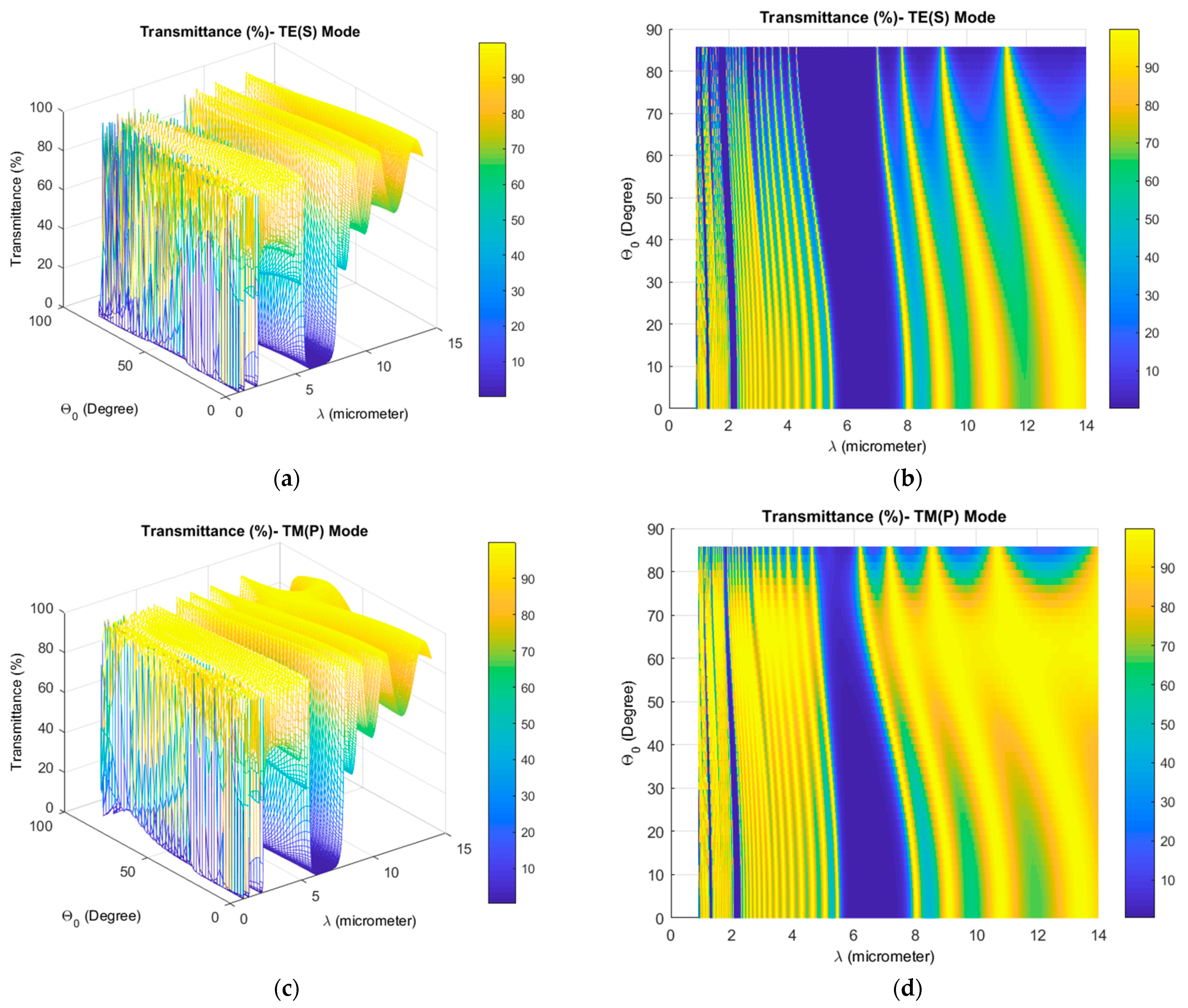
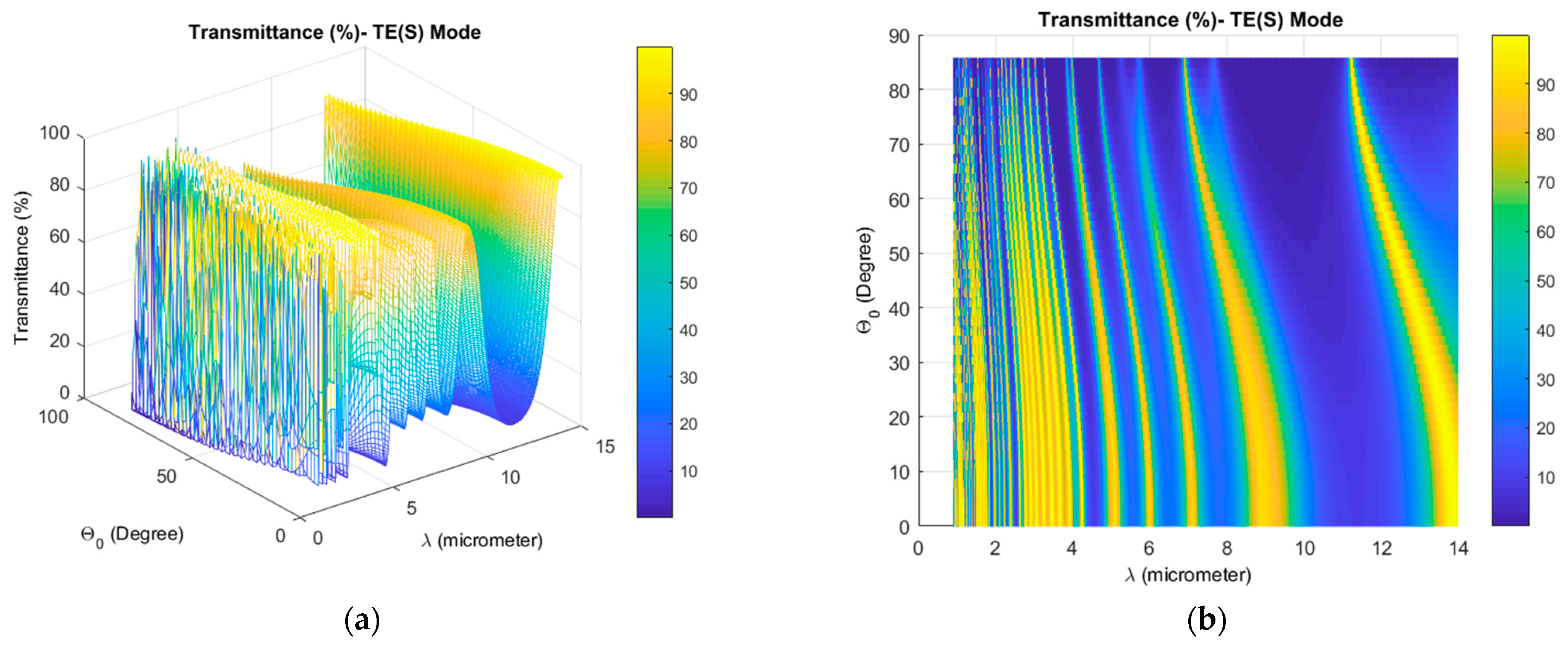
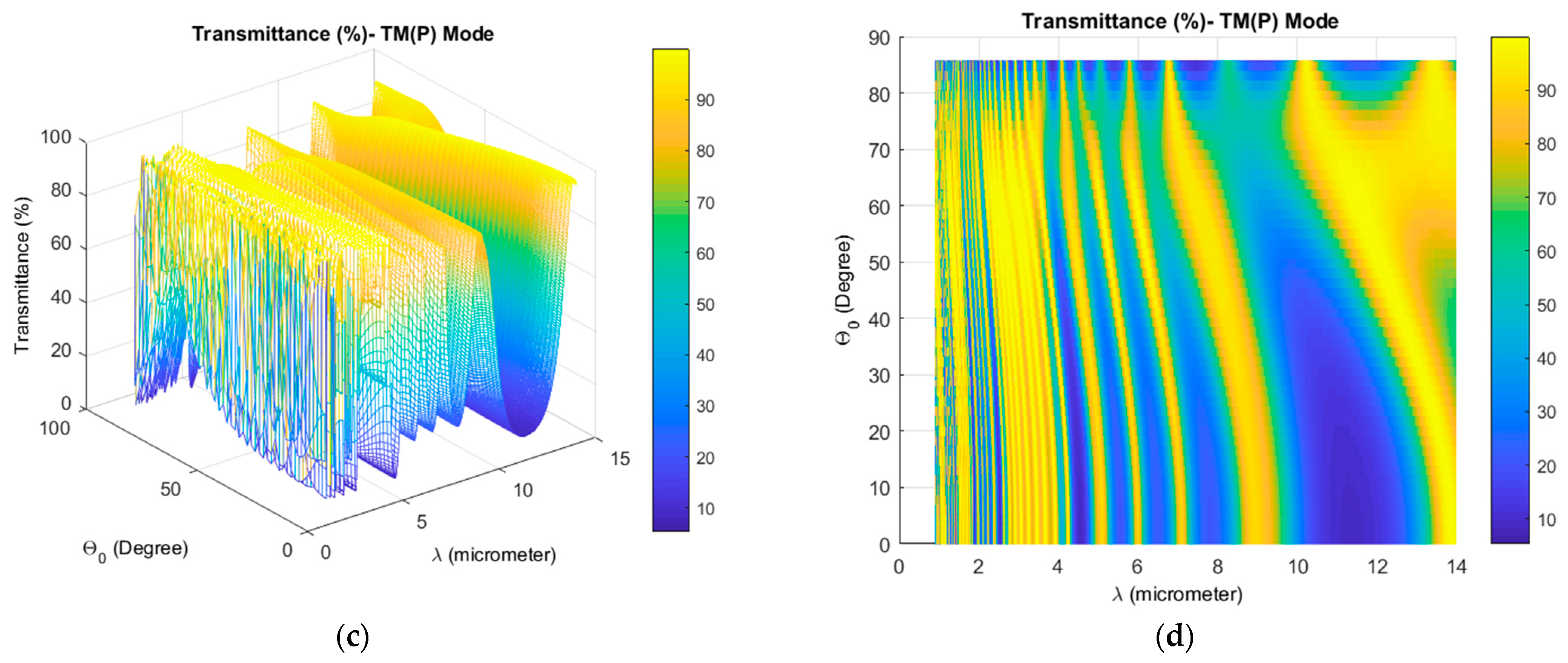
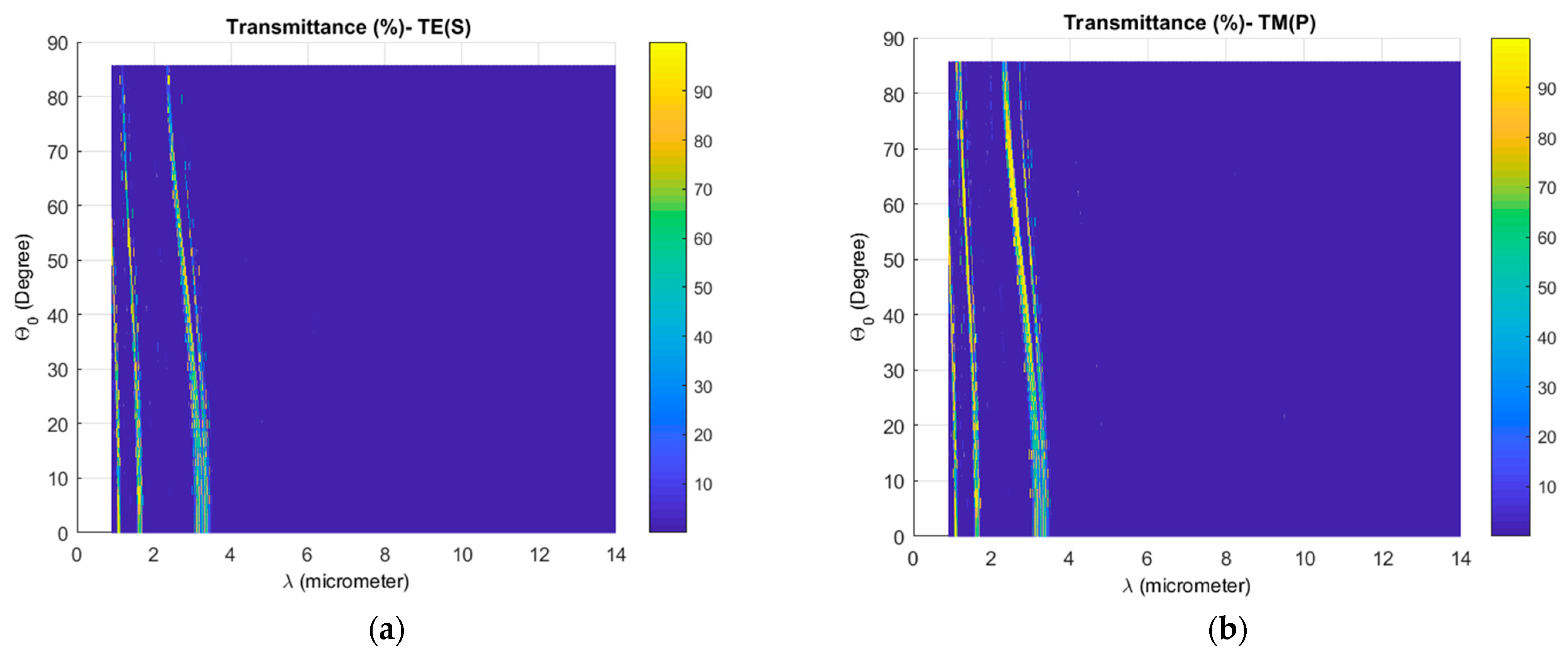
3. Results and Discussions
3.1. Material Effect
3.2. Iteration Effect
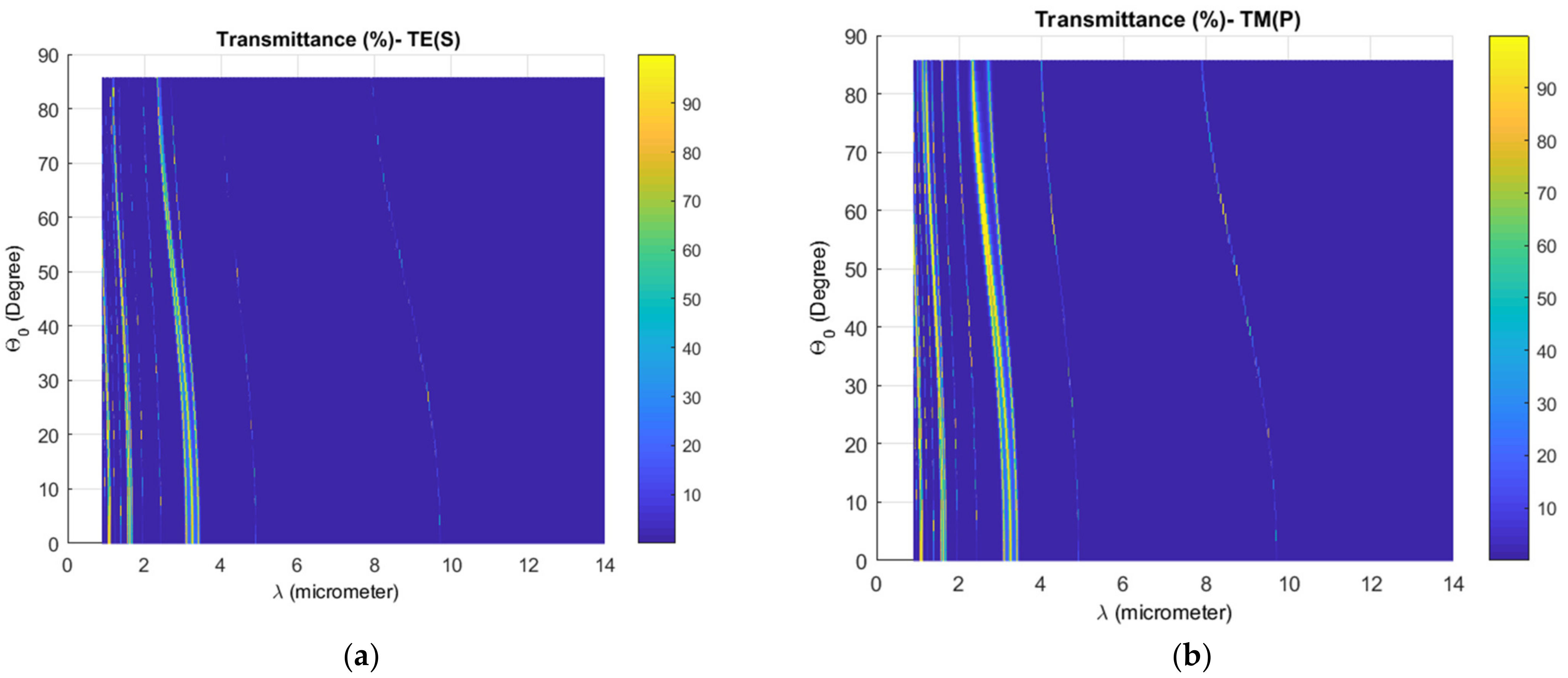
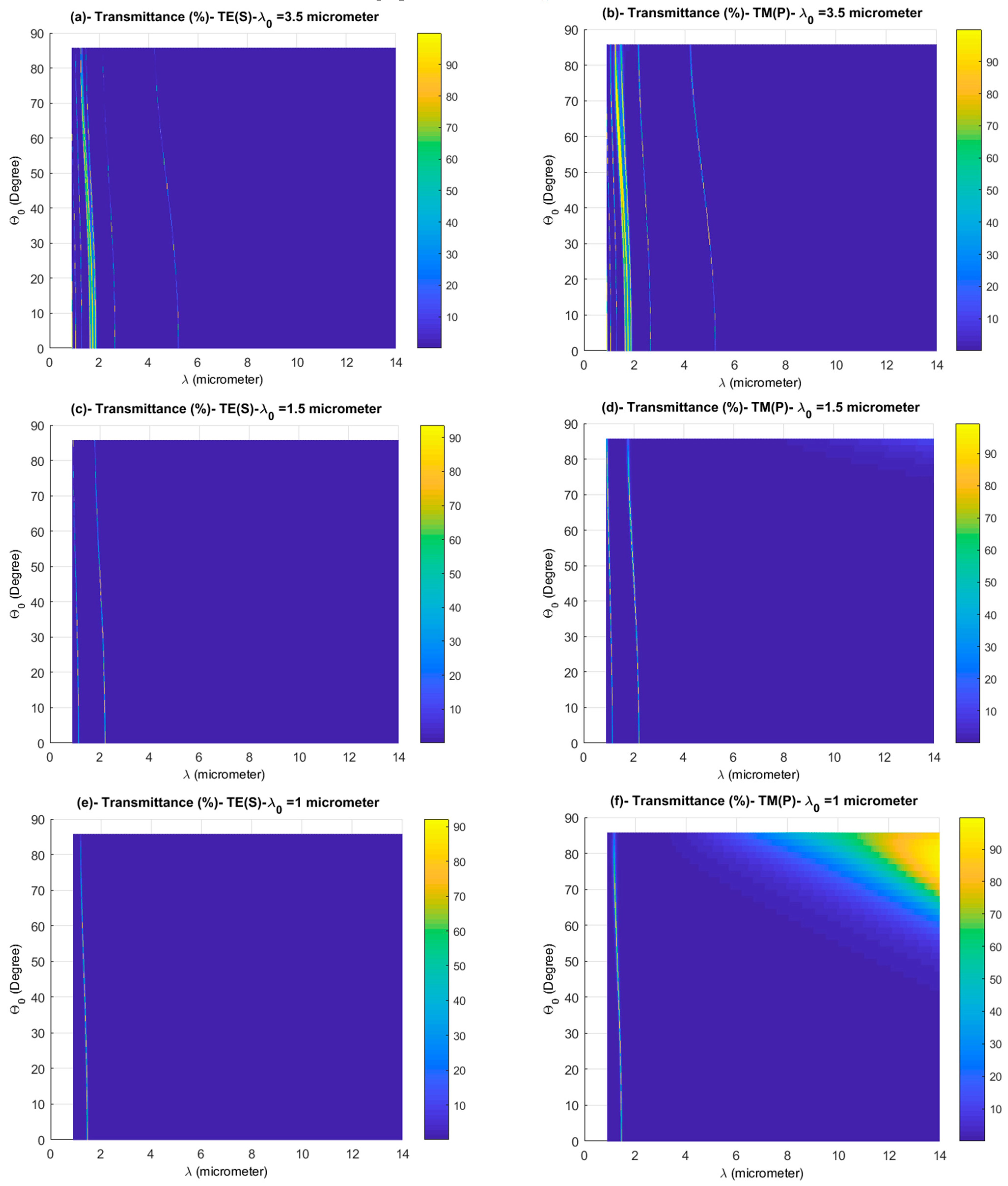
3.3. Reference Wavelength Effect
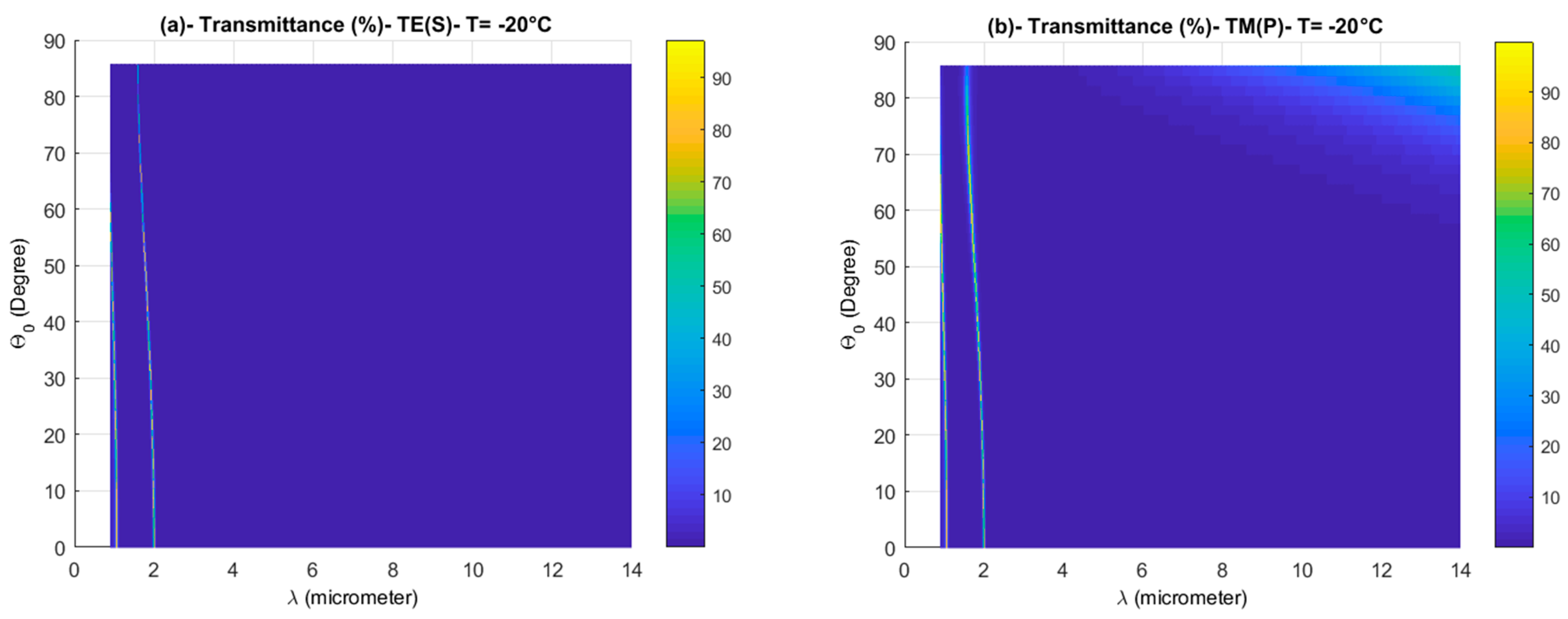
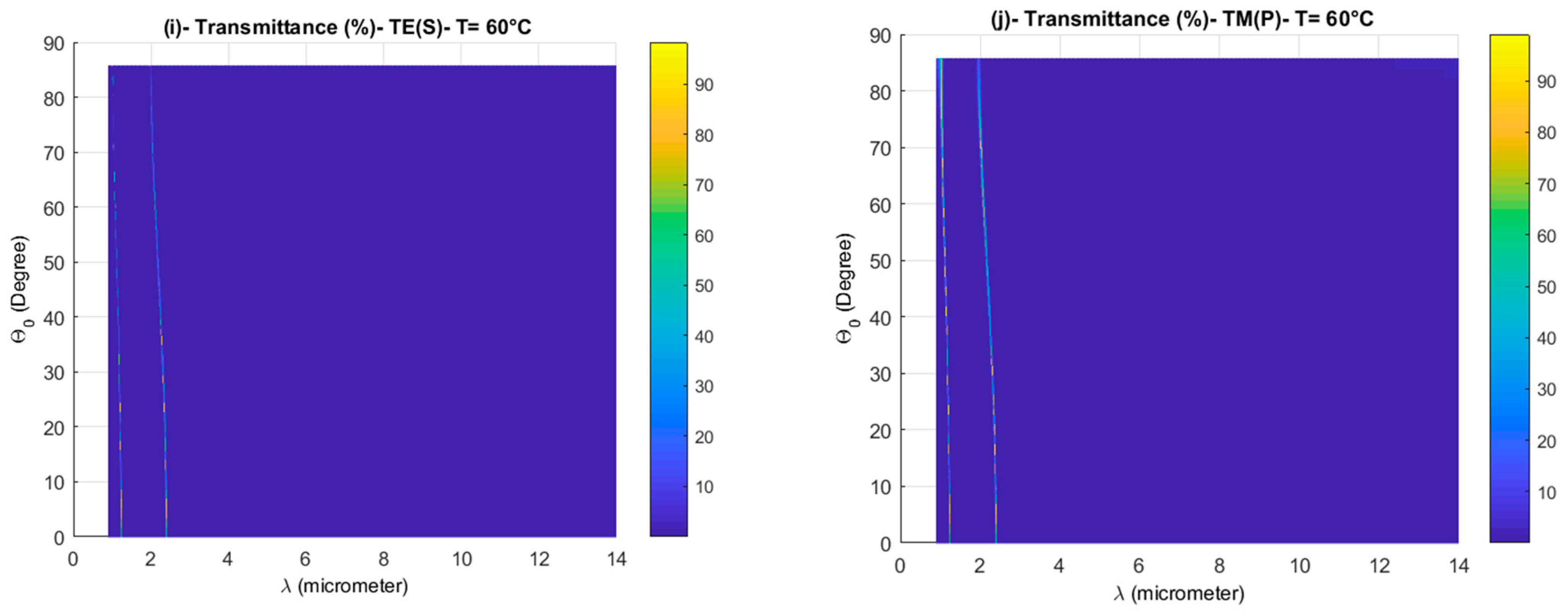
3.4. Temperature Effect
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Ramaswami, R. Optical fiber communication: From transmission to networking. IEEE Commun. Mag. 2002, 40, 138–147. [Google Scholar] [CrossRef]
- Byrnes, J. (Ed.) Unexploded Ordnance Detection and Mitigation, 2nd ed.; Springer: Dordrecht, The Netherlands, 2009; p. 21. [Google Scholar]
- Corsi, C. History highlights and future trends of infrared sensors. J. Mod. Opt. 2010, 57, 1663–1686. [Google Scholar] [CrossRef]
- Frodella, W.; Gigli, G.; Morelli, S.; Lombardi, L.; Casagli, N. Landslide Mapping and Characterization through Infrared Thermography (IRT): Suggestions for a Methodological Approach from Some Case Studies. Remote Sens. 2017, 9, 1281. [Google Scholar] [CrossRef]
- Wien, W. XXX. On the division of energy in the emission-spectrum of a black body. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1897, 43, 214–220. [Google Scholar] [CrossRef]
- Mehra, J.; Rechenberg, H. Part 1 The Fundamental Equations of Quantum Mechanics 1925–1926 Part 2 The Reception of the New Quantum Mechanics 1925–1926 In The Historical Development of Quantum Theory, 1st ed.; Springer: New York, NY, USA, 1982; Volume 4, p. 322. [Google Scholar]
- Bowley, R.; Sanchez, M.; Knox, R.S. Introductory Statistical Mechanics, 2nd ed.; Oxford University Press: Oxford, UK, 2000; p. 368. [Google Scholar]
- Ribbing, C.G. Controlling thermal radiation from surfaces. In Optical Thin Films and Coatings; Woodhead Publishing: Cambridge, UK, 2013; Volume 2013, pp. 357–390. [Google Scholar]
- Forsberg, C.H. Radiation heat transfer. In Heat Transfer Principles and Applications; Routledge: London, UK, 2021; Volume 2021, pp. 343–389. [Google Scholar]
- Brandão, E.; Costa, C.; Vasconcelos, M.; Anselmo, D.; Mello, V. Octonacci photonic quasicrystals. Opt. Mater. 2015, 46, 378–383. [Google Scholar] [CrossRef]
- Silva, E.; Costa, C.; Vasconcelos, M.; Anselmo, D. Transmission spectra in graphene-based octonacci one-dimensional photonic quasicrystals. Opt. Mater. 2019, 89, 623–629. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Ben Ali, N.; Kanzari, M. Tunable narrowband optical filters using superconductor/dielectric generalized Thue-Morse photonic crystals. Microelectron. Eng. 2019, 213, 41–46. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Ben Ali, N.; Belhadj, W.; Kanzari, M. Photonic Band Gap Properties of One-dimensional Generalized Fibonacci Photonic Quasicrystal Containing Superconductor Material. J. Supercond. Nov. Magn. 2019, 32, 3541–3547. [Google Scholar] [CrossRef]
- 17Segovia-Chaves, F.; Vinck-Posada, H.; Trabelsi, Y.; Ben Ali, N. Transmittance spectrum in a one-dimensional photonic crystal with Fibonacci sequence superconductor–semiconductor. Optik 2020, 217, 164803. [Google Scholar] [CrossRef]
- 18Ali, N.B.; Trabelsi, Y.; Kanzari, M. Stop band filter by using hybrid quasi-periodic one dimensional photonic crystal in microwave domain. IJMOT 2009, 4, 195–204. [Google Scholar]
- Hu, C.-A.; Liu, J.-W.; Wu, C.-J.; Yang, T.-J.; Yang, S.-L. Effects of superconducting film on the defect mode in dielectric photonic crystal heterostructure. Solid State Commun. 2013, 157, 54–57. [Google Scholar] [CrossRef]
- Srivastava, S.K. Study of defect modes in 1d photonic crystal structure containing high and low Tc superconductor as a defect layer. J. Supercond. Nov. Magn. 2014, 27, 101–114. [Google Scholar] [CrossRef]
- Wu, J.; Gao, J. Low temperature sensor based on one-dimensional photonic crystals with a dielectric-superconducting pair defect. Optik 2015, 126, 5368–5371. [Google Scholar] [CrossRef]
- Asmi, R.; Ali, N.B.; Kanzari, M. Numerical investigation of light localization in generalized Thue–Morse one-dimensional photonic crystal. J. Photon. Energy 2016, 6, 34501. [Google Scholar] [CrossRef]
- Srinivasan, K.; Ali, N.B.; Trabelsi, Y.; Rajan, M.M.; Kanzari, M. Design of a modified single-negative metamaterial structure for sensing application. Optik 2019, 180, 924–931. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, N.B.; Trabelsi, Y.; Alsaif, H.; Bouazzi, Y.; Kanzari, M. Optimized Omnidirectional High-Reflectance Using Octonacci Photonic Crystal for Thermographic Sensing Applications. Photonics 2021, 8, 169. https://doi.org/10.3390/photonics8050169
Ali NB, Trabelsi Y, Alsaif H, Bouazzi Y, Kanzari M. Optimized Omnidirectional High-Reflectance Using Octonacci Photonic Crystal for Thermographic Sensing Applications. Photonics. 2021; 8(5):169. https://doi.org/10.3390/photonics8050169
Chicago/Turabian StyleAli, Naim Ben, Youssef Trabelsi, Haitham Alsaif, Yasssine Bouazzi, and Mounir Kanzari. 2021. "Optimized Omnidirectional High-Reflectance Using Octonacci Photonic Crystal for Thermographic Sensing Applications" Photonics 8, no. 5: 169. https://doi.org/10.3390/photonics8050169
APA StyleAli, N. B., Trabelsi, Y., Alsaif, H., Bouazzi, Y., & Kanzari, M. (2021). Optimized Omnidirectional High-Reflectance Using Octonacci Photonic Crystal for Thermographic Sensing Applications. Photonics, 8(5), 169. https://doi.org/10.3390/photonics8050169




