Dispersion Optimization of Silicon Nitride Waveguides for Efficient Four-Wave Mixing

Abstract

Silicon nitride waveguides have emerged as an excellent platform for photonic applications, including nonlinear optical signal processing, owing to their relatively high Kerr nonlinearity, negligible two photon absorption, and wide transparent bandwidth. In this paper, we propose an effective approach using 3D finite element method to optimize the dispersion characteristics of silicon nitride waveguides for four-wave mixing (FWM) applications. Numerical studies show that a flat and low dispersion profile can be achieved in a silicon nitride waveguide with the optimized dimensions. Near-zero dispersion of 1.16 ps/km/nm and 0.97 ps/km/nm at a wavelength of 1550 nm are obtained for plasma-enhanced chemical vapor deposition (PECVD) and low-pressure chemical vapor deposition (LPCVD) silicon nitride waveguides, respectively. The fabricated micro-ring resonator with the optimized dimensions exhibits near-zero dispersion of −0.04 to −0.1 ps/m/nm over a wavelength range of 130 nm which agrees with the numerical simulation results. FWM results show that near-zero phase mismatch and high conversion efficiencies larger than −12 dB using a low pump power of 0.5 W in a 13-cm long silicon nitride waveguide are achieved.

1. Introduction

With the rapid development of the modern optical communication, the technology of integrated photonic devices is continuously developing. Four-wave mixing (FWM), as an important third-order nonlinear optical process, can be used for wavelength conversion and optical signal processing in integrated waveguides, and has received intense investigations on different platform [1]. Materials such as silicon, silicon dioxide, silicon-rich silica, silicon nitride, and nonlinear polymer have been used for FWM applications. The refractive index of silicon is higher, and the optical band gap (1.1 eV) is smaller. However, the conversion efficiency and signal processing speed of the FWM effect in pure silicon are limited by the nonlinear loss (two photon absorption induced free carrier absorption) [2,3]. Silicon dioxide has a smaller refractive index, but the nonlinear index is very low (2.7 × 10⁻²⁰ m²/W at 1550 nm), thus it needs a long waveguide to achieve high nonlinear effect. As an alternative choice, silicon nitride waveguides have a moderately high index contrast, a relatively high Kerr nonlinearity, and a negligible two photon absorption around telecom wavelengths, which makes it a potential candidate for photonic integration platforms [4,5,6,7]. Moreover, silicon nitride has a wide transparent window ranging from visible to near infrared wavelengths [8]. As a consequence, excellent silicon nitride-based nonlinear optical applications have been demonstrated, including optical frequency combs [9,10], broadband supercontinuum generation [11], self-phase modulation [12], and FWM-based wavelength conversion [13]. Usually, silicon nitride thin films can be prepared by PECVD or low-LPCVD [4].

The dispersion properties of the waveguides are significant for the ultrafast nonlinear applications [14,15,16,17]. The lack of dispersion management might lower the wavelength conversion efficiency and limit the tuning range of the FWM process. In principle, near-zero dispersion over a wavelength range is required to achieve phase matching for high FWM conversion efficiencies [18,19]. Note that other third-order nonlinear applications, such as optical frequency combs, broadband supercontinuum generation, self-phase modulation, and cross-phase modulation also require dispersion engineering for phase matching. Both the material dispersion and waveguide dispersion contribute to the total dispersion. The waveguide dispersion can be tailored by controlling the structure parameters of the waveguide [10,11,12,17]. The phase matching conditions are mainly dominated by second-order dispersion, which is usually described by the dispersion coefficient D.

In this paper, systematic analyses on the dispersion properties of PECVD and LPCVD silicon nitride channel waveguides are conducted, and the geometric parameters of the waveguides to obtain near-zero dispersions for phase matching are optimized. The fabricated silicon nitride micro-ring resonator with optimized parameter shows near-zero dispersion of −0.07 ps/m/nm at 1550 nm and a flat dispersion profile over a 130 nm wavelength range. FWM results show that the optimized silicon nitride waveguide exhibits a high conversion efficiency larger than −12 dB.

2. Waveguide Dispersion Analysis Principle

The silicon nitride channel waveguide is designed on silicon substrate with a SiO₂ claddings. The thicknesses of the bottom and top claddings are 3 μm. The width and the thickness of the core are denoted by w and t, respectively. The relationships between the effective refractive index and the group refractive index and the dispersion coefficient can be expressed by following equations [20]:

$$n_g=n_{\mathrm{eff}}-\lambda \frac{d{n}_{\mathrm{eff}}}{d\lambda }{n}_g=n_{\mathrm{eff}}-\lambda \frac{d{n}_{\mathrm{eff}}}{d\lambda }$$

(1)

$$D\left(\lambda \right)=\frac{1}{c}\frac{d{n}_g}{d\lambda }=-\frac{\lambda }{c}\frac{d^2{n}_{\mathrm{eff}}}{d{\lambda }^2}=-\frac{2\pi c}{{\lambda }^2}{\beta }_2$$

(2)

where n_eff is the effective refractive index, n_g is the group refractive index, λ is the wavelength, c is the speed of the light, β₂ is the group velocity dispersion. The effective refractive index of the waveguide depends on the waveguide width. thickness and the material refractive index. By analyzing the spectrum of n_eff, the group refractive index and dispersion of the waveguide can be extracted according to Equations (1) and (2).

3. Results and Discussion

3.1. Waveguide Dispersion Optimiation

The PECVD silicon nitride is deposited at temperature of 350 °C with a gas flow ratio of SiH₄:NH₃:N₂=6:3:189 sccm. The LPCVD silicon nitride is prepared by using dichlorosilane (DCS) and ammonia (NH₃) at 800 °C with a DCS to NH₃ ratio of 0.3 [17]. The material refractive indices are shown in Figure 1. The data will be used in effective refractive index and dispersion calculation. The CVD deposited silicon nitride film can be silicon-rich or nitrogen-rich. Due to the different deposition temperature and gas ratio, there is a relatively large difference between refractive indices of silicon nitride films prepared by PECVD and LPCVD [21,22].

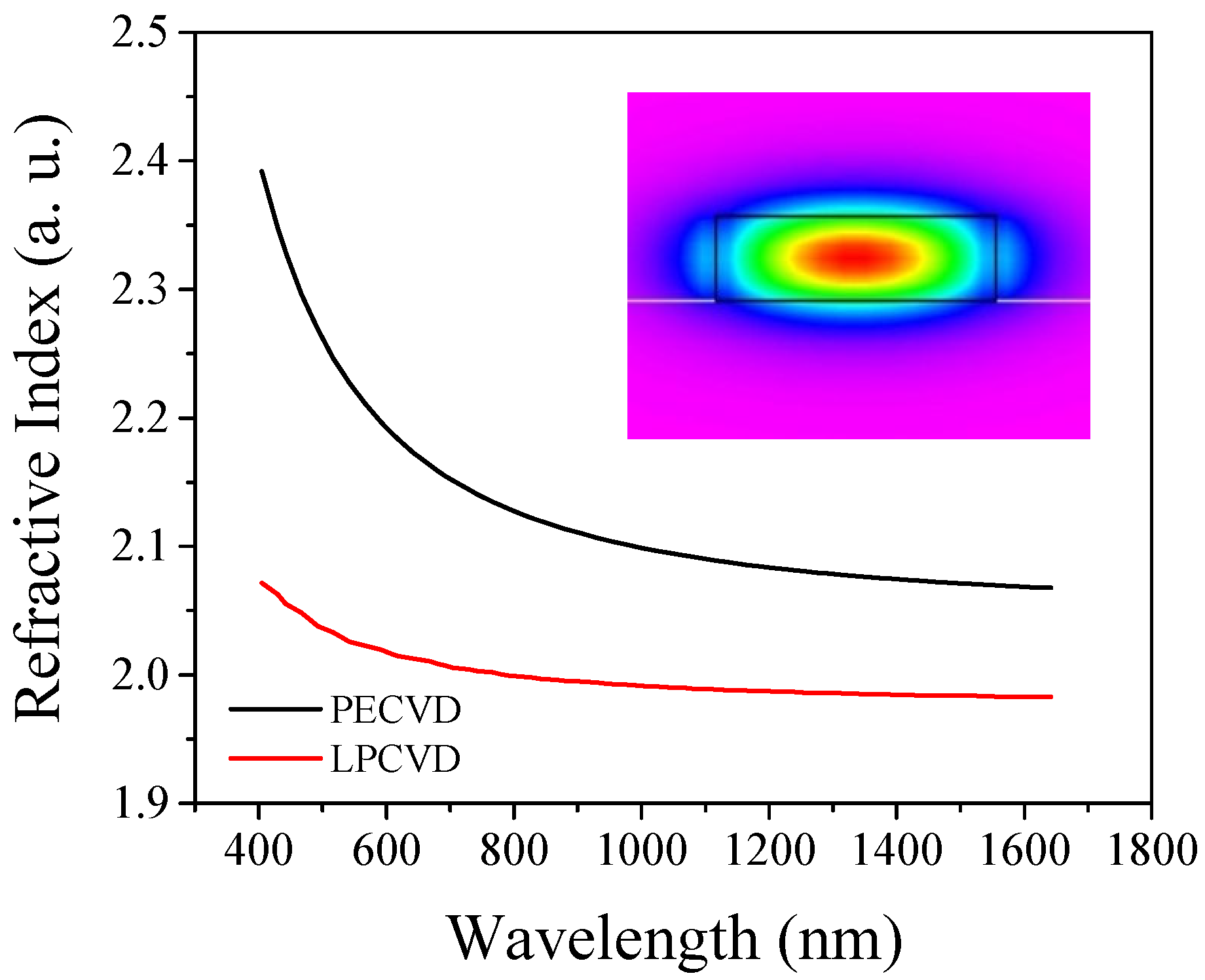
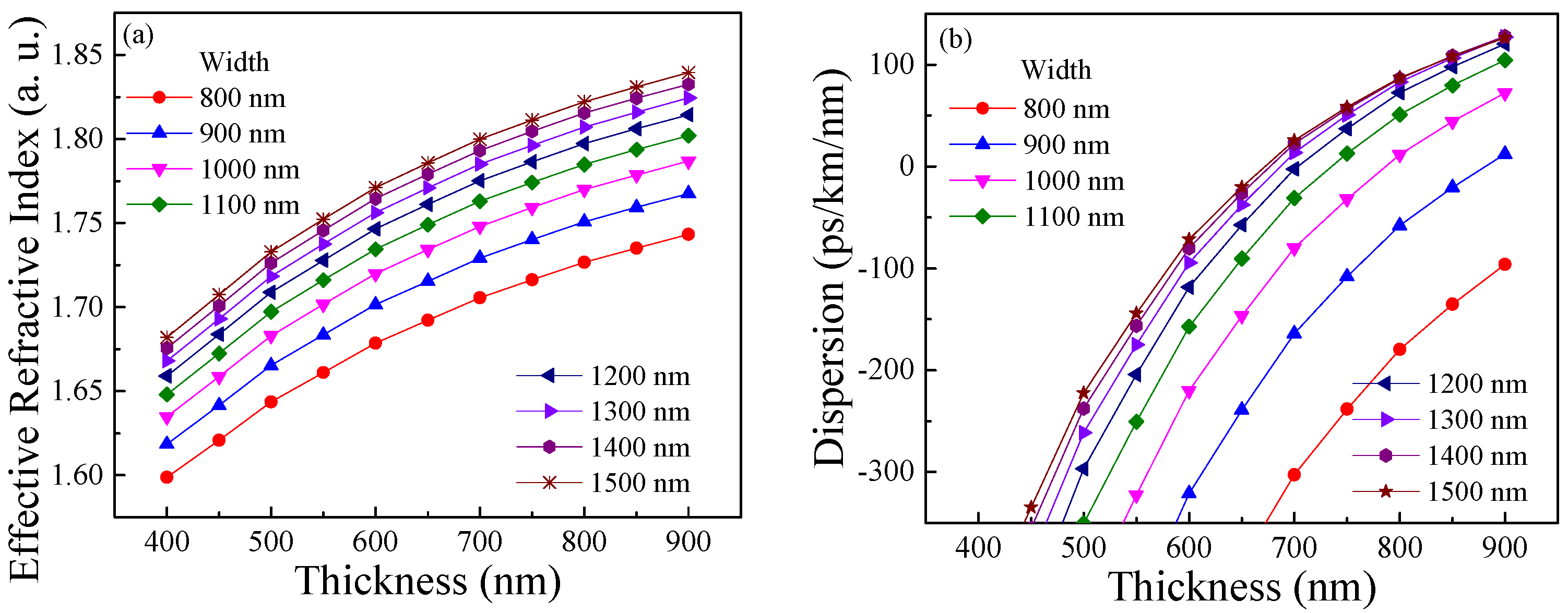
3.1.1. Dispersion of Silicon Nitride Thin Film Waveguide of PECVD

In this study, only the dispersion of the fundamental TE mode is studied because TM modes become TE modes if the waveguide rotates 90°. The filed distribution of the silicon nitride channel waveguide is calculated by using 3D finite element method (3D-FEM). The insert in Figure 1 shows the field distribution of the fundamental mode of the PECVD silicon nitride waveguide at 1550 nm with a width of 710 nm and a thickness of 1250 nm. It can be seen that the optical power is well confined in the core of the waveguide.

The effective refractive index of the mode is obtained from the mode calculation. Figure 2 shows the effective refractive index and dispersion of the waveguides with different width and thickness at the wavelength of 1550 nm. Note that the dispersion includes the waveguide dispersion and material dispersion. It can be seen that the effective refractive index of the waveguide increases with the width and thickness increasing because more power is confined in the waveguide core while the cross-section is larger.

The dispersion increases with the width and thickness increasing. The dispersion increases slowly with the width while the width is larger than 1200 nm. This is because the optical mode distribution is well confined in the waveguide core and weakly affected by the width increase. For the same reason, the thickness dependence of the dispersion will exhibit a similar characteristic. For TE mode, the dispersion changes faster with the thickness than with the width. However, the optimization of the width is easier than that of the thickness because it can be simply realized by designing the photolithograph pattern. Moreover, a very large thickness of the silicon nitride film will add much difficulty to the dry etching of the device. Therefore, a tradeoff between the device fabrication and the dispersion engineering should be made. While the width changing is not enough to get a target dispersion especially an anomalous dispersion (D > 0), the thickness should be changed during experimental optimization.

According to Figure 2b, near-zero dispersions can be easily obtained while the thickness is around 700 nm and the width is around 1200 nm. We choose the waveguide parameters as t = 710 nm and w = 1250 nm which offers an obvious fabrication tolerance. Thus, the dispersion of the selected dimension is slightly larger than zero which might satisfy the phase matching requirement of FWM. It should be noted that the core dimension of the waveguide does not meet the condition of single-mode propagation. However, the power of the high order mode distributes to the edge and attenuates very fast due to transmission loss. Therefore, the high order mode dispersion of the waveguide can be ignored and the dimension supports effective nonlinear interaction between the fundamental mode and the materials. The spectrum of the dispersion of the selected waveguide is shown in Figure 3. The dispersion is near zero (±20 ps/km/nm) over a 100 nm wavelength range around 1550 nm, and is close to zero (~1.16 ps/km/nm) at 1550 nm, which can offer an excellent phase matching condition.

3.1.2. Dispersion of Silicon Nitride Thin Film Waveguide of LPCVD

In this section, we analyze the dispersion of channel waveguides of silicon nitride deposited by using LPCVD. Figure 4a shows the dispersion of the waveguide with different width and thickness at the wavelength of 1550 nm. It can be seen that the dispersion increases with the width and thickness. The zero dispersion point can be found on the curve of w = 1100 nm. Therefore, the waveguide with thickness of 790 nm and width of 1100 nm was selected, which are close to the optimized parameters of PECVD silicon nitride waveguide. The dispersion spectrum of the optimized waveguide is shown in Figure 4b. It shows flat and low dispersion over a wide wavelength range, and a near-zero dispersion of 0.97 ps/km/nm at the wavelength of 1550 nm is obtained.

Compared Figure 2 and Figure 4, it can be seen that PECVD and LPCVD silicon nitride waveguides exhibit similar dispersion characteristics. Even though the refractive index characteristics are different, near-zero dispersion can be obtained to meet the phase matching for FWM, in which the thickness is in the range of 700 nm to 800 nm and the width is in the range of 1100 nm to 1300 nm. If the dispersion is optimized for TM mode in silicon nitride waveguide, a larger waveguide thickness (>1 μm) will be required because of the rotational relationship between TM and TE modes. The larger thickness might add more difficulty to the film deposition and cause more side wall roughness during etching [4].

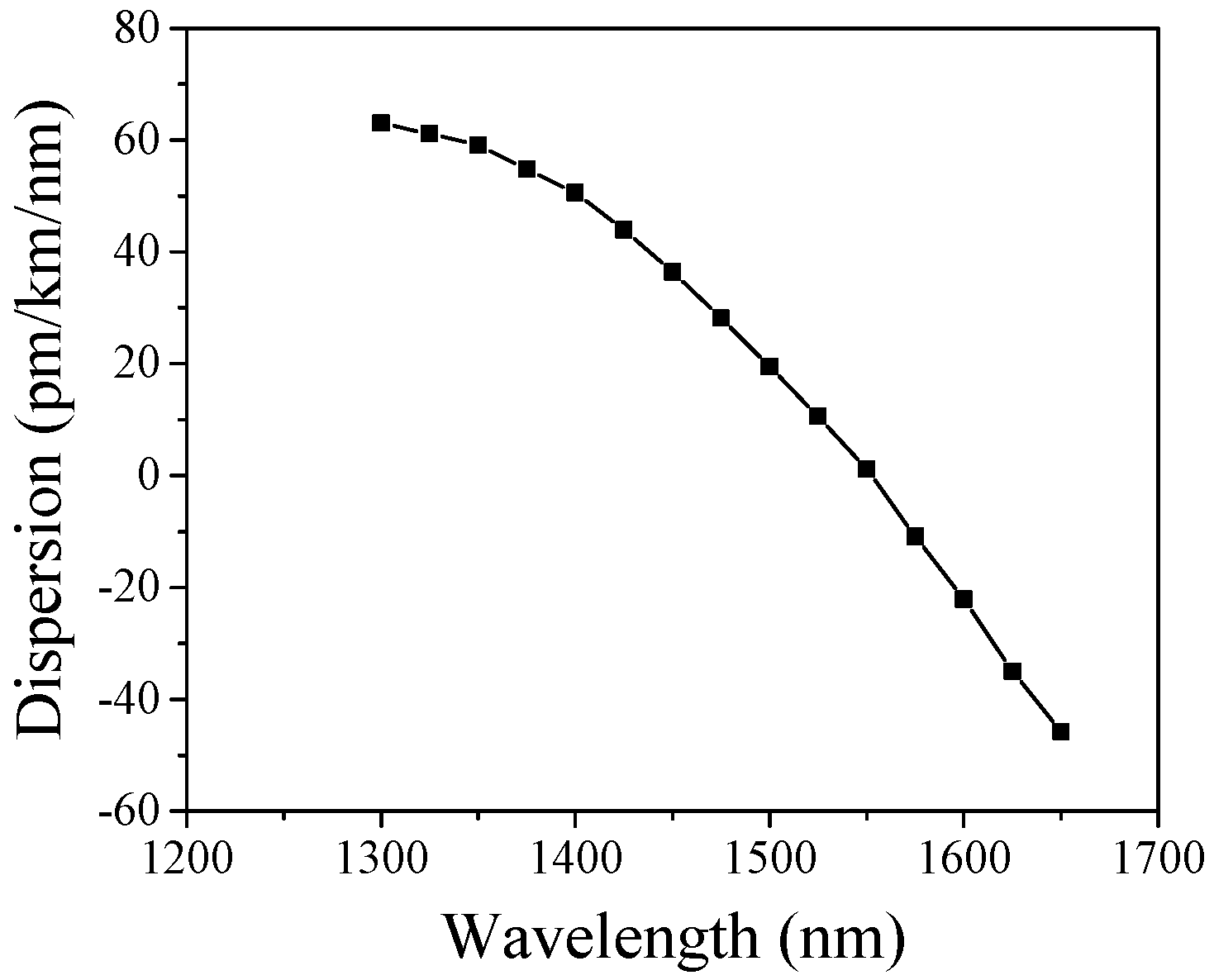
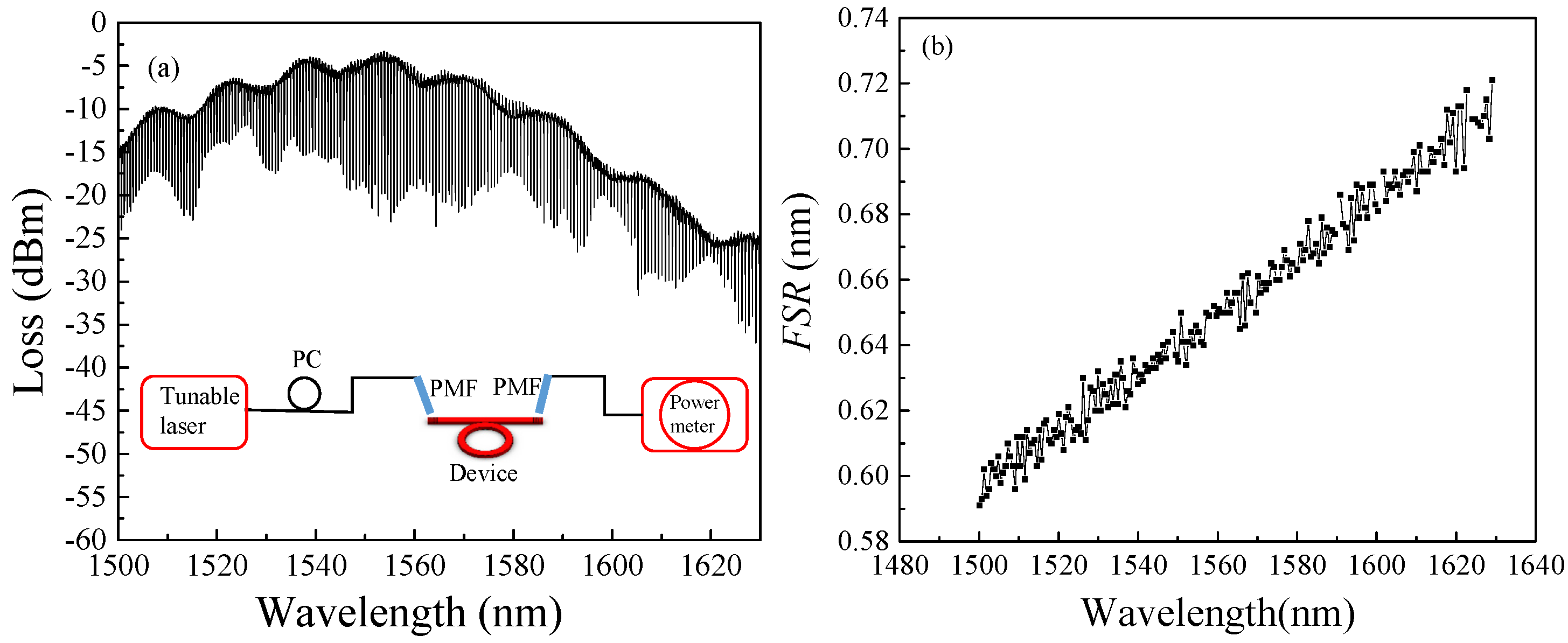
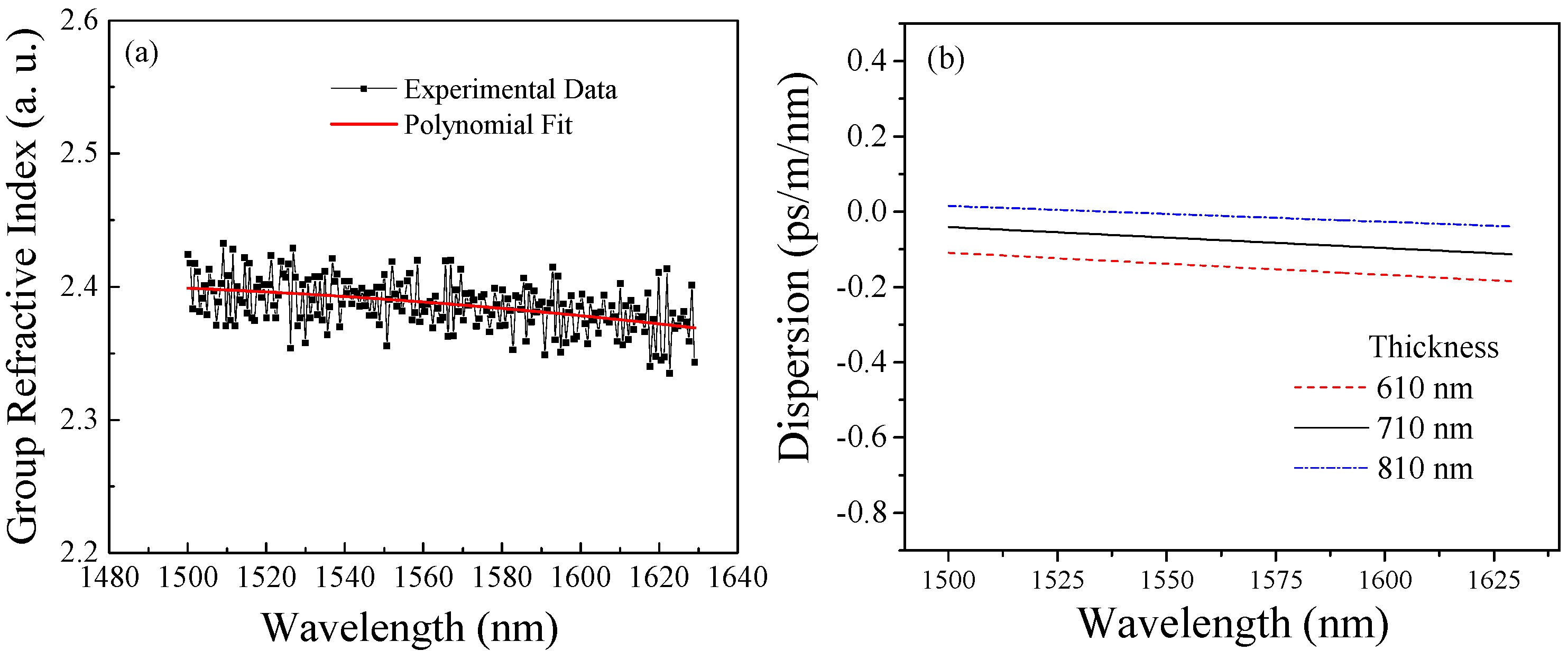
3.2. Waveguide Fabrication and Experimental Characterization

The dispersion of waveguides can be experimentally analyzed by measuring the spectrum of an interference waveguide structure such as an MZI interferometer or a micro-ring resonator. Therefore, we fabricate a micro-ring resonator on a standard 4-inch silicon wafer with a 3 μm-thick SiO₂ layer according to the optimized parameters. The radium of the ring, the waveguide width, the gap between the bus waveguide and the micro-ring are 250 μm, 1250 nm and 150 nm, respectively. The 710 nm-thick silicon nitride film is firstly deposited on the wafer at a temperature of 350 °C with a gas flow ratio of SiH₄:NH₃:N₂ = 6:3:189 sccm by using the PECVD (SAMCO, PD-220NL). A 500 nm-thick positive photoresist ARP6200 is then spin-coated on the wafer at the speed of 1500 rpm. After baking at 150 °C for 1 min, the waveguide structure is then patterned by electronic beam lithography (EBL, Elionix, ELS-G100) and etched 710 nm onto the silicon nitride layer by ion coupling plasma (ICP, SAMCO, RIE-400iPB) with the gas of CHF₃. The gap flow, bias power and ICP power are 6 sccm, 50 W, and 50 W, respectively. After removing the photoresist, a 3 μm-thick SiO₂ layer is then deposited on the sample as a top cladding at 150 °C by using liquid source chemical vapor deposition (LSCVD, SAMCO, PD100ST) [23]. Figure 5 illustrates the schematic illustration, micrograph and the SEM image in the coupling zone of the micro-ring resonator. The light coupling was conducted by using waveguide grating couplers which offer excellent design and application flexibilities [24]. The grating couplers are optimized at 1550 nm and the coupling efficiency is about −3.5 dB. The fabricated device agrees well with the design.

In order to measure the transmission spectrum of the micro-ring resonator, light from a tunable laser (SANTEC TSL550) is pumped into the input waveguide. The wavelength is swept over a range of 130 nm and the spectrum is recorded by an optical power meter (SANTEC MPM200) with 1 pm wavelength resolution and shown in Figure 6a. The insert shows the experimental setup. According to the spectrum data, the free spectral range (FSR) is extracted and shown in Figure 6b. It can be seen that FSR increases gradually with the wavelength. Note that, the transmission loss of the waveguide is estimated to be 1.82 dB/cm by measuring the fiber-to fiber losses of waveguides with different lengths.

The relationship between the group refractive index and FSR can be written as [25]:

$$n_g=\frac{{\lambda }^2}{2\pi RFSR}$$

(3)

where R is the radius of the ring. According to Equation (3), the group refractive index is calculated and shown in Figure 7a. The red line is the polynomial fitting of the data. By substituting the fitting into Equation (2), the dispersion is calculated and shown in Figure 7b. It shows a flat and low dispersion profile within −0.04 to −0.1 ps/m/nm from wavelength 1500 nm to 1630 nm (a range of 130 nm). Near-zero dispersion of −0.07 ps/m/nm at the wavelength of 1550 nm is achieved. The dispersion decreases with the wavelength which is similar to the simulation results shown in Figure 3 and Figure 4. The wavelength dependence of the dispersion is near linear in Figure 7b, which is a bit different to those shown in Figure 3 and Figure 4 at short wavelengths. It can be explained that the material dispersion which is very linear in the wavelength range as shown in Figure 1 contributes much to the total dispersion of the fabricated device due to the relatively small waveguide size of the micro-ring resonator.

Dispersions of the waveguides with thicknesses of 610 nm and 810 nm are also measured and shown in Figure 7b. Simulation and experiment results show that near-zero anomalous dispersion (D > 0) can be realized by tailoring the dimensions of the waveguides. Sometimes, anomalous dispersion is required for phase matching [10,18]. Especially in the case of large loss existing, the anomalous dispersion can compensate the phase mismatching caused by the linear and nonlinear losses. As demonstrated before, only increasing the width might be incapable of resulting in an anomalous dispersion if the thickness is small. In order to get a near-zero anomalous dispersion, the thickness of 810 nm or larger values is suitable.

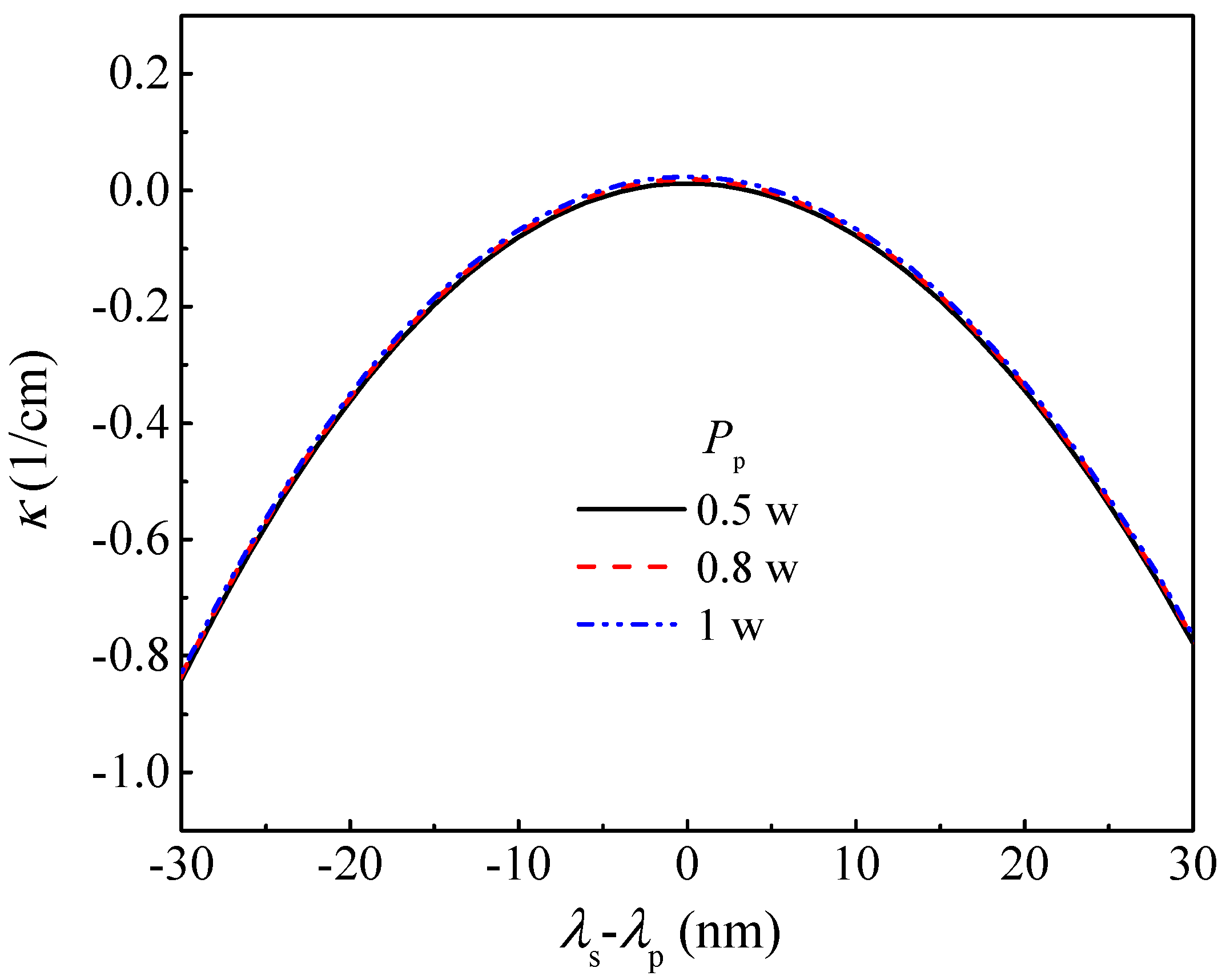
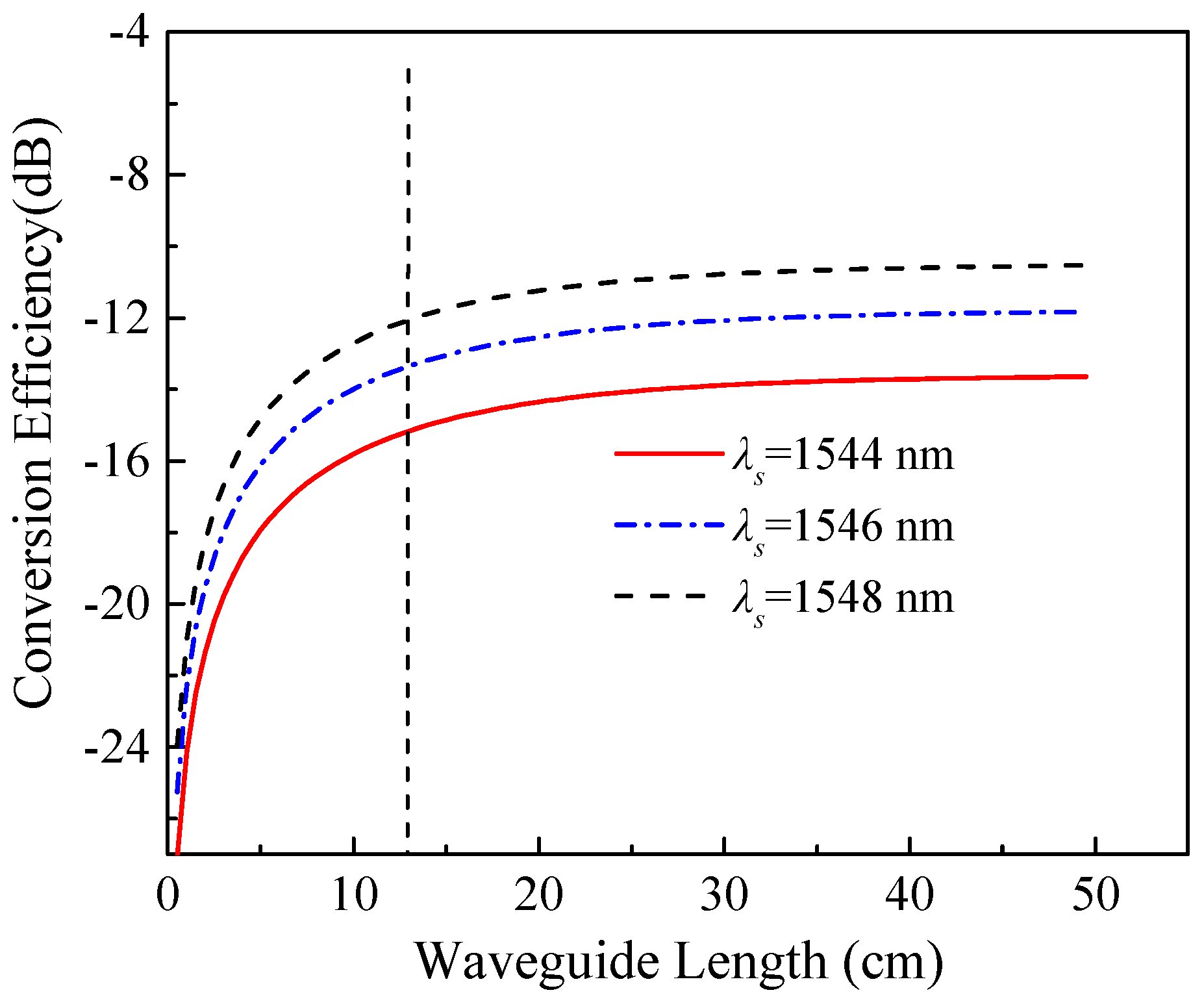
3.3. Phase Mismatch and Conversion Efficiency of the Waveguide

The phase mismatch of the waveguide for FWM can be expressed as [26,27,28]:

$$\kappa =\mathsf{\Delta }\beta +2\gamma P_P={\beta }_s+{\beta }_c-2{\beta }_p+2\gamma P_P\approx {\beta }_2{({\omega }_s-{\omega }_p)}^2+2\gamma P_P$$

(4)

where β_p,s,c and ω_p,s,c are the wavenumbers and frequencies of the interaction optical waves, P_p is the pump power. the first and second terms, Δβ and 2γP_p, are referred to as linear and nonlinear phase mismatch, respectively. γ is the waveguide nonlinear coefficient and is defined as [29]:

$$\gamma =\frac{2\pi n_2}{\lambda A_{\mathrm{eff}}}$$

(5)

where n₂ is the nonlinear refractive index, A_eff is effective mode area of the waveguide. According to the mode distribution, γ is calculated to be 1.19 m⁻¹W⁻¹ at 1550 nm by assuming n₂ = 2.6 × 10⁻¹⁹ m²W⁻¹ for silicon nitride.

The phase mismatch depends on the dispersion, frequency difference, waveguide nonlinear coefficient and input pump power. Because the value of γ is positive and not too large, a near-zero dispersion especially anomalous dispersion can make the phase mismatch close to zero. Figure 8 shows the phase mismatch of the waveguide with different input pump power. The near-zero phase mismatch (±0.2 cm⁻¹) is obtained over a 30 nm wavelength range near the pump wave, which is attributed to the optimized near-zero anomalous dispersion of the silicon nitride waveguide. It also shows a weak phase mismatch dependence on the pump power, which means that the conversion efficiency can be effectively improved by increasing the pump power.

The coupled equations of the FWM process can be expressed as [27,30]:

$$\frac{d{A}_p}{dz}=-\frac{1}{2}\alpha A_p+j\gamma {\left|A_p\right|}^2{A}_p$$

(6)

$$\frac{d{A}_s}{dz}=-\frac{1}{2}\alpha A_s+2j\gamma {\left|A_p\right|}^2{A}_s+j\gamma A_i^{*}{A}_p^{2}exp\left(-j\mathsf{\Delta }\beta z\right)$$

(7)

$$\frac{d{A}_i}{dz}=-\frac{1}{2}\alpha A_i+2j\gamma {\left|A_p\right|}^2{A}_i+j\gamma A_s^{*}{A}_p^{2}exp\left(-j\mathsf{\Delta }\beta z\right)$$

(8)

where A_p,s,c are the amplitude of the interaction optical waves, α is the transmission loss factor, z is the coordinate along the transmission direction. The conversion efficiency (CE) defined as the power ratio of the output idler power to signal power are calculated. Figure 9 shows the CE dependence on the waveguide length with an input pump power of 0.5 W. It can be seen that CE as high as −12 dB can be obtained with a length of 13 cm. The CE increases slowly while the length is larger than 13 cm because the accumulated transmission loss in a very long waveguide attenuates the generated idler power. Moreover, the optical power in a very long waveguide changes obviously during transmission due to the nonnegligible loss. The phase mismatch increases with the transmission distance. Therefore, as can be seen in Figure 9, the CE changes more obviously with the input signal wavelength while the length is larger. The CE decreases with the input signal wavelength decreasing because the wavelength difference between the pump and signal waves enlarges the phase mismatch as shown in Figure 8.

4. Conclusions

In this paper, we analyzed the group velocity dispersion of the silicon nitride waveguides. In order to find the near-zero dispersion points for the phase matching of FWM-based application, we optimize the core dimension of the silicon nitride waveguide. The effective refractive index and the dispersion of the waveguide increase with the width and thickness increasing, and the dispersion decreases with the wavelength increasing. The optimum core dimension of the PECVD silicon nitride waveguide is 710 nm × 1250 nm and the corresponding dispersion is 1.16 ps/km/nm. The optimized core dimension of the LPCVD silicon nitride waveguide is 790 × 1100 nm and the corresponding dispersion is 0.97 ps/km/nm. Results show that the dimensions of the PECVD and LPCVD silicon nitride for the phase matching of FWM are similar.

The dispersion of a PECVD silicon nitride micro-ring resonator is experimentally characterized with the core dimensions of t = 710 nm and w = 1250 nm. Results show that a near-zero dispersion of −0.07 ps/m/nm at the wavelength of 1550 nm is obtained which is consistent with the theoretical results. Owing to the optimized dispersion of the waveguides, near-zero phase mismatch over a wavelength range of 30 nm is obtained, which ensures high CEs larger than −12 dB with a low input pump power of 0.5 W in a 13 cm long silicon nitride waveguide.