Precise Optical Modulation and Its Application to Optoelectronic Device Measurement
Abstract
1. Introduction
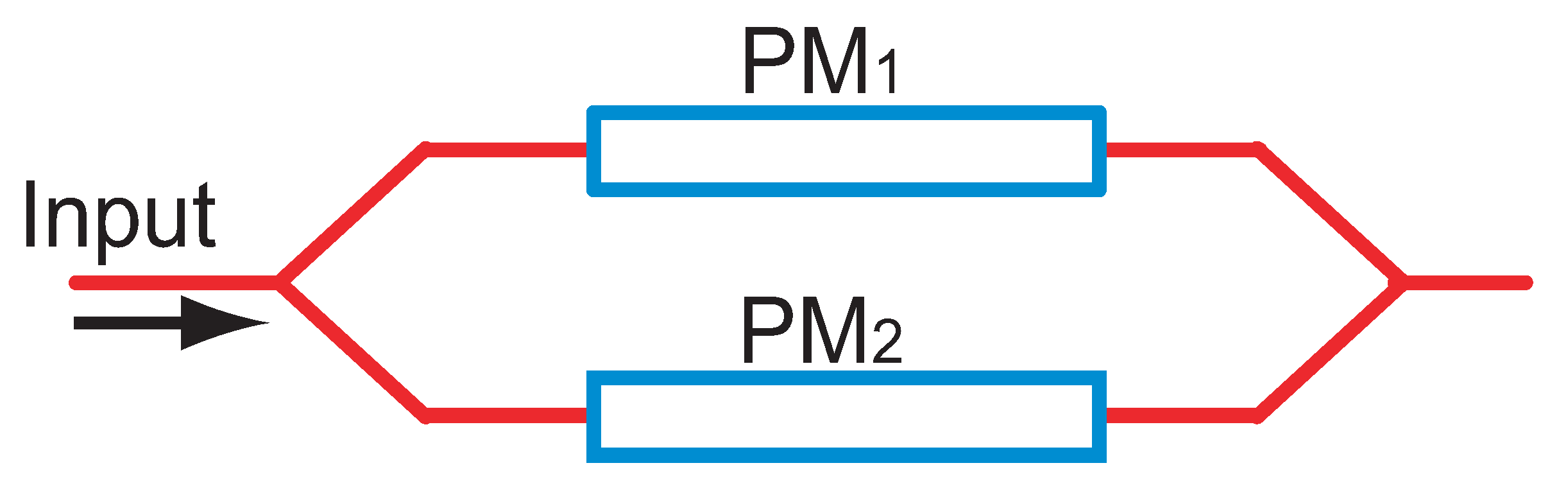
2. Intensity Modulation by a Balanced Mach-Zehnder Modulator
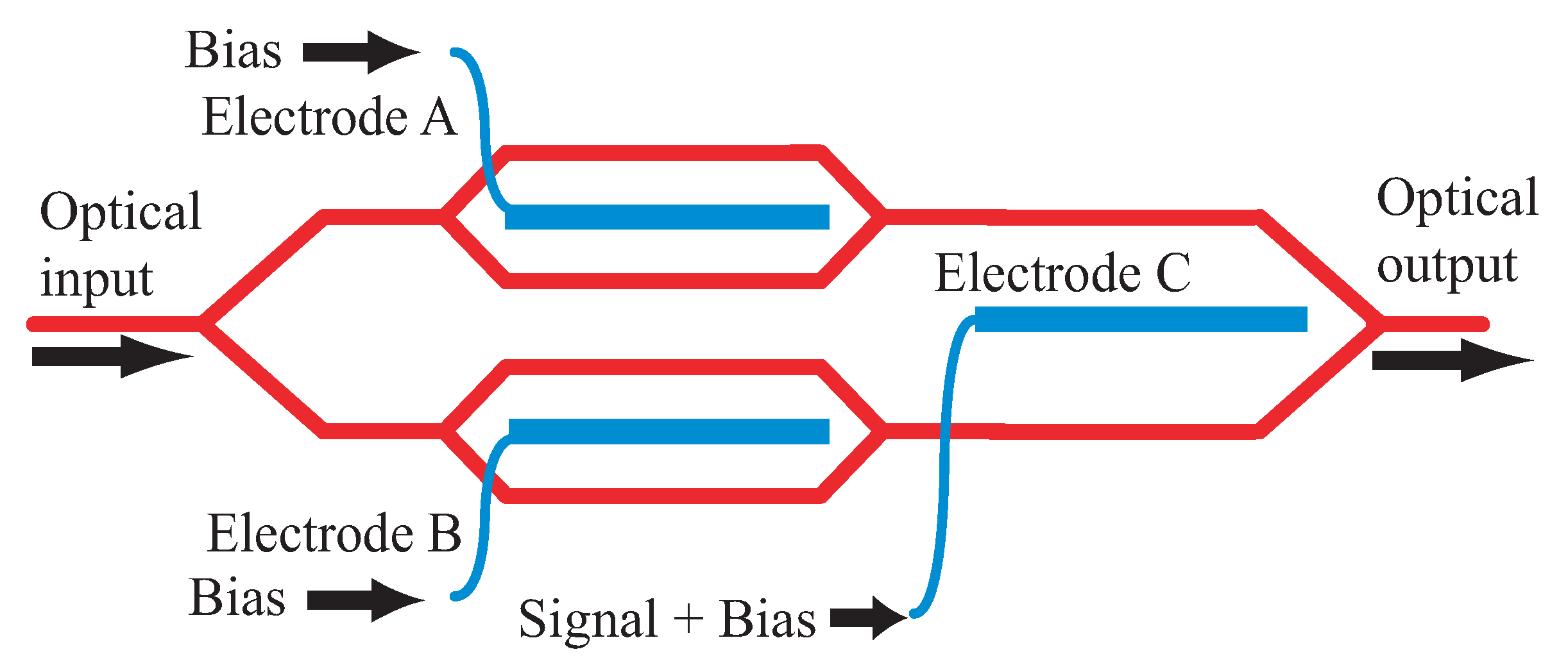
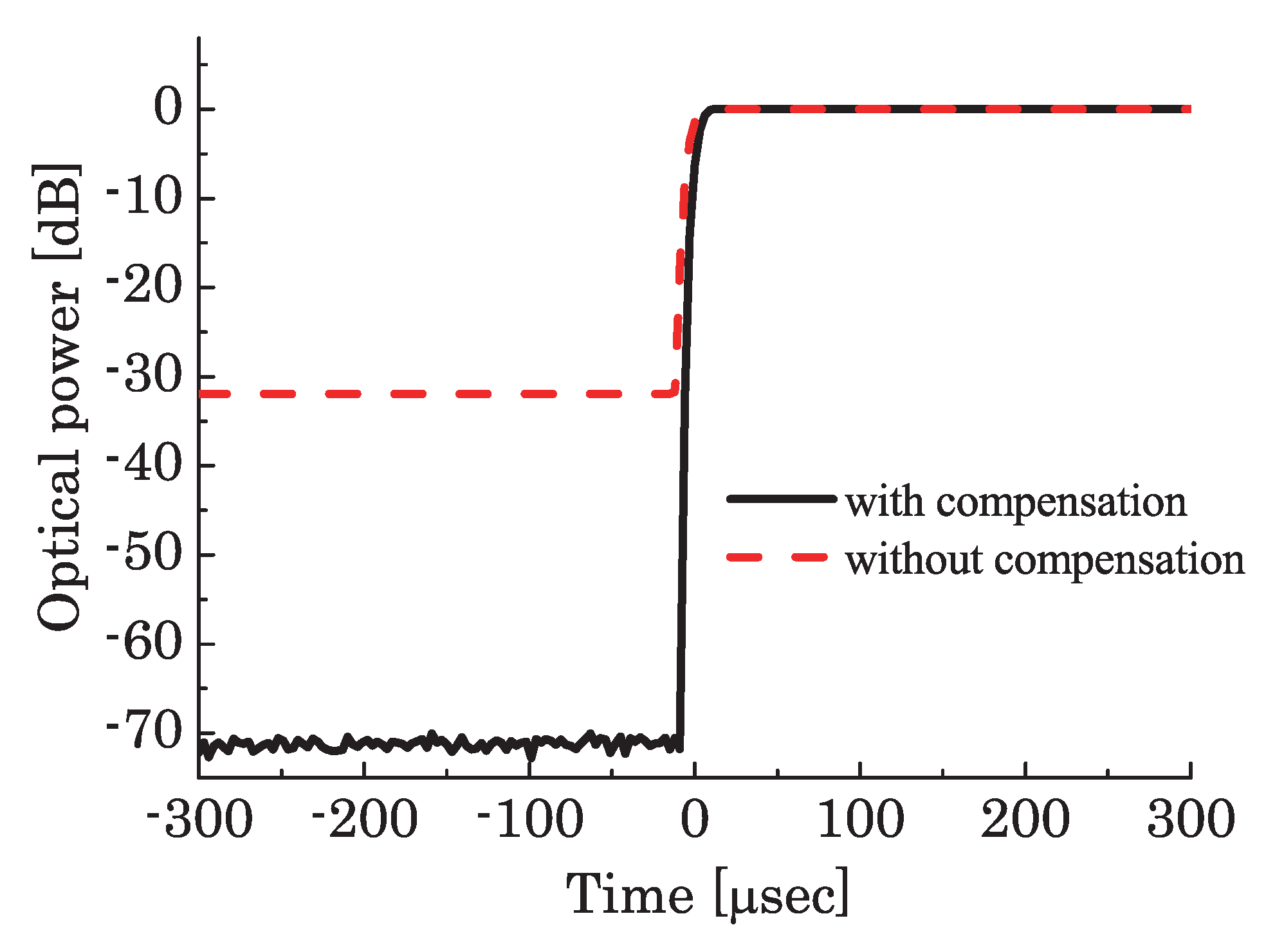
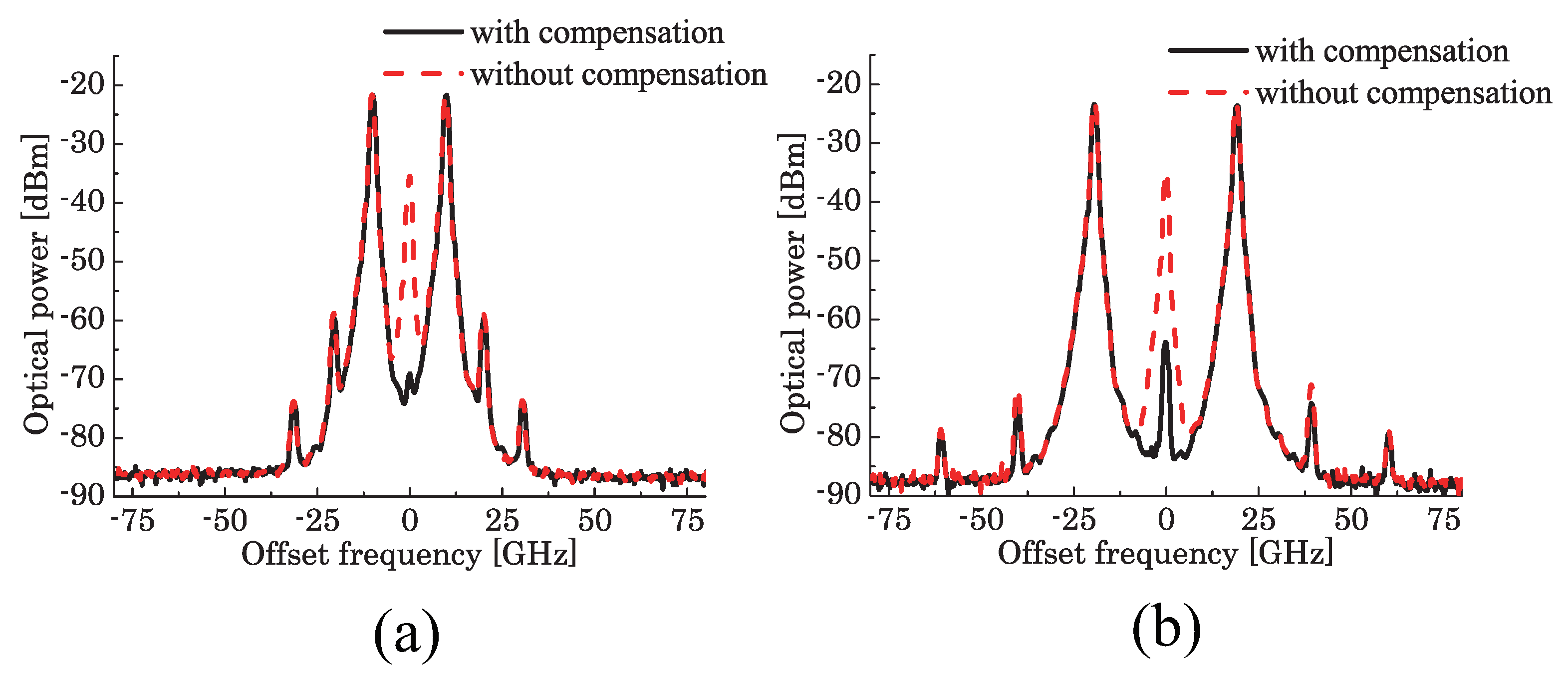
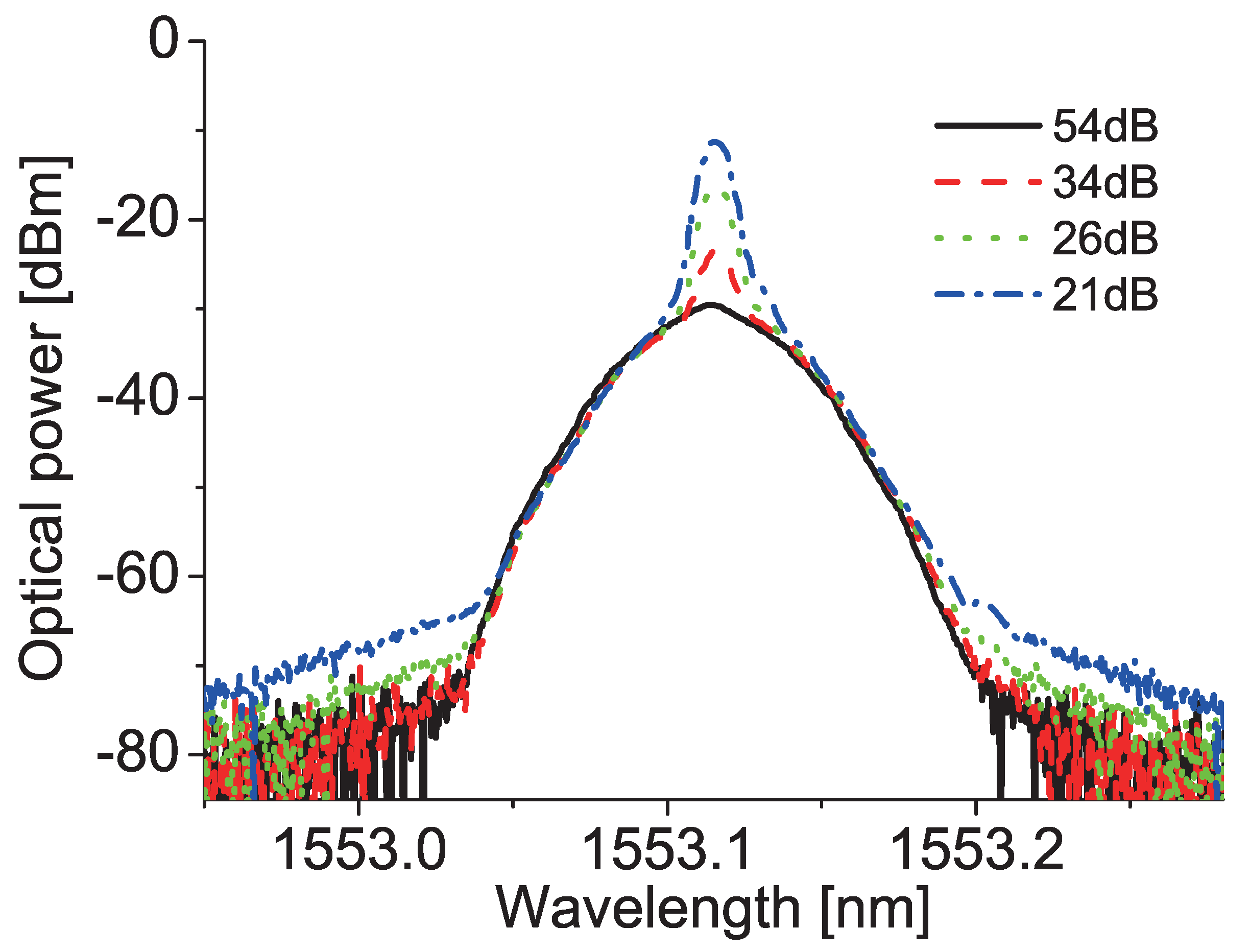
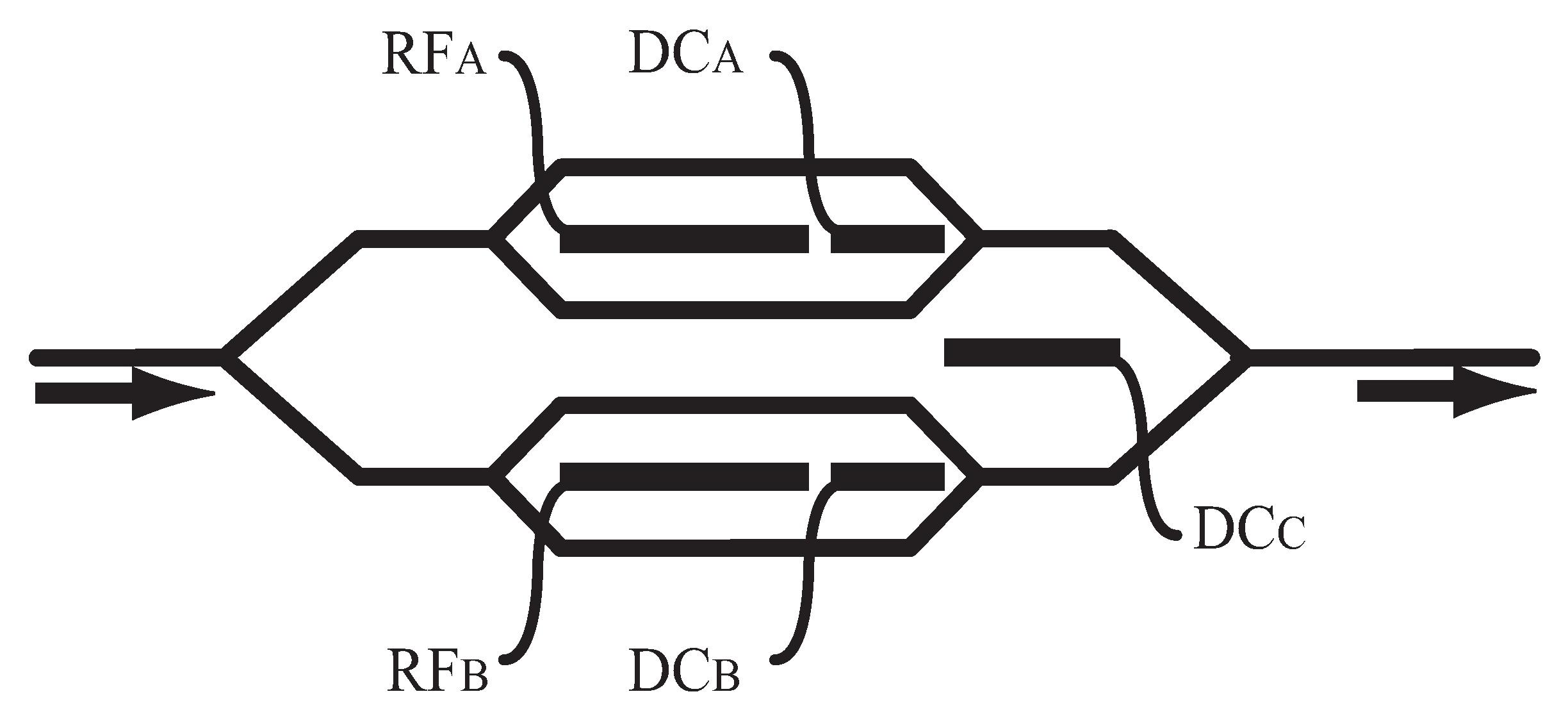
3. Active Trimming for High Extinction-Ratio Intensity Modulation
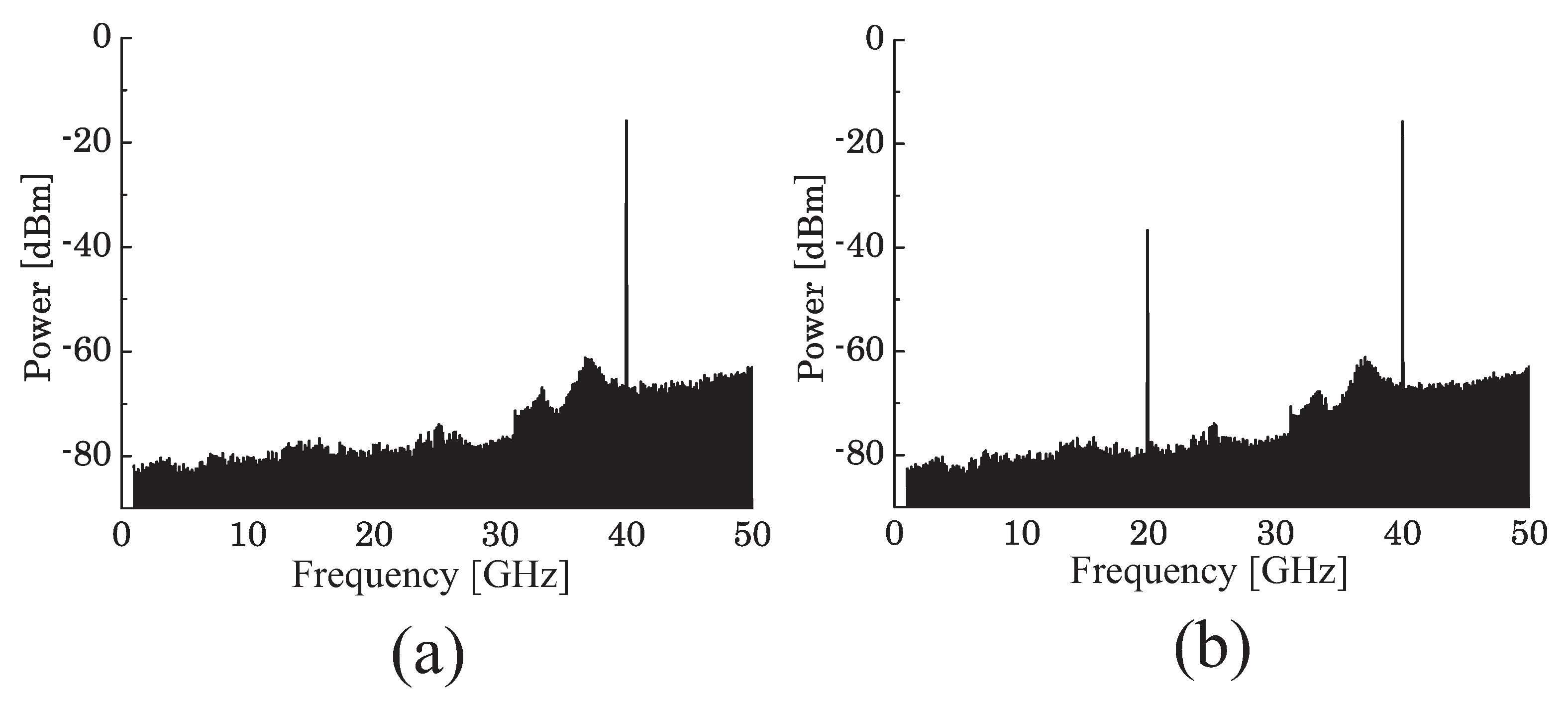
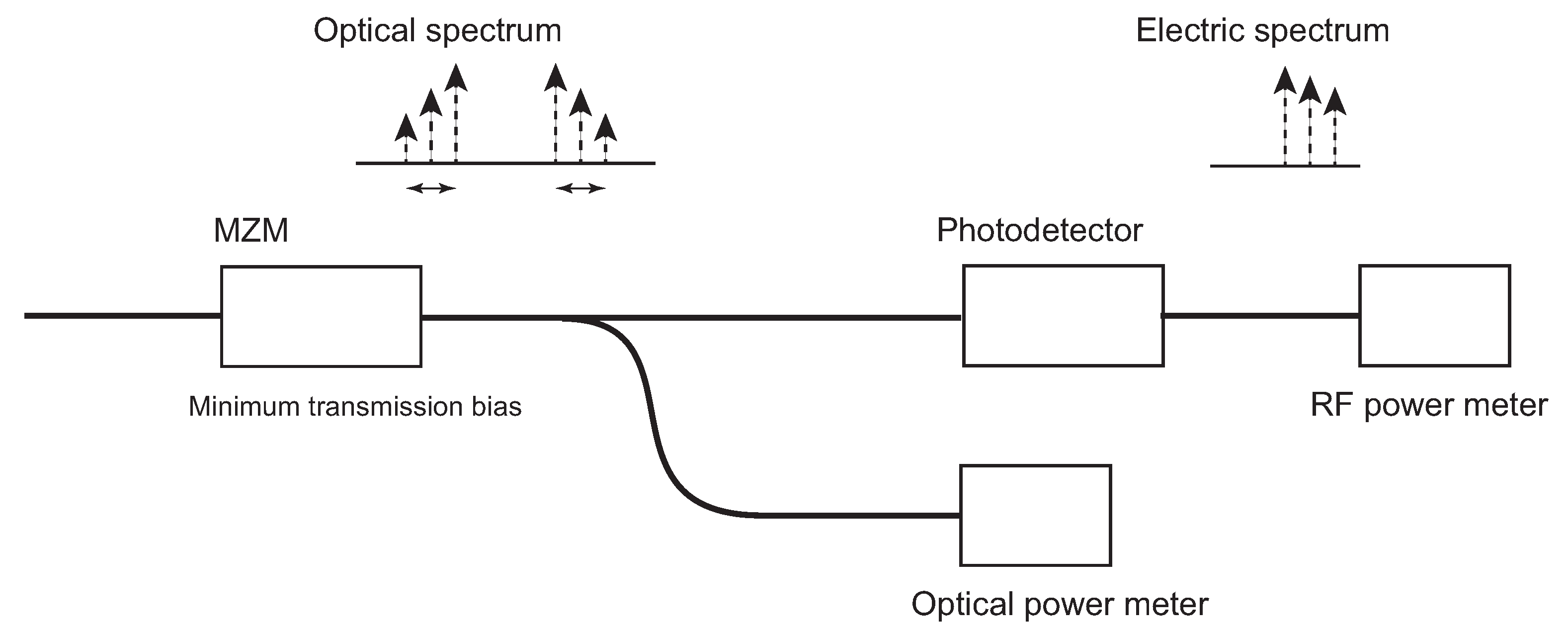
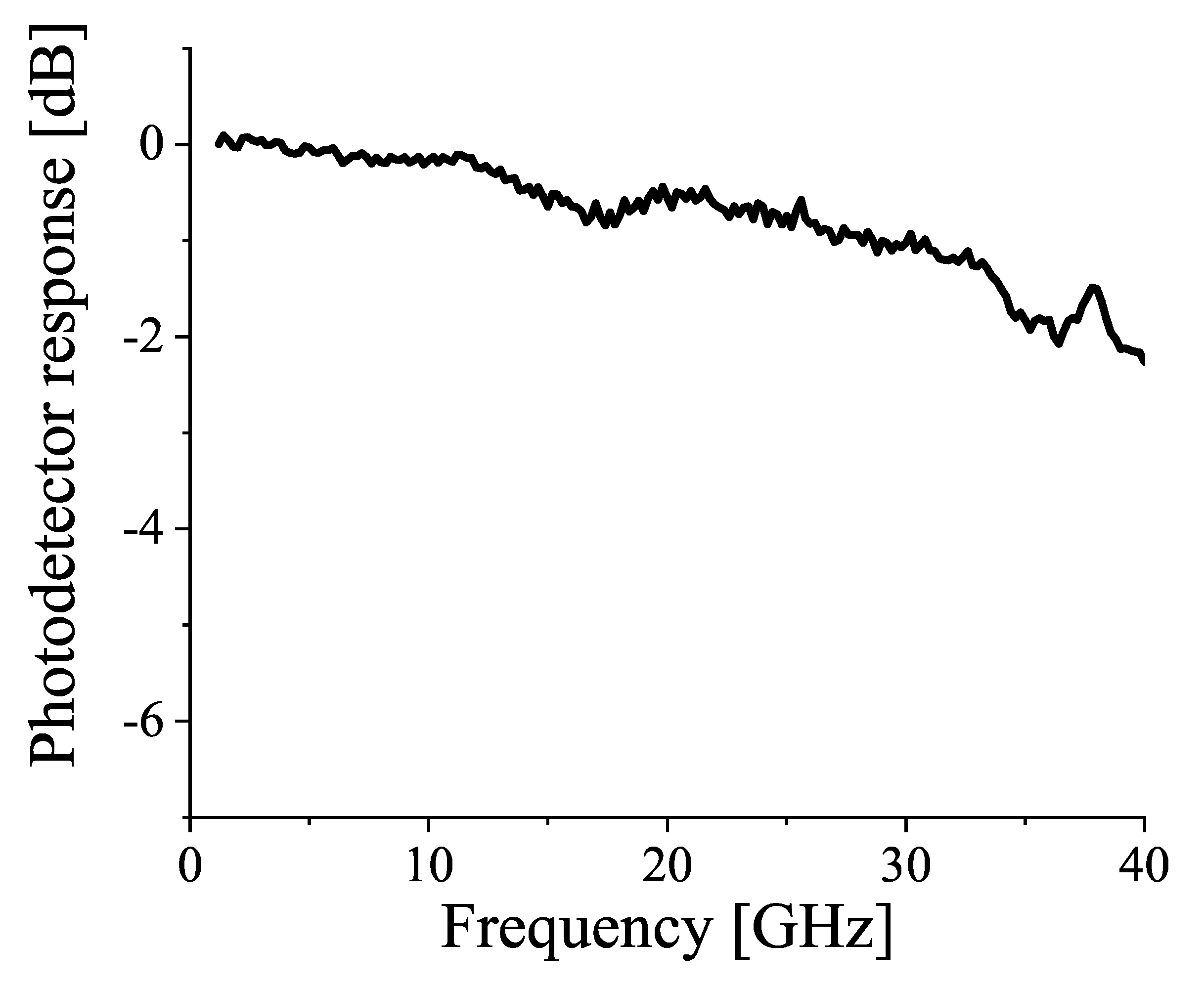
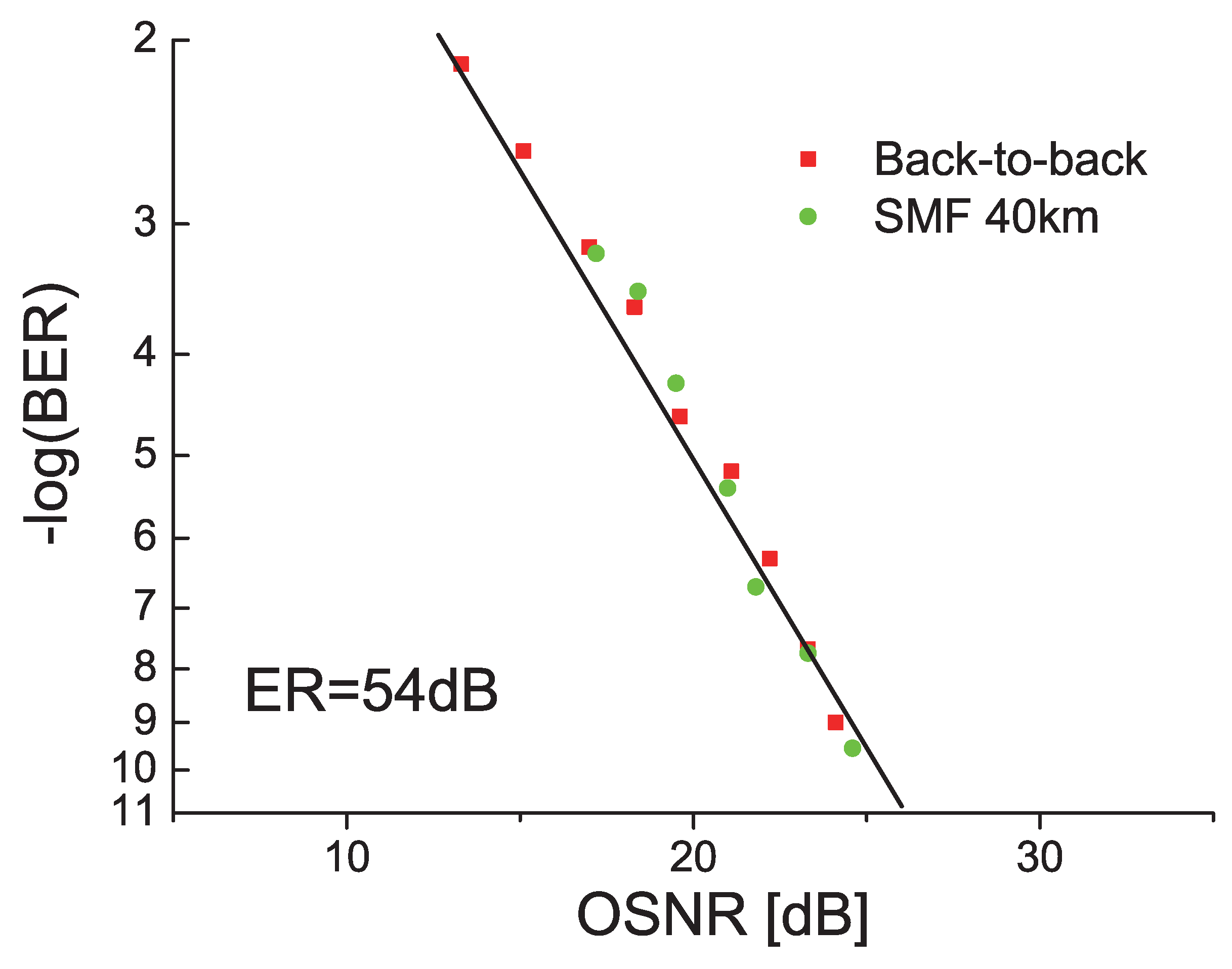
4. Photodetector Response Measurement by Optical Two-Tone Signals
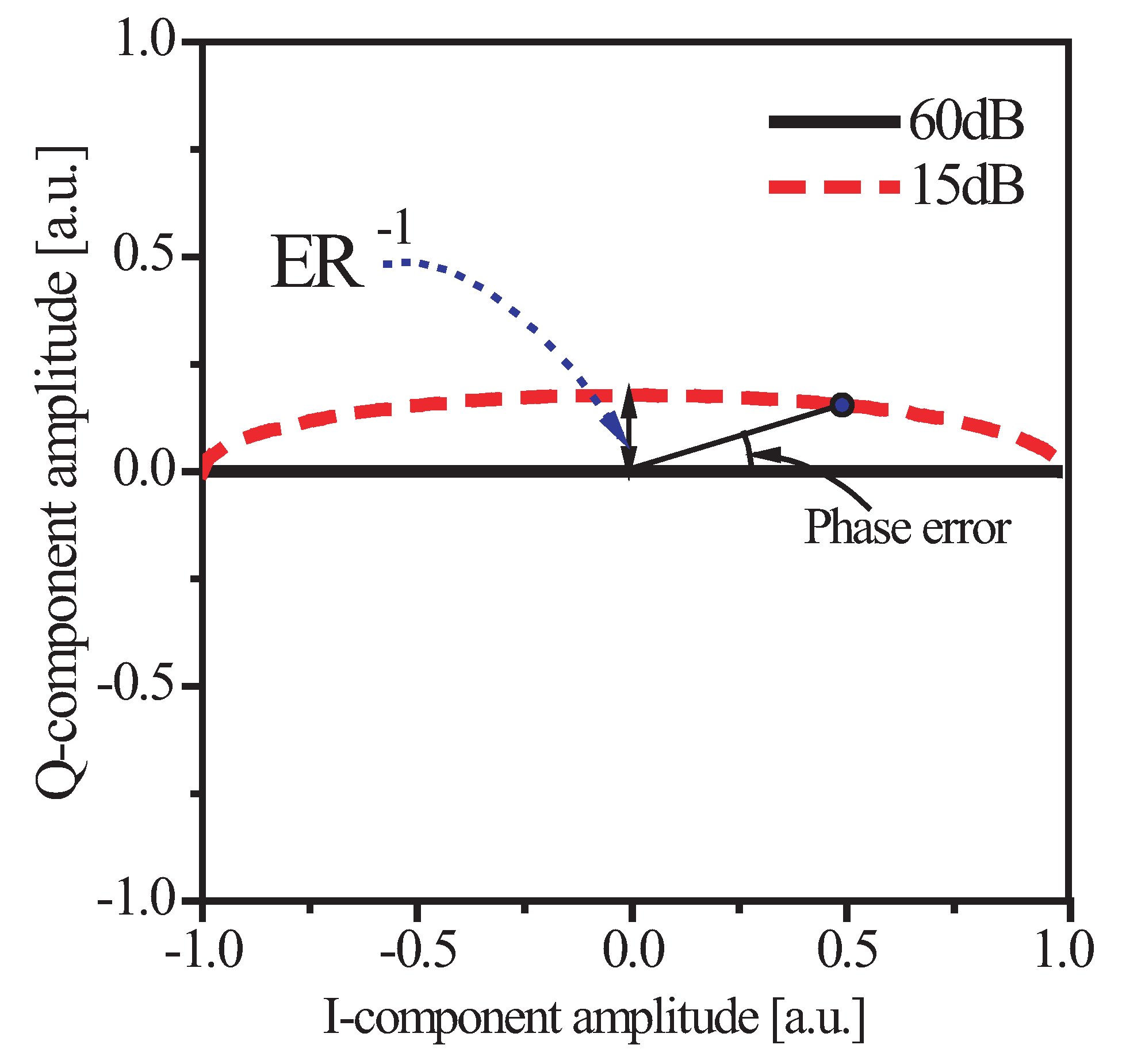
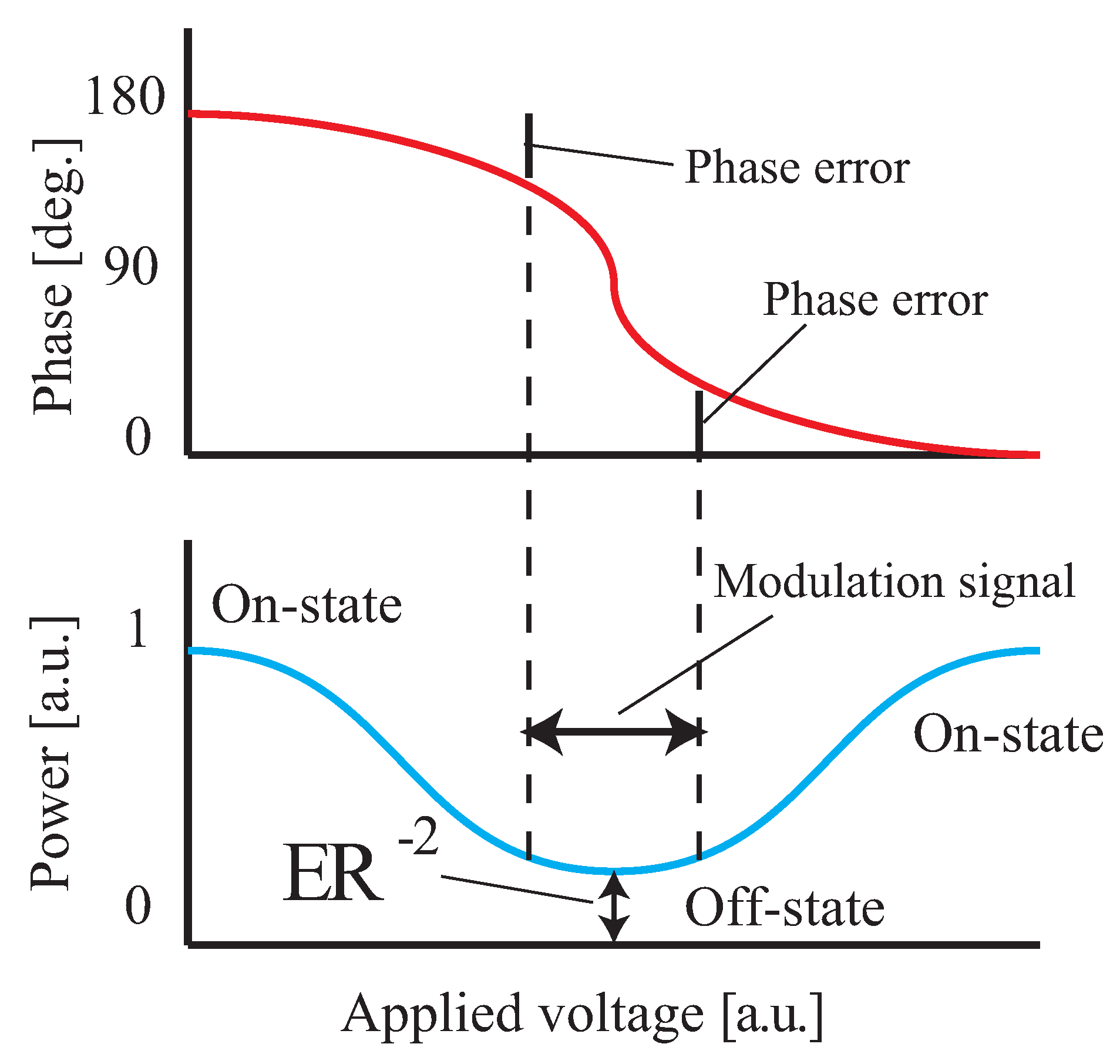
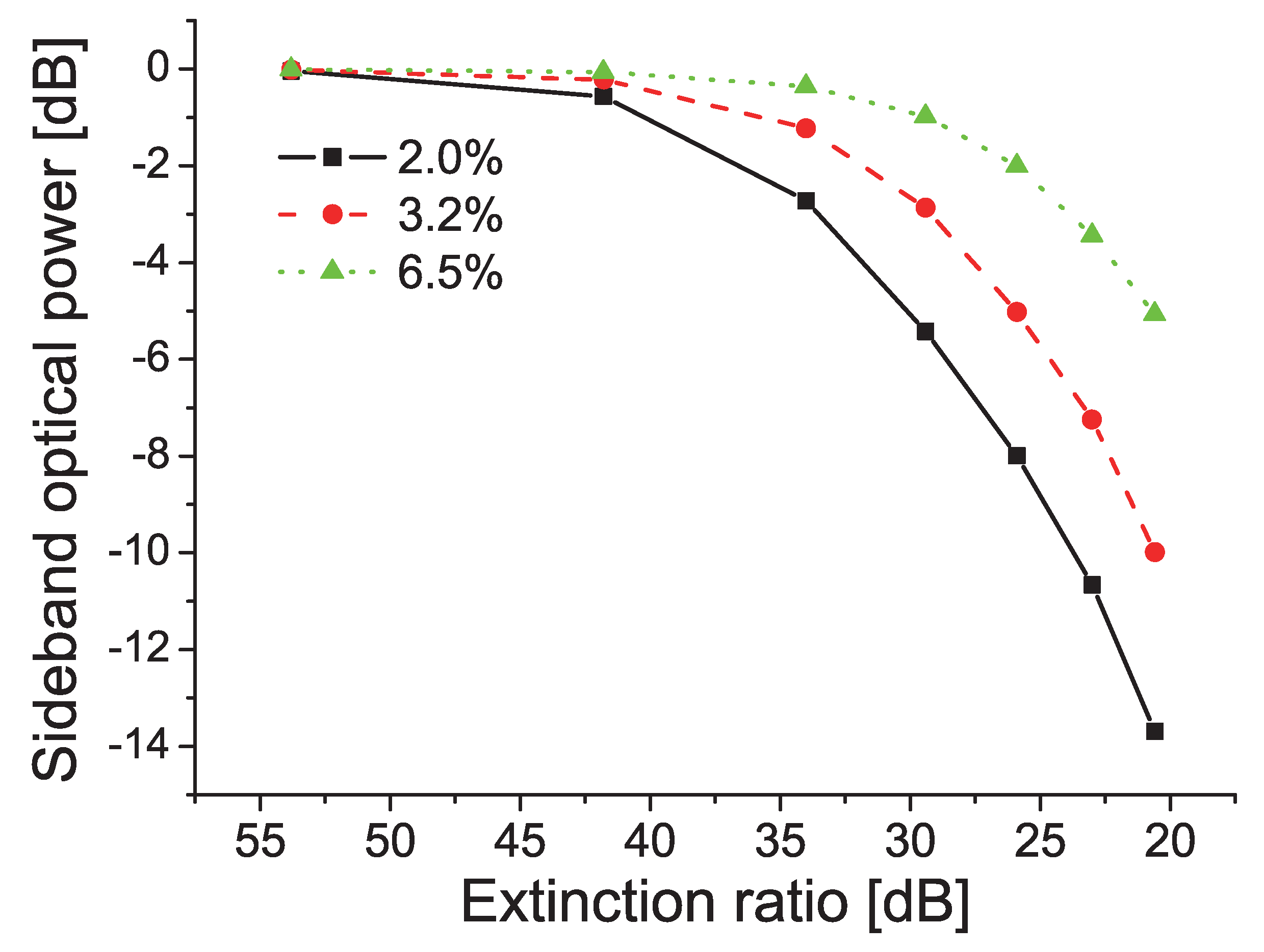
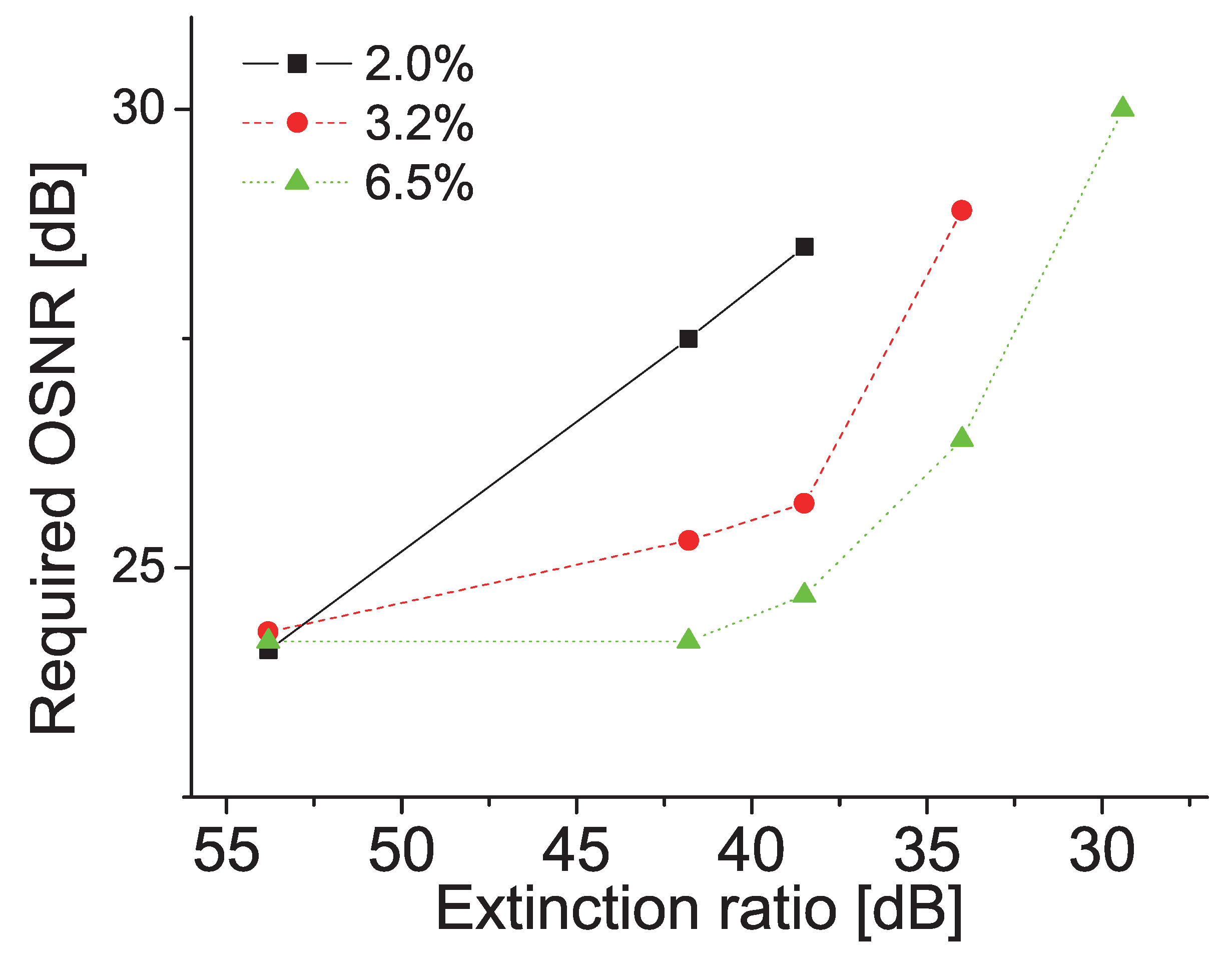
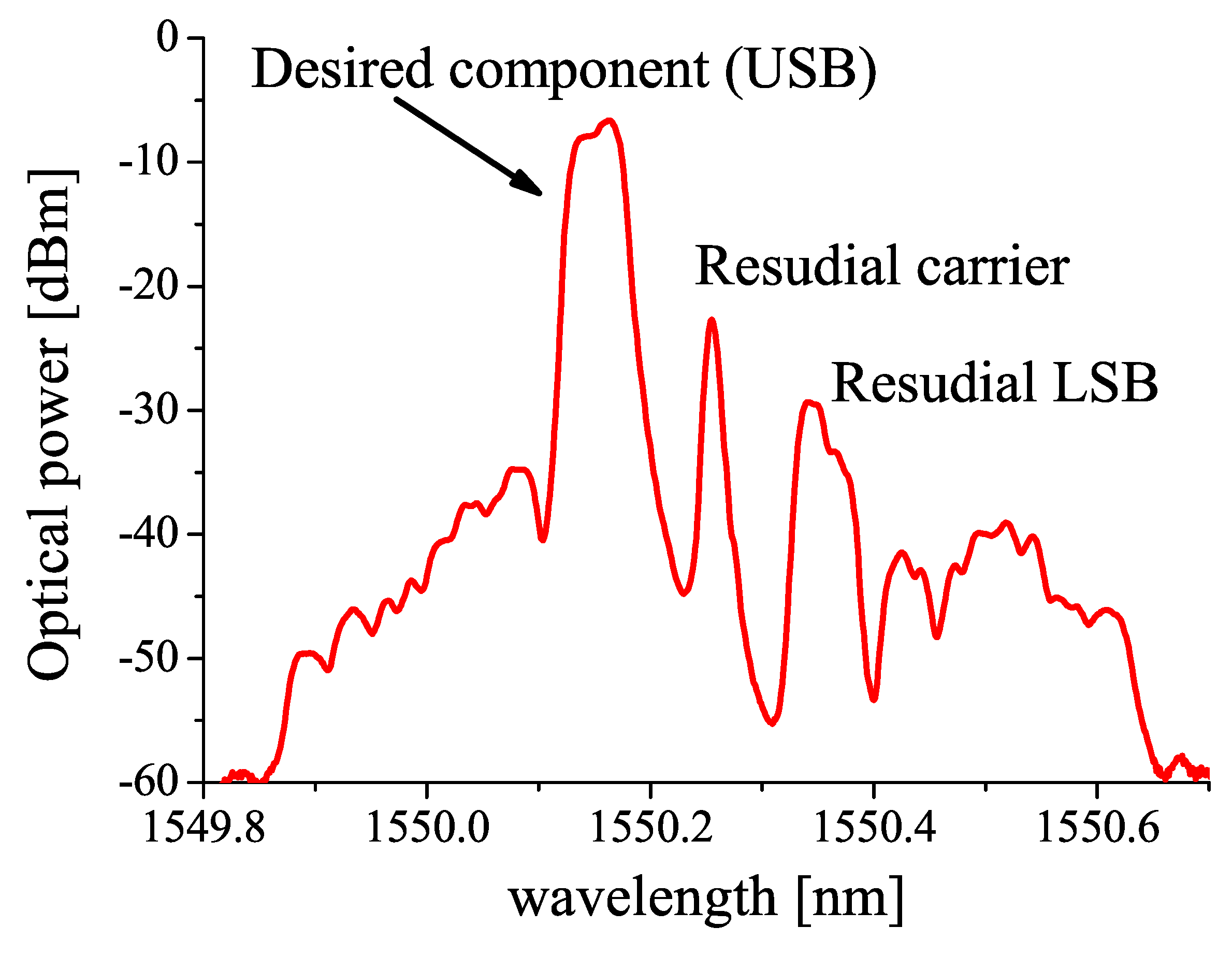
5. ER-Induced Phase Error in Optical Modulation
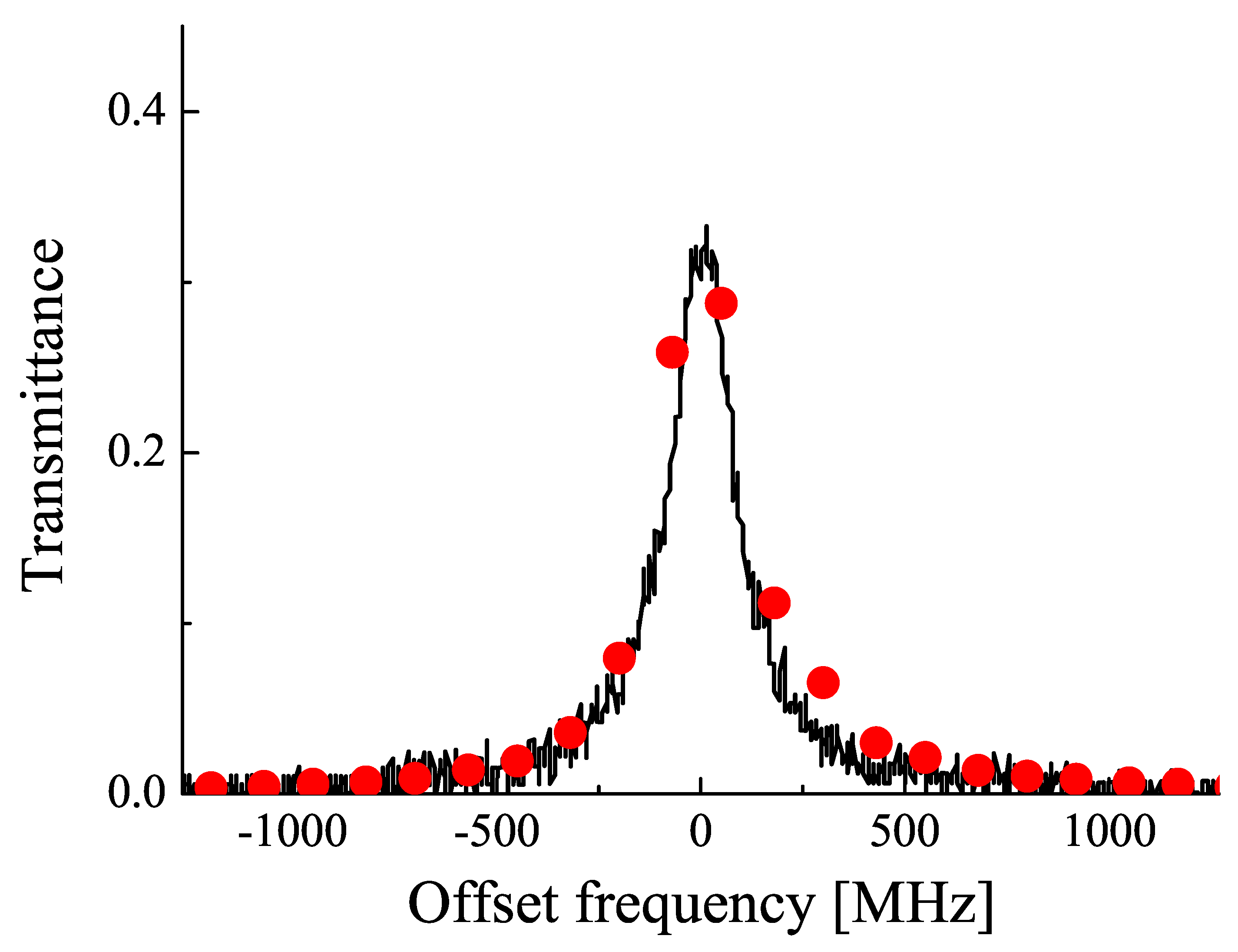
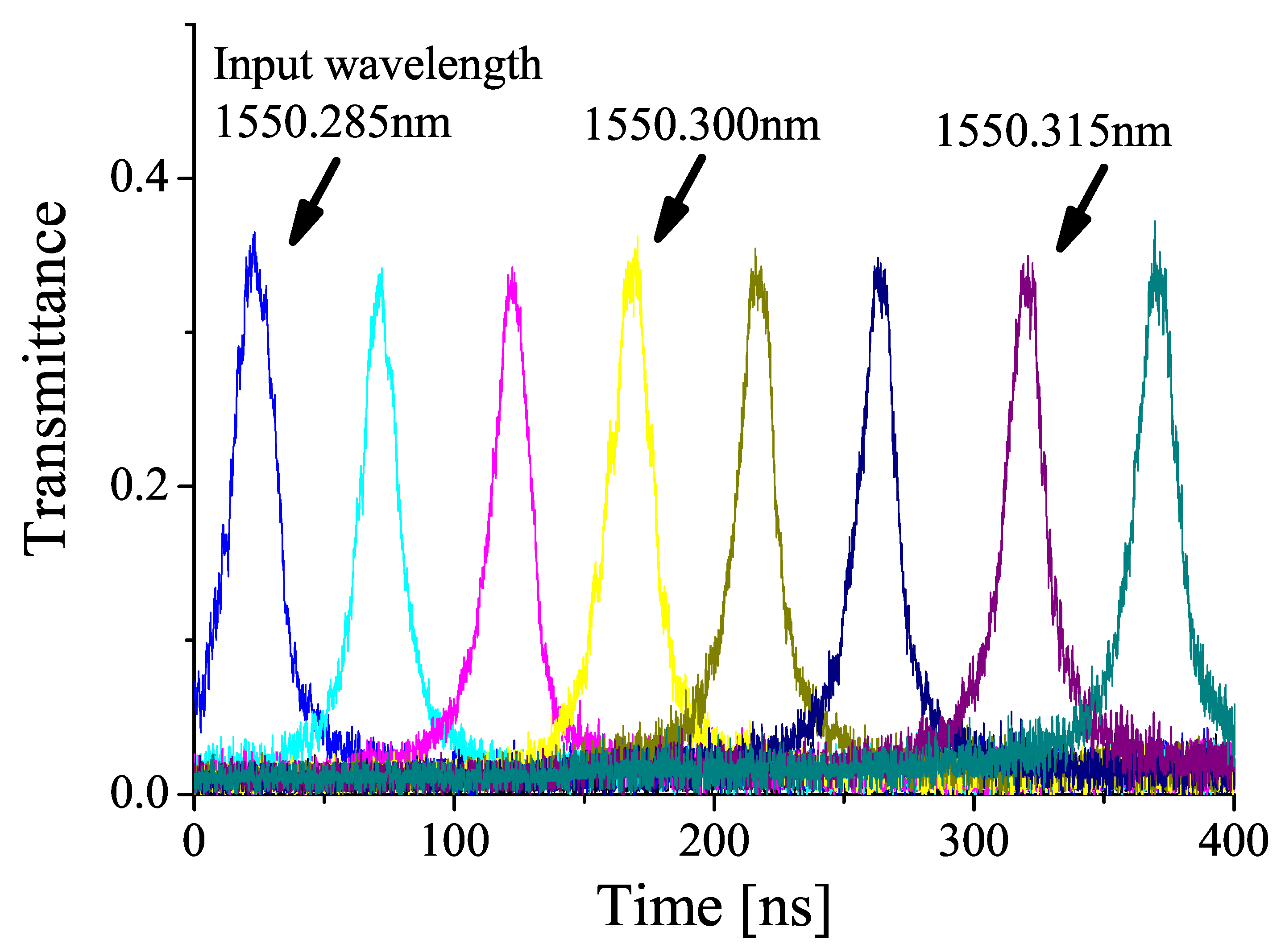
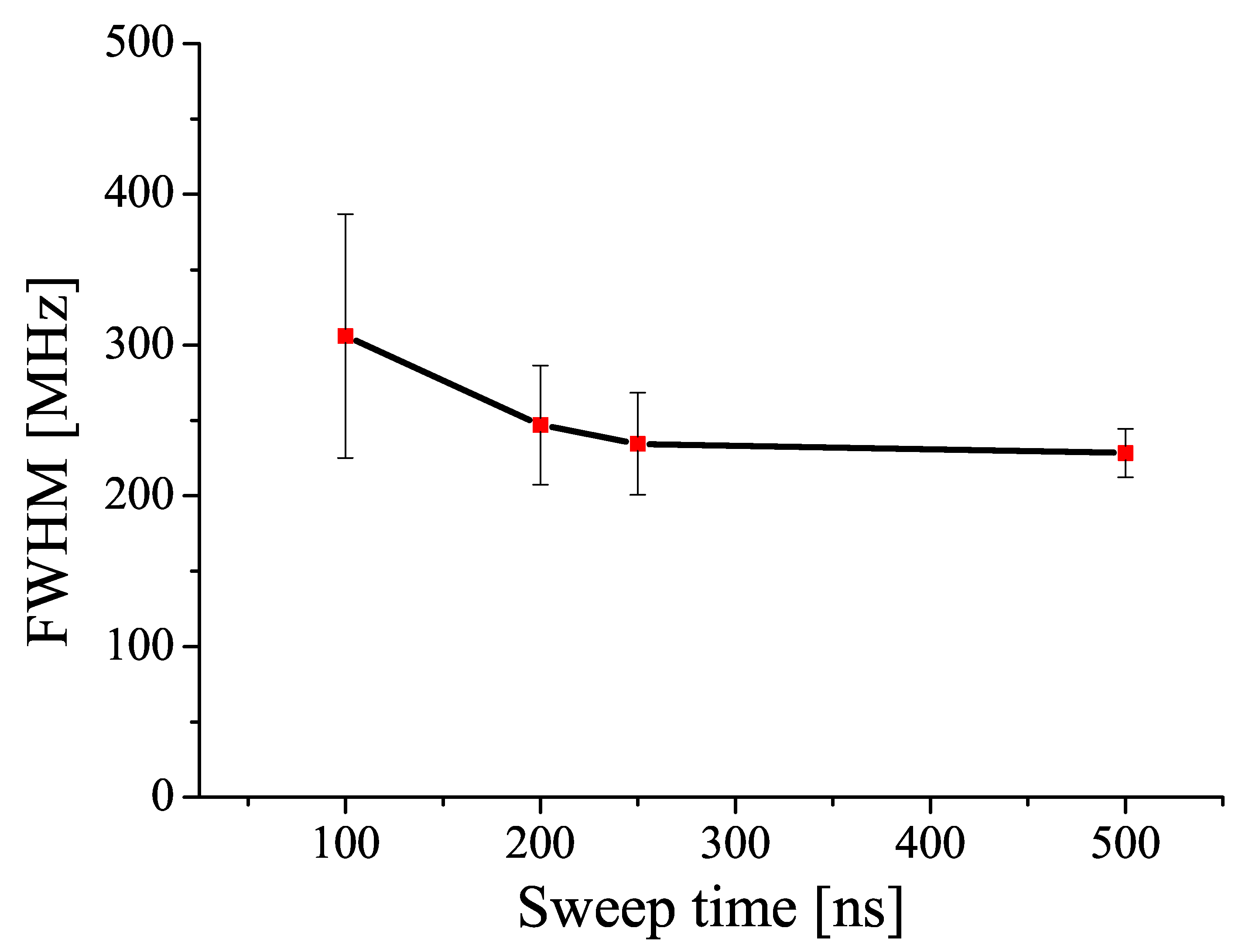
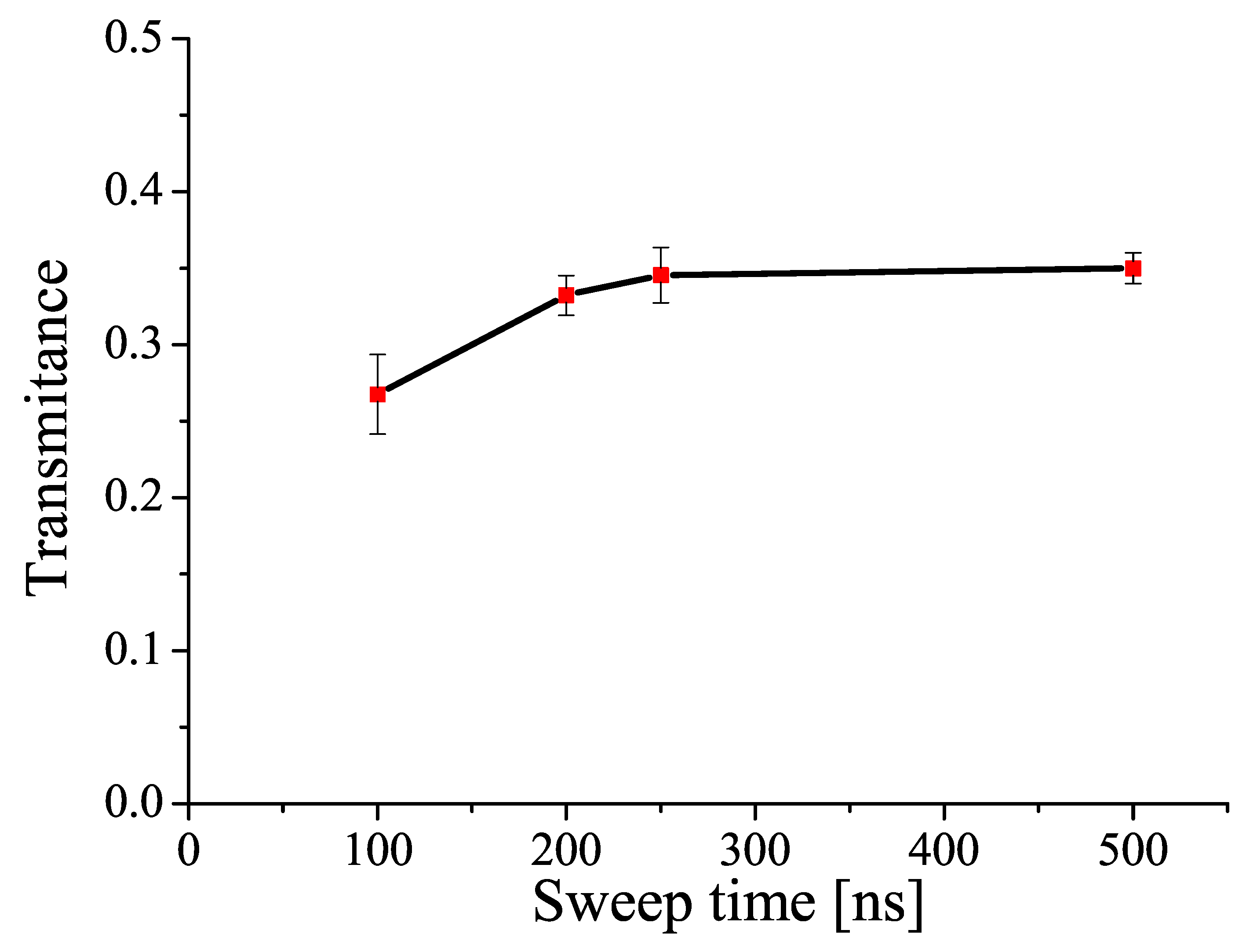
6. Rapid Optical Frequency Sweep for Device Characterization
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Kawanishi, T.; Sakamoto, T.; Izutsu, M. High-Speed Control of Lightwave Amplitude, Phase, and Frequency by Use of Electrooptic Effect. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 79–91. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Kanno, A.; Kawanishi, T.; Izutsu, M.; Nakajima, H. Precise Optical Modulation Using Extinction-Ratio and Chirp Tunable Single-Drive Mach?Zehnder Modulator. J. Light. Technol. 2017, 35, 4781–4788. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, L.; Ruan, X.; Yang, F.; Ming, H.; Li, Y. High Baud Rate Transmission With Silicon Photonic Modulators. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 1–9. [Google Scholar] [CrossRef]
- Lu, G.-W.; Zhang, H.-B.; Shinada, S.; Hong, J.; Cheng, Y.; Yokoyama, S. Power-Efficient O-Band 40 Gbit/s PAM4 Transmitter Based on Dual-Drive Cascaded Carrier-Depletion and Carrier-Injection Silicon Mach-Zehnder Modulator With Binary Driving Electronics at CMOS Voltages. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 1–8. [Google Scholar] [CrossRef]
- Ogiso, Y.; Ozaki, J.; Ueda, Y.; Wakita, H.; Nagatani, M.; Yamazaki, H.; Nakamura, M.; Kobayashi, T.; Kanazawa, S.; Hashizume, Y.; et al. 80-GHz Bandwidth and 1.5-V Vπ InP-Based IQ Modulator. J. Light. Technol. 2020, 38, 249–255. [Google Scholar] [CrossRef]
- Irmscher, S.; Lewen, R.; Eriksson, U. InP-InGaAsP high-speed traveling-wave electroabsorption modulators with integrated termination resistors. IEEE Photonics Technol. Lett. 2002, 14, 923–925. [Google Scholar] [CrossRef]
- Kawanishi, T.; Kanno, A.; Freire, H.S.C. Wired and Wireless Links to Bridge Networks: Seamlessly Connecting Radio and Optical Technologies for 5G Networks. IEEE Microw. Mag. 2018, 19, 102–111. [Google Scholar] [CrossRef]
- Kawanishi, T. Wired and Wireless Seamless Access Systems for Public Infrastructure; Artech House: Norwood, MA, USA, 2020. [Google Scholar]
- Kawanishi, T.; Sakamoto, T.; Tsuchiya, M.; Izutsu, M. High extinction ratio optical modulator using active intensity trimmers. In Proceedings of the 2005 31st European Conference on Optical Communication, ECOC 2005, Glasgow, UK, 25–29 September 2005; Volume 4, pp. 841–842. [Google Scholar] [CrossRef]
- Kawanishi, T.; Sakamoto, T.; Chiba, A.; Tsuchiya, M.; Toda, H. Ultra high extinction-ratio and ultra low chirp optical intensity modulation for pure two-tone lightwave signal generation. In Proceedings of the 2008 Conference on Lasers and Electro-Optics and 2008 Conference on Quantum Electronics and Laser Science, San Jose, CA, USA, 4–9 May 2008; pp. 1–2. [Google Scholar]
- Kawanishi, T.; Sakamoto, T.; Chiba, A.; Izutsu, M. Study of precise optical modulation using Mach-Zehnder interferometers for advanced modulation formats. In Proceedings of the 33rd European Conference and Exhibition of Optical Communication, Berlin, Germany, 16–20 September 2007; pp. 1–2. [Google Scholar] [CrossRef]
- Kawanishi, T.; Sakamoto, T.; Chiba, A.; Izutsu, M.; Winzer, P.J. Duobinary signal generation using high-extinction ratio modulation. In Proceedings of the OFC/NFOEC 2008-2008 Conference on Optical Fiber Communication/National Fiber Optic Engineers Conference, San Diego, CA, USA, 24–28 February 2008; pp. 1–3. [Google Scholar] [CrossRef]
- Kawanishi, T.; Sakamoto, T.; Izutsu, M. Optical frequency sweep technique using single sideband modulation. In Proceedings of the 2005 31st European Conference on Optical Communication, ECOC 2005, Glasgow, UK, 25–29 September 2005; Volume 3, pp. 635–636. [Google Scholar] [CrossRef]
- Kawanishi, T.; Sakamoto, T.; Fonseca, D.; Cartaxo, A.; Monteiro, P.; Izutsu, M. Fine Transmittance/Reflectivity Measurement System Using Single-Sideband Frequency Sweeper with Ultra-Wideband Hilbert Transformer. In Proceedings of the 2006 European Conference on Optical Communications, Cannes, France, 24–28 September 2006; pp. 1–2. [Google Scholar] [CrossRef]
- Kawanishi, T.; Sakamoto, T.; Izutsu, M. Fast optical frequency sweep for ultra-fine real-time spectral domain measurement. Electron. Lett. 2006, 42, 999–1000. [Google Scholar] [CrossRef]
- Inagaki, K.; Kawanishi, T.; Izutsu, M. Optoelectronic frequency response measurement of photodiodes by using high-extinction ratio optical modulator. IEICE Electron. Express 2012, 9, 220–226. [Google Scholar] [CrossRef]
- Inagaki, K.; Kawanishi, T.; Iwai, H.; Oikawa, Y. Development of lightwave frequency response analyzer for characterizing O/E conversion devices. In Proceedings of the 2014 International Topical Meeting on Microwave Photonics (MWP) and the 2014 9th Asia-Pacific Microwave Photonics Conference (APMP), Hokkaido, Japan, 20–23 October 2014; pp. 113–116. [Google Scholar] [CrossRef]
- Winzer, P.J.; Raybon, G.; Doerr, C.R.; Duelk, M.; Dorrer, C. 107-Gb/s optical signal generation using electronic time-division multiplexing. J. Light. Technol. 2006, 24, 3107–3113. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawanishi, T. Precise Optical Modulation and Its Application to Optoelectronic Device Measurement. Photonics 2021, 8, 160. https://doi.org/10.3390/photonics8050160
Kawanishi T. Precise Optical Modulation and Its Application to Optoelectronic Device Measurement. Photonics. 2021; 8(5):160. https://doi.org/10.3390/photonics8050160
Chicago/Turabian StyleKawanishi, Tetsuya. 2021. "Precise Optical Modulation and Its Application to Optoelectronic Device Measurement" Photonics 8, no. 5: 160. https://doi.org/10.3390/photonics8050160
APA StyleKawanishi, T. (2021). Precise Optical Modulation and Its Application to Optoelectronic Device Measurement. Photonics, 8(5), 160. https://doi.org/10.3390/photonics8050160




