Abstract
With the increase in the popularity of cloud computing and big data applications, the amount of sensitive data transmitted through optical networks has increased dramatically. Furthermore, optical transmission systems face various security risks at the physical level. We propose a novel key distribution scheme based on signal-to-noise ratio (SNR) measurements to extract the fingerprint of the fiber channel and improve the physical level of security. The SNR varies with time because the fiber channel is affected by many physical characteristics, such as dispersion, polarization, scattering, and amplifier noise. The extracted SNR of the optical fiber channel can be used as the basis of key generation. Alice and Bob can obtain channel characteristics by measuring the SNR of the optical fiber channel and generate the consistent key by quantization coding. The security and consistency of the key are guaranteed by the randomness and reciprocity of the channel. The simulation results show that the key generation rate (KGR) can reach 25 kbps, the key consistency rate (KCR) can reach 98% after key post-processing, and the error probability of Eve’s key is ~50%. In the proposed scheme, the equipment used is simple and compatible with existing optic fiber links.
1. Introduction
With the sharp increase in the speed and distance of optical communications, optical networks have become more accessible; accordingly, more threats and higher risks may be posed. A reliable key distribution system is required to solve this problem and ensure communication security. Traditional public key-based key distribution security primarily depends on the complexity of an algorithm, such as the RSA algorithm [1,2]. However, traditional cryptography is susceptible to the rapid progress of hardware and algorithms. The robustness of these algorithms faces severe challenges with the development of computer systems, especially quantum computers [3,4]. Quantum key distribution (QKD) is theoretically considered as the only solution to guarantee absolute security at the physical level [5,6,7,8]. However, QKD requires highly sensitive optical detection equipment instead of optical amplifiers. Therefore, it is still challenging to realize QKD at longer distances and higher key rates.
A promising and cost-effective approach is to take advantage of the unpredictable and random characteristics of the transmission channel to convert the random characteristics of the environment into a secure key. In this approach, the key is only highly correlated to the legitimate users (Alice and Bob), but not to the signal being eavesdropped on by Eve. This idea has already been put into practice in wireless and fiber-optic communications systems. In a wireless communication system, for key generation, the random fading effects of the wireless channel are utilized [9,10], such as received signal strength, channel impulse response, and frequency phase in key distribution schemes [11,12].
Unlike wireless communication, the optic fiber links have stronger resistance to environmental disturbance. The proposed method achieves the implementation of a classical physical layer secure key distribution (SKGD) with unique fiber characteristics, which extracts the key from the fiber channel characteristics. For the key distribution scheme based on chaotic synchronization, the security has been improved [13,14], but it is incompatible with the existing optic fiber link configuration, and the key distribution distance is short. The SKGD scheme based on the unique characteristics of the physical layer has the advantages of high security, low cost, and a simple structure. The polarization mode dispersion (PMD) depends on the birefringence distribution in instantaneous space [15,16,17,18] and fluctuates randomly in the link, providing a random source for key generation. Eve close to the legitimate party can easily cause information disclosure because the PMD can only produce a favorable effect when the distance is long enough. Based on the key distribution scheme of the optical fiber interferometer [19,20], the interferometer is exposed to the public and vulnerable to active intrusion attacks. As a result, other solutions that can guarantee high security and easy implementation have not been fully explored.
Recently, researchers have proposed a key generation scheme based on the bit error rate (BER) measurement of physical channel characteristics [21,22]. The scheme takes advantage of the physical channel’s randomness to ensure the security of the key and does not change the structure of the existing optic fiber link. However, this scheme requires a high BER in order for the normal transmission to be affected. We propose a key distribution measurement scheme based on the SNR characteristics of the physical layer of the optical fiber channel without affecting the normal transmission. The combination of key distribution and encryption transmission is realized by simulation. The final KGR can reach 25 kbps, and the KCR can reach 98%. Fingerprint SNR is used as the random source of key extraction in the system, and the uniqueness of the fiber channel ensures the high security of the generated key.
2. Key Generation Scheme for Optical Fiber Communication
2.1. Channel Model
As shown in Figure 1, the signal sent by the legitimate client Alice is , while the legitimate receiver Bob receives the signal sequence . The eavesdropping signal obtained by Eve is . The legitimate receiver obtains the SNR by comparing the signal from the receiver with that from the transmitter. According to information theory, the mutual information between Eve and Alice as Equation (1) should be as small as possible for reliable transmission. Eve cannot correctly obtain Alice’s key information, indicating that the key of communication negotiation is secure when .
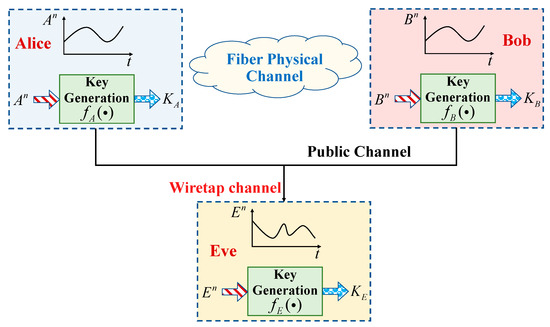
Figure 1.
Key generation model diagram.
The keys generated by Alice, Bob, and Eve are , , and , respectively, to achieve the security of the physical layer. Assuming that the coefficient of key consistency is large enough for n to satisfy the following relation, the system is secure [9,23].
In the best case, the key consistency rate approached in Equation (2) indicates that the completion of the key generated by Alice and Bob is consistent. Equation (3) indicates that Eve receives the information irrespective of the key generated by the legitimate. The maximum security key capacity is shown in Equation (4). The key capacity is when the communication between legitimate parties is normal, and the generated key capacity is when Eve eavesdrops. The maximum value is obtained by subtracting from .
The security capacity under the Gaussian Tap channel is shown in Equation (5), where is the power of the signal, and are, respectively, the noise variance of Bob and Eve stealing channels in the normal transmission main channel.
2.2. Channel Model
Figure 2 shows the proposed key generation scheme based on the SNR measurement in the optical fiber loop. Due to the changes in temperature, external stress, and physical parameters, the measured SNR fluctuates randomly. Specific physical layer channel features are extracted as follows: Alice and Bob simultaneously measure the SNR parameter changes in the fiber loop. Data from Alice and Bob are transmitted in the fiber loop link through time-division multiplexing. Alice and Bob occupy different time slots, i.e., even and odd symmetric time slots, respectively. First, Alice generates random data and random ground state through a PRNG. Afterwards, the DSP module of the transmitter generates the signal from the signal and the ground state . The signal reaches the Bob terminal after transmission in the optical fiber. Bob’s DSP module processes the received signal with a random ground state to generate the data . After the data signal is transmitted in the optical fiber, the signal with channel noise reaches Alice. The receiver’s DSP module generates data based on the received signal and random ground state . The SNR performance of the fiber loop can be obtained by comparing the data with . Similarly, Bob can measure the fiber loop simultaneously to acquire the SNR change rate of the fiber loop backlink.
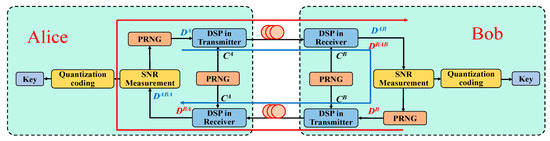
Figure 2.
Schematic diagram of key generation principle at the physical layer. PRNG: pseudo-random number generator. DSP: digital signal processing.
2.3. Key Evaluation Index
In this paper, the SNR as the channel physical layer feature is introduced to evaluate the system performance. The calculation of the SNR is shown as follows: The bit resolution of signal quantization is N, the quantization noise variance is , and the signal’s power is . The expression of SNR is shown in Equation (6) [24].
Alice and Bob obtain the SNR through the loopback measurement and then quantize it to generate the key. As presented in Equation (7), is the average value of the SNR, and is the quantization coefficient.
KGR is the number of keys generated in a period divided by the test time. The details are shown in Equation (8).
R is the signal transmission rate of 10 Gb/s, and is the segment length of the received signal. Moreover, denotes the outliers during quantization corresponding to the number of key bits generated after each symbol is quantized as 0.3, and is the discarding rate of privacy amplification (i.e., bit rate discarded in privacy amplification).
The KCR is the consistency rate of the key generated by Alice and Bob, and the partition length of the key is , as shown in Equation (9).
The key error rate (KER) is the error rate of the key generated by Alice and Eve, as shown in Equation (10).
2.4. Key Generation Process
The key quantization optimization process is shown in Figure 3. Alice and Bob extract channel characteristics of the SNR, quantify and code to generate the key, and generate the key with excellent consistency and security after post-processing. The specific steps are as follows:
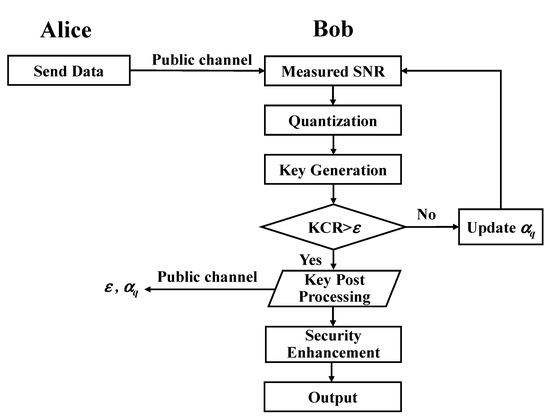
Figure 3.
Optimized key generation factors ε and αq.
Step 1: Bob calculates the channel’s SNR through loopback measurements;
Step 2: The characteristic information SNR is quantized to generate a consistency key by encoding. The specific steps are shown in Equation (2);
Step 3: The key’s consistency is judged, and the consistency factor is set as = 0.95. If , it will proceed to the next step; otherwise, the quantization factor will be updated and it will go back to the beginning;
Step 4: After the key is post-processed, Bob transmits the quantization coefficient and consistency factor ε to Alice through the public channel;
Step 5: To increase the security of the generated key, data with length 0 or length 1 are discarded, and the key sequence KB with good randomness and consistency is obtained;
Step 6: Bob shares the optimized parameters and ε with Alice, and Alice generates the key sequence KA in the same way.
3. Key Distribution Simulation Platform Setup
As shown in Figure 4, the data transmission rate of the scheme is 10 Gbps, the optic fiber link is 200 km, the laser transmitting power is 1 mW, and the wavelength is 1550 nm. The sending process of the scheme is as follows: Firstly, Alice obtains the orthogonal frequency division multiplexing signal encrypted by quantum noise stream through DSP processing. Next, the signal is converted from digital to analogue through the arbitrary waveform generator (AWG), and the electrical signal is modulated onto an optical carrier using an I/Q modulator. The signal amplified by erbium-doped fiber amplifier (EDFA) enters the optic fiber link to Bob’s terminal. It is demodulated by the coherent receiver and sampled by a 20 GSa/s oscilloscope (OSC). Bob converts the signal to analogue through AWG and then modulates it to the optical carrier using the I/Q modulator. After passing through the amplifier and optic fiber link, Alice’s coherent receiver carries out coherent demodulation on the signal. The demodulated data are sent to an OSC for sampling (sampling rate = 20 GSa/s). Finally, Alice performs DSP processing on the sampled signal. There are simulation-specific parameters, as listed in Table 1.
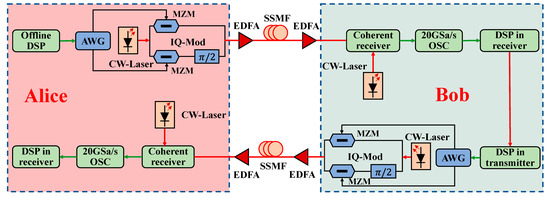
Figure 4.
System simulation platform. MZM: Mach–Zehnder modulator. SSMF: standard single mode fiber.

Table 1.
Simulation parameter list.
4. Analysis of Simulation Results
4.1. Random Analysis
The National Institute of Standards and Technology (NIST) random test results of key sequences are illustrated in Figure 5a to evaluate the randomness of key bits. We randomly selected a set of keys from the key sequence as the key test sequence, and 10 NIST sub-tests [25]. The return threshold of all 10 of the NIST sub-tests is above 0.99, which indicates that the key sequence has true randomness. In addition, for some tests that return multiple thresholds, we only give the minimum value. Figure 5b describes the 0/1 ratio performance of Alice and Bob’s key bits as a function of the SNR sampling interval. Alice quantifies the key to receive the 0, 1 key. The noise sources, such as laser, optical amplifier, and physical fiber parameters, determine the randomness of the fiber channel. Consequently, the probability of keys 0 and 1 fluctuates around 0.5, further verifying the key’s randomness.
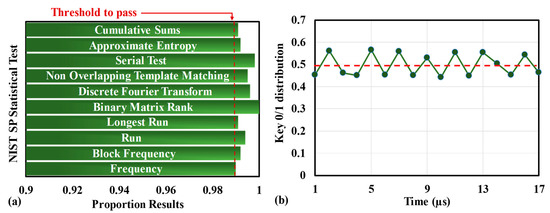
Figure 5.
(a) Key NIST test results, and (b) 0/1 distribution probability of the key.
4.2. Consistency Analysis
Key consistency comes from precise channel reciprocity, so Alice and Bob share a highly related key source. According to the physical characteristics of the reciprocity of the channel, a consensus key is generated. The reciprocity of the channel mainly improves the consistency of the key. The metric characteristic of the channel generated by the key is the SNR. As shown in Figure 6a, the KGR of the system first increases and then decreases. With the increase in the SNR sampling interval, the calculation of BER requires more data bits, leading to the decrease in the KGR. When the sampling time is 2 μs, the maximum KGR is 25 kbps. The amount of data obtained at each sampling point is relatively insignificant when the sampling interval is very small, leading to a relatively severe miscalculation of SNR. Therefore, the SNR values calculated by Alice and Bob are inconsistent, which affects the KGR. When the sampling interval is large, the SNR value calculated within the same amount of time is relatively small, leading to a relatively low KGR rate. Therefore, it is necessary to set a reasonable sampling interval to obtain a relatively high KGR. It is obvious that faster fluctuation of channels corresponds to a smaller sampling interval, thus extracting more channel feature and generating more secret keys.
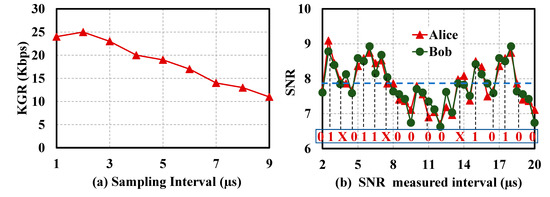
Figure 6.
(a) KGR change curve and (b) key extraction quantization curve.
In Figure 6b, red represents the sampling value measured by Alice, and green characterizes the sampling value measured by Bob. It is evident that the change curves of Alice and Bob almost coincide, and the curve consistency is significant since they simultaneously measure the same fiber. As a result, we quantize the sample value to one and zero when it is greater and less than the mean, respectively. In addition, if the sample value is near the mean, we discard the data.
Furthermore, the KGR changes when varying the transmission power, sampling interval, and system’s laser power. The signal transmission rate is altered to extract more channel features, and the KGR increases when the transmission rate is relatively low. However, the KGR does not increase and tends to be stable when the transmission rate increases to a certain extent. The sampling interval is varied to find the maximum KGR from different sampling intervals. At this time, the change in the KGR should be non-linear to determine the suitable KGR.
As shown in Figure 7, the relationship between the length of the selected data and the consistency is direct. The smaller the data block length is, the worse the key consistency is. By quantifying the SNR, the consistency of the initial keys obtained by Alice and Bob is as above. The SNR interval gradually increases with key consistency, and the obtained key consistency rate reaches 98% when the SNR interval is greater than 1.4 μs. As the SNR measurement interval increases, the error curve is smoother, and the fluctuation reduces, so the key consistency quantized by Alice and Bob is enhanced. The extracted keys can be subjected to off-line DSP to eliminate the influence of the inconsistency between the two key sequences of Alice and Bob.
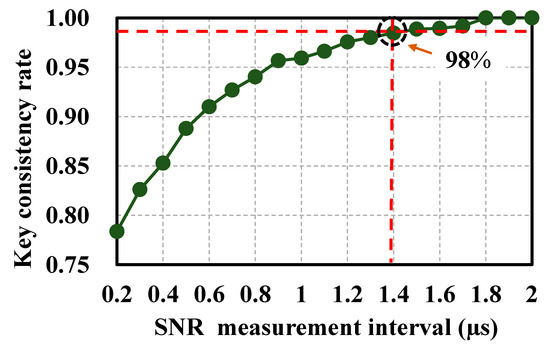
Figure 7.
Influence of SNR measurement interval on Alice–Bob consistency.
More extensive data are needed to calculate the SNR required to increase the KCR at both ends, because the longer the data, the more stable the SNR and the higher the KCR. If the selected data are too long, the KGR for generating the key decreases, in that the calculated SNR drops for extensive data. Therefore, a reasonable SNR measurement interval should be selected to strike a balance between the KCR and the KGR.
4.3. Security Analysis
As shown in Figure 8a, the measured SNR value for Alice and Bob is approximately 10, while Eve’s SNR is around −30. Alice and Bob loop back the measurement, and they know the initial key to decrypt the signal. Eve can only intercept information from the optical fiber without the initial key, so the SNR is low.
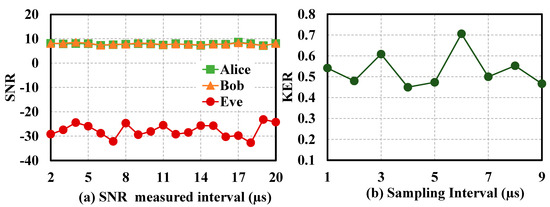
Figure 8.
(a) The measured value curve of Alice and Bob Eve SNR, and (b) the change curve of the error rate of Eve key.
As shown in Figure 8b, Eve quantifies the key for SNR and Alice, then she obtains the key for comparison. The error rate of receiving the key is about 50%, so Eve cannot obtain the correct key. Moreover, the correlation coefficient between Alice and Eve is , indicating that the key generated by the system has superior security. Alice and Eve’s SNR is not the same, since Eve measures the SNR through different equipment and lines from Alice and Bob. The SNR is a variable that can be used to negotiate keys to ensure the generated keys are unique.
5. Conclusions
In this paper, a key generation scheme based on the SNR characteristic of the optical fiber channel’s physical layer is proposed. In the scheme, the rate of SNR change is obtained using loopback measurements, and the changed SNR is compared with the threshold system to judge whether the system is attacked and the legitimate equipment can be correctly authenticated. If Eve launches an active attack on the system, it impacts the security and reliability of the generated key. Therefore, we can use physical layer authentication for intrusion detection. The simulation results show that the KGR can reach 25 kbps, and the KCR can reach 98%. The correlation coefficient of BER measurement samples of Alice and Eve is relatively low. The correlation coefficient and the KER of Eve is only 50%, indicating that this system has high security. Due to the physical characteristics of using the SNR as a key distribution scheme, normal communication requirements can be guaranteed to set the SNR values. The scheme can be used together with other security methods in the higher network layer, to enhance communication security and withstand active intrusion attacks. It has excellent application value and is suitable for popularization.
Author Contributions
Conceptualization, X.W. and B.W.; methodology, X.W.; software, B.W., K.Z. and H.S.; validation, X.W., B.W. and K.Z.; formal analysis, H.S.; investigation, H.S.; resources, R.L.; data curation, R.L.; writing—original draft preparation, X.W. and F.Z.; writing—review and editing, F.Z.; visualization, F.Z.; supervision, J.Z.; project administration, X.W.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the NSFC (Grant No.:61831003), University Natural Science Research Project of Anhui Province (Grant No.: KJ2019A0616), and the Key Projects in Natural Science of West Anhui University (Grant No.: WXZR201719). The authors are thankful for the funding support from the Anhui Provincial Quality Engineering Project (Grant No.: 2020jyxm2152).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study does not report any data.
Acknowledgments
We acknowledge the support given by Kai Wang and Shuang Wei during the project.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analysis, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Katz, J.; Lindell, Y. Introduction to Modern Cryptography; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Shor, P. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Patra, B.; Incandela, R.M.; Van Dijk, J.P.G.; Homulle, H.A.R.; Song, L.; Shahmohammadi, M.; Staszewski, R.B.; Vladimirescu, A.; Babaie, M.; Sebastiano, F.; et al. Cryo-CMOS Circuits and Systems for Quantum Computing Applications. IEEE J. Solid-State Circuits 2017, 53, 309–321. [Google Scholar] [CrossRef]
- Lo, H.-K.; Curty, M.; Tamaki, K. Secure quantum key distribution. Nat. Photon. 2014, 8, 595–604. [Google Scholar] [CrossRef]
- Korzh, B.; Lim, C.C.W.; Houlmann, R.; Gisin, N.; Li, M.J.; Nolan, D.A.; Sanguinetti, B.; Thew, R.; Zbinden, H. Provably secure and practical quantum key distribution over 307 km of optical fibre. Nat. Photon. 2015, 9, 163–168. [Google Scholar] [CrossRef]
- Lucamarini, M.; Yuan, Z.L.; Dynes, J.F.; Shields, A.J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nat. Cell Biol. 2018, 557, 400–403. [Google Scholar] [CrossRef] [PubMed]
- Hwang, W.-Y. Quantum Key Distribution with High Loss: Toward Global Secure Communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef]
- Zhang, J.; Duong, T.Q.; Marshall, A.; Woods, R. Key Generation from Wireless Channels: A Review. IEEE Access 2016, 4, 614–626. [Google Scholar] [CrossRef]
- Bottarelli, M.; Epiphaniou, G.; Ben Ismail, D.K.; Karadimas, P.; Al-Khateeb, H. Physical characteristics of wireless communication channels for secret key establishment: A survey of the research. Comput. Secur. 2018, 78, 454–476. [Google Scholar] [CrossRef]
- Premnath, S.N.; Jana, S.; Croft, J.; Gowda, P.L.; Clark, M.; Kasera, S.K.; Patwari, N.; Krishnamurthy, S. Secret Key Extraction from Wireless Signal Strength in Real Environments. IEEE Trans. Mob. Comput. 2013, 12, 917–930. [Google Scholar] [CrossRef]
- Liu, Y.; Draper, S.C.; Sayeed, A.M. Exploiting Channel Diversity in Secret Key Generation from Multipath Fading Randomness. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1484–1497. [Google Scholar] [CrossRef]
- Sasaki, T.; Kakesu, I.; Mitsui, Y.; Rontani, D.; Uchida, A.; Sunada, S.; Yoshimura, K.; Inubushi, M. Common-signal-induced synchronization in photonic integrated circuits and its appli-cation to secure key distribution. Opt. Express 2017, 25, 26029–26044. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Cheng, M.; Luo, C.; Deng, L.; Zhang, M.; Fu, S.; Tang, M.; Shum, P.; Liu, D. Semiconductor-laser-based hybrid chaos source and its application in secure key distribution. Opt. Lett. 2019, 44, 2605–2608. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Hajomer, A.A.E.; Yang, X.; Hu, W. Error-free secure key generation and distribution using dynamic Stokes parameters. Opt. Express 2019, 27, 29207–29216. [Google Scholar] [CrossRef]
- Hajomer, A.A.E.; Zhang, L.; Yang, X.; Hu, W. Accelerated key generation and distribution using polarization scrambling in optical fiber. Opt. Express 2019, 27, 35761–35773. [Google Scholar] [CrossRef]
- Hajomer, A.A.E.; Zhang, L.; Yang, X.; Hu, W. Post-Processing Protocol for Physical-Layer Key Generation and Distribution in Fiber Networks. IEEE Photon. Technol. Lett. 2020, 32, 901–904. [Google Scholar] [CrossRef]
- Zaman, I.U.; Lopez, A.B.; Al Faruque, M.A.; Boyraz, O. Physical Layer Cryptographic Key Generation by Exploiting PMD of an Optical Fiber Link. J. Light. Technol. 2018, 36, 5903–5911. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Ma, P.Y.; Blow, E.C.; Mittal, P.; Prucnal, P.R. Accelerated secure key distribution based on localized and asymmetric fiber interfer-ometers. Opt. Express 2019, 27, 32096–32110. [Google Scholar] [CrossRef] [PubMed]
- Kravtsov, K.; Wang, Z.; Trappe, W.; Prucnal, P.R. Physical layer secret key generation for fiber-optical networks. Opt. Express 2013, 21, 23756–23771. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Li, Y.; Zhao, Y.; Yang, X. Secure Key Distribution System Based on Optical Channel Physical Features. IEEE Photon. J. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Lei, C.; Zhang, J.; Li, Y.; Zhao, Y.; Wang, B.; Gao, H.; Li, J.; Zhang, M. Long-haul and High-speed Key Distribution Based on One-way Non-dual Arbitrary Basis Transformation in Optical Fiber Link. In Proceedings of the Optical Fiber Communication Conference and Exhibition(OFC), San Diego, CA, USA, 8–12 March 2020; p. W2A.51. [Google Scholar]
- Maurer, U.M. Secret key agreement by public discussion from common information. IEEE Trans. Inf. Theory 1993, 39, 733–742. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, J.; Li, Y.; Gao, G.; Zhao, Y.; Zhang, H. Single-carrier QAM/QNSC and PSK/QNSC transmission systems with bit-resolution limited DACs. Opt. Commun. 2019, 445, 29–35. [Google Scholar] [CrossRef]
- Fratalocchi, A.; Fleming, A.; Conti, C.; Di Falco, A. NIST-certified secure key generation via deep learning of physical unclonable functions in silica aerogels. Nanophotonics 2020, 10, 457–464. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).