Abstract
Radiation metrology is crucial in space, for instance in monitoring the conditions on-board space vehicles. The energy released in matter by ionizing radiation is due to the atomic and molecular ionization processes, which have been investigated for several decades from both a theoretical and an experimental point of view. Electronic excitation and ionization cross-section are of particular interest in radiation physics, because of their role in the radiation–matter interaction process. Recently, experimental findings have shown that the interplay with a laser field can strongly modify the electronic interaction probabilities and emission spectra. These phenomena are still not completely understood from a theoretical point of view, and the available empirical data concern a few, simple atomic species. We represent a possible dosimetric effect of the interaction with laser light, inferring from experiments the characteristics of laser-assisted cross-sections. Using a Monte-Carlo calculation for simulating the micro-dosimetric aspects of the irradiation of a simple geometry, we show the need of new experimental data and more detailed theoretical approaches to these phenomena in complex molecular systems.
1. Introduction
Electron-impact ionization dynamics of atoms and molecules play a crucial role in several scientific and practical application fields, ranging from spectroscopy and radiation metrology to radiation chemistry and the biological effect of ionizing radiations. Understanding the ionization dynamics requires a detailed knowledge of the corresponding cross-sections. Experimentally, a well-established approach to obtain a detailed description of the interaction probabilities, and consequently, a comprehensive characterization of the electron impact ionization dynamics, is given by the so-called (e,2e) studies, in which the two outgoing electrons are detected in coincidence [1,2].
Recently [3], it was discovered that the presence of a laser field strongly influences the electron-impact triple-differential cross-section (TDCS), the cross-section differential in the solid angles of both electrons and the energy of one of them, which is measured in the (e, 2e) experiments. At a first attempt, the authors of [3] were unable to reproduce theoretically the empirical data they measured. In fact, their description of the electron-impact ionization dynamics was based on the so-called First-Born Approximation (FBA), which does not take into account the important correlation effect, as for instance, the collective and single particle degree of freedom excited in the target wave function (dubbed dressed wave-function) and the absorption (or emission) of a photon in the ionization process. The cited article deepens its roots in older studies describing multiphoton ionization, starting from the 1930s [4]. In the last decade, several research efforts have produced considerable advances in describing laser-assisted electron impact ionization of simple atoms and molecules [5,6], even if the treatment of complex targets remains challenging.
The possibility of tuning, to some extent, the ionization cross-section with the aid of a laser would affect several scientific fields, including radiation physics. As a matter of fact, electronic scattering is the core of the quantum few-body dynamics exploited in Monte Carlo (MC) simulation of radiation transport, which are routinely used in ionizing radiation dosimetry [7].
In this paper, starting from an educated guess on the effect of a non-resonant laser field on the electron-impact ionization cross-section in water, some consideration will be made to its potential dosimetric effect, using a simulated irradiation of a simple cylindrical phantom. The main issue one has to solve consists in filling the gap between the theoretical, detailed approach used for describing the laser-assisted process and the semi-empirical method, which has to be used in MC codes in order to reproduce the experimental value of macroscopic dosimetric quantities.
The document is organized as follows. The second section reviews some of the theoretical approaches used to describe the laser-assisted electron impact process. A brief account of the theoretical fundamentals underlying ionization cross-section calculation is given. The same section also describes the semi-empirical methods used for calculating the electronic inelastic scattering cross-sections when radiation travels through matter. The discussion emphasizes the issue arising in the passage from gas-phase to condensed-phase.
Third and fourth sections of the article discuss a simplistic calculation trying to infer a possible micro- and nano-dosimetric effect of laser-assisted electron scattering. The focal point is the need of new experimental data, because even from tiny modifications to the cross-sectional model can result in considerable radiological differences. A section on perspective research completes the paper.
2. Electron-Atom Scattering Cross-Section
Some elements are given here, concerning the theoretical treatment of atomic scattering both in vacuum and condensed matter. How scattering is formally treated, and which issues arise, from both a theoretical and a computational point of view, when condensed matter and laser-field interaction come into play, are briefly described.
In particular, the First-Born Approximation is introduced, because this approach is generally detailed enough for describing the inelastic scattering in vacuum. In the literature, however, it has been pointed out that FBA cannot be employed for describing ionization in the presence of a laser field, because it does not take into account the correlations induced by the interaction, as it will be evident from the Lippmann–Schwinger equation. As a matter of fact, the simple model proposed here is based on the literature results obtained considering a more detailed description of the transition operator.
Moreover, issues arise in passing to condensed matter, where the scattering description is more complex with respect to the vacuum condition, even if one does not consider the presence of a laser field. We present the standard, semiempirical approach used for describing particle passage through matter. We assume, in our model, that this approach is valid for describing even multiple scattering in the presence of a laser field, and build the description of the laser-assisted electron ionization in condensed matter applying the features observed in the vacuum scattering case in the MC code. This is a working hypothesis of our model, and it could be worthy to spend some theoretical research efforts to understand the implications of this assumption.
2.1. Theory of (e, 2e) Collisions
In the Heisenberg picture, one may consider a scattering problem as taking an initial wavefunction to a final wavefunction through a scattering operator, S, defined such that
Hence, the S operator contains all the information on the evolution of the system from its initial to final state. It is useful to define the so-called S-matrix, representing the operator within an uncorrelated basis, , with indicating the non-interacting target state vector and the infinitely-distant plane-wave projectile. When the final state of Equation (1) can be considered one of these non-interacting projectile-target states, as is not the case within condensed-phase matter, the scattering matrix element reads [8]
where V represents the target–projectile interaction potential. The second term in Equation (2) defines an element of the Transition (T) matrix, equivalent to the definition of an operator
The Lippmann–Schwinger equation for this operator can be written as
where is the Green’s function corresponding to outgoing spherical wave boundary conditions. Equation (4) is formally equivalent to the infinite (Born) series
Truncating Equation (5) to include k terms is known as the k-th Born approximation, which provides an increasingly accurate description of the coupling between reaction channels.
The First-Born approximation is the most widely used form of the series 5, in both theoretical and experimental works, given the simplicity of the approach. The magnitude of the error of FBA is inversely proportional to the projectile energy, and in the low-energy regime (<10 keV) of the secondaries (-rays), it is necessary to include at least the second-order term. This method is usually dubbed the Second-Born Approximation (SBA). SBA has been shown, in the literature, to be crucial for correctly taking into account the laser-dressing of the wave function [9].
More sophisticated theoretical approaches exist, determining a non-perturbative treatment of the wave-function dressing [10]. However, as reported in the following section, one of the most complex aspects to be tackled in MC simulation of radiation passing through matter is the effect of the condensed-matter phase.
A useful element for our speculative treatment on the effect of laser-light excitation in particle scattering is reported in [9]. The article reviews the calculation of the ionization TDCS of a simple atomic system exploiting first- and Second-Born approximations. Figure 1 reports one of the proposed results.
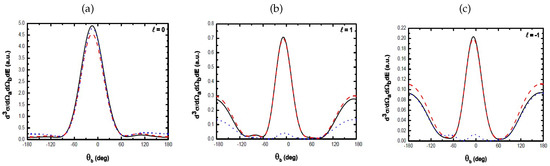
Figure 1.
Triple-differential cross-sections corresponding to the laser-assisted electron-impact ionization process of atomic hydrogen as a function of the ejected angle . The incident electron energy is = 40 eV, the ejected electron energy is = 5 eV, and the scattering angle is . The laser is set to to eV and the electric field strength is V/cm. The laser polarization vector of the field is set parallel to the wave vector of the incident electron. Red, dashed line: Second-Born approximation results; Continuous line: First-Born approximation results. Blue, dotted line: results obtained by ignoring the dressing of the target. () : no-photon net exchange; () one photon absorption; () one photon emission (taken from [9]).
At a first glance, the figure demonstrates one of the characteristics of the process, confirmed by experiments. Ejected electrons can be divided in two different groups: the first, generally dubbed “binary encounter”, is associated with a two-body scattering of the incoming and ejected electrons, in which there is essentially no interaction with the atomic nucleus. In this process, the two electrons scatter on opposite sides of the initial electron direction. In Figure 1, binary encounter electrons are those within the angular range . A second group of electrons, after the interaction, emerge on opposite sides with respect to the electrons of the binary encounter. These particles, called “recoil”, are thought to originate from a further interaction of the two electrons, the scattered and the ionized ones, with both the nucleus and the remaining part of the electron cloud. In this sense, recoil electron pairs are binary encounters which encompass a reflection due to potential the ion.
Without claiming to be exhaustive, in this work, we try to figure out what a potential radiological effect of low-energy, laser-assisted electron scattering could be, exploiting the difference between recoil and binary encounter electron scattering. A laser field seems to enhance the probability of binary encounters over the recoil process, even in those interactions involving a net photon exchange, which would otherwise be associated with recoil electrons.
Clearly, this is just one of the effects which the laser light could have on the scattering process, since it could even change the differential and total cross-section of the process, completely redefining the physical effects of the radiation–matter interaction, in particular the imparted dose and the link between dose and damage.
However, even such a simple change in the angular distribution of the emitted electrons could have an appreciable effect from a nano-dosimetric point of view, leading to a hypothetical change in those impairments induced by ionization clustering. Later in this article it is discussed how modifying the angular emission probability within an MC code induces differences in these clusters. It is worthy to recall that there is no claim of generality concerning this effect, but the potential impact discussed urges the availability of new experimental data on the subject.
2.2. Inelastic Scattering Cross-Sections in MC Code
Ionization cross-sections of target atoms are essential for a detailed and realistic simulation of particle slowing-down in passing through matter. A condensed state of aggregation modifies gas-phase inelastic electron cross-section, an effect that MC codes needs to correctly take into account for a realistic prediction of delivered dose [11].
Almost all the MC codes available for practical purposes simulate the human body to be composed of liquid water. Despite this fact, direct measurements of scattering cross-sections in liquid water are not available. Indirect approaches are generally based on the complex dielectric response function of the material, where E and represent, respectively, the energy and momentum transfer to the target.
The importance of this constitutive relation, linking the electric field in the vacuum to its counterpart within matter, comes from the need, in condensed media, to take into account polarization effects, which determine the screened character of the Coulomb interaction potential. This heuristic—and classical—statement implies, from a practical point of view, that theoretical models relate the double-differential cross-section to the Energy-Loss-Function, . For example, in the non-relativistic Plane-Wave Born Approximation (PWBA), it can be shown [12] that the inverse electron inelastic mean-free path, , reads
where is the Bohr radius, T the kinetic energy of the incident electron, and the proper double-differential cross-section can be derived from , dividing it by the number density of target atoms, N.
Plane-Wave Born Approximation, which implies an incident plane-wave whose cross-section is calculated using the First-Born Approximation, is not perfectly applicable to the condensed matter case, where incident particles originate from previous interactions. There are, however, more sophisticated approaches taking into account correlation in projectiles and targets [12], determining a closer fit to optical [13] and inelastic X-ray scattering [14] data. Fit to experimental data is the key to success for the approaches based on a complex dielectric function for MC computational dosimetry, because it provides a semiempirical way for handling correlations in wave functions due to the aggregation state. In such models, free-parameters of dielectric function are extrapolated at the optical limit, , while non-zero momentum transfer, whose data are incomplete for IXS and not available in classical experiments, may be obtained by exploiting the so-called extension algorithms [15].
According to this simple and effective approach, several models of the dielectric function have been constructed, allowing calculations of inelastic electron diffusion in condensed-phase media. Dielectric function models are commonly based on the theory of homogeneous electron gas, which is relatively simple to handle. The properties of the system are generally described in the framework of the Random-Phase Approximation (RPA), which considers the Hamiltonian as being composed of a self-consistent electronic mean-field term and an interaction allowing correlation up to two-particle two-holes of the mean low-energy state of the many-body system.
3. Radiation Dosimetry with Laser-Assisted Ionizations
In this section, we try to figure out what the dosimetric impact of laser-assisted electron scattering could be, in order to give an estimation of the importance of obtaining new experimental data. From the discussion developed above, concerning the theoretical basis of charged-particle scattering in condensed matter, it is evident that the calculation that we will develop does not pretend to be accurate, but could be, in some aspects, realistic if the net effect of the laser field on the electron scattering would be, among the others, to change the electron angular emission distribution.
In order to simulate the presence of the laser field, the Born ionization model of the MC code was modified to enhance the emission of secondaries with an angle of degrees with respect to the primary particle. The irradiation of a microscopic volume, representing the cell nucleus, was then simulated with 1 MeV protons. Since only the angular distribution of secondaries was modified, no change is expected in the microdosimetric aspects of the simulated irradiation.
As a matter of fact, in Figure 2, the specific and lineal energy distributions for the “laser-assisted” and “normal” scattering case have been shown. Again, in a real irradiation, these distributions are likely to be different, since the total and energy-differential cross-sections would probably change; however, to date, there are no experimental data for a similar set-up. In other terms, Figure 2 shows a limit of applicability of the simple model proposed here, which is not able to describe the micro-dosimetric consequences of the interaction with a laser field.
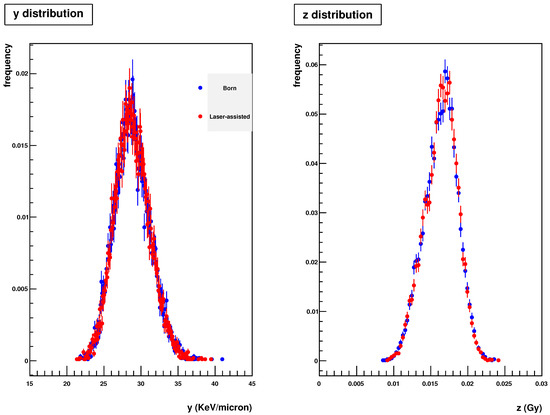
Figure 2.
Simulated specific and lineal energy distributions for a 1 MeV irradiation of a micrometric volume (“cell nucleus”); • Born ionization process; • “laser-assisted” ionization process.
What have been found to appreciably change are the distributions of the physical quantities related to the clustering of ionizations, represented in Figure 3. The first effect of the laser field, intended as the modified angular distribution of secondaries, can be recognised in the number of clusters decreasing by about . The importance of this information is not in the quantity, given that our model is based on a simple approximation, but on the qualitative effect of a sensible decrease in the number of clusters.
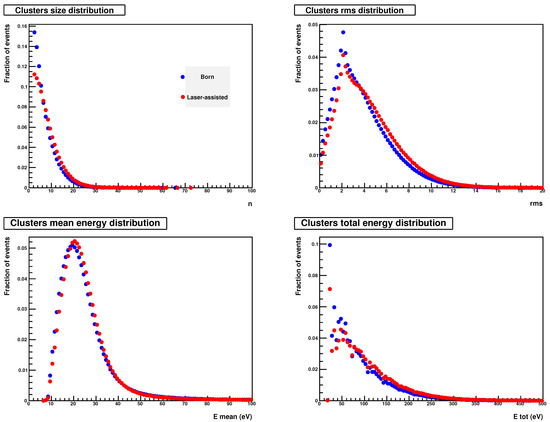
Figure 3.
Simulated distributions of physical quantities describing the nanometric clusters of ionization for a 1 MeV irradiation of a micrometric volume (“cell nucleus”); • Born ionization process; • “laser-assisted” ionization process.
For the sake of clarity, as discussed in the following section, “ionization cluster” refers here to a set of ionization events that are found to be close in space with a density-based scanning algorithm.
It is well known that the irradiation with hadrons is characterized by a heterogeneous track structure, whose features are strongly correlated with the distributions of the physical quantities associated with ionization clusters, as their size, mean radius, mean and total energy content. In other words, the trace a heavy charged particle leaves passing through matter is related to the spectra and angular distributions of the electrons it ionizes. These distributions are crucial, at the same time, for the clusterization of the ionization event induced by the secondary electrons themselves. From these clusters the effectiveness of the ionizing radiation depends on the damage, because for a given volume, a larger number of ionizations implies a higher energy imparted.
Physical quantities associated with clusters, reported in Figure 3, exhibit some modifications related to the different spatial distribution of the secondaries that we have used for miming the effect of the laser field, even if the energy imparted to the whole target volume is comparable with the irradiation without a laser, as shown in Figure 2. The smaller number of clusters, then, is associated with an equivalent total number of ionizations in the entire volume. This determines an increased mean number of events for each cluster, resulting in a larger cluster mean radius and an augmented total energy associated with each bunch of events. The ratio of clusters mean energy with clusters’ mean radius, indicating the mean energy imparted to a given nanoscopic volume, is increased.
According to our model, then, the presence of a laser field could result in a spatially concentrated and more effective “damage” associated with the irradiation. Does the polarization of the incoming electromagnetic field induce some orientation effect, determining the degree of concentration of the ionization clusters? Empirical data on nano- and micro-dosimety of ionizing radiation coupled with lasers could shed some light on the phenomenon described in this article, and eventually clarify how the modification in the physics of the subatomic interaction could have an effect on the mechanism of the overall energy release on the different length scale.
Concretely, a simple attempt could be made for evidencing the effect of laser light on ionization-cluster formation, using a new experimental set-up recently employed for measuring cluster distributions. In [16], F. Vasi and U. Schneider reported a complete set of experimental data on the number of ionization clusters with increasing complexities —i.e., composed of an increasing number of ionizations that occurred close in space—formed by a 5 MeV alpha particle and measured with an innovative ceramic nanodosimeter.
The new device, developed starting from previous attempts of constructing a nano-dosimeter small and simple enough to deploy [17,18,19], has the intriguing characteristic of being simple enough to be replicated in almost every physics laboratory, without the need for reproducing the relatively large facilities which have been employed since the beginning of this century for measuring the size distributions of ionization clusters produced by the interaction of ionizing radiation with atoms and molecules [20,21,22,23].
The idea is that an end-user experimentalist could try to reproduce the measures reported in [16], adding a laser field interacting with the low-pressure propane ionized by the -radiation of the Americium, and verifying if the size distribution of the ionization clusters, obtained with the Bayes theorem, does change. In our opinion, however, two important remarks must be made at this point: (i) first, the compact nanodosimeter employs low-pressure propane, which is know to have tissue-equivalent properties in the interaction with ionizing radiation, but the effect of the laser field on gaseous propane could not be the same as on liquid water; (ii) as reported above, the size distribution measured with the compact nanodosimeter is estimated using the Bayes theorem, which seems to induce a detection efficiency that decreases with the dimension of the sensitive volume, apparently posing a limit on the dimension of clusters that could be measured. However, one could imagine an experiment at one of the larger facilities, which could even serve for validation purposes.
Finally, from a theoretical point of view, in our opinion there should be some research effort for understanding if the semi-empirical approach currently used in MC calculation for condensed-matter phases is still valid when describing ionization occurring in presence of the laser field.
4. Materials and Methods
Data on the simulated irradiation with 1 MeV proton particles have been gathered using the Monte-Carlo toolkit Geant4 [24]. Geant4 is a versatile and powerful toolkit capable of simulating the passage of particles through matter, and including a large variety of physical models—driven by theory or data—for the passage of each particle type through matter, with an energy ranging from a few eV to several TeV, and the possibility for the user to construct a detailed geometrical model of the target [25,26].
In our work, the library of computational models called Geant4-DNA [27] has been used for obtaining a nano-metric accuracy in the description of the energy deposition. The simulations that can be performed with this package allow the calculation of all elementary interactions on an event-by-event basis. This means that the process of energy deposition within matter can be followed, down to the eV scale, taking into account all the energy deposits produced by the primary particles and all their secondary electrons.
In the calculation performed for this article, a threshold of 9 eV was used. This choice allows a detailed description of the energy deposition, which at low energy is due in particular to the secondary electrons, while reducing the computational time. The material which has been used for simulating a biological tissue is liquid water. The associated molecular structure, for which the inverse electron inelastic mean-free path of Equation (6) depends on the complex dielectric function, was characterized by five ionization and five excitation shells.
The target volume chosen for the proton irradiation was a homogeneous cylinder with an ellipsoidal basis and height h = 2 µm. A similar volume has been used elsewhere [28] for simulating a typical endothelium cell nuclei. Using a micro-metric target volume, it has been possible to study the energy deposition process at both the micro-metric and nano-metric length scale. In particular, as discussed above, the characteristics of the nano-metric energy deposition are closely related to the so-called track structure of the radiation.
In particular, at the micro-dosimetric level, the distributions of the specific and lineal energy, z and y, have been calculated, with indicating the total energy deposit in the target volume, m the mass of the volume itself, and l the length of the path followed by the primary ionizing particle through the target. The specific and lineal energy for each particle have been calculated as and , respectively.
On the other hand, at the nano-metric level, the detailed energy deposit process was studied through the clusterization of the single ionization events. The distributions of the physical parameters associated with these clusters, namely their complexity, total and mean energy and root mean square (rms) have been produced and analyzed. In order to determine the clusters of ionizations produced by the passage of each primary particle, the structure in space of the events has been analyzed with a density-based scanning algorithm, DBSCAN [29].
This algorithm divides all the ionization in a first set of clusters, analysing their distance according to a reference length chosen by the user as a model parameter. This first set of clusters is characterized by a given complexity, spatial extension and energy content, which are different from those of the final set of clusters. As a matter of fact, clusters belonging to the first set are analyzed again, and can then be merged pairwise into a single entity if their distance lies within the reference length parameter. The algorithm then iterates until it does not find any other cluster to merge. In our calculation, we have considered a reference length, for the initial cluster’s extension, of 3.2 nm, which is associated in literature with a DNA segment of 10 base pairs [30]. This value has been used because a future comparison with the biological data on DNA strand breaks could be foreseen.
5. Conclusions and Perspectives
This article has presented some speculative prevision on the possible effect of a laser-assisted exposure to ionizing radiation. The calculations presented are based on a working hypothesis concerning some of the characteristics of the electron–electron ionization process in the presence of an electromagnetic laser field. Without any claims of generality, we tried to determine a realistic consequence of such a concurrent electromagnetic interaction, evidencing the need of new empirical data on the subject
Trivially, the first perspective research following our discussion concerns an experimental verification on the effect described. Eventually, implications of the laser-assisted irradiation in the medical field could relate to the effectiveness of radiation therapy and the mitigation of its side consequences, but clearly the development of a new technology based on the exploitation of a physical phenomenon is limited by several practical aspects, particularly in bio-med sciences.
Finally, the effect of a laser field on radiation-induced damage could be employed in detectors used for spectroscopy and metrological applications, particularly in the complex radiation environment found in space, where the discussed ionization process could be, for instance, exploited to enhance the useful lifetime of sensitive elements.
Author Contributions
The research article was conceived by D.B., who also prepared the original draft; scientific and redaction contributions came from F.L., M.Q. and L.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FBA | First-Born Approximation |
| MC | Monte-Carlo |
| MDPI | Multidisciplinary Digital Publishing Institute |
| PWBA | Plane-Wave Born Approximation |
| RPA | Random-Phase Approximation |
| SBA | Second-Born Approximation |
| TDCS | Triple-differential Cross-Section |
References
- Ehrhardt, H.; Schulz, M.; Tekaat, T.; Willmann, K. Ionization of Helium: Angular Correlation of the Scattered and Ejected Electrons. Phys. Rev. Lett. 1969, 22, 89. [Google Scholar] [CrossRef]
- Amaldi, U., Jr.; Egidi, A.; Marconero, R.; Pizzella, G. Use of a Two Channeltron Coincidence in a New Line of Research in Atomic Physics. Rev. Sci. Instrum. 1969, 40, 1001. [Google Scholar] [CrossRef]
- Höhr, C.; Dorn, A.; Najjari, B.; Fischer, D.; Schröter, C.D.; Ullrich, J. Electron Impact Ionization in the Presence of a Laser Field: A kinematically Complete (nγe,2e) Experiment. Phys. Rev. Lett. 2005, 94, 153201. [Google Scholar] [CrossRef]
- Milonni, P.W.; Sundaram, B. I Atoms in Strong Fields: Photoionization and Chaos. Prog. Opt. 1993, 31, 1–137. [Google Scholar]
- Zammit, M.C.; Fursa, D.V.; Bray, I. Convergent-close-coupling formalism for positron scattering from molecules. Phys. Rev. A 2013, 87, 020701. [Google Scholar] [CrossRef]
- Abdurakhmanov, I.B.; Kadyrov, A.S.; Fursa, D.V.; Avazbaev, S.K.; Bailey, J.J.; Bray, I. Antiproton-impact ionization of Ne, Ar, Kr, Xe, and H2O. Phys. Rev. A 2015, 91, 022712. [Google Scholar] [CrossRef]
- Naga, I.E.; Pater, P.; Seuntjens, J. Monte Carlo role in radiobiological modelling of radiotherapy outcomes. Phys. Med. Biol. 2012, 57, R75. [Google Scholar]
- McDowell, M.R.C.; Coleman, J.P. Introduction to the Theory of Ion-Atom Collisions; North-Holland Pub. Co.: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Makhoute, A.; Khalil, D.; Ajana, I. Laser-Assisted (e, 2e) collisions in the Symmetric/Asymmetric Coplanar Geometry. Atoms 2019, 7, 40. [Google Scholar] [CrossRef]
- Bray, I.; Stelbovics, A.T. Convergent close-coupling calculations of electron-hydrogen scattering. Phys. Rev. A 1992, 46, 6995–7011. [Google Scholar] [CrossRef] [PubMed]
- Kyriakou, I.; Šefl, M.; Nourry, V.; Incerti, S. The impact of new Geant4-DNA cross section models on electron track structure simulations in liquid water. J. Appl. Phys. 2016, 119, 194902. [Google Scholar] [CrossRef]
- Emfietzoglou, D.; Kyriakou, I.; Garcia-Molina, R.; Abril, I.; Nikjoo, H. Inelastic cross sections for low-energy electrons in liquid water: Exchange and correlation effects. Radiat. Res. 2013, 180, 499–513. [Google Scholar] [CrossRef]
- Heller, J.M.; Hamm, R.N.; Birkhoff, R.D.; Painter, L.R. Collective oscillation in liquid water. J. Chem. Phys. 1974, 60, 3483–3486. [Google Scholar] [CrossRef]
- Hayashi, H.; Watanabe, N.; Udagawa, Y.; Kao, C.C. The complete optical spectrum of liquid water measured by inelastic x-ray scattering. Proc. Natl. Acad. Sci. USA 2000, 97, 6264–6266. [Google Scholar] [CrossRef]
- Fernández-Varea, J.M.; Mayol, R.; Liljequist, D.; Salvat, F. Inelastic scattering of electrons in solids from a generalized oscillator strength model using optical and photoelectric data. J. Phys. Condens. Matter 1993, 5, 3593–3610. [Google Scholar] [CrossRef]
- Vasi, F.; Schneider, U. First Measurements of Ionization Cluster-Size Distributions with a Compact Nanodosimeter. Med. Phys. 2021. Accepted Author Manuscript. [Google Scholar] [CrossRef] [PubMed]
- Casiraghi, M.; Bashkirov, V.A.; Hurley, R.F.; Schulte, R.W. Characterisation of a track structure imaging detector. Rad. Prot. Dos. 2015, 166, 223–227. [Google Scholar] [CrossRef] [PubMed]
- Casiraghi, M.; Bashkirov, V.; Hurley, F.; Schulte, R. A novel approach to study radiation track structure with nanometer-equivalent resolution. Eur. Phys. J. D 2014, 68, 111. [Google Scholar] [CrossRef]
- Vasi, F.; Casiraghi, M.; Bashkirov, V.; Giesen, U.; Schulte, R. Development of a single ion detector for radiation track structure studies. J. Instrum. 2016, 11, 329. [Google Scholar] [CrossRef]
- Nardo, L.; Alkaa, A.; Khamphan, C.; Conte, V.; Colautti, P.; Sgur, P.; Tornielli, G. A detector for track-nanodosimetry. Nucl. Instrum. Methods Phys. Res. A 2002, 484, 312–326. [Google Scholar] [CrossRef]
- Shchemelinin, S.; Garty, G.; Breskin, A.; Chechik, R.; Schulte, R. Ion-counting nanodosimetry: A new method for assessing radiation damage to DNA. Nucl. Instrum. Methods Phys. Res. A 2002, 477, 527–530. [Google Scholar] [CrossRef]
- Garty, G.; Shchemelinin, S.; Breskin, A.; Chechik, R.; Assaf, G.; Orion, I.; Bashkirov, V.; Schulte, R.; Grosswendt, B. The performance of a novel ion-counting nanodosimeter. Nucl. Instrum. Methods Phys. Res. A 2002, 492, 212–235. [Google Scholar] [CrossRef]
- Pszona, S.; Kula, J.; Marjanska, S. New method for measuring ion clusters produced by charged particles in nanometre track sections of DNA size. Nucl. Instrum. Methods Phys. Res. A 2000, 447, 601–607. [Google Scholar] [CrossRef]
- Agostinelli, S.; The Geant4 Collaboration. GEANT4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Loffredo, F.; Vardaci, E.; Quarto, M.; Roca, V.; Pugliese, M. Validation of electromagnetic and hadronic physical processes in the interaction of a proton beam with matter: A Solar Particle Events case study with an Al slab. Adv. Space Res. 2017, 59, 393. [Google Scholar] [CrossRef]
- Loffredo, F.; Vardaci, E.; Roca, V.; Pugliese, M. Space missions: Comparison of shielding effectiveness among different materials using 1 GeV protons. Mater. Res. Express 2019, 6, 01654. [Google Scholar] [CrossRef]
- Incerti, S.; Baldacchino, G.; Bernal, M.; Capra, R.; Champion, C.; Francis, Z.; Guèye, P.; Mantero, A.; Mascialino, B.; Moretto, P.; et al. The geant4-dna project. Int. J. Mod. Sim. Sci. Comp. 2010, 1, 157–178. [Google Scholar] [CrossRef]
- Bianco, D.; Villagrasa, C.; Santos, M.D. Multi-scale analysis of simulated proton and alpha irradiation. Rad. Prot. Dos. 2015, 164, 444–448. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Friedland, W.; Jacob, P.; Bernhardt, P.; Paretzke, H.G.; Dingfelder, M. Simulation of DNA damage after proton irradiation. Radiat. Res. 2013, 159, 401410. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).