Abstract
Metals, semiconductors, metamaterials, and various two-dimensional materials with plasmonic dispersion exhibit numerous exotic physical effects in the presence of an external bias, for example an external static magnetic field or electric current. These physical phenomena range from Faraday rotation of light propagating in the bulk to strong confinement and directionality of guided modes on the surface and are a consequence of the breaking of Lorentz reciprocity in these systems. The recent introduction of relevant concepts of topological physics, translated from condensed-matter systems to photonics, has not only given a new perspective on some of these topics by relating certain bulk properties of plasmonic media to the surface phenomena, but has also led to the discovery of new regimes of truly unidirectional, backscattering-immune, surface-wave propagation. In this article, we briefly review the concepts of nonreciprocity and topology and describe their manifestation in plasmonic materials. Furthermore, we use these concepts to classify and discuss the different classes of guided surface modes existing on the interfaces of various plasmonic systems.
1. Introduction
Various metals, gas plasmas, highly doped semiconductors, and metamaterials that can be modelled as weakly interacting gases of charged particles do not support light propagation within their bulk at frequencies lower than their plasma frequency, a direct consequence of their negative permittivity in this regime. However, at the interface between such a plasmonic material and a dielectric, collective charge oscillations coupled to electromagnetic fields result in surface-plasmon-polariton modes that are strongly confined to the two-dimensional (2D) interface and evanescently decay in the bulk. Analogous to the everyday experience of seeing surface gravity waves propagating in all directions on the surface of a water body that is perturbed by a dropped pebble, these surface plasmon-polaritons do not have any preferential direction when propagating on a homogenous isotropic 2D interface. Conversely, if the plasmonic material is magnetized, the resulting Lorentz force affects the motion of the charged particles and breaks this isotropy and symmetry, modifying the dispersion of bulk and surface modes. Notably, a magnetic bias opens a frequency window where backward-propagating surface waves are prohibited [1,2,3,4,5,6]. These unidirectional surface plasmon-polariton modes on magnetized plasma-dielectric interfaces, known as surface magneto-plasmons, were first discovered several decades ago, and are just one example of the host of unidirectional surface modes existing on complex (anisotropic, chiral, nonreciprocal) plasmonic materials. Such plasmonic platforms combine the advantages of subwavelength light confinement and enhancement offered by plasmonics with the backscattering-immune transport characteristics of unidirectional waves, and they are being increasingly investigated for novel or enhanced functionalities, such as compact Faraday rotation, isolation, and circulation [7,8,9,10] and extreme light-matter interactions, field enhancement, and giant nonlinear effects [11,12,13,14], to name a few. In this article, we review the rich physics of unidirectional surface modes on complex plasmonic materials, relating them to the properties of the bulk modes, and distinguishing between various classes of surface waves based on the concepts of reciprocity and topology.
Before studying these different types of surface waves in detail, let us briefly introduce some general concepts related to the principle of reciprocity and how ideas of topological wave-physics enter the problem. Reciprocity in electromagnetics is the general principle that the ratio of the field detected by a detector to the field emitted by a source are the same if the source and detector are interchanged [15,16,17]. For reciprocal media, such as a simple non-biased plasmonic material, the dispersion of any eigenmode (including surface modes) does not depend on the sign of the wavevector , , as shown in Figure 1a,b. This strict symmetry condition rules out the possibility of realizing truly unidirectional surface waves on reciprocal media, irrespective of any consideration related to the topological nature of the material (more on this below). We stress that, although lossy plasmonic materials break time-reversal symmetry at the macroscopic level, they cannot overcome this limitation, since breaking time-reversal symmetry is not equivalent to breaking reciprocity (the two concepts are equivalent only for lossless media), as further elucidated in [15]. Therefore, the only way to realize an asymmetric surface-plasmon-polariton dispersion is to break reciprocity, as shown in Figure 1c,d, which is achieved by biasing the system with an external physical quantity that is odd upon time reversal, for example an external magnetic field or a drift current [15].
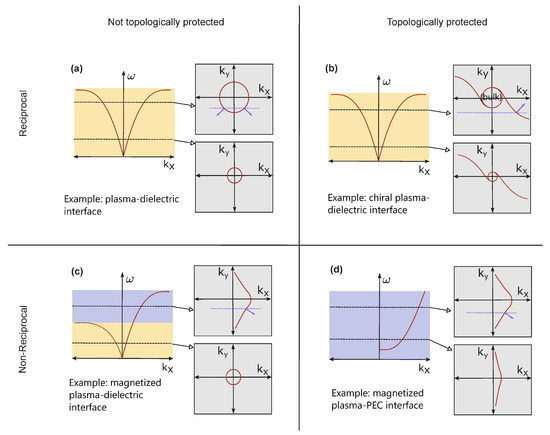
Figure 1.
Reciprocal/nonreciprocal and topological/nontopological surface plasmon-polariton modes. (a,b) Model dispersion diagrams of reciprocal surface plasmon-polaritons that can be classified as topologically trivial and non-trivial, respectively. The equifrequency contours of the dispersion surfaces for these modes at two different frequency values are plotted on the right insets. It can be seen that the dispersion curves are symmetric in momentum space for both cases, , but contrary to (a), the topologically protected mode in (b) does not backscatter (within a certain angular range) for defects that preserve the component of momentum, as indicated by the dashed blue line. Blue arrows denote the group velocity vector for a certain value of momentum. (c,d) Examples of non-reciprocal surface plasmon-polariton modes. The equifrequency contours are strongly asymmetric in both cases, but the backward-propagating mode is completely absent (within a bulk-mode bandgap) only in the topologically protected case in (d).
Non-reciprocity alone is, however, not sufficient to generate truly one-way surface modes. For instance, surface magneto-plasmons on a magnetized plasma-dielectric interface exhibit an asymmetric dispersion, as seen in Figure 1c, but become unidirectional only in a small range of frequencies. Furthermore, the inherent nonlocal effects in the plasma material tend to close this one-way frequency window, as we shall discuss in the next sections. Other types of surface plasmon-polaritons, however, exhibit stronger forms of unidirectionality, as in the case of surface modes at the interface between a magnetized plasma and an opaque medium [18,19,20], or the edge modes of magnetically biased graphene [21]. In these cases, strict unidirectionality is usually related to the opening of a bulk-mode bandgap and to some underlying topological invariant number associated with the bulk modes, i.e., an integer quantity that is preserved under continuous deformations that do not close this bandgap. The most common topological invariant in nonreciprocal systems is the so-called Chern number, which can often be intuitively interpreted as a winding number for the modal evolution in momentum space (after a full circuit in momentum space, an eigenmode does not have to go back exactly to its original form; instead it may acquire an additional phase, the Berry phase, equal to , where C is the Chern number for that mode). This evolution-winding is robust against perturbations that do not close the bandgap. As a result, if two media with a common bandgap but different topological properties are interfaced, the bandgap has to close at the interface to allow for a change in the topological invariants, which results in the emergence of unidirectional, topologically protected, surface modes at the interface whose dispersion span the entire bandgap. Interestingly, the so-called bulk-edge correspondence principle predicts that the net number of unidirectional surface modes on an interface between two materials is equal to the difference between their respective gap Chern numbers (the sum of the Chern numbers of all the modes below the bandgap) [20]. As discussed in the following, the interface between a magnetized plasma and a trivial opaque material is an example of such a topological system, with a difference in gap Chern number equal to unity [18,19,20], which results in a single unidirectional surface mode spanning the bandgap (Figure 1d), with no backward-propagating mode in this frequency interval (these properties make this system the analogue of “quantum Hall insulators” in condensed-matter physics). Consequently, the strong, topologically protected, unidirectional nature of these surface modes ensures defect-immune light propagation with no backscattering.
At this point, we would like to underscore the fact that nonreciprocal and topological media are overlapping but distinct classes of (meta)materials. Indeed, although reciprocal plasmonic materials cannot support strictly unidirectional surface modes due to the symmetry of their dispersion relation, , their surface plasmon-polariton modes may or may not exhibit some form of topological protection against certain defects. Two contrasting examples are the surface plasmon-polaritons on conventional isotropic plasmonic media, which are not protected against defects, and the surface modes on three-dimensional chiral plasmonic metamaterials, which are instead topologically protected against certain kinds of defects despite the reciprocal nature of the system. Moreover, it was first recognized by Bliokh et al. [22,23] and Van Mechelen and Jacob [24] that the free-space solutions of Maxwell’s equations exhibit an intrinsic “quantum spin Hall effect”, which manifests in the form of surface modes, for example conventional surface plasmon-polaritons, possessing a transverse spin angular momentum that is locked to their linear momentum. However, despite this unidirectional form of spin transport, such surface plasmon-polariton modes, due to their bosonic nature, are not unidirectional (as shown in Figure 1a) and not topologically immune to backscattering. On the other hand, the interface between some three-dimensional chiral plasmonic materials and vacuum supports surface waves with hyperbolic-like equifrequency contours that are ultimately associated with other topological properties of the bulk modes, i.e., the existence of “Weyl point degeneracies”. For the particular example in Figure 1b, this results in a surface mode that is backscattering-immune, for a limited range of propagation angles, in the presence of defects with certain symmetries. We therefore denote this surface mode as “topologically protected” although it must be noted that this is a relatively weak form of protection, especially compared with the case of strictly unidirectional surface modes in nonreciprocal topological platforms.
These preliminary considerations highlight the great richness of nonreciprocal and/or topological plasmonic materials and the electromagnetic modes they support. We hope this article will provide the reader with a general overview of these exciting topics within this broad area of research. This review is organized as follows: we analyze plasmonic materials with reciprocity broken by external static magnetic fields in Section 2 and by direct electric currents in Section 3. We discuss the bulk modes and surface modes supported by these materials and classify the surface modes on the basis of their topological protection against defects. Finally, in Section 4 we briefly discuss the surface modes on certain chiral plasmonic platforms that are reciprocal but nevertheless topologically nontrivial.
2. Non-Reciprocal Modes of Magnetized Plasmonic Media
2.1. Bulk Properties–Constraints on Permittivity Tensor, Dispersion Diagram, Topological Properties
A magnetized plasma or plasmonic material is one of the simplest examples of a nonreciprocal, gyrotropic, homogenous medium. For a static magnetic bias along the z direction, its relative permittivity tensor (under a time-harmonic convention) can generally be written as [25],
The permittivity tensor of a magnetized plasma is necessarily asymmetric, according to the Onsager-Casimir Principle [26], and it can be written as the sum of a diagonal matrix and an antisymmetric matrix that depends on the gyrotropy parameter . The asymmetry of this permittivity tensor directly implies that the material breaks Lorentz reciprocity, which opens the possibility to realize a number of useful functionalities that cannot be achieved with reciprocal media, for example true isolation. The intensity of relevant nonreciprocal effects, however, depend on the relative strength of the diagonal and off-diagonal tensor elements, which are constrained by some general physical considerations. In this section, we briefly review some of these considerations, as they are relevant to the nonreciprocal properties of electromagnetic waves in the bulk of the material, which are in turn responsible for nonreciprocal and topological effects related to surface modes.
The diagonal and off-diagonal elements in Equation (1) are not entirely arbitrary and independent, but rather fundamentally related by certain physical constraints. Notably, the passivity condition (electromagnetic energy may be dissipated, not generated, by the material) implies that the matrix is negative semi-definite (its eigenvalues are negative or zero) [27,28], which then implies that the imaginary part of the tensor diagonal elements are nonpositive. More significantly, it can be directly proven from the passivity condition that the absolute value of the imaginary part of the off-diagonal element is bounded by the imaginary part of the diagonal element (primed and double-primed symbols refer to the real part and imaginary part, respectively). This leads to the interesting observation that if the diagonal elements are purely real, the off-diagonal elements cannot cause absorption, hence the material is lossless.
Another relevant physical condition is that the time-averaged electromagnetic energy stored in a medium must be positive and not smaller than the energy stored by the same electromagnetic fields in vacuum (as discussed in [29], this can be rigorously proven by requiring that the medium is causal, i.e., it reacts to a field only after the field is applied, and passive). In the low-loss case (), this means that the matrix is positive semi-definite (its eigenvalues are positive or zero) [28]. This energy condition is then useful to relate the real parts of the tensor elements,
A corollary of (2) is that if we consider the case of vacuum, , or any material with relative permittivity close to unity and negligible dispersion, gyrotropic effects must vanish ( must be zero).
The permittivity tensor elements can be optimized to realize plasmonic systems of maximal nonreciprocity/gyrotropy. How to define “maximal gyrotropy” depends on the physical quantity that describes a given nonreciprocity effect. For instance, for nonreciprocal thermal emitters, it is required to maximize the gyrotropy ratio in order to increase the efficiency of photonic heat engines [30]. If dispersion is required to be negligible, Equation (2) suggests that the off-diagonal element is necessarily bounded by . On the contrary, highly dispersive regions near resonance allow to take virtually any value, without violating the energy constraint in Equation (2). As an example, we can see how the ratio can be maximized in the case of a standard Drude model for a magnetized plasmonic material, for which the permittivity tensor elements are given by,
where is the plasma frequency that characterizes the plasma medium, is the cyclotron frequency, which depends on the strength of the magnetic field bias, and is the loss coefficient; in the following we assume (low-loss condition). At the cyclotron frequency , both parameters are peaked and , so the ratio is not maximized. Interestingly, instead, it can be easily verified that, at the “modified plasma frequency” (due to the magnetic bias) , the parameter is near zero. Therefore, at , maximal gyrotropy ratio can be realized, such that,
As shown in Figure 2b, this optimal gyrotropy ratio for is then maximized if, and takes the value . This hints at the possibility of realizing strongly nonreciprocal devices (for, e.g., strongly asymmetrical emission/absorption) by suitably designing the parameters of the material and the operating frequency.
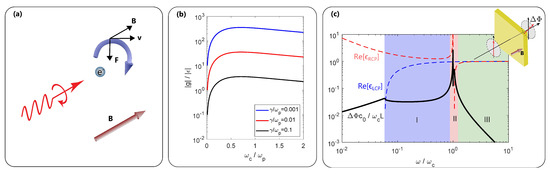
Figure 2.
Nonreciprocity in magnetized plasmonic materials. (a) Due to the Lorentz force, a magnetic bias B moves the free electrons of a plasma in circular motion (cyclotron motion). Circularly polarized (CP) electromagnetic waves of opposite handedness interact differently with these rotating electrons; hence, at the macroscopic level, a different effective permittivity is “seen” by left-handed CP and right-handed CP waves. (b) Gyrotropy ratio as a function of the cyclotron frequency for different values of the loss coefficient. This ratio, which indicates the strength of certain nonreciprocal effects, can be maximized with a proper choice of parameters, ad discussed in the text. (c) Dispersion behavior of the Faraday rotation angle (solid black) for a plasmonic material with . The dashed lines represent the permittivity of the eigenmodes in the bias direction. The RCP mode exhibits a resonance at . At resonance (red region), Faraday rotation is peaked, however, losses and dispersion are significant. The high-frequency region (green) is the most common regime of operation for magneto-plasmonic components, while the region below resonance (blue) is promising for broadband dispersionless nonreciprocity.
Another important manifestation of bulk nonreciprocity in magnetized plasmonic materials is the phenomenon of Faraday rotation. This is a nonreciprocal rotation of the plane of polarization of a linearly polarized wave propagating in the direction of the bias, which originates from the different permittivities and phase velocities experienced by the left- and right-handed circularly polarized (LCP, RCP) eigenmodes of a gyrotropic medium. Importantly, if the bias is kept fixed, the rotation accumulated by a time-reversed wave during a backward-propagating trip does not ‘unwind’ the rotation acquired during the forward-propagation trip, which implies that the total rotation during a roundtrip is not zero. This property has been widely used to realize many nonreciprocal devices such as isolators, gyrators, and circulators. The Faraday rotation angle can be expressed as [25], where and are the permittivity eigenvalues for LCP and RCP modes, respectively, L is the propagation length in the magnetized plasmonic medium and is the speed of light in vacuum. Maximizing the Faraday rotation angle for a certain length is another relevant challenge for the realization of superior nonreciprocal devices. Interestingly, Faraday rotation exhibits a rich dispersion behavior that can be classified into three main parameter regions of interest, as shown in Figure 2c. The region most commonly studied in the literature is the far-from-resonance high-frequency regime, (region III, green) [31]. The main drawback of operating in this region, however, is that Faraday rotation is highly dispersive at high frequencies, , which prevents the realization of broadband nonreciprocal functionalities. Another potential region of interest is near the cyclotron resonance (region II, red) where Faraday rotation is maximized; however, near resonance, dispersion is even stronger and losses are also maximized. A third region of interest is below resonance (region I, blue) and exists only if , which guarantees that both LCP/RCP modes are propagative (positive permittivity values) at these frequencies. This condition has been demonstrated, for example, in n-doped Indium Antimonide (InSb) at THz frequencies [32,33]. It has been recently shown in Ref. [13] that operating in this region allows realizing strong nonreciprocal effects at the subwavelength scale that are also remarkably broadband since Faraday rotation turns out to be almost frequency-independent in this regime, as seen in Figure 2c. Using a moderate magnetic bias, compact (sub-wavelength) nonreciprocal components can then be realized in this parameter region with low losses at room temperature [13].
Bulk dispersion characteristics of magnetized plasma:
Since the bulk-edge correspondence principle of topological physics [20] relates the existence and number of topologically protected surface states to the topological invariant properties of the bulk bands, in the remainder of this section, we describe the bulk dispersion curves and topological invariant (Chern number) of nonreciprocal plasmas. The dispersion curves for a homogenous magnetized plasmonic material can be calculated by substituting the gyrotropic permittivity from Equation (1) into the source-free Maxwell’s equations and solving for the allowed plane-wave eigensolutions and their dispersion relation, which relates the eigenfrequency to the modal wavevector in an implicit form. Equivalently, the electric and magnetic fields and microscopic current density (instead of the macroscopic permittivity) can be expressed as suitable eigenstates forming an eigenvalue problem with the eigenfrequency as the explicit solution, as described in Refs. [34,35]. The eigenfrequency for each plane wave, and therefore the dispersion diagram, can then be calculated by diagonalizing the corresponding Hamiltonian for each value of wavevector. Calculating the Berry curvature and topological invariants is easier using this Hamiltonian approach since the formulas from condensed-matter physics [36] can be applied with minimal modifications.
Using the lossless Drude model and setting the cyclotron frequency to as an example, we have plotted in Figure 3a the complete dispersion diagram for plane-wave propagation along () and perpendicular () to the magnetic bias. Since the system is rotationally symmetric around the direction of the applied magnetic field these two propagation directions are sufficient to describe fully its dispersion characteristics. The band structure has four bands for positive frequencies, and identical four bands for negative frequencies and one trivial band at zero frequency (not depicted in Figure 3a). While the presence of the negative-frequency bands may not be important for practical applications, they need to be considered for the Chern number calculations [21,37].
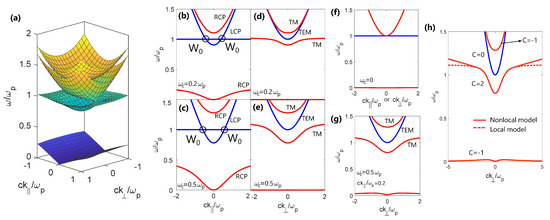
Figure 3.
Bulk dispersion characteristics of a magnetized plasmonic material. (a) Dispersion surfaces calculated using a standard Drude model for a plasma with a magnetic bias with strength (warmer colors correspond to higher frequency). (b–g) Cross sections of the dispersion diagram in (a) for varying magnetic field strengths and directions. Weyl points are indicated as W0. (h) Dispersion curves for propagation perpendicular to the magnetic field, calculated using a hydrodynamic model and compared to the local Drude model. The topological Chern numbers are indicated next to each band. We have assumed a small non-zero momentum along the bias to ensure that the lowest band is clearly visible. In all the dispersion diagrams for propagation perpendicular to the bias, TM modes are indicated in red and TEM modes are indicated in blue.
The impact of the strength of the applied magnetic field on these bulk bands is depicted in Figure 3b–g. When there is no magnetic bias there are only two bands, one flat band corresponding to the longitudinal motion of the free ions at the plasma frequency and one parabolic band for transverse plane waves (Figure 3f). In the presence of a magnetic field, for propagation along the bias (Faraday configuration), plotted in Figure 3b,c, the bulk longitudinal mode is unaffected by the Lorentz force but the degeneracy of the transverse modes is lifted. As described in the previous section, this is because the circularly polarized eigenmodes propagate with different phase velocities along the bias. Moreover, the appearance of a mode well below the plasma frequency can be seen as the cyclotron frequency is increased in Figure 3c. This mode creates a window for low-frequency wave propagation in magnetized plasmas, of particular importance in ionospheric science, and is known as a “whistler mode” [25] since its frequency is within the audible acoustic range. Finally, the intersection of the longitudinal and the LCP mode, indicated as W0 in Figure 3b,c, are linear degeneracies in 3D momentum space called “Weyl points” that are sources and sinks of Berry curvature and are associated to an integer quantized topological charge (additional details in the next section) [34,35].
For propagation perpendicular to the magnetic bias (Voigt configuration; Figure 3d,e), the eigenmodes are either transverse electromagnetic waves (denoted as TEM in Figure 3), or transverse-magnetic (TM) waves with both transverse and longitudinal components of the electric field. Since the electric field of the TEM mode drives charged particles in the plasma along the direction of the applied magnetic field, this mode and its dispersion curve are unaffected by the applied magnetic field as seen in Figure 3d–f. This is in contrast with the two TM bands, which have a dispersion relation given by , and are separated by a band gap that is directly proportional to the strength of the applied magnetic field [25].
Finally, all variables in Figure 3 and the rest of this review have been normalized using the plasma frequency of the material to underscore that the results are universal and can be applied to any material that follows a Drude dispersion in a certain spectral region. Typical materials of this type include noble metals for visible wavelengths [38], highly doped oxide semiconductors, such as transparent conducting oxides, for infrared [39,40,41], other semiconductors such as n-type InSb for terahertz applications [42], and gas plasmas or plasmonic metamaterials [43] (e.g., wire media [44]) at microwaves and lower frequencies.
Chern number calculations:
To classify the modes of magnetized plasmonic media based on their topological properties, the relevant topological invariant, that is, the Chern number, of each of the bands described above can be calculated by integrating the Berry curvature over the entire k space. Although the Brillouin zone for this homogenous system is not compact unlike in a periodic system, the calculation of the Chern number is valid as the momentum space can be mapped to a compact Riemann sphere with the south pole corresponding to and the north pole at , as discussed in [45]. The main caveat in this calculation is that the Hamiltonian has to be sufficiently “well behaved” for large wavevectors. Interestingly, it has been shown that the standard Drude model is not well behaved in this asymptotic region and the resultant Chern number of the TM band below the TM bandgap in Figure 3h is not an integer [18,19,37,45]. Indeed, it can also be seen that this dispersion band is not entirely physical since it becomes flat and approaches a constant frequency for arbitrarily large wavevectors, which implies an infinite density of states [46]. This problem can be solved by introducing a high-wavevector cutoff in the permittivity model, which regularizes the behavior by correctly making the material response vanish for diverging wavevectors (in a realistic material, a field with very fast spatial, or temporal, variation cannot polarize the microscopic constituents of the medium). In the literature, this regularization has been implemented in three equivalent ways: (i) forcing the material response of the biased plasmonic material to approach a “well behaved” local response, such as that of vacuum, for wavevectors larger than the cut-off value [45]; (ii) adding an odd viscosity term to constraint the material response at large wavelengths [47]; and (iii) using a more accurate model for a realistic plasma such as the hydrodynamic model [46,48]. Each of these methods results in a spatially dispersive material response (i.e., function of wavevector) that is well behaved as , and they lead to the same bulk-band Chern numbers that are shown in Figure 3h. Note that only the TM bands in the plane orthogonal to the bias are topologically nontrivial (non-zero Chern number) and, as we will discuss in the next section, they are associated with the emergence of topologically protected surface modes in certain configurations.
2.2. Surface States—Transparent, Opaque and Other Interfaces
The types of surface modes that exist on magnetically biased plasmonic materials can be loosely categorized into three types, based on the material with which they share a boundary: (i) transparent dielectric interfaces (including vacuum), (ii) opaque interfaces, and (iii) boundaries between magnetized plasmas with different relative bias. An opaque interface here can refer to the boundary between the plasma and a material with a trivial bulk-mode bandgap such as a perfect electric conductor (PEC), perfect magnetic conductor (PMC), a suitable photonic crystal, or a Drude metal with a relatively large plasma frequency. In the following we will review the surface states on each of these interfaces and discuss their unidirectionality and topological protection.
Magnetized plasma—Transparent medium:
The surface plasmon-polariton modes (SPP) on a plasma-dielectric interface are the most well studied class of surface waves in plasmonics. Here the dielectric medium can refer to vacuum or any material that does not have a photonic bandgap around the frequency of interest. We first review the SPPs that exist, on an interface, in the direction orthogonal to the applied magnetic field, as illustrated in Figure 4a, and we then discuss the more general case of SPPs propagating in an arbitrary direction on the two-dimensional interface.
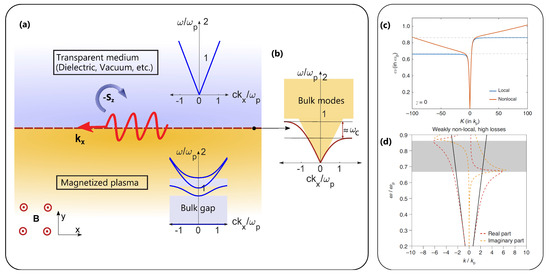
Figure 4.
Unidirectional surface plasmon-polariton modes on an interface between a semi-infinite magnetized plasmonic medium and a transparent medium, in the plane orthogonal to the bias. (a) Geometry of the interface in the plane orthogonal to the applied magnetic field (geometry, bias, and SPP fields are invariant in the out-of-plane (z) direction). Inset: Typical bulk-mode dispersions. The blue arrow marks the direction of rotation of the electric field vector in the xy plane, associated with a transverse spin for the propagating SPP. (b) Typical SPP dispersion calculated using a standard local Drude model. (c) SPP dispersion calculated using a non-local hydrodynamic model for the plasma. (d) SPP dispersion in a weakly non-local plasma with high losses. (c,d) reproduced with permission from [46,57], respectively.
In the presence of a static magnetic bias, the two counterpropagating SPP modes propagating in a direction orthogonal to the applied magnetic field have asymmetric dispersion curves as illustrated in Figure 4b. If the plasmonic material is described by a local Drude model, the two counterpropagating SPP dispersion bands asymptotically approach two different constant frequency values. This leads to a frequency window, of width proportional to the strength of the applied magnetic field, where SPPs can only propagate in one direction. We also note that these SPP modes, being TM waves with respect to the propagation direction, have an electric field oscillating in cycloidal motion (elliptically polarized) in the plane of propagation, leading to a transverse spin angular momentum locked to its linear momentum. In other words, the spin direction is uniquely determined by the propagation direction, in drastic contrast with the longitudinal spin of conventional elliptically polarized plane waves. We stress, however, that spin-momentum locking is not a consequence of the broken reciprocity in magnetized plasmas, but is a common property of the evanescent fields of guided surface waves found on a variety of material interfaces, as mentioned in the Introduction [22,23,24] (an exception is the case of nontraveling surface modes with zero in-plane wavevector, such as Tamm plasmon polaritons found on the interface between a plasmonic medium and a photonic crystal, at a frequency within the photonic-crystal bandgap [49,50,51]).
The existence of the unidirectional frequency window in Figure 4b crucially depends on the group velocity of the counterpropagating mode asymptotically tending to zero for large wavevectors. This behavior is however unphysical [46,52], as mentioned in the previous section for bulk modes, and it can be regularized by modifying the simplistic Drude model that was used to derive the permittivity in Equation (3) to include the convective and diffusive transport effects of an electron gas [46,52,53,54,55,56]. For example, using the popular hydrodynamic model of a free-electron gas and neglecting diffusion effects, the induced free-electron current J is governed by the following equation, in the presence of an external magnetic bias in the z direction,
Here, is the non-local parameter, associated with a pressure term responsible for convective currents, which ultimately results in the upward bending of the SPP dispersion, as shown in Figure 4c, preventing the SPP modes from asymptotically approaching a constant value. In theory, this closes the unidirectional frequency window and rules out the existence of strictly unidirectional SPPs on biased plasma-dielectric interfaces, as there is always a counterpropagating SPP mode with a relatively larger wavevector. However, in practice, material losses affect modes with larger wavevectors more strongly, which may lead to a situation in which the SPP mode propagating in one direction is underdamped, whereas the nonlocality-induced counterpropagating mode is overdamped, as shown in Figure 4d. This may result in SPP propagation that can be considered, for all practical purposes, unidirectional in a small frequency range [52,57]. We stress, however, that the central conclusion of recent works in this area is that the unidirectional properties of these surface modes depend on the relative strength of dissipative and nonlocal effects in a given plasmonic material, and more realistic material models are necessary to make accurate predictions [57].
Note that the origin of these quasi-unidirectional SPP modes on a magnetized plasma-dielectric interface cannot be linked to topological considerations [57]. Indeed, in this configuration the surface modes do not emerge within a non-trivial bulk-mode bandgap opened by the breaking of reciprocity (unlike other forms of surface waves discussed in the following sections) and the transparent medium at the interface does not even have a bulk-mode bandgap in the same frequency region. In this case, SPPs exist also in the reciprocal case, and the magnetic bias has mainly the effect of making their dispersion asymmetrical; however, as we have discussed above, the presence of a counterpropagating mode in realistic non-local plasma models confirms that, despite the breaking of reciprocity, these surface modes are not strictly unidirectional and lack topological protection from back-scattering.
Next, we describe the SPP propagation and dispersion properties in arbitrary directions on the 2D interface between a dielectric and a plasmonic material magnetized in the plane of the interface, as illustrated in Figure 5a. The 2D surface mode dispersion shown in Figure 5b matches the 1D SPP dispersion for propagation orthogonal to the bias in Figure 4b. Moreover, it can be seen in Figure 5b that, for low frequencies, the equifrequency contours are closed loops, just slightly anisotropic, and the SPP modes are allowed to propagate omnidirectionally. As the frequency approaches the unidirectional window described previously, the equifrequency contours become more elliptical and the SPP modes propagate with stronger anisotropy. Finally, within the unidirectional window, we see from Figure 5b that the equifrequency contours become open and no backward-propagating mode exist in the −x direction, at least in the local case [58] (in the nonlocal case, the equifrequency contours close for very large values of wavevector). Furthermore, due to the hyperbolic-like shape of the equifrequency contours, a point source near the surface would launch SPPs propagating as narrow diffraction-less beams [59]. This is because the asymptotic part of the equifrequency contours tend to dominate the response, resulting in highly collimated energy flow (group velocity vectors are normal to the equifrequency contour), as shown in Figure 5c. For additional details on this interesting behavior, analogous to diffractionless wave propagation in hyperbolic metamaterials, but with the additional benefit of quasi-unidirectionality, we refer the interested readers to Ref. [59].
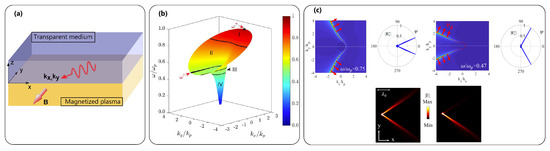
Figure 5.
Surface plasmon-polariton modes in arbitrary directions on the two-dimensional interface between a magnetized plasmonic material and a transparent medium. (a) Three-dimensional geometry under consideration with an applied magnetic field in the y-direction. (b) 2D dispersion diagram of the SPP mode calculated using a standard local Drude model for . The black lines are the equifrequency contours at select frequencies. (c) Top: Equifrequency contours in wavevector space and corresponding SPP propagation patterns (for z-directed point source excitation) in the plane of the interface. Arrows indicate the group velocity of the dominant components of the SPP mode. Two diffraction-less beams are present on the interface at frequencies within the unidirectional window in (b). Bottom: Simulated SPP propagation patterns excited by a z-directed linearly polarized (left) and circularly polarized (right) dipole. Since the two beams have nearly orthogonal transverse spins, a suitably oriented circularly polarized dipole source can be used to strongly excite only one of the beams. (b,c) reproduced with permission from [58,59], respectively.
Weyl points in the high magnetic field regime:
While the nonreciprocal effects reviewed above do not require a minimum bias intensity applied to the plasmonic material, qualitatively different effects arise for sufficiently large bias. Notably, it was recently shown that if the cyclotron frequency is larger than the plasma frequency of the material (which is feasible, for example, in solid-state plasmas with small effective electron mass, e.g., InSb at THz frequencies [60]), two new Weyl points appear in the 3D bulk-mode band structure at the plasma frequency [34,35] (see Figure 6b,c). This is in addition to the two Weyl points that were described in Section 2.1, which are present for any non-zero cyclotron frequency. The high-cyclotron-frequency Weyl points have recently been experimentally confirmed by mapping the photonic dispersion of magnetized InSb at a surprisingly low field strength of 0.19T due to the low effective mass of charge carriers in InSb [60].
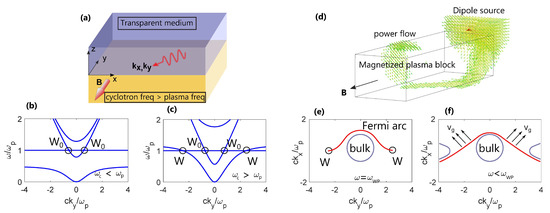
Figure 6.
Topological surface plasmon-polariton modes on a 2D interface between a transparent medium and a magnetized plasmonic medium with . (a) Three-dimensional geometry under consideration with an applied magnetic field in the y-direction. (b,c) Bulk band dispersion for a magnetized plasma along the magnetic bias. There are two Weyl points (W0) for at the intersection of the longitudinal-mode band and one of the transverse-mode bands (b), and four inversion-symmetry-related Weyl points (W0 and W) for (c). For details, see Refs. [34,35]. (d) Simulated surface wave propagation on a three-dimensional nonreciprocal plasmonic block with . The surface wave is unidirectional and topologically protected, resulting in zero backscattering from the edges of the block. (e,f) Equifrequency contours (Fermi arcs) of the surface modes at the frequency of the Weyl points (e) and at a lower frequency (f), for . The Fermi arcs are indicated in red color and the group velocity vectors are indicated with black arrows. The surface mode dispersion is not symmetric in momentum space as expected for a system with broken reciprocity. Furthermore, at low frequencies (f), the surface modes propagate with low diffraction, due to the hyperbolic-like equifrequency contour, as confirmed in the simulation in panel (d).
Since Weyl points are monopoles of Berry curvature, any cross-section between two oppositely charged Weyl points in momentum space has a non-zero total Berry curvature, potentially resulting in topologically protected unidirectional surface modes, as discussed in more details in Ref. [61]. This manifests as open equifrequency contours for the surface modes, called Fermi arcs, that terminate at the projection of the Weyl points on the plane of the interface. As a relevant example, the Fermi arc dispersion for propagation on the interface between a magnetized plasma with and vacuum is plotted for two different frequencies in Figure 6e,f. It can be seen that, while the equifrequency contour indeed terminates at the Weyl points at the plasma frequency, for lower frequencies the Fermi arc has an open hyperbolic-like shape similar to the equifrequency contours in Figure 5c, with straight asymptotes for large wavevectors resulting in highly directive surface modes [62] (note, however, that the SPPs in Figure 5c and Figure 6f exist in different parameter regimes, and , respectively, and have different properties). As seen in numerical simulations in Figure 6d, this topological surface mode is able to propagate around a 3D magnetized plasma block with no back-scattering and essentially no diffraction. Note that, despite the absence of a complete bulk-mode bandgap in this case, the source dipole strongly excites the non-reciprocal surface mode (and the free-space radiation modes), whereas the bulk modes of the plasmonic block are only weakly excited and rapidly dissipate due to their large wavevector. Alternatively, meta-couplers may also be used to couple to the topological surface mode in a more directional fashion [63]. We also stress that this topological mode does not occur if , since high-cyclotron-frequency Weyl points and the corresponding Fermi arcs are not present in that regime, and the SPP modes that do exist for (conventional surface magneto-plasmons) are not topologically protected, as seen in the previous section.
Magnetized plasma—Opaque medium:
Different types of surface modes emerge in a configuration in which the magnetized plasmonic material is interfaced with an opaque medium, instead of a transparent material (Figure 7a). The opaque medium here refers to any medium that, in a certain frequency range, does not admit any propagating wave solution, but only evanescent waves or zero fields, for example a PEC or PMC layer, a reciprocal metal/plasma with negative permittivity at the frequency of interest or a photonic crystal operating within a bandgap [64]. In general, since light cannot propagate in opaque materials, their dispersion characteristics can be described as equivalent to a trivial insulator (with a potentially infinite bulk-mode bandgap, as in the idealized PEC or PMC cases). The bulk-edge correspondence principle of topological physics then dictates that the net number of unidirectional surface modes existing within the common bulk-mode bandgap of two materials at the interface is equal to the difference between the gap Chern number of their respective bandgaps. The “gap Chern number” is defined as the sum of the Chern numbers of all the bulk bands below the bandgap. This principle only dictates the net number of unidirectional surface modes (with some relevant exceptions discussed below), whereas their actual dispersion characteristics depend on the specific properties of the opaque medium and the resulting boundary conditions.
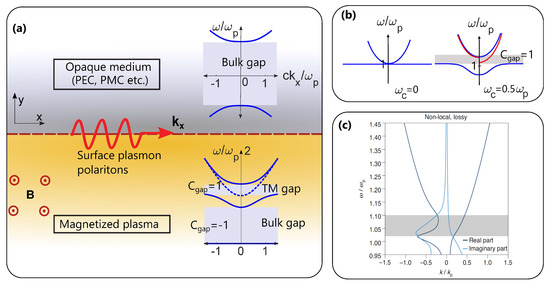
Figure 7.
Topologically protected surface plasmon-polariton modes on an interface between a semi-infinite magnetized plasmonic medium and an opaque medium, in the plane orthogonal to the bias. (a) Geometry of the interface in the plane orthogonal to the applied magnetic field (geometry, bias, and SPP fields are invariant in the out-of-plane (z) direction). Inset: Typical bulk-mode dispersion diagrams. The gap Chern numbers for the magnetized plasma are calculated by summing the Chern numbers of all the bands below the gap (see Figure 3). (b) Bulk-mode and surface-mode dispersion diagrams for a plasma-metal interface for a plasmonic material with zero magnetic bias (left) and non-zero bias (right). The bulk modes are indicated in blue and the single topological unidirectional surface mode that spans the bulk-mode bandgap is indicated in red. Note that the plasma bulk-mode dispersion is only gapped for TM-polarized waves (solid blue lines) as shown in the dispersion diagram in the bottom inset of panel (a). (c) Topological SPP dispersion diagram calculated using a non-local, lossy hydrodynamic model. Although nonlocality does not affect the topological mode, large losses result in an overdamped counterpropagating mode. (c) reproduced with permission from [57].
As an example, the dispersion curve of the surface mode existing on the interface between a magnetized plasma and a trivial opaque metal, for propagation orthogonal to the magnetic bias, is shown in Figure 7b. The difference between the gap Chern numbers, for the frequency range corresponding to the TM bandgap of the magnetized plasma, is −1. This follows from the fact that the sum of all the bulk band Chern numbers below this gap for a magnetized plasma is −1 (see Figure 3h), and zero for the trivial metal. The presence of one unidirectional surface mode within the gap, as seen in in Figure 7b, confirms the predictions of the bulk-edge correspondence principle. Although this unidirectional mode has been known for nearly five decades [3], its topological origin was discovered only recently [45,65,66]. Importantly, unlike the topologically trivial SPP modes described above (Figure 4 and Figure 5), these topological surface modes are robust to non-local effects and do not lose their strict unidirectionality even if strong nonlocalities are taken into account [52,57]. This can also be explained by recognizing that their unidirectional nature depends on their dispersion behavior for small wavevectors (asymmetry in lower-frequency cut-offs, as seen in Figure 7b), and not on their behavior for large wavevectors (asymmetry in flat dispersion asymptotes) which is much more affected by the presence of nonlocal effects that depend on k. Thanks to their topological robustness, even the presence of large sharp defects and discontinuities does not lead to the backscattering of these unidirectional surface modes. This property can be used to reroute waves around large objects with arbitrarily complex shape [67,68] or concentrate light at broadband “field hotspots” using terminated one-way structures [12]. We note, however, that large losses in the plasmonic material may result in the appearance of an overdamped counterpropagating mode, as seen in Figure 7c [57].
Similarly robust unidirectional surface modes have also been predicted to emerge on an interface between a magnetized plasma and a photonic crystal with a common bulk-mode bandgap [64]. Another interesting example of topological surface modes has been explored in magnetized gaseous plasmas at the smooth interface between plasma and vacuum [18]. For a fixed non-zero wavevector along the direction of the magnetic bias, , electromagnetic waves cannot propagate in vacuum in the orthogonal -direction for any frequency lower than , resulting in an effective bandgap similar to an opaque medium. In this case too, a single topological surface plasmon-polariton mode spanning the entire bandgap is realized, as long as the considered value of is preserved [18].
Finally, since a PMC is topologically equivalent to any other trivial opaque medium, it should support the same number of one-way surface states at an interface with a magnetized plasma (one topological surface mode, as in Figure 7b). However, at a PMC boundary the tangential magnetic field needs to vanish and, therefore, there can be no TM surface waves at the interface between a biased plasma and a PMC, directly contradicting the predictions of the bulk-edge correspondence. This apparent paradox was resolved recently in Ref. [48], where the authors showed that the expected surface mode does exist, but with a diverging wavevector, spanning the bandgap in the asymptotic part of the spatial spectrum for . This behavior is again regularized by the introduction of nonlocal effects; however, the surface mode remains very highly localized [48].
Magnetized plasmas with oppositely directed magnetic bias:
In magnetized plasmas, reversing the direction of the magnetic field reverses the sign of the bulk band Chern numbers given in Figure 3h. Therefore, the difference in gap Chern numbers for the common bandgap between two plasmonic materials with oppositely directed magnetic fields is double that at an interface with a trivial opaque medium. For propagation orthogonal to the magnetic field, for instance, the TM bandgap described in the previous sections now supports two unidirectional propagating surface modes instead of one [20]. Moreover, it has been shown that on a 2D interface between two 3D plasmonic materials, the shape of the Fermi arcs described in the previous section can be modified by changing the relative angle between the magnetic biases in the two materials [69].
Other considerations:
One crucial difference between periodic systems and continuum systems such as magnetized plasmas is that the wavevector (momentum) of the eigenmodes of a periodic system is bounded due to a finite Brillouin zone (hence, momentum space is compact), which has relevant implications for the calculation of topological invariants, as discussed in Section 2.1, and for the bulk-edge correspondence principle Although a proof of this principle for continuum systems has been provided in [20], edge/surface modes may be located in the asymptotic part of the spatial spectrum [48,70], as in the plasma-PMC case mentioned above, which also need to be properly accounted for when applying the principle. Some methods to accurately count surface modes have been proposed such as by assuming a thin vacuum layer between the two materials [19,52], which brings the “missing” surface mode back to finite values of wavenumber. Other methods are based on the scattering matrix describing the system, as discussed in [70]. From a practical standpoint, however, the correspondence principle can be physically violated for all practical purposes, in certain configurations, since highly confined surface modes with large wavevector are very rapidly attenuated even if all materials are assumed perfect, with zero intrinsic bulk losses, due to confinement-induced Landau damping at interfaces or radiation leakage [48]. Finally, we also note that other ways of realizing topological surface modes in continuous plasmonic platforms have been theoretically demonstrated in Refs. [71,72] by introducing a suitable nonlocal response in the gyrotropy parameter; interestingly, the dispersion of these edge states does not depend on the other material at the interface.
2.3. Edge States on Two-Dimensional Biased Plasmas
Apart from the previously reviewed 3D plasmonic materials, thin films such as graphene and high-mobility semiconductor heterojunctions that can be modelled as a 2D electron gas (2DEG) in certain spectral regions have also been known to support surface plasmon-polariton modes [73]. The collective charge oscillations in 2DEGs are confined to a 2D plane, which results in distinctly different dispersion characteristics, as compared to 3D surface plasmon-polaritons [74]. Interestingly, analogous to the unidirectional SPP modes on finite magnetized plasmonic materials, finite 2DEGs have been known for decades to support edge modes on their one-dimensional boundaries in the presence of an orthogonal magnetic field [75,76,77].
Recently, these properties have also been connected to topological wave physics. Specifically, it was shown that the presence of an orthogonal magnetic bias not only breaks reciprocity, but also opens a non-trivial bandgap in the bulk-mode dispersion around zero frequency, with a gap Chern number equal to [21,78], as shown in Figure 8. The unidirectional edge modes of the magnetized 2DEG are then tied to the topological properties of the bulk-mode bandgap through the bulk-edge correspondence, and are therefore topologically protected against defects that do not close this bandgap. Furthermore, the boundary between two 2DEGs that are magnetized along opposite directions has a gap Chern number difference equal to and supports two unidirectional edge modes (Figure 8). The presence of these two modes, as predicted by the bulk-edge correspondence principle, was recently experimentally validated in a GaAs—AlGaAs heterostructure [78].
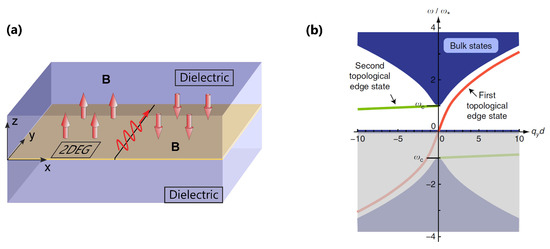
Figure 8.
Unidirectional edge modes at the interface between two 2DEGs with oppositely directed external magnetic bias. (a) Geometry of the structure. (b) Bulk-mode and edge-mode dispersion diagram. Two edge modes propagating in the same direction (same sign of group velocity) are present in the bulk-mode bandgap. Since the gap Chern number for a single magnetized 2DEG is , the gap Chern number difference for the common bandgaps in this system is , correctly predicting the net number of unidirectional edge modes according to the bulk-edge correspondence principle. (b) reproduced with permission from [21].
3. Current-Induced Unidirectional Surface Waves on Plasmonic Media
In the previous sections, we discussed the most common method to break Lorentz reciprocity, in order to achieve unidirectional propagation in different plasmonic configurations. This approach based on an external magnetic bias, however, suffers from practical limitations, such as the necessity of a typically large magnetic field bias and the bulkiness of the biasing circuits or external permanent magnets, which hinders the integrability of nonreciprocal plasmonic elements in miniature systems. Moreover, gyrotropic effects are relatively weak at very high frequencies, such as in the optical domain. Consequently, in recent years there has been a growing interest to realize magnetic-free nonreciprocal components that are compatible with integrated systems and can operate at high frequencies with good performance. For example, approaches to break reciprocity based on certain spatio-temporal modulations have become a very active area of research [79], especially for microwave and millimeter-wave systems, but they are challenging to scale and implement in nanophotonics.
Another interesting approach that has received recent attention in the literature is based on biasing a conducting material with a direct electric current , which, just like the magnetic field, is also a physical quantity with odd symmetry under time reversal, and therefore it can be used to break Lorentz reciprocity [80,81,82]. In particular, the forced drift movement of free electrons in the conducting material produces a Doppler shift such that the frequency in the dispersive material permittivity changes to , where is the electron drift velocity and is the wavenumber of an electromagnetic wave propagating in the current direction. As a result, the plasma permittivity becomes nonlocal (i.e., spatially dispersive), and the material responds differently for oppositely propagating waves, , which is a clear sign of nonreciprocity.
The current bias drastically affects the dispersion of surface plasmon-polariton modes, making it strongly asymmetric, as shown in Figure 9. However, the dispersion characteristics of SPPs on a plasmonic material with current-induced-nonreciprocity is fundamentally different from the case of SPPs on a magnetically biased plasma. For the case of a plasma-dielectric interface, as shown in Figure 4, the magnetic field bias introduces an asymmetry in the flat dispersion asymptotes, upward or downward, depending on the propagation direction, which opens a unidirectional window for SPP propagation (at least in the local case) with bandwidth that depends on the cyclotron frequency (i.e., the strength of the magnetic bias). On the contrary, the Doppler frequency shift introduced by the current bias tilts the SPP dispersion curve, depending on the drift velocity , as shown in Figure 9b. Interestingly, this implies that the unidirectional window for SPPs has, in theory, no upper bound, if absorption and the presence of other surface/bulk modes is neglected. An important advantage of this method is that the needed values of the electric current are realistic for high-mobility plasmonic platforms, for example graphene in the mid-infrared, while the frequency range of operation is not strictly limited by the bias as in the gyrotropic case.
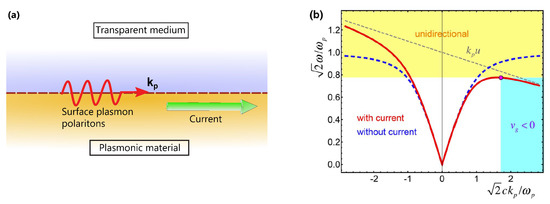
Figure 9.
Current-induced unidirectional surface plasmon-polariton modes at a plasma-vacuum interface. (a) Geometry of the system. (b) Surface modes dispersion diagram with and without current bias. Interestingly, the system supports a region of zero and negative group velocity, due to highly confined surface plasmon-polaritons being dragged backward by the electron flow. A fundamental difference between the SPP modes on a magnetized plasma (Figure 4) and on a current-biased plasma is that here the unidirectional region has no upper frequency limit in the ideal lossless case (losses will make the dispersion bands bend backward as in Figure 4d). (b) reproduced with permission from [81].
The case of graphene is particularly promising, thanks to its very high electron mobility, which allows achieving drift velocities several orders of magnitude larger than in typical metals [80]. Graphene is also a unique candidate for reconfigurable systems due to its excellent tunability properties. The results in Ref. [80] show that, although graphene SPPs have a different dispersion diagram compared to SPPs on three-dimensional plasmonic media as in Figure 9b (without flat asymptotes), biasing a graphene sheet with a direct electric current still produces a similar tilt of the dispersion diagram, opening a frequency range where graphene SPPs propagate unidirectionally. Additionally, this unidirectional propagation regime in graphene has been shown to be robust even if nonlocal effects are significant [80], and the current bias tend to increase the propagation length of the graphene SPPs. For these reasons, drift-biased high-mobility plasmonic materials have large potential to become an important platform for realizing nonreciprocal plasmonic devices at optical frequencies.
4. Topologically Protected Surface Waves on Reciprocal Plasmonic Media
Breaking reciprocity is not the only way to realize topologically non-trivial phases of matter in plasmonic materials, which again underscores the distinction between nonreciprocal and topological properties. As a relevant example, we note that the topologically non-trivial Weyl phase (characterized by the presence of Weyl points) can be realized in two ways, by breaking reciprocity (as in Figure 6) or by breaking parity symmetry in 3D materials [61]. In plasmonic media it has been shown that parity symmetry can be broken, and Weyl points emerge, if a suitable anisotropic chiral coupling between the electric and magnetic fields is introduced [35,83,84]. These properties have been realized in various reciprocal plasmonic metamaterials [83,84,85] using helical metal-elements to introduce chirality. The dispersion diagram of the resultant plasmonic metamaterial has Weyl degeneracies that are connected by Fermi arcs, corresponding to topological surface modes at an interface with a trivial insulator [85]. For more details on the topological properties of these Weyl points in chiral plasmonic materials and their differences and similarities with the Weyl points in a magnetized plasma, we refer the interested reader to Ref [35].
The equifrequency contour for the surface states realized at the interface between the chiral plasmonic metamaterial proposed in [85] and vacuum are reproduced in Figure 10b. Comparing the Fermi arcs in this figure to those in a typical nonreciprocal plasmonic material in Figure 10a, it can be seen that, in the former, the equifrequency contour is unaffected by the transformation as expected in reciprocal systems. Since this symmetry rules out strict unidirectionality, a natural question that follows is, in what sense are these modes topologically protected? For the specific system described in Figure 10b, we see that any defect on the interface that is invariant along the y-direction, and therefore preserves the component of the wavevector, cannot backscatter surface waves within a certain range of , corresponding to a certain angular range for surface waves incident on the defect. As mentioned in the Introduction, this is a weaker form of topological protection as compared to nonreciprocal topological plasmonic systems; however, it provides a degree of robustness that is not available to simple surface plasmon-polaritons on isotropic reciprocal plasmas (Figure 10c) despite their spin-momentum-locking property. Indeed, spin-polarized propagation is not enough to provide topological protection to backscattering since the bosonic nature of light does not forbid interaction between spins in the presence of generic defects. Outside the field of plasmonics, in other electromagnetic/photonic systems this problem has been circumvented by introducing pseudospin degrees of freedom and designing suitable photonic crystals and metamaterials with symmetries that guarantee pseudospin-momentum locking and prevent pseudospin mixing, resulting in defect-immune edge-state propagation, analogous to quantum spin Hall topological insulators in condensed-matter physics [86].
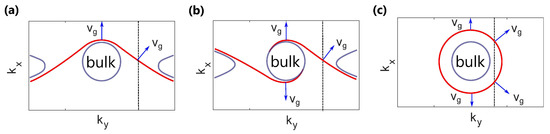
Figure 10.
Bulk- and surface- mode equifrequency contours for different classes of materials at an interface with vacuum: (a) typical magnetized plasma (reproduced from Figure 6f), (b) typical chiral reciprocal plasma, and (c) reciprocal, non-chiral, isotropic plasma. The surface states and bulk states are indicated in red and blue color respectively, and the group velocity vectors are indicated with blue arrows. Since the chiral plasma preserves reciprocity, the equifrequency contour obeys the symmetry condition . Thus, if a surface mode in case (b) is propagating in the x direction, it can reflect backwards in the presence of defects, but not in case (a), as indicated by the group velocity arrows in the two panels. However, the surface mode in (b) is robust against certain defects that preserve , leading to no backscattering within a range of values for . As an example, the dashed line in (b) shows that, if a certain value of is preserved, no backward-propagating mode can be excited with the same . This is in contrast with the surface plasmon-polaritons on a reciprocal isotropic plasma (c) which can backscatter in the presence of generic defects.
In addition, it has been recently shown that losses do not have the same impact on reciprocity-broken and parity-broken topological plasmonic systems. Parity-broken plasmonic materials such as the one described in Ref. [83] can undergo a topological transition to a trivial state induced by moderate levels of losses, whereas reciprocity-broken plasmonic materials such as magnetized plasmas will remain topologically non-trivial in the presence of similar (and much higher) losses [35]. Despite these shortcomings associated with their weaker form of topological protection, reciprocal plasmonic materials with non-trivial topological properties have the clear advantage of not requiring an external bias, and may find application in many scenarios that only require backscattering-immunity for certain defects.
5. Conclusions
In this article, we have reviewed the rich physics of nonreciprocal and topological plasmonic materials and the properties of the bulk and surface modes that they support. Due to subwavelength confinement, surface plasmon-polariton modes have the unique potential to strongly enhance light-matter interactions and bridge the gap between micro-scale optical waveguides and the nano-scale realm. At such length scales, defect-immune unidirectional wave-routing may have tremendous importance in applications that require high density of plasmonic waveguides, or rapid transitions to small mode volumes as in plasmonic-based optical modulators. As we have extensively discussed, different classes of surface plasmon-polariton modes, depending on the properties of the plasmonic material and its interfaces, exhibit varying degrees of unidirectionality and robustness in the presence of defects, losses, and nonlocal effects. For these reasons, we believe that nonreciprocal and topological plasmonics may offer a rich and diverse array of options for robust subwavelength waveguiding applications and to enhance light-matter interactions in new and extreme ways. We also stress, however, that accurate and realistic material models that properly account for dissipation and nonlocal effects [57] are crucial to make correct predictions regarding the unidirectional and topological properties of these platforms.
Author Contributions
Writing—original draft preparation, K.S. and M.I.A.; writing—review and editing, F.M.; visualization, K.S.; supervision, F.M.; project administration, F.M.; funding acquisition, F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation (1741694) and Air Force Office of Scientific Research (FA9550-19-1-0043).
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Trivelpiece, A.W.; Gould, R.W. Space Charge Waves in Cylindrical Plasma Columns. J. Appl. Phys. 1959, 30, 1784–1793. [Google Scholar] [CrossRef]
- Adachi, S.; Mushiake, Y. Surface waves along a perfectly conducting plane covered with semi-infinite magneto-plasma. J. Res. Natl. Bur. Stand. Sect. Radio Sci. 1965, 69, 171. [Google Scholar] [CrossRef]
- Seshadri, S.R.; Pickard, W.F. Surface Waves on an Anisotropic Plasma Sheath. IEEE Trans. Microw. Theory Tech. 1964, 12, 529–541. [Google Scholar] [CrossRef]
- Aers, G.C.; Boardman, A.D. The theory of semiconductor magnetoplasmon-polariton surface modes: Voigt geometry. J. Phys. C Solid State Phys. 1978, 11, 945–959. [Google Scholar] [CrossRef]
- Brion, J.J.; Wallis, R.F.; Hartstein, A.; Burstein, E. Theory of Surface Magnetoplasmons in Semiconductors. Phys. Rev. Lett. 1972, 28, 1455–1458. [Google Scholar] [CrossRef]
- Camley, R.E. Nonreciprocal surface waves. Surf. Sci. Rep. 1987, 7, 103–187. [Google Scholar] [CrossRef]
- Chin, J.Y.; Steinle, T.; Wehlus, T.; Dregely, D.; Weiss, T.; Belotelov, V.I.; Stritzker, B.; Giessen, H. Nonreciprocal plasmonics enables giant enhancement of thin-film Faraday rotation. Nat. Commun. 2013, 4, 1599. [Google Scholar] [CrossRef]
- Davoyan, A.R.; Engheta, N. Nonreciprocal Rotating Power Flow within Plasmonic Nanostructures. Phys. Rev. Lett. 2013, 111, 047401. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Wang, Q.J.; Zhang, Y. Broadly tunable one-way terahertz plasmonic waveguide based on nonreciprocal surface magneto plasmons. Opt. Lett. 2012, 37, 1895–1897. [Google Scholar] [CrossRef] [PubMed]
- You, Y.; Xiao, S.; Wu, C.; Zhang, H.; Deng, X.; Shen, L. Unidirectional-propagating surface magnetoplasmon based on remanence and its application for subwavelength isolators. Opt. Mater. Express 2019, 9, 2415–2425. [Google Scholar] [CrossRef]
- Chettiar, U.K.; Davoyan, A.R.; Engheta, N. Hotspots from nonreciprocal surface waves. Opt. Lett. 2014, 39, 1760–1763. [Google Scholar] [CrossRef]
- Gangaraj, S.A.H.; Jin, B.; Argyropoulos, C.; Monticone, F. Broadband Field Enhancement and Giant Nonlinear Effects in Terminated Unidirectional Plasmonic Waveguides. Phys. Rev. Appl. 2020, 14, 054061. [Google Scholar] [CrossRef]
- Abdelrahman, M.I.; Monticone, F. Broadband and giant nonreciprocity at the subwavelength scale in magnetoplasmonic materials. Phys. Rev. B 2020, 102, 155420. [Google Scholar] [CrossRef]
- Mann, S.A.; Mekawy, A.; Alù, A. Broadband Field Localization, Density of States, and Nonlinearity Enhancement in Nonreciprocal and Topological Hotspots. Phys. Rev. Appl. 2021, 15, 034064. [Google Scholar] [CrossRef]
- Caloz, C.; Alù, A.; Tretyakov, S.; Sounas, D.; Achouri, K.; Deck-Léger, Z.-L. Electromagnetic Nonreciprocity. Phys. Rev. Appl. 2018, 10, 047001. [Google Scholar] [CrossRef]
- Remer, L.; Mohler, E.; Grill, W.; Lüthi, B. Nonreciprocity in the optical reflection of magnetoplasmas. Phys. Rev. B 1984, 30, 3277–3282. [Google Scholar] [CrossRef]
- Potton, R.J. Reciprocity in optics. Rep. Prog. Phys. 2004, 67, 717–754. [Google Scholar] [CrossRef]
- Parker, J.B.; Marston, J.B.; Tobias, S.M.; Zhu, Z. Topological Gaseous Plasmon Polariton in Realistic Plasma. Phys. Rev. Lett. 2020, 124, 195001. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Bulk-edge correspondence for topological photonic continua. Phys. Rev. B 2016, 94, 205105. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Proof of the Bulk-Edge Correspondence through a Link between Topological Photonics and Fluctuation-Electrodynamics. Phys. Rev. X 2019, 9, 011037. [Google Scholar] [CrossRef]
- Jin, D.; Lu, L.; Wang, Z.; Fang, C.; Joannopoulos, J.D.; Soljačić, M.; Fu, L.; Fang, N.X. Topological magnetoplasmon. Nat. Commun. 2016, 7, 13486. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Smirnova, D.; Nori, F. Quantum spin Hall effect of light. Science 2015, 348, 1448–1451. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Nori, F. Transverse spin of a surface polariton. Phys. Rev. A 2012, 85, 061801. [Google Scholar] [CrossRef]
- Van Mechelen, T.; Jacob, Z. Universal spin-momentum locking of evanescent waves. Optica 2016, 3, 118–126. [Google Scholar] [CrossRef]
- Ishimaru, A. Dispersion and Anisotropic Media. In Electromagnetic Wave Propagation, Radiation, and Scattering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017; pp. 233–283. [Google Scholar]
- McIsaac, P.R. A General Reciprocity Theorem. IEEE Trans. Microw. Theory Tech. 1979, 27, 340–342. [Google Scholar] [CrossRef]
- Lindell, I.V.; Dahl, F.M. Conditions for the parameter dyadics of lossy bianisotropic media. Microw. Opt. Technol. Lett. 2001, 29, 175–178. [Google Scholar] [CrossRef]
- Lindell, I.V.; Sihvola, A.H.; Puska, P.; Ruotanen, L.H. Conditions for the parameter dyadics of lossless bianisotropic media. Microw. Opt. Technol. Lett. 1995, 8, 268–272. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Chapter IX—The electromagnetic wave equations. In Electrodynamics of Continuous Media, 2nd ed.; Pergamon: Amsterdam, The Netherlands, 1984; Volume 8, pp. 257–289. [Google Scholar]
- Zhao, B.; Guo, C.; Garcia, C.A.C.; Narang, P.; Fan, S. Axion-Field-Enabled Nonreciprocal Thermal Radiation in Weyl Semimetals. Nano Lett. 2020, 20, 1923–1927. [Google Scholar] [CrossRef]
- Sommerfeld, A. Lectures on Theoretical Physics; Academic Press: Cambridge, MA, USA, 1950; Available online: http://books.google.com/books?id=VgFRAAAAMAAJ (accessed on 9 April 2021).
- Arikawa, T.; Wang, X.; Belyanin, A.A.; Kono, J. Giant tunable Faraday effect in a semiconductor magneto-plasma for broadband terahertz polarization optics. Opt. Express 2012, 20, 19484–19492. [Google Scholar] [CrossRef]
- Wang, X.; Belyanin, A.A.; Crooker, S.A.; Mittleman, D.M.; Kono, J. Interference-induced terahertz transparency in a semiconductor magneto-plasma. Nat. Phys. 2010, 6, 126–130. [Google Scholar] [CrossRef]
- Gao, W.; Yang, B.; Lawrence, M.; Fang, F.; Béri, B.; Zhang, S. Photonic Weyl degeneracies in magnetized plasma. Nat. Commun. 2016, 7, 12435. [Google Scholar] [CrossRef]
- Shastri, K.; Monticone, F. Dissipation-induced topological transitions in continuous Weyl materials. Phys. Rev. Res. 2020, 2, 033065. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Topological classification of Chern-type insulators by means of the photonic Green function. Phys. Rev. B 2018, 97, 115146. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer US: New York, NY, USA, 2007. [Google Scholar]
- Yu, H.; Peng, Y.; Yang, Y.; Li, Z.-Y. Plasmon-enhanced light–matter interactions and applications. NPJ Comput. Mater. 2019, 5, 45. [Google Scholar] [CrossRef]
- West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for better plasmonic materials. Laser Photonics Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative Plasmonic Materials: Beyond Gold and Silver. Adv. Mater. 2013, 25, 3264–3294. [Google Scholar] [CrossRef] [PubMed]
- Chochol, J.; Postava, K.; Čada, M.; Pištora, J. Experimental demonstration of magnetoplasmon polariton at InSb(InAs)/dielectric interface for terahertz sensor application. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Boltasseva, A.; Atwater, H.A. Low-Loss Plasmonic Metamaterials. Science 2011, 331, 290–291. [Google Scholar] [CrossRef]
- Simovski, C.R.; Belov, P.A.; Atrashchenko, A.V.; Kivshar, Y.S. Wire Metamaterials: Physics and Applications. Adv. Mater. 2012, 24, 4229–4248. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Chern invariants for continuous media. Phys. Rev. B 2015, 92, 125153. [Google Scholar] [CrossRef]
- Buddhiraju, S.; Shi, Y.; Song, A.; Wojcik, C.; Minkov, M.; Williamson, I.A.D.; Dutt, A.; Fan, S. Absence of unidirectionally propagating surface plasmon-polaritons at nonreciprocal metal-dielectric interfaces. Nat. Commun. 2020, 11, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Souslov, A.; Dasbiswas, K.; Fruchart, M.; Vaikuntanathan, S.; Vitelli, V. Topological Waves in Fluids with Odd Viscosity. Phys. Rev. Lett. 2019, 122, 128001. [Google Scholar] [CrossRef]
- Gangaraj, S.A.H.; Monticone, F. Physical Violations of the Bulk-Edge Correspondence in Topological Electromagnetics. Phys. Rev. Lett. 2020, 124, 153901. [Google Scholar] [CrossRef] [PubMed]
- Kaliteevski, M.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef]
- Goto, T.; Dorofeenko, A.V.; Merzlikin, A.M.; Baryshev, A.V.; Vinogradov, A.P.; Inoue, M.; Lisyansky, A.A.; Granovsky, A.B. Optical Tamm States in One-Dimensional Magnetophotonic Structures. Phys. Rev. Lett. 2008, 101, 113902. [Google Scholar] [CrossRef] [PubMed]
- Bikbaev, R.G.; Vetrov, S.Y.; Timofeev, I.V. Hybrid Tamm and surface plasmon polaritons in resonant photonic structure. J. Quant. Spectrosc. Radiat. Transf. 2020, 253, 107156. [Google Scholar] [CrossRef]
- Gangaraj, S.A.H.; Monticone, F. Do truly unidirectional surface plasmon-polaritons exist? Optica 2019, 6, 1158–1165. [Google Scholar] [CrossRef]
- Mortensen, N.A.; Raza, S.; Wubs, M.; Søndergaard, T.; Bozhevolnyi, S.I. A generalized non-local optical response theory for plasmonic nanostructures. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef]
- Raza, S.; Bozhevolnyi, S.I.; Wubs, M.; Mortensen, N.A. Nonlocal optical response in metallic nanostructures. J. Phys. Condens. Matter 2015, 27, 183204. [Google Scholar] [CrossRef]
- Fernández-Domínguez, A.I.; Wiener, A.; García-Vidal, F.J.; Maier, S.A.; Pendry, J.B. Transformation-Optics Description of Nonlocal Effects in Plasmonic Nanostructures. Phys. Rev. Lett. 2012, 108, 106802. [Google Scholar] [CrossRef]
- Maack, J.R.; Mortensen, N.A.; Wubs, M. Size-dependent nonlocal effects in plasmonic semiconductor particles. EPL Europhys. Lett. 2017, 119, 17003. [Google Scholar] [CrossRef]
- Monticone, F. A truly one-way lane for surface plasmon polaritons. Nat. Photonics 2020, 14, 461–465. [Google Scholar] [CrossRef]
- Pakniyat, S.; Holmes, A.M.; Hanson, G.W.; Gangaraj, S.A.H.; Antezza, M.; Silveirinha, M.G.; Jam, S.; Monticone, F. Non-Reciprocal, robust surface plasmon polaritons on gyrotropic interfaces. IEEE Trans. Antennas Propag. 2020, 68, 3718–3729. [Google Scholar] [CrossRef]
- Gangaraj, S.A.H.; Hanson, G.W.; Silveirinha, M.G.; Shastri, K.; Antezza, M.; Monticone, F. Unidirectional and diffractionless surface plasmon polaritons on three-dimensional nonreciprocal plasmonic platforms. Phys. Rev. B 2019, 99, 245414. [Google Scholar] [CrossRef]
- Wang, D.; Yang, B.; Gao, W.; Jia, H.; Yang, Q.; Chen, X.; Wei, M.; Liu, C.; Navarro-Cía, M.; Han, J.; et al. Photonic Weyl points due to broken time-reversal symmetry in magnetized semiconductor. Nat. Phys. 2019, 15, 1150–1155. [Google Scholar] [CrossRef]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Shastri, K.; Monticone, F. Robust surface-wave propagation and leaky-wave radiation based on three-dimensional topological plasmonic materials. In Proceedings of the Active Photonic Platforms XI, San Diego, CA, USA, 11–15 August 2019; Volume 11081, p. 1108107. [Google Scholar]
- Ding, F.; Bozhevolnyi, S.I. A Review of Unidirectional Surface Plasmon Polariton Metacouplers. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–11. [Google Scholar] [CrossRef]
- Yu, Z.; Veronis, G.; Wang, Z.; Fan, S. One-Way Electromagnetic Waveguide Formed at the Interface between a Plasmonic Metal under a Static Magnetic Field and a Photonic Crystal. Phys. Rev. Lett. 2008, 100, 023902. [Google Scholar] [CrossRef]
- Gangaraj, S.A.H.; Silveirinha, M.G.; Hanson, G.W. Berry Phase, Berry Connection, and Chern Number for a Continuum Bianisotropic Material From a Classical Electromagnetics Perspective. IEEE J. Multiscale Multiphysics Comput. Tech. 2017, 2, 3–17. [Google Scholar] [CrossRef]
- Gangaraj, S.A.H.; Nemilentsau, A.; Hanson, G.W. The effects of three-dimensional defects on one-way surface plasmon propagation for photonic topological insulators comprised of continuum media. Sci. Rep. 2016, 6, 30055. [Google Scholar] [CrossRef]
- Hayran, Z.; Gangaraj, S.A.H.; Monticone, F. Topologically protected broadband rerouting of propagating waves around complex objects. Nanophotonics 2019, 8, 1371–1378. [Google Scholar] [CrossRef]
- Pakniyat, S.; Liang, Y.; Xiang, Y.; Cen, C.; Chen, J.; Hanson, G.W. Indium antimonide—Constraints on practicality as a magneto-optical platform for topological surface plasmon polaritons. J. Appl. Phys. 2020, 128, 183101. [Google Scholar] [CrossRef]
- Xia, L.; Gao, W.; Yang, B.; Guo, Q.; Liu, H.; Han, J.; Zhang, W.; Zhang, S. Stretchable Photonic ‘Fermi Arcs’ in Twisted Magnetized Plasma. Laser Photonics Rev. 2018, 12, 1700226. [Google Scholar] [CrossRef]
- Tauber, C.; Delplace, P.; Venaille, A. Anomalous bulk-edge correspondence in continuous media. Phys. Rev. Res. 2020, 2. [Google Scholar] [CrossRef]
- Van Mechelen, T.; Jacob, Z. Quantum gyroelectric effect: Photon spin-1 quantization in continuum topological bosonic phases. Phys. Rev. A 2018, 98, 023842. [Google Scholar] [CrossRef]
- Van Mechelen, T.; Jacob, Z. Unidirectional Maxwellian spin waves. Nanophotonics 2019, 8, 1399–1416. [Google Scholar] [CrossRef]
- Stern, F. Polarizability of a Two-Dimensional Electron Gas. Phys. Rev. Lett. 1967, 18, 546–548. [Google Scholar] [CrossRef]
- Jablan, M.; Buljan, H.; Soljačić, M. Plasmonics in graphene at infrared frequencies. Phys. Rev. B 2009, 80, 245435. [Google Scholar] [CrossRef]
- Chiu, K.W.; Quinn, J.J. Plasma oscillations of a two-dimensional electron gas in a strong magnetic field. Phys. Rev. B 1974, 9, 4724–4732. [Google Scholar] [CrossRef]
- Mast, D.B.; Dahm, A.J.; Fetter, A.L. Observation of Bulk and Edge Magnetoplasmons in a Two-Dimensional Electron Fluid. Phys. Rev. Lett. 1985, 54, 1706–1709. [Google Scholar] [CrossRef] [PubMed]
- Glattli, D.C.; Andrei, E.Y.; Deville, G.; Poitrenaud, J.; Williams, F.I.B. Dynamical Hall Effect in a Two-Dimensional Classical Plasma. Phys. Rev. Lett. 1985, 54, 1710–1713. [Google Scholar] [CrossRef] [PubMed]
- Jin, D.; Xia, Y.; Christensen, T.; Freeman, M.; Wang, S.; Fong, K.Y.; Gardner, G.C.; Fallahi, S.; Hu, Q.; Wang, Y.; et al. Topological kink plasmons on magnetic-domain boundaries. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef]
- Sounas, D.L.; Alù, A. Non-reciprocal photonics based on time modulation. Nat. Photonics 2017, 11, 774–783. [Google Scholar] [CrossRef]
- Morgado, T.A.; Silveirinha, M.G. Drift-Induced Unidirectional Graphene Plasmons. ACS Photonics 2018, 5, 4253–4258. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Rodríguez-Fortuño, F.J.; Bekshaev, A.Y.; Kivshar, Y.S.; Nori, F. Electric-current-induced unidirectional propagation of surface plasmon-polaritons. Opt. Lett. 2018, 43, 963–966. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Gomez-Diaz, J.S. Nonreciprocal and collimated surface plasmons in drift-biased graphene metasurfaces. Phys. Rev. B 2019, 100, 081410. [Google Scholar] [CrossRef]
- Xiao, M.; Lin, Q.; Fan, S. Hyperbolic Weyl Point in Reciprocal Chiral Metamaterials. Phys. Rev. Lett. 2016, 117, 057401. [Google Scholar] [CrossRef]
- Gao, W.; Lawrence, M.; Yang, B.; Liu, F.; Fang, F.; Béri, B.; Li, J.; Zhang, S. Topological Photonic Phase in Chiral Hyperbolic Metamaterials. Phys. Rev. Lett. 2015, 114, 037402. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Guo, Q.; Tremain, B.; Barr, L.E.; Gao, W.; Liu, H.; Béri, B.; Xiang, Y.; Fan, D.; Hibbins, A.P.; et al. Direct observation of topological surface-state arcs in photonic metamaterials. Nat. Commun. 2017, 8, 1–7. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Mousavi, S.H.; Tse, W.-K.; Kargarian, M.; MacDonald, A.H.; Shvets, G. Photonic topological insulators. Nat. Mater. 2012, 12, 233–239. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).