Abstract
Photonic Hilbert transformers are fundamental components for optical computing and signal processing. Here, for the first time we propose all-optical arbitrary-order Hilbert transformers using phase-modulated fiber Bragg gratings (PM-FBGs) in transmission to our best knowledge. The PM-FBG is a kind of fiber grating, whose coupling strength remains almost uniform and period varies along the fiber length. For demonstration, we have designed and numerically simulated 0.5th-order, first-order, and 1.5th-order photonic Hilbert transformers, respectively. The profiles of those PM-FBGs are obtained employing quasi-Newton optimization algorithm. Simulation results show that the designed three Hilbert transformers are all in good agreement with the ideal results in bandwidths up to 500 GHz and can tolerate a large range of input pulse width.
1. Introduction
All-optical signal processing for computing and networking has attracted increasingly attention because it gives a solution to overcome the future speed limitation imposed by the present electronics-based systems. Similar to electronic circuit, optical signal processing circuit also needs the basic building blocks, for example photonic Hilbert transformer (PHT). Hilbert transformation is a fundamental signal processing operation, and through PHT, the Hilbert transform of an input temporal optical waveform can be obtained.
The order of a PHT can be integer or fractional. Both of them can find numerous applications in many areas such as single-sideband (SSB) modulation, characterization of broadband microwave signals, and widely tunable filtering [1,2,3]. For example, PHT can be used to construct the analytic signal needed for SSB modulation from a real signal. While fractional PHT (FrPHT) offers a new degree of freedom and its fractional phase can be used as a secret key in SSB modulation [4]. PHT was firstly introduced by Emami and implemented using multitap fiber optics [5], and FrPHT was firstly introduced by Christian and implemented using asymmetrical fiber Bragg grating [6]. Up to now, various approaches for the generation of PHT and FrPHT have been proposed, including fiber Bragg grating (FBG) [7,8,9], long period grating (LPG) [10], waveguide Bragg grating (WBG) [11], planar Bragg grating (PBG) [12], on-chip photonic crystal nanocavity (PCN) [13], and integrated Kerr micro-comb source [14]. Compared to other schemes, fiber-grating-based PHTs offer the advantages of simplicity, relatively low cost, low insertion loss, and full compatibility with fiber optics systems. In all fiber-grating-based PHTs, FBG-based PHTs are more tolerant to environmental changes compared with LPG-based PHTs [15].
Phase-modulated fiber Bragg grating (PM-FBG) is a complex kind of FBG, whose strength is almost uniform along the fiber length while it has a complex phase response, corresponding to a complex period. However, this grating period can be directly encoded into the phase mask, which makes it easier to be fabricated and reproduced in practice process. A number of devices based on PM-FBG have been designed and demonstrated through simulation and experiments, such as virtual Gires–Tournois etalons [16], pulse shaper [17], and photonic temporal differentiator [18]. In particular, PM-FBGs with a length of 9 cm applied to delay line interferometer [19] and format conversion [20] have been fabricated using a UV laser direct-writing system, where the gratings are created pitch by pitch, and the coupling coefficient profile and the varied period are realized by controlling the on/off of an acoustic optical modulator and moving the phase mask/fiber.
In this paper, for the first time we propose arbitrary-order PHTs based on phase-modulated fiber Bragg gratings in transmission to our best knowledge. Taking the transfer function of Hilbert transformer as the spectral response we needed, the coupling coefficient and period of PM-FBG can be calculated by inverse synthesis method. Since the designed PM-FBGs working in transmission, a coupler or circulator is not needed to separate the reflected light from incident light, which improves the energy efficiency and reduces the cost and complexity of the whole setup [8,21,22,23,24]. What is more, the PM-FBGs may also use athermal packaging to significantly reduce the possible influence of temperature changes [19], which can make them operate stably in practical applications.
2. Principle and Method
The spectral response (SR) of the PM-FBG that we will design can be expressed as transfer function of Hilbert transformer .
where n is the order of the Hilbert transformer and can be integer or fractional, and is the central frequency. Since FBG in transmission is a minimum-phase filter, the amplitude response and phase response are related by means of logarithmic Hilbert transform [25]. If the desired spectral response is a minimum phase function, we can get the required amplitude and phase response simultaneously. Unfortunately, the transfer function of an arbitrary-order PHT is not a minimum-phase function. Thus, we have to convert the non-minimum-phase function to a minimum-phase function firstly and we can apply the method proposed in [26]. The method is based on the fact that any causal temporal function with a dominant peak around or close to the origin will be either a minimum-phase function or close to one [27]. Therefore, the non-minimum-phase function can be converted into minimum-phase function using the following equation:
where and are the amount of power of the delta function and the designed PHT, respectively, and is the relative delay. The parameters and are constrained by the physical parameters of the grating (namely the maximum reflectivity of the FBG: ) and related by the following expression:
The time delay is introduced to separate the two signals and need to be selected properly, which limits the bandwidth of the desired PHT.
As examples, we have designed three PHTs with order n being 0.5, 1, and 1.5, respectively. We set the length of the fiber grating , the amount of power of the delta function and the designed PHT , and the time delay for all the examples. What is more, the PHT devices are designed to operate at the central wavelength of 1550 nm and with a bandwidth ranging from 1548 nm to 1552 nm (corresponding to a frequency domain bandwidth of 500 GHz). Theoretically, there is no limit to the length of the grating. Longer grating length could be chosen with a smaller coupling coefficient to obtain the similar design result. However, one should note that the grating length is usually limited by the translation range and accuracy of the fabrication system in practice. The amplitudes of transmission spectral response corresponding to different orders are shown in Figure 1, from which we can see that the SR amplitude is symmetric about the central wavelength of 1550 nm and oscillates with the same period on each side of the central wavelength. The main difference for different orders appears around the central part, where the amplitude decreases as the order increases. However, the overall shapes of amplitudes are roughly the same. Consequently, PHTs with any orders could be designed through the same process with different grating period distributions involved in the results.
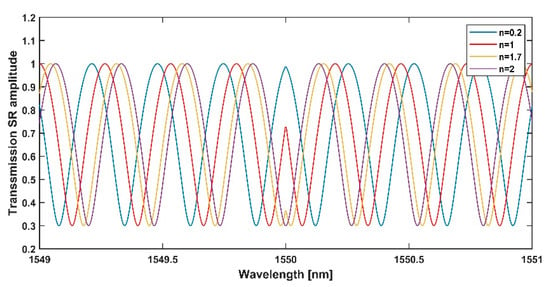
Figure 1.
Amplitudes of transmission spectral response corresponding to different orders.
The coupling coefficients and grating periods of the designed PM-FBGs can be calculated using quasi-Newton optimization algorithm, which is an algorithm for finding local maxima and minima of an input function. The quasi-Newton method is an alternative of Newton’s method and is used when the Hessian matrix of the input function is unavailable or is too expensive to compute at every iteration [28]. The iteration steps of the quasi-Newton method are as follows:
Step1: Define an initial point , let , the iteration direction .
Step2: Obtain the step length :
Let
If , then is the minimum point. The calculation will stop. Otherwise, go to step3.
Step3: Let , , using the following equation:
Let
Return to step 2.
Here, the input function is defined as the error between the desired transmission spectral response and the simulated spectral response using parameters of the grating profiles we have calculated. For each iteration, the quasi-Newton method makes the error smaller, which means we are closer to what we want. When the error is small enough, the optimization algorithm will stop.
3. Design Results and Discussion
3.1. 0.5th-Order Photonic Hilbert Transformer
When , according to Equations (1) and (2) the transfer function and the minimum-phase function corresponding to it would be
The coupling coefficient and grating period obtained by quasi-Newton method are shown in Figure 2a. It can be seen from Figure 2a that the coupling coefficient is almost uniform along the grating length, while the grating period variation oscillates in the range of −1.7 nm to 2 nm. The maximum of the coupling coefficient is 320 m−1. According to the obtained grating profile in Figure 2a, we calculate the simulated spectrum response of designed PM-FBG employing transfer matrix method and compare it with the ideal SR in Figure 2b. From Figure 2b, we can see that the simulated SR agrees well with the ideal SR in a bandwidth of 4 nm, which means that the PM-FBG we designed could realize the function of a 0.5th-order photonic Hilbert transformer.
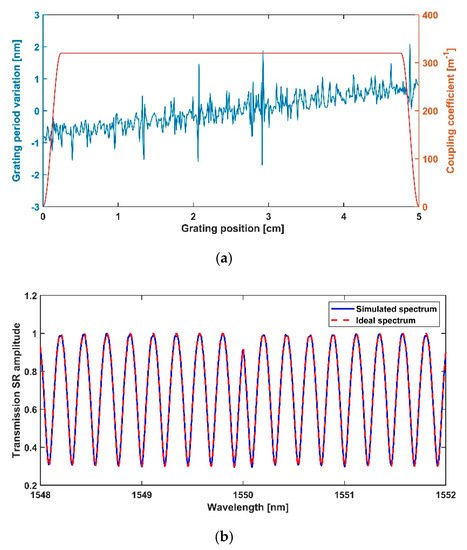
Figure 2.
(a) Grating period (blue line) and coupling coefficient (red line) of the designed 0.5th-order photonic Hilbert transformer (PHT) and (b) comparison between ideal spectrum (dashed red line) and simulated spectrum (blue line).
3.2. First-Order Photonic Hilbert Transformer
When , the transfer function and the minimum-phase function corresponding to it would be
The coupling coefficient and grating period of the PM-FBG we designed to realize the function of a first-order photonic Hilbert transformer are shown in Figure 3a. From Figure 3a, we can see that the grating period variation oscillates in the range of −1.9 nm to 1.6 nm and the maximum of the coupling coefficient is 350 m−1. Figure 3b shows the comparison between ideal SR and simulated SR of the designed PM-FBG, which is calculated using the obtained grating profile in Figure 3a and employing the transfer matrix method. Obviously, the simulated SR of our designed PM-FBG agrees well with the ideal SR in a bandwidth of 4 nm.
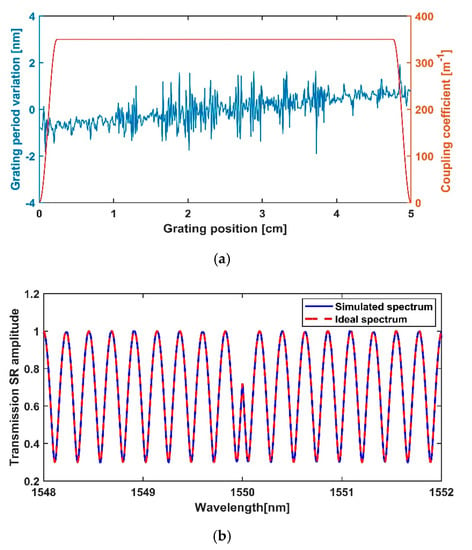
Figure 3.
(a) Grating period (blue line) and coupling coefficient (red line) of the designed first-order PHT and (b) comparison between ideal spectrum (dashed red line) and simulated spectrum (blue line).
3.3. 1.5th-Order Photonic Hilbert Transformer
When , the transfer function and the minimum-phase function corresponding to it would be
Adopting the same design process as the 0.5th-order and first-order PHT, the obtained coupling coefficient and grating period of a 1.5th-order PHT are shown in Figure 4a. The coupling coefficient is almost uniform along the grating length and the maximum is 310 m−1, while the grating period variation oscillates in the range of −2.5 nm to 2.2 nm. Figure 4b shows the comparison between ideal SR and simulated SR of the designed PM-FBG. It still can be seen that the simulated SR agrees well with the ideal SR in a bandwidth of 4 nm.
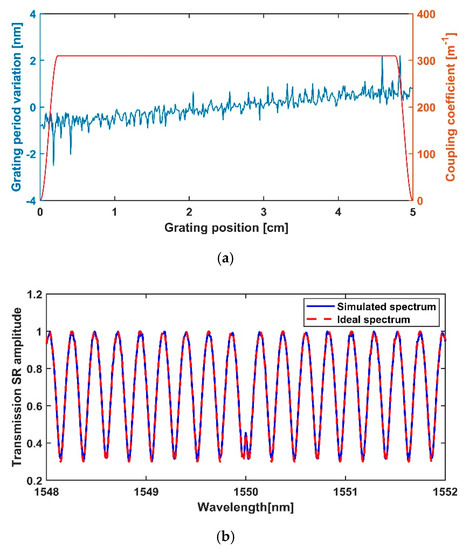
Figure 4.
(a) Grating period (blue line) and coupling coefficient (red line) of the designed 1.5th-order PHT and (b) comparison between ideal spectrum (dashed red line) and simulated spectrum (blue line).
We also numerically demonstrate the functionality of the designed PM-FBGs by launching a 3 ps-full-width at half-maximum (FWHM) input Gaussian pulse centered at to the designed PM-FBGs. The obtained output temporal waveforms are presented in Figure 5. Figure 5a shows the input 3 ps-FWHM Gaussian pulse. Figure 5b–d show the obtained output pulse of designed 0.5th-order PHT, first-order PHT, and 1.5th-order PHT, respectively. In each output pulse, there are two parts. The left part of the pulse is a copy of the input Gaussian pulse and the right part of the pulse is the obtained Hilbert transformed pulse. If needed, we can use a time gating device to get only Hilbert transformed pulse at the output. It is also seen in Figure 5 that each of these three Hilbert transformed pulses has split into two peaks. For the first-order PHT, the amplitudes of the peaks are similar. For the 0.5th-order PHT, the right peak of the Hilbert transformed pulse is greater, while for 1.5th-order PHT, the left is greater.
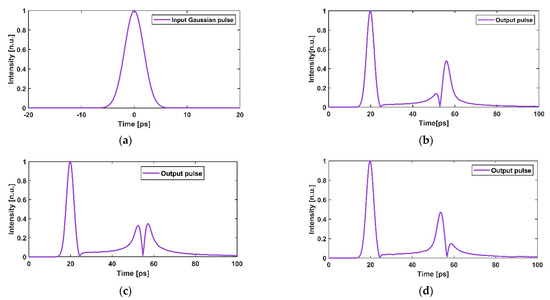
Figure 5.
Temporal responses of the designed phase-modulated fiber Bragg gratings (PM-FBGs): (a) 3 ps-full-width at half-maximum (FWHM) input Gaussian pulse; output pulse of the designed (b) 0.5th-order PHT; (c) first-order PHT; and (d) 1.5th-order PHT.
In order to get a clear view of the results of the designed PM-FBGs, we zoom in the obtained Hilbert transformed pulses and compare them with the ideal Hilbert transformed pulses in Figure 6. It can be seen from Figure 6 that the output temporal waveform results of the designed PM-FBGs agree well with that of the ideal 0.5th-order PHT, first-order PHT, and 1.5th-order PHT, respectively.
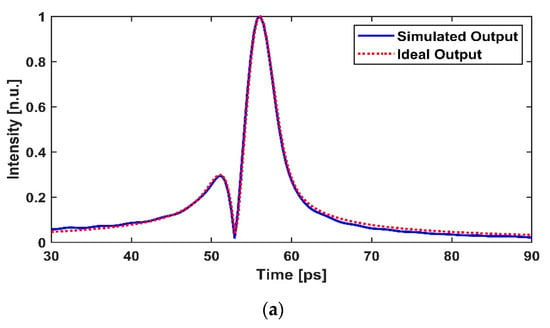
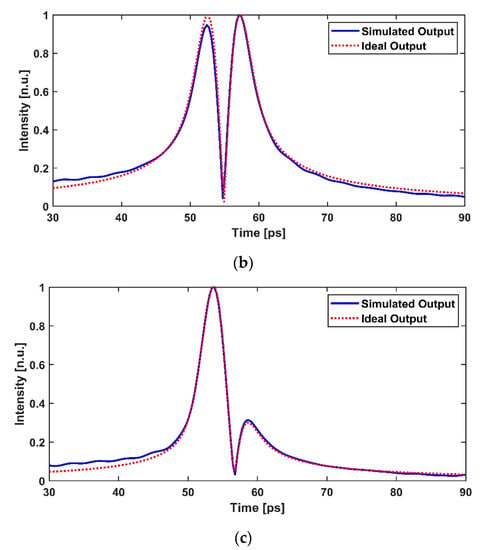
Figure 6.
Comparison between the ideal (dashed red line) and simulated (blue line) output pulses for (a) 0.5th-order PHT; (b) first-order PHT; and (c) 1.5th-order PHT.
Finally, in order to evaluate the performance of the three designed PHT devices, we calculate the cross-correlation () coefficient using the following formula:
where and represent the amplitude envelopes of the temporal output waveforms of the designed PHT and the ideal PHT, respectively. The coefficient provides a precise estimate of the level of similarity between the obtained waveform and the ideal waveform, thus allowing one to infer the time-bandwidth product capabilities of the proposed design [26].
The coefficients of the three PHT devices are shown in Figure 7. For 0.5th-order PHT, when the FWHM of the input Gaussian pulse ranges between 1.1 ps and 9.5 ps, the coefficient is larger than 90%, which means the numerically obtained temporal output waveform is extremely correlated with the ideal. For first-order PHT, the range is 1.1 ps to 9.3 ps, and for 1.5th-order PHT is 1.1 ps to 10.3 ps. For the designed 0.5th-order PHT, first-order PHT, and 1.5th-order PHT, the maximum coefficient is about 0.9868, 0.9876, and 0.9904, respectively. Those calculated coefficient values further confirm that the designed 0.5th-order, first-order, and 1.5th-order PHTs based on PM-FBGs can perform very accurate Hilbert transformation and tolerate the input pulse width.
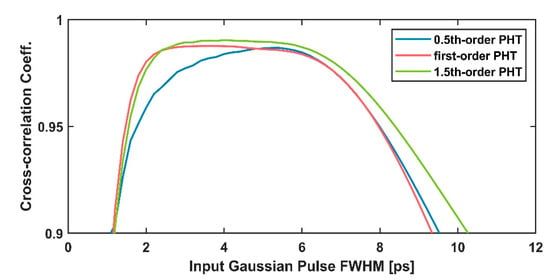
Figure 7.
Cross-correlation coefficients between the ideal and numerically obtained temporal output waveforms as a function of the FWHM of the input Gaussian pulse for the three designed PHTs.
4. Conclusions
In conclusion, we have demonstrated a new approach of designing arbitrary-order PHTs using phase-modulated FBGs in transmission. As examples, we have designed three PHTs: 0.5th-order PHT, first-order PHT, and 1.5th-order PHT. The quasi-Newton method has been employed to obtain the grating periods of the designed PM-FBGs, which makes the design versatile and can be applied in any kind of grating design. The obtained grating periods of these three PHTs are complex and oscillate up and down. We have demonstrated the three PHT devices have very good performance in a usable bandwidth up to 500 GHz and have a good tolerance to input pulse width. Moreover, the bandwidth can be further increased with the increase of the grating period variation range. An optical circulator or coupler is not required owing to the designed PM-FBGs work in transmission, which gives the benefits of high energetic efficiency and simplicity. Compared to other types of FBG-based PHTs proposed before [9], the fabrication method of the PM-FBG-based PHTs could be easier and have greater reproducibility, since the grating periods of a PM-FBG could be directly encoded into a phase mask. In addition, the maximum cross-correlation coefficient can reach above 0.985, and the coefficient values confirm that the PM-FBG-based PHTs can tolerate a larger range of input pulse width.
Author Contributions
Conceptualization, X.S.; methodology, X.S. and X.L.; software, Y.L.; validation, Y.L.; formal analysis, X.L. and Y.L.; investigation, X.L. and Y.L.; data curation, X.L. and Y.L.; writing—original draft preparation, Y.L. and X.L.; writing—review and editing, X.S. and L.Z.; funding acquisition, X.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China, grant number 2018YFE0117400 and National Natural Science Foundation of China (NSFC), grant number 61775074.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sima, C.; Gates, J.C.; Zervas, M.N.; Smith, P.G.R. Review of photonic Hilbert transformers. Front. Optoelectron. 2013, 6, 234. [Google Scholar] [CrossRef][Green Version]
- Emami, H.; Sarkhosh, N.; Bui, L.A.; Mitchell, A. Wideband RF photonic in-phase and quadrature-phase generation. Opt. Lett. 2008, 33, 98–100. [Google Scholar] [CrossRef]
- Bazargani, H.P.; Fernández-Ruiz, M.R.; Azaña, J. Tunable, nondispersive optical filter using photonic Hilbert transformation. Opt. Lett. 2014, 39, 5232–5235. [Google Scholar] [CrossRef] [PubMed]
- Tseng, C.C.; Pei, S.C. Design and application of discrete-time fractional Hilbert transformer. IEEE Trans. Circuits Syst. II Exp. Briefs 2000, 47, 1529–1533. [Google Scholar] [CrossRef]
- Emami, H.; Sarkhosh, N.; Bui, L.A.; Mitchell, A. Amplitude independent RF instantaneous frequency measurement system using photonic Hilbert transform. Opt. Express 2008, 16, 13707–13712. [Google Scholar] [CrossRef] [PubMed]
- Cuadrado-Laborde, C. Proposal and design of a photonic in-fiber fractional Hilbert transformer. IEEE Photon. Technol. Lett. 2010, 22, 33–35. [Google Scholar] [CrossRef]
- Li, M.; Yao, J.P. All-fiber temporal photonic fractional Hilbert transformer based on a directly designed fiber Bragg grating. Opt. Lett. 2010, 35, 223–225. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Yao, J.P. Experimental demonstration of a wideband photonic temporal Hilbert transformer based on a single fiber Bragg grating. IEEE Photon. Technol. Lett. 2010, 22, 1559–1561. [Google Scholar] [CrossRef]
- Fernández-Ruiz, M.R.; Wang, L.; Azaña, J.; Burla, M.; Carballar, A.; LaRochelle, S. THz-bandwidth photonic Hilbert transformers based on fiber Bragg gratings in transmission. Opt. Lett. 2015, 40, 41–44. [Google Scholar] [CrossRef]
- Ashrafi, R.; Azana, J. Terahertz bandwidth all-optical Hilbert transformers based on long-period gratings. Opt. Lett. 2012, 37, 2604–2606. [Google Scholar] [CrossRef]
- Bazargani, H.P.; Burla, M.; Chrostowski, L.; Azaña, J. Photonic Hilbert transformers based on laterally apodized integrated waveguide Bragg gratings on a SOI wafer. Opt. Lett. 2016, 41, 5039–5042. [Google Scholar] [CrossRef] [PubMed]
- Sima, C.T.; Gates, J.C.; Holmes, C.; Mennea, P.L.; Zervas, M.N.; Smith, P.G.R. Terahertz bandwidth photonic Hilbert transformers based on synthesized planar Bragg grating fabrication. Opt. Lett. 2013, 38, 3448–3451. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Zheng, A.; Zhang, Y.; Xia, J.; Tan, S.; Yang, T.; Zhang, X. Photonic Hilbert transformer employing on-chip photonic crystal nanocavity. J. Lightwave Technol. 2014, 32, 3704–3709. [Google Scholar] [CrossRef]
- Tan, M.; Xu, X.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. Microwave and RF Photonic Fractional Hilbert Transformer Based on a 50 GHz Kerr Micro-Comb. J. Lightwave Technol. 2019, 37, 6097–6104. [Google Scholar] [CrossRef]
- James, S.W.; Tatam, R.P. Optical fibre long-period grating sensors: Characteristics and application. Meas. Sci. Technol. 2003, 14, 49–61. [Google Scholar] [CrossRef]
- Shu, X.; Sugden, K.; Bennion, I. Virtual Gires-Tournois etalons realized with phase-modulated wideband chirped fiber gratings. Opt. Lett. 2007, 32, 3546–3548. [Google Scholar] [CrossRef]
- Preciado, M.A.; Shu, X.; Sudgen, K. Proposal and design of phase-modulated fiber gratings in transmission for pulse shaping. Opt. Lett. 2013, 38, 70–72. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Shu, X. Design of Arbitrary-Order Photonic Temporal Differentiators Based on Phase-Modulated Fiber Bragg Gratings in Transmission. J. Lightwave Technol. 2017, 35, 2926–2932. [Google Scholar] [CrossRef]
- Preciado, M.A.; El-Taher, A.; Sugden, K.; Shu, X. Spatially distributed delay line interferometer based on transmission Bragg scattering. Opt. Lett. 2019, 44, 4319–4322. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Xu, Z.; Preciado, M.A.; Gbadebo, A.; Zhang, L.; Xiong, J.; Yu, Y.; Cao, H.; Shu, X. Transmissive Fiber Bragg Grating-Based Delay Line Interferometer for RZ-OOK to NRZ-OOK Format Conversion. IEEE Access 2019, 7, 140300–140304. [Google Scholar] [CrossRef]
- Margulis, W.; Lindberg, R.; Laurell, F.; Hedin, G. Intracavity interrogation of an array of fiber Bragg gratings. Opt. Express 2021, 29, 111–118. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Tang, J.; Cheng, C.; Cai, L.; Guo, H.; Yang, M. Simultaneously distributed temperature and dynamic strain sensing based on a hybrid ultra-weak fiber grating array. Opt. Express 2020, 28, 34309–34319. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xu, B.; Wang, D.N.; Li, Y.; Gong, H.; Wang, Z. High-Resolution Sensing System Based on Fiber Bragg Grating Fabry–Perot Interferometer and Frequency-Domain Demodulation. IEEE Sens. J. 2019, 19, 4451–4457. [Google Scholar] [CrossRef]
- Yu, J.; Wu, Z.; Yang, X.; Han, X.; Zhao, M. Tilted Fiber Bragg Grating Sensor Using Chemical Plating of a Palladium Membrane for the Detection of Hydrogen Leakage. Sensors 2018, 18, 4478. [Google Scholar] [CrossRef]
- Skaar, J. Synthesis of fiber Bragg gratings for use in transmission. J. Opt. Soc. Am. A 2001, 18, 557–564. [Google Scholar] [CrossRef]
- Fernández-Ruiz, M.R.; Carballar, A.; Azaña, J. Arbitrary Time-Limited Optical Pulse Processors Based on Transmission Bragg Gratings. IEEE Photon. Technol. Lett. 2014, 26, 1754–1757. [Google Scholar] [CrossRef]
- Ozcan, A.; Digonnet, M.J.F.; Kino, G.S. Characterization of fiber Bragg gratings using spectral interferometry based on minimum-phase functions. J. Light. Technol. 2006, 24, 1739–1757. [Google Scholar] [CrossRef]
- Bonnans, J.F.; Gilbert, J.C.; Lemaréchal, C.; Sagastizabal, C.A. Numerical Optimization—Theoretical and Practical Aspects, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 51–56. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).