Focusing a Vortex Laser Beam with Polarization Conversion

Abstract

We show that when strongly focusing a linearly polarized optical vortex with the topological charge 2 (or −2) in the near-focus region, there occurs not only a reverse energy flow (where the projection of the Poynting vector is negative) but the right- (or left-) handed circular polarization of light as well. Notably, thanks to spin–orbital conversion, the on-axis polarization vector handedness is the same as that of the transverse energy flow, i.e., anticlockwise (clockwise). An absorbing spherical microparticle centered on the optical axis placed in the focus may be expected to rotate anticlockwise (clockwise) around its axis and its center of masses. We also show that in the case of sharp focusing of light with linear polarization (without an optical vortex) before and after focus, the light has an even number of local regions with left- and right-handed circular (elliptical) polarizations. Theoretical predictions are corroborated by the numerical simulation.

1. Introduction

When strongly focusing a circularly polarized Gaussian beam, a near-focus orbital energy flow has been generated thanks to spin–orbital conversion [1,2,3,4,5,6,7]. In the original plane, such a beam has no orbital angular momentum (OAM), only having a non-zero on-axis projection of the spin angular momentum (SAM) vector thanks to circular polarization. However, a non-zero longitudinal component of the electric vector that occurs in the strong focus leads to the generation of a transverse energy flow, which produces the non-zero longitudinal OAM component. Behavioral patterns of SAM and OAM in the tight focus of optical vortices were studied in References [8,9,10,11,12]. On the other hand, there have been publications concerned with a reverse energy flow in the tight focus of optical vortices [13,14,15,16] and some laser beams such as vector X-waves [17], non-paraxial Airy beams [18], Weber beams [19], vector Bessel beams [20], and fractional Bessel vortex beams [21].

It should be noted that it was shown in [14] that when sharp focusing of linearly polarized light (without an optical vortex) in the peripheral part in the focal plane (in “dark rings”, where the energy flux is zero), a reverse energy flow is formed. But the value of the reverse flow in [14] (in modulus) is a small part (1–2%) of the value of the forward flow. In this work, due to the presence of an optical vortex with a topological charge of 2 (or −2), the reverse flow was formed on the optical axis (and not at the periphery), and its magnitude (in modulus) was approximately equal to 30% of the maximum value of the forward energy flux. Moreover, the reverse flow on the optical z-axis, as in this work, takes place at any z before and after the focal spot. In addition, the reverse flow in [14] was a toroidal flow of energy. Such a flow of energy “makes a loop” around the “dark ring”, where it is equal to zero. The longitudinal size of this “loop” along the optical z-axis is approximately equal to the depth of focus.

In this work, using Richard–Wolf formulae, we derived analytical relationships to describe projections of the Poynting vector (the energy flow) and the SAM vector when tightly focusing a linearly polarized optical vortex with a topological charge of 2. In the original plane, all SAM vector components of such a beam were zero, but they all became non-zero near the strong focus. This can be explained by the effect inverse to the spin–orbital conversion. Thus, in the case under study, thanks to the orbital–spin conversion, the original linearly polarized vortex beam generates a circularly polarized vortex beam in the tight focus. It is important to mention that a vortex beam with the topological charge (TC) m = 2 has a specific feature—that of generating an on-axis reverse energy flow in the tight focus (characterized by the negative longitudinal projection of the Poynting vector). Moreover, there will be non-zero on-axis intensity. At any m > 2, except for m = 1 and m = 2, both the on-axis intensity of light and energy flow are zero.

We note that for spin–orbital coupling to occur, the beam needs to propagate in a medium and because of this throughout the text below, we use the notion of spin–orbital conversion. Thanks to the beam rays converging to the focus, there appears a non-zero longitudinal projection of the electric field vector that, combined with the transverse components, produces a transverse energy flow (although the original energy flow only has a longitudinal component), which, in turn, produces a longitudinal projection of the OAM vector. In the focus, two transverse projections (x and y components) of the electric field vector (E-vector) have a relative phase shift of π, generating a circularly polarized beam, which, in turn, generates the longitudinal component of the SAM vector.

2. Energy Flow and SAM in the Strong Focus

Previously, relationships to describe projections of the electric and magnetic fields in the vicinity of the tight focus of an original linearly polarized optical vortex with an arbitrary integer TC m have been derived [6]. In this case, a near-axis reverse energy flow in the focus was shown to occur at any m ≥ 2. However, with the reverse energy flow being maximal on the optical axis only at m = 2, below, we look into focusing a linearly polarized optical vortex with TC m = 2. Based on the Richards–Wolf theory [14], it is possible to derive projections of the electric field vector in the tight focus of an aplanatic optical system. If the original light field is given by:

$$E=A(\theta )e^{i2\phi }\left(\begin{array}{l}1\\ 0\end{array}\right),H=A(\theta )e^{i2\phi }\left(\begin{array}{l}0\\ 1\end{array}\right),$$

(1)

where E and H are the electric and magnetic field of Jones vectors, projections of the electric field vector in the focal plane will be given by [6]:

$$\begin{array}{rl}& E_x=i{e}^{2i\phi }(I_{0,2}+\frac{1}{\sqrt{2}}{e}^{2i\phi }{I}_{2,4}+\frac{1}{\sqrt{2}}{e}^{-2i\phi }{I}_{2,0}),\\ & E_y=-e^{2i\phi }(-\frac{1}{\sqrt{2}}{e}^{2i\phi }{I}_{2,4}+\frac{1}{\sqrt{2}}{e}^{-2i\phi }{I}_{2,0}),\\ & E_z=2e^{2i\phi }(\frac{1}{\sqrt{2}}{e}^{i\phi }{I}_{1,3}-\frac{1}{\sqrt{2}}{e}^{-i\phi }{I}_{1,1}),\end{array}$$

(2)

where:

$$\begin{array}{l}{I}_{\nu ,\mu }=\left(\frac{\pi f}{\lambda }\right){\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}{\sin }^{\nu +1}(\frac{\theta }{2}){\cos }^{3-\nu }(\frac{\theta }{2})}\times \\ \times {\cos }^{1/2}(\theta )A(\theta )e^{ikz\cos \theta }{J}_{\mu }(x)d\theta ,\end{array}$$

(3)

and λ is the incident wavelength, f is the focal length of the aplanatic system, x = krsinθ, J_μ(x) is the first-kind Bessel function, and NA = sinθ₀ is the numerical aperture. Assuming the initial amplitude A(θ) to be a real function, it can be given by a constant (plane wave) or a Gaussian beam.

$$A(\theta )=\exp \left(\frac{-{\gamma }^2{\sin }^2\theta }{{\sin }^2{\theta }_0}\right),$$

(4)

where γ is constant. Equation (4) shows an example of the dependence of the initial field amplitude on the tilt angle to the optical axis θ. The vortex phase of the initial field is seen from Equation (1) to be described by a linear function of the azimuthal angle ϕ. The results of this work almost did not depend on the type of Function (4). Instead of (4), the function A(θ) can be the constant: A(θ) = A₀.

Note that in [22], using the theory developed in [14], similar equations were obtained, but for a different case. In [22], sharp focusing of light with left- (or right)-handed circular polarization and with an optical vortex with a topological charge of −2 (or 2) was considered. It was shown that in the focal plane near the optical axis, where the reverse energy flow is formed, polarization inversion occurs: the initial left-handed circular polarization turns into right-handed circular polarization. Conversely, if the initial field is right-handed circularly polarized, then there is left-handed circular polarization near the optical axis in the focus. In this section, we obtain new formulas that do not follow from the formulas obtained in [22]. We seek to derive projections of the SAM vector [10]:

$$\mathbf{S}=\frac{1}{16\pi \omega }\mathrm{Im}({\mathbf{E}}^{*}\times \mathbf{E}),$$

(5)

where Im is the imaginary part of the number, E* denotes complex conjugation of the electric field vector, $\times$ is the vector multiplication sign, and ω is the cyclic frequency of light. In the following, for simplicity, we omitted the constant (1/8πω). Substituting (2) into (5) yields expressions for projections of the SAM vector in the focal plane (z = 0) for an initially linearly polarized optical vortex (m = 2), Equation (1):

$$\begin{array}{l}{S}_x=\left(I_{1,1}{I}_{2,0}-I_{1,3}{I}_{2,4}\right)\sin \phi +\\ +\left(I_{1,1}{I}_{2,4}-I_{1,3}{I}_{2,0}\right)\sin 3\phi ,\\ S_y=-\left(I_{1,1}{I}_{2,0}-I_{1,3}{I}_{2,4}\right)\cos \phi -\\ -\left(I_{1,1}{I}_{2,4}-I_{1,3}{I}_{2,0}\right)\cos 3\phi -\\ -\sqrt{2}{I}_{2,0}\left(I_{1,1}-I_{1,3}\right)\cos \phi ,\\ S_z=\frac{1}{2}\left(I_{2,0}-I_{2,4}\right)\times \\ \times \left(I_{2,0}+I_{2,4}+\sqrt{2}{I}_{0,2}\cos 2\phi \right).\end{array}$$

(6)

From Equation (6), the on-axis longitudinal projection of the SAM vector is seen to be non-zero and positive:

$$S_z(r=z=0)=\frac{1}{2}{I}_{2,0}^2.$$

(7)

This means that the light wave in the focus near the optical axis has right-handed circular polarization (electric vector rotates anticlockwise). From the last equation in (6), the light is also seen to be inhomogeneously polarized in the focal plane. For instance, light will be linearly polarized on the radii where the inequality $I_{2,0}=I_{2,4}$ holds, because $S_z=0$. Meanwhile, in the regions where $S_z<0$, the light wave will be left-handed circularly polarized. Along the rays in the focal plane outgoing from the center at angles ϕ: π/4, 3π/4, 5π/4, and 7π/4, alternating polarization states will occur, being right-handed circular at $I_{2,0}^2>I_{2,4}^2$, linear at $I_{2,0}^2=I_{2,4}^2$, and left-handed circular at $I_{2,0}^2<I_{2,4}^2$. From the first two equations of Equation (6), it is seen that at ϕ = πn, n = 1,2, …$S_x=0$ and at ϕ = π/2 + πn, n = 1,2, … $S_y=0$. This means that in the longitudinal planes yz and xz, light is circularly (or elliptically) polarized near the strong focus.

Next, let us consider expressions for projections of the Poynting vector (energy flow) $P=\frac{c}{2\pi }\mathrm{Re}\left(E*\times H\right)$ [14], where c is the speed of the light in the vacuum (next, we omit the constant c/π) in the focal plane when focusing an optical vortex (m = 2) with linear original polarization (1):

$$\begin{array}{l}{P}_x=-Q(r)\sin \phi ,\\ P_y=Q(r)\cos \phi ,\\ P_z=\frac{1}{2}\left(I_{0,2}^2-I_{2,4}^2-I_{2,0}^2\right),\\ Q(r)=\frac{1}{2}\left[I_{1,3}\left(I_{0,2}+I_{2,4}\right)+I_{1,1}\left(I_{0,2}+I_{2,0}\right)\right].\end{array}$$

(8)

From the comparison of (6) and (8), the focal-plane distribution of the SAM vector is seen to be radially asymmetric because the original light is linearly polarized, whereas the distribution of the longitudinal projection of the energy flow is circularly symmetric. We note that, as is the case with the SAM distribution, the intensity distribution in the focal plane is also radially asymmetric:

$$\begin{array}{l}I={\left|E_x\right|}^2+{\left|E_y\right|}^2+{\left|E_z\right|}^2=\\ =I_{2,0}^2+I_{0,2}^2+I_{2,4}^2+2I_{1,1}^2+2I_{1,3}^2-\\ -2I_{1,1}{I}_{1,3}\cos \phi +\sqrt{2}{I}_{0,2}\left(I_{2,0}+I_{2,4}\right)\cos 2\phi \end{array}$$

(9)

being non-zero on the optical axis: ($I(r=0)=I_{2,0}^2$). From Equation (8), it follows that the on-axis energy flow equals in magnitude the longitudinal projection of the SAM vector in Equation (7) but opposite in sign:

$$P_z(r=z=0)=-S_z(r=z=0)=-\frac{1}{2}{I}_{2,0}^2.$$

(10)

Hence, we infer that the on-axis energy flow is negative in the focus (being directed oppositely to the incident light beam). Equation (8) also suggests that the transverse energy flow rotates anticlockwise around the optical axis:

$$P_r=0,P_{\phi }=Q(r).$$

(11)

Directly on the optical axis, the transverse energy flow is zero ($P_{\phi }(r=0)=Q(0)=0$). Hence, we can infer that in the focal plane near the optical axis both the transverse energy flow and the polarization vector rotate anticlockwise. However, as distinct from the zero on-axis value of the transverse energy flow of (11), the longitudinal component of the SAM of (7) takes the almost maximum positive value on the axis. If an absorbing microsphere centered on the optical axis is placed in the focus, the longitudinal SAM projection may be expected to make the microsphere rotate about the optical axis anticlockwise [23]. Since the intensity distribution on the optical axis has a minimum (but not zero) value in a region with a diameter of about 400 nm (considering the numerical aperture of the focusing lens to be NA = 0.95), the diameter of an absorbing spherical particle, which is placed in the center, should be less than 400 nm (in this work, we used a bead with a diameter of 300 nm). Note that all values in this work (i.e., intensity, energy flux, and spin angular momentum) are given in arbitrary units (a.u.).

Below, we demonstrate that if the TC of the linearly polarized optical axis changes sign (m = −2), the on-axis reverse energy flow in the focus will still occur, whereas the longitudinal SAM component will become negative. Actually, instead of Equation (2), projections of the electric field in the focus for the initial linearly polarized optical vortex (m = −2) will be given by:

$$\begin{array}{l}{E}_x=i{e}^{-2i\phi }\left(I_{0,2}+\frac{1}{\sqrt{2}}{e}^{2i\phi }{I}_{2,4}+\frac{1}{\sqrt{2}}{e}^{-2i\phi }{I}_{2,0}\right),\\ E_y=-e^{-2i\phi }\left(-\frac{1}{\sqrt{2}}{e}^{2i\phi }{I}_{2,4}+\frac{1}{\sqrt{2}}{e}^{-2i\phi }{I}_{2,0}\right),\\ E_z=2e^{-2i\phi }\left(\frac{1}{\sqrt{2}}{e}^{i\phi }{I}_{1,3}-\frac{1}{\sqrt{2}}{e}^{-i\phi }{I}_{1,1}\right).\end{array}$$

(12)

Making use of Equation (12), the longitudinal components of the Poynting vector and the SAM vector can be defined as:

$$P_z=\frac{1}{2}\left(I_{0,2}^2-I_{2,4}^2-I_{2,0}^2\right),$$

(13)

$$S_z=-\frac{1}{2}\left(I_{2,0}-I_{2,4}\right)\left(I_{2,0}+I_{2,4}+\sqrt{2}{I}_{0,2}\cos 2\phi \right).$$

The comparison of (6), (8), and (12) suggests that when the sign of the optical vortex is reversed, the longitudinal component of the energy flow vector remains unchanged and the longitudinal SAM component only changes its sign. This means that a reverse on-axis energy flow and a negative on-axis projection of the SAM vector (left-handed circular polarization) occurs in the focus:

$$P_z(r=z=0)=S_z(r=z=0)=-\frac{1}{2}{I}_{2,0}^2.$$

(14)

Thus, thanks to the effect of orbital–spin conversion, in the focal plane of a strongly focused linearly polarized optical vortex is observed an on-axis reverse energy flow and the right-handed (m = 2) or left-handed (m = −2) circular polarization of light. Notably, the on-axis polarization vector and the transverse energy flow have the same handedness: anticlockwise (m = 2) or clockwise (m = −2).

The above-described reasoning can be shortly summarized as follows. In the initial plane, there is a linearly polarized optical vortex that only has a longitudinal component of OAM (with the electric field vector having only components in the original plane (Equation (1)), with all SAM vector projections being equal to zero. The angular momentum vector is known to be composed of the sum of OAM and SAM vectors and conserve upon free-space propagation [4,5,10]. Therefore, thanks to all projections of the SAM vector becoming non-zero in the tight focus, all projections of the OAM vector in the focus may also be expected to become non-zero.

3. Numerical Simulation

In the numerical simulation, an incident beam of wavelength λ = 633 nm is passed through an 8 µm aperture. The field is described by a linearly polarized plane wave of unit intensity and a phase vortex with m = 2 (Figure 1), multiplied by a spherical wave converging at a distance of f = 1.31 µm (NA = 0.95):

$$\begin{array}{l}{E}_x=\exp \left(i\left(kf-m\phi -\omega t\right)\right),\\ E_y=0.\end{array}$$

(15)

Assuming the above-defined original field, the intensity pattern depicted in Figure 2 is observed in the focal plane. The FDTD-aided numerical simulation was conducted using the FullWAVE software. The calculation was conducted for λ/30 mesh along all three axes, with the initial field containing 601 × 601 pixels. By taking an odd number of pixels, we ensured symmetry of the field relative to the origin.

Figure 2 suggests that in the strong focus of a linearly polarized wave, there was a 0.3 µm × 0.27 µm region (on the x- and y-axis, respectively), where the projection of the Poynting vector on the optical axis was negative. From Figure 2e, it can also be seen that in this region a gradual linear-to-circular on-axis polarization conversion occurred, with the E-vector rotating anticlockwise on and near the axis. On the edges of this central region, there were two regions where the E-vector rotated clockwise: X = 0, −0.2 µm < Y < −0.1 µm, and 0.1 µm < Y < 0.2 µm. In addition, in the distribution pattern of the Poynting vector, there was a ring with an approximate radius of 0.66 µm (e.g., 0.622 µm < X < 0.693 µm at Y = 0) in which the Poynting vector projection was also negative (Figure 2d). Within the ring, linear-to-circular polarization conversion also occurred, with the E-vector rotating clockwise as seen from Figure 2e.

Figure 3 depicts a two-dimensional distribution of the SAM vector projection Sz (Equation (5)) alongside its x- and y-axis profiles on the optical axis. The z-axis projection of the SAM vector is seen to be non-zero and positive on the optical axis within the region 0.267 µm < X < 0.267 µm and −0.13 µm < Y < 0.13 µm.

Let us calculate torque acting on the microparticle with complex refraction number from the light field in a rigorous case (without dipole or Rayleigh approximation). The torque M acting from light on the microparticle relative to an arbitrary point A(x,y,z) appear and will be equal to [24]:

$$M={\displaystyle \underset{S}{\oint }\left[r\times \left(\sigma \cdot n\right)\right]dS},$$

(16)

where r is a radius-vector from the point A(x,y,z) to a point of integration on the surface S, n is an external normal vector to the surface S, A is the point relative to which the torque M is calculated, and $\sigma$ is the Maxwell stress tensor, the components of which in the CGS system can be written as [22]:

$${\sigma }_{ik}=\frac{1}{4\pi }\left(\frac{{\left|E\right|}^2+{\left|H\right|}^2}{2}{\delta }_{ik}-E_i{E}_k-H_i{H}_k\right),$$

(17)

where $E_i,H_i$—electric and magnetic fields components (i, k = x, y, z), and ${\delta }_{ik}$—Kronecker symbol (${\delta }_{i=k}=1$, ${\delta }_{i\ne k}=0$). The projections of the E and H fields both inside and outside the microparticle satisfy the Maxwell equations, if calculated using the FDTD method. The refraction number of the bead is complex, and the imaginary part describes the absorption of the light inside it.

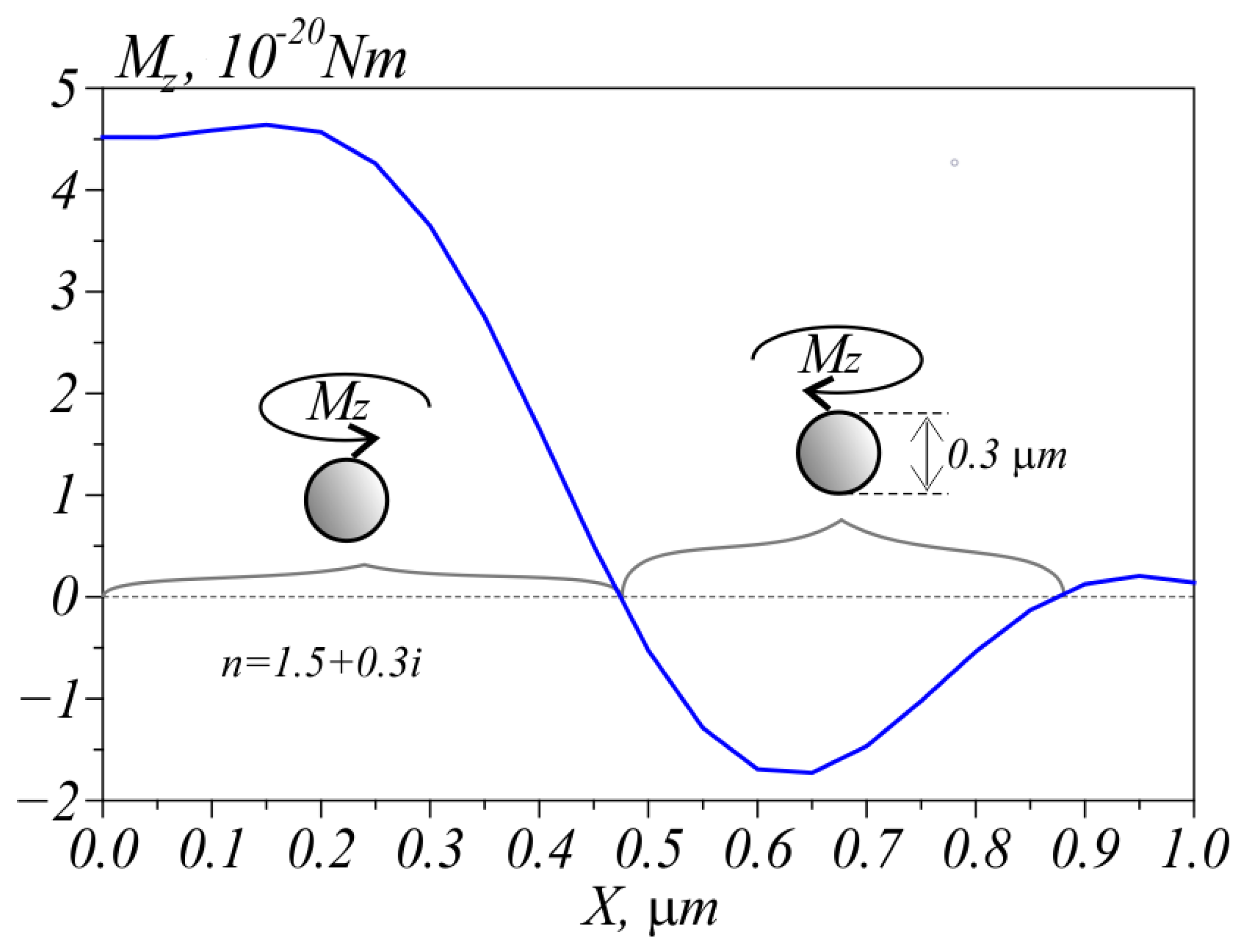
An absorbing microparticle placed in the field depicted in Figure 2 may be expected to experience a torque, making it rotate around its center of mass thanks to circular polarization. Shown in Figure 4 is the result of calculating the projection of a torque M_z exerted on a 0.3 µm microparticle (with refractive index n = 1.5 + 0.3i) relative to the optical z-axis. For a 100 mW incident beam, the numerical simulation was conducted on a λ/30 mesh over the whole field, with a smaller mesh of λ/80 utilized immediately in the microparticle neighborhood on all three coordinate axes in the region −1.5 µm < X < 1.5 µm, −0.65 µm < Y < 0.65 µm, and 0.3 µm < Z < 2.3 µm.

From Figure 4, the torque is seen to be maximal near the center (at distance of approximately X = 0.2 µm), making the microparticle rotate anticlockwise according to the on-axis polarization handedness. Note that the maximal torque value M_z > 0 coincides with the maximal value of the longitudinal SAM component S_z seen in Figure 4 on the horizontal x-axis (Figure 3b). Then, as the particle is moved off the center in the positive direction of the x-axis, the torque decreased and reversed its sign, before again becoming maximal in the absolute value at a point X = ~0.6 µm and having clockwise handedness (the ring region where Sz was negative in Figure 2c,d). From Figure 2e, the polarization was seen to again become elliptical with the E-vector rotating clockwise, similar to the torque M_z handedness.

4. Circular Polarization Formation under Sharp Focusing of Linearly Polarized Light

It is known that when focusing light with linear polarization, we obtain light with linear polarization in the focal plane too. Although it was shown in [14] that if we consider the polarization in the longitudinal plane, for example, XZ (or YZ), then in these planes we have light with elliptical polarization. In this section, using the projections of the Stokes vector calculated before and after the focus, we show that when focusing light with linear polarization (without an optical vortex), there are regions in which the polarization vector rotates clockwise and counterclockwise. In this section, we describe the simulation of the sharp focusing of the linearly polarized plane wave with a wavelength of λ = 633 nm by an aplanatic lens with a numerical aperture of NA = 0.95. The initial linear polarization was directed along the y-axis. 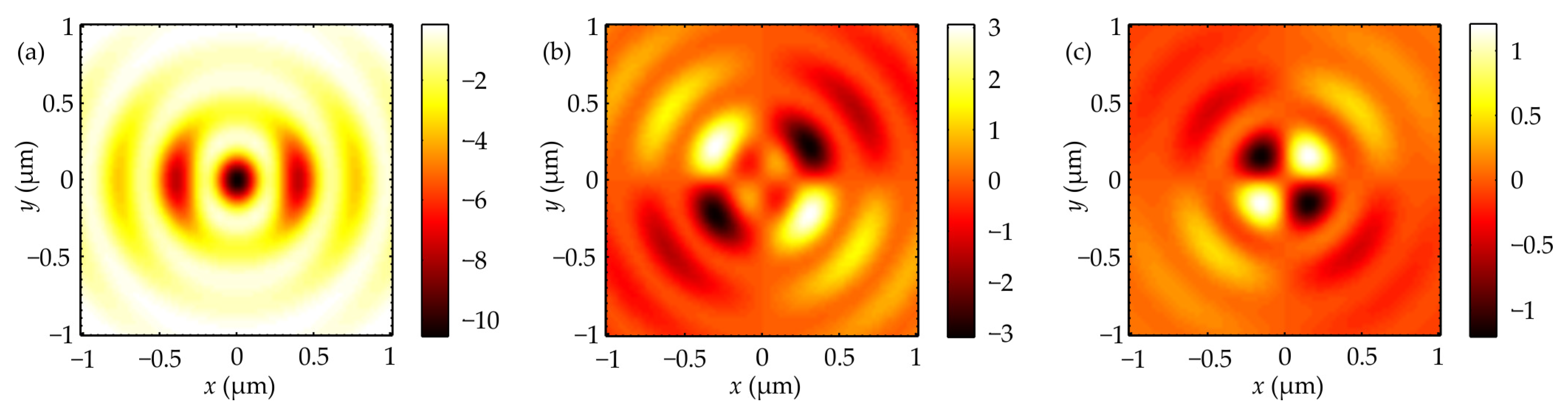We used the Richards–Wolf integral [14] to calculate the distribution of electric field components near the sharp focus. Then, we calculated the distribution of Stokes vector components:

$$\begin{array}{l}{s}_1=E_x{E}_x^{*}-E_y{E}_y^{*}\\ s_2=2\mathrm{Re}\left(E_x{E}_y^{*}\right)\\ s_3=2\mathrm{Im}\left(E_x{E}_y^{*}\right)\end{array}$$

(18)

It can be seen from a comparison of (5) and (18) that the third component of the Stokes vector and the longitudinal component of the SAM vector coincided (up to constants). The distributions of the Stokes vector components (s₁, s₂, s₃) at the distances z = −λ before the focal plane and z = λ after the focal plane are shown in Figure 5 and Figure 6, respectively. The third component of the Stokes vector (18) shows the existence of circular (elliptical) polarization. For example, dark or bright regions on Figure 5c (located at an angle of ±45° to the x-axis) show that the polarization vector rotates clockwise or anticlockwise in these areas.

It is seen from Figure 5 and Figure 6 that the first two components of the Stokes vector are the same; however, the third component changed the sign to the opposite. For example, after propagation through the focal plane, the direction of the rotation was reversed, e.g., in the first quarter, the light before the focal plane had left-handed circular polarization, and after the focal plane it had right-handed circular polarization. The right-handed circular polarization before the focal plane was located in the 2nd and 4th quadrants, and the left-handed circular polarization was located in the 1st and 3rd quadrants (Figure 5c).

5. Conclusions

In this work, based on the Richards–Wolf theory, we derived analytical expressions for projections of the Poynting vector and SAM vector close to the strong focus of a linearly polarized optical vortex with TC m = +2 and m = −2. The relations derived suggest that near the optical axis in the focal plane, there occurs a reverse energy flow. In the reverse energy flow region, the right- (for m = 2) or left-handed (m = −2) polarization of light was observed. In the meantime, inhomogeneous polarization was found at the periphery of the focal plane, where polarization was alternating from right-handed circular (or elliptical) to left-handed circular (or elliptical) and to linear. At the same time, close to the optical axis, the handedness of the polarization vector rotation coincided with that of the transverse energy flow rotation: with both rotating anticlockwise at m = 2 and clockwise at m = −2. The generation of circular polarization in the reverse energy flow region enabled the latter to be detected. Actually, if an absorbing microparticle is placed near the focus in the reverse energy flow region, the SAM will cause it to rotate around its center of mass. With the on-axis transverse energy flow being zero, it will hardly contribute to the microparticle rotation. The handedness of the microparticle rotation will be defined by the TC sign of the vortex beam. We also showed that in the case of sharp focusing of linearly polarized light (without an optical vortex) in the planes before and after the focus, there are regions (approximately 300 nm in size) in which the polarization vector rotates clockwise or counterclockwise. When passing through the focus, these areas change places.