Multi-Wavelength Optical Patterning for Multiscale Materials Design
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Azopolymer Thin Films
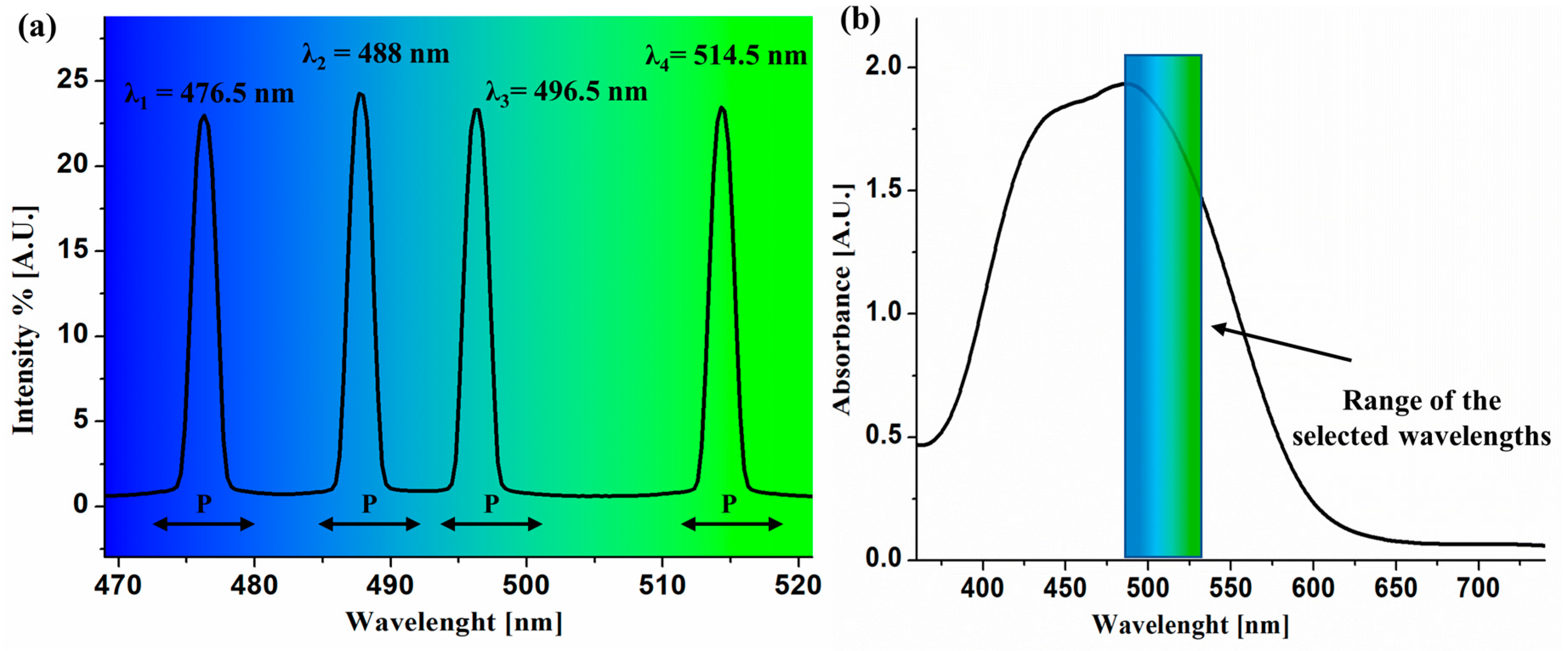
2.2. Multi-Wavelength Interferometry
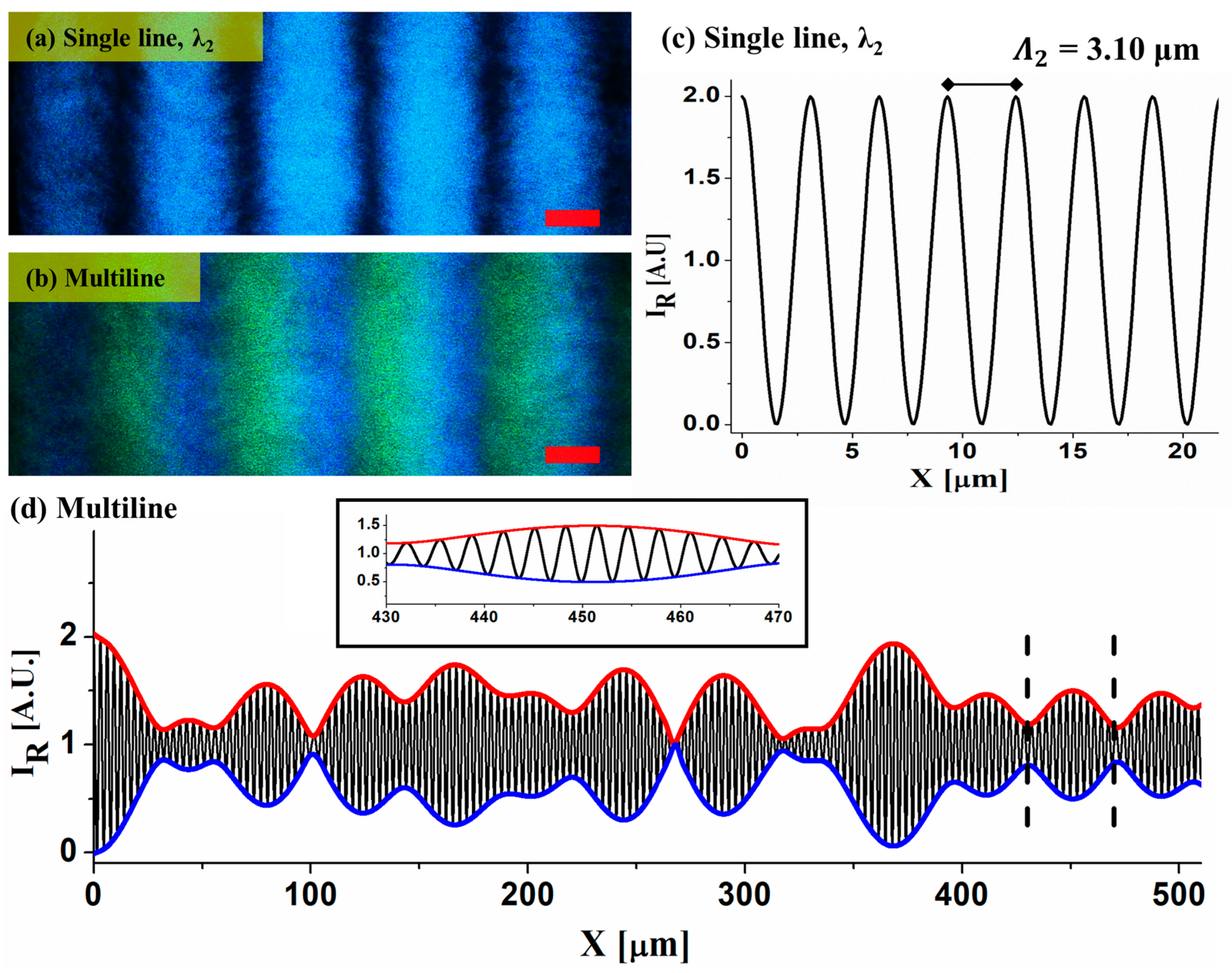
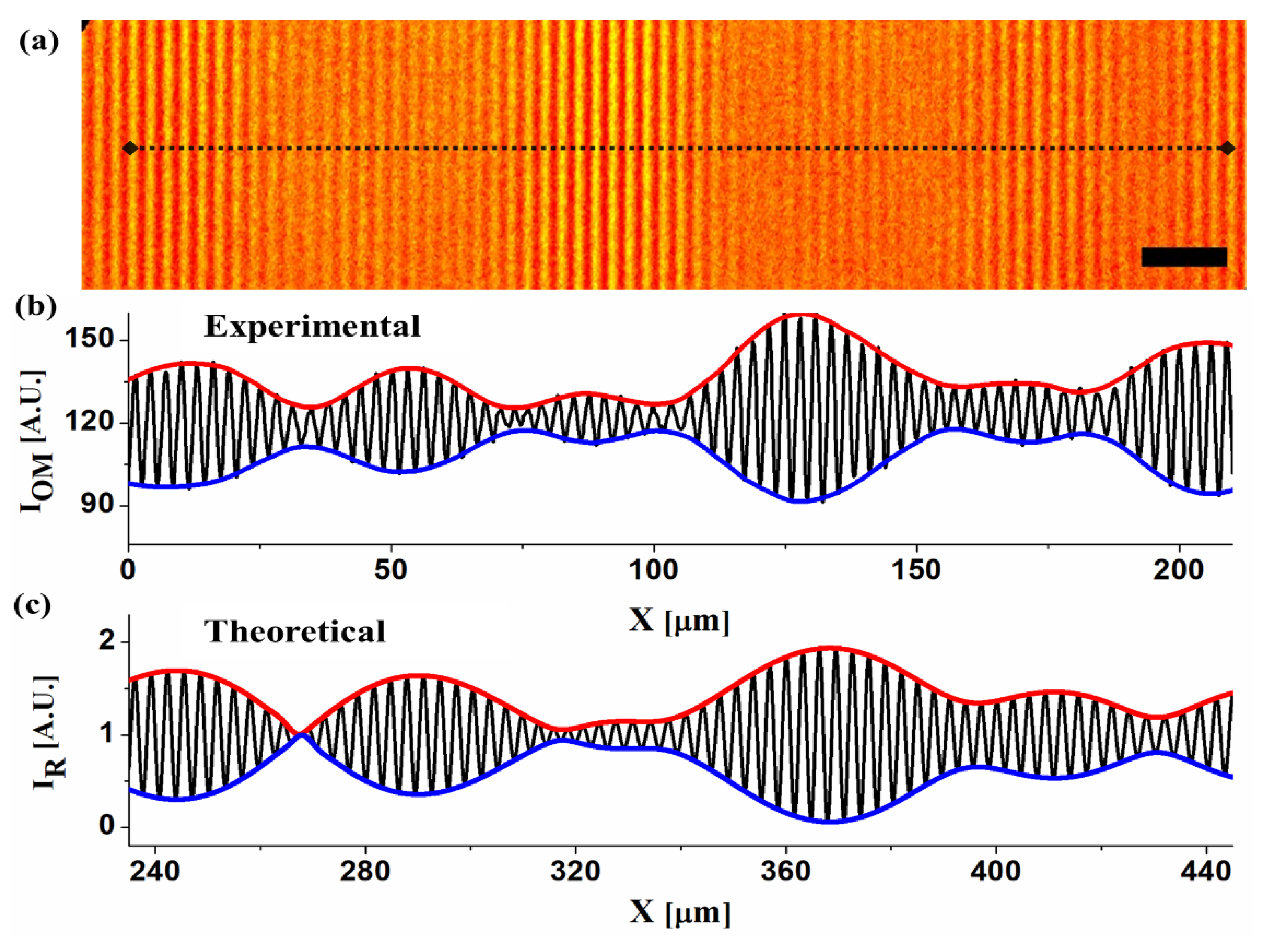
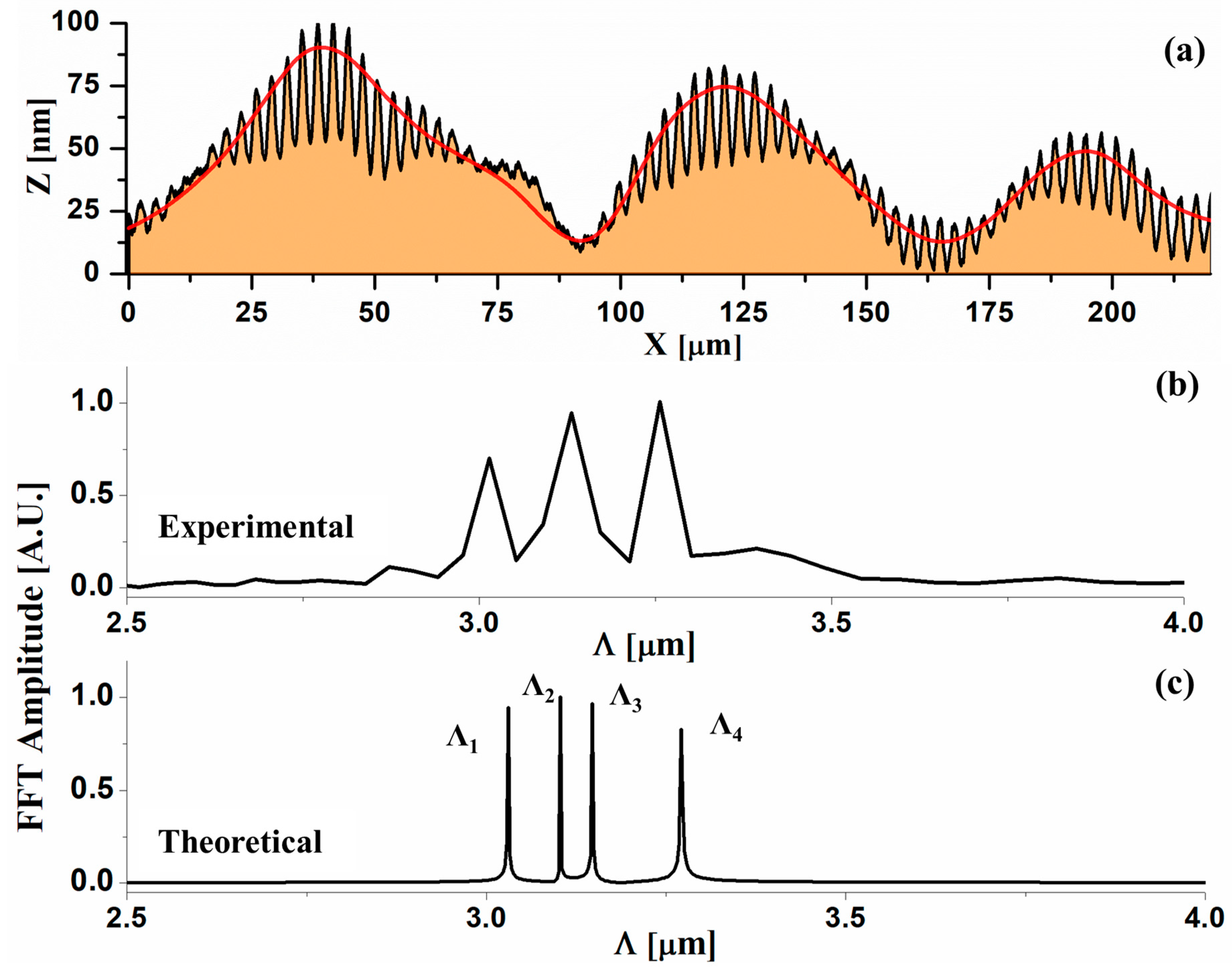
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Salvatore, M.; Oscurato, S.L.; Maddalena, P.; Ambrosio, A. Light-Induced Complex Surface Structuring of Azobenzene-Containing Materials; Elsevier Inc.: Amsterdam, The Netherlands, 2020; ISBN 9780128168653. [Google Scholar]
- Jelken, J.; Santer, S. Light induced reversible structuring of photosensitive polymer films. RSC Adv. 2019, 9, 20295–20305. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Tang, G.; Hua, D.; Xiong, R.; Han, J.; Jiang, S.; Zhang, Q.; Huang, C. Stimuli-responsive bio-based polymeric systems and their applications. J. Mater. Chem. B 2019, 7, 709–729. [Google Scholar] [CrossRef] [PubMed]
- Katz, J.S.; Burdick, J.A. Light-Responsive Biomaterials: Development and Applications. Macromol. Biosci. 2010, 10, 339–348. [Google Scholar] [CrossRef] [PubMed]
- Knipe, J.M.; Peppas, N.A. Multi-responsive hydrogels for drug delivery and tissue engineering applications. Regen. Biomater. 2014, 1, 57–65. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Municoy, S.; Álvarez Echazú, M.I.; Antezana, P.E.; Galdopórpora, J.M.; Olivetti, C.; Mebert, A.M.; Foglia, M.L.; Tuttolomondo, M.V.; Alvarez, G.S.; Hardy, J.G.; et al. Stimuli-Responsive Materials for Tissue Engineering and Drug Delivery. Int. J. Mol. Sci. 2020, 21, 4724. [Google Scholar] [CrossRef]
- Gao, Z.; Han, Y.; Wang, F. Cooperative supramolecular polymers with anthracene‒endoperoxide photo-switching for fluorescent anti-counterfeiting. Nat. Commun. 2018, 9, 3977. [Google Scholar] [CrossRef]
- Yang, T.; Zuo, Y.; Feng, S. Rational design of photo-chromic molecule for constructing polysiloxane-based fluorescent films and anti-counterfeiting. Mater. Des. 2021, 207, 109867. [Google Scholar] [CrossRef]
- Zeng, H.; Wani, O.M.; Wasylczyk, P.; Priimagi, A. Light--Driven, Caterpillar--Inspired Miniature Inching Robot. Macromol. Rapid Commun. 2018, 39, 1700224. [Google Scholar] [CrossRef]
- Zhou, P.; Chen, L.; Yao, L.; Weng, M.; Zhang, W. Humidity- and light-driven actuators based on carbon nanotube-coated paper and polymer composite. Nanoscale 2018, 10, 8422–8427. [Google Scholar] [CrossRef]
- Mesaritakis, C.; Akriotou, M.; Kapsalis, A.; Grivas, E.; Chaintoutis, C.; Nikas, T.; Syvridis, D. Physical Unclonable Function based on a Multi-Mode Optical Waveguide. Sci. Rep. 2018, 8, 9653. [Google Scholar] [CrossRef]
- Chaintoutis, C.; Akriotou, M.; Mesaritakis, C.; Komnios, I.; Karamitros, D.; Fragkos, A.; Syvridis, D. Optical PUFs as physical root of trust for blockchain--driven applications. IET Softw. 2019, 13, 182–186. [Google Scholar] [CrossRef]
- Perera-Costa, D.; Bruque, J.M.; González-Martín, M.L.; Gómez-García, A.C.; Vadillo-Rodríguez, V. Studying the Influence of Surface Topography on Bacterial Adhesion using Spatially Organized Microtopographic Surface Patterns. Langmuir 2014, 30, 4633–4641. [Google Scholar] [CrossRef] [PubMed]
- Oscurato, S.L.; Salvatore, M.; Maddalena, P.; Ambrosio, A. From nanoscopic to macroscopic photo-driven motion in azobenzene-containing materials. Nanophotonics 2018, 7, 1387–1422. [Google Scholar] [CrossRef]
- Zhao, Y.; Ikeda, T. (Eds.) Smart Light-Responsive Materials; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; ISBN 9780470439098. [Google Scholar]
- Pagliusi, P.; Audia, B.; Provenzano, C.; Piñol, M.; Oriol, L.; Cipparrone, G. Tunable Surface Patterning of Azopolymer by Vectorial Holography: The Role of Photoanisotropies in the Driving Force. ACS Appl. Mater. Interfaces 2019, 11, 34471–34477. [Google Scholar] [CrossRef]
- Yadavalli, N.S.; Korolkov, D.; Moulin, J.-F.; Krutyeva, M.; Santer, S. Probing Opto-Mechanical Stresses within Azobenzene-Containing Photosensitive Polymer Films by a Thin Metal Film Placed Above. ACS Appl. Mater. Interfaces 2014, 6, 11333–11340. [Google Scholar] [CrossRef] [PubMed]
- Bandara, H.M.D.; Burdette, S.C. Photoisomerization in different classes of azobenzene. Chem. Soc. Rev. 2012, 41, 1809–1825. [Google Scholar] [CrossRef] [PubMed]
- Audia, B.; Pagliusi, P.; Provenzano, C.; Roche, A.; Oriol, L.; Cipparrone, G. Influence of Photoanisotropies on Light-Controllable Structuration of Azopolymer Surface. ACS Appl. Polym. Mater. 2020, 2, 1597–1604. [Google Scholar] [CrossRef]
- Nedelchev, L.; Ivanov, D.; Berberova, N.; Strijkova, V.; Nazarova, D. Polarization holographic gratings with high diffraction efficiency recorded in azopolymer PAZO. Opt. Quantum Electron. 2018, 50, 212. [Google Scholar] [CrossRef]
- Park, K.J.; Park, J.H.; Huh, J.-H.; Kim, C.H.; Ho, D.H.; Choi, G.H.; Yoo, P.J.; Cho, S.M.; Cho, J.H.; Lee, S. Petal-Inspired Diffractive Grating on a Wavy Surface: Deterministic Fabrications and Applications to Colorizations and LED Devices. ACS Appl. Mater. Interfaces 2017, 9, 9935–9944. [Google Scholar] [CrossRef]
- Nair, S.; Escobedo, C.; Sabat, R.G. Crossed Surface Relief Gratings as Nanoplasmonic Biosensors. ACS Sens. 2017, 2, 379–385. [Google Scholar] [CrossRef]
- Fedele, C.; Mäntylä, E.; Belardi, B.; Hamkins-Indik, T.; Cavalli, S.; Netti, P.A.; Fletcher, D.A.; Nymark, S.; Priimagi, A.; Ihalainen, T.O. Azobenzene-based sinusoidal surface topography drives focal adhesion confinement and guides collective migration of epithelial cells. Sci. Rep. 2020, 10, 15329. [Google Scholar] [CrossRef]
- Schedl, A.E.; Probst, P.T.; Meichner, C.; Neuber, C.; Kador, L.; Fery, A.; Schmidt, H.-W. Confinement templates for hierarchical nanoparticle alignment prepared by azobenzene-based surface relief gratings. Soft Matter 2019, 15, 3872–3878. [Google Scholar] [CrossRef] [PubMed]
- Probst, C.; Meichner, C.; Kreger, K.; Kador, L.; Neuber, C.; Schmidt, H.-W. Athermal Azobenzene-Based Nanoimprint Lithography. Adv. Mater. 2016, 28, 2624–2628. [Google Scholar] [CrossRef]
- Bian, S.; Williams, J.M.; Kim, D.Y.; Li, L.; Balasubramanian, S.; Kumar, J.; Tripathy, S. Photoinduced surface deformations on azobenzene polymer films. J. Appl. Phys. 1999, 86, 4498–4508. [Google Scholar] [CrossRef]
- Tofini, A.; Levesque, L.; Lebel, O.; Sabat, R.G. Erasure of surface relief gratings in azobenzene molecular glasses by localized heating using a CO2 laser. J. Mater. Chem. C 2018, 6, 1083–1091. [Google Scholar] [CrossRef]
- Ubukata, T.; Isoshima, T.; Hara, M. Wavelength-Programmable Organic Distributed-Feedback Laser Based on a Photoassisted Polymer-Migration System. Adv. Mater. 2005, 17, 1630–1633. [Google Scholar] [CrossRef]
- Krüger, J.; Bolle, N.; Calvelo, T.; Bergmann, S.; Abourahma, H.; McGee, D.J. Optical reconfiguration of surface relief gratings on supramolecular polymer films using grating translation and superposition. J. Appl. Phys. 2019, 125, 243108. [Google Scholar] [CrossRef]
- Yadavalli, N.S.; Saphiannikova, M.; Santer, S. Photosensitive response of azobenzene containing films towards pure intensity or polarization interference patterns. Appl. Phys. Lett. 2014, 105, 051601. [Google Scholar] [CrossRef]
- Leibold, J.; Sabat, R.G. Fabrication of micrometer-scale surface relief gratings in azobenzene molecular glass films using a modified Lloyd’s mirror interferometer. Opt. Mater. 2019, 96, 109315. [Google Scholar] [CrossRef]
- Ogiwara, A.; Hirokari, T. Formation of anisotropic diffraction gratings in a polymer-dispersed liquid crystal by polarization modulation using a spatial light modulator. Appl. Opt. 2008, 47, 3015. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, U.; Pagliusi, P.; Provenzano, C.; Lepera, E.; Cipparrone, G. Liquid crystal microlens arrays recorded by polarization holography. Appl. Opt. 2015, 54, 3303. [Google Scholar] [CrossRef] [PubMed]
- Do, D.B.; Lin, J.H.; Lai, N.D.; Kan, H.-C.; Hsu, C.C. Fabrication of three-dimensional polymer quadratic nonlinear grating structures by layer-by-layer direct laser writing technique. Appl. Opt. 2011, 50, 4664. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.-A.; Wang, C.-H.; Zhang, Y.-S.; Mo, T.-S.; Huang, S.-Y.; Hsieh, X.-L.; Wong, Y.-J.; Lin, J.-D.; Lee, C.-R. Control of Large-Area Orderliness of a 2D Supramolecular Chiral Microstructure by a 1D Interference Field. ACS Appl. Mater. Interfaces 2021, 13, 44916–44924. [Google Scholar] [CrossRef]
- Oscurato, S.L.; Salvatore, M.; Borbone, F.; Maddalena, P.; Ambrosio, A. Computer-generated holograms for complex surface reliefs on azopolymer films. Sci. Rep. 2019, 9, 6775. [Google Scholar] [CrossRef] [Green Version]
- Ruffato, G.; Rossi, R.; Massari, M.; Mafakheri, E.; Capaldo, P.; Romanato, F. Design, fabrication and characterization of Computer Generated Holograms for anti-counterfeiting applications using OAM beams as light decoders. Sci. Rep. 2017, 7, 18011. [Google Scholar] [CrossRef] [Green Version]
- Jean-Michel, D. Three coloured differential interferometry. Appl. Opt. 1997, 13. [Google Scholar] [CrossRef]
- Desse, J.-M.; Albe, F.; Tribillon, J.-L. Real-time color holographic interferometry. Appl. Opt. 2002, 41, 5326. [Google Scholar] [CrossRef]
- Van der Veen, R.C.A.; Tran, T.; Lohse, D.; Sun, C. Direct measurements of air layer profiles under impacting droplets using high-speed color interferometry. Phys. Rev. E 2012, 85, 026315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Born, M.; Wolf, E.; Bhatia, A.B.; Clemmow, P.C.; Gabor, D.; Stokes, A.R.; Taylor, A.M.; Wayman, P.A.; Wilcock, W.L. Principles of Optics; Cambridge University Press: Cambridge, MA, USA, 1999; ISBN 9780521642224. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Audia, B.; Pagliusi, P.; Mazzulla, A.; Cipparrone, G. Multi-Wavelength Optical Patterning for Multiscale Materials Design. Photonics 2021, 8, 481. https://doi.org/10.3390/photonics8110481
Audia B, Pagliusi P, Mazzulla A, Cipparrone G. Multi-Wavelength Optical Patterning for Multiscale Materials Design. Photonics. 2021; 8(11):481. https://doi.org/10.3390/photonics8110481
Chicago/Turabian StyleAudia, Biagio, Pasquale Pagliusi, Alfredo Mazzulla, and Gabriella Cipparrone. 2021. "Multi-Wavelength Optical Patterning for Multiscale Materials Design" Photonics 8, no. 11: 481. https://doi.org/10.3390/photonics8110481
APA StyleAudia, B., Pagliusi, P., Mazzulla, A., & Cipparrone, G. (2021). Multi-Wavelength Optical Patterning for Multiscale Materials Design. Photonics, 8(11), 481. https://doi.org/10.3390/photonics8110481




