Silicon-Based Optoelectronics Enhanced by Hybrid Plasmon Polaritons: Bridging Dielectric Photonics and Nanoplasmonics
Abstract
1. Introduction
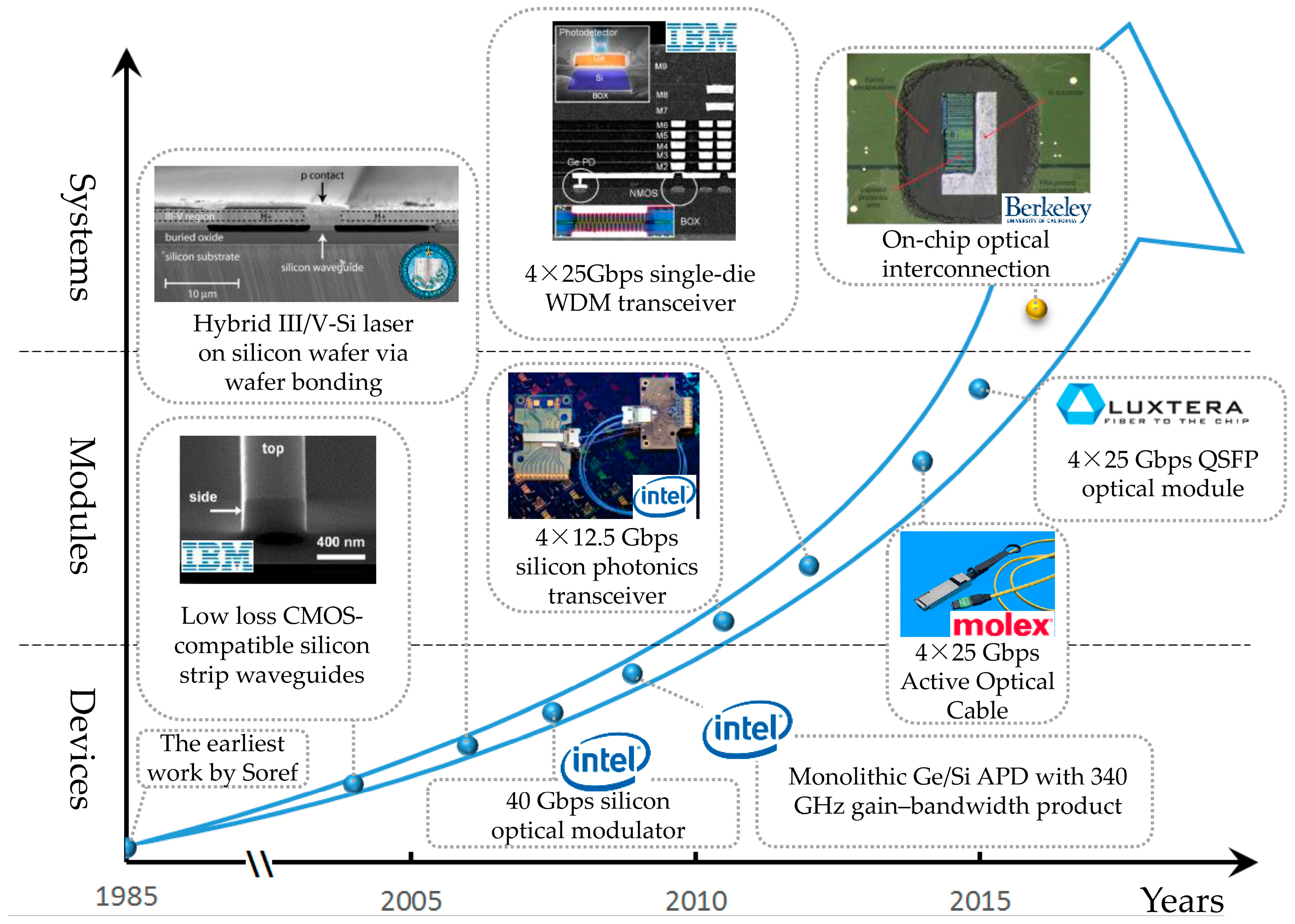
1.1. Silicon-Based Optoelectronics
1.2. Plasmonics
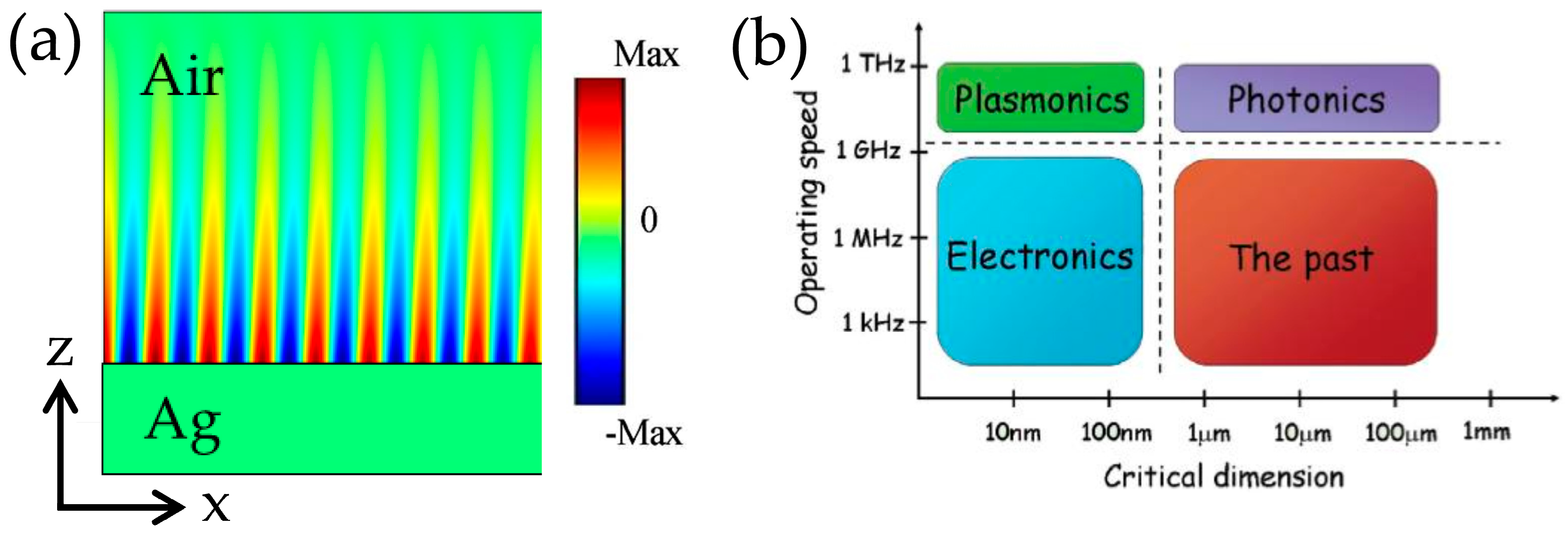
1.2.1. Fundamental Principles of Plasmonics
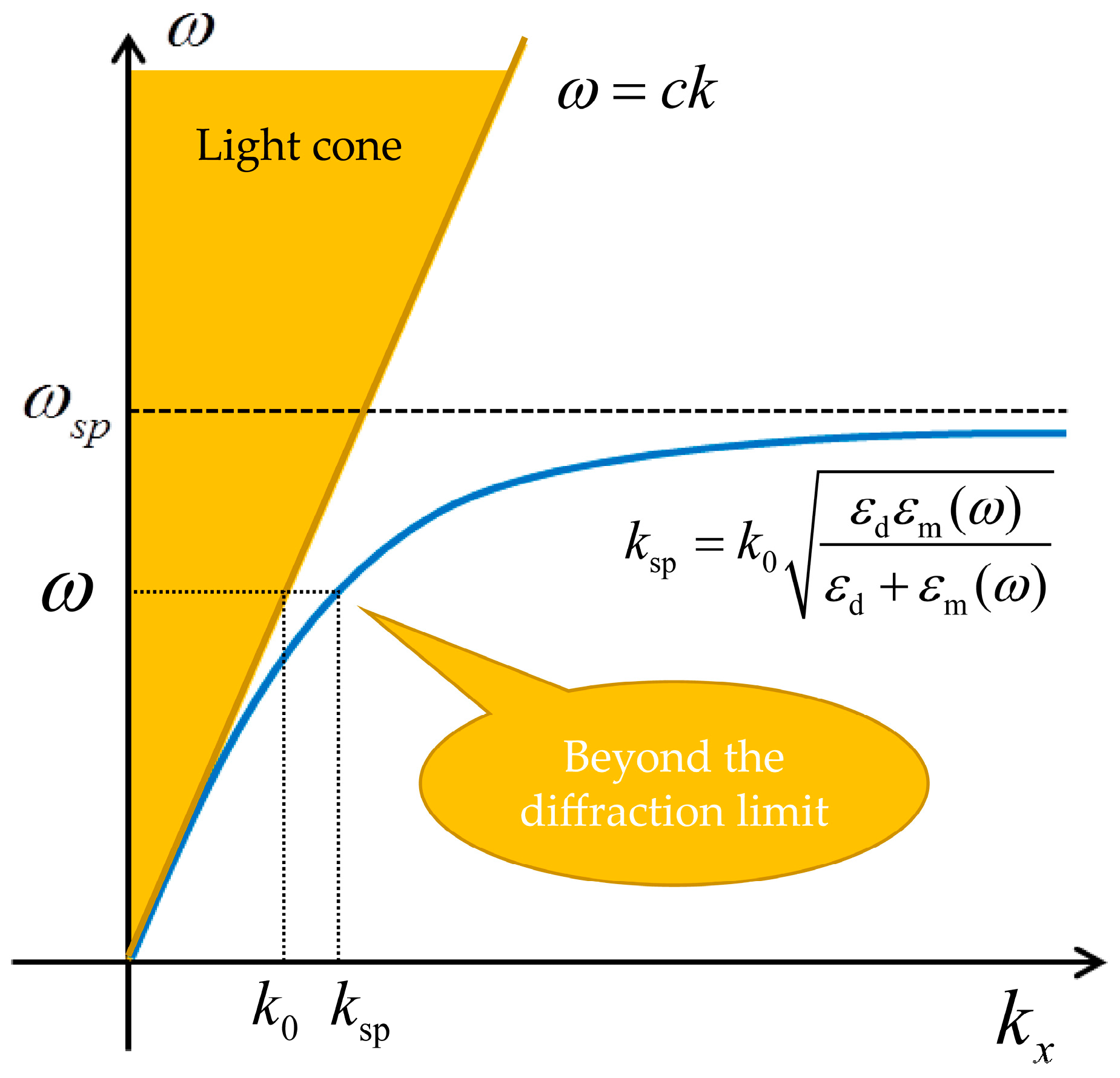
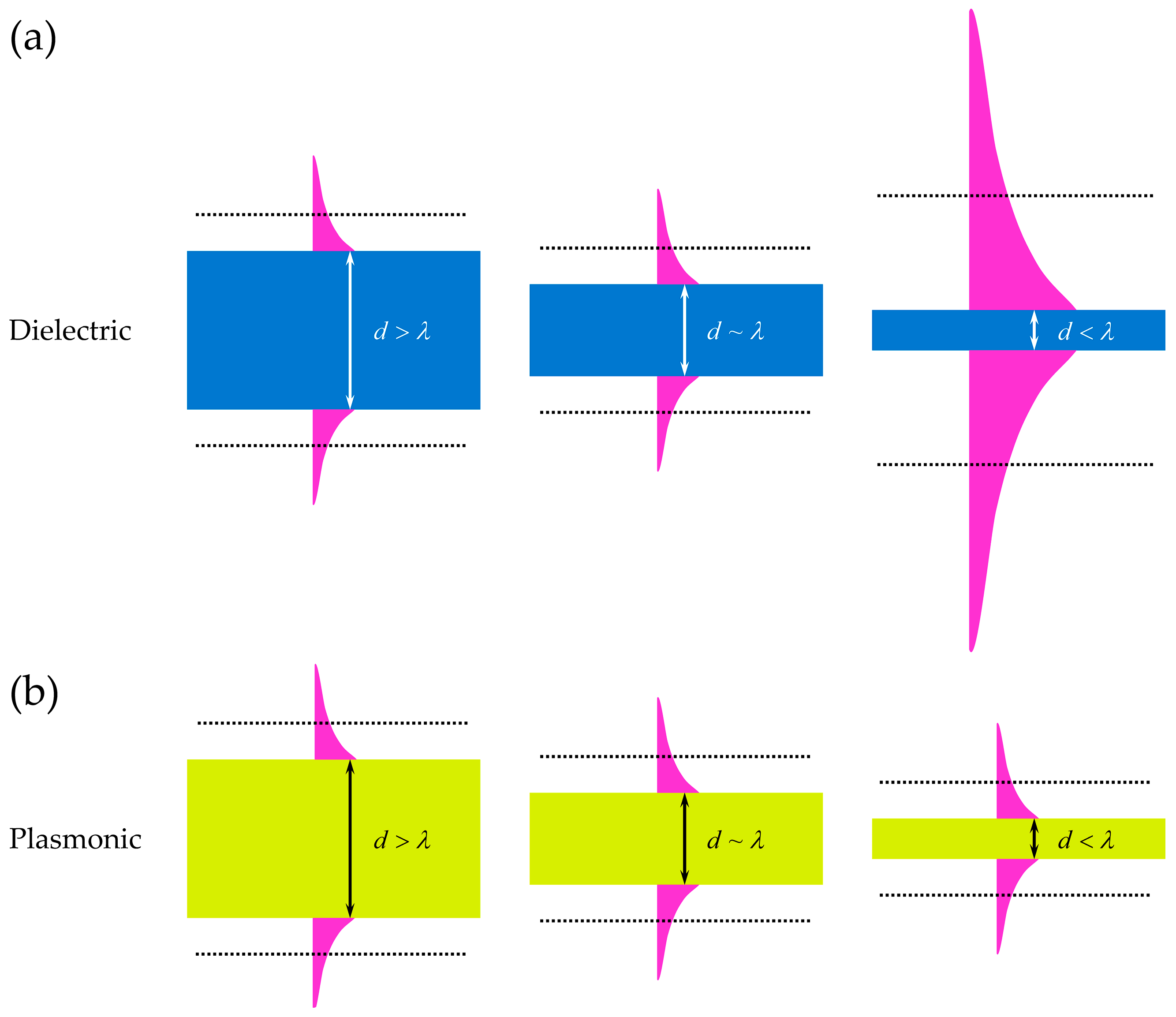
1.2.2. Surface Plasmon Subwavelength Optics
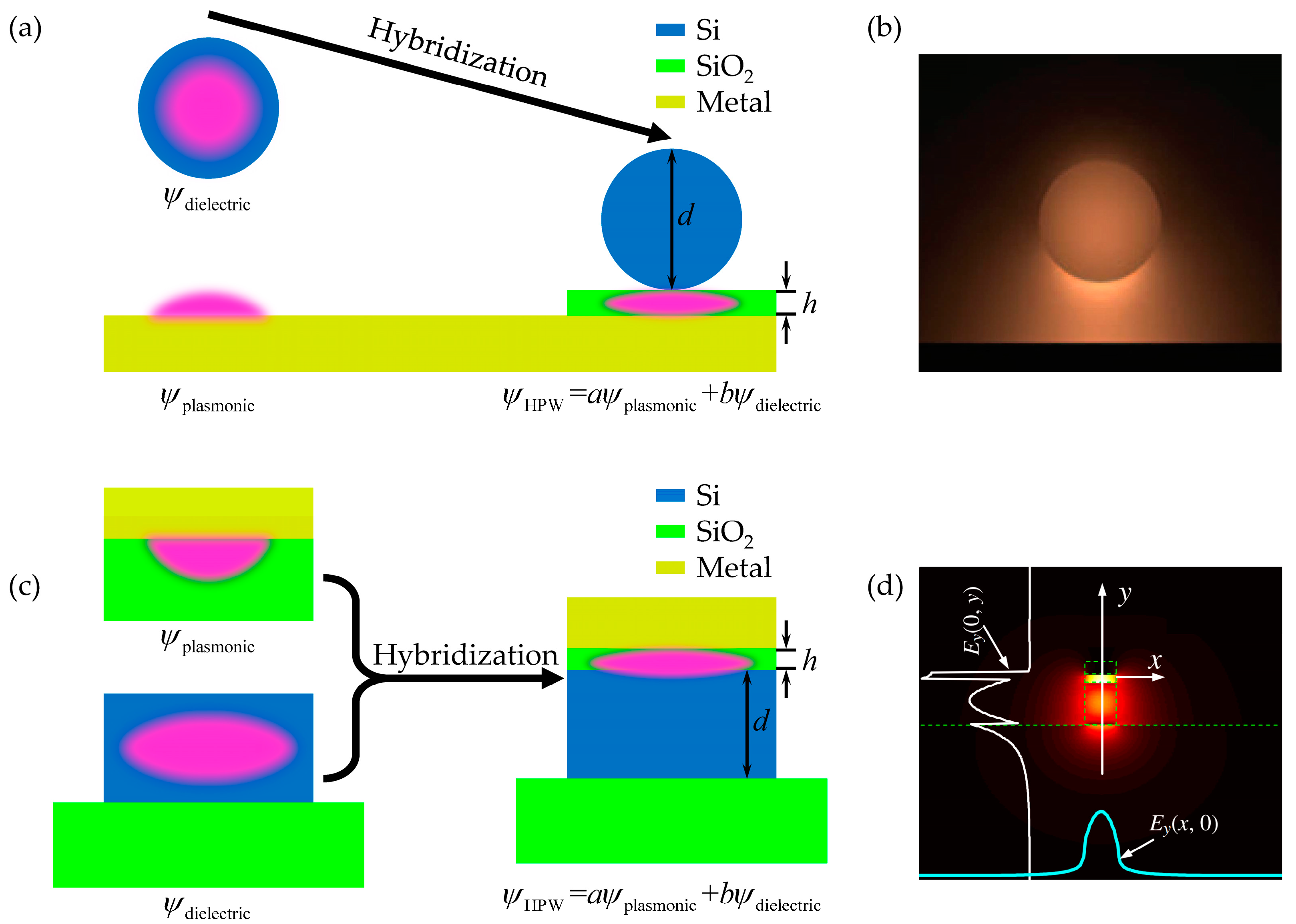
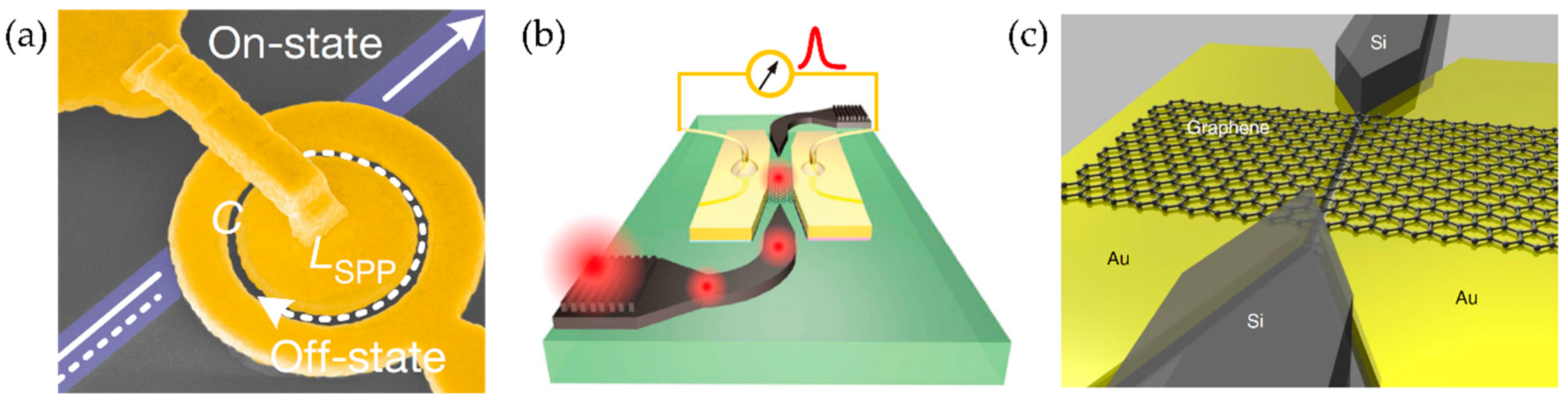
2. Hybrid Plasmon Polaritons (HPPs)
3. HPPs Enhancing the Silicon Photonic Circuits
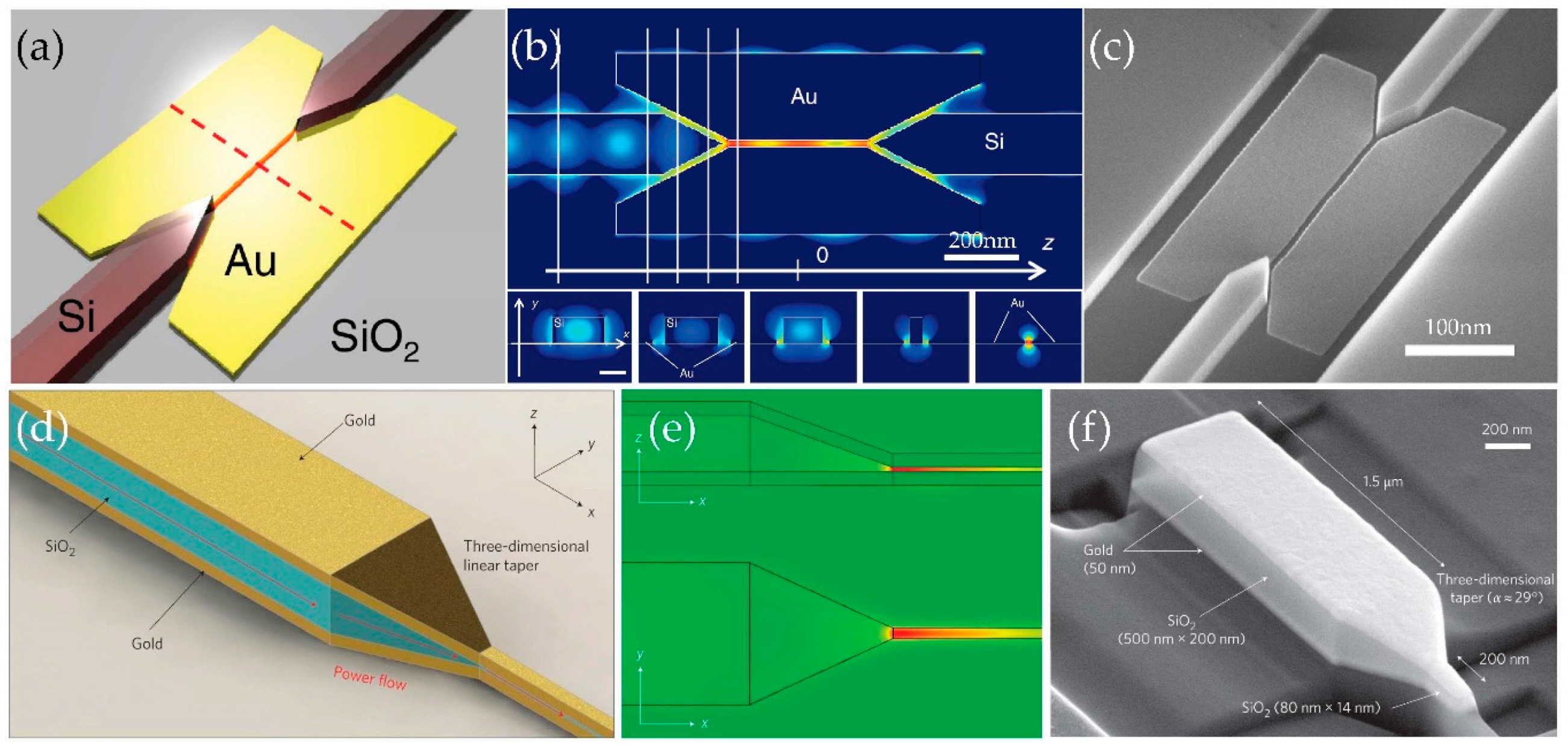
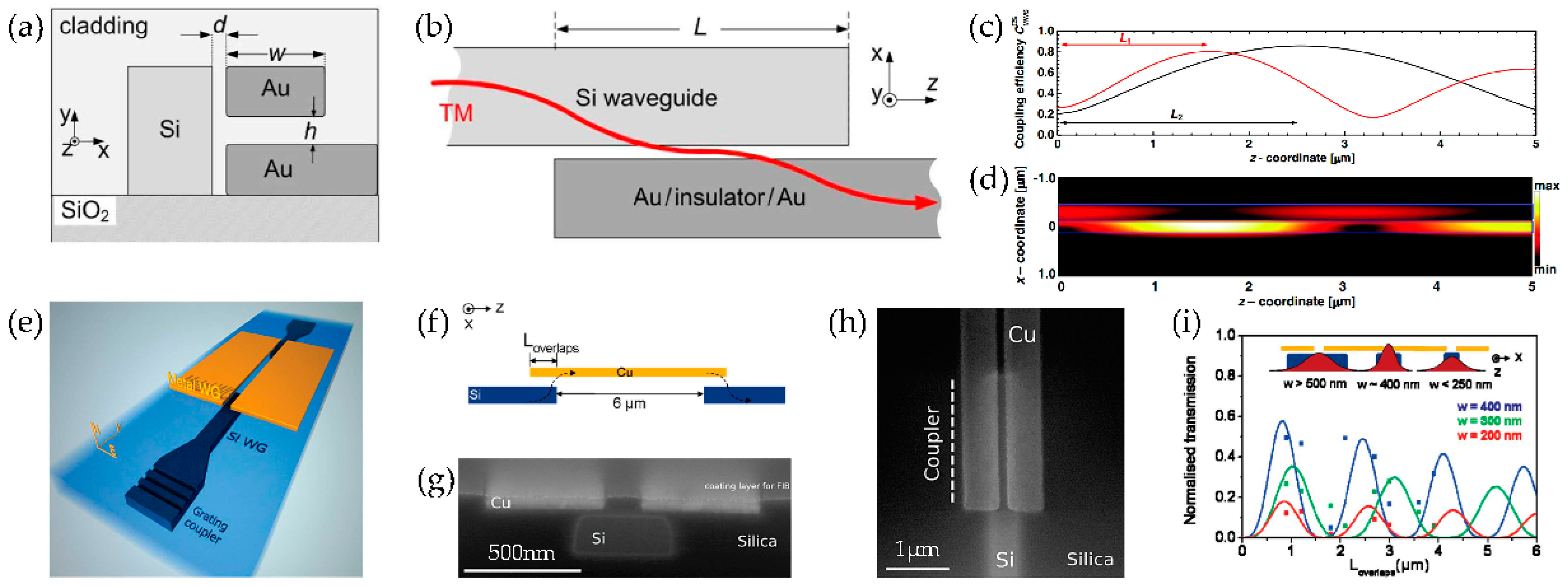
3.1. Tapered Coupling Design
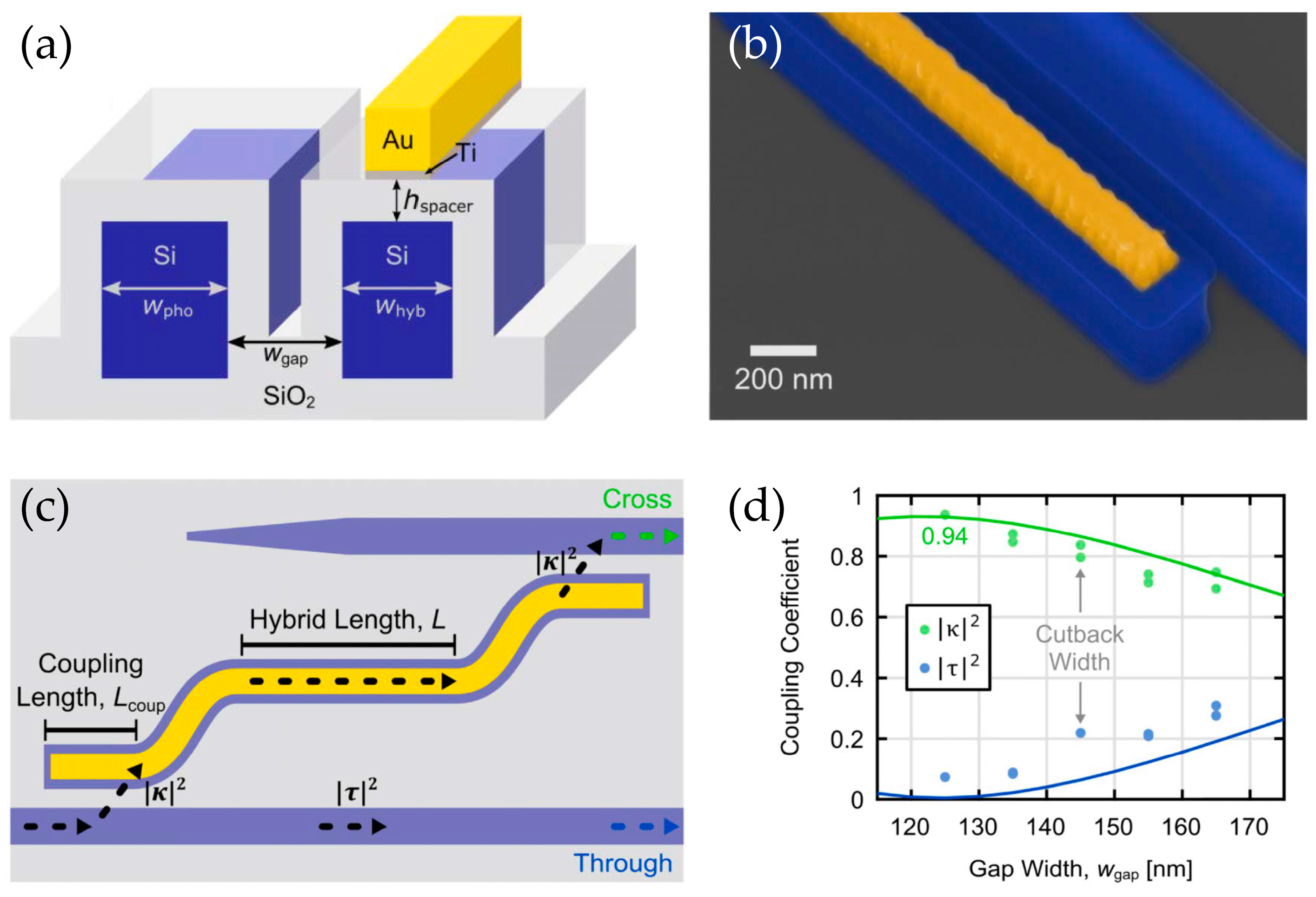
3.2. Directional Coupling Design
4. Prospects and Challenges of HPPs
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Z.; Yin, B.; Michel, J. On-chip light sources for silicon photonics. Light Sci. Appl. 2015, 4, e358. [Google Scholar] [CrossRef]
- Reed, G.T.; Mashanovich, G.; Gardes, F.Y.; Thomson, D.J. Silicon optical modulators. Nat. Photonics 2010, 4, 518–526. [Google Scholar] [CrossRef]
- Liu, D.; Tang, J.; Meng, Y.; Li, W.; Zhu, N.; Li, M. Ultra-low Vpp and high-modulation-depth InP-based electro–optic microring modulator. J. Semicond. 2021, 42, 82301. [Google Scholar] [CrossRef]
- Dai, D.; Bowers, J.E. Silicon-based on-chip multiplexing technologies and devices for Peta-bit optical interconnects. Nanophotonics 2014, 3, 283–311. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Dai, D. Multimode silicon photonics. Nanophotonics 2019, 8, 227–247. [Google Scholar] [CrossRef]
- Son, G.; Han, S.; Park, J.; Kwon, K.; Yu, K. High-efficiency broadband light coupling between optical fibers and photonic integrated circuits. Nanophotonics 2018, 7, 1845–1864. [Google Scholar] [CrossRef]
- Marchetti, R.; Lacava, C.; Carroll, L.; Gradkowski, K.; Minzioni, P. Coupling strategies for silicon photonics integrated chips [Invited]. Photonics Res. 2019, 7, 201–239. [Google Scholar] [CrossRef]
- Dai, D.; Bauters, J.; Bowers, J.E. Passive technologies for future large-scale photonic integrated circuits on silicon: Polarization handling, light non-reciprocity and loss reduction. Light Sci. Appl. 2012, 1, e1. [Google Scholar] [CrossRef]
- Su, L.; Ouyang, W.; Fang, X. Facile fabrication of heterostructure with p-BiOCl nanoflakes and n-ZnO thin film for UV photodetectors. J. Semicond. 2021, 42, 52301. [Google Scholar] [CrossRef]
- Yin, Z.; Hu, X.; Zeng, J.; Zeng, Y.; Peng, W. Self-powered circularly polarized light detector based on asymmetric chiral metamaterials. J. Semicond. 2020, 41, 122301. [Google Scholar] [CrossRef]
- Sun, C.; Wade, M.T.; Lee, Y.; Orcutt, J.S.; Alloatti, L.; Georgas, M.S.; Waterman, A.S.; Shainline, J.M.; Avizienis, R.R.; Lin, S.; et al. Single-chip microprocessor that communicates directly using light. Nature 2015, 528, 534–538. [Google Scholar] [CrossRef]
- Intel. The 50G Silicon Photonics Link; White Paper; Intel: Santa Clara, CA, USA, 2010. [Google Scholar]
- Vlasov, Y.A.; McNab, S.J. Losses in single-mode silicon-on-insulator strip waveguides and bends. Opt. Express 2004, 12, 1622–1631. [Google Scholar] [CrossRef]
- Fang, A.W.; Park, H.; Cohen, O.; Jones, R.; Paniccia, M.J.; Bowers, J.E. Electrically pumped hybrid AlGaInAs-silicon evanescent laser. Opt. Express 2006, 14, 9203–9210. [Google Scholar] [CrossRef] [PubMed]
- Assefa, S.; Shank, S.; Green, W.; Khater, M.; Kiewra, E.; Reinholm, C.; Vlasov, Y. A 90nm CMOS integrated Nano-Photonics technology for 25Gbps WDM optical communications applications. In Proceedings of the 2012 International Electron Devices Meeting, San Francisco, CA, USA, 10–13 December 2012; pp. 33–38. [Google Scholar]
- Molex Active Optical Cable. Available online: https://www.molex.com/molex/products/family (accessed on 23 August 2021).
- Liao, L.; Liu, A.; Rubin, D.; Basak, J.; Chetrit, Y.; Nguyen, H.; Cohen, R.; Izhaky, N.; Paniccia, M. 40 Gbit/s silicon optical modulator for high-speed applications. Electron. Lett. 2007, 43, 1196–1197. [Google Scholar] [CrossRef]
- Kang, Y.; Liu, H.; Morse, M.; Paniccia, M.J.; Zadka, M.; Litski, S.; Sarid, G.; Pauchard, A.; Kuo, Y.; Chen, H.; et al. Monolithic germanium/silicon avalanche photodiodes with 340 GHz gain–bandwidth product. Nat. Photonics 2009, 3, 59–63. [Google Scholar] [CrossRef]
- Luxtera 100G (4 × 26) PSM4 QSFP Module. Available online: http://www.luxtera.com/luxtera/products (accessed on 23 August 2021).
- Zhou, Z.; Chen, R.; Li, X.; Li, T. Development trends in silicon photonics for data centers. Opt. Fiber Technol. 2018, 44, 13–23. [Google Scholar] [CrossRef]
- International Technology Roadmap for Semiconductors 2.0, 2015 ed.; Beyond CMOS. In 2015; ITRS: New York, NY, USA, 2015.
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef]
- Sorger, V.J.; Oulton, R.F.; Ma, R.; Zhang, X. Toward integrated plasmonic circuits. MRS Bull. 2012, 37, 728–738. [Google Scholar] [CrossRef]
- Brongersma, M.L.; Shalaev, V.M. The Case for Plasmonics. Science 2010, 328, 440. [Google Scholar] [CrossRef]
- Berini, P. Figures of merit for surface plasmon waveguides. Opt. Express 2006, 14, 13030–13042. [Google Scholar] [CrossRef] [PubMed]
- Conway, J.A.; Sahni, S.; Szkopek, T. Plasmonic interconnects versus conventional interconnects: A comparison of latency, crosstalk and energy costs. Opt. Express 2007, 15, 4474–4484. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Bertolotti, M.; Sibilia, C.; Guzman, A.M. Evanescent Waves in Optics: An Introduction to Plasmonics; Springer: Berlin/Heidelberg, Germany, 2017; Volume 206. [Google Scholar]
- Ritchie, R.H. Plasma Losses by Fast Electrons in Thin Films. Phys. Rev. 1957, 106, 874–881. [Google Scholar] [CrossRef]
- Ozbay, E. Plasmonics: Merging Photonics and Electronics at Nanoscale Dimensions. Science 2006, 311, 189–193. [Google Scholar] [CrossRef]
- Khattak, H.K.; Bianucci, P.; Slepkov, A.D. Linking plasma formation in grapes to microwave resonances of aqueous dimers. Proc. Natl. Acad. Sci. USA 2019, 116, 4000. [Google Scholar] [CrossRef]
- Rotenberg, N.; Kuipers, L. Mapping nanoscale light fields. Nat. Photonics 2014, 8, 919–926. [Google Scholar] [CrossRef]
- Yu, H.; Peng, Y.; Yang, Y.; Li, Z. Plasmon-enhanced light–matter interactions and applications. NPJ Comput. Mater. 2019, 5, 45. [Google Scholar] [CrossRef]
- Wang, Y.; Plummer, E.W.; Kempa, K. Foundations of Plasmonics. Adv. Phys. 2011, 60, 799–898. [Google Scholar] [CrossRef]
- Enoch, S.; Bonod, N. Plasmonics: From Basics to Advanced Topics; Springer: Berlin/Heidelberg, Germany, 2012; Volume 167. [Google Scholar]
- Bozhevolnyi, S.I.; Martin-Moreno, L.; Garcia-Vidal, F. Quantum Plasmonics. In Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 2016; p. 185. [Google Scholar]
- Coronado, E.A.; Schatz, G.C. Surface plasmon broadening for arbitrary shape nanoparticles: A geometrical probability approach. J. Chem. Phys. 2003, 119, 3926–3934. [Google Scholar] [CrossRef]
- Sambles, J.R.; Bradbery, G.W.; Yang, F. Optical excitation of surface plasmons: An introduction. Contemp. Phys. 1991, 32, 173–183. [Google Scholar] [CrossRef]
- Beyond the diffraction limit. Nat. Photonics 2009, 3, 361. [CrossRef]
- Stockman, M.I.; Kneipp, K.; Bozhevolnyi, S.I.; Saha, S.; Dutta, A.; Ndukaife, J.; Kinsey, N.; Reddy, H.; Guler, U.; Shalaev, V.M.; et al. Roadmap on plasmonics. J. Opt. 2018, 20, 43001. [Google Scholar] [CrossRef]
- Stockman, M.I. Nanoplasmonics: The physics behind the applications. Phys. Today 2011, 64, 39–44. [Google Scholar] [CrossRef]
- Kneipp, K. Surface-enhanced Raman scattering. Phys. Today 2007, 60, 40–46. [Google Scholar] [CrossRef]
- Feng, J.; Siu, V.S.; Roelke, A.; Mehta, V.; Rhieu, S.Y.; Palmore, G.T.R.; Pacifici, D. Nanoscale Plasmonic Interferometers for Multispectral, High-Throughput Biochemical Sensing. Nano Lett. 2012, 12, 602–609. [Google Scholar] [CrossRef]
- Chung, T.; Lee, S.; Song, E.Y.; Chun, H.; Lee, B. Plasmonic Nanostructures for Nano-Scale Bio-Sensing. Sensors 2011, 11, 10907–10929. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Ji, D.; Song, H.; Zhang, N.; Hu, Y.; Anthopoulos, T.D.; Di Fabrizio, E.M.; Xiao, S.; Gan, Q. Light–Matter Interaction within Extreme Dimensions: From Nanomanufacturing to Applications. Adv. Opt. Mater. 2018, 6, 1800444. [Google Scholar] [CrossRef]
- Schuller, J.A.; Barnard, E.S.; Cai, W.; Jun, Y.C.; White, J.S.; Brongersma, M.L. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193–204. [Google Scholar] [CrossRef]
- Knoll, B.; Keilmann, F. Near-field probing of vibrational absorption for chemical microscopy. Nature 1999, 399, 134–137. [Google Scholar] [CrossRef]
- Kawata, S.; Inouye, Y.; Verma, P. Plasmonics for near-field nano-imaging and superlensing. Nat. Photonics 2009, 3, 388–394. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Nanofocusing of electromagnetic radiation. Nat. Photonics 2014, 8, 13–22. [Google Scholar] [CrossRef]
- Lee, B.; Kim, S.; Kim, H.; Lim, Y. The use of plasmonics in light beaming and focusing. Prog. Quant. Electron. 2010, 34, 47–87. [Google Scholar] [CrossRef]
- Kim, S.; Lim, Y.; Kim, H.; Park, J.; Lee, B. Optical beam focusing by a single subwavelength metal slit surrounded by chirped dielectric surface gratings. Appl. Phys. Lett. 2008, 92, 13103. [Google Scholar] [CrossRef]
- Fu, Y.; Zhou, W.; Lim, L.E.N.; Du, C.L.; Luo, X.G. Plasmonic microzone plate: Superfocusing at visible regime. Appl. Phys. Lett. 2007, 91, 61124. [Google Scholar] [CrossRef]
- Mote, R.G.; Yu, S.F.; Ng, B.K.; Zhou, W.; Lau, S.P. Near-field focusing properties of zone plates in visible regime—New insights. Opt. Express 2008, 16, 9554–9564. [Google Scholar] [CrossRef]
- Shi, H.; Wang, C.; Du, C.; Luo, X.; Dong, X.; Gao, H. Beam manipulating by metallic nano-slits with variant widths. Opt. Express 2005, 13, 6815–6820. [Google Scholar] [CrossRef]
- Min, C.; Wang, P.; Jiao, X.; Deng, Y.; Ming, H. Beam focusing by metallic nano-slit array containing nonlinear material. Appl. Phys. B 2008, 90, 97–99. [Google Scholar] [CrossRef]
- Jia, S.; Wu, Y.; Wang, X.; Wang, N. A Subwavelength Focusing Structure Composite of Nanoscale Metallic Slits Array With Patterned Dielectric Substrate. IEEE Photonics J. 2014, 6, 1–8. [Google Scholar] [CrossRef]
- Wang, B.; Wu, X.; Zhang, Y. Multiple-Wavelength Focusing and Demultiplexing Plasmonic Lens Based on Asymmetric Nanoslit Arrays. Plasmonics 2013, 8, 1535–1541. [Google Scholar] [CrossRef]
- Meinzer, N.; Barnes, W.L.; Hooper, I.R. Plasmonic meta-atoms and metasurfaces. Nat. Photonics 2014, 8, 889–898. [Google Scholar] [CrossRef]
- Yin, L.; Vlasko-Vlasov, V.K.; Pearson, J.; Hiller, J.M.; Hua, J.; Welp, U.; Brown, D.E.; Kimball, C.W. Subwavelength Focusing and Guiding of Surface Plasmons. Nano Lett. 2005, 5, 1399–1402. [Google Scholar] [CrossRef]
- Nomura, W.; Ohtsu, M.; Yatsui, T. Nanodot coupler with a surface plasmon polariton condenser for optical far/near-field conversion. Appl. Phys. Lett. 2005, 86, 181108. [Google Scholar] [CrossRef]
- Liu, Z.; Steele, J.M.; Srituravanich, W.; Pikus, Y.; Sun, C.; Zhang, X. Focusing Surface Plasmons with a Plasmonic Lens. Nano Lett. 2005, 5, 1726–1729. [Google Scholar] [CrossRef] [PubMed]
- Stockman, M.I. Nanofocusing of Optical Energy in Tapered Plasmonic Waveguides. Phys. Rev. Lett. 2004, 93, 137404. [Google Scholar] [CrossRef] [PubMed]
- Babadjanyan, A.J.; Margaryan, N.L.; Nerkararyan, K.V. Superfocusing of surface polaritons in the conical structure. J. Appl. Phys. 2000, 87, 3785–3788. [Google Scholar] [CrossRef]
- Issa, N.A.; Guckenberger, R. Optical Nanofocusing on Tapered Metallic Waveguides. Plasmonics 2007, 2, 31–37. [Google Scholar] [CrossRef]
- Krüger, M.; Schenk, M.; Hommelhoff, P. Attosecond control of electrons emitted from a nanoscale metal tip. Nature 2011, 475, 78–81. [Google Scholar] [CrossRef]
- Nerkararyan, K.V. Superfocusing of a surface polariton in a wedge-like structure. Phys. Lett. A 1997, 237, 103–105. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Vernon, K.C. Adiabatic nano-focusing of plasmons by sharp metallic wedges. Appl. Phys. B 2007, 86, 7–17. [Google Scholar] [CrossRef]
- Durach, M.; Rusina, A.; Stockman, M.I.; Nelson, K. Toward Full Spatiotemporal Control on the Nanoscale. Nano Lett. 2007, 7, 3145–3149. [Google Scholar] [CrossRef]
- Vernon, K.C.; Gramotnev, D.K.; Pile, D.F.P. Adiabatic nanofocusing of plasmons by a sharp metal wedge on a dielectric substrate. J. Appl. Phys. 2007, 101, 104312. [Google Scholar] [CrossRef]
- Verhagen, E.; Kuipers, L.K.; Polman, A. Plasmonic Nanofocusing in a Dielectric Wedge. Nano Lett. 2010, 10, 3665–3669. [Google Scholar] [CrossRef] [PubMed]
- Gramotnev, D.K.; Tan, S.J.; Kurth, M.L. Plasmon Nanofocusing with Negative Refraction in a High-Index Dielectric Wedge. Plasmonics 2014, 9, 175–184. [Google Scholar] [CrossRef]
- Gramotnev, D.K. Adiabatic nanofocusing of plasmons by sharp metallic grooves: Geometrical optics approach. J. Appl. Phys. 2005, 98, 104302. [Google Scholar] [CrossRef]
- Pile, D.F.P.; Vogel, M.W.; Zhang, X.; Gramotnev, D.K. Local electric field enhancement during nanofocusing of plasmons by a tapered gap. Phys. Rev. B 2007, 75, 35431. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Vogel, M.W.; Stockman, M.I. Optimized nonadiabatic nanofocusing of plasmons by tapered metal rods. J. Appl. Phys. 2008, 104, 34311. [Google Scholar] [CrossRef]
- Pile, D.F.P.; Gramotnev, D.K. Adiabatic and nonadiabatic nanofocusing of plasmons by tapered gap plasmon waveguides. Appl. Phys. Lett. 2006, 89, 41111. [Google Scholar] [CrossRef]
- Volkov, V.S.; Bozhevolnyi, S.I.; Devaux, E.; Ebbesen, T.W. Bend loss for channel plasmon polaritons. Appl. Phys. Lett. 2006, 89, 143108. [Google Scholar] [CrossRef]
- Bozhevolnyi, S.I.; Volkov, V.S.; Devaux, E.; Laluet, J.; Ebbesen, T.W. Channel plasmon subwavelength waveguide components including interferometers and ring resonators. Nature 2006, 440, 508–511. [Google Scholar] [CrossRef] [PubMed]
- Volkov, V.S.; Bozhevolnyi, S.I.; Devaux, E.; Laluet, J.; Ebbesen, T.W. Wavelength Selective Nanophotonic Components Utilizing Channel Plasmon Polaritons. Nano Lett. 2007, 7, 880–884. [Google Scholar] [CrossRef] [PubMed]
- Dionne, J.A.; Sweatlock, L.A.; Sheldon, M.T.; Alivisatos, A.P.; Atwater, H.A. Silicon-Based Plasmonics for On-Chip Photonics. IEEE J. Sel. Top. Quant. 2010, 16, 295–306. [Google Scholar] [CrossRef]
- Ebbesen, T.W.; Genet, C.; Bozhevolnyi, S.I. Surface-plasmon circuitry. Phys. Today 2008, 61, 44–50. [Google Scholar] [CrossRef]
- Charbonneau, R.; Lahoud, N.; Mattiussi, G.; Berini, P. Demonstration of integrated optics elements based on long-ranging surface plasmon polaritons. Opt. Express 2005, 13, 977–984. [Google Scholar] [CrossRef]
- Huang, K.C.Y.; Seo, M.; Sarmiento, T.; Huo, Y.; Harris, J.S.; Brongersma, M.L. Electrically driven subwavelength optical nanocircuits. Nat. Photonics 2014, 8, 244–249. [Google Scholar] [CrossRef]
- Maradudin, A.A.; Novikov, I.V. Channel polaritons. Phys. Rev. B 2002, 66, 35403. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Pile, D.F.P. Single-mode subwavelength waveguide with channel plasmon-polaritons in triangular grooves on a metal surface. Appl. Phys. Lett. 2004, 85, 6323–6325. [Google Scholar] [CrossRef]
- Volkov, V.S.; Devaux, E.; Ebbesen, T.W.; Bozhevolnyi, S.I. Channel Plasmon-Polariton Guiding by Subwavelength Metal Grooves. Phys. Rev. Lett. 2005, 95, 46802. [Google Scholar] [CrossRef]
- Neutens, P.; Lagae, L.; Borghs, G.; Van Dorpe, P. Electrical Excitation of Confined Surface Plasmon Polaritons in Metallic Slot Waveguides. Nano Lett. 2010, 10, 1429–1432. [Google Scholar] [CrossRef]
- Melikyan, A.; Koehnle, K.; Lauermann, M.; Palmer, R.; Koeber, S.; Muehlbrandt, S.; Schindler, P.C.; Elder, D.L.; Wolf, S.; Heni, W.; et al. Plasmonic-organic hybrid (POH) modulators for OOK and BPSK signaling at 40 Gbit/s. Opt. Express 2015, 23, 9938–9946. [Google Scholar] [CrossRef]
- Melikyan, A.; Alloatti, L.; Muslija, A.; Hillerkuss, D.; Schindler, P.C.; Li, J.; Palmer, R.; Korn, D.; Muehlbrandt, S.; Van Thourhout, D.; et al. High-speed plasmonic phase modulators. Nat. Photonics 2014, 8, 229–233. [Google Scholar] [CrossRef]
- Haffner, C.; Heni, W.; Fedoryshyn, Y.; Niegemann, J.; Melikyan, A.; Elder, D.L.; Baeuerle, B.; Salamin, Y.; Josten, A.; Koch, U.; et al. All-plasmonic Mach–Zehnder modulator enabling optical high-speed communication at the microscale. Nat. Photonics 2015, 9, 525–528. [Google Scholar] [CrossRef]
- Haffner, C.; Chelladurai, D.; Fedoryshyn, Y.; Josten, A.; Baeuerle, B.; Heni, W.; Watanabe, T.; Cui, T.; Cheng, B.; Saha, S.; et al. Low-loss plasmon-assisted electro-optic modulator. Nature 2018, 556, 483–486. [Google Scholar] [CrossRef]
- Sorger, V.J.; Lanzillotti-Kimura, N.D.; Ma, R.; Zhang, X. Ultra-compact silicon nanophotonic modulator with broadband response. Nanophotonics 2012, 1, 17–22. [Google Scholar] [CrossRef]
- Dionne, J.A.; Diest, K.; Sweatlock, L.A.; Atwater, H.A. PlasMOStor: A Metal−Oxide−Si Field Effect Plasmonic Modulator. Nano Lett. 2009, 9, 897–902. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Radko, I.P.; Mazurski, N.; Desiatov, B.; Beermann, J.; Albrektsen, O.; Levy, U.; Bozhevolnyi, S.I. On-Chip Detection of Radiation Guided by Dielectric-Loaded Plasmonic Waveguides. Nano Lett. 2015, 15, 476–480. [Google Scholar] [CrossRef]
- Neutens, P.; Van Dorpe, P.; De Vlaminck, I.; Lagae, L.; Borghs, G. Electrical detection of confined gap plasmons in metal–insulator–metal waveguides. Nat. Photonics 2009, 3, 283–286. [Google Scholar] [CrossRef]
- Falk, A.L.; Koppens, F.H.L.; Yu, C.L.; Kang, K.; de Leon Snapp, N.; Akimov, A.V.; Jo, M.; Lukin, M.D.; Park, H. Near-field electrical detection of optical plasmons and single-plasmon sources. Nat. Phys. 2009, 5, 475–479. [Google Scholar] [CrossRef]
- Raether, H. Surface Plasmons; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Dionne, J.A.; Lezec, H.J.; Atwater, H.A. Highly Confined Photon Transport in Subwavelength Metallic Slot Waveguides. Nano Lett. 2006, 6, 1928–1932. [Google Scholar] [CrossRef]
- Spasenović, M.; Polman, A.; Kuipers, L.K.; Verhagen, E. Nanowire Plasmon Excitation by Adiabatic Mode Transformation. Phys. Rev. Lett. 2009, 102, 203904. [Google Scholar] [CrossRef]
- Pile, D.F.P.; Ogawa, T.; Gramotnev, D.K.; Okamoto, T.; Haraguchi, M.; Fukui, M.; Matsuo, S. Theoretical and experimental investigation of strongly localized plasmons on triangular metal wedges for subwavelength waveguiding. Appl. Phys. Lett. 2005, 87, 61106. [Google Scholar] [CrossRef]
- Steinberger, B.; Hohenau, A.; Ditlbacher, H.; Stepanov, A.L.; Drezet, A.; Aussenegg, F.R.; Leitner, A.; Krenn, J.R. Dielectric stripes on gold as surface plasmon waveguides. Appl. Phys. Lett. 2006, 88, 94104. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Li, Q.; Yan, M.; Qiu, M. Broadband coupler between silicon waveguide and hybrid plasmonic waveguide. Opt. Express 2010, 18, 13173–13179. [Google Scholar] [CrossRef]
- Li, Q.; Song, Y.; Zhou, G.; Su, Y.; Qiu, M. Asymmetric plasmonic-dielectric coupler with short coupling length, high extinction ratio, and low insertion loss. Opt. Lett. 2010, 35, 3153–3155. [Google Scholar] [CrossRef] [PubMed]
- Dai, D.; He, S. A silicon-based hybrid plasmonic waveguide with a metal cap for a nano-scale light confinement. Opt. Express 2009, 17, 16646–16653. [Google Scholar] [CrossRef] [PubMed]
- Sorger, V.J.; Ye, Z.; Oulton, R.F.; Wang, Y.; Bartal, G.; Yin, X.; Zhang, X. Experimental demonstration of low-loss optical waveguiding at deep sub-wavelength scales. Nat. Commun. 2011, 2, 331. [Google Scholar] [CrossRef]
- Oulton, R.F.; Sorger, V.J.; Genov, D.A.; Pile, D.F.P.; Zhang, X. A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation. Nat. Photonics 2008, 2, 496–500. [Google Scholar] [CrossRef]
- Lou, F.; Dai, D.; Thylen, L.; Wosinski, L. Design and analysis of ultra-compact EO polymer modulators based on hybrid plasmonic microring resonators. Opt. Express 2013, 21, 20041–20051. [Google Scholar] [CrossRef] [PubMed]
- Bian, Y.; Gong, Q. Low-loss light transport at the subwavelength scale in silicon nano-slot based symmetric hybrid plasmonic waveguiding schemes. Opt. Express 2013, 21, 23907–23920. [Google Scholar] [CrossRef] [PubMed]
- Adhem, K.; Avrutsky, I. Local field enhancement on demand based on hybrid plasmonic-dielectric directional coupler. Opt. Express 2016, 24, 5699–5708. [Google Scholar] [CrossRef]
- Alam, M.Z.; Aitchison, J.S.; Mojahedi, M. Theoretical Analysis of Hybrid Plasmonic Waveguide. IEEE J. Sel. Top. Quant. 2013, 19, 4602008. [Google Scholar] [CrossRef]
- He, X.; Ning, T.; Lu, S.; Zheng, J.; Li, J.; Li, R.; Pei, L. Ultralow loss graphene-based hybrid plasmonic waveguide with deep-subwavelength confinement. Opt. Express 2018, 26, 10109–10118. [Google Scholar] [CrossRef] [PubMed]
- Chelladurai, D.; Doderer, M.; Koch, U.; Fedoryshyn, Y.; Haffner, C.; Leuthold, J. Low-loss hybrid plasmonic coupler. Opt. Express 2019, 27, 11862–11868. [Google Scholar] [CrossRef] [PubMed]
- Prodan, E.; Radloff, C.; Halas, N.J.; Nordlander, P. A Hybridization Model for the Plasmon Response of Complex Nanostructures. Science 2003, 302, 419. [Google Scholar] [CrossRef]
- Haus, H.A.; Huang, W. Coupled-mode theory. Proc. IEEE 1991, 79, 1505–1518. [Google Scholar] [CrossRef]
- Nishihara, H.; Haruna, M.; Suhara, T. Optical Integrated Circuits; McGraw Hill Professional: New York, NY, USA, 1989; Volume 1. [Google Scholar]
- Hardy, A.; Streifer, W. Coupled mode theory of parallel waveguides. J. Lightwave Technol. 1985, 3, 1135–1146. [Google Scholar] [CrossRef]
- Breukelaar, I.G. Surface Plasmon-Polaritons in Thin Metal Strips and Slabs: Waveguiding and Mode Cutoff. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2004. [Google Scholar]
- Shahbazyan, T.V.; Stockman, M.I. Plasmonics: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ginzburg, P.; Arbel, D.; Orenstein, M. Gap plasmon polariton structure for very efficient microscale-to-nanoscale interfacing. Opt. Lett. 2006, 31, 3288–3290. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Shakya, J.; Lipson, M. Subwavelength confinement in an integrated metal slot waveguide on silicon. Opt. Lett. 2006, 31, 2133–2135. [Google Scholar] [CrossRef]
- Ono, M.; Taniyama, H.; Xu, H.; Tsunekawa, M.; Kuramochi, E.; Nozaki, K.; Notomi, M. Deep-subwavelength plasmonic mode converter with large size reduction for Si-wire waveguide. Optica 2016, 3, 999–1005. [Google Scholar] [CrossRef]
- Choo, H.; Kim, M.; Staffaroni, M.; Seok, T.J.; Bokor, J.; Cabrini, S.; Schuck, P.J.; Wu, M.C.; Yablonovitch, E. Nanofocusing in a metal–insulator–metal gap plasmon waveguide with a three-dimensional linear taper. Nat. Photonics 2012, 6, 838–844. [Google Scholar] [CrossRef]
- Zhu, K.; Xu, P.; Sun, P.; Liu, X.; Li, H.; Zhou, Z. An Ultra-compact Broadband TE-pass Nanofocusing Structure. In Proceedings of the Asia Communications and Photonics Conference/International Conference on Information Photonics and Optical Communications 2020 (ACP/IPOC), Beijing, China, 24–27 October 2020; p. M151A. [Google Scholar]
- Zhu, K.; Xu, P.; Sun, P.; Liu, X.; Li, H.; Zhou, Z. Low Loss, High Extinction Ratio Plasmonic Spot Size Converter. In Proceedings of the Asia Communications and Photonics Conference/International Conference on Information Photonics and Optical Communications 2020 (ACP/IPOC), Beijing, China, 24–27 October 2020; p. M31A. [Google Scholar]
- Tian, J.; Yu, S.; Yan, W.; Qiu, M. Broadband high-efficiency surface-plasmon-polariton coupler with silicon-metal interface. Appl. Phys. Lett. 2009, 95, 13504. [Google Scholar] [CrossRef]
- Han, Z.; Elezzabi, A.Y.; Van, V. Experimental realization of subwavelength plasmonic slot waveguides on a silicon platform. Opt. Lett. 2010, 35, 502–504. [Google Scholar] [CrossRef]
- Veronis, G.; Fan, S. Theoretical investigation of compact couplers between dielectric slab waveguides and two-dimensional metal-dielectric-metal plasmonic waveguides. Opt. Express 2007, 15, 1211–1221. [Google Scholar] [CrossRef] [PubMed]
- Briggs, R.M.; Grandidier, J.; Burgos, S.P.; Feigenbaum, E.; Atwater, H.A. Efficient Coupling between Dielectric-Loaded Plasmonic and Silicon Photonic Waveguides. Nano Lett. 2010, 10, 4851–4857. [Google Scholar] [CrossRef] [PubMed]
- Conway, J. Efficient Optical Coupling to the Nanoscale. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 2006. [Google Scholar]
- Yu, J.; Ohtera, Y.; Yamada, H. Highly efficient coupler for dielectric slot waveguides and hybrid plasmonic waveguides. Jpn. J. Appl. Phys. 2018, 57, 052202. [Google Scholar] [CrossRef]
- Chen, C.T.; Xu, X.; Hosseini, A.; Pan, Z.; Subbaraman, H.; Zhang, X.; Chen, R.T. Design of Highly Efficient Hybrid Si-Au Taper for Dielectric Strip Waveguide to Plasmonic Slot Waveguide Mode Converter. J. Lightwave Technol. 2015, 33, 535–540. [Google Scholar] [CrossRef]
- Zhu, B.Q.; Tsang, H.K. High Coupling Efficiency Silicon Waveguide to Metal–Insulator–Metal Waveguide Mode Converter. J. Lightwave Technol. 2016, 34, 2467–2472. [Google Scholar] [CrossRef]
- Feng, N.; Dal Negro, L. Plasmon mode transformation in modulated-index metal-dielectric slot waveguides. Opt. Lett. 2007, 32, 3086–3088. [Google Scholar] [CrossRef]
- Zhu, S.; Liow, T.Y.; Lo, G.Q.; Kwong, D.L. Silicon-based horizontal nanoplasmonic slot waveguides for on-chip integration. Opt. Express 2011, 19, 8888–8902. [Google Scholar] [CrossRef]
- Ginzburg, P.; Arbel, D.; Tein, M.O. Efficient Coupling of Nano-Plasmonics to Micro-Photonic Circuitry. In Proceedings of the Conference on Lasers and Electro-Optics/Quantum Electronics and Laser Science and Photonic Applications Systems Technologies, Baltimore, MD, USA, 22–27 May 2005; p. N5. [Google Scholar]
- Ginzburg, P.; Arbel, D.; Orenstein, M. Surface Plasmon Assisted Interfacing between Nano and Micro Scale Photonic Circuits. In Proceedings of the Integrated Photonics Research and Applications/Nanophotonics for Information Systems, San Diego, CA, USA, 10–13 April 2005; p. A5. [Google Scholar]
- Yang, R.; Wahsheh, R.A.; Lu, Z.; Abushagur, M.A.G. Efficient light coupling between dielectric slot waveguide and plasmonic slot waveguide. Opt. Lett. 2010, 35, 649–651. [Google Scholar] [CrossRef]
- Wu, M.; Han, Z.; Van, V. Conductor-gap-silicon plasmonic waveguides and passive components at subwavelength scale. Opt. Express 2010, 18, 11728–11736. [Google Scholar] [CrossRef]
- Lau, B.; Swillam, M.A.; Helmy, A.S. Hybrid orthogonal junctions: Wideband plasmonic slot-silicon waveguide couplers. Opt. Express 2010, 18, 27048–27059. [Google Scholar] [CrossRef]
- Shi, P.; Zhou, G.; Chau, F.S. Enhanced coupling efficiency between dielectric and hybrid plasmonic waveguides. J. Opt. Soc. Am. B 2013, 30, 1426–1431. [Google Scholar] [CrossRef]
- Lee, S.; Park, J.; Kang, M.; Lee, B. Highly efficient plasmonic interconnector based on the asymmetric junction between metal-dielectric-metal and dielectric slab waveguides. Opt. Express 2011, 19, 9562–9574. [Google Scholar] [CrossRef]
- Heydari, M.B.; Asgari, M.; Jafari, N. Novel analytical model for nano-coupler between metal–insulator–metal plasmonic and dielectric slab waveguides. Opt. Quant. Electron. 2018, 50, 432. [Google Scholar] [CrossRef]
- Liu, Y.; Lai, Y.; Chang, K. Plasmonic Coupler for Silicon-Based Micro-Slabs to Plasominc Nano-Gap Waveguide Mode Coversion Enhancement. J. Lightwave Technol. 2013, 31, 1708–1712. [Google Scholar] [CrossRef]
- Lim, H.J.; Kwon, M.S. Efficient Coupling Between Photonic and Dielectric-Loaded Surface Plasmon Polariton Waveguides with the Same Core Material. IEEE Photonics J. 2014, 6, 1–9. [Google Scholar] [CrossRef][Green Version]
- Desiatov, B.; Goykhman, I.; Levy, U. Plasmonic nanofocusing of light in an integrated silicon photonics platform. Opt. Express 2011, 19, 13150–13157. [Google Scholar] [CrossRef]
- Wahsheh, R.A.; Abushagur, M.A.G. Experimental and theoretical investigations of an air-slot coupler between dielectric and plasmonic waveguides. Opt. Express 2016, 24, 8237–8242. [Google Scholar] [CrossRef] [PubMed]
- Brimont, A.; Vicente Galán, J.; Maria Escalante, J.; Martí, J.; Sanchis, P. Group-index engineering in silicon corrugated waveguides. Opt. Lett. 2010, 35, 2708–2710. [Google Scholar] [CrossRef]
- Bryant, G.H. Propagation in Corrugated Waveguides. Proc. Inst. Electr. Eng. 1969, 116, 203–213. [Google Scholar] [CrossRef]
- Hochberg, M.; Baehr-Jones, T.; Walker, C.; Scherer, A. Integrated plasmon and dielectric waveguides. Opt. Express 2004, 12, 5481–5486. [Google Scholar] [CrossRef] [PubMed]
- Melikyan, A.; Kohl, M.; Sommer, M.; Koos, C.; Freude, W.; Leuthold, J. Photonic-to-plasmonic mode converter. Opt. Lett. 2014, 39, 3488–3491. [Google Scholar] [CrossRef] [PubMed]
- Delacour, C.; Blaize, S.; Grosse, P.; Fedeli, J.M.; Bruyant, A.; Salas-Montiel, R.; Lerondel, G.; Chelnokov, A. Efficient Directional Coupling between Silicon and Copper Plasmonic Nanoslot Waveguides: Toward Metal−Oxide−Silicon Nanophotonics. Nano Lett. 2010, 10, 2922–2926. [Google Scholar] [CrossRef]
- Ding, Y.; Cheng, Z.; Zhu, X.; Yvind, K.; Dong, J.; Galili, M.; Hu, H.; Mortensen, N.A.; Xiao, S.; Oxenløwe, L.K. Ultra-compact integrated graphene plasmonic photodetector with bandwidth above 110 GHz. Nanophotonics 2020, 9, 317–325. [Google Scholar] [CrossRef]
- Ono, M.; Hata, M.; Tsunekawa, M.; Nozaki, K.; Sumikura, H.; Chiba, H.; Notomi, M. Ultrafast and energy-efficient all-optical switching with graphene-loaded deep-subwavelength plasmonic waveguides. Nat. Photonics 2020, 14, 37–43. [Google Scholar] [CrossRef]




| Frequency region | Very high frequency | Optical frequency | Very low frequency | At plasma frequency |
 | 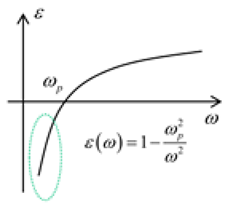 | is complex | 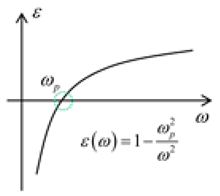 | |
| Relative permittivity | ||||
| Refractive index | n is real | n is complex | ||
| Properties of Metal | 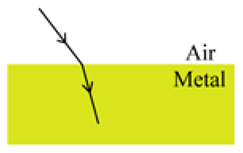 Metal is like dielectric |  Fields decay exponentially |  Fields decay rapidly | Only collective longitudinal oscillations of free electrons exist (called volume plasmons) |
| Waveguide Type | Schematics 1 | Free Space Wavelength λ (nm) | ||
|---|---|---|---|---|
| Metal–insulator–metal (MIM) [98] |  | 685 | 10% | 5 |
| Insulator–metal–insulator (IMI) [99] |  | 1550 | 14% | 14 |
| Triangular metal wedge [100] |  | 633 | - | 2 |
| Dielectric stripe on metal [101] |  | 800 | - | 10 |
| Ref. | Dielectric Waveguide Type and Core Size | Plasmonic Waveguide Type and Core Size | Taper Length /nm | λ/nm | Coupling Loss/dB | Propagation Loss /(dB × μm −1) | Field Enhancement |
|---|---|---|---|---|---|---|---|
| [123] | Si-strip 400 nm × 220 nm | HPW 60 nm × 20 nm | 1080 | 1550 | <0.8 | - | 135.5 |
| [124] | Si-strip 400 nm × 220 nm | HPW 20 nm × 40 nm | - | 1550 | <0.7 | - | 75 |
| [102] | Si-strip 450 nm × 250 nm | HPW 200 nm × 250 nm | 400 | 1550 | 1.5 | - | - |
| [121] * | Si-strip 400 nm × 200 nm | Au-air-Au 50 nm × 20 nm | 600 | 1500–1600 | 1.7 | 1.8 | 41 |
| [125] * | Si-strip 450 nm × 250 nm | Au-air-Au 200 nm × 250 nm | 958.9 | 1460–1540 | 4.5 | 2.5 | - |
| [122] * | SiO2-strip 500 nm × 200 nm | Au- SiO2-Au 80 nm × 14 nm | 1500 | 830 | 1.3 | 4.9 | 400 |
| [126] * | Si-strip 300 nm × 340 nm | Au-PMMA-Au 200 nm × 200 nm | >2500 | 1550 | 5.2 | 0.78 | - |
| [119] | SiO2-strip 1250 nm in width | Au- SiO2-Au 50 nm in width | 6000 | 1550 | 1.5 | - | - |
| [127] | Si-strip 300 nm in width | Ag-air-Ag 50 nm in width | 400 | 1550 | 0.3 | - | - |
| [128] * | Si-ridge 740 nm × 220 nm | Dielectric-loaded 500 nm × 560 nm | ~2000 | 1550 | 1 | 0.09 | - |
| [129] | SiO2-slab 50 nm in thickness | Ag- SiO2-Ag 1 nm in thickness | ~428 | 476 | ~2 | ~109 | ~350 |
| [130] | Si-slot 650 nm in width | HPW 300 nm in width | 50 | 1550 | ~0.5 | - | - |
| [131] | Si-strip 450 nm × 250 nm | Au-SU8-Au 250 nm × 250 nm | 1700 | 1550 | 0.3 | 0.32 | - |
| [132] * | Si-strip 450 nm × 230 nm | Au-PMMA-Au 80 nm × 180 nm | 5400 | 1640 | 4 | 1.8 | - |
| [133] | Si-strip 450 nm × 300 nm | HPW 350 nm × 300 nm | 500 | 1400–1700 | <0.1 | 0.1 | 16 |
| [120] * | Si-strip 450 nm × 250 nm | Au-Si-Au 150 nm × 250 nm | 4000 | 1550 | 2.5 | 0.8 | - |
| [134] * | Si-strip 500 nm × 340 nm | HPW 45 nm × 340 nm | 1000 | 1550 | 0.4 | 0.63 | - |
| [135] | SiO2-strip 1250 nm in width | Au- SiO2-Au 50 nm in width | 2500 | 1550 | 1.5 | - | - |
| [136] | SiO2-strip 1250 nm in width | Au- SiO2-Au 50 nm in width | 6000 | 1550 | <2 | - | - |
| [137] * | Si-slot 460 nm × 260 nm | Au-air-Au 80 nm × 260 nm | - | 1550 | 3.7 | 2 | - |
| [138] * | Si-strip 1000 nm × 340 nm | HPW 200 nm × 440 nm | 1000 | 1550 | 0.97 | 0.1 | - |
| [139] * | Si-strip 400 nm × 340 nm | Ag-air-Ag 50 nm × 340 nm | - | 1530–1590 | ~1.5 | ~3.6 | - |
| [140] | Si-strip with SiN 400 nm × 390 nm | HPW 200 nm × 460 nm | 300 | 1300–1650 | <0.5 | ~0.2 | - |
| [141] | Si-strip 1000 nm × 370 nm | Ag- SiO2-Ag 1000 nm × 100 nm | 540 | 1550 | ~0.6 | - | - |
| [142] | Si-slab 300 nm in width | Ag-air-Ag 63 nm in width | - | 1550 | 1.2 | - | - |
| [143] | Si-slab 1250 nm in width | Ag-Si-Ag 50 nm in width | 1500 | 1550 | 0.3 | - | - |
| [144] * | Si-strip 2500 nm × 900 nm | HPW 500 nm × 900 nm | 4000 | 1550 | 1.1 | 0.083 | - |
| [145] * | Si-strip 900 nm × 250 nm | Au-Si-Au 50 nm × 200 nm | 2000 | 1552 | ~1.2 | - | ~10 |
| [146] * | Si-strip 460 nm × 250 nm | Au-air-Au 80 nm × 250 nm | 50 | 1260–1620 | ~2.8 | ~2 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, P.; Xu, P.; Zhu, K.; Zhou, Z. Silicon-Based Optoelectronics Enhanced by Hybrid Plasmon Polaritons: Bridging Dielectric Photonics and Nanoplasmonics. Photonics 2021, 8, 482. https://doi.org/10.3390/photonics8110482
Sun P, Xu P, Zhu K, Zhou Z. Silicon-Based Optoelectronics Enhanced by Hybrid Plasmon Polaritons: Bridging Dielectric Photonics and Nanoplasmonics. Photonics. 2021; 8(11):482. https://doi.org/10.3390/photonics8110482
Chicago/Turabian StyleSun, Pengfei, Pengfei Xu, Kejian Zhu, and Zhiping Zhou. 2021. "Silicon-Based Optoelectronics Enhanced by Hybrid Plasmon Polaritons: Bridging Dielectric Photonics and Nanoplasmonics" Photonics 8, no. 11: 482. https://doi.org/10.3390/photonics8110482
APA StyleSun, P., Xu, P., Zhu, K., & Zhou, Z. (2021). Silicon-Based Optoelectronics Enhanced by Hybrid Plasmon Polaritons: Bridging Dielectric Photonics and Nanoplasmonics. Photonics, 8(11), 482. https://doi.org/10.3390/photonics8110482





