Research on X-ray Fluorescence Enhanced Fluoroscopy Imaging Technology
Abstract
:1. Introduction
1.1. Principles and Limitations of Fluoroscopy Imaging
1.2. Introduction to X-ray Fluorescence and Its Imaging
1.3. Literature Research on Enhanced Imaging
1.4. The Idea of Using Fluorescence to Enhance Fluoroscopy Imaging
1.5. Technical Feasibility Analysis
2. Methods
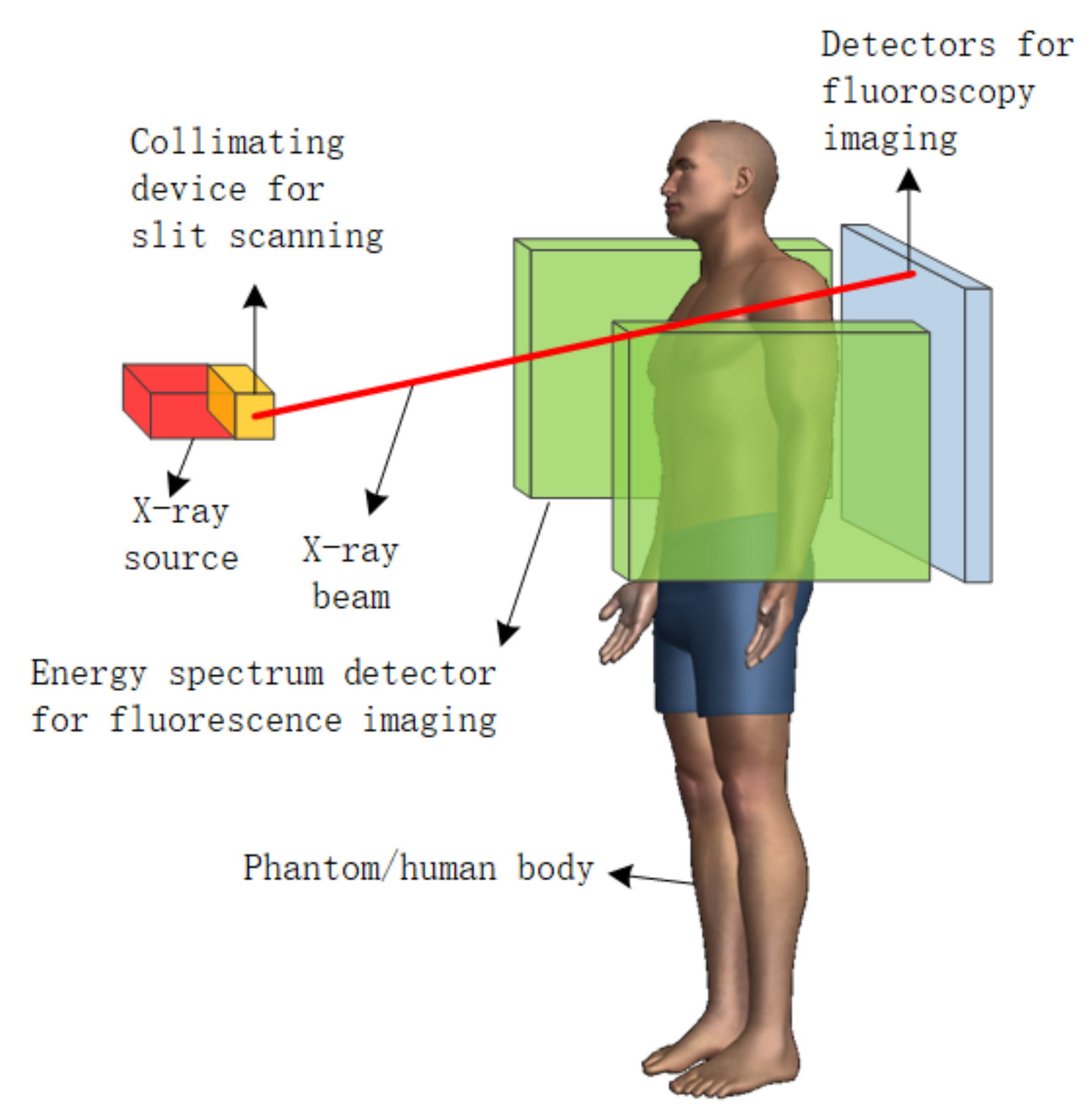
2.1. Pencil Beam Spot Scanning Method
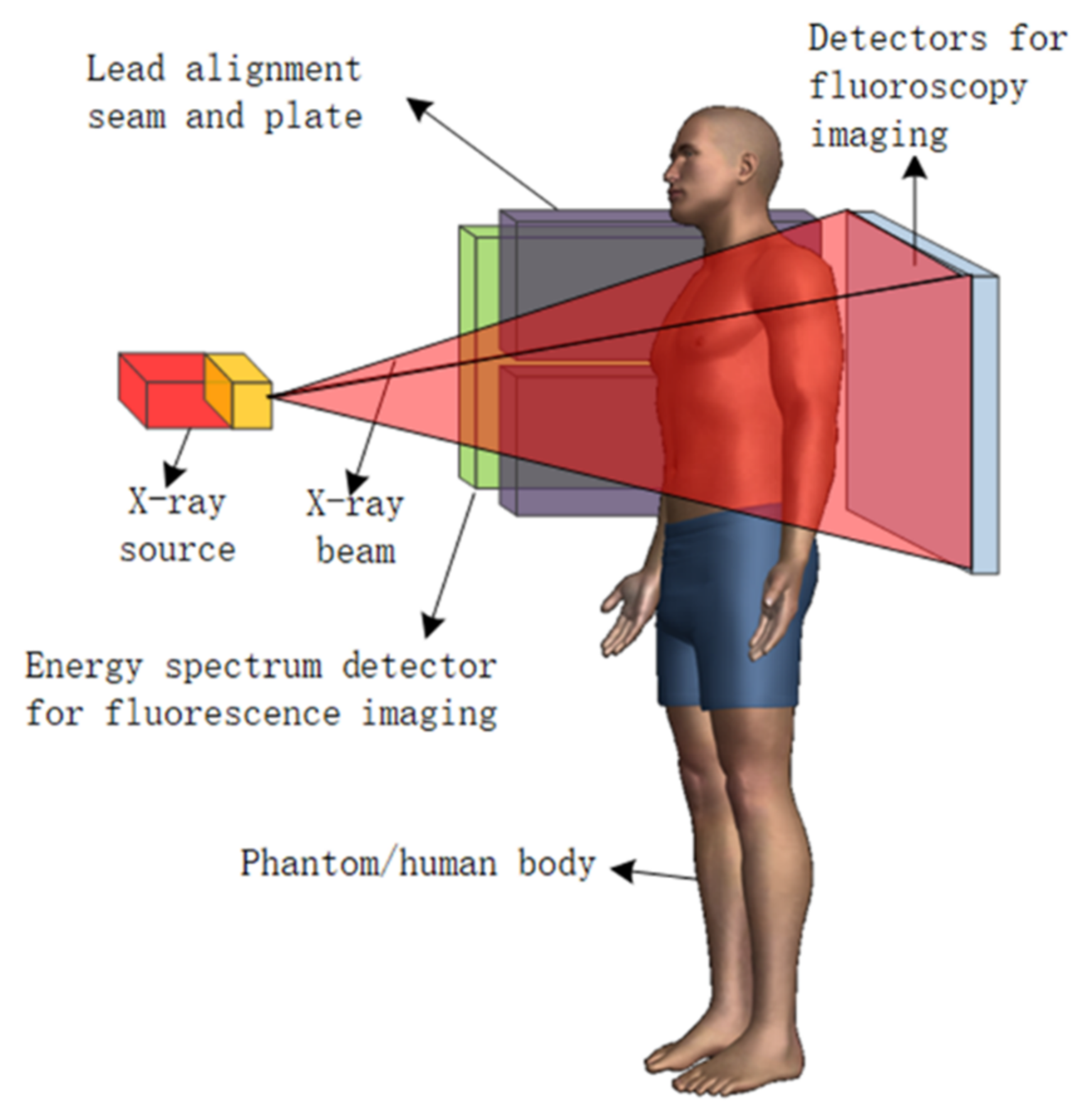
2.2. Cone-Beam Collimation Method
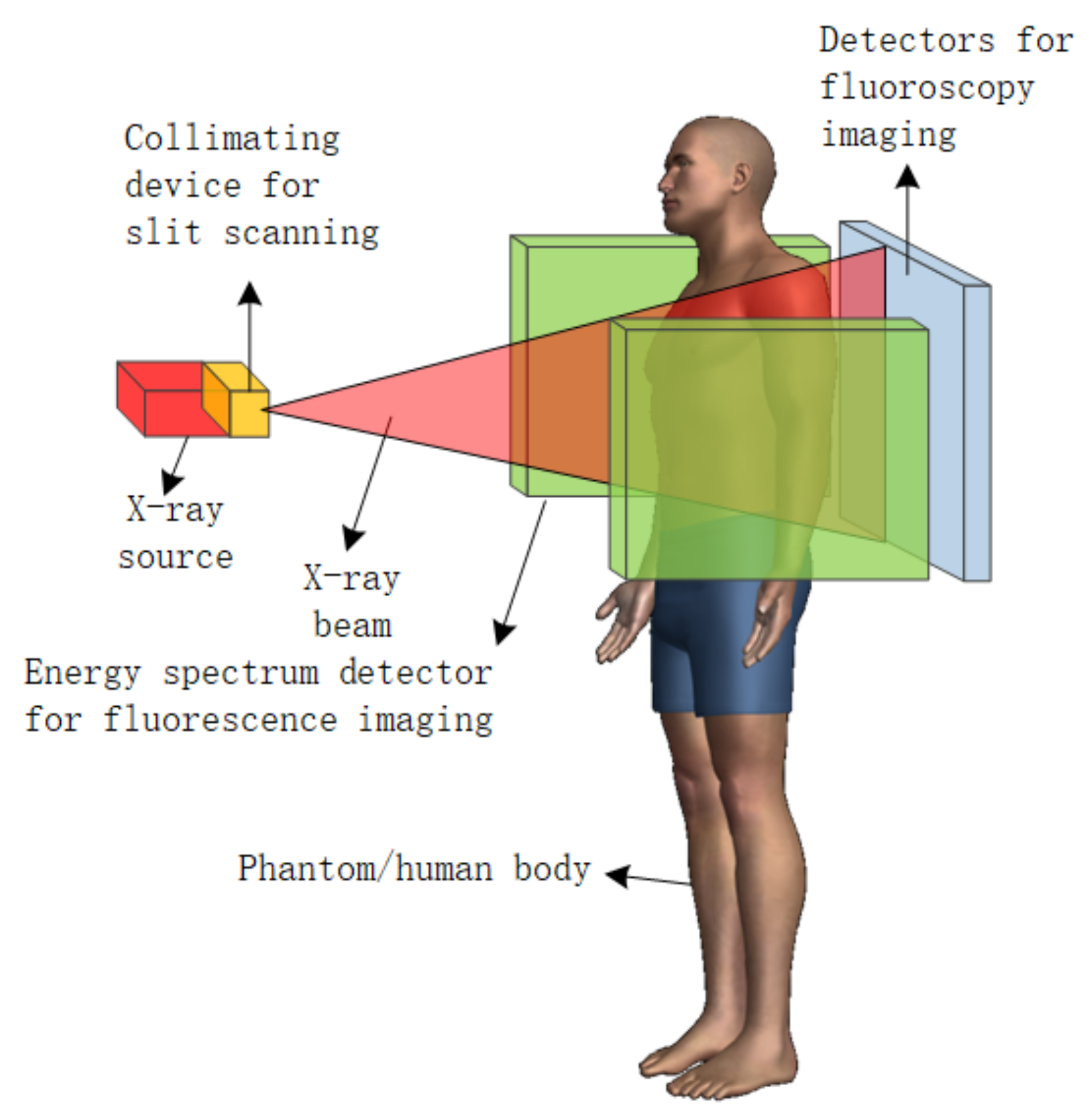
2.3. Slit Scanning Method
3. Settings and Parameters
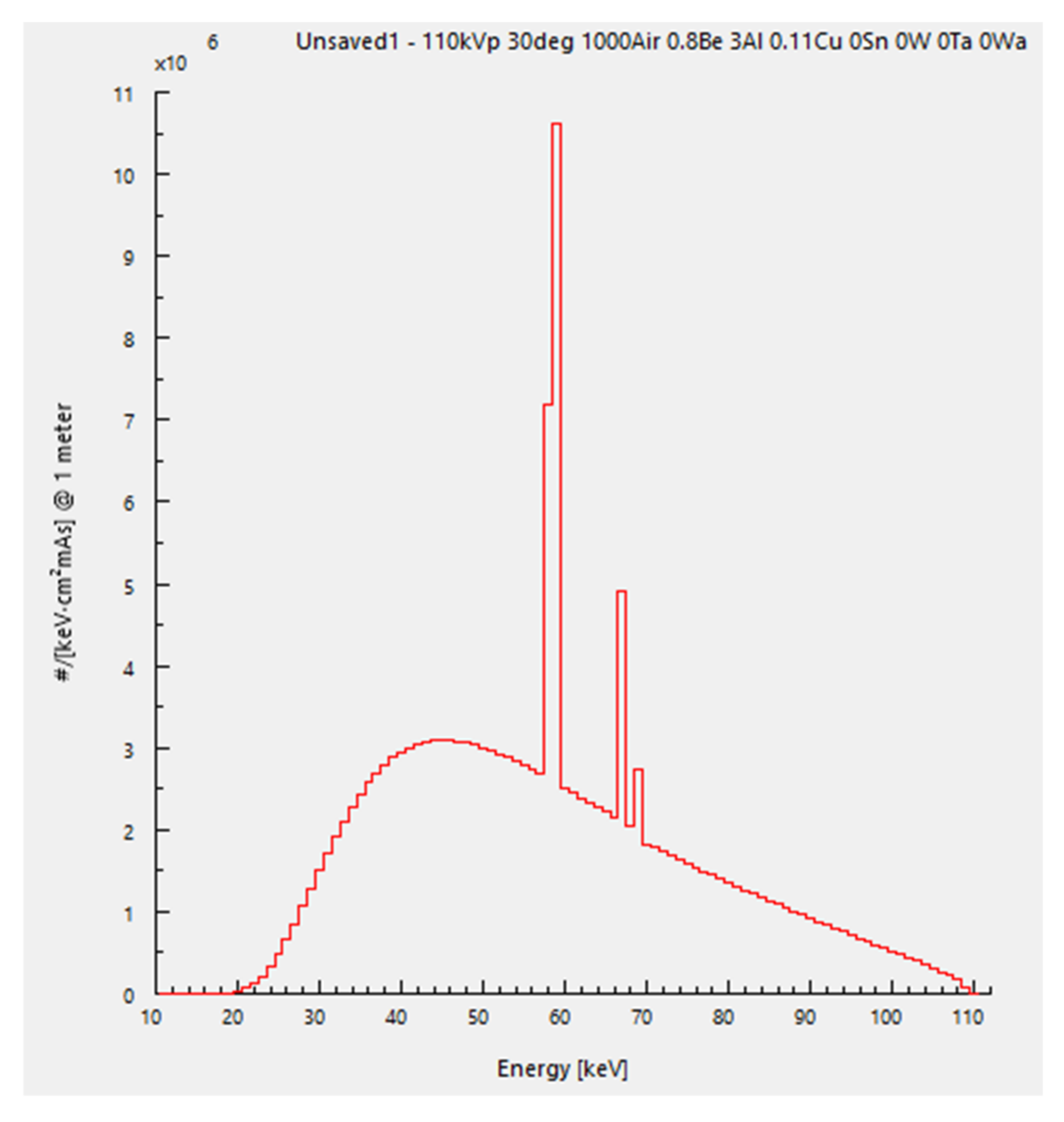
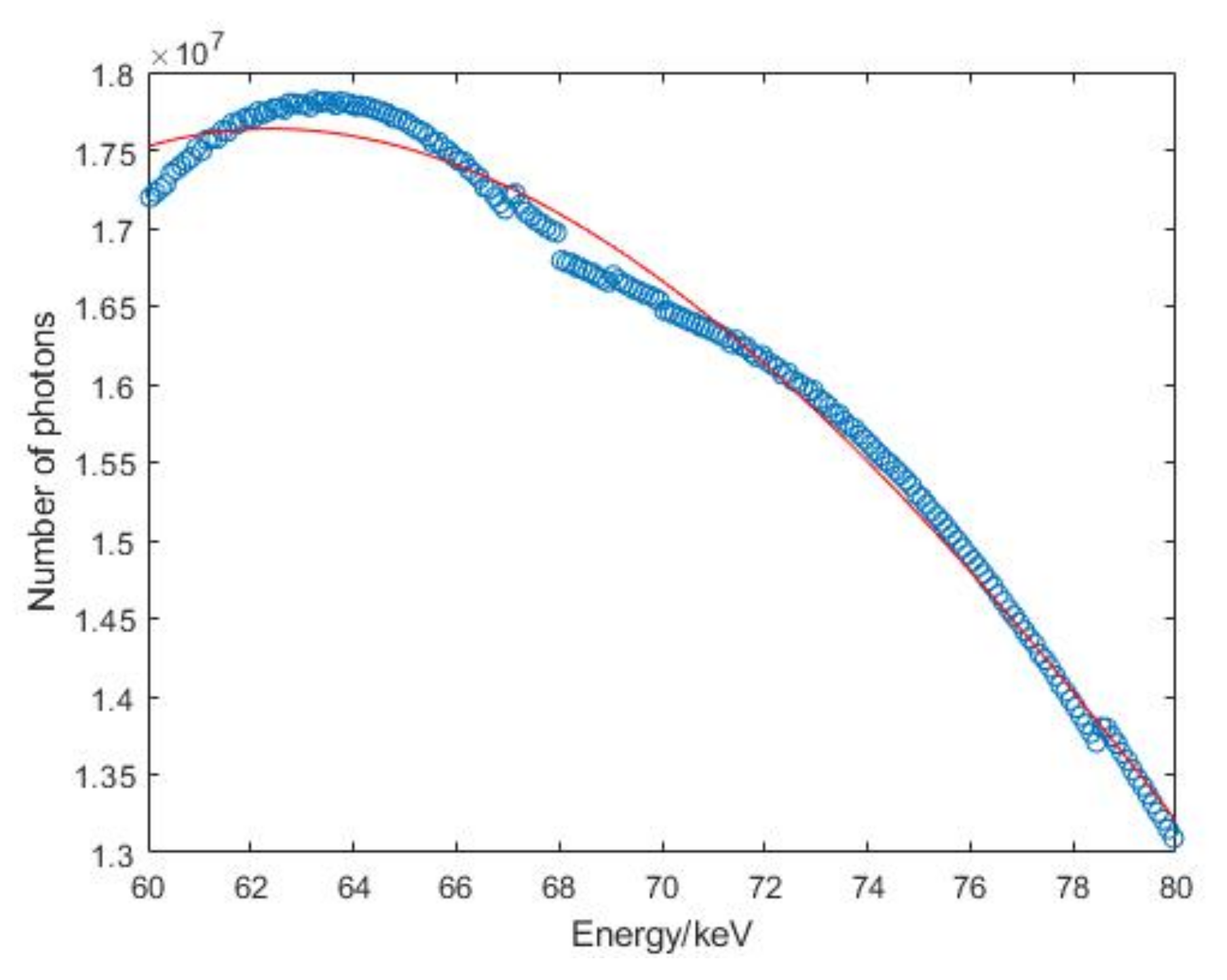
3.1. X-ray Source Tube Voltage and Energy Spectrum
3.2. Phantom and Simulaition Structure
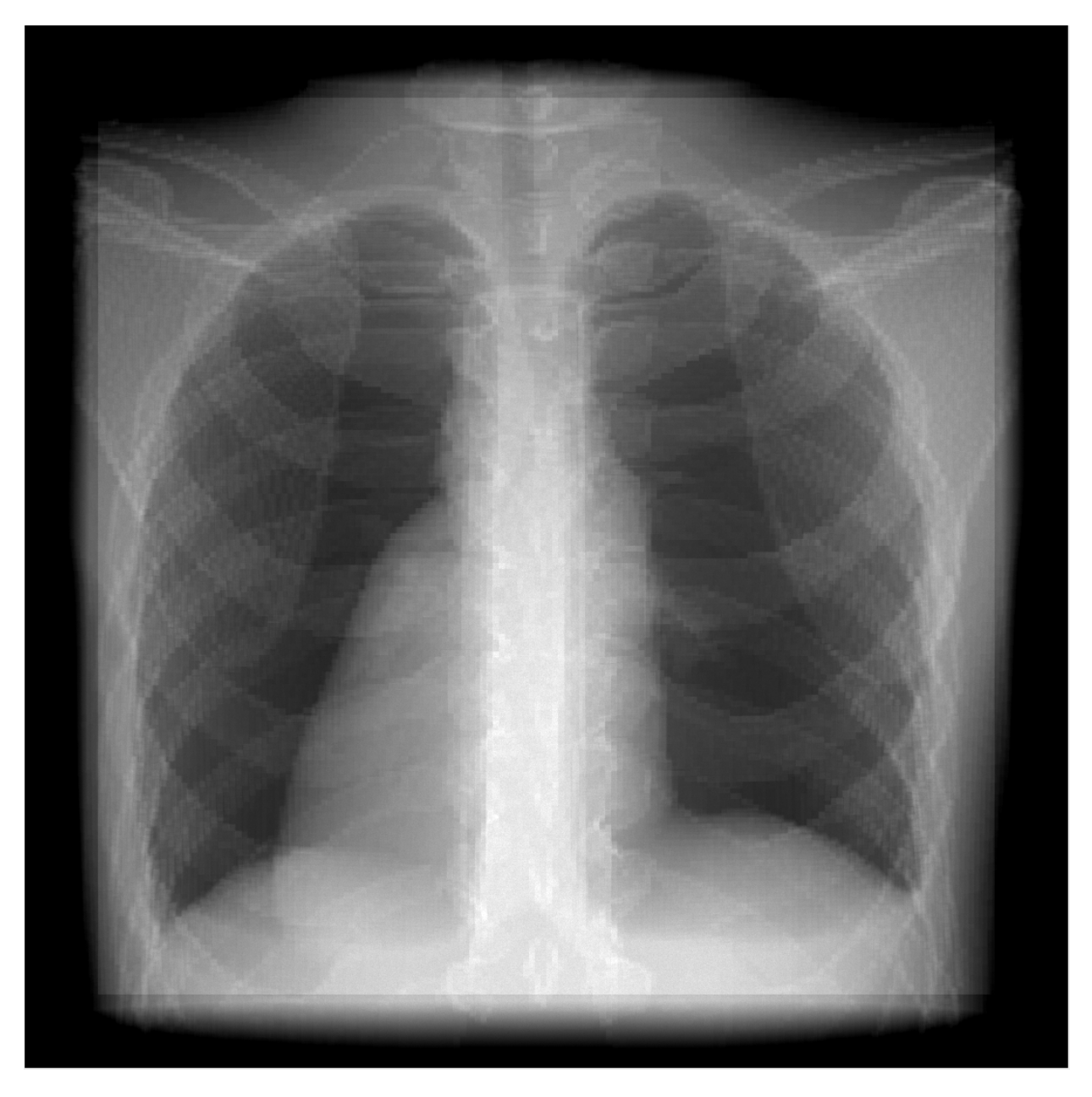
3.2.1. Phantom
3.2.2. Detectors
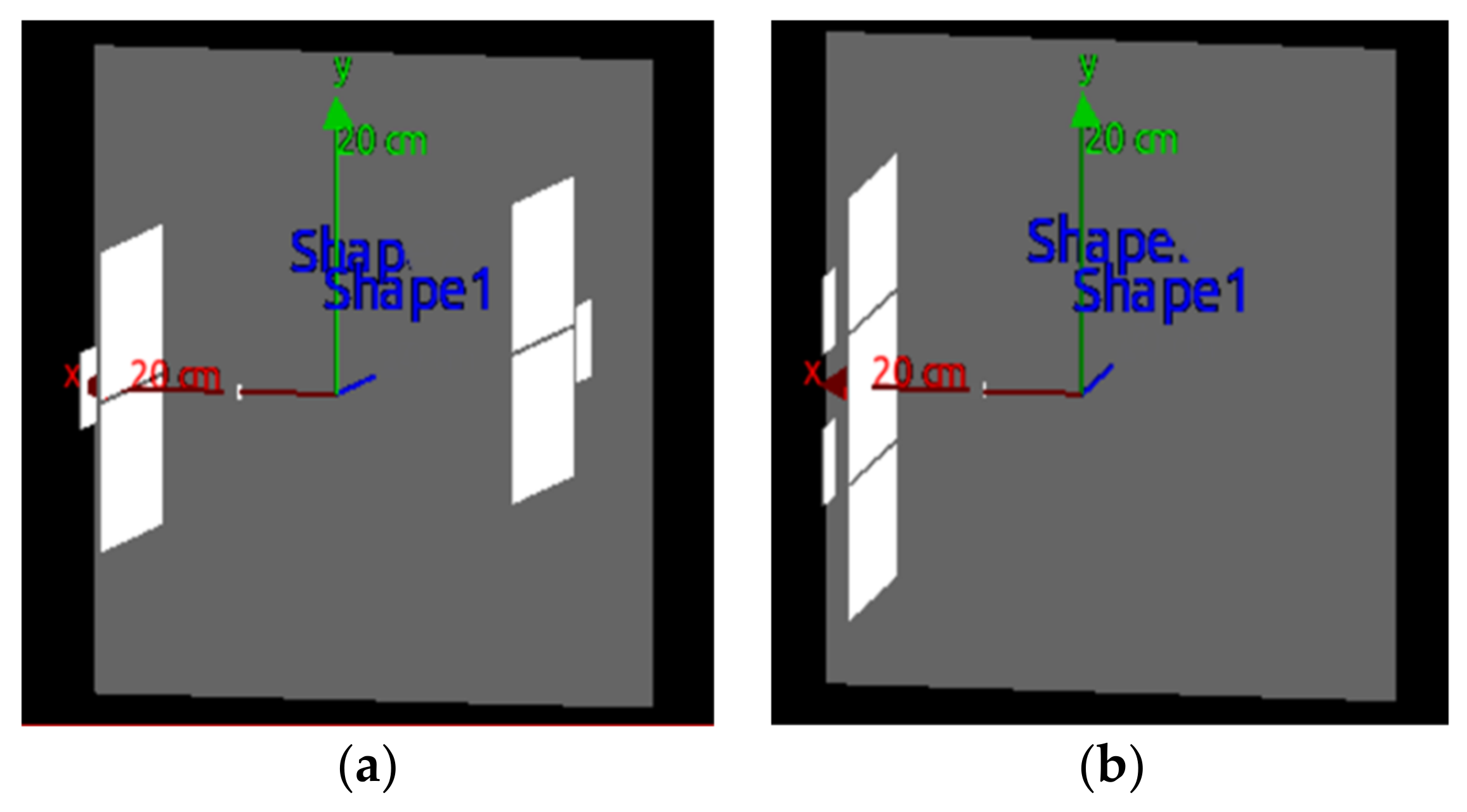
3.2.3. Structure of Simulation Design
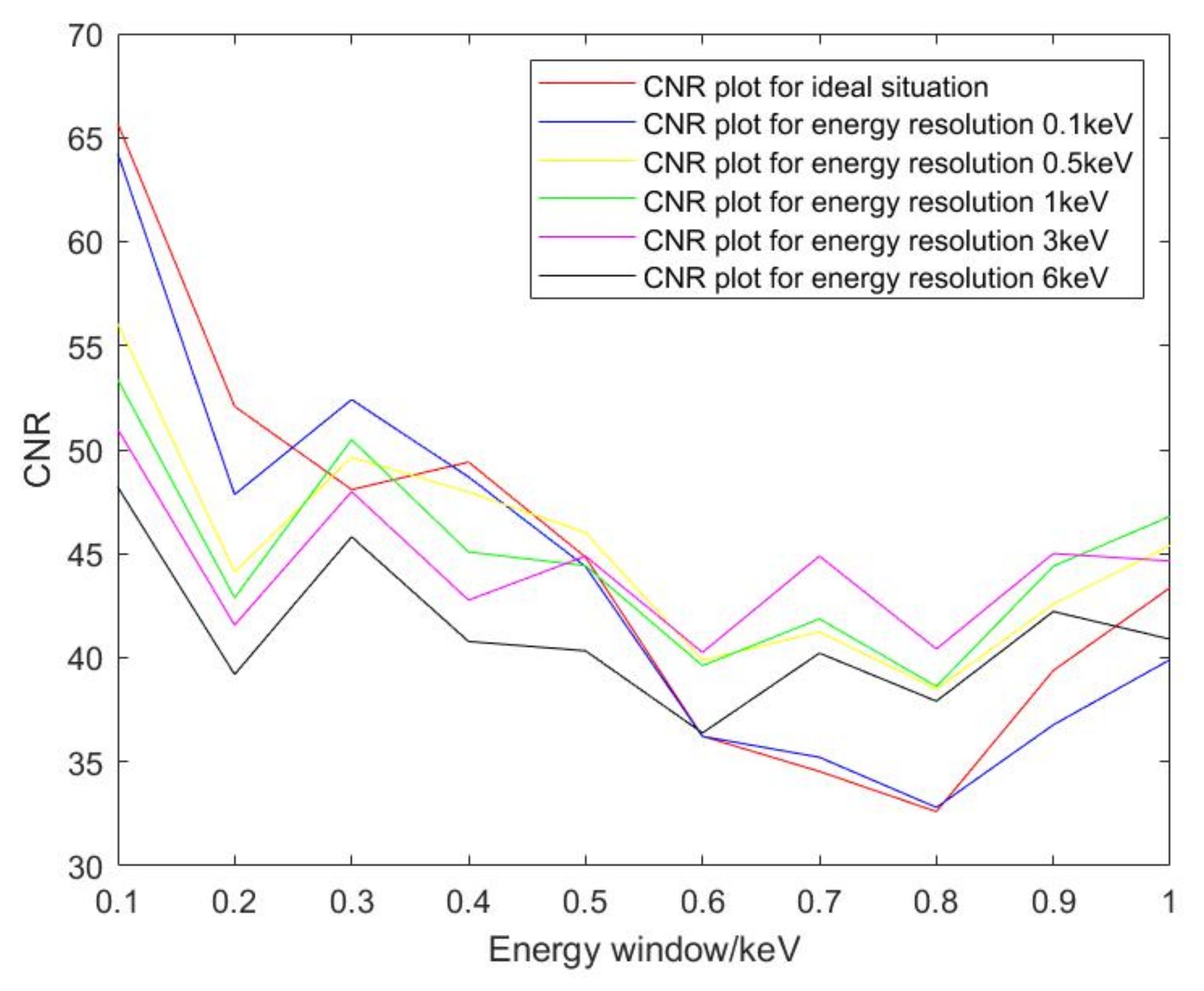
3.2.4. Energy Resolution
3.3. Number of Photons
3.4. Selection of Contrast Agents
3.5. Concentration of Agents
4. Results
4.1. Results of Pencil Beam Spot Scanning Method
4.1.1. Comparison of Fluorescence Detectors
4.1.2. De-Scattering
4.1.3. Convolution Denoising
4.1.4. Dual Mode Enhancement Result
4.2. Results of Cone-Beam Collimation Method
4.3. Results of Slit Scanning Method
5. Discussions
5.1. Phantom
5.2. Influence of Energy Resolutions and Energy Windows
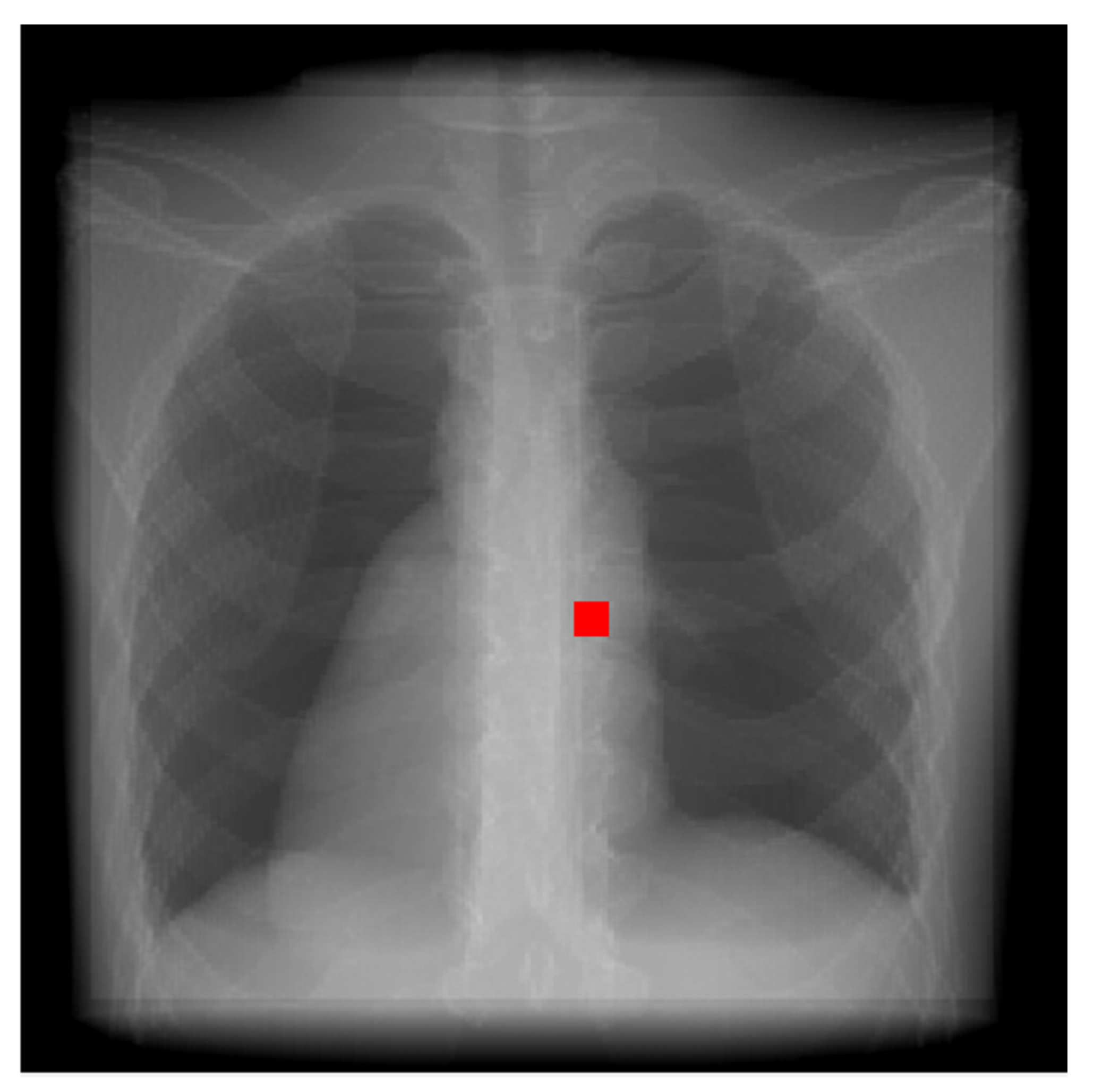
5.3. Position of the Lesion
5.4. False Positive
5.5. Other Areas for Improvement
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reddy, B.S.; Premachand, K.; Rao, P.V.R.; Parthasaradhi, K. Z-dependence of photoelectric cross-section in the energy region of absorption edges (6.4 ÷ 136.47) keV. Il Nuovo Cim. A 1992, 105, 735–739. [Google Scholar] [CrossRef]
- Yue, Z.G.; Wei, W.; You, Z.X.; Yang, Q.Z.; Yue, H.; Su, Z.G.; Ma, G.H. Iron Oxide Nanotubes for Magetically Guided Delivery and pH-Activated Release of Insoluble Anticancer Drugs. Adv. Funct. Mater. 2011, 21, 3446–3453. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, S.; Fang, W.; Li, L. The latest development of X-ray fluorescence computed tomography. Chin. J. Stereol. Image Anal. 2018, 23, 102–116. [Google Scholar]
- Rui, X. Synthesis of Nanoparticles as A Contrast Agent for CT and Application in Imaging; Jilin University: Changchun, China, 2014. [Google Scholar]
- Gang, X.; Zhengping, Q.; Minghua, Z.; Xiaoming, C.; Shengli, G. A single-source approach to Bi2S3 and Sb2S3 nanorods via a hydrothermal treatment. Cryst. Growth Des. 2004, 4, 513–516. [Google Scholar]
- Popovtzer, R.; Agrawal, A.; Kotov, N.; Popovtzer, A.; Balter, J.; Carey, T.; Kopelman, R. Targeted Gold Nanoparticles Enable Molecular CT Imaging of Cancer. Nano Lett. 2008, 8, 4593–4596. [Google Scholar] [CrossRef] [Green Version]
- Manohar, N.; Reynoso, F.J.; Diagaradjane, P.; Krishnan, S.; Cho, S.H. Quantitative imaging of gold nanoparticle distribution in a tumor-bearing mouse using benchtop x-ray fluorescence computed tomography. Sci. Rep. 2016, 6, 22079. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grüner, F.; Blumendorf, F.; Schmutzler, O.; Staufer, T.; Bradbury, M.; Wiesner, U.; Rosentreter, T.; Loers, G.; Lutz, D.; Richter, B.; et al. Localising functionalised gold-nanoparticles in murine spinal cords by X-ray fluorescence imaging and background-reduction through spatial filtering for human-sized objects. Sci. Rep. 2018, 8, 16561. [Google Scholar] [CrossRef] [Green Version]
- Schmutzler, O.; Graf, S.; Behm, N.; Mansour, W.; Blumendorf, F.; Staufer, T.; Körnig, C.; Salah, D.; Kang, Y.; Peters, J.; et al. X-ray Fluorescence Uptake Measurement of Functionalized Gold Nanoparticles in Tumor Cell Microsamples. Int. J. Mol. Sci. 2021, 22, 3691. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Li, L.; Chen, J.; Chen, Z.; Zhang, W.; Lu, H. Quantitative Imaging of Gd Nanoparticles in Mice Using Benchtop Cone-Beam X-ray Fluorescence Computed Tomography System. Int. J. Mol. Sci. 2019, 20, 2315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.; Li, L.; Chen, Z. Scattering Noise Model Enhanced EM-TV Algorithm for Benchtop X-ray Fluorescence Computed Tomography Image Reconstruction. IEEE Access 2019, 7, 113589–113595. [Google Scholar] [CrossRef]
- Li, L.; Zhang, S.; Li, R.; Chen, Z. Full-field fan-beam x-ray fluorescence computed tomography with a conventional x-ray tube and photon-counting detectors for fast nanoparticle bioimaging. Opt. Eng. 2017, 56, 043106. [Google Scholar] [CrossRef]
- Liang, L.; Ruizhe, L.; Siyuan, Z.; Zhiqiang, C. Simultaneous X-ray fluorescence and K-edge CT imaging with photon counting detectors. Proc. SPIE 2016. [Google Scholar] [CrossRef]
- Sokolov, K.; Follen, M.; Aaron, J.; Pavlova, I.; Malpica, A.; Lotan, R.; Richards-Kortum, R. Real-time vital optical imaging of precancer using anti-epidermal growth factor receptor antibodies conjugated to gold nanoparticles. Cancer Res. 2003, 63, 1999–2004. [Google Scholar]
- Cho, S.H. Estimation of tumour dose enhancement due to gold nanoparticles during typical radiation treatments: A preliminary Monte Carlo study. Phys. Med. Biol. 2005, 50, N163. [Google Scholar] [CrossRef]
- Jones, B.L.; Krishnan, S.; Cho, S.H. Estimation of microscopic dose enhancement factor around gold nanoparticles by Monte Carlo calculations. Med. Phys. 2010, 37, 3809–3816. [Google Scholar] [CrossRef]
- Feifei, L.; Zihou, L.; Xiaodong, J.; Aiguo, W.; Weiqiang, C.; Qiang, L. Radiosensitizing Effect of Gadolinium Oxide Nanoparticles on Human Non-small Cell Lung Cancer A549 Cells. Nucl. Phys. Rev. 2019, 36, 373. [Google Scholar] [CrossRef]
- Hurtado, S.; León, M.G.; García-Tenorio, R. Monte Carlo simulation of the response of a germanium detector for low-level spectrometry measurements using GEANT4. Appl. Radiat. Isot. 2004, 61, 139–143. [Google Scholar] [CrossRef]
- Poludniowski, G.; Landry, G.; Deblois, F.; Evans, P.M.; Verhaegen, F. SpekCalc: A program to calculate photon spectra from tungsten anode x-ray tubes. Phys. Med. Biol. 2009, 54, N433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, L.; Rui, Q.; Zhen, W.; Li, C.; Yang, B.; Liu, H.; Ren, L.; Li, J. Calculation of conversion coefficients using Chinese adult reference phantoms for air submersion and ground contamination. Phys. Med. Biol. 2017, 62, 2276–2314. [Google Scholar]
- Lu, W.; Wu, Z.; Qiu, R.; Li, C.; Yang, B.; Gao, S.; Ren, L.; Li, J. Physical Dosimetric Reconstruction of a Radiological Accident at Nanjing (China) for Clinical Treatment Using THUdose. Health Phys. 2017, 113, 327–334. [Google Scholar] [CrossRef] [PubMed]
- Yong, H.; Lei, Y.; Ruji, Y.; Ohno, R. The Principle of Cadmium Telluride(CdTe)Detector and Medical Application. Shanghai J. Biomed. Eng. 2005, 4, 221–225. [Google Scholar]
- Kuang, Y.; Pratx, G.; Bazalova, M.; Meng, B.; Qian, J.; Xing, L. First demonstration of multiplexed x-ray fluorescence computed tomogra-phy (XFCT) imaging. IEEE Trans. Med. Imaging 2013, 32, 262–267. [Google Scholar] [CrossRef] [PubMed]
- Ichihara, T.; Ogawa, K.; Motomura, N.; Kubo, A.; Hashimoto, S. Compton scatter compensation using the triple-energy window method for single-and dual-isotope SPECT. J. Nucl. Med. 1993, 34, 2216–2221. [Google Scholar] [PubMed]
- Perkins, S.T.; Cullen, D.; Chen, M.H.; Rathkopf, J.; Scofield, J.; Hubbell, J.H. Tables and Graphs of Atomic Subshell and Relaxation Data Derived from the LLNL Evaluated Atomic Data Library (EADL), Z = 1–100; US Department of Energy, Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1991.















| Peak Energy | Energy Bin/keV | Theta | Anode Material | Air | Al | Cu |
|---|---|---|---|---|---|---|
| 110 keV | 1 | 30° | Tungsten | 1000 mm | 3 mm | 0.11 mm |
| Peak Energy | Material Type | Tumor Size | Simulation Photons | Concentration |
|---|---|---|---|---|
| 110 keV | Au | 1 cm3 | 1012 | 5 mg/mL |
| 110 keV | Au | 1 cm3 | 1012 | 0.5 mg/mL |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Li, L.; Qiu, R.; Chen, Z. Research on X-ray Fluorescence Enhanced Fluoroscopy Imaging Technology. Photonics 2021, 8, 441. https://doi.org/10.3390/photonics8100441
Yan Z, Li L, Qiu R, Chen Z. Research on X-ray Fluorescence Enhanced Fluoroscopy Imaging Technology. Photonics. 2021; 8(10):441. https://doi.org/10.3390/photonics8100441
Chicago/Turabian StyleYan, Zhenyao, Liang Li, Rui Qiu, and Zhiqiang Chen. 2021. "Research on X-ray Fluorescence Enhanced Fluoroscopy Imaging Technology" Photonics 8, no. 10: 441. https://doi.org/10.3390/photonics8100441
APA StyleYan, Z., Li, L., Qiu, R., & Chen, Z. (2021). Research on X-ray Fluorescence Enhanced Fluoroscopy Imaging Technology. Photonics, 8(10), 441. https://doi.org/10.3390/photonics8100441





