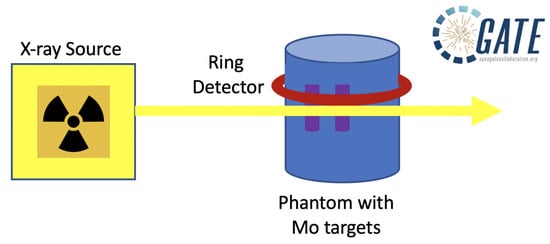
X-ray Fluorescence Computed Tomography (XFCT) Imaging with a Superfine Pencil Beam X-ray Source
Abstract
1. Introduction
2. Materials and Methods
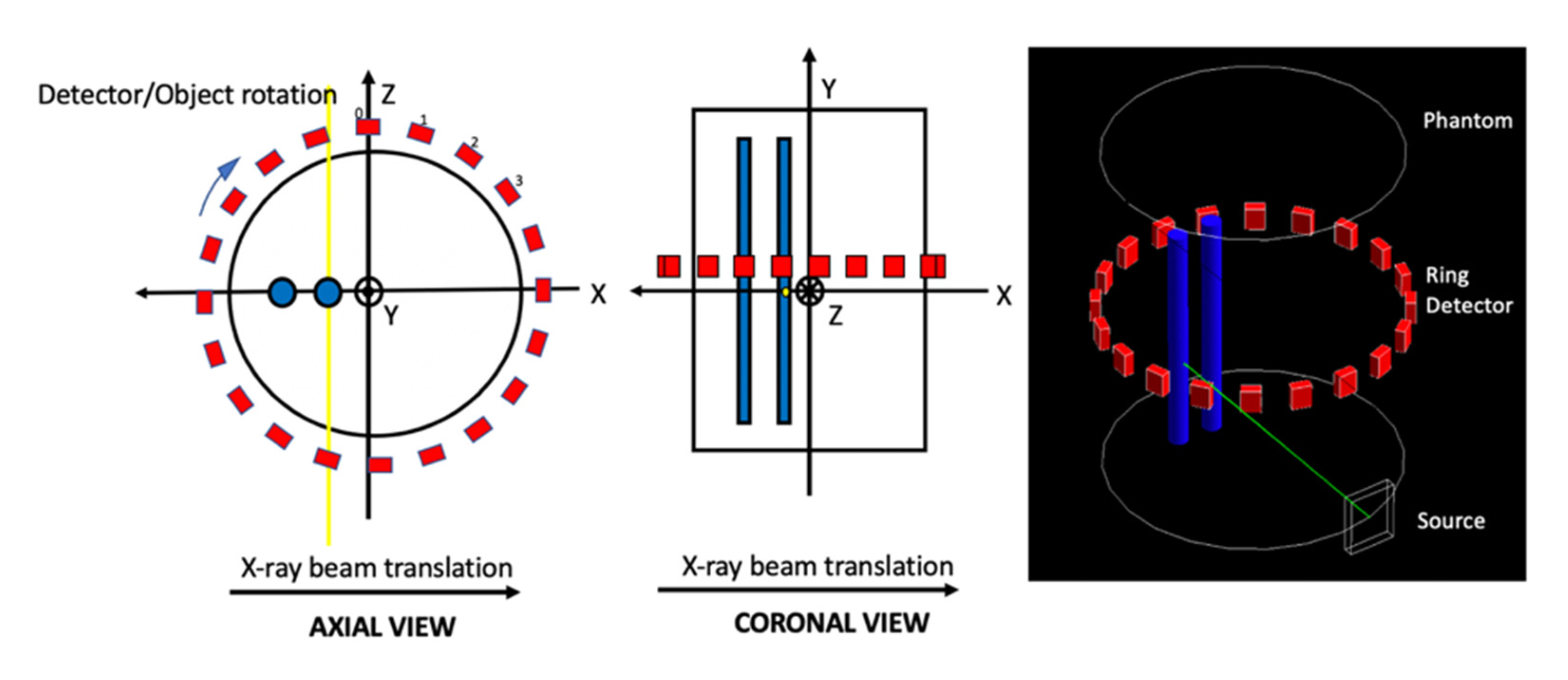
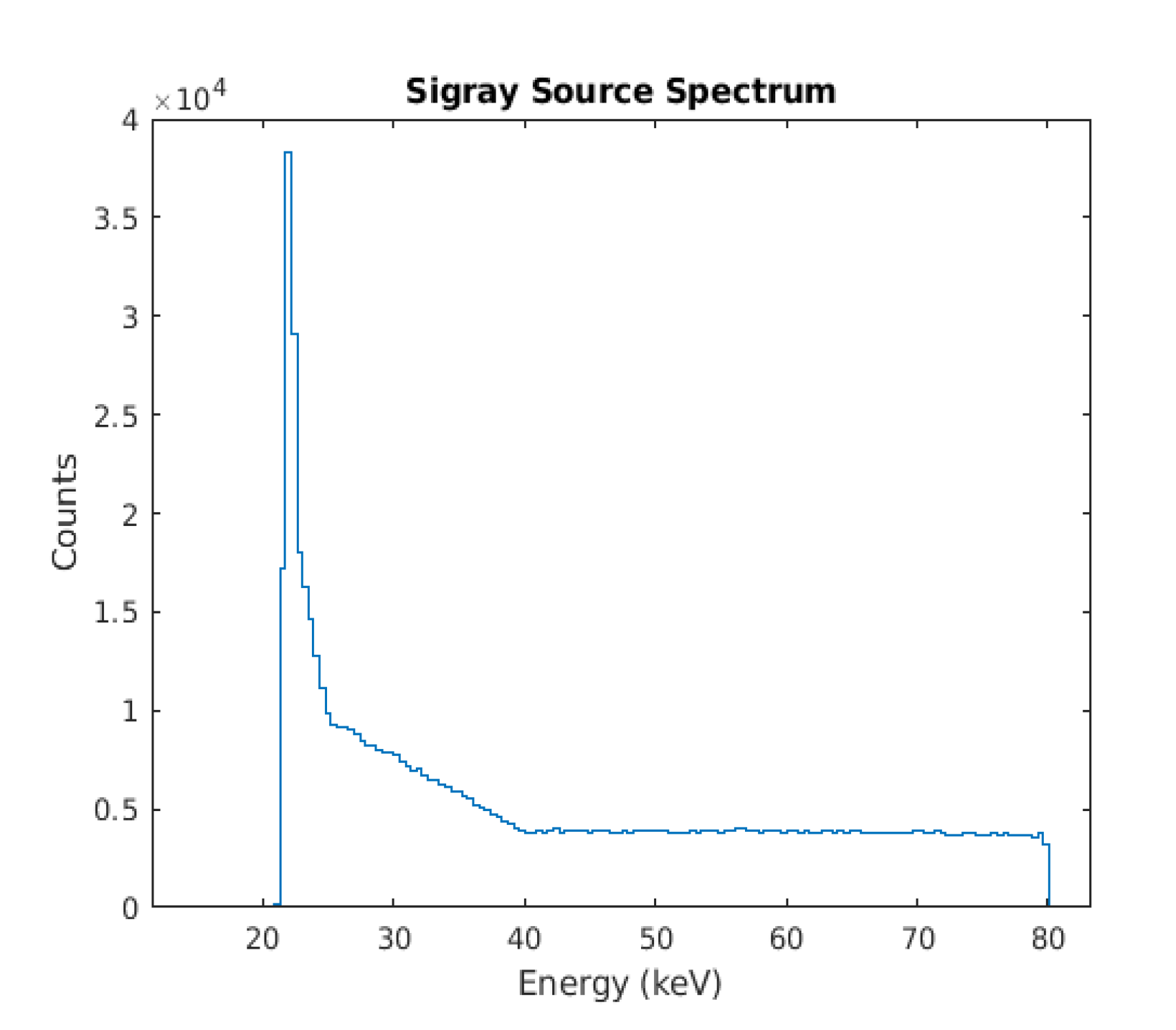
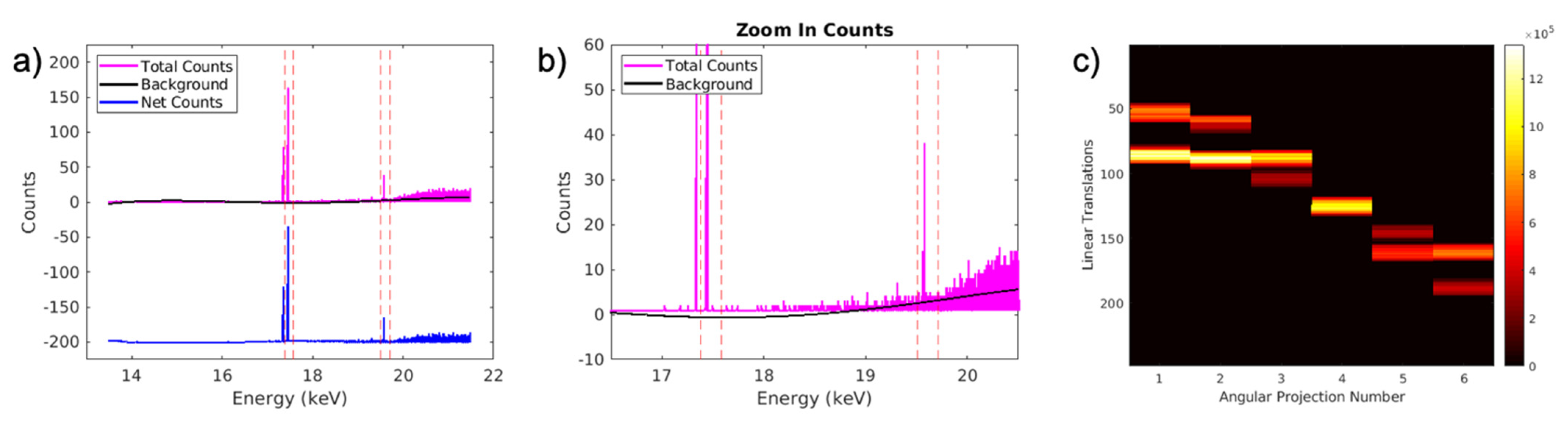
2.1. GATE Simulation
2.2. System Matrix and Reconstruction Algorithms
2.3. High Spatial Resolution Imaging
2.4. Reconstruction Algorithm Performance with Different Angular Projection Number
2.5. Reconstruction Algorithm Comparison
2.6. Image Quality Evaluation Criteria
3. Results
3.1. Effects of Detector Number and Detector Placement
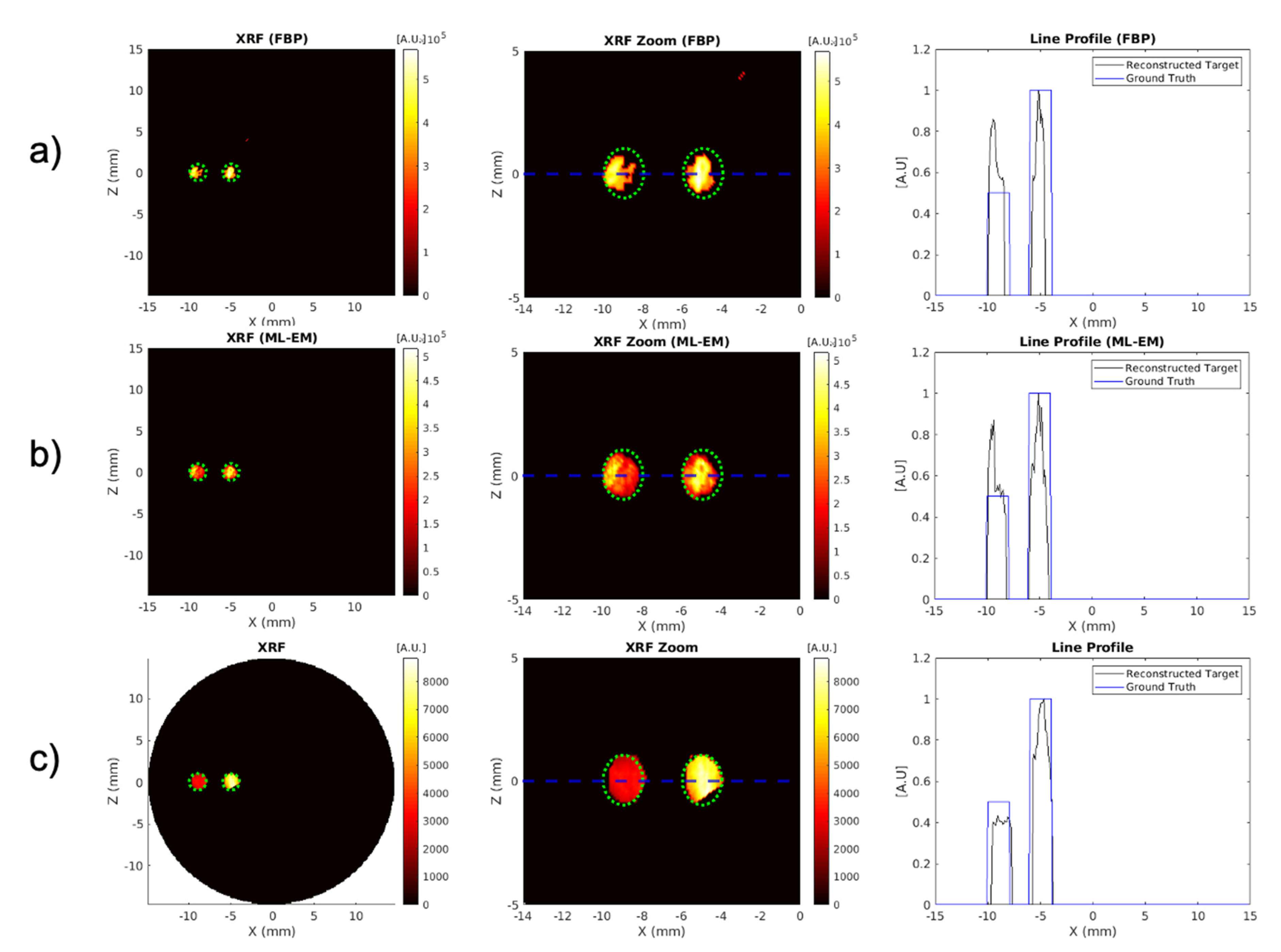
3.2. Reconstruction Algorithm Comparison
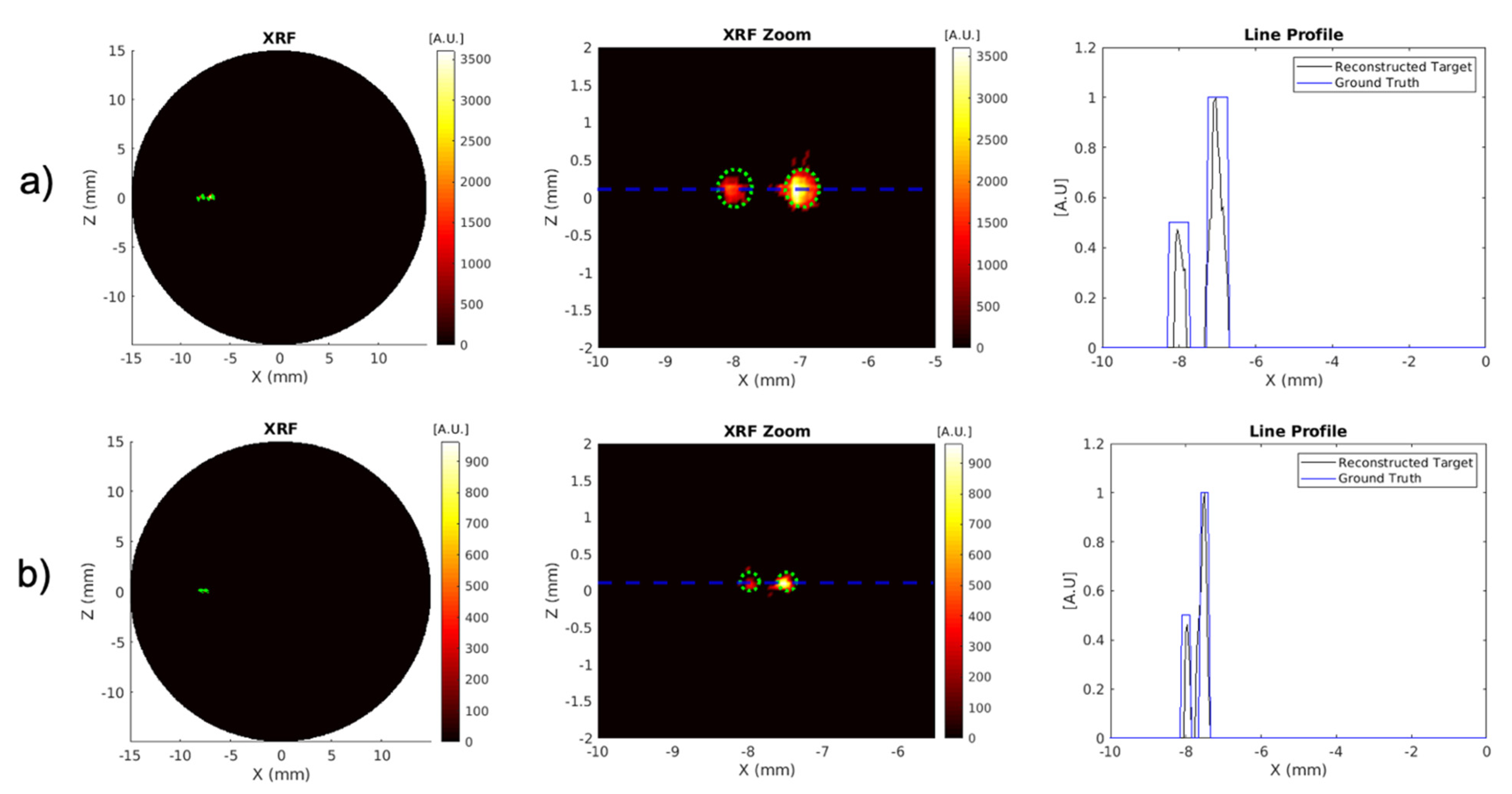
3.3. High Spatial Resolution Imaging
3.4. Reconstruction Algorithm Performance with Different Angular Projection Number
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, L.; Ahmed, M.F.; Jayarathna, S.; Feng, P.; Wei, B.; Cho, S.H. A detector’s eye view (DEV)-based OSEM algorithm for benchtop X-ray fluorescence computed tomography (XFCT) image reconstruction. Phys. Med. Biol. 2019, 64. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Li, L.; Chen, J.; Chen, Z.; Zhang, W.; Lu, H. Quantitative imaging of gd nanoparticles in mice using benchtop cone-beam X-ray fluorescence computed tomography system. Int. J. Mol. Sci. 2019, 20, 2315. [Google Scholar] [CrossRef] [PubMed]
- Jones, B.L.; Cho, S.H. The feasibility of polychromatic cone-beam X-ray fluorescence computed tomography (XFCT) imaging of gold nanoparticle-loaded objects: A Monte Carlo study. Phys. Med. Biol. 2011, 56, 37193730. [Google Scholar] [CrossRef] [PubMed]
- Dunning, C.A.S.; Bazalova-Carter, M. Optimization of a table-top X-ray fluorescence computed tomography (XFCT) system. Phys. Med. Biol. 2018, 63, 235013. [Google Scholar] [CrossRef] [PubMed]
- Vernekohl, D.; Xing, L. X-ray Excited Fluorescent Materials for Medical Application. Top. Med. Chem. 2014, 9, 1–68. [Google Scholar] [CrossRef]
- Larsson, J.C.; Vogt, C.; Vågberg, W.; Toprak, M.S.; Dzieran, J.; Arsenian-Henriksson, M.; Hertz, H.M. High-spatial-resolution X-ray fluorescence tomography with spectrally matched nanoparticles. Phys. Med. Biol. 2018, 63. [Google Scholar] [CrossRef] [PubMed]
- Shilo, M.; Reuveni, T.; Motiei, M.; Popovtzer, R. Nanoparticles as computed tomography contrast agents: Current status and future perspectives. Nanomedicine 2012, 7. [Google Scholar] [CrossRef] [PubMed]
- Hainfeld, J.F.; Slatkin, D.N.; Smilowitz, H.M. The use of gold nanoparticles to enhance radiotherapy in mice. Phys. Med. Biol. 2004, 49. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; He, P.; Deng, L.; Chen, M.; Wei, B. Monte Carlo Simulation for Polychromatic X-ray Fluorescence Computed Tomography with Sheet-Beam Geometry. Int. J. Biomed. Imaging 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Bazalova, M.; Kuang, Y.; Pratx, G.; Xing, L. Investigation of X-ray fluorescence computed tomography (XFCT) and K-edge imaging. IEEE Trans. Med. Imaging 2012, 31, 1620–1627. [Google Scholar] [CrossRef] [PubMed]
- Cheong, S.K.; Jones, B.L.; KSiddiqi, A.; Liu, F.; Manohar, N.; Cho, S.H. X-ray fluorescence computed tomography (XFCT) imaging of gold nanoparticle-loaded objects using 110 kVp X-rays. Phys. Med. Biol. 2010, 55, 647–662. [Google Scholar] [CrossRef] [PubMed]
- Dunning, C.A.S.; Bazalova, M. Design of a combined X-ray fluorescence Computed Tomography (CT) and photon-counting CT table-top imaging system. J. Instrum. 2020, 15, P06031. [Google Scholar] [CrossRef]
- Defrise, M.; Kinahan, P.E.; Michel, C.J. Image Reconstruction Algorithms in PET. In Positron Emission Tomography; Bailey, D.L., Townsend, D.W., Valk, P.E., Maisey, M.N., Eds.; Springer: London, UK, 2005. [Google Scholar]
- Zhang, W.; Romero, I.O.; Li, C. Time domain X-ray luminescence computed tomography: Numerical simulations. Biomed. Opt. Express. 2019, 10, 372. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Martínez-Dávalos, A.; Cherry, S.R. Numerical simulation of X-ray luminescence optical tomography for small-animal imaging. J. Biomed. Opt. 2014, 19, 046002. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zhu, D.; Li, C. Nonconvex regularizations in fluorescence molecular tomography for sparsity enhancement. Phys. Med. Biol. 2014, 59, 2901–2912. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Li, C. Accelerated image reconstruction in fluorescence molecular tomography using a nonuniform updating scheme with momentum and ordered subsets methods. J. Biomed. Opt. 2016, 21, 016004. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jan, S.; Santin, G.; Strul, D.; Staelens, S.; Assié, K.; Autret, D.; Avner, S.; Barbier, R.; Bardiès, M.; Bloomfield, P.M.; et al. GATE: A simulation toolkit for PET and SPECT. Phys. Med. Biol. 2004, 49, 4543–4561. [Google Scholar] [CrossRef] [PubMed]
- Achterhold, K.; Bech, M.; Schleede, S.; Potdevin, G.; Ruth, R.; Loewen, R.; Pfeiffer, F. Monochromatic computed tomography with a compact laser-driven X-ray source. Sci. Rep. 2013, 3, 3–6. [Google Scholar] [CrossRef] [PubMed]
- Brun, R.; Rademakers, F. ROOT-An Object Oriented Data Analysis Framework, Proceedings AIHENP’96 Workshop, Lausanne, September 1996. Nucl. Inst. Methods Phys. Res. A 1997, 389, 81–86. Available online: http://root.cern.ch/ (accessed on 18 June 2021). [CrossRef]
- Fessler, J.A. Michigan Image Reconstruction Toolbox. Available online: https://web.eecs.umich.edu/~fessler/code/index.html (accessed on 18 June 2021).
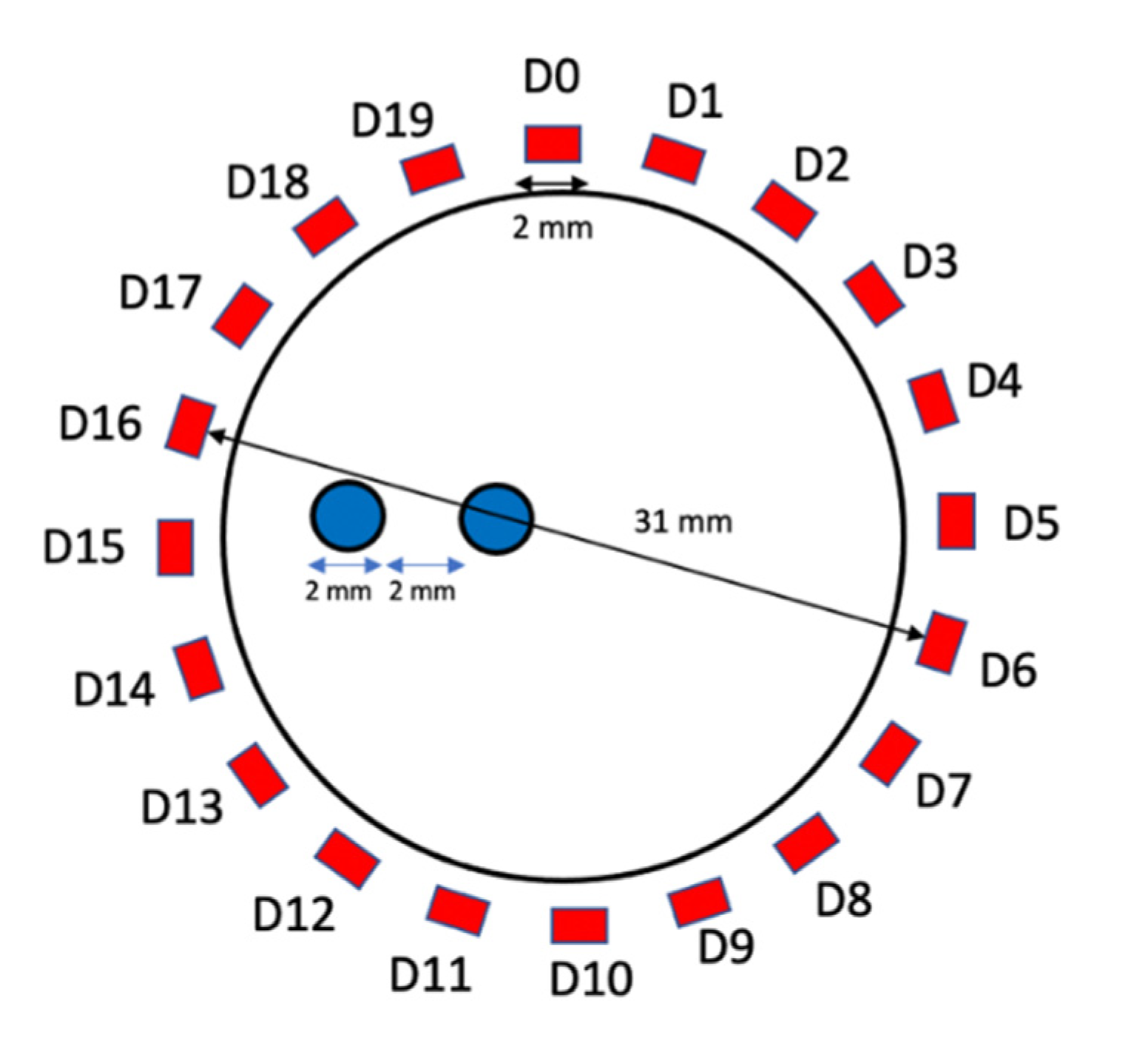
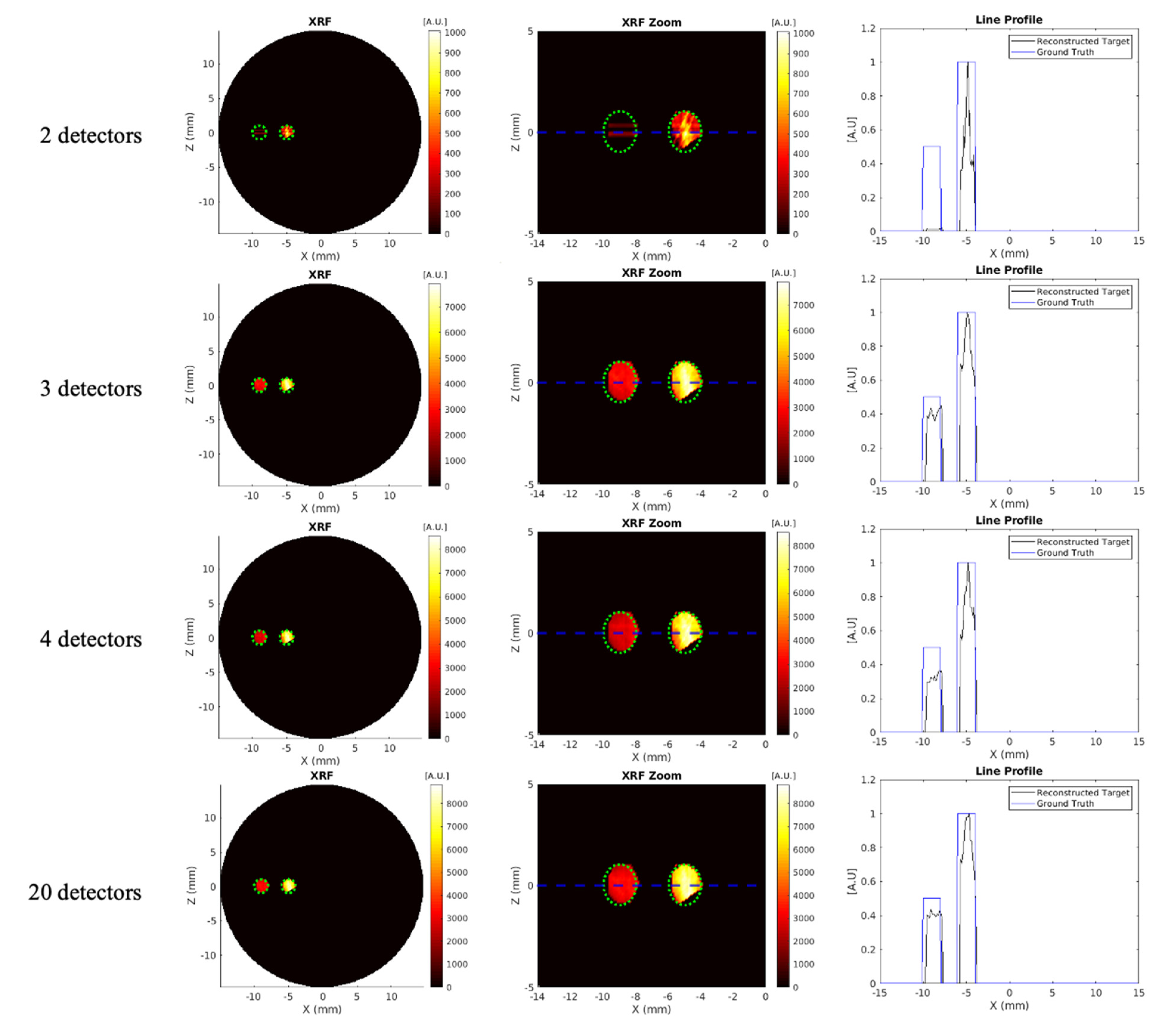
| Detector Number | Target Contrast Ratio (Ground Truth = 2) | DICE (%) (Ground Truth = 100%) | MSE | CNR5, CNR10 |
|---|---|---|---|---|
| 2 (D0, D4) * | 6.910 | 71.805 | 2.229 × 10−3 | 1.649, 11.396 |
| 2 (D9, D14) | 2.415 | 88.737 | 1.105 × 10−3 | 38.267, 92.413 |
| 3 (D0, D9, D14) * | 2.430 | 88.737 | 1.113 × 10−3 | 37.418, 90.907 |
| 3 (D3, D12, D17) | 2.025 | 88.737 | 1.078 × 10−3 | 18.196, 36.840 |
| 4 (D0, D5, D10, D15) * | 2.887 | 88.737 | 1.116 × 10−3 | 24.616, 71.068 |
| 4 (D3, D8, D13, D18) | 1.774 | 88.737 | 1.030 × 10−3 | 24.567, 43.577 |
| 20 (D0 to D19) * | 2.389 | 88.737 | 1.061 × 10−3 | 43.516, 103.936 |
| Reconstruction Method | Reconstruction Time (s) | Target Contrast Ratio (Ground Truth = 2) | DICE (%) (Ground Truth = 100%) | MSE | CNR5, CNR10 |
|---|---|---|---|---|---|
| FBP | 0.479048 | 2.410 | 64.918 | 2.422 × 10−3 | 2.447, 5.897 |
| ML-EM | 661.2517 | 1.5713 | 89.170 | 1.645 × 10−3 | 12.879, 20.237 |
| fNUMOS | 0.015264 | 2.389 | 88.737 | 1.061 × 10−3 | 43.516, 103.936 |
| Target Size (mm) | Detector Number | Target Contrast Ratio (Ground Truth = 2) | DICE (%) (Ground Truth = 100%) | MSE | CNR5, CNR10 |
|---|---|---|---|---|---|
| 0.25 | 20 (D0 to D19) | 2.981 | 38.89 | 5.710 × 10−5 | 4.650, 13.861 |
| 2 (D9, D14) | 4.071 | 37.68 | 5.796 × 10−5 | 2.003, 8.153 | |
| 0.50 | 20 (D0 to D19) | 2.030 | 66.67 | 1.197 × 10−4 | 7.445, 15.110 |
| 2 (D9, D14) | 1.662 | 67.13 | 1.283 × 10−4 | 5.474, 9.098 |
| Number of Projections | Detector Number | Target Contrast Ratio (Ground Truth = 2) | DICE (%) (Ground Truth = 100%) | MSE | CNR5, CNR10 |
|---|---|---|---|---|---|
| 3 | 20 (D0 to D19) | 2.201 | 55.07 | 1.874 × 10−4 | 15.208, 33.476 |
| 2 (D9, D14) | 3.220 | 49.18 | 1.993 × 10−4 | 2.066, 6.654 | |
| 6 | 20 (D0 to D19) | 1.825 | 65.67 | 1.528 × 10−4 | 4.923, 8.983 |
| 2 (D9, D14) | 1.750 | 53.97 | 1.763 × 10−4 | 4.859, 8.506 | |
| 10 | 20 (D0 to D19) | 2.186 | 57.14 | 1.472 × 10−4 | 32.853, 71.801 |
| 2 (D9, D14) | 2.161 | 59.62 | 1.377 × 10−4 | 61.394, 132.651 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero, I.O.; Fang, Y.; Lun, M.; Li, C. X-ray Fluorescence Computed Tomography (XFCT) Imaging with a Superfine Pencil Beam X-ray Source. Photonics 2021, 8, 236. https://doi.org/10.3390/photonics8070236
Romero IO, Fang Y, Lun M, Li C. X-ray Fluorescence Computed Tomography (XFCT) Imaging with a Superfine Pencil Beam X-ray Source. Photonics. 2021; 8(7):236. https://doi.org/10.3390/photonics8070236
Chicago/Turabian StyleRomero, Ignacio O., Yile Fang, Michael Lun, and Changqing Li. 2021. "X-ray Fluorescence Computed Tomography (XFCT) Imaging with a Superfine Pencil Beam X-ray Source" Photonics 8, no. 7: 236. https://doi.org/10.3390/photonics8070236
APA StyleRomero, I. O., Fang, Y., Lun, M., & Li, C. (2021). X-ray Fluorescence Computed Tomography (XFCT) Imaging with a Superfine Pencil Beam X-ray Source. Photonics, 8(7), 236. https://doi.org/10.3390/photonics8070236