Analysis of the Spatial Properties of Correlated Photon in Collinear Phase-Matching

Abstract

In this paper, the spatial properties of correlated photon in collinear phase-matching in the process of spontaneous parametric down conversion (SPDC) are researched. Based on the study of the phase-matching angle, non-collinear angle, and correlated photon wavelength, a theoretical model of non-collinear angular variation is derived, which can be used to estimate and predict the width of the correlated photon ring. The experimental measurement is carried out with CMOS camera, and the measurement results are consistent with the theoretical simulation results, which verifies the rationality of theoretical reasoning. Meanwhile, the change of the correlated photon divergence angle outside the crystal is studied, the closer the wavelength is to the degenerate, the smaller the measurement value of the divergence angle, which is agreement with the theoretical simulation. The results of the study play a reference role in the evaluation of the spatial properties of correlated photon and lay a foundation for the measurement of the correlated photon number rate and the calibration of a photodetector.

1. Introduction

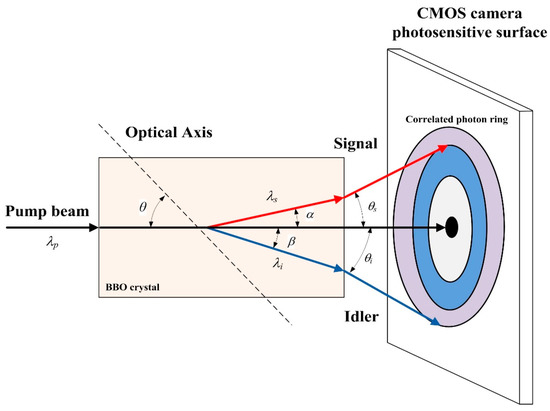
Spontaneous parametric down conversion (SPDC) is a nonlinear optical process in which a higher energy photon from laser beam splits into a pair of lower energy photons in the nonlinear crystal [1,2,3,4,5]. The photon pairs are produced simultaneously, but the properties of the individual photon are free and different, depending on the electric field and intensity of the higher energy photon during the down conversion process [6,7]. The two photons, called entangled photons or correlated photons [8], have a strict entanglement property in polarization time and space [9], which has been applied in quantum cryptography, quantum simulation, and quantum metrology [10,11,12,13,14,15,16,17]. In recent years, it is used for the absolute measurement of the quantum efficiency of photodetectors in the time-correlated single photon counting regime without relying on the calibrated standards [18,19,20,21,22]. During this process, the emission cone properties of correlated photons, such as spectral range, non-collinear angle, and divergence angle, play an important role in the selection of photosensitive surface of photodetector and the determination of its position. The SPDC of the down conversion process has two types depending on whether the correlated photons have the same or orthogonal polarization. If produced correlated photon pairs have the same polarization, but opposite to the pump, it is labelled as type-I down conversion, and vice versa, labelled as type-II down conversion [23,24,25]. Moreover, the pair of photons generated propagate in the same direction as the pumped photons, which is collinear phase-matching. Conversely, when the photon pairs travel in a different direction than the pump, it is the non-collinear phase-matching. The collinear phase-matching is a special case of non-collinear phase-matching. Compared with non-collinear phase-matching, the near-optical axis two-photon field of the collinear phase-matching can be carried out around the same propagation direction, and the spatial entanglement states are simple and easy to understand [2,26,27]. Also, the presence of Poynting vector walk-off effect will cause the spatial offset of the correlated photon increasing and reduce the conversion efficiency; for the collinear phase-matching, the spatial shape of the correlated photons due to the walk-off effect can be negligible [27,28].

In the previous literature [29,30,31,32,33], spectral bandwidth and gain bandwidth models were constructed from crystal length, group velocity, and group velocity dispersion, etc. However, the model of the non-collinear angular variation, correlated photon ring width, and divergence angle is not perfect in terms of the construction and analysis of the system from the aspects of phase-matching angle, non-collinear angle, and phase mismatch. In this paper, we analyze the spatial properties of the emitted photons in collinear phase-matching via non-collinear angular variation and divergence angular spectrum. Under the condition of the degenerate wavelength collinear phase-matching, we first theoretically calculate the relationship between phase matching angle, non-collinear angle, and parametric wavelength, construct a model of non-collinear angular variation and ring width of correlated photon. Then, combined with the experimental measurement results, the correctness and rationality of the theoretical simulation results are proven. Moreover, combining the non-collinear angle with Snell’s Law [34] to calculate the divergence angle outside the crystal at different wavelengths, and the experiment verifies the rationality of the theory. The properties and influence factors of SPDC process emission photons in uniaxial crystals with collinear phase-matching can be better informed. It lays a foundation for optimizing the SPDC process and carrying out correlated photon rate measurement and detector calibration.

2. Theoretical Estimation of the Correlated Photon Ring Properties

The SPDC process where the pump photon at energy ℏω_p splits into a correlated photon pair of signal and idler within the uniaxial crystal of BBO (β-BaB₂O₄: barium metaborate) which energies are respectively ℏω_s and ℏω_i, does follow energy conservation and momentum conservation rules so that [35]:

$$\hslash {\omega }_p=\hslash {\omega }_s+\hslash {\omega }_i$$

(1)

$$k_p=k_s+k_i$$

(2)

where ℏ is the Planck constant; ω_j and $k_j$ are the angular frequency and the wave vector for the pump, signal and idler modes (j = p, s, i). The Equation (2) is also known as the phase-matching condition. In order to achieve the maximum conversion efficiency, Equations (1) and (2) need to be met simultaneously.

Figure 1 denotes the produced correlated photon ring profile due to a pump beam interacts with the BBO crystal. Equation (2) is rewritten as the wave vector models of pump and parametric (signal and idler):

$$k_p=k_s\cos \alpha +k_i\cos \beta$$

(3)

$$k_s\sin \alpha =k_i\sin \beta$$

(4)

$$k_j=\frac{2\pi n_j}{{\lambda }_j}(j=p,s,i)$$

(5)

where α and β are the angles of signal and idler with pump beam, respectively. In addition to this the α (or β) is non-collinear angle in the crystal and it is called collinear phase-matching as α = β = 0°, which is a limit case of the non-collinear interaction scheme. The n_j and λ_j stand for the refraction index and wavelength, respectively. Thus, the relation of three wavelengths of signal (s), idler (i) and pump (p): $\frac{1}{{\lambda }_p}=\frac{1}{{\lambda }_s}+\frac{1}{{\lambda }_i}$ is satisfied.

Figure 1. A pump beam interacts with the BBO crystal to produce a correlated photon ring, and the profile is recorded by the CMOS camera photosensitive surface.

In the paper, the SPDC process occurs for a pump wavelength of 266 nm and interacts with the nonlinear crystal. It is assumed that the generated parametric photons have a wavelength range of 400 nm–794 nm, and the signal wavelength λ_s is 400 nm–532 nm. Then, the sum of the vector modes of parametric photons is K_sum:

$$K_{sum}=\frac{2\pi }{{\lambda }_s}\left[n_s+\frac{n_i}{{\lambda }_p}\left({\lambda }_s-{\lambda }_p\right)\right]$$

(6)

where n_s and n_i are the refraction index of parametric photons.

For negative uniaxial BBO crystals with n_e < n_o, type I down conversion refers to the generated two-photon pairs with ordinary state, whose refractive index does not depend on the propagation direction. However, the pump beam as extraordinary state and the refractive index n_p(θ) associates with the propagation direction of light [36]:

$$n_p\left(\theta \right)=\frac{n_p^o\cdot n_p^e}{\sqrt{{\left(n_p^o\sin \theta \right)}^2+{\left(n_p^e\cos \theta \right)}^2}}$$

(7)

where n_p^o and n_p^e respectively represent the main refractive index of pump beam in the crystal, which can be calculated by the Sellmeier formulas of the BBO crystal [37,38]. The θ is the angle between the vector direction of extraordinary light (e light) and the optical axis of the crystal, also known as phase-matching angle.

The variation of K_sum and θ at different signal wavelength is illustrated in Figure 2. It is clearly observed that the K_sum is inversely proportional to λ_s, but θ is directly proportional to λ_s. That is, with the increase of the signal wavelength, the sum of the vector modes of parametric decreases while the phase-matching angle increases. As a result, when the maximum value K_sum-max is 3.9735 × 10⁷ m⁻¹ at 400 nm and minimum value K_sum-min is 3.9547 × 10⁷ m⁻¹ at 532 nm. The pump vector mode is at minimum, k_p(θ) = K_sum-min, according to Equations (6) and (7), the minimum value of refractive index n_p(θ)_min and the maximum value of phase-matching angle θ_max are 1.6742 and 47.6339° respectively. Similarly, k_p(θ) = K_sum-max, namely, the maximum refractive index n_p(θ)_max and the minimum phase-matching angle θ_min are 1.6822 and 44.4721°, respectively.

Figure 2. The dependence of the sum of the vector modes of parametric K_sum and phase-matching angle θ on different signal wavelength λ_s.

As the phase-matching angle changes between 44.4721° and 47.6339°, the wavelengths of signal and idle which output from the back of the crystal also changes, as shown in Figure 3. In the case of collinear phase-matching, the parametric wavelengths are 400 nm (for the signal photon) and 794 nm (for the idler photon) at 44.4721°. In order to satisfy the conservations of energy and momentum of the Equations (1) and (2), with the increase of phase-matching angle θ, λ_s increase while λ_i decrease, all the way to θ is 47.6339°, λ_s = λ_i = 532 nm (for the degenerate photon pair). Of course, not only does the parametric photon pair with strict collinear phase-matching, but the satisfied non-collinear phase-matching condition can be emitted.

Figure 3. The curve of the wavelengths λ of signal and idler changing with the change of phase-matching angle θ. The black curve in the lower part represents the wavelength of signal λ_s (400 nm ≤ λ_s ≤ 532 nm), while the red curve in the upper part represents the wavelength of idler λ_i (532 nm < λ_i ≤ 794 nm).

The key point of the correlated photon rate measurement and detector calibration using the SPDC is to determine the location and properties of the correlated photon ring. For this, it is important to concentrate on the study of the spatial distribution properties of the correlated photons within and outside the BBO crystal, which is the type I phase-matching of the degenerate wavelength collinear (λ_s = λ_i = 2λ_p = 532 nm). When the pump beam interacts with the crystal surface at a certain angle, the correlated photons that satisfy the phase-matching requirements are produced, and the photons at different wavelengths correspond to different non-collinear angles, then, travel behind the crystal along different divergence angles. It is conical in space and ring-shaped on the photosensitive surface of the CMOS camera, which is perpendicular to the direction of the pump beam propagation. Moreover, the degenerate correlated photon pair is co-propagation with the pump, that is, 0° of non-collinear angle, and the projection on the camera’s photosensitive surface is beam-like, as shown in Figure 1.

From Equation (2), with the perfect phase-matching, the value of phase mismatch of three wave vectors (pump, signal and idler) in the crystal is 0, expressed as $\Delta k=0$, and $\Delta k=k_s+k_i-k_p$. In practical applications, there are many factors such as pump beam dispersion, cutting angle deviation and crystal temperature instability, and $\Delta k\ne 0$, which reduces the efficiency of crystal conversion. In general, specifies the absolute value of the maximum phase mismatch mode allows $\left|\Delta k\right|=\frac{\pi }{L}$, where L is the length of the interaction of three waves in the crystal [29,39]. From the previous analysis, it can be determined that in the process of SPDC, the phase-matching angle of the crystal meeting the conditions can emit correlated photons with a wide spectral range, as shown in Figure 3. The laser of 266 nm pumps the BBO crystal of phase-matching angle of 47.6339°, generated the correlated photons in 532 nm collinear while others noncollinear, and carries out a research of spatial distribution characteristics. Also, the spectral range emitted from the crystal is wide, however, the non-collinear angle variations of different wavelength correlated photons that satisfy the phase-matching criterial has a range, set as Δα (as signal) and Δβ (as idler). The smaller the value of Δα (or Δβ), the narrower the correlated photon ring received on the CMOS camera’s photosensitive surface, and the converse is wider.

In this part, assume that the three waves satisfy completely the phase matching conditions (θ = 47.6339°), which is $\Delta k=k_s\cos {\alpha }_0+k_i\cos {\beta }_0-k_p=0$, and the non-collinear angles of signal and idler are α₀ and β₀, respectively. As the modification of correlated photon wavelengths, the corresponding non-collinear angle modifies as shown in Figure 4. It can be seen that the correlated photons of different wavelengths propagate along different non-collinear angles. When the wavelength of both ends approaches the degenerate wavelength at 532 nm, the non-collinear angle decreases, and it is 0° at the point of 532 nm. This phenomenon conforms to the condition of complete phase matching.

Figure 4. The relationship between the wavelength and the non-collinear angle of the correlated photon in the complete phase matching.

In the actual process, if the pump beam in the crystal direction remains the same, the signal along the non-collinear angle (α₀+Δα), corresponding idler will along (β₀+Δβ). At this point, the phase mismatch Δk_act satisfies:

$$\Delta k_{act}=k_s\cos \alpha +k_i\cos \beta -k_p$$

(8)

where, α is the actual propagation direction of signal, which is the sum of non-collinear angle α₀ that is completely phase matching and the non-collinear angular variation Δα. Similarly, β is the actual propagation direction of idler and it is the sum of non-collinear angle β₀ that is completely phase matching and the variation Δβ.

In order to research the variation of signal non-collinear angle, Δk_act is expanded in a Taylor series:

$$\Delta k_{act}=\Delta k+\frac{\partial \Delta k}{\partial \alpha }\cdot \Delta \alpha +\frac{1}{2!}\frac{{\partial }^2\Delta k}{\partial {\alpha }^2}\cdot \Delta {\alpha }^2+\cdot \cdot \cdot$$

(9)

The maximum phase mismatch is taken for Δk_act, and Equation (9) of Δk_act expansion through second-order approximation can be rewritten as:

$$\Delta k+\frac{\partial \Delta k}{\partial \alpha }\cdot \Delta \alpha +\frac{1}{2!}\frac{{\partial }^2\Delta k}{\partial {\alpha }^2}\cdot \Delta {\alpha }^2+\frac{\pi }{L}=0$$

(10)

with

$$\{\begin{array}{l}\frac{\partial \Delta k}{\partial \alpha }=-k_s\cdot \sin {\alpha }_0-k_i\cdot \sin {\beta }_0\cdot \frac{\partial \beta }{\partial \alpha }\\ \frac{{\partial }^2\Delta k}{\partial {\alpha }^2}=-k_s\cdot \cos {\alpha }_0-k_i\cdot \cos {\beta }_0\cdot {\left(\frac{\partial \beta }{\partial \alpha }\right)}^2-k_i\cdot \sin {\beta }_0\cdot \frac{{\partial }^2\beta }{\partial {\alpha }^2}\\ \frac{\partial \beta }{\partial \alpha }=\frac{n_i{\lambda }_s}{n_s{\lambda }_i}\cdot \frac{\cos {\beta }_0}{\cos {\alpha }_0}\\ \frac{{\partial }^2\beta }{\partial {\alpha }^2}=\frac{n_i{\lambda }_s}{n_s{\lambda }_i}\cdot \frac{-\sin {\beta }_0}{\cos {\alpha }_0}\cdot \frac{\partial \beta }{\partial \alpha }+\frac{n_i{\lambda }_s}{n_s{\lambda }_i}\cdot \cos {\beta }_0\cdot \frac{\sin {\alpha }_0}{{\cos }^2{\alpha }_0}\end{array}$$

(11)

Simplifying Equation (10), the variation of signal non-collinear angle (Δα) can be written as:

$$\Delta \alpha =\frac{g_s-h_s}{w}$$

(12)

with

$$\{\begin{array}{l}{g}_s=2\pi \cdot \left[\frac{n_s}{{\lambda }_s}\cdot \sin {\alpha }_0+{\left(\frac{n_i}{{\lambda }_i}\right)}^2\cdot \frac{{\lambda }_s}{n_s}\cdot \frac{\sin {\beta }_0\cos {\beta }_0}{\cos {\alpha }_0}\right]\\ w=-2\pi \cdot \left[\frac{n_s}{{\lambda }_s}\cdot \cos {\alpha }_0+{\left(\frac{n_i{\lambda }_s}{n_s{\lambda }_i}\right)}^2\cdot \frac{n_i}{{\lambda }_i}\cdot \frac{\cos 2{\beta }_0\cos {\beta }_0}{{\cos }^2{\alpha }_0}\right]+\frac{n_i{\lambda }_s}{n_s{\lambda }_i}\cdot \tan \alpha \cdot \frac{\cos {\beta }_0}{\cos {\alpha }_0}\\ f=2w\cdot \frac{\pi }{L}\\ h_s=\sqrt{g_s^2-f}\end{array}$$

(13)

In a similar way, the variation of idler non-collinear angle can be deduced which is similar to Equation (12). According to the above reasoning process, the variation of the non-collinear angle of the correlated photon is bound up with the non-collinear angle with complete phase matching and the action length of the three waves in the crystal.

3. Experimental Measurement

In this part, an experimental platform is built to measure the properties of the angular distribution of the correlated photons generated by a BBO crystal, which verifies the theoretical research on the non-collinear angular variation through experimental method. The layout of the experimental measurement setup is shown in Figure 5.

Figure 5. Experimental measurement setup.

The pump source is a continuous laser of 266 nm with the maximum power up to 55 mW. The quartz prism (vertex angle of 70°) and the dichroscope (reflectivity of 98% in the wavelength of 266 nm) eliminate the residual 532 nm in the pump beam of 266 nm. Moreover, the G-T represents the Glan-Taylor polarizer made of α-BBO and it is plated with 200 nm to 400 nm anti-reflection film, which modifies the polarization ratio of the pump, increases the proportion of e light in type-I SPDC, and further increases the correlated photon number generated. The zero-order half-wave plate is used to change the phase difference of 1/2 wavelength to realize the opening and closing of the correlated photons generation process. A plano-convex lens with a focal distance of 150 mm focuses the pump beam at the entrance of the nonlinear crystal.

The nonlinear crystal used negative uniaxial BBO is 2 mm long, cut for type-I collinear phase-matching at θ = 47.63°. Of course, the crystal phase-matching condition also can be turned to $n\left(\omega \right)=n_p\left(2\omega \right)$(n(ω) and n_p(2ω) said the refractive index of the correlated photon and the pump) due to $k_{s,i}=n\left(\omega \right)\cdot \frac{\omega }{c}$(k_s,i and ω are, respectively, the wave number and frequency of the correlated photon, c is the photon propagation speed in a vacuum). The results show that the phase-matching condition can be regarded as the refractive index of the correlated photon in the crystal is equivalent to that of the pump. In the case that most nonlinear optical crystals in the visible are in normal dispersion, and the higher the wave frequency, the greater the refractive index, namely $n\left(\omega \right)<n_p\left(2\omega \right)$. Therefore, the phase-matching condition cannot be satisfied theoretically when the wave beam propagates in isotropic medium. However, for the anisotropic BBO crystal, due to the birefringence effect, two waves with different refractive indices are allowed to propagate in the same direction, and the phase matching can be realized by the effect in the normal dispersion range.

The long-pass filter (with a transmittance of over 95% across the spectrum from 400 nm to 794 nm) and the band-pass filter are represented as LP-F and BP-F, respectively, whose functions are to eliminate any residual radiation at the continuous laser and selecting the wavelength of the correlated photons. Moreover, the non-collinear angular variation and the divergence angular distribution are recorded by means of the imaging device of CMOS camera, whose effective area is 13.312 mm × 13.312 mm and readout mode is chosen 4 × 4, placed in the behind of BP-F. Observe the spectral distribution of correlated photons emitted from the back of BBO crystal, and the results will be presented in Figure 6. It can be found that the signal and idler wavelength of 472 nm and 610 nm are a pair of correlated photons. It is observed that the same ring images appear as the theoretical analysis, in which the spot in each central same area is composed by 266 nm pump not eliminated completely. Although the detection sensitivity of CMOS camera in 400 nm to 794 nm is at least 6 times higher than 266 nm, however, the correlated number is 8 orders of magnitude lower than the pump, the ring cannot be seen without the filters. The results of the theoretical calculations, experimental measurements, and detailed explanations will be developed in the next section.

Figure 6. (a–i) Experimental results of the correlated photon rings with different wavelengths. (a) λ = 415 nm, (b) λ = 472 nm, (c) λ = 550 nm, (d) λ = 572 nm, (e) λ = 605 nm, (f) λ = 610 nm, (g) λ = 685 nm, (h) λ = 700 nm, (i) λ = 710 nm.

4. Results Analysis

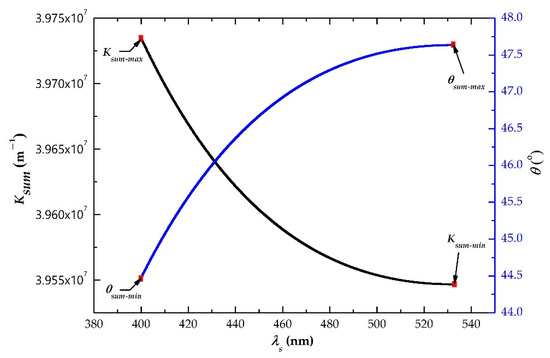
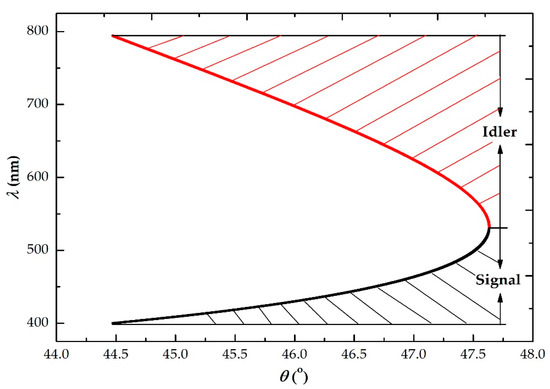
According to theoretical analysis, the correlated photon ring width is related to the non-collinear angular variation, that is, the ring width at different wavelengths is different, and the corresponding non-collinear angular variation is also different. In this section, first using the Equation (12) to calculate the 415 nm, 472 nm, 550 nm, 572 nm, 605 nm, 610 nm, 685 nm, 700 nm, and 710 nm, a total of nine wavelengths corresponding non-collinear angular variation, we find that the theoretical results have a floating range. Then, the ring profile measured by CMOS camera is processed, and the width values can be obtained with the image processing technology, finally converted into the non-collinear angular variation behind crystal (not exuded). Figure 7a shows the theoretical simulations and experimental measurements of the non-collinear angular variation at different correlated photon wavelengths. The black and red curves represent the theoretical values and the measured values of non-collinear angular variation, respectively. Figure 7b illustrates the error bars of the experimental data. It can be observed that the measured values are less than the theoretical simulation, which is the result of the theoretical research under the premise of the largest phase mismatch. Also, it provides reference and guidance for predicting the maximum width and position of correlated photon rings. The non-collinear angular variations of 472 nm, 550 nm and 572 nm are simulated theoretically, higher than the other wavelengths, and the experimental results are consistent with the theory. Meanwhile, with the decrease of signal wavelength and the increase of idler wavelength, the difference between the theoretical and measured values of the non-collinear angular variation decreases. At the wavelengths of 685 nm and 550 nm, the difference between theory and measured data are minimum 0.0168° and maximum 0.1906°, respectively. The reason is that the closer the non-collinear angle is to the degenerate wavelength, the greater the influence of the experimental conditions such as phase-matching angle, pump incident angle, and diameter.

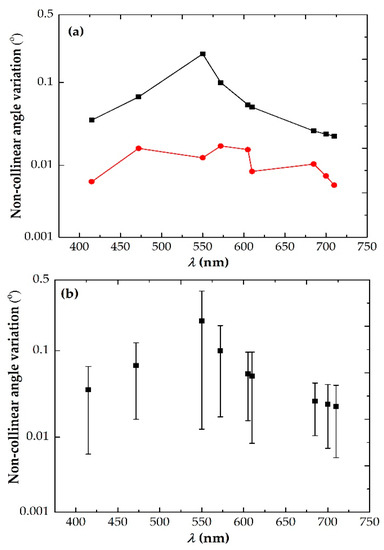
Figure 7. (a) Theoretical simulation and experimental measurement of the noncollinear angular variation at different photon wavelengths. The curves of black and red respectively represent the theoretical values and the measured values of non-collinear angular variation. (b) The error bars of the experimental data of the non-collinear angle variation.

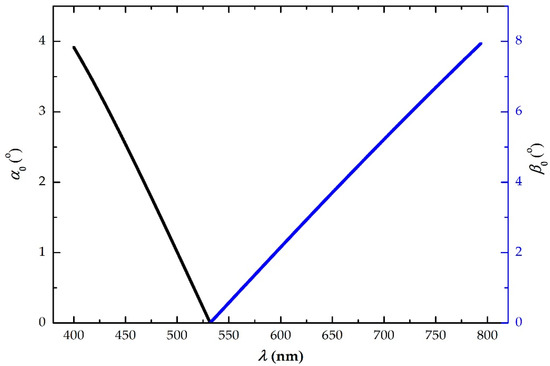
The location and size of the ring need to determine before calibrating the photodetector using correlated photons. To understand and determine the position and size of the ring before using correlated photons to carry out the photodetector calibration, another physical quantity, divergence angle, describing the spatial properties of the correlated photons, is introduced. It is the included angle between the outer circle of the correlated photon and the pump beam emitted from the back of the crystal, which is half of the apex angle of the spatial propagation cone, and in Figure 6, is expressed as θ_s /θ_i representing respectively the divergence angle of signal or idler. The non-collinear angle is the between the propagation direction of the correlated photon in the crystal and the pump beam, while the divergence angle is another form of its existence outside the crystal. And the conversion between the two angles can be made by Snell’s Law. Therefore, measured values of divergence angles at different wavelengths are obtained based on the correlated photon rings in the above experiment, however, the theoretical simulations require combining Equations (3)–(5) and Snell’s Law, as presented in Figure 8. At both ends of the degenerate wavelength of 532 nm (415 nm ≤ λ < 532 nm and 550 nm ≤ λ ≤ 710 nm), the divergence angle decreases as the wavelength of signal increases, while is diametrically opposite for the relationship between the idler wavelength and divergence angle, which is increases as the wavelength of idler increases. When the correlated photon wavelengths are 472 nm, 550 nm and 572 nm (near degeneracy), the measured average of the divergence angle differs by 1.73° from the theoretical. On the one hand, it has an error of 0.25° between the cutting angle and phase-matching angle which causes the degeneracy wavelength to shift. On the other hand, the effect of non-collinear angle on the phase-matching angle of degenerate collinear wavelength is significant. It can be seen from Figure 7 that the non-collinear angular variation mean of the three wavelengths is 0.0156°, which is greater than the others.

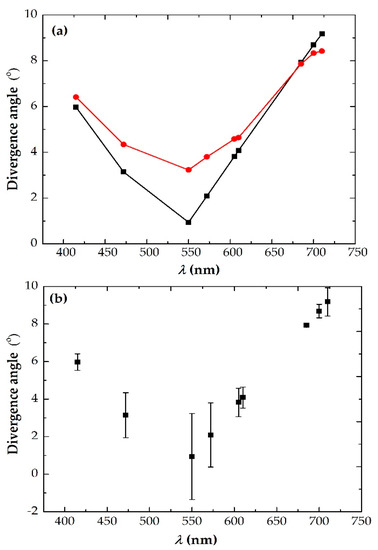
Figure 8. (a) Theoretical simulation and experimental measurement of the divergence angular spectrum at different photon wavelengths. The black curve represents the theoretical values, and the red curve is the experimental results. (b) The error bars of the experimental data of the divergence angle.

5. Discussions

The main result of this work is based on the quantity expression of phase-matching condition, and the theory studies the second-order change of the non-collinear angle with the wavelength of the correlated photons. At the same time, the parameters of the characterization spatial properties (the non-collinear angle of correlated photon, spectral width, divergence angle) are quantitatively described and analyzed without varying the parameters such as pump and crystal. In the experiment, a pair of correlated photon images can be observed and recorded, which verifies the process of producing the correlated photons in SPDC satisfying the law of energy conservation. However, the previous works mainly studied the spatial distribution of correlated photons produced by varying the pump parameters (such as, focusing on pump beam and changing pump spectral width) during the process of SPDC, which influenced the spatial symmetry of the two-photon field [25,40,41,42]. Also, a qualitative study was implemented for the spatial characteristics of correlated photons under the condition that the diameter, near field and far field of pump were considered [43]. Moreover, the spectral characteristics of the type-I SPDC, which were in the three commonly phase-matching conditions (collinear degenerate, noncollinear degenerate and collinear nondegenerate), were reported, and the relationship between spectroscopy and photon freedom entanglement was studied, which provided the theoretical guidance for the application of quantum ghost imaging [44], interference effect [45,46], and other techniques. The entangled two-photon field generated by SPDC phase matching in BBO crystal was explored in depth by Karan et al [47], who summarized the effects of various crystal and pump parameters on the entangled two-photon field, in order to illustrate how various experimental parameters affect the photon pairs generated. Finally, the two-photon wave function was derived based on angle-orbital angular momentum and the two-photon angular Schmidt spectrum was calculated. From the perspective of quantum electrodynamics, Forbes et al [48] quantitatively analyzed the degenerate down conversion mechanism of localized and nonlocalized, providing a reasonable explanation for the uncertainty of the position-momentum of the correlated photon propagation.

The spatial properties of the SPDC in type-I BBO uniaxial crystal with degenerate wavelength collinear phase-matching are investigated theoretically and experimentally. Based on the quantity expression of phase-matching condition, the relationship between the non-collinear angle and the correlated photon wavelength has been presented. Also, the theoretical process of the non-collinear angular variation is derived and analyzed, and the results have a floating range of 0.0235°–0.2032°. Then, the spatial divergence angle coming out of the crystal, is calculated. Of course, the correlated photon rings are measured by CMOS cameras and the measured image can be converted to the corresponding measurements of non-collinear angular variations and divergence angles. The experimental measurement results verify the correctness of the numerical simulation of non-collinear angular variation in the range. As for the divergence angle, the measurements at both ends of the degenerate wavelength 532 nm (except for three nearby wavelengths) are consistent with the theoretical simulation. And the non-collinear angular variation mean of three correlated photon wavelengths near the degenerate wavelength is larger than others, which also has a great influence on the phase-matching angle of the degenerate wavelength collinear. Moreover, at the phase-matching angle 47.63°, the measured divergence angle decreases with the increase of signal and increases with the increase of idler, and the result is agreement with theoretical analysis. The theoretical analysis model of the spatial properties of the correlated photon pairs established in the paper will lay a foundation for a deeper understanding of the positions and characteristics of parametric photons in advance in the photodetector calibration process.