Abstract
As water is normally used as the immersion medium in optically trapped microsphere microscopy, the high-refractive-index barium titanate glass (BTG) microsphere shows a better imaging performance than the low-index polystyrene (PS) or melamine formaldehyde (MF) microsphere, but it is difficult to be trapped by single-beam optical trapping due to its overly high refractive index. In this study, coated BTG microspheres with a PS coating have been computationally explored for the combination of optical trapping with microsphere-assisted microscopy. The PS coating thickness affects both the optical trapping efficiency and photonic nanojet (PNJ) property of the coated BTG sphere. Compared to the uncoated BTG sphere, the coated BTG sphere with a proper PS coating thickness has a highly improved trapping efficiency which enables single-beam optical trapping, and a better PNJ with a higher optical intensity and a narrower full width at half maximum (FWHM) corresponding to better imaging performance. These coated BTG spheres also have an advantage in trapping efficiency and imaging performance over conventional PS and MF spheres. The coated BTG microsphere is highly desirable for optically trapped microsphere super-resolution microscopy and potentially beneficial to other research areas, such as nanoparticle detection.
1. Introduction
Optical microscopes are widely used in the fields of life science and nano-technology. Due to the optical diffraction limit, conventional optical microscopy has a 200 nm resolution in the visible spectrum which has greatly hampered its applications in many research fields. To break the optical diffraction limit, several techniques have been developed, including a near-field scanning optical microscopy [1], solid immersion lens [2], superoscillatory lens [3] and fluorescent microscopy [4].
In 2011, Wang et al. demonstrated that a traditional optical microscope together with transparent fused silica (SiO2) microspheres () can gain a 100-nm resolution in air under white light illumination [5]. Then, a polystyrene (PS) microsphere () was used to overcome the optical diffraction limit in both air [6] and water [7]. Darafsheh et al. realized optical super-resolution imaging by using high-refractive-index barium titanate glass (BTG) microspheres () totally immersed in a liquid environment [8], and they also studied the influence of immersion medium on imaging performance in microsphere-assisted microscopy [9]. This label-free super-resolution imaging technique has attracted many research groups across the world, demonstrating sub-diffraction discerning ability in nanostructure detections and biological observations [10,11,12,13]. The super-resolution mechanism of microsphere-assisted microscopy is still a heated topic [14,15,16]. Early in 2004, the dielectric microsphere was regarded as a potential new visible-light super-resolution technique through a phenomenon known as “photonic nanojet” (PNJ), which has a narrow waist and an extraordinarily high optical intensity formed on the shadow-side surface of a plane-wave-illuminated dielectric microsphere [17]. The full width at half maximum (FWHM) and the maximum optical intensity () of the PNJ are related to the size of the microsphere, the incident wavelength and the refractive index contrast (RIC) between the microsphere and immersion medium [18]. Ultralong PNJ can be obtained by a two-layer dielectric microsphere [19], a graded-index microsphere [20] and a liquid-filled hollow microcylinder [21]. Meanwhile, an ultra-narrow PNJ can be gained by overstepping the upper refractive index [22], a dielectric cylinder, with a glass cuboid [23] and a nanohole-structured mesoscale dielectric sphere [24]. It is responsible for switching the PNJ on and off for a microsphere with an incident focused beam [25]. The PNJ theory is regarded as a part of the super-resolution mechanism, and there is a qualitative relation between PNJ property and imaging performance [26,27,28]. It has been investigated that the PNJ greatly benefits high-resolution optical imaging, and the resolution power of PNJ is quantified [29]. We can use the PNJ property of the sphere to characterize the imaging performance, which would help us in selecting a proper microsphere for practical microsphere-assisted microscopy.
To control the position of the microsphere for site-specific imaging and large field-of-view scanning imaging, a non-contact optical manipulation technique of microparticles, named optical trapping (also known as optical tweezers), can be introduced [30]. A schematic of a normal optical system for the combination of single-beam optical trapping with microsphere-assisted microscopy is shown in Figure 1a, including an optical trapping part and an illumination part with the same objective. The laser beam () is highly focused by the objective to trap the microsphere, and the charge-coupled detector (CCD) captures the magnified image of the sample surface through the trapped microsphere under an illumination (). The inset in Figure 1a shows the scheme of typical optical trapping of a microsphere in a Gaussian beam. Optically-trapped microspheres have been widely used for imaging applications. Early in 1997, a micro-objective, made of a 25-μm PS microsphere, was manipulated by single-beam optical tweezers to produce locally magnified (or reduced) images of a specific area [31]. Furthermore, Stanescu et al. investigated the magnification property of a laser-trapped PS sphere in water [32]. An optically-trapped SiO2 sphere with a diameter of 8 μm was used to image the sample surface and detected the defect successfully [33]. Recently, our group focused on the selection of microsphere types for the combination of optical trapping with microsphere-assisted microscopy, and finally, the low-index PS sphere and melamine formaldehyde (MF) sphere () were optically-trapped for super-resolution imaging of a 139-nm line-width silicon nanostructure grating [34]. Optically-trapped microsphere microscopy holds an advantage in super-resolution imaging through the non-contact optical manipulation of dielectric microspheres.
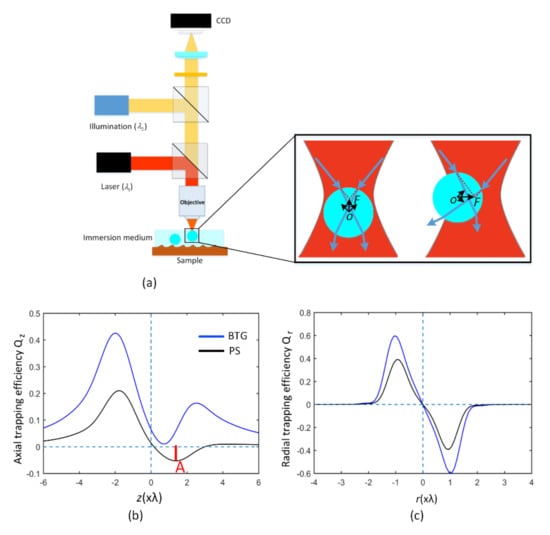
Figure 1.
(a) Schematic of a normal optical system for the combination of single-beam optical trapping with microsphere-assisted microscopy. The same objective is utilized for both the optical trapping and the observation. The inset in (a) shows force on the microsphere in optical trapping with a Gaussian beam, in which the sphere is dragged toward to the region of high intensity. Axial (b) and radial (c) trapping forces of a barium titanate glass (BTG) sphere (blue line) and polystyrene (PS) sphere (black line) in optical trapping as a function of displacement from the focus. The force is given in terms of the dimensionless trapping efficiency which can be converted to actual force by multiplying by , where is the immersion index, is the beam power at the focus and is the light speed in free space. A linearly polarized 1064-nm Gaussian beam is used as the trapping beam, focused by an objective with numerical aperture of 1.0. These two spheres in water have the same radius of 0.8 μm. The maximum reverse axial force A is shown in (b) and it characterizes the trap strength. The PS sphere can be trapped easily, while the BTG sphere is hard to trap.
In optically-trapped microsphere microscopy, the microsphere is not only the object of optical trapping, but also the one to be used for magnified or super-resolution imaging. The refractive index of the sphere is fairly important because it affects both the optical trapping property and the imaging performance of the sphere. On the one hand, for single-beam optical trapping in water, the refractive index of the used sphere is required be less than 1.73 [35], and too high of a refractive index will make it difficult to realize stable optical trapping. For example, the axial force and radial force acting on two index-different spheres as a function of sphere position are illustrated in Figure 1b,c, respectively. The maximum reverse axial force A characterizes the trap strength, which determines whether or not the sphere can be trapped. We can see that the low-index PS sphere in water can be trapped easily, while the high-refractive-index BTG sphere is hard to trap in three dimensions because its high refractive index strongly increases the scattering force, which pushes the sphere away from the focused laser spot. An alternative method to trap high-index spheres has been proposed by counter-propagating optical tweezers in which the scattering forces are eliminated [36], but such a setup is complicated. On the other hand, for imaging applications of microspheres in water, the high refractive index of the BTG sphere is beneficial to produce a sharper PNJ and a better imaging quality (higher resolution and better image contrast) than that of the low-index SiO2, PS and MF spheres. Even with the same RIC, the BTG sphere in a liquid droplet produces a highly focused PNJ and a better image contrast compared with a low-index soda lime glass sphere () in air [9]. There seems to exist a contradiction for the combination of single-beam optical trapping with microsphere-assisted microscopy when using high-refractive-index BTG spheres, and existing optically-trapped microsphere microscopy using low-index spheres in water may suffer from poor imaging performance, e.g., inadequate discerning ability and low image contrast.
In this study, high-refractive-index BTG microspheres with uniform PS coatings have been computationally explored for optically trapped microsphere microscopy. An antireflection coating on a high-refractive-index sphere can improve the trapping efficiency of the sphere efficiently [35,37]. From numerical simulations, we found that coating thickness plays an important role and it affects both the optical trapping efficiency and the PNJ property of the coated BTG sphere. Compared to an uncoated BTG sphere, a coated BTG sphere with a proper PS coating thickness in water has a highly improved trapping efficiency, and a better PNJ with a higher and a narrower FWHM which corresponds to a better imaging performance. For coated BTG spheres with a specific core radius of 2.5 μm, the maximum axial trapping efficiency can be enhanced over 10-fold by proper PS coating, and the PNJ properties (FWHM and ) are also improved by the coating. In addition, coated BTG spheres also have an advantage in trapping efficiency and imaging performance over conventional low-index PS and MF spheres. A coated BTG sphere enables single-beam optical trapping for enhanced trapping efficiency and also produces a better PNJ property related to better imaging performance, making it highly desirable for optically-trapped microsphere super-resolution microscopy.
2. Model of a Coated Sphere
A model of the coated microsphere is illustrated in Figure 2. The sphere consists of an inner core of radius and an outer coating of radius . The refractive indices of the inner core and the outer coating are and , respectively. The coated sphere is totally immersed in a liquid medium with . The incident electric field can be a Gaussian beam for optical trapping or a plane wave for PNJ generation.
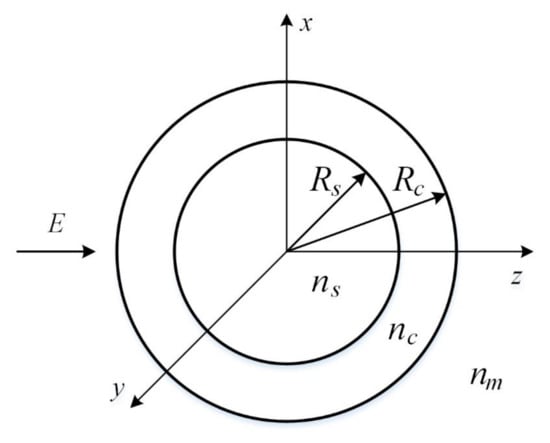
Figure 2.
Model of a coated microsphere.
In the following simulations, is set to 1.9 corresponding to the BTG sphere, and deionized water () is used as immersion medium. The PS material () is used as a coating and the coating thickness varies. The coating index is almost equal to the geometric mean of the indices from the core and the medium, and the geometric mean is normally used for an optimal single-layer planar antireflection coating [38].
One should note that the refractive index of the core of the coated sphere is set to 1.9 in numerical simulations; for other high-index spheres with a different refractive index, such as BTG spheres () and TiO2 spheres (), similar analysis could be implemented by considering the optical trapping performance and the PNJ property of the coated sphere simultaneously.
3. Optical Trapping of Coated Spheres
3.1. Relationship between the Optical Trapping Forces and the Refractive Index Difference Δn
Normally, there are two optical forces acting on a sphere in a focused laser beam: one is the gradient force , which attracts the sphere towards the focus, and the other is the scattering force, which tends to push the sphere away from the focus. A sphere can be trapped if the gradient force is larger than the scattering force. In the Rayleigh regime (), the gradient force of a single uncoated sphere is considered to be proportional to refractive index mismatch —the difference between the refractive index of the sphere and the immersion medium [39]:
where .
A larger gradient force can be generated by spheres with a higher refractive index, attracting spheres more strongly toward the focal region of optical trapping.
However, the scattering force is related to the reflectivity of the sphere, and it is proportional to , the square of the refractive index difference between the refractive index of the sphere and the immersion medium:
It is apparent that the scattering force increases more quickly with the refractive index mismatch than the gradient force. Therefore, for spheres with a high refractive index, the scattering force dominates, which pushes spheres away from the focus in the direction of light propagation. This limits the maximum refractive index of spheres that are able to be trapped in single-beam optical tweezers.
In the geometric optics regime (), by some proper assumptions, such as neglecting interferences and multiple reflections, considering the reflection and refraction of a single light ray incident at an angle with respect to the normal of the sphere surface, researchers also found that the gradient force by a single ray is proportional to the :
Furthermore, the corresponding scattering force by the reflected light ray is proportional to :
Summing the overall light rays preserves the scaling.
In the Mie regime (), including spheres we mainly consider in this research, although the force relations cannot be described correctly by the Rayleigh scattering or geometric approximation, one can still find that for spheres in this regime, the scattering force depends more strongly on the refractive index mismatch than on the gradient force.
Antireflection coating on a high-refractive-index sphere serves as a simple and effective way to reduce the scattering force, eventually making high-index spheres trappable by single-beam optical trapping [35,37]. As illustrated in Figure 2, the refractive index of the antireflection coating is the between that of the sphere and the immersion medium (typical deionized water): , where . Without the coating, we have only one sphere–water interface, . With the coating, we get two interfaces: a water–coating interface, , and a coating–sphere core interface, . According to the Fresnel equations, the reflectivity is proportional to the square of the refractive index mismatch . The sum of the squares is less than the square of the sum, so the total sum of the reflectivity at the two interfaces is smaller than that at the sphere–water interface:
The scattering force is proportional to the reflectivity, and it can thus be reduced by the antireflection coating with a refractive index equal to the geometric mean of the indices from the sphere core and the immersion medium.
3.2. Optical Trapping Simulations of Coated BTG Spheres with PS Coating
To calculate the optical forces on particles in optical trapping, we used the optical tweezers toolbox [40]. A Gaussian beam with wavelength nm was used as the trapping beam, and it was focused by an objective with NA 1.0. The core radius was set in a range of 0.5 μm–5 μm for a wide enough field of view (FOV) in microsphere-assisted microscopy, and the coating thickness was varied from to (corresponding to 0 nm–669 nm, ) with an interval value of . The trap strength could be determined by the maximum reverse restoring force (i.e., maximum reverse axial force in Figure 1b). The dependence of trap strength on sphere size with four different PS coating thickness is shown in Figure 3. The oscillations that appeared in the profiles result from the interference effect [35,41]. For comparison, the force on the uncoated BTG sphere with the same core radius was also calculated, and we can see that uncoated BTG spheres cannot be optically trapped at all sizes. See Video S1 for improvements in axial trapping efficiency and Video S2 for improvements in radial trapping efficiency of coated BTG spheres with varied PS coating thickness. This suggests that the improvement from the coating is not overly sensitive to the coating thickness [35]. This may not be suitable for high-index BTG spheres. When varies from to (about 100 nm–234 nm), the overall enhancement in first increases and then decreases (almost all coated BTG spheres can be trapped regardless of their radii). With (167 nm), the greatest overall improvement in is obtained as shown in Figure 3c, and the overall enhancement brought by the PS coating is over 3-fold compared to the uncoated BTG spheres. When exceeds (234 nm), the improvement of for large coated BTG spheres gradually weakens, and the minimal improvement occurs at (335 nm) in which almost all coated BTG spheres with core radius larger than 3 μm cannot be trapped, as seen in Figure 3e. With the increasement of , the second greatest overall improvement in can be gained at (535 nm) as illustrated in Figure 3g. The coating thickness affects the axial trapping efficiency obviously, and it has a small impact on the radial trapping efficiency . Note that , which normally exceeds broadly, is high enough for stable radial trapping. Therefore, in this research we will pay more attention to the effect of PS coating on axial trapping efficiency . Through proper PS coating, the optical trapping efficiency of the high-index BTG sphere has been highly improved, which demonstrates that the antireflection coating on a high-index sphere is very useful for single-beam optical trapping.
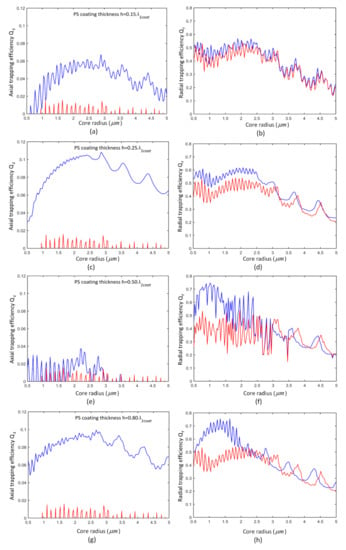
Figure 3.
Maximum axial trapping efficiency and maximum radial trapping efficiency for coated (in blue) and uncoated (in red) high-refractive BTG spheres with a varied PS coating thickness. The BTG core radius was set in a range of 0.5 μm–5 μm. Four different PS coating thickness are illustrated: for (a,b); for (c,d); for (e,f); for (g,h).
As shown in Figure 4, similar improvements in and have also been demonstrated for a coated BTG sphere with a specific core radius of 2.5 μm. It is apparent that the coat thickness affects the improvement in axial trapping efficiency . With varying , the corresponding maximum and minimum occur in due to the destructive or constructive interferences formed by the light reflected from the inside and outside surfaces [35]. The maximum improvement in (0.1053) occurs at a coating thickness of 181 nm (), and the second maximal improvement in (0.088) occurs at of 535 nm (). When is close to 381 nm (), the improvement in axial trapping efficiency almost vanishes, resulting in even smaller than that of the uncoated BTG sphere (). With a proper coat thickness, we can gain an effective enhancement in for high-refractive-index BTG spheres, and this highly-improved trapping efficiency will enable us to trap coated BTG spheres with single-beam optical tweezers.
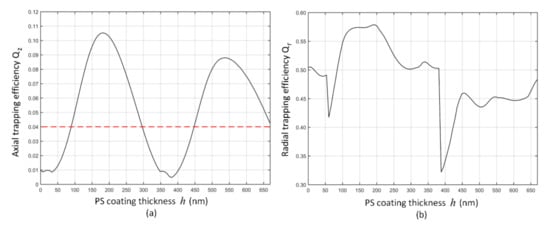
Figure 4.
Axial (a) and radial (b) trapping efficiency for a coated BTG sphere with a core radius of 2.5 μm, as the PS coating thickness varies.
4. PNJ in Coated Spheres
4.1. Electromagnetic Fields in a Multilayered Sphere
Based on the Mie theory, for an x-polarized incident plane wave with an amplitude propagating in the z direction, the electric and magnetic fields can be calculated for a multilayered sphere with layers, where corresponds to the core region. Each layer has a size parameter and a refractive index contrast , where is the out radius of the layer, is the refractive of the layer and is the refractive index of the immersion medium outside the whole multilayered sphere. The whole space could be divided into two regions: one is the region inside the multilayered sphere, and the other region is the immersion medium outside the sphere. From a physical point of view, the electric fields can be regarded as a superposition of inward and outward waves. For example, and can be expressed in term of complex spherical eigenvectors [42]:
where . , , and () are the vector spherical harmonics, and here, we use only the first kind of spherical Bessel function () and the first kind of spherical Hankel function (). The subscripts and denote even and odd modes, respectively; is the order of vector spherical harmonics.
The expansion of the electric fields in the region is given by:
where is the angular frequency and is the magnetic permeability. The expansion coefficients (,, and ) can be determined by matching the tangential components of electromagnetic fields at all of the interfaces [43].
The internal electric field in the core region () is in the form:
In the region outside the sphere, the total external fields are considered to be the superposition of the incident field and the scattered field, . By the Mie theory, they can be expressed by:
where and are the scattering coefficients. By comparing equations, we have , , and .
4.2. PNJ Property of Coated BTG Spheres with PS Coating
The coated BTG sphere with a PS coating in Figure 2 can be regarded as one type of multilayered sphere. Based on the Mie theory, we will now study the intensity distributions of PNJs for coated BTG spheres with a PS coating. For the incident wave, a linearly polarized plane wave ( nm in vacuum) propagates along the z-axial. We suppose that the coated BTG sphere has a core radius of 2.5 μm, the same as the radius in Figure 4, and the thickness of the PS coating is varied from 0 nm to 669 nm.
Figure 5 shows the intensity distributions of PNJs generated on the shadow sides of four BTG spheres with different PS coating thicknesses . The coating thickness affects the focusing performance of the PNJ, as shown in Figure 5a–e. The uncoated BTG sphere () has a maximum optical intensity of 165, where is the incident optical intensity. At positions of maximum optical intensity, we obtained the corresponding FWHMs of PNJs. Figure 5f–j show the FWHMs of PNJs corresponding to Figure 5a–e. With of 282 nm, the coated BTG sphere possesses a PNJ with a FWHM of 298 nm, which seems worse compared to that of the uncoated BTG sphere. Meanwhile, some values of PS coating thickness led to a better PNJ with a higher and a narrower FWHM. Using a proper coating thickness, we can obtain a focused PNJ with a narrower FWHM and a higher . With of 188 nm, we obtained a better PNJ (, FWHM = 220 nm as shown in Figure 5b,g) related to better imaging performance. When was 450 nm, we also obtained a better PNJ with a FWHM of 222 nm (Figure 5i), and the enhancement in (Figure 5d) was over 1.45 fold compared to that of the uncoated BTG sphere (Figure 5a). With of 535 nm, we obtained a better PNJ with a FWHM of 234 nm (Figure 5j), and the enhancement in (Figure 5e) was over 1.62 fold compared to that of the uncoated BTG sphere.
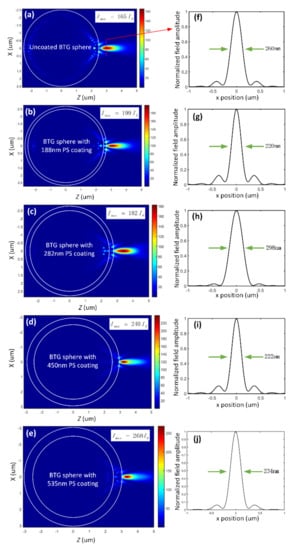
Figure 5.
Intensity distributions and full widths at half maximum (FWHMs) around a 2.5 μm-core-radius BTG sphere with different PS coating thickness: (a) uncoated BTG sphere, (b) BTG sphere with 188-nm PS coating thickness, (c) BTG sphere with 282-nm PS coating thickness, (d) BTG sphere with 450-nm PS coating thickness and (e) BTG sphere with 535-nm PS coating thickness. (f–j) FWHMs of photonic nanojets (PNJs) at the maximum intensity donated by the dashed line in (a–e). is the intensity of the incident wave.
Figure 6 shows the relative change of FWHMs and of PNJs of coated BTG spheres (core radius 2.5 μm) with varied PS coating thickness, and the uncoated BTG sphere with a radius of 2.5 μm is used for comparation. It can be seen that with PS coating, the coated BTG spheres normally show a higher (blue line in Figure 6). The wave additionally focuses due to the increase in the curvature of the radiation wave front going through the core, leading to an enhancement in at the focal waist of the coated sphere [44]. The increase in in our study results from two aspects: (1) the reduction in backscattered light; (2) the increase in the sphere volume. The latter is likely to be the main reason for the rapid increase in with a large PS coating thickness (like above 400 nm). The FWHM varied with the increase in (red line in Figure 6), and all FWHMs were less than 300 nm (). When varied from 0 nm to 400 nm, the FWHM of the PNJs showed a random varying trend. Note that once the leads to a widened FWHM, the increase in corresponding is relatively small. When was in the range of 400 nm to 669 nm, the FWHMs of the coated BTG spheres were always narrower than that of the uncoated BTG sphere, and the relative change in was more than 20%.
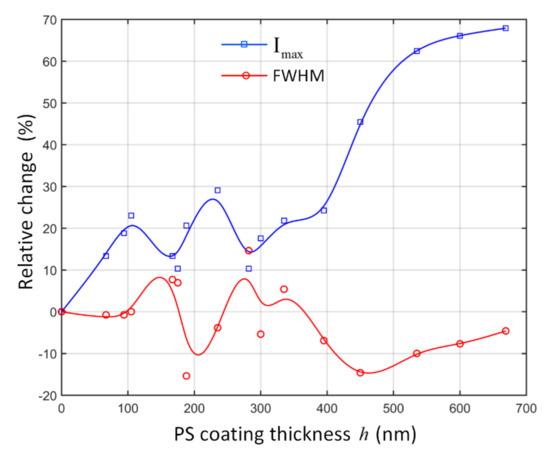
Figure 6.
Relative change of the FWHM and maximum optical intensity of PNJs for a 2.5 μm-core-radius BTG sphere with different PS coating thickness. The corresponds to the uncoated BTG sphere.
5. Proper PS Coating Thickness for Coated BTG Spheres
From numerical simulations for optical trapping and PNJ generation of coated BTG spheres with a PS coating, we can see that the PS coating thickness affects both the optical trapping (Figure 4) and the PNJ property (Figure 5 and Figure 6). A proper PS coating thickness is beneficial to obtain an improved optical trapping efficiency and a better PNJ property of the coated BTG sphere simultaneously, and it is desirable for optically-trapped microsphere microscopy. Actually, the biggest problem of the high-index BTG spheres used for optically-trapped microsphere microscopy is that it cannot be trapped by single-beam optical tweezers. Now, how to decide the proper coating thickness? One simple principle to decide proper PS coating thickness is illustrated as below: first, the selected should ensure a high trapping efficiency which makes the high-index spheres trappable. Then, once the selected leads to a better PNJ property, the selected will be the proper PS coating thickness .
For the coated BTG sphere with a core radius of 2.5 μm in Figure 4, Figure 5 and Figure 6, the considered range of PS coating thickness was set at 90 nm–295 nm and 447 nm–669 nm, corresponding to the highly enhanced (larger than 0.04) above the dashed line in Figure 4a. The value of 0.04 was selected because the average of the PS sphere (which is commonly considered to be trapped easily) with a radius range of 0.5 μm–5 μm in the same condition is no more than 0.04 as shown in Figure 7a. As for the first considered range of (90 nm–295 nm), we can see that the FWHM of PNJ varies randomly, and the is enhanced. Some values of around 188 nm which lead to a highly improved (about 0.10) and a narrower FWHM (close to 220 nm) could be selected as the proper PS coating thickness . For the second considered range of (447 nm–669 nm), we can see that the in this range leads to a better PNJ with a reduced FWHM (less than 250 nm) and an highly enhanced , thus being an appropriate PS coating thickness . Meanwhile, this relatively wide range of values of will reduce the difficulty of fabrication of such coated BTG spheres. With a proper thickness of PS coating, the coated BTG sphere will enable usage of single-beam optical tweezers and also possess a better imaging performance.
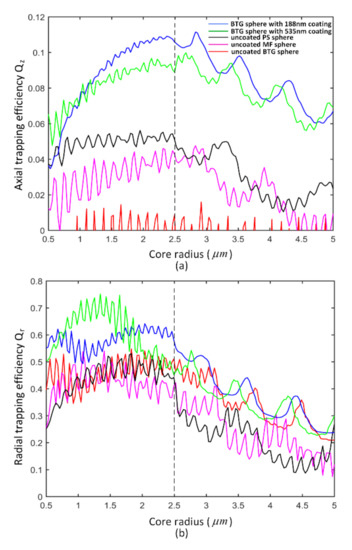
Figure 7.
Axial (a) and radial (b) trapping efficiency of different microspheres, including the uncoated PS/melamine formaldehyde (MF)/BTG spheres and two coated BTG spheres.
Coated BTG spheres with two specific values (188 nm and 535 nm) of are considered to show the superiority of proper PS coating thickness in more detail. The value of 188 nm is close to the value of (181 nm) corresponding to the maximum improvement in in Figure 4a, and the of 535 nm equals to the value of for the second biggest improvement in Figure 4a. Despite these two values being optimized for the BTG sphere with a specific core radius of 2.5 μm, they also work for BTG spheres with other core radii.
First, we will compare the trapping performances of the coated spheres with those of the uncoated spheres. Particularly, uncoated low-index PS and MF spheres normally used for optically-trapped microsphere microscopy are also considered in comparison. The axial trapping efficiency and radial trapping efficiency of different microspheres are illustrated in Figure 7a,b, respectively. As seen in Figure 7a, for uncoated spheres, the overall decreases as the index of sphere increases. With a 188 nm/535 nm PS coating, BTG spheres show much better trapping performance than uncoated BTG spheres, and they also perform better than uncoated low-index PS and MF spheres. The improved trapping performance of the coated high-index sphere is mainly due to the reduced scattering force which originates from the suppression of backscattering by the antireflection coating [45]. Coated BTG spheres indeed possess much higher trapping efficiency which enables single-beam optical trapping.
As for PNJ property, it is commonly believed that high-index BTG spheres have an advantage over low-index PS and MF spheres with the same radius in a water medium [8,9], and a high-index sphere is beneficial for producing a PNJ with a smaller FWHM and a higher . The coated BTG spheres with proper possess a better PNJ related to better imaging performance than uncoated BTG spheres. To save computation time, PNJ simulations of related spheres with a wide range of radius are omitted here.
For spheres with a specific core radius of 2.5 μm (dotted line in Figure 7), the optical trapping efficiency and the PNJ property of five different spheres (the uncoated PS/MF/BTG spheres and two coated BTG spheres) are summarized in Table 1. For the coated BTG sphere with a proper PS coat thickness of 188 nm, we observed a highly improved axial trapping efficiency . The enhancement in is over 10-fold compared to that of the uncoated BTG sphere (), and about 2-fold compared to the uncoated PS sphere () and MF sphere (). Meanwhile, we obtained a better PNJ (, FWHM = 220 nm) compared to that of the uncoated PS/MF/BTG spheres. Compared with the uncoated BTG sphere (, FWHM = 260 nm), the increased by about 21%, and the FWHM decreased by about 15%. Compared with the uncoated MF sphere (, FWHM = 346 nm), the increased by about 83%, and the FWHM decreased by about 36%. Compared with the uncoated PS sphere (, FWHM = 376 nm), the increased by about 173%, and the FWHM decreased by about 41%. It is apparent that the coated BTG sphere with a proper PS coating thickness of 188 nm benefits both the enhancement of optical trapping efficiency and the generation of a better PNJ.

Table 1.
Optical trapping efficiency and PNJ property of different microspheres in water.
With another proper of 535 nm, the for the coated BTG sphere was about 0.088 times highly enhanced for optical trapping, and a better PNJ (, FWHM = 234 nm) was also obtained. The effects of a 535-nm PS coating on optical trapping efficiency and PNJ property are similar to that of a 188-nm PS coating. The large causes an increasement of sphere volume leading to a rapid enhancement of . This coated BTG sphere with relatively large proper also improved the axial trapping efficiency and benefitted the generation of an enhanced PNJ.
It is worthwhile to note that besides the core radius of 2.5 μm, other core radii of coated BTG spheres could be investigated in a similar way to find the ideal coating thickness. The coated BTG sphere with a proper PS coating thickness shows a significant improvement in trapping efficiency and produces a better PNJ, corresponding to an enhanced imaging performance compared to that of the uncoated PS/MF/BTG spheres. This provides us with an opportunity to use coated BTG spheres for optically-trapped microsphere super-resolution microscopy.
6. Conclusions
There are several comments that can be concluded from above analysis, i.e.,
- (a)
- Besides the PS coating, we also used SiO2 material for the coating of BTG spheres. Although the refractive index of SiO2 () varies by about 0.13 compared to the ideal value of coating, the effects of SiO2 coating on optical trapping efficiency (see Figure S1) and PNJ property (see Figure S2) of the coated BTG sphere with a core radius of 2.5 μm are similar to that of PS coating. The overall improvement in axial trapping efficiency with an SiO2 coating is smaller than that with a PS coating, and this may be explained by the fact that the refractive index of SiO2 coating deviates from ideal value. With a proper SiO2 coating thickness, we can also obtain a highly enhanced axial trapping efficiency and a better PNJ property (see Table S1). The SiO2 coating provides us with an alternative coating material to fabricate coated BTG spheres, and it also enables us to use single-beam optical tweezers to trap coated BTG spheres for super-resolution microscopy.
- (b)
- A BTG sphere with a PS coating or SiO2 coating can be synthesized with existing procedures [46] in future work. The coated sphere enables single-beam optical trapping with a lower NA objective and a much lower laser power [37], and the lower NA objective, in turn, is beneficial to show the enhanced power of microspheres in imaging resolution.
In conclusion, we have computationally studied coated BTG spheres with a PS coating for optically-trapped microsphere super-resolution microscopy. The coating’s thickness has an influence on both trapping efficiency and PNJ property of the coated BTG sphere. The PS coating shows a favorable performance in trapping efficiency enhancement as its index is closer to the ideal refractive index (geometric mean of the indices from the BTG core and the water medium). Compared to the uncoated PS, MF and BTG spheres, the coated BTG sphere, with the proper thickness of PS coating, can enhance the trapping efficiency effectively and produce a better PNJ with a narrower FWHM and a higher optical intensity, corresponding to a better imaging performance. The coated high-refractive-index BTG sphere is highly desirable for optically-trapped microsphere super-resolution microscopy, and potentially useful for other research areas like nanoparticle detection.
Supplementary Materials
The following are available online at https://www.mdpi.com/2304-6732/7/4/84/s1, Figure S1: Axial (a) and radial (b) trapping efficiency for a coated BTG sphere with a core radius of 2.5 μm, as the SiO2 coating thickness varies; Figure S2: Relative change of the FWHM and maximum optical intensity of PNJs for a 2.5 μm-core-radius BTG sphere with different SiO2 coating thickness. Table S1: Optical trapping efficiency and PNJ property of five different microspheres in water. Video S1: Axial trapping efficiency with varied PS coating thickness; Video S2: Radial trapping efficiency with varied PS coating thickness.
Author Contributions
Methodology, X.L., S.H. and Y.T.; simulations, X.L.; analysis, X.L., and Y.T.; writing—original draft preparation, X.L.; writing—review and editing, S.H. and Y.T.; project administration, S.H.; funding acquisition, S.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (61705232, 61675206, 61845201,61975211,61875166), and in part by the Sichuan Science and Technology Program (18ZDZX0164, 2020JDJQ0005).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Inouye, Y.; Kawata, S. Near-field scanning optical microscope with a metallic probe tip. Opt. Lett. 1994, 19, 159–161. [Google Scholar] [CrossRef] [PubMed]
- Terris, B.D.; Mamin, H.J.; Rugar, D.; Studenmund, W.R.; Kino, G.S. Near-field optical data storage using a solid immersion lens. Appl. Phys. Lett. 1994, 65, 388–390. [Google Scholar] [CrossRef]
- Rogers, E.T.F.; Lindberg, J.; Roy, T.; Savo, S.; Chad, J.E.; Dennis, M.R.; Zheludev, N.I. A super-oscillatory lens optical microscope for subwavelength imaging. Nat. Mater. 2012, 11, 432–435. [Google Scholar] [CrossRef] [PubMed]
- Betzig, E.; Patterson, G.H.; Sougrat, R.; Lindwasser, O.W.; Olenych, S.; Bonifacino, J.S.; Davidson, M.W.; Lippincott-Schwartz, J.; Hess, H.F. Imaging intracellular fluorescent proteins at nanometer resolution. Science 2006, 313, 1642–1645. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, W.; Li, L.; Luk’yanchuk, B.; Khan, A.; Liu, Z.; Chen, Z.; Hong, M. Optical virtual imaging at 50 nm lateral resolution with a white-light nanoscope. Nat. Commun. 2011, 2, 218. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Li, L.; Ben-Aryeh, Y.; Wang, Z.; Guo, W. Overcoming the diffraction limit induced by microsphere optical nanoscopy. J. Opt. 2013, 15, 125710. [Google Scholar] [CrossRef]
- Li, J.; Liu, W.; Li, T.; Rozen, I.; Zhao, J.; Bahari, B.; Kante, B.; Wang, J. Swimming microrobot optical nanoscopy. Nano Lett. 2016, 16, 6604–6609. [Google Scholar] [CrossRef]
- Darafsheh, A.; Walsh, G.F.; Dal Negro, L.; Astratov, V.N. Optical super-resolution by high-index liquid-immersed microspheres. Appl. Phys. Lett. 2012, 101, 141128. [Google Scholar] [CrossRef]
- Darafsheh, A. Influence of the background medium on imaging performance of microsphere-assisted super-resolution microscopy. Opt. Lett. 2017, 42, 735–738. [Google Scholar] [CrossRef]
- Zhou, Y.; Tang, Y.; Deng, Q.; Zhao, L.; Hu, S. Contrast enhancement of microsphere-assisted super-resolution imaging in dark-field microscopy. Appl. Phys. Express 2017, 10, 082501. [Google Scholar] [CrossRef]
- Wang, F.; Liu, L.; Yu, H.; Wen, Y.; Yu, P.; Liu, Z.; Wang, Y.; Li, W.J. Scanning superlens microscopy for non-invasive large field-of-view visible light nanoscale imaging. Nat. Commun. 2016, 7, 13748. [Google Scholar] [CrossRef] [PubMed]
- Perrin, S.; Li, H.; Leong-Hoi, A.; Lecler, S.; Montgomery, P. Illumination conditions in microsphere-assisted microscopy. J. Microsc. 2019, 274, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Du, B.; Xia, J.; Wu, J.; Zhao, J.; Zhang, H. Switchable Photonic Nanojet by Electro-Switching Nematic Liquid Crystals. Nanomaterials 2019, 9, 72. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhou, Y.; Li, Y.; Hong, M. Microsphere enhanced optical imaging and patterning: From physics to applications. Appl. Phys. Rev. 2019, 6, 021304. [Google Scholar] [CrossRef]
- Wang, Z.; Luk’yanchuk, B. Super-resolution imaging and microscopy by dielectric particle-lenses. In Label-Free Super-Resolution Microscopy; Astratov, V., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 371–406. [Google Scholar]
- Ben-Aryeh, Y. Increase of resolution by use of microspheres related to complex snell’s law. J. Opt. Soc. Am. A 2016, 33, 2284–2288. [Google Scholar] [CrossRef]
- Chen, Z.; Taflove, A.; Backman, V. Photonic nanojet enhancement of backscattering of light by nanoparticles: A potential novel visible-light ultramicroscopy technique. Opt. Express 2004, 12, 1214–1220. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.S.; Paniagua-Domínguez, R.N.; Minin, I.; Minin, O.; Wang, Z. Refractive index less than two: Photonic nanojets yesterday, today and tomorrow [invited]. Opt. Mater. Express 2017, 7, 1820–1847. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, L.V.; Shen, J.-T. Ultralong photonic nanojet formed by a two-layer dielectric microsphere. Opt. Lett. 2014, 39, 4120–4123. [Google Scholar] [CrossRef]
- Kong, S.-C.; Taflove, A.; Backman, V. Quasi one-dimensional light beam generated by a graded-index microsphere. Opt. Express 2009, 17, 3722–3731. [Google Scholar] [CrossRef]
- Gu, G.; Zhou, R.; Chen, Z.; Xu, H.; Cai, G.; Cai, Z.; Hong, M. Super-long photonic nanojet generated from liquid-filled hollow microcylinder. Opt. Lett. 2015, 40, 625–628. [Google Scholar] [CrossRef]
- Gu, G.; Song, J.; Liang, H.; Zhao, M.; Chen, Y.; Qu, J. Overstepping the upper refractive index limit to form ultra-narrow photonic nanojets. Sci. Rep. 2017, 7, 5635. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Twardowski, P.; Gérard, P.; Duo, Y.; Fontaine, J.l.; Lecler, S. Ultra-narrow photonic nanojets through a glass cuboid embedded in a dielectric cylinder. Opt. Express 2018, 26, 3723–3731. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Liu, Z.; Minin, O.V.; Minin, I.V. Deep Subwavelength-Scale Light Focusing and Confinement in Nanohole-Structured Mesoscale Dielectric Spheres. Nanomaterials 2019, 9, 186. [Google Scholar] [CrossRef] [PubMed]
- Neves, A.A.R. Photonic nanojets in optical tweezers. J. Quant. Spectrosc. Radiat. Transf. 2015, 162, 122–132. [Google Scholar] [CrossRef]
- Yang, H.; Trouillon, R.l.; Huszka, G.; Gijs, M.A.M. Super-resolution imaging of a dielectric microsphere is governed by the waist of its photonic nanojet. Nano Lett. 2016, 16, 4862–4870. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Moullan, N.; Auwerx, J.; Gijs, M.A.M. Super-resolution biological microscopy using virtual imaging by a microsphere nanoscope. Small 2014, 10, 1712–1718. [Google Scholar] [CrossRef] [PubMed]
- Hou, B.; Zhang, L. Liquid microdroplet as an optical component to achieve imaging of 100 nm nanostructures on a far-field microscope. J. Opt. 2018, 20, 055606. [Google Scholar] [CrossRef]
- Zhen, Z.; Huang, Y.; Feng, Y.; Shen, Y.; Li, Z. An ultranarrow photonic nanojet formed by an engineered two-layer microcylinder of high refractive-index materials. Opt. Express 2019, 27, 9178–9188. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef]
- Sasaki, M.; Kurosawa, T.; Hane, K. Micro-objective manipulated with optical tweezers. Appl. Phys. Lett. 1997, 70, 785–787. [Google Scholar] [CrossRef]
- Stanescu, S.; Galieni, V.; Ho, C.-H.; Goh, G.; Vilain, S.; Guo, W.; Sheppard, A.; Wang, T.; Li, L. Optical Tweezers Microsphere-Lens Super Resolution Imaging System. In Proceedings of the Optics in the Life Sciences Congress, San Diego, CA, USA, 2 April 2017; Optical Society of America: San Diego, CA, USA, 2017; p. BoW3A.1. [Google Scholar]
- Michihata, M.; Kim, J.; Takahashi, S.; Takamasu, K.; Mizutani, Y.; Takaya, Y. Surface imaging technique by an optically trapped microsphere in air condition. NanoManuf. Metrol. 2018, 1, 32–38. [Google Scholar] [CrossRef]
- Liu, X.; Hu, S.; Tang, Y.; Xie, Z.; Liu, J.; He, Y. Selecting a Proper Microsphere to Combine Optical Trapping with Microsphere-Assisted Microscopy. Appl. Sci. 2020, 10, 3127. [Google Scholar] [CrossRef]
- Hu, Y.; Nieminen, T.A.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Antireflection coating for improved optical trapping. J. Appl. Phys. 2008, 103, 093119. [Google Scholar] [CrossRef]
- van der Horst, A.; van Oostrum, P.D.J.; Moroz, A.; van Blaaderen, A.; Dogterom, M. High trapping forces for high-refractive index particles trapped in dynamic arrays of counterpropagating optical tweezers. Appl. Opt. 2008, 47, 3196–3202. [Google Scholar] [CrossRef]
- Jannasch, A.; Demirörs, A.F.; van Oostrum, P.D.J.; van Blaaderen, A.; Schäffer, E. Nanonewton optical force trap employing anti-reflection coated, high-refractive-index titania microspheres. Nat. Photonics 2012, 6, 469–473. [Google Scholar] [CrossRef]
- Walheim, S.; Schäffer, E.; Mlynek, J.; Steiner, U. Nanophase-separated polymer films as high-performance antireflection coatings. Science 1999, 283, 520–522. [Google Scholar] [CrossRef]
- Bormuth, V.; Jannasch, A.; Ander, M.; van Kats, C.M.; van Blaaderen, A.; Howard, J.; Schäffer, E. Optical trapping of coated microspheres. Opt. Express 2008, 16, 13831–13844. [Google Scholar] [CrossRef]
- Nieminen, T.A.; Loke, V.L.Y.; Stilgoe, A.B.; Knöner, G.; Brańczyk, A.M.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Optical tweezers computational toolbox. J. Opt. A Pure Appl. Opt. 2007, 9, S196–S203. [Google Scholar] [CrossRef]
- Stilgoe, A.B.; Nieminen, T.A.; Knöner, G.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. The effect of mie resonances on trapping in optical tweezers. Opt. Express 2008, 16, 15039–15051. [Google Scholar] [CrossRef]
- Yang, W. Improved recursive algorithm for light scattering by a multilayered sphere. Appl. Opt. 2003, 42, 1710–1720. [Google Scholar] [CrossRef]
- Bohren, L.C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Geints, Y.E.; Panina, E.K.; Zemlyanov, A.A. Control over parameters of photonic nanojets of dielectric microspheres. Opt. Commun. 2010, 283, 4775–4781. [Google Scholar] [CrossRef]
- Wang, N.; Li, X.; Chen, J.; Lin, Z.; Ng, J. Gradient and scattering forces of anti-reflection-coated spheres in an aplanatic beam. Sci. Rep. 2018, 8, 17423. [Google Scholar] [CrossRef] [PubMed]
- Demirörs, A.F.; Jannasch, A.; van Oostrum, P.D.J.; Schäffer, E.; Imhof, A.; van Blaaderen, A. Seeded growth of titania colloids with refractive index tunability and fluorophore-free luminescence. Langmuir 2011, 27, 1626–1634. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).