Optical Forces Acting on a Double DNA-Like Helix, Its Unwinding and Strands Rupture

Abstract

In this paper we study electromagnetic forces induced on DNA and DNA-like helices by external electromagnetic waves. We consider simultaneously occurring forces and torques, interconnected and acting along the double helix axis. Since the DNA molecule has an absorption band in the ultraviolet and visible range near wavelengths ${\lambda }_{1res}=280$ nm and ${\lambda }_{2res}=500$ nm, we expect that it may be possible to selectively apply engineered forces to DNA molecules using appropriate illumination by light in these frequency ranges. The optical forces are simulated for DNA fragments consisting of 20 and 35 turns. Fragments of this length are convenient for direct sequencing and subsequent use in experiments and in practice. It is shown that repulsion forces can arise between the strands of the double DNA-like helix in the field of external electromagnetic waves. Such forces are characteristic of a DNA-like helix with its specific pitch angle and are not inherent in double helices with more straightened or more compressed turns. These repulsion forces, acting along the entire helix, both for electric charges and for electric currents, can lead to damage and rupture of the strands in the double helix. In addition, there can also exist forces and moments of forces directed along the helix axis, which simultaneously stretch and unwind a double helix. The double helix equilibrium under the action of optical forces is also of interest from another point of view, i.e., for optimizing the structure of artificial magnetics and bianisotropic metamaterials for applications in all frequency ranges.

1. Introduction

This article is based on research carried out in recent years on the effects of electromagnetic radiation on a DNA molecule. These studies show that a DNA molecule can be significantly damaged by electromagnetic radiation with its special characteristics, such as intensity, pulse duration, frequency, and others. Although we are talking about the effect of electromagnetic waves of various ranges, the mechanism of these effects has not yet been studied at the level of electromagnetic theory. This article addresses the challenge of applying the laws of classical electromagnetism to describe the light wave effects on a double DNA-like helix and to calculate the forces acting on the strands. It is impossible to solve such a problem without considering the specific conductivity mechanism of the DNA molecule. At present, a clear conclusion about the electrical conductivity of the DNA molecule has not been drawn, since it exhibits very different conducting properties under various conditions, like an insulator, conductor, or semiconductor. Therefore, the article uses a model of a DNA-like helix as a perfect electric conductor, which can serve as a basis for further more in-depth studies and comparison with experimental data.

Over the past few years, the studies of various states of a DNA molecule have intensified: supercoiled, relaxed, and linear states have been studied [1,2,3,4]. Various possible mechanisms of the DNA molecule transitions between these states have been considered, including transitions under the influence of electrons or intense infrared (IR) radiation. These transitions can occur as a result of ruptures of one or both strands forming a double helix of the DNA molecule.

The studies of various aspects of the DNA replication process, including mechanical ones, are also of high interest. For example, a recently published article [5] discusses the mechanical and topological properties of chromatin, allowing DNA strands to be separated without entanglement. The possible superhelix location relative to a moving replisome is studied, at which there is a soft separation of the strands, and the DNA replication occurs without damaging the genes. A very important feature studied in [5] is the simultaneous presence of the force that straightens the molecule, and the torque that unwinds the double helix in the replication process. The effects of electromagnetic forces acting in the process of the DNA replication remain outside the scope of article [5] and other studies.

In this paper, we study electromagnetic forces induced in DNA molecules by external electromagnetic waves. We use the electrodynamic approach and consider simultaneously occurring forces and torques, interconnected and acting along the double helix axis. The reason for the occurrence of such forces is no longer the effect of the replisome, as in [5], but the effect of an external electromagnetic wave.

Seeking possibilities to manipulate DNA molecules (move, rotate, unwind, break the strands, etc.) with the use of mechanical forces created by light illumination can potentially offer a new molecular-scale tool in addition to the chemical means. According to the experimental data, the DNA molecule exhibits strong absorption for some wavelengths of the electromagnetic field in the ultraviolet and visible ranges. Such absorption can be considered as the excitation of a strong polarization current in the helices, because the absorbing centers (atoms and molecules) are present periodically in the helix along its entire length. When interacting with the wave, they provide certain effective current along the entire helix. Effective electric currents along DNA helices create forces applied to the DNA strands, which can be potentially used to manipulate the molecule. Since the DNA molecule has an absorption band in the ultraviolet and visible range near wavelengths ${\lambda }_{1res}=280$ nm and ${\lambda }_{2res}=500$ nm [6,7,8], we expect that it may be possible to selectively apply engineered forces to DNA molecules using appropriate illumination by light in these frequency ranges.

To analyze mechanical forces exerted on DNA helices by incident light and the danger of “improper” helix unwinding and strands rupture, we can use methods of classical electrodynamics, considering effective electric current existing in a double helix.

The electrical conductivity of the DNA molecule and its mechanisms keep drawing researchers’ attention [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29], but they have not been fully studied yet. The water cover where a DNA molecule is located can lead to electrical conductivity of the macromolecule. In addition, not only the conduction current, but also the polarization current can occur in the DNA molecule. Conductivity mechanisms of DNA molecules and their details remain outside the scope of this article. For such molecule, supercoiled, relaxed, and linear states are possible [1,2,3,4], the last of which is considered in this paper.

This research represents a step towards studying the possibilities of activating the DNA molecule under the influence of an external electromagnetic field, the wavelength of which is much longer than the length of the helical turn, and belongs to the optical range. At the same time, the length of the entire helix can be close to half the wavelength, and thereby the conditions for resonant interaction can be satisfied. DNA molecule is a macromolecule in which atoms, molecules, and other molecular formations are periodically arranged. These molecules and atoms are activated at certain frequencies, and the cases when these frequencies coincide with a half-wave resonance for the full length of the helix are important to us. The question then arises whether a half-wave resonance can appear in the DNA molecule or in its segment due to the periodically located absorption centers.

The double helix equilibrium under action of optical forces is of interest from another point of view, i.e., for optimizing the structure of metamaterials. Metal helices as elements of metamaterials are widely used due to their properties of inducing strong electric and magnetic responses which can be tuned by tailoring the helix geometry. Therefore, the metamaterials based on helices have intrinsic capabilities of controlling the basic electromagnetic characteristics of the field in a wide range depending on specific goals [30,31,32,33,34].

A special place among helices take bifilar helices consisting of two helical conductors. These conductors are arranged mutually symmetrically: the second helix is rotated with respect to the first helix on 180 degrees around a common helix axis (X axis). Electric currents in such bifilar helices are more balanced than in the case of single helices, which leads to the symmetry of properties of metamaterials, as some components of the tensors of dielectric susceptibility and magnetic susceptibility vanish. At the same time, the question about the stability of the bifilar helix arises, since the electrical currents in the two spirals are close to each other and can interact strongly [35,36,37,38].

A double-stranded helix with its optimal pitch angle has the highest polarizabilities among other optimal helices. This structural advantage can be beneficial when creating, for example, metamaterials with negative refraction and metasurfaces with low reflection and high absorption [39,40], controlling the polarization state or the transmission phase, etc. [41,42,43].

The excitation states of a long bifilar helix with quasi-stationary distributions of electric currents have already been studied earlier in [44,45]. Whereas the article by Semchenko et al. [44] studies a two-fold symmetrical double stranded helix, paper [45] is devoted to an asymmetrical DNA-like helix. This particular excitation state is realized when the wavelength of excitation is much longer than the length of the helical turn. From a mechanical point of view, the torsion and stresses in the double stranded helix are of particular importance for resonant excitation.

In this paper, the issue of the double DNA-like helix equilibrium in a linear state, as well as the danger of “improper” unwinding of the helix and strands rupture under the external wave action are considered in the framework of classical electrodynamics. The interaction of currents and charges in two helices is studied in the case when the wavelength of the electromagnetic field significantly exceeds the length of the helical turn. A standing electromagnetic wave is expected to arise in a double helix, in which the antinodes of the electric current and charge alternate. Numerical simulation of a linear segment of a double DNA-like helix, consisting of 20 turns, was carried out under the half-wave resonance conditions for the full length of one strand in a straightened condition. The resonant frequency and direction of the electric current in both strands forming a double helix have been determined. Analytical expressions have been obtained for all components of the forces acting on an arbitrary element of one helix from the side of another helix, considered in its entirety. The mutual shift of the helices along their axis, which takes place in a real helix of the DNA molecule, is taken into account. It is shown that this relative shift of two helices leads to the simultaneous existence of the force and the force moment acting on each helix and directed along their common axis. These axial components of the force and the force moment are mutually proportional. These interrelated force and force moments can result in unwinding of the double helix and its separation into two separate strands without damage. A similar “soft” unwinding of the double helix, without damaging it, occurs during the DNA replication under the helicase or unwinding protein action.

Earlier work [5] did not consider the peculiarities of electromagnetic forces acting in the DNA replication process. Mechanical aspects of axial stretching and lateral unfastening of a double-helix DNA molecule are considered in [46], but without the analysis of electromagnetic forces.

Based on classical electrodynamics, the assumption about the role of the mutual shift of two helices relative to their common axis in the DNA molecule has been made in this paper. The radial components of the interaction forces of electric currents and charges have been calculated, and their dependence on the pitch angle of the double helix has been determined. These radial components of the forces describe the mutual attraction or repulsion of two helices and exist both for a symmetrical double helix and in the case of mutual shift of two helices along their common axis.

2. The Distribution of Electric Currents and Charges in a Double Helix and the Formation of a Standing Wave

Long helices containing a large number of turns are under consideration. At the same time, these helices have a finite length, so a standing wave of the electric current is established in each of them as a result of waves reflection from the ends of the helices. We assume that the incident wave is quasimonochromatic, and the excitation time is long enough to excite the resonant mode of the helix.

When this condition is satisfied, the electric current strength in the first and second helices can be written as

$$I_1\left(l_1,t\right)=I_{1max}\cos \left(k{l}_1\right)\cos \left(\omega t\right), I\left(l,t\right)=I_{max}\cos \left(kl\right)\cos \left(\omega t\right),$$

(1)

where $l_1$ and $l$ are the coordinates counted along the first and second helical line; $I_{1max}$ and $I_{max}$ are the amplitudes of current standing waves; $k=\frac{\omega }{c}$ is the wavenumber; $\omega$ is the cyclic current frequency. Since the second helix is shifted to the first one along the axis $X$ by $x_s$, the following relations are satisfied

$$l\sin \alpha =x-x_s,l_1\sin \alpha =x_1,$$

(2)

where $\alpha$ is the helix pitch angle with respect to the plane, perpendicular to the X axis. This angle satisfies the relations

$$\mathrm{tg}\alpha =\frac{h}{2\pi r},\sin \alpha =\frac{h}{P},P=\sqrt{{(2\pi r)}^2+h^2},$$

(3)

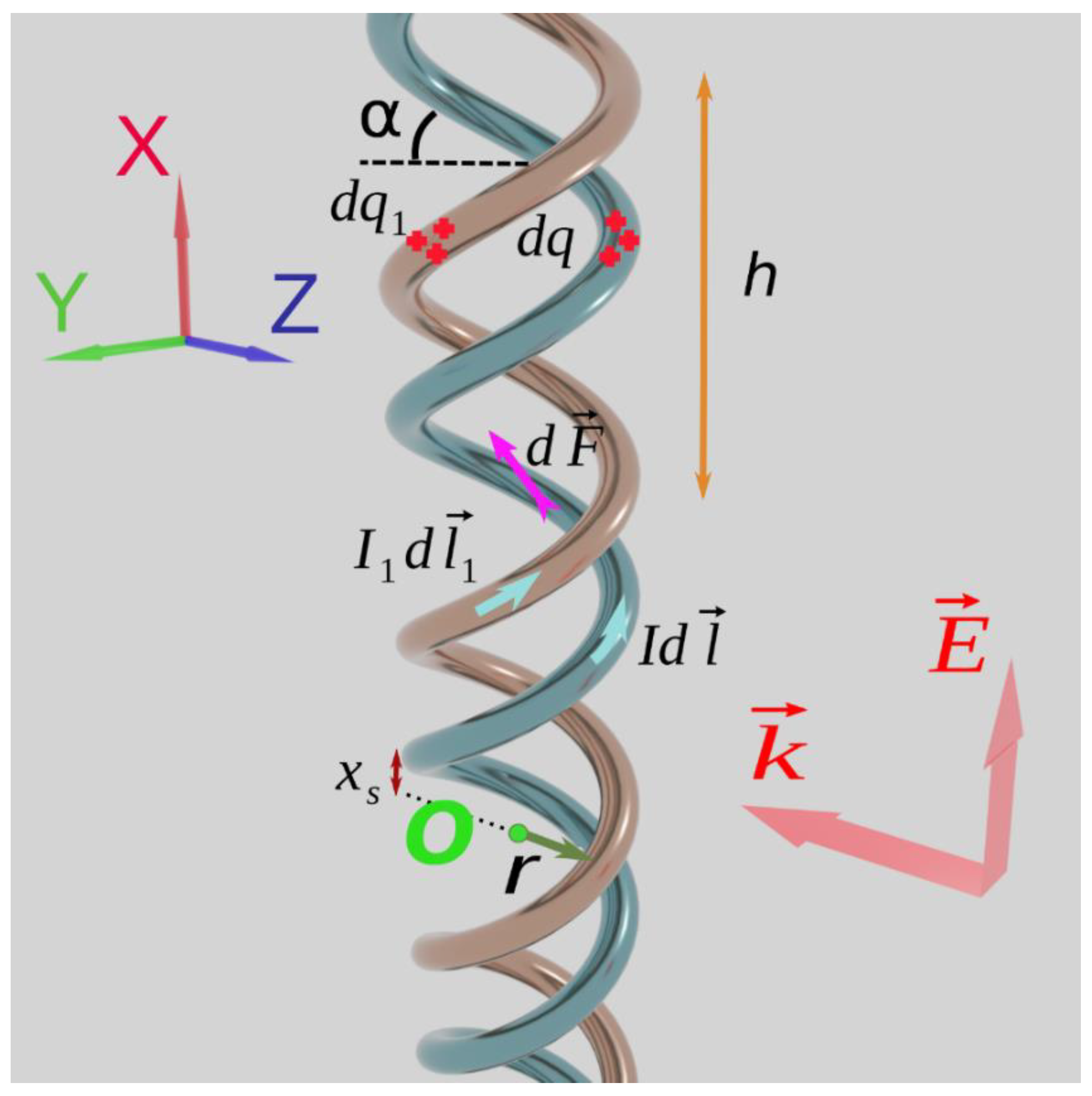
where $r$ is the helical turn radius; $h=\frac{2\pi }{\left|q\right|}$ is the helix pitch; $q$ is the helix specific winding, which is positive ($q>0$) for a right-handed helix and negative ($q<0$) for a left-handed helix; P is the helical turn length. The schematic of a double DNA-like helix with mutual shift of the helices along axis X is shown in Figure 1.

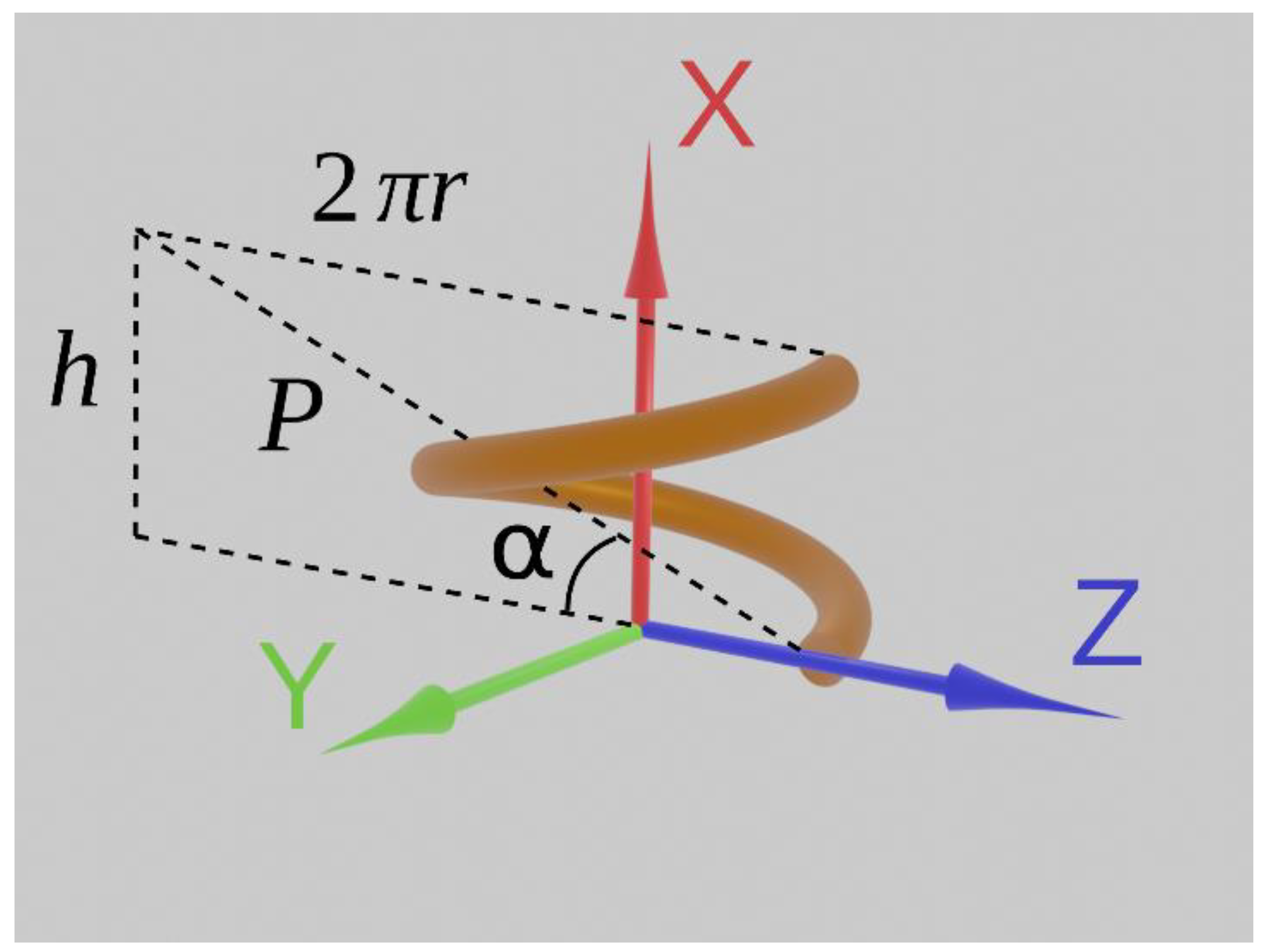
The length of the helical turn can be calculated using the Pythagorean theorem (see Figure 2).

An important relation also follows from the drawing of the helical turn in expanded form

$$\cot \alpha =\pm qr,$$

(4)

which will be often used in subsequent calculations. Here, the “$+$” sign is used in the case of a right-handed helix, and the “$-$“sign is true for a left-handed helix.

The distribution of electric charges in the helix also forms a standing wave, and can be calculated based on the continuity equation

$$\frac{1}{S_0}\frac{\partial I}{\partial l}+\frac{\partial \rho }{\partial t}=0,$$

(5)

where $S_0$ is the effective cross section of the helix conductor and $\rho$ is the electric charge volume density. Now it is possible to write for two helices

$${\rho }_1\left(l_1,t\right)=\frac{1}{S_{0}c}{I}_{1max}\sin \left(k{l}_1\right)\sin \left(\omega t\right),\rho \left(l,t\right)=\frac{1}{S_{0}c}{I}_{max}\sin \left(kl\right)\sin \left(\omega t\right).$$

(6)

In the case of a perfect conductor, the volume charge density $\rho$ vanishes, and the surface charge density $\sigma$ acquires the main importance. Therefore, when considering a perfect conductor in all formulae, it is necessary to perform the replacement $\rho S_0\to \sigma 2\pi r_0$, where $S_0=\pi r_0^2$, and $r_0$ is the radius of the conductor section.

3. The Interaction Force of Electric Currents Arising in Two Strands, and the Moment of This Force

First, we consider the interaction of low-frequency currents for which the length of the electromagnetic wave $\lambda$ significantly exceeds the length of the helical turn $P$:

$$\lambda >>P,$$

(7)

where $\lambda =\frac{2\pi c}{\omega }$. For low-frequency currents in two strands, the force of their interaction can be calculated using the Ampere law, and the magnetic field induction can be calculated on the basis of the Biot–Savart law:

$$d{\overrightarrow{F}}^{mag}=[Id\overrightarrow{l}\overrightarrow{B}],\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\int \frac{[I_{1}d{\overrightarrow{l}}_1\overrightarrow{R}]}{R^3}.$$

(8)

On the right-hand side of Formula (8), we do not take into account the retardation of electromagnetic waves as they propagate along the helix, since the retardation effects are in this case negligible. Below, we consider a segment of a double helix containing 20 turns and satisfying the condition of half-wave resonance. For such a helix segment, the maximum possible retardation time is ${\tau }_{ret}^{max}=\frac{L^{max}}{c}=\frac{20P}{c}=\frac{\lambda }{2c}=\frac{T}{2}$, where $T=\frac{1}{\nu }$ is the period of the electromagnetic wave. This is the retardation time of the waves for the full length of the helix. However, the magnetic induction created by the current element decreases in space with increasing distance according to the law $B~\frac{1}{R^2}$. Moreover, forces created by distant parts of the two helical conductors tend to cancel. Therefore, as shown by numerical calculations, only two adjacent turns of the helix, close to the observation point, have a significant effect on the current in the helix. In this case, the effective retardation time of the waves decreases significantly and can be estimated as ${\tau }_{ret}^{eff}=\frac{L^{eff}}{c}=\frac{2P}{c}=\frac{\lambda }{20c}=\frac{T}{20}$. These quantitative estimates show that we can ignore the effect of electromagnetic wave retardation in this calculation.

If inequality (7) is not satisfied, then high-frequency excitation of the helix takes place. In this case, it is necessary to introduce the vector potential $\overrightarrow{A}=\frac{{\mu }_0}{4\pi }{{\displaystyle \int }}_L\frac{I_1\overrightarrow{d{l}_1}}{R}$, using which one can calculate the magnetic induction by the formula $\overrightarrow{B}=rot\overrightarrow{A}$. However, in the limiting low-frequency case, this calculation method leads to the same result as relations (8).

Here, $d{\overrightarrow{F}}^{mag}$ is the Ampere force acting on a physically small current element $Id\overrightarrow{l}$ in the second helix from the side of the entire first helix; square brackets denote the vector product, $d{\overrightarrow{l}}_1$ and $d\overrightarrow{l}$ are physically small elements of the first and second helices, $\overrightarrow{B}$ is induction of the magnetic field produced by the entire first helix at the point location of the second helix element $d\overrightarrow{l}$, $\overrightarrow{R}$ is a radius vector drawn from the element of the first helix $d{\overrightarrow{l}}_1$ to that of the second helix $d\overrightarrow{l}$, ${\mu }_0$ is a magnetic constant, and integration is carried out along the entire first helix.

Choosing the direction of the coordinate axes as shown in Figure 3, and the reference point of the polar angle $\varphi$ from the Y axis, it is possible to write the relations for the components of the vector $d{\overrightarrow{l}}_1$ characterizing a physically small element of the first helix as

$$d{l}_{1x}=dx=\pm \sin \alpha \cdot d{l}_1, d{l}_{1y}=\pm \cot \alpha \cdot \sin \varphi \cdot dx,d{l}_{1z}=\pm \cot \alpha \cdot \cos \varphi \cdot dx,$$

(9)

$$\varphi =qx+\frac{\pi }{2},$$

(10)

where the “$+$” sign corresponds to a right-handed helix, and the “$-$“ sign is valid for a left-handed helix.

We consider an asymmetric DNA-like helix in which two helices are mutually shifted along their common axis by $x_s$. As the experimental data show [47], a real DNA helix has the following parameters: $r={10}^{-9}\mathrm{m}$, $h=3.4\cdot {10}^{-9} \mathrm{m}$, and thus $q=1.85\cdot {10}^9 \frac{\mathrm{rad}}{\mathrm{m}}$. According to a paper by Watson et al. [48], the rotation angle of the second helix with respect to the symmetrical position is $u_s=53 \mathrm{deg}=0.93 \mathrm{rad}$. Since the following relations are satisfied for the helix

$$u=q{x}_1,u_s=q{x}_s,$$

(11)

we obtain

$$x_s=0.5\cdot {10}^{-9}\mathrm{m}=\frac{1}{2}r,u_s=\frac{1}{2}\cot {\alpha }_{exp},$$

(12)

where ${\alpha }_{exp}=28.4 \mathrm{deg}$ is a double DNA helix pitch angle, obtained from the experimental data in [47].

The Ampere force acting on the current element $Id\overrightarrow{l}$ in the second helix from the side of the entire first helix has a maximum value at the point where the current antinode is found, for example, when $l=0$ at point A. It is for this point that the magnetic interaction of two helices is most pronounced. Point A, located on the second helix, has coordinates $\left(x_s,0,-r\right)$. Then, the radius vector $\overrightarrow{R}$ drawn from an arbitrary element of the first helix $d{\overrightarrow{l}}_1$ to point A can be expressed as

$$\overrightarrow{R}={\overrightarrow{R}}_0+x_s{\overrightarrow{x}}_0-r{\overrightarrow{z}}_0,$$

(13)

where ${\overrightarrow{x}}_0,{\overrightarrow{y}}_0,{\overrightarrow{z}}_0$ are unit vectors of the Cartesian coordinate system; ${\overrightarrow{R}}_0$ is a radius vector drawn from an arbitrary element of the first helix $d{\overrightarrow{l}}_1$ to the origin of the coordinate system. Figure 3 shows that the components of the vector ${\overrightarrow{R}}_0$ are

$$R_{0x}=-x,R_{0y}=-r\cos \varphi ,R_{0z}=-r\sin \varphi .$$

(14)

Based on Formulae (13) and (14), the modulus of the radius vector $\overrightarrow{R}$ can be calculated as

$$R={({(x-x_s)}^2+2r^2\left(1+\sin \varphi \right))}^{\frac{1}{2}}.$$

(15)

Since the second helix is rotated relative to the first one in a double DNA helix, a relation similar to Formula (10) holds for the second helix:

$$\varphi =q\left(x-x_s\right)+\frac{3\pi }{2}.$$

(16)

Then, the components of the second helix element $d\overrightarrow{l}$ at point A, when $x=x_s$, is possible to write in the form similar to Formula (9):

$$d{l}_x=dx,d{l}_y=\pm \cot \alpha \cdot dx,d{l}_z=0,$$

(17)

where the “$+$” sign stands for a right-handed helix, and the “$-$” sign corresponds to a left-handed helix. Using relations (17), we obtain the Ampere force components (8) acting on a physically small current element $Id\overrightarrow{l}$ in the second helix at point A, where there is a maximum current strength in a standing wave, from the side of the entire first helix:

$$d{F}_x^{mag}=Id{l}_y{B}_z,d{F}_y^{mag}=-Id{l}_x{B}_z,d{F}_z^{mag}=I\left(d{l}_x{B}_y-d{l}_y{B}_x\right).$$

(18)

Formulae (17) and (18) imply the following relation between the components of the magnetic interaction force:

$$\frac{d{F}_x^{mag}}{d{F}_y^{mag}}=\mp \cot \alpha ,$$

(19)

where the upper sign corresponds to a right-handed helix, and the lower sign is valid for a left-handed helix. It is very important that relation (19) holds for arbitrary values $I$ and $\overrightarrow{B}$, i.e., for any values of constant or quasi-stationary (low-frequency) electric currents in two helices.

All the force components $d{\overrightarrow{F}}^{mag}$ at the point of the second helix can be written in a cylindrical coordinate system:

$$d{F}_y=d{F}_{\varphi },d{F}_z=-d{F}_r,$$

(20)

and $d{F}_x$ component does not change. Thus, the force component $d{F}_z^{mag }$ is directed along the radius of the helical turn to the center of the turn, i.e., when $d{F}_z^{mag}>0$ there is attraction of the helices, and when $d{F}_z^{mag}<0$ the helices are mutually repelled. The force component $d{F}_x^{mag}$ is directed along the axis of the double helix and can lead to compression or stretching of the second helix. The force component $d{F}_{\varphi }^{mag}$ is in the polar plane and can cause the second helix rotation.

Let us introduce the force moment acting on the second helix element

$$d\overrightarrow{M}=[\overrightarrow{r}d\overrightarrow{F}].$$

(21)

Now, considering Formula (7), relation (19) can be transformed to the form

$$\langle d{F}_x^{mag}\rangle {}_t=-q\langle d{M}_x^{mag}\rangle {}_t,$$

(22)

which is true both for a right-handed helix $(q>0)$ and a left-handed one $(q<0)$. Here, angle brackets with index t denote the time averaging operation.

For further calculations, it is convenient to perform a change of the variable $u=q{x}_1$, i.e., to take into account relations (11). Integrating over the entire length of the first helix and averaging the force in time, we obtain all three components of the Ampere force acting on the current element $Id\overrightarrow{l}$:

$$\langle d{F}_x^{mag}\rangle {}_t=\frac{{\mu }_0}{4\pi r}\frac{1}{2}{I}_{max}{I}_{1max}dl\cos \alpha ·{\cot }^2\alpha {{\displaystyle \int }}_{-\infty }^{+\infty }{\frac{\cos (\frac{P}{\lambda }u)\left(\sin u+\left(u_s-u\right)\cos u\right)du}{{({(u_s-u)}^2+2{\cot }^2\alpha \left(1+\cos u\right))}^{\frac{3}{2}}}}_{},$$

(23)

$$\langle d{F}_y^{mag}\rangle {}_t=-\mathrm{tg}\alpha \cdot \langle d{F}_x^{mag}\rangle {}_t,$$

(24)

$$\langle d{F}_z^{mag}\rangle {}_t=\frac{{\mu }_0}{4\pi r}\frac{1}{2}{I}_{max}{I}_{1max}dl\sin \alpha ·{\cot }^2\alpha {{\displaystyle \int }}_{-\infty }^{+\infty }\frac{\cos \left(\frac{P}{\lambda }u\right)\left(\left(1-{\cot }^2\alpha \right)\left(1+\cos u\right)-\left(u_s-u\right)\sin u\right)du}{{\left({\left(u_s-u\right)}^2+2{\cot }^2\alpha \left(1+\cos u\right)\right)}^{\frac{3}{2}}}.$$

(25)

When deriving Formulae (23)–(25), it was suggested that the currents in two helices pass in the same direction relative to the helices’ axis. In each particular case, the direction of these currents depends on the conditions of the helix activation. Integration is carried out in infinite limits, i.e., very long helices, consisting of a large number of turns, are considered.

Formulae (23)–(25) show the following: (1) the pitch angle of the double helix $\alpha$, which is often found in these formulae, is a very important parameter; (2) the ratio of the helical turn length to the wavelength of the electromagnetic field $\frac{P}{\lambda }$ is also an important characteristic, while $P$ and $\lambda$ do not appear individually; (3) factor $\frac{{\mu }_0}{4\pi r}{I}_{max}{I}_{1max}dl$ is characteristic for describing the interaction of two currents located at distance $2r$ from each other; (4) the coefficient $\frac{1}{2}$ appeared due to averaging the Ampere force in time; (5) the helix specific winding $q$ and the helix pitch $h$ do not explicitly appear in these formulae. This form of Formulae (23)–(25) is very convenient and universal, as they can be applied also to DNA-like helices, exhibiting, for example, resonance properties in the microwave range, for which $q\approx {10}^2 {\mathrm{m}}^{-1}$, $h\approx {10}^{-2}\mathrm{m}$. These formulae in the same form can also be used for a real DNA helix, for which $q\approx {10}^9 {\mathrm{m}}^{-1}$, $h\approx {10}^{-9} \mathrm{m}$.

Formula (22) shows that the force and the force moment, acting on the current element in the second helix along its axis from the side of the first helix, exist simultaneously and are inextricably linked. If the mutual shift of the helices is absent, i.e., $u_s=0$, the sub-integral function in Formula (23) becomes odd, and both quantities in Formula (22) vanishes. At the same time, the radial component of the magnetic force, which is responsible for the attraction or repulsion of the currents in two helices, continues to exist for a symmetric helix, because the sub-integral function in Formula (25) is even when $u_s=0$. Thus, the mutual shift of the helices leads to the occurrence of magnetic force and force moment acting on currents along the helical axis.

The force with different components and the moment of force acting on each helix can affect the balance of the double helix. This should be taken into account when designing the metamaterials based on DNA-like helices, as well as when studying the processes occurring in a real DNA helix, for example, during its replication.

4. The Interaction Force of Electric Charges Induced in Two Strands, and the Moment of This Force

Let us also consider the interaction of electric charges in the strands of a double DNA-like helix. This force takes the maximum value for a physically small element of the helix on which the antinode of the electric charge is located, for example, when $l=\frac{\lambda }{4}$ in Formula (1). It is for this reason that the electrical interaction of two helices is most pronounced. As the low-frequency approximation is considered here, therefore, the interaction force of electric charges can be determined using the Coulomb law

$$d{\overrightarrow{F}}^{el}=\frac{1}{4\pi {\epsilon }_0}dq\int \frac{d{q}_1}{R^3}\overrightarrow{R}.$$

(26)

Here, $d{\overrightarrow{F}}^{el}$ is the Coulomb force acting on a physically small charge $dq$ on the second helix from the side of the entire first helix; $d{q}_1$ is a certain elementary charge on the first helix; $\overrightarrow{R}$ is a radius vector drawn from the elementary charge $d{q}_1$ to the charge $dq$; ${\epsilon }_0$ is the electric constant, integration is carried out along the entire first helix. Electric charges on physically small elements of the first and second helices can be written as

$$d{q}_1={\rho }_1{S}_{0}d{l}_1={\rho }_1{S}_0\frac{d{x}_1}{\sin \alpha },dq=\rho S_{0}dl=\rho S_0\frac{dx}{\sin \alpha },$$

(27)

where ${\rho }_1$ and $\rho$ are electric charge volume density for the first and the second helices, respectively.

If condition (7) is not valid, then we have a case of high-frequency interaction. In this case, in addition to the vector potential $\overrightarrow{A}$, the expression for which is given after equations (8), it is also necessary to introduce the scalar potential $\phi =\frac{1}{4\pi {\epsilon }_0}{{\displaystyle \int }}_V\frac{{\rho }_{1}dV}{R}$, on the basis of which the electric field strength can be calculated by the formula $\overrightarrow{E}=-grad \phi - \frac{\partial \overrightarrow{A}}{\partial t}$. However, when passing to the limit of low frequencies, this method of calculation gives the same result as Formula (26). In the most general case, the Maxwell stress tensor can also be used to calculate the forces of electromagnetic interaction. However, at low frequencies of the electromagnetic field, that fundamental way of calculating leads to the same result as the Coulomb and Biot–Savart laws applied in this article.

It is possible to shift the origin of coordinates along axis $X$ by $x_{el}=\frac{\lambda }{4}\sin \alpha$ for computational convenience. Point A will be in the place of the maximum electric charge volume density in the second helix. Similar to Formula (5), it is possible to write the values ${\rho }_1$ and $\rho$ considering the shift of the coordinates’ origin:

$${\rho }_1\left(l_1,t\right)=\frac{1}{S_{0}c}{I}_{1max}\cos \left(k{l}_1\right)\sin \left(\omega t\right),\rho \left(l,t\right)=\frac{1}{S_{0}c}{I}_{max}\cos \left(kl\right)\sin \left(\omega t\right).$$

(28)

By calculating the integral in Formula (26) along the whole length of the first helix and finding the average value of the force in time, we obtain all three components of the Coulomb force acting on the charge element dq:

$$\langle d{F}_x^{el}\rangle {}_t=\frac{{\mu }_0}{4\pi r}\frac{1}{2}{I}_{max}{I}_{1max}dl\frac{\cot \alpha }{\sin \alpha }{{\displaystyle \int }}_{-\infty }^{+\infty }{\frac{\cos (\frac{P}{\lambda }u)\left(u_s-u\right)du}{{({(u_s-u)}^2+2{\cot }^2\alpha \left(1+\cos u\right))}^{\frac{3}{2}}}}_{},$$

(29)

$$\langle d{F}_y^{el}\rangle {}_t=\frac{{\mu }_0}{4\pi r}\frac{1}{2}{I}_{max}{I}_{1max}dl\frac{{\cot }^2\alpha }{\sin \alpha }{{\displaystyle \int }}_{-\infty }^{+\infty }{\frac{\cos (\frac{P}{\lambda }u)\sin udu}{{({(u_s-u)}^2+2{\cot }^2\alpha \left(1+\cos u\right))}^{\frac{3}{2}}}}_{},$$

(30)

$$\langle d{F}_z^{el}\rangle {}_t=-\frac{{\mu }_0}{4\pi r}\frac{1}{2}{I}_{max}{I}_{1max}dl\frac{{\cot }^2\alpha }{\sin \alpha }{{\displaystyle \int }}_{-\infty }^{+\infty }{\frac{\cos (\frac{P}{\lambda }u)\left(1+\cos u\right)du}{{({(u_s-u)}^2+2{\cot }^2\alpha \left(1+\cos u\right))}^{\frac{3}{2}}}}_{}.$$

(31)

When deriving Formulae (29)–(31), as before, the currents in two helices passing in the same direction relative to the helices’ axis were considered. The direction of these currents in each particular case depends on the conditions of the helix excitation.

The important issue for us is whether the relation for the force and the moment of force is satisfied in the interaction of electric charges in a double helix, similar to Formula (22), which we obtained for the Ampere force. If Formula (22) follows directly from expressions (18) and (19), a similar relation is not noticeable in an explicit form in Formulae (29) and (30). Let us consider the auxiliary integral

$$Int={{\displaystyle \int }}_{-\infty }^{+\infty }\frac{\left(u_s-u+{\cot }^2\alpha \sin u\right)du}{{({(u_s-u)}^2+2{\cot }^2\alpha \left(1+\cos u\right))}^{\frac{3}{2}}}$$

(32)

and introduce the function $w={(u_s-u)}^2+2{\cot }^2\alpha \left(1+\cos u\right)$. When calculating the derivative $\frac{dw}{du}=-2\left(u_s-u\right)-2{\cot }^2\alpha \cdot \sin u$, we obtain

$$Int=-\frac{1}{2}{{\displaystyle \int }}_{-\infty }^{+\infty }\frac{dw}{w^{\frac{3}{2}}}={\frac{1}{w^{\frac{1}{2}}}|}_{-\infty }^{+\infty }=0.$$

(33)

Multiplying Formula (30) by $\cot \alpha$, summing the result up with Formula (29) and taking into account relation (33), we obtain the relation for the electric force and the moment of force, similar to Formula (22):

$$\langle d{F}_x^{el}\rangle {}_t=-q\langle d{M}_x^{el}\rangle {}_t.$$

(34)

It should be noted that Formula (34) is valid for arbitrary values of electric charges in two helices, if these charges are constant or change slowly.

Consequently, the force and the moment of force acting on the charge element in the second helix along its axis from the side of the first helix are mutually proportional, i.e., they exist simultaneously. Both quantities in Formula (34) become zero for a symmetric double helix, i.e., when $u_s=0$. At the same time, the radial component of the electric force, which describes the attraction or repulsion of charges in two helices, exists both for mutually shifted and symmetrically arranged helices. Thus, the mutual shift of the helices leads to the occurrence of the electric force and the moment of force acting on the charges along the helix axis.

5. Radial and Axial Components of Magnetic and Electric Forces: Attraction and Repulsion of Two Helices

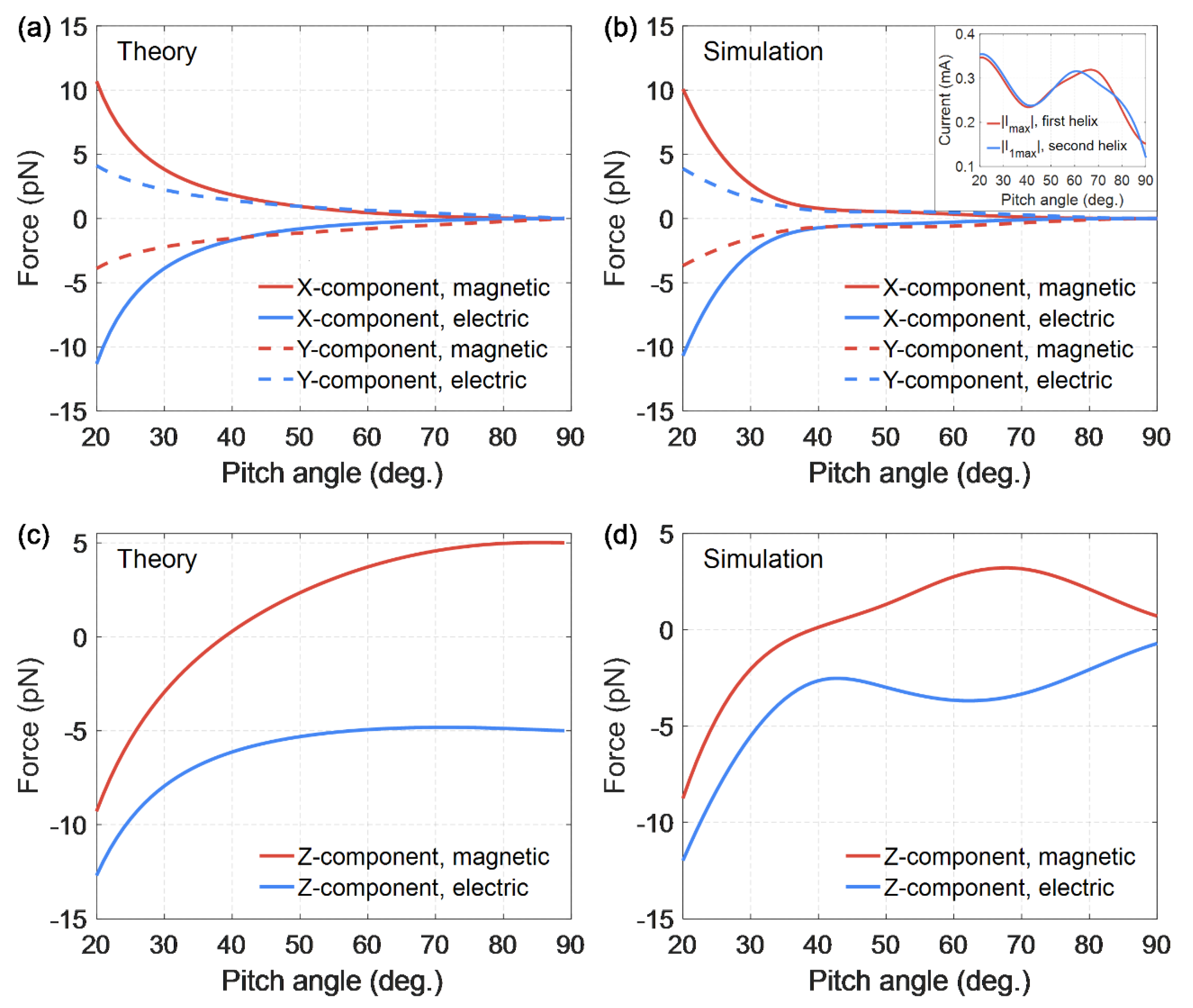
Also of interest is the dependence on the helix pitch angle of all the components (X, Y, and Z) of the forces (23)–(25) and (29)–(31) produced by both magnetic and electric fields (see Figure 4). Wolfram Mathematica was used for numerical calculations of analytical formulae, and ANSYS HFSS software was used for numerical simulations of forces. Figure 4 show good agreement between theory and simulations. We should recall that electric and magnetic forces at various points of the double helix are considered, so these forces are analyzed individually. The magnetic force is considered in the antinode of the electric current, where this force has a maximum value, and the electric force is zero. Similarly, the electric force is considered in the antinode of the electric charge, where this force reaches its maximum and the magnetic force is zero. The positive Z-component of the magnetic or electric force means the radial attraction of the elementary part of the second helix to the first one, while the negative value of Z component means the radial repulsion force. Figure 4 demonstrates an interesting feature: there exists a certain equilibrium helix pitch angle (${\alpha }_0\approx 38 \mathrm{deg}$) at which Z-component of the magnetic force vanishes, which means that there is no radial attraction or repulsion of the elementary current in the second helix with respect to the entire first helix [44]. At this particular angle ${\alpha }_0$, the radial component of the magnetic interaction force of the helices’ changes sign. Hence, the helices with stretched turns, for which $\alpha >{\alpha }_0$, are mutually attracted. This fact corresponds to a well-known limiting case $\alpha \to \frac{\pi }{2}$, when there is an attraction of two straight long conductors in which currents flow in the same direction. On the contrary, the helices with more compressed turns, for which $\alpha <{\alpha }_0$, are repelled along the helix radius, if currents flow in the same direction relative to the helix axis.

As for the electric force component Z, it is negative for all the pitch angles of the double helix, which means mutual radial repulsion of the charges in two helices.

The pitch angle of the DNA helix, according to experimental data, is ${\alpha }_{exp}=28.4 \mathrm{deg}$ [47,48]. Figure 4 shows that for such a pitch angle ${\alpha }_{exp}$ with the same direction of currents in two helices, radial repulsion forces arise between the strands of the double helix. Firstly, electric charges are repelled, having the same sign in two strands: $\langle d{F}_z^{el}\rangle {}_t<0$. Secondly, since the inequality ${\alpha }_{exp}<{\alpha }_0$ is satisfied, the electric currents that have the same direction in two strands relative to the axis of the helix are repelled as well: $\langle d{F}_z^{mag}\rangle {}_t<0$. Therefore, the repulsion forces act along the entire double helix, both in the antinode regions of the electric charge and in the antinode regions of the electric current. This radial repulsion force, acting along the entire helix, can lead to damage and rupture of the strands in the double helix.

If the inequality holds for the pitch angle of the helix $\alpha \ge 80 \mathrm{deg}$, the turns of the double helix are very stretched. Then Z-components of electric and magnetic forces are approximately equal to each other with the opposite sign. This equality ensures the equilibrium of two strands, which in their shape are close to straight conductors, at any distance between them. Relative to the Z axis, perpendicular to the strands, the electric charges in two strands are mutually repulsive, as they have the same signs. In this case, the electric currents are mutually attracted, since they have the same direction, with the same force.

The X- and Y-components of electric and magnetic forces become significant for more compressed turns. The X-component of the electric force exceeds the Z-component of the electric force in modulus, if $\alpha \le 20 \mathrm{deg}$. At the same time, the X-component of the magnetic force becomes more significant compared to the Z-component of the magnetic force in modulus, if $\alpha \le 45 \mathrm{deg}$. The X-component of forces may lead to the helix compression or stretching and the Y-components may result in the helix winding or unwinding. As Figure 4 shows, the X- and Y-components of the electric and magnetic forces behave symmetrically with a change in the pitch angle of the double helix. The X-component of the electric force is approximately equal to the X-component of the magnetic force, taken with a minus sign, for all the pitch angles of the helix. The same approximate equality is true for the Y-components of electric and magnetic forces. These properties of the forces ensure the equilibrium of the double helix strands relative to X and Y axes (the electric charges in two strands are mutually repulsive, and the electric currents are mutually attracted with the same force).

If the helix pitch angle tends to zero, the forces components, as the graphs show, have a singularity. The helical turns become very compressed, practically flat, at such pitch angles, and two helices overlap each other. The distance between them tends to zero, and therefore the interaction forces increase unlimitedly.

6. The Tangential Component of the Force Acting on the Helix

Above, we considered Point A, at which the current strength or charge density have maximum values, i.e., the antinode region of the electric current or the charge. Only magnetic or only electric force acts at this point. It is also necessary to consider another helix point, shifted relative to the antinode of the current and the charge. For computational convenience, we shift the origin of coordinates, which was previously in the helix center, along the axis of the helix by $-x_c$. Now the helix center will have a coordinate $x_c$. Introducing $u_c=q{x}_c$ similarly to Formula (11), we actually characterize the position of the helix center in the new coordinate system by the rotation angle of the helix, expressed in radians. Using Formulae (1), (3), and (11), we can write the electric current force in the first and second helices in form

$$I_1\left(u,t\right)=I_{1max}\cos \left(\frac{P}{\lambda }\left(u-u_c\right)\right)\cos \left(\omega t\right), I\left(u,t\right)=I_{max}\cos \left(\frac{P}{\lambda }\left(u-u_c-u_s\right)\right)\cos \left(\omega t\right).$$

(35)

Since the second helix has a shift relative to the first one, let us consider, as before, the point on the second helix with the coordinate $x=x_s$, $u=u_s$. Similarly to Formulae (23)–(25), we obtain all three components of the Ampere force acting on the current element $Id\overrightarrow{l}$ in the second helix from the side of the entire first helix, depending on the distance to the origin of coordinates, expressed in the rotation angles of the helix:

$$\langle d{F}_x^{mag}{\left(u_c\right)\rangle }_t=\frac{{\mu }_0}{8\pi r}{I}_{max}{I}_{1max}dl\cos \left(\frac{P}{\lambda }{u}_c\right)\frac{{\cos }^3\alpha }{{\sin }^2\alpha }{{\displaystyle \int }}_{-\infty }^{+\infty }\frac{\cos \left(\frac{P}{\lambda }\left(u-u_c\right)\right)\left(\sin u+\left(u_s-u\right)\cos u\right)du}{{\left({\left(u_s-u\right)}^2+2{\cot }^2\alpha \left(1+\cos u\right)\right)}^{\frac{3}{2}}},$$

(36)

$$\langle d{F}_y^{mag}{\left(u_c\right)\rangle }_t=-\mathrm{tg}\alpha \cdot \langle d{F}_x^{mag}{\left(u_c\right)\rangle }_t,$$

(37)

$$\begin{array}{cc}\langle d{F}_z^{mag}{\left(u_c\right)\rangle }_t& \\ =\frac{{\mu }_0}{8\pi r}{I}_{max}{I}_{1max}& dl\cos \left(\frac{P}{\lambda }{u}_c\right)\frac{{\cos }^2\alpha }{\sin \alpha }\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\frac{\cos \left(\frac{P}{\lambda }\left(u-u_c\right)\right)\left(\left(1-\mathrm{co}{t}^2\alpha \right)\left(1+\cos u\right)-\left(u_s-u\right)\sin u\right)}{{\left({\left(u_s-u\right)}^2+2{\cot }^2\alpha \left(1+\cos u\right)\right)}^{\frac{3}{2}}}\end{array}$$

(38)

Similar to Formula (6), it is possible to write the electric charge volume density for two helices

$$\begin{array}{c}\hfill {\rho }_1\left(u,t\right)=\frac{1}{S_{0}c}{I}_{1max}\sin \left(\frac{P}{\lambda }\left(u-u_c\right)\right)\sin \left(\omega t\right),\hfill \\ \hfill \rho \left(u,t\right)=\frac{1}{S_{0}c}{I}_{max}\sin \left(\frac{P}{\lambda }\left(u-u_c-u_s\right)\right)\sin \left(\omega t\right).\hfill \end{array}$$

(39)

By analogy with expressions (29)–(31), it is possible to write all three components of the Coulomb force acting on the charge element $dq$ in the second helix from the side of the entire first helix, at point $x=x_s$, $u=u_s$, depending on the angular distance to the origin of coordinates:

$$\langle d{F}_x^{el}{\left(u_c\right)\rangle }_t=-\frac{{\mu }_0}{8\pi r}{I}_{max}{I}_{1max}dl\sin \left(\frac{P}{\lambda }{u}_c\right)\frac{\cos \alpha }{{\sin }^2\alpha }{{\displaystyle \int }}_{-\infty }^{+\infty }\frac{\sin \left(\frac{P}{\lambda }\left(u-u_c\right)\right)\left(u_s-u\right)du}{{\left({\left(u_s-u\right)}^2+2{\cot }^2\alpha \left(1+\cos u\right)\right)}^{\frac{3}{2}}},$$

(40)

$$\langle d{F}_y^{el}{\left(u_c\right)\rangle }_t=-\frac{{\mu }_0}{8\pi r}{I}_{max}{I}_{1max}dl\sin \left(\frac{P}{\lambda }{u}_c\right)\frac{{\cos }^2\alpha }{{\sin }^3\alpha }{{\displaystyle \int }}_{-\infty }^{+\infty }\frac{\sin \left(\frac{P}{\lambda }\left(u-u_c\right)\right)\sin udu}{{\left({\left(u_s-u\right)}^2+2{\cot }^2\alpha \left(1+\cos u\right)\right)}^{\frac{3}{2}}},$$

(41)

$$\langle d{F}_z^{el}{\left(u_c\right)\rangle }_t=\frac{{\mu }_0}{8\pi r}{I}_{max}{I}_{1max}dl\sin \left(\frac{P}{\lambda }{u}_c\right)\frac{{\cos }^2\alpha }{{\sin }^3\alpha }{{\displaystyle \int }}_{-\infty }^{+\infty }\frac{\sin \left(\frac{P}{\lambda }\left(u-u_c\right)\right)\left(1+\cos u\right)du}{{\left({\left(u_s-u\right)}^2+2{\cot }^2\alpha \left(1+\cos u\right)\right)}^{\frac{3}{2}}}.$$

(42)

At this point, shifted relative to the antinode of the current and the antinode of the charge, the forces of electric and magnetic interaction of two helices exist simultaneously, and the total force can be found as

$$d{\overrightarrow{F}}^{sum}=d{\overrightarrow{F}}^{el}+d{\overrightarrow{F}}^{mag}.$$

(43)

For the selected coordinate system, the forces component $d{F}_z$ of electric and magnetic interaction is radial for a double helix. The tangential component $d{F}_{\tau }$ of these forces is also of interest. It is possible to determine the ratio for the tangential component of the force acting on a physically small element of the second helix from the side of the entire first helix

$$d{F}_{\tau }=\pm d{F}_x\sin \alpha +d{F}_y\cos \alpha ,$$

(44)

which is true for both magnetic and electric forces, as well as for the total force. Here, as above, the “$+$” sign corresponds to a right-handed helix, and the “$-$” sign corresponds to a left-handed one. Using Formulae (43) and (44), and averaging in time, we arrive at

$$\begin{array}{c}\hfill <d{F}_{\tau }^{sum}\left(u_c\right){>}_t=\pm \left(<d{F}_x^{el}\left(u_c\right){>}_t+<d{F}_x^{mag}\left(u_c\right){>}_t\right)\sin \alpha +(<d{F}_y^{el}\left(u_c\right){>}_t+<\hfill \\ \hfill d{F}_y^{mag}\left(u_c\right){>}_t)\cos \alpha ,\hfill \end{array}$$

(45)

where Formulae (36)–(38) should be substituted with (40)–(42).

By setting the tangential component to zero

$$d{F}_{\tau }=0,$$

(46)

we get another equilibrium condition for each of the two helices, which means no strand tension or compression. Using relations (44) and (46), we arrive at Formula (19) already known to us, which has been derived above for the magnetic force components. Thus, relations (19), (22), (24), and (34) obtained above are equivalent to Formula (46) and indicate the absence of the tangential component of the electric and (or) magnetic interaction force. Therefore, Formula (46) is true only for the direct currents and constant charges existing in the helix, or, at low-frequency (quasistationary) electromagnetic oscillations, in the areas of current antinode or charge antinode. When variable electric charges and currents are excited in the helix, relation (46) is not satisfied, and the following inequality occurs

$$d{F}_{\tau }\ne 0$$

(47)

In this case, the tangential component of the forces becomes more significant with the increasing frequency of electromagnetic oscillations, which can lead to damage and rupture of the helix.

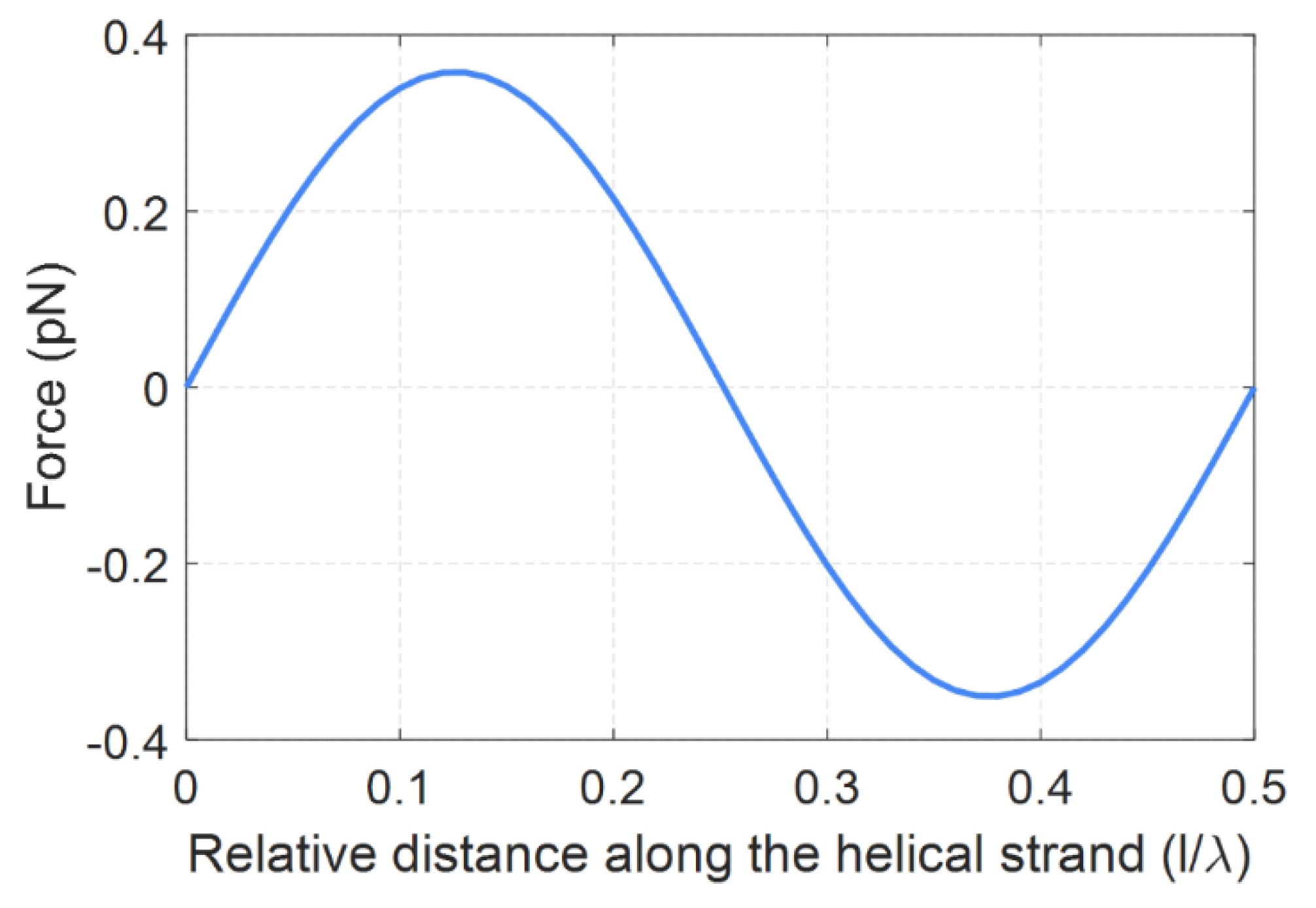
Calculating the force, by Formula (45) we obtain the graph of the tangential component of force depending on the relative distance along the helix line. This distance is expressed in wavelengths of the electromagnetic field and varies from 0 to 0.5. The graph is made for a right-handed helix providing that $\lambda \approx {10}^{2}P$.

As it is shown in Figure 5, the tangential component of the total force $d{F}_{\tau }^{sum}$ takes the maximum value at points located in the middle between the charge antinode and the current antinode. These points are at a distance approximately $l=\frac{\lambda }{8}$ from the current antinode and from the charge antinode. Comparing Figure 4 and Figure 5 shows that the tangential force is inferior in magnitude to Z-components by about 10 times and 23 times, and also to X-and Y-components by approximately 6 and 11 times.

7. Simulation of a Double DNA-Like Helix as an Ideal Conductor under Half-Wave Resonance Conditions in the External Wave Field

Let us consider a double DNA-like helix with the parameters corresponding to a real DNA molecule in the external wave field. At the same time, we assume that a double helix has conductive properties, and consider it as an ideal conductor. ANSYS HFSS software is used for numerical simulations of electromagnetic properties of DNA-like helices. The helix pitch angle is $\alpha { }_{exp}=28.4 \mathrm{deg}$, the radius is $r=1 \mathrm{mm}$ (in a real DNA molecule $r=1 \mathrm{nm}$), and the radius of the conductor section is $r_0=0.1 \mathrm{mm}$. In reality, DNA strands can contain hundreds of turns, in our case there is a limit to twenty turns. The length of such a helix is $L=142.9 \mathrm{mm}$. Assume that the double helix is excited by a linearly polarized wave, for which the electric field vector oscillates parallel to the helix axis, and the wave vector is directed perpendicular to the helix axis, as shown in Figure 1. Let us analyze the radiation emitted by helix conductors. In cases where the length of the conductor, when straightened, is equal to the integer number of half waves, i.e., $L=n\frac{\lambda }{2}$ for integer values of n, the resonance is possible for the electric current in the helix and, therefore, for the wave radiated by the helix. When n = 1, the so-called “main” or half-wave resonance is possible. Resonance frequencies obtained during simulation may differ from the values calculated theoretically.

Figure 6 shows the graphs of the electric field intensity of the radiated wave in the far zone, depending on the frequency. The strength module of the radiated field is averaged over all radiation directions. Blue lines in the graphs indicate the expected resonant frequencies calculated theoretically for odd values n = 1, 3, 5, 7, 9. When considering the even values of n, the integer number of waves fits along the entire length of the conductor. In this case, all the radiators the conductor can be split into create mutually compensating fields in the surrounding space. The total wave radiated by the entire conductor is very weak.

The simulation shows that pronounced resonances occur for the wave radiated by the helix. A half-wave resonance manifests itself most strongly. The helix radiates as usual at a half-wave resonance frequency; the radiation pattern is similar to a conventional electric dipole radiator. For short helices containing several turns, the simulation and theoretical calculation give close values for resonant frequencies. For long helices, e.g., 20 turns, there is a significant difference between the resonance frequencies obtained during the simulation process or theoretical calculation. This difference in resonance frequencies can be explained by the very close mutual arrangement of the strands in the double DNA-like helix. For example, for a helix consisting of 20 turns, under conditions of half-wave resonance, the ratio of the distance between the strands to the wavelength is $\frac{2r}{\lambda }=7·{10}^{-3}$. Such a small distance between the strands can lead to a strong interaction of currents and charges in the double helix and, consequently, to a shift of resonant frequencies, which we see in Figure 6.

It follows from Figure 6 that the intensities of the waves radiated at frequencies ${\nu }_1$ and ${\nu }_3$ (the fields of the main and the next modes) have a ratio $\frac{E_{\nu 3}}{E_{\nu 1}}=0.41$. Using the theory of dipole radiation, it can be shown that the effective electric charges arising upon activation of the main and higher-order modes are related in magnitude as $\frac{q_{\nu 3}}{q_{\nu 1}}~\frac{E_{\nu 3}}{E_{\nu 1}}{(\frac{{\nu }_1}{{\nu }_3})}^2~4.6·{10}^{-2}$. The same relationship is true for the effective electric currents. Consequently, Formulae (1) and (6) are justified for the consideration of only the main mode, and joint analysis of all modes is not required.

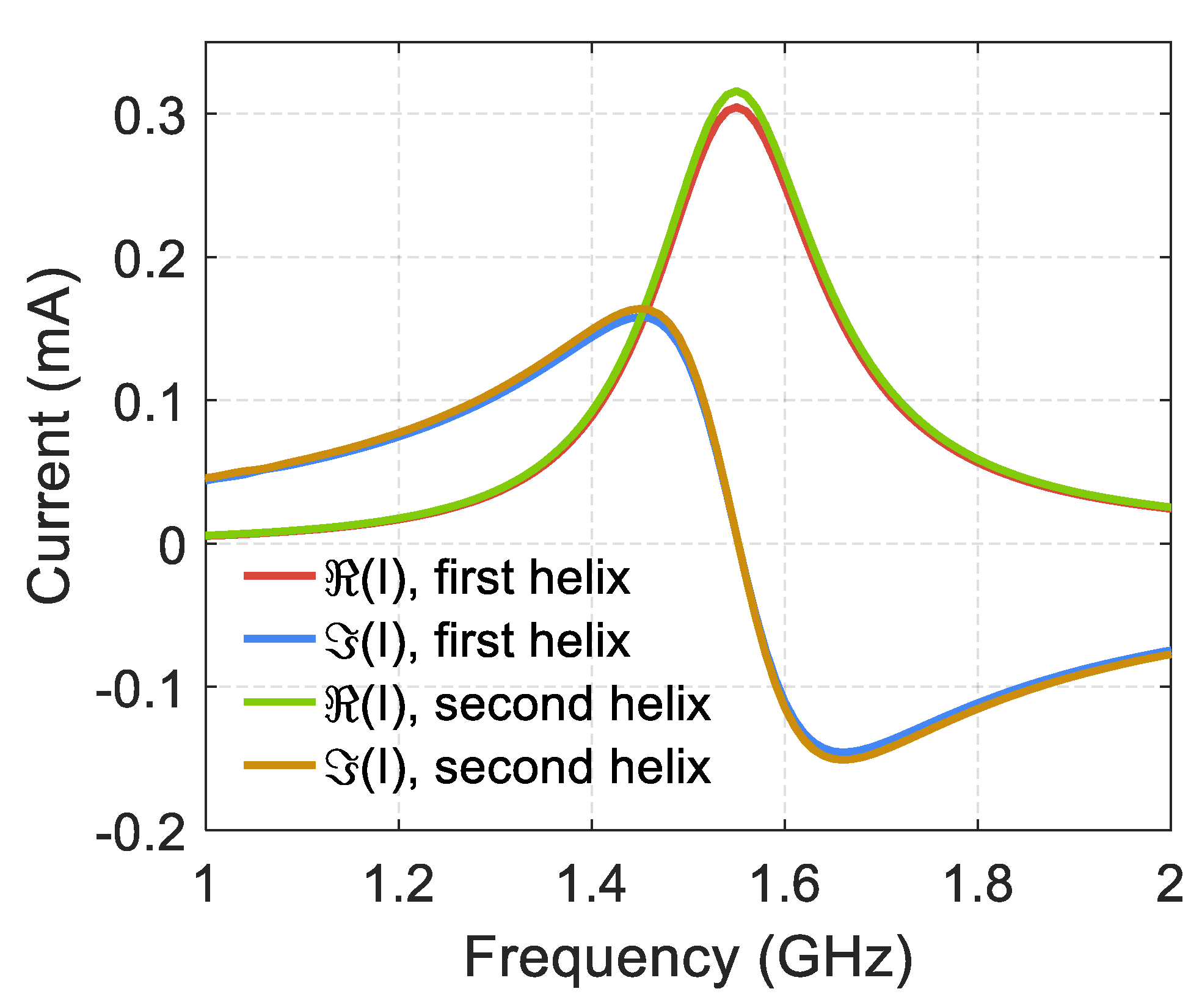
Figure 7 shows the frequency dependence for the real and the imaginary parts of electric currents in two strands of a double DNA-like helix containing 20 turns, near the half-wave resonance, in the helix center. We have used the theorem on the circulation of the magnetic field strength vector for the determination of electric currents. The magnetic field vector was integrated along the contours for both strands of the double helix (the plane is orthogonal to the axis of the double helix). These contours cover the conductors and are located in the horizontal plane for the helix shown in Figure 1 and Figure 3a. From Figure 7 it follows that the electric currents in two strands are almost equal to each other and have the same sign, i.e., they pass in the same direction relative to the helix axis. This feature of electric currents in two strands was used above when calculating the forces of interaction between the strands in a double DNA-like helix.

Numerical modeling shows that the spatial distribution of electric currents and charges is usual for the half-wave resonance and is described by harmonic functions depending on the coordinate l along the helical conductor. The current has a maximum in the center of the helix and monotonously decreases to zero at the ends of the helix. The electric charge density has maxima at the ends of the helix and vanishes at the center of the helix.

The distribution of electric charge in a double DNA-like helix was obtained using ANSYS HFSS software. The simulation was performed at the frequency $\nu =1.55 \mathrm{GHz}$, at which the current in two strands reaches its maximum value due to resonance, as shown in Figure 7. Simulation results show that, under the condition of the considered half-wave resonance, the incident wave induces electric charges of the same sign in the two strands of the double helix, if we consider the points of the two helices, which are mutually symmetric with respect to the axis of the double helix. This feature was used above when calculating the forces of interaction between the strands in a double DNA-like helix. At the resonant current strength $I_{max}=0.3 \mathrm{mA}$, which corresponds to results shown in Figure 7, simulation gives the maximum value of the surface charge density at the edges of the helix ${\sigma }_{max}~{10}^{-9}\frac{C}{m^2}$. These values are consistent with Formula (6) and confirm the excitation of only one main mode of current oscillations in the helix. With the considered current direction, positive charges are induced in the upper parts of the two strands, and, respectively, in the lower parts there are negative charges. With such a distribution of electric charges, there is a mutual radial repulsion of the two strands in a double helix, and this repulsive force acts along the entire length of the helix. Consequently, the simulation is consistent with the results shown in Figure 4b, confirming our conclusion about the mutual radial repulsion of the strands in the double helix at the half-wave resonance. This repulsion of strands is caused not only by the interaction of identically directed electric currents (this force is significant mainly in the central part of the helix, where the currents are strong). The reason for the repulsion of the strands is also the interaction of same-sign charges (this force is important mainly at the ends of the helices, where the charge density is high).

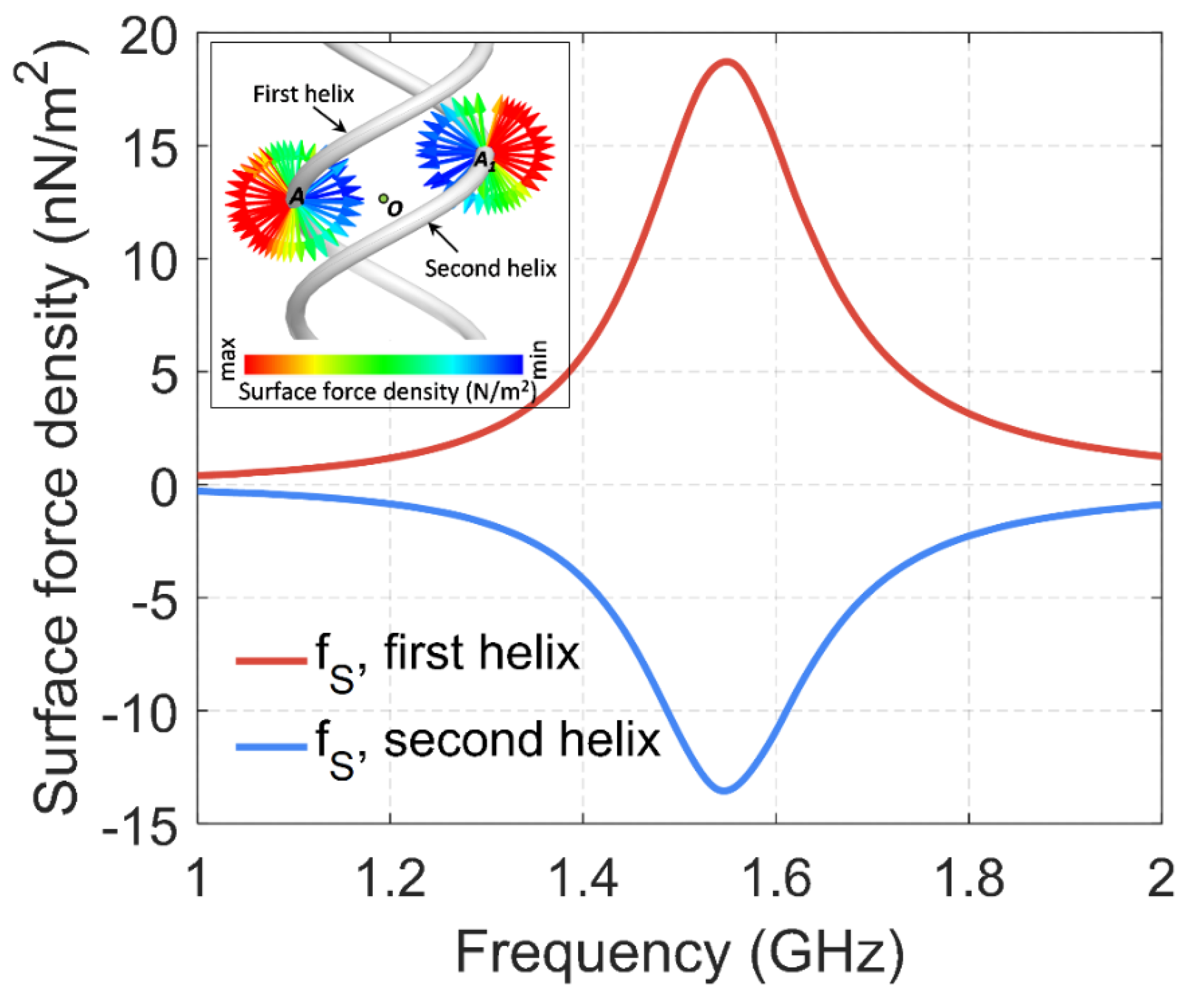
We also modeled the surface density of the forces of interaction of two helices using ANSYS HFSS software and Maxwell’s stress tensor. The simulation results for the middle of the helices are shown in Figure 8. The results are consistent with Figure 4c,d and show mutual radial repulsion of two strands in a double helix, confirming the presented theoretical calculations.

Let us note again the following interesting fact. At the considered half-wave resonance, an antinode of the electric current appears in the central part of the two helices, and the radial repulsion of the two strands is caused by the interaction of currents. These two currents have the same direction relative to the axis of the helix, as a result of their excitation by a wave incident from a side. If such currents existed in two straight parallel conductors, they would be mutually attracted, as is known from the classical theory of magnetism. However, since currents with the same direction pass in the strands of a DNA-like helix, they are radially repelled, which is a consequence of the specific geometry of the DNA-like helix.

We have carried out numerical simulations of metallic DNA-like helices as perfect conductors in the microwave range. We believe that the results of this study can be qualitatively applied to a real DNA molecule in the optical range. Perhaps this transition appears too bold for readers, but it has the right to exist for the following reasons. (1) The electrodynamic similarity, which allows objects and structures to be scaled and predicted their electromagnetic properties in a different frequency range. (2) The various electrically conductive properties of a real DNA molecule, that can be a dielectric, conductor, or semiconductor depending on external conditions. Therefore, the model of a DNA-like helix as a perfect conductor, which is used in the article, can serve as a basis for further, more in-depth studies and comparison with experimental data.

The linear state of the DNA molecule is under consideration here, and we attempt to study the possibility of its excitation under the action of the external electromagnetic field, the wavelength of which is much longer than the length of the helical turn and belongs to the optical range. The length of each helical strand can be close to half the wavelength. This circumstance can enable resonant interaction. Molecules and atoms, being the DNA constituents and located periodically, are activated at certain wavelengths. Thus, the cases when these wavelengths coincide with half-wave resonance for the full length of each helical strand really matter in this research. For example, it is well known that a DNA molecule has an absorption band in the ultraviolet region near the wavelengths ${\lambda }_{1res}=280 \mathrm{nm}$, and ${\lambda }_{2res}=500 \mathrm{nm}$ [6,7,8]. Since the length of one DNA helix turn is $P=7.14 \mathrm{nm}$, the segments of the DNA molecule containing approximately 20 turns and 35 turns can satisfy the condition of a half-wave resonance and undergo the electromagnetic wave activation. Fragments of this length are convenient for direct sequencing and subsequent use in experiments and in practice. The pitch angle of the DNA helix can be calculated using experimental data, and it is ${\alpha }_{exp}=28.4 \mathrm{deg}$ [47,48]. As shown in Section 5, specifically Figure 4, it follows that under the half-wave resonance condition created by an external wave, radial repulsion forces arise between the strands of a double helix. An important feature is the same currents direction in two strands relative to the double helix axis. This direction of currents is confirmed by numerical simulation in this section. The obtained repulsion forces act along the entire activated part of the double helix, because not only electric charges with the same sign in two strands are repelled. Electric currents are repelled as well, having the same direction in two strands relative to the helix axis. Such radial repulsion forces can cause strands damage and rupture in the double helix.

The interaction forces between two strands in a double DNA-like helix have been under consideration above. Such forces are the result of the interaction of electric charges and (or) electric currents arising in the strands. The forces acting on both strands by the external electromagnetic wave are studied below in this section.

The distribution of electric charges in a double helix at a half-wave resonance is shown schematically in Figure 1. When the electric vector direction of the incident wave is upward, as shown in the figure, mainly positive charges are concentrated in the upper part of the helix, and negative charges are concentrated in the lower part of the helix. Therefore, the following relations for the electric forces, acting in an external field on any elements of the helix in its lower and upper parts, can be obtained:

$$d{F}_{\left(bot\right)x}^{el}<0, d{F}_{\left(top\right)x}^{el}>0.$$

(48)

Formula (48) indicate helix stretching along its axis under the influence of the electric field of the incident wave under the half-wave resonance condition. Using relations (48) and (34) for a right-handed helix, i.e., when $q>0$, we arrive at the formulae for the moments of the electric forces acting in an external field on arbitrary elements of the strands in the lower and upper parts of the helix:

$$d{M}_{\left(bot\right)x}^{el}>0, d{M}_{\left(top\right)x}^{el}<0.$$

(49)

Relations (49) indicate unwinding of a right-handed helix under the influence of the electric field of the incident wave under the half-wave resonance condition.

Thus, under the half-wave resonance condition, not only radial repulsion forces arise between the strands of the double helix, which act along the entire length of the activated helix part. In addition, forces and moments of forces can also arise directed along the helix axis, which simultaneously stretch and unwind a double helix.

If we consider metallic double helices as elements of metamaterials, then the conduction electrons are well activated in the microwave and in the terahertz ranges, as well as at higher frequencies, up to the plasma frequency. In this case, a half-wave resonance may occur for the entire length of the wire forming the helix. According to this study, the equilibrium of a double helix in an external electromagnetic field substantially depends on its pitch angle. This fact should be taken into account when designing metamaterials based on DNA-like helices.

8. Conservation Laws in the Media and Structures with Helical Symmetry

The relation

$$F_x+q{M}_x=0,$$

(50)

obtained above independently for the forces of electric and magnetic interaction in a double helix, has a deep meaning. It can be shown that for the structures with helical symmetry, this relation is a consequence of the conservation laws of fundamental physical quantities. For example, in classical monograph [49], the particle motion in the field of an infinite homogeneous cylindrical helix is considered. Since the particle moves in the inhomogeneous and anisotropic field, the particle momentum and its moment of momentum, considered separately, do not conserve. At the same time, the Lagrange function of the particle does not change when it rotates around the helical axis (X-axis) by angle $\delta \varphi$ and simultaneously transfers along this axis at a distance $\frac{1}{q}\delta \varphi$. Therefore, it follows from the Noether theorem that the conservation law is satisfied:

$$p_x+q{m}_x=\mathrm{const}.$$

(51)

Thus, the conserved quantity is a linear combination of the particle momentum projection on the helix axis $p_x$ and the same projection of the moment of momentum $m_x={[\overrightarrow{r},\overrightarrow{p}]}_x$. Let us highlight again that the conservation laws are not satisfied for the particle momentum and moment of momentum projections on the helix axis, taken separately. Considering changes in $\mathsf{\Delta }{p}_x$ and $\mathsf{\Delta }{m}_x$ in an arbitrary time period $\mathsf{\Delta }t$, using conservation law (51), relation (50) can be obtained for the projections of the force and the force moment on the helix axis.

Conservation law (51) and relation for the force and the force moment (50) are valid not only in mechanics, but also in electrodynamics. In particular, paper [50] and monograph [51] consider the propagation of light in cholesteric liquid crystals, which are characterized by helical symmetry. It is shown that the Lagrange function for the electromagnetic field

$$L=\frac{1}{2}(\overrightarrow{E}\overrightarrow{D}-\overrightarrow{B}\overrightarrow{H})$$

(52)

is invariant with respect to helical rotation around the axis of the cholesteric helix. This invariance satisfies conservation law (51), where

$$\overrightarrow{p}=[\overrightarrow{D},\overrightarrow{B}],\overrightarrow{m}=[\overrightarrow{r}[\overrightarrow{D},\overrightarrow{B}]]$$

(53)

are the vectors of the particle momentum density and the moment of momentum density of the electromagnetic field.

Analytical and numerical calculations show that relations (19), (22), (24), and (34) are satisfied accurately only if there are direct electric currents and constant charges in a double helix. In this case, there is a helical symmetry of the entire system of currents and charges, as well as electric and magnetic fields. If alternating electric currents and charges are excited in a double helix, the helical symmetry is broken, and Formulae (19), (22), (24), and (34) are true only in a certain approximation. The lower the frequency of the electromagnetic field, the higher the accuracy of these relations.

9. Conclusions

This paper considers a double DNA-like helix in the field of the incident electromagnetic wave, which creates a half-wave resonance in the helical strands. The length of one double helix strand is approximately equal to half the wavelength of the incident electromagnetic field. This resonance type is well known in radiophysics for both conductors and dielectrics, and therefore it can be realized in DNA-like helices depending on the conductivity type similar to metals, organic semiconductors, or dielectrics. It is shown that forces and moments of forces that are interrelated with each other can occur simultaneously at such a resonance in a double DNA-like helix under the influence of the incident electromagnetic wave. These forces and torques can create the risk of both “improper” unwinding of the helix and rupture of its threads. By “improper” helix unwinding we mean the process that is different from a “soft” one that does not damage the separation of two strands which occurs under the helicase action during the DNA replication.

The equilibrium of a double DNA-like helix, which is in a linear state, and the danger of “improper” helix unwinding and strands rupture are considered based on the laws of classical electrodynamics. Two basic properties make it possible to consider a helix as DNA-like in a geometric sense. Firstly, the helix pitch angle relative to the plane, which is perpendicular to the helix axis, corresponds to well-known experimental data and is approximately equal to the value $\alpha { }_{exp}=28.4 \mathrm{deg}$. Secondly, two strands of the helix are mutually shifted along the helix axis by value $x_s=\frac{1}{2}r$ equal to half the helix radius, which is also known from the previous experiments.

Incident electromagnetic waves induce certain effective electric current in a double helix. As experimental data show, the DNA molecule exhibits strong absorption for the wavelengths ${\lambda }_{1res}=280 \mathrm{nm}$ and ${\lambda }_{2res}=500 \mathrm{nm}$ [6,7,8]. Such absorption can be considered as excitation of a strong current in the helices, because the absorbing centers (atoms and molecules) are present periodically in the helix along its entire length, and when interacting with the wave, they provide some effective current along the entire helix. The interaction of currents and charges in two helices is studied in the low-frequency case, when the wavelength of the electromagnetic field significantly exceeds the length of the helical turn. Based on the laws of Coulomb, Biot–Savart, and Ampere, the analytical expressions are obtained for all the forces components acting on an arbitrary element of one helix from the side of the other one, considered in its entirety. The results can be used both in the design of metamaterials based on DNA-like helices, and in the study of a real DNA molecule.

The mutual shift of the helices along their axis, which takes place in a real helix of the DNA molecule, is taken into account. It is shown that when two strands interact, their relative shift leads to simultaneous existence of the force and the moment of force acting on each helix and directed along their common axis. These axial components of the force and the moment of force are mutually proportional.

The radial components of the interaction forces of electric currents and charges have been calculated, and their dependence on the double helix pitch angle has been obtained. These radial components of the forces describe the mutual attraction or repulsion of two helices and exist both for a symmetrical double helix and in the case of mutual shift of two helices along their common axis. It has been shown that there exists a certain equilibrium helix pitch angle (${\alpha }_0\approx 38\mathrm{deg}$) at which the radial component of the magnetic force vanishes, which means the absence of radial attraction or repulsion of the elementary current in the second helix with respect to the entire first helix [44,45]. At this particular angle α₀ the force radial component of the helices’ magnetic interaction changes sign.

A numerical simulation of the linear segment of a double DNA-like helix, consisting of 20 turns, has been done, wherein the helix is considered as an ideal conductor. The total length of each straightened strand is expected to be approximately equal to half the wavelength of the electromagnetic field, i.e., the half-wave resonance condition is satisfied.

These studies are a step in studying the possibility of activating a DNA molecule under the influence of an external electromagnetic field, the wavelength of which is much longer than the length of the helical turn, and belongs to the optical range. At the same time, the length of each helical strand can be close to half the wavelength, and thereby the conditions for resonant interaction can be satisfied. We have made an attempt to justify the half-wave resonance based on the DNA molecule structure. The molecules and atoms, which are present in the DNA periodically, are activated at certain frequencies, and the cases when these frequencies coincide with a half-wave resonance for the full length of the helix are important. For example, the DNA molecule has an absorption band in the ultraviolet and visible range near wavelengths ${\lambda }_{1res}=280$ nm and ${\lambda }_{2res}=500$ nm. Consequently, the segments of the DNA molecule containing approximately 20 turns and 35 turns can satisfy the half-wave resonance condition and undergo activation by an electromagnetic wave. Fragments of this length are convenient for direct sequencing and subsequent use in experiments and in practice. In this case, radial repulsion forces arise between the strands of the double helix. These repulsion forces act along the entire excited part of a double helix, because not only electric charges with the same sign in two strands are repelled. Electric currents are repelled as well, having the same direction in two strands relative to the helix axis. Such a radial repulsion force, acting along the entire length of the DNA, can lead to strands damage and rupture of the double helix. To provide a better picture of these repulsive forces, supplementary materials with figures are attached, where a double DNA-like helix with its specific geometry is compared with two straight parallel conductors. This information helps to understand the fundamental difference between the forces arising under the action of an external electromagnetic wave in a pair of straight parallel conductors and in a double DNA-like helix.

In addition, there can exist forces and moments of forces directed along the helix axis, which simultaneously stretch and unwind a double helix.

At the same time, we know that “soft”, non-destructive unwinding and separation of the strands in a DNA double helix is possible. This process can be during the DNA replication under the helicase or unwinding protein action [5,48]. While studying the replication, first of all its mechanical and biological aspects are usually considered. However, without considering the electromagnetic forces, the pattern of the DNA replication remains incomplete. In this regard, the result obtained in this article appear promising: the direction of the radial force of electric currents attraction or repulsion in two helical strands depends on the double helix pitch angle. The critical pitch angle of the double helix, at which the radial force of the magnetic interaction of two helices changes its direction, is ${\alpha }_0\approx 38 \mathrm{deg}$ [44,45]. At the same time, the DNA helix in its natural condition is characterized by the pitch angle $\alpha {}_{exp}=28.4 \mathrm{deg}$ [47,48]. Since the helicase is in close proximity to DNA, it can carry oppositely directed electric currents in the helical strands (similar to the current source in a two-wire line). Then, the inequality ${\alpha }_{exp}< {\alpha }_0$ is satisfied at the beginning of the replication, when the DNA is still in its natural condition. This means that the electric currents in two helices, having the opposite direction, are mutually attracted along the helix radius. Later, during the replication process, certain straightening of the helical strands and an increase in the double helix pitch angle to a new value α₁ may occur. The inequality ${\alpha }_1> {\alpha }_0$ can be achieved at which oppositely directed electric currents in two helices begin to repel mutually along the double helix radius. Such repulsion is necessary to separate two strands in space and to continue replication. Note that this article considers the activation of electric currents in a double helix under the electromagnetic wave influence from a remote source. Such currents can have the same direction in two helical strands, which is radically different from the helicase action, which is found in close proximity to the DNA.

The obtained relation between the axial components of the force and the moment of this force, which is true for both electric and magnetic forces, has a deep meaning. This relation is a consequence of the conservation laws of fundamental physical quantities for the structures with helical symmetry. For example, in the simplest case, it is possible to consider an elementary electric charge or a current element moving in the field of constant charges or constant currents located on the helix line. Then, for this moving particle, the conserved quantity is a linear combination of the particle momentum projection on the helix axis $p_x$ and the same projection of the moment of momentum $m_x={[\overrightarrow{r},\overrightarrow{p}]}_x$. Note that the conservation laws are not satisfied for the particle momentum and moment of momentum projections on the helix axis, taken separately.

Metal double DNA-like helices, as well as helices with different winding directions, right-handed and left-handed [52], can be used as elements of metamaterials. In metal helices, conduction electrons are well activated in the microwave and in the terahertz range, as well as at higher frequencies, up to the plasma frequency. In this case, half-wave resonance and other types of resonances may arise for the entire length of the wire forming the helix. It has been shown that the equilibrium of the double helix in an external electromagnetic field substantially depends on its pitch angle. This fact should be taken into account when designing the metamaterials based on DNA-like helices and studying electro (opto)-mechanical effects in chiral and racemic structures.