Optical Bistability in an Optomechanical System with N-Type Atoms under Nonresonant Conditions
Abstract
1. Introduction
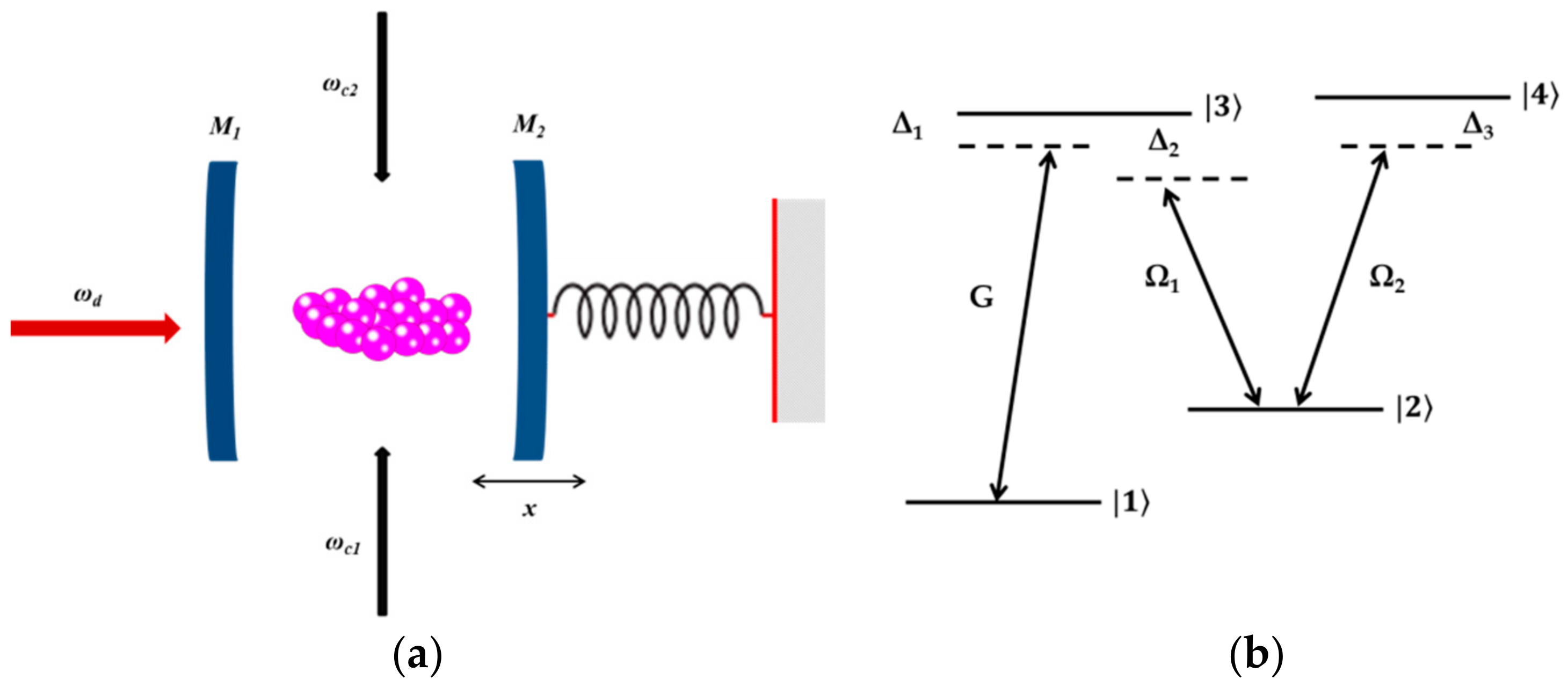
2. Theoretical Model
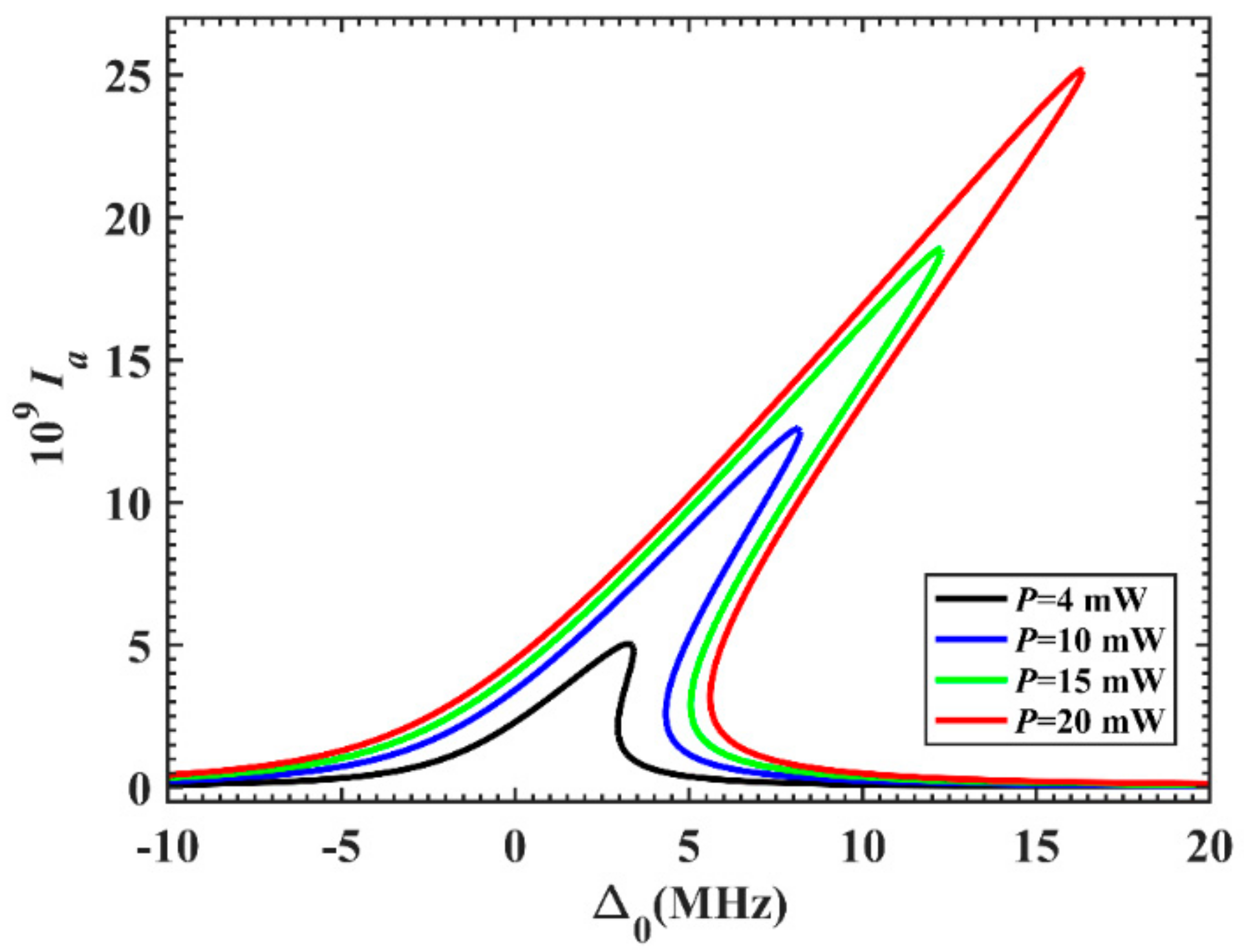
3. Numerical Simulations and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mancini, S.; Tombesi, P. Quantum noise reduction by radiation pressure. Phys. Rev. A 1994, 49, 4055–4065. [Google Scholar] [CrossRef] [PubMed]
- Kronwald, A.; Marquardt, F.; Clerk, A.A. Dissipative optomechanical squeezing of light. New J. Phys. 2014, 16, 063058. [Google Scholar] [CrossRef]
- Huang, S.M.; Chen, A.X. Quadrature-squeezed light and optomechanical entanglement in a dissipative optomechanical system with a mechanical parametric drive. Phys. Rev. A 2018, 98, 063843. [Google Scholar] [CrossRef]
- Vitali, D.; Gigan, S.; Ferreira, A.; Bohm, H.R.; Tombesi, P.; Guerreiro, A.; Vedral, V.; Zeilinger, A.; Aspelmeyer, M. Optomechanical entanglement between a movable mirror and a cavity field. Phys. Rev. Lett. 2007, 98, 030405. [Google Scholar] [CrossRef] [PubMed]
- Xiong, H.; Wu, Y. Fundamentals and applications of optomechanically induced transparency. Appl. Phys. Rev. 2018, 5, 031305. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Huang, S.M. Electromagnetically induced transparency in mechanical effects of light. Phys. Rev. A 2010, 81, 041803. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, B.; Ozdemir, S.K.; Liu, Y.X.; Jing, H.; Lü, X.Y.; Liu, Y.L.; Yang, L.; Nori, F. Giant nonlinearity via breaking parity-time symmetry: A route to low-threshold phonon diodes. Phys. Rev. B 2015, 92, 115407. [Google Scholar] [CrossRef]
- Xiong, H.; Si, L.G.; Wu, Y. Precision measurement of electrical charges in an optomechanical system beyond linearized dynamics. Appl. Phys. Lett. 2017, 110, 171102. [Google Scholar] [CrossRef]
- Fiore, V.; Yang, Y.; Kuzyk, M.C.; Barbour, R.; Tian, L.; Wang, H. Storing optical information as a mechanical excitation in a silica optomechanical resonator. Phys. Rev. Lett. 2011, 107, 133601. [Google Scholar] [CrossRef]
- Van Thourhout, D.; Roels, J. Optomechanical device actuation through the optical gradient force. Nat. Photonics 2010, 4, 211–217. [Google Scholar]
- Chen, A.X.; Nie, W.J.; Li, L.; Zeng, W.; Liao, Q.H.; Xiao, X.B. Steady-state entanglement in levitated optomechanical systems coupled to a higher order excited atomic ensemble. Opt. Commun. 2017, 403, 97–102. [Google Scholar] [CrossRef]
- Sete, E.A.; Eleuch, H. Controllable nonlinear effects in an optomechanical resonator containing a quantum well. Phys. Rev. A 2012, 85, 043824. [Google Scholar] [CrossRef]
- Sete, E.A.; Eleuch, H.; Ooi, C.H.R. Entanglement between exciton and mechanical modes via dissipation-induced coupling. Phys. Rev. A 2015, 92, 033843. [Google Scholar] [CrossRef]
- Xiong, W.; Jin, D.Y.; Qiu, Y.Y.; Lam, C.H.; You, J.Q. Cross-Kerr effect on an optomechanical system. Phys. Rev. A 2016, 93, 023844. [Google Scholar] [CrossRef]
- Sarma, B.; Sarma, A.K. Ground-state cooling of micromechanical oscillators in the unresolved-sideband regime induced by a quantum well. Phys. Rev. A 2016, 93, 033845. [Google Scholar] [CrossRef]
- Huang, S.M.; Chen, A.X. Improving the cooling of a mechanical oscillator in a dissipative optomechanical system with an optical parametric amplifier. Phys. Rev. A 2018, 98, 063818. [Google Scholar] [CrossRef]
- Han, Y.; Cheng, J.; Zhou, L. Electromagnetically induced transparency in a cavity optomechanical system with an atomic medium. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 165505. [Google Scholar] [CrossRef]
- Qi, T.; Han, Y.; Zhou, L. Electromagnetically induced transparency in cavity optomechanical system with Λ-type atomic medium. J. Mod. Opt. 2013, 60, 431–436. [Google Scholar] [CrossRef]
- Li, Y.; Sun, C.P. Group velocity of a probe light in an ensemble of Λ atoms under two-photon resonance. Phys. Rev. A 2004, 69, 051802. [Google Scholar] [CrossRef]
- Chang, Y.; Shi, T.; Liu, Y.; Sun, C.P.; Nori, F. Multistability of electromagnetically induced transparency in atom-assisted optomechanical cavities. Phys. Rev. A 2011, 83, 063826. [Google Scholar] [CrossRef]
- Groblacher, S.; Hammerer, K.; Vanner, M.R.; Aspelmeyer, M. Observation of strong coupling between a micromechanical resonator and an optical cavity field. Nature 2009, 460, 724–727. [Google Scholar] [CrossRef] [PubMed]
- Li, J.H.; Lu, X.Y.; Luo, J.M.; Huang, Q.J. Optical bistability and multistability via atomic coherence in a N-type atomic medium. Phys. Rev. A 2006, 74, 035801. [Google Scholar] [CrossRef]
- Vogell, B.; Kampschulte, T.; Rakher, M.T.; Faber, A.; Treutlein, P.; Hammerer, K.; Zoller, P. Long distance coupling of a quantum mechanical oscillator to the internal states of an atomic ensemble. New J. Phys. 2015, 17, 043044. [Google Scholar] [CrossRef]
- Mann, N.; Pelster, A.; Thorwart, M. Tuning the order of the nonequilibrium quantum phase transition in a hybrid atom-optomechanical system. New J. Phys. 2019, 21, 113037. [Google Scholar] [CrossRef]
- Jiang, C.; Bian, X.; Cui, Y.; Chen, G. Optical bistability and dynamics in an optomechanical system with a two-level atom. J. Opt. Soc. Am. B 2016, 33, 2099. [Google Scholar] [CrossRef]
- Chen, B.; Wang, X.F.; Yan, J.K.; Zhu, X.F.; Jiang, C. Controllable optical bistability in a three-mode optomechanical system with atom-cavity-mirror couplings. Superlattice Microst. 2018, 113, 301. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Deng, L.; Chen, A. Optical Bistability in an Optomechanical System with N-Type Atoms under Nonresonant Conditions. Photonics 2020, 7, 122. https://doi.org/10.3390/photonics7040122
Gao Y, Deng L, Chen A. Optical Bistability in an Optomechanical System with N-Type Atoms under Nonresonant Conditions. Photonics. 2020; 7(4):122. https://doi.org/10.3390/photonics7040122
Chicago/Turabian StyleGao, Yan, Li Deng, and Aixi Chen. 2020. "Optical Bistability in an Optomechanical System with N-Type Atoms under Nonresonant Conditions" Photonics 7, no. 4: 122. https://doi.org/10.3390/photonics7040122
APA StyleGao, Y., Deng, L., & Chen, A. (2020). Optical Bistability in an Optomechanical System with N-Type Atoms under Nonresonant Conditions. Photonics, 7(4), 122. https://doi.org/10.3390/photonics7040122



