Asymmetric Carrier Divider with an Irregular RF Phase on DD-MZ Modulator for Eliminating Dispersion Power Fading in RoF Communication

Abstract

The main problem of intensity modulation (IM) in radio-over-fiber (RoF) communication is dispersion power fading (DPF), which occurs when the signal is transmitted through a dispersive link that causes a sideband cancelation effect. The DPF level of the RoF link is determined by the deviation factor (DF). The optical single-sideband (OSSB) modulation scheme, which is generated by driving one of the dual-drive Mach–Zehnder modulators (DD-MZMs), is usually used to overcome DPF. The DF value of OSSB modulation at modulation index m = 0.1 increases from 0.008 to 0.930 at m = 1. It can be said that this method is only effective at reducing DF at low m. However, as well-known information of the DD-MZM system, high-efficiency optic–electric conversions can be obtained at high m values, but DF will increase. Therefore, reducing the DPF value for high m ≥ 0.1 is interesting. It is known that in wireless communication, to reduce the impact of fading, direct signals are amplified and signals with irregular phases are used. Moreover, this paper proposes the DD-MZM with an asymmetric carrier divider as a direct signal and combines it with an irregular radio frequency (RF) phase to reduce the DPF at high m. The carrier that is generated by laser diode (LD) power (P_IN) is divided asymmetrically as power modulation (P_DD-MZM) and carrier arm (CA) power (P_CA). Furthermore, the minimum DF is obtained when the P_IN is separated as 75% for P_CA and 25% for P_DD-MZM with an irregular RF signal of θ = 48° and a bias point value of γ = ¾. As a result, with the same power as OSSB, this proposed structure produces DF at m = 0.1 and m = 1 with values of 0.008 and 0.03, or it can reduce DF of 96.7% at m = 1. The mathematical model and simulation model have very good agreement, which validates the proposed method.

1. Introduction

A system that can transmit radio frequency (RF) signals (X_TX(t)) through optical fiber used to support wireless communication services, known as radio-over-fiber (RoF), has been developed recently. The transmission is completed by modulating the optical source (E_in(t)) using X_TX(t), which is transmitted using the electro-optic (E/O) converter located in the central office (CO). At the receiver, the RF signal is recovered using an optoelectric (O/E) converter located in the radio access point (RAP). Recovered RF signals (X_rec(t)) are then transmitted wirelessly from RAP to the mobile station (MS). The conversion of RF signals to optics can be performed by modulating the optical source directly or modulating the optical carrier externally. Either direct or external modulation can be used to modulate the intensity (amplitude) or phase of the optical carrier. The recovery of the RF signal at the receiver on intensity modulation (IM) is recognized as direct detection (DD), whereas in phase modulation, it is known as coherent detection [1].

The IM on the RoF link produces an optical signal with a double sideband spectrum. The optical double sideband (ODSB) is an optical signal with a spectrum consisting of an optical carrier and upper and lower sidebands located around the optical carrier. When the ODSB signal is transmitted through a fiber link, the chromatic dispersion of the fiber causes the sideband and optical carrier to propagate at different speeds. This leads to the modulated signal at the receiver (E_RX(t)) experiencing a different phase between the sideband component and optical carrier by ϕ. The proportion of ϕ follows the length of the fiber (L), the frequency of the RF signal (f_m) and the wavelength (λ_c) used. The phase difference between the sideband and optical carrier causes the O/E process to generate two identical RF signals but with a different phase of 2ϕ, resulting in constructive and deconstructive interference on the recovered RF signal. Destructive interference causes a reduction in recovered RF signal power, which is known as dispersion power fading (DPF). If ϕ = π/2, the sideband cancelation effect occurs, which causes a massive loss of power or deep fade [2].

There are several methods for overcoming the DPF, such as carrier phase shift (CPS) [3,4,5,6,7,8]. The CPS method uses a carrier phase shift of the E_TX(t) signal at the transmitter. The phase of the carrier (ϕ) is adjusted such that ϕ at the receiver is zero. However, this method has disadvantages because ϕ is different due to the change in L, f_m, and λ_c. Thus, it is always necessary to reset ϕ every system change, and it is not a convenient or robust solution. Furthermore, optical carrier suppression (OCS) was proposed by [9,10,11,12,13,14,15,16]. The OCS modulation system is modulated with upper and lower sidebands but without carrier components. At the OCS, X_rec(t) is generated from the beating upper sideband and lower sideband with a distance of 2f_m, so the frequency of X_rec(t) is 2f_m. However, this method has drawbacks, such as requiring additional devices, such as downconverters, to convert X_rec(t) frequency to its initial value. Machine learning can also be used to overcome DPF. This method has been successfully implemented for short-range transmission [17,18]. However, it also has some disadvantages, one of which is a complicated configuration on the receiver side.

The reduction in DPF can be overcome using optical single-sideband (OSSB) modulation. OSSB modulation has advantages such as not requiring frequency translation [19] or inconvenient phase receiver adjustment. OSSB modulation scheme can be generated by filtering one of the sideband modulated optical signals [20]. This method, however, highly dependents on the optical wavelength. The OSSB modulation scheme can be produced with DD-MZM by driving one of its arms using the RF signal that is given a bias voltage ½ of the switching voltage and driving another arm using a signal with a regular phase (θ) of 90° [15,21,22,23,24]. DD-MZM is an E/O converter frequently used in RoF links due to its ability to generate various optical schemes with just a simple configuration.

The mathematical model of OSSB modulation is usually developed based on the Bessel function [15]. Based on this function, the low DPF at OSSB can be obtained if the system generates the carrier signal and +1st order sideband only. To produce this condition, the OSSB modulation must be operated at low m ≤ 0.1 because higher m will generate more sideband orders. A higher number of sideband orders will automatically increase the DPF. However, the OSSB is only effective at low m ≤ 0.1. However, to increase the efficiency of optic–electric conversions at the OSSB, a high m value is needed [22]. Therefore, it will be interesting to reduce the DPF value at high m = 1.

In wireless communication, increasing the direct signal power [25] and using irregular phases can reduce the effect of fading. Then, the concept of suppressing fading in wireless communication can be applied to RoF communication to suppress the effect of DPF. As a novelty, this paper proposes an asymmetric carrier divider as a direct signal with an irregular RF phase on a DD-MZ modulator for eliminating DPF, as shown in Figure 1. In detail, the optical source generated using a laser diode (LD), E_in(t) is divided using an optical splitter (OS) with asymmetrical values such as power modulation (P_DD-MZM) and carrier arm (CA) power (P_CA). The signal at P_DD-MZM is modulated using DD-MZM, and the modulated signal (E_DD-MZM(t)) is generated. The signal at the CA is added to E_DD-MZM(t) using an optical combiner (OC), which produces the transmitted signal (E_TX(t)). The E_TX(t) is transmitted using fiber link H(f) and produces received signal (E_RX(t)). The E_RX(t) is detected and recovered using a photodetector (PD) and produces X_rec(t). This proposed method is called an asymmetric carrier divider system.

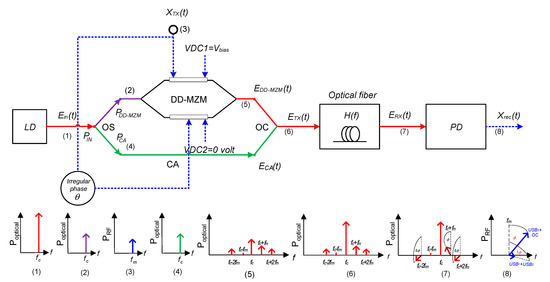
Figure 1. The proposed asymmetric carrier divider with irregular RF phase on DD-MZ modulator.

Furthermore, to further reduce the DPF value that is caused by multi-sideband order, this paper also proposes the irregular RF phase. Therefore, the optimum E_DD-MZM(t) spectrum can be generated by adjusting the DD-MZM arm to produce a low DPF. The DPF level is determined using the deviation factor (DF). DF is the quantity of recovered RF signal power variation at the receiver that is measured over a certain range of fiber lengths. The smaller the DF is, the lower the DPF level or the smaller the effect of chromatic dispersion towards the RoF link.

Therefore, we combine the asymmetric carrier divider system with the irregular RF phase on the DD-MZ modulator. Therefore, the combination of the optimum value of the power ratio and the optimum value of the irregular phase will reduce DF at RoF communication significantly.

Furthermore, the significant contributions of this paper are as follows:

• The laser diode (LD) power (P_IN) carrier is divided asymmetrically as the power modulation (P_DD-MZM) and carrier arm power (P_CA). The power P_CA is used to compensate for the power of the carrier of the optical field of the DD-MZM output, which is reduced due to increasing m.
• The RF signal with an irregular phase (θ) was applied to the DD-MZ modulator. Therefore, the optimum E_DD-MZM(t) spectrum can be generated by adjusting the DD-MZM arm.
• The minimum DF is obtained when the P_IN is separated as 75% for P_CA and 25% for P_DD-MZM with an irregular RF signal of θ = 48° and bias point value of γ = ¾. This proposed structure produces DF at m = 0.1 and m = 1 value are 0.008 and 0.03, or it reduced DF of 96.7% compared to OSSB.
• The proposed system was successfully applied without additional power or filter, and the additional power or filter managed to increase the cost and complexity of RAP. Moreover, θ is independent of fiber length. Our proposed model is applied for single fiber, not for routing scenarios with many nodes.
• The proposed mathematical model of the system is developed based on the Bessel function. This model can be used to evaluate all the parameters. Furthermore, the model is validated using simulation, and it has very good agreement, which validates the proposed method.
• Nevertheless, the current paper has some limitations: (1) We used the comparison between numerical and simulation models without experiment due to the unavailability of devices, but this model was successfully verified and had a good agreement; (2) Our proposed method was focused on optical signals modulated by RF sine waves [22,26,27,28,29]; (3) To eliminate the dispersion, we focused on the received RF power; (4) We assumed that the optic arm length is less than 1 m; therefore, the phase did not change significantly; (5) In this study, we investigated up to 16 scenarios, and the DD-MZM modulator was used with the best performance in the C4 scenario; and (6) As a consideration, the paper’s proposed method focused not only on asymmetric power divider but also on the optimal phase. Therefore, the minimum DF was obtained by combining the irregular phase and the power divider to reduce DF by 96.7%. We think that the global optimum DF results will also be similar to the proposed case in this scenario. Moreover, we also must consider the availability of the optical divider in the market.

2. Optical Field of DD-MZM Output

2.1. DD-MZM with Basic Configuration

Mach–Zehnder modulator (MZM) is an external IM generally used on fiber optic links. MZM can be driven on one or both arms. MZM that is driven on both arms is known as dual-drive MZM (DD-MZM). With the configuration illustrated in Figure 2, DD-MZM can produce several modulation schemes shapes. E_in(t) generated by the laser diode (LD) is equally divided into both arms (upper and lower arms). The MZM upper arm is driven by the RF signal (X_TX(t)) and is given an additional DC voltage of V_bias. The lower arm of the MZM is driven by the same X_TX(t) signal, but its phase is shifted using an electrical phase shifter (EPS) of θ without an additional DC voltage.

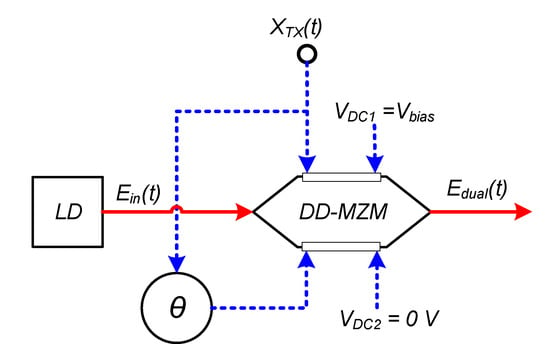
Figure 2. Basic configuration of DD-MZM to generate various modulation schemes.

Assuming that the extinction ratio (ER) of DD-MZM is extremely high, and the optical signal has the same polarization at every point, the optical field of DD-MZM output E_dual(t) can be approximated by [30]

$$E_{dual}\left(t\right)\approx \frac{1}{2}\sqrt{2P_{in}}{e}^{j2\pi f_{c}t}\left\{e^{\left(j\pi \frac{V_{up}\left(t\right)}{V_{\pi }}\right)}+e^{\left(j\pi \frac{V_{down}\left(t\right)}{V_{\pi }}\right)}\right\}$$

(1)

where V_π is the MZM switching voltage, P_in is the optical power output of LD, f_c is the continuous optical wave frequency, V_up(t) is the upper signal drive and V_down(t) is the lower signal drive.

X_TX(t) is given by

$$X_{TX}\left(t\right)=V_m\cos 2\pi f_{m}t$$

(2)

where V_m is the RF signal amplitude, f_m is the RF signal frequency, V_up(t)) and V_down(t) of DD-MZM are given by

$$V_{up}\left(t\right)=V_m\cos \left(2\pi f_{m}t\right)+V_{bias}$$

(3)

$$V_{down}\left(t\right)=V_m\cos \left(2\pi f_{m}t+\theta \right)$$

(4)

where θ is the phase of the EPS in radians. By substituting Equations (3) and (4) into Equation (1)

$$E_{dual}\left(t\right)\approx \frac{1}{2}\sqrt{2P_{in}}{e}^{j2\pi f_{c}t}\left\{e^{\left(j\pi \frac{V_m}{V_{\pi }}\cos \left(2\pi f_{m}t\right)+j\pi \frac{V_{bias}}{V_{\pi }}\right)}+e^{\left(j\pi \frac{V_m}{V_{\pi }}\cos \left(2\pi f_{m}t+\theta \right)\right)}\right\}$$

(5)

is obtained. For simplification, Equation (5) can be rewritten as

$$\begin{gathered} E_{dual}\left(t\right)=\frac{1}{2}\sqrt{2P_{in}}{e}^{j2\pi f_{c}t}\left\{e^{\left(jm\cos \left(2\pi f_{m}t\right)+j\pi \gamma \right)}+e^{jm\cos \left(2\pi f_{m}t+\theta \right)}\right\} \\ =\frac{1}{2}\sqrt{2P_{in}}{e}^{j2\pi f_{c}t}\left\{e^{jm\cos \left(2\pi f_{m}t\right)}.e^{j\pi \gamma }+e^{jm\cos \left(2\pi f_{m}t+\theta \right)}\right\} \end{gathered}$$

(6)

where $m=\pi \frac{V_m}{V_{\pi }}$ is the DD-MZM modulation index, and $\gamma =\frac{V_{bias}}{V_{\pi }}$ is the normalized bias voltage.

To simplify the analysis, Equation (6) is written as

$$E_{dual}\left(t\right)=\frac{1}{2}\sqrt{2P_{in}}{e}^{j2\pi f_{c}t}\left\{A.e^{\left(j\pi \gamma \right)}+B\right\}$$

(7)

where

$$A=e^{jm\cos \left(2\pi f_{m}t\right)}$$

(8)

$$B=e^{jm\cos \left(2\pi f_{m}t+\theta \right)}$$

(9)

By applying Jacobi Anger expansion [31], where

$$e^{jm\cos x}={\displaystyle \sum }_{n=-\infty }^{\infty }{j}^n{J}_n\left(m\right)e^{jnx}$$

(10)

and

$$e^{jm\sin x}={\displaystyle \sum }_{n=-\infty }^{\infty }{J}_n\left(m\right)e^{jnx}$$

(11)

Equations (8) and (9) become

$$A={\displaystyle \sum }_{n=-\infty }^{\infty }{j}^n.J_n\left(m\right).e^{jn\left(2\pi f_{m}t\right)}$$

(12)

$$B={\displaystyle \sum }_{n=-\infty }^{\infty }{j}^n.J_n\left(m\right).e^{jn\left(2\pi f_{m}t+\theta \right)}$$

(13)

where J_n(m) is the nth Bessel function of the first kind; therefore, Equation (6) can be stated as

$$\begin{gathered} E_{dual}\left(t\right)=\frac{1}{2}\sqrt{2P_{in}}{e}^{j2\pi f_{c}t}\left\{\begin{array}{c}{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{j}^n.J_n\left(m\right).e^{jn\left(2\pi f_{m}t\right)}.e^{j\pi \gamma }+{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{j}^n.J_n\left(m\right).e^{jn\left(2\pi f_{m}t+\theta \right)}\end{array}\right\} \\ =\frac{1}{2}\sqrt{2P_{in}}\left\{{\displaystyle \sum }_{n=-\infty }^{\infty }{j}^n.J_n\left(m\right).\left(e^{j\pi \gamma }+e^{jn\theta }\right).e^{j2\pi \left(f_c+n{f}_m\right)t}\right\} \end{gathered}$$

(14)

From Equation (14), it can be seen that the DD-MZM output optical field consists of a carrier and sideband with infinite order. In accordance with the Bessel function, the proportion of carrier and sideband depends on the modulation index m used. The greater m is, the carrier power decreases, and more sideband orders are formed. Various forms of modulation schemes can be generated by setting parameters θ and γ.

The OSSB modulation scheme can be generated by setting the value of γ = ½ and θ = 90°. With this arrangement, the lower sideband of order (4n + 1) is suppressed, where n = 0, 1, 2, … [15]. The equation E_dual(t) for OSSB modulation is given by

$$E_{dual-OSSB}\left(t\right)=\frac{1}{2}\sqrt{2P_{in}}\left\{{\displaystyle \sum }_{n=-\infty }^{\infty }{j}^n.J_n\left(m\right).\left(e^{j\frac{\pi }{2}}+e^{jn\frac{\pi }{2}}\right).e^{j2\pi \left(f_c+n{f}_m\right)t}\right\}$$

(15)

2.2. DD-MZM with Carrier Arm (CA)

The effectiveness of OSSB modulation to overcome DPF diminishes with increasing m; when m increases, the carrier power of the DD-MZM output optical field decreases, and more sideband orders are formed. To compensate for the decreased carrier power due to increasing m, the DD-MZM series is added with a carrier arm (CA), as portrayed in Figure 1. The continuous optical wave signal generated by LD is shared using an optical splitter (OS); one part is used as an optical input of DD-MZM, and the other part is forwarded to CA to be recombined with DD-MZM output using an optical combiner (OC). The optical signal on DD-MZM is modulated by the RF signal with a similar configuration to DD-MZM with a detailed configuration, as shown in Figure 1.

The comparison of LD power entered into DD-MZM and the total LD power is expressed as

$$r=\frac{P_{DD-MZM}}{P_{in}}=\frac{P_{in}-P_{CA}}{P_{in}}$$

(16)

where P_in, P_DD-MZM, and P_CA are the power sharing ratio, LD output power, and power input into DD-MZM and power input into CA, respectively. Thus, the DD-MZM output optical field (E_DD-MZM(t)) can be expressed as

$$E_{DD-MZM}\left(t\right)=\frac{r}{2}\sqrt{2P_{in}}\left\{{\displaystyle \sum }_{n=-\infty }^{\infty }{j}^n.J_n\left(m\right).\left(e^{j\pi \gamma }+e^{jn\theta }\right).e^{j2\pi \left(f_c+n{f}_m\right)t}\right\}$$

(17)

We assume that the optic arm length is less than 1 m. Therefore, the phase of P_CA does not change significantly. The CA optical field (E_CA(t)) can be expressed as

$$E_{CA}\left(t\right)=\left(1-r\right)\sqrt{2P_{in}}{e}^{j2\pi f_{c}t}$$

(18)

The optical field output of OC (E_TX(t)) is the sum of E_DD-MZM(t) with E_CA(t), given by

$$\begin{array}{c}{E}_{TX}\left(t\right)=E_{DD-MZM}\left(t\right)+E_{CA}\left(t\right)\hfill \\ =\sqrt{2P_{in}}\left\{\left(1-r\right)e^{j2\pi f_{c}t}+\frac{r}{2}{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}\left(e^{j\pi \gamma }+e^{jn\theta }\right).j^n.J_n\left(m\right).e^{j2\pi \left(f_c+n{f}_m\right)t}\right\}\hfill \end{array}$$

(19)

From Equation (19), it can be seen that the optical signal spectrum of the DD-MZM output with CA comprises an optical carrier with infinite sideband order. Various forms of modulation schemes can still be generated by setting the parameter θ and γ. The magnitude of carrier power compensation of the DD-MZM output optical field that decreases because the increasing m can be adjusted by regulating the value of r. The optical field of the DD-MZM output with CA will always have a carrier even if J₀(m) is zero.

3. C/N Penalty of RoF Link

The DPF of the RoF link can be seen through the carrier-to-noise (C/N) penalty curve. The C/N penalty in this paper is defined by the ratio between RF power received at distance L or P_rec(L) compared to the output power at MZM modulator, and it has distance L = 0 or $P_{rec}\left(L=0\right)$. The difference value between Prec (L) and Prec (L = 0) occurs because of the relative phase difference between sideband and carrier. Therefore, the noise term is the phase noise. Moreover, the C/N penalty was also introduced by [32,33,34]. To calculate the C/N penalty of the RoF link, it is necessary to initially model and derive the P_rec(L) value. The RoF link model that uses DD-MZM with CA as the E/O converter can be seen in Figure 1. The RoF link consists of DD-MZM with CA as the E/O converter, a dispersive optical fiber with H(f) response and photodetector (PD) as the O/E converter.

To simplify the analysis, Equation (19) can be rewritten as

$$E_{TX}\left(t\right)=A_c{e}^{j2\pi f_{c}t}+{\displaystyle \sum }_{n=1}^{\infty }\left\{A_{ln}{e}^{j2\pi \left(f_c-n{f}_m\right)t}+A_{un}{e}^{j2\pi \left(f_c+n{f}_m\right)t}\right\}$$

(20)

where

$$A_c=\sqrt{2P_{in}}\left\{(\left(1-r\right)+\frac{r}{2}.J_0\left(m\right).\left(e^{j\pi \gamma }+1\right)\right\},$$

$$A_{ln}=\sqrt{2P_{in}}.\frac{r}{2}.j^n.J_n\left(m\right).\left(e^{j\pi \gamma }+e^{-jn\theta }\right),\mathrm{and}$$

$$A_{un}=\sqrt{2P_{in}}.\frac{r}{2}.j^n.J_n\left(m\right).\left(e^{j\pi \gamma }+e^{jn\theta }\right).$$

The transfer function of the dispersive fiber link is given by [35]

$$H\left(f\right)=e^{\frac{j\pi DL{\lambda }_c^2{\left(f-f_c\right)}^2}{c}}$$

(21)

where D is the chromatic dispersion in ps/(nm.km). The ${\lambda }_c=c/f_c$ is the optical wavelength, f is the frequency offset of the optical carrier, c is the speed of light in a vacuum, and L is the fiber length. When E_TX(t) is transmitted through the fiber link, there is a phase difference between the optical carrier and the first-order sideband, $\varphi ,$ given by

$$\varphi =\frac{\pi DL{\lambda }_c^2{f}_m^2}{c}$$

(22)

while the phase difference between the optical carrier and any random sideband is the square of the frequency range $\left(\pm n{f}_m\right)$ given by [36]

$${\varphi }_n=n^2\varphi$$

(23)

Therefore, the optical field arriving at the receiver (E_RX(t)) can be expressed as

$$E_{RX}\left(t\right)=A_c{e}^{j2\pi f_{c}t}+{\displaystyle \sum }_{n=1}^{\infty }\left\{A_{ln}{e}^{j2\pi \left(f_c-n{f}_m\right)t}+A_{un}{e}^{j2\pi \left(f_c+n{f}_m\right)t}\right\}.e^{j{n}^2\varphi }$$

(24)

At the receiver, E_RX(t) is detected using a photodetector, which is a squared envelope operator, given by [2]

$${\left|E_{RX}\left(t\right)\right|}^2=E_{RX}\left(t\right).E_{RX}^{*}\left(t\right)$$

(25)

By simply taking the f_m term,

$$\begin{array}{c}{\left|E_{RX}\left(t\right)\right|}^2=e^{j2\pi f_{m}t}\left\{A_c{A}_{l1}^{*}{e}^{-j\varphi }+A_c^{*}{A}_{u1}{e}^{j\varphi }+A_{l1}{A}_{l2}^{*}{e}^{-j3\varphi }+A_{u1}^{*}{A}_{u2}{e}^{j3\varphi }+A_{l2}{A}_{l3}^{*}{e}^{-j5\varphi }+A_{u2}^{*}{A}_{u3}{e}^{j5\varphi }+\dots \right\}\hfill \\ =e^{j2\pi f_{m}t}\left\{{\displaystyle {\displaystyle \sum }_{n=0}^{\infty }}{A}_{ln}{A}_{l\left(n+1\right)}^{*}{e}^{-j\left(2n+1\right)\varphi }+A_{un}^{*}{A}_{u\left(n+1\right)}{e}^{j\left(2n+1\right)\varphi }\right\}\hfill \end{array}$$

(26)

is obtained, where A_l0 = A_u0 = A_c.

The photodetector output (X_rec(t)) electrical current is equivalent to the real part of Equation (26) [35]; therefore,

$$X_{rec}\left(t\right)\approx \left\{{\displaystyle \sum }_{n=0}^{\infty }{A}_{ln}{A}_{l\left(n+1\right)}^{*}{e}^{-j\left(2n+1\right)\varphi }+A_{un}^{*}{A}_{u\left(n+1\right)}{e}^{j\left(2n+1\right)\varphi }\right\}\cos 2\pi f_{m}t$$

(27)

The X_rec(t) power is the square of the amplitude term in Equation (27) [2], so that the recovered RF signal power as the L function, P_rec(L), is given by

$$P_{rec}\left(L\right)={\left\{{\displaystyle \sum }_{n=0}^{\infty }{A}_{ln}{A}_{l\left(n+1\right)}^{*}{e}^{-j\left(2n+1\right)\varphi }+A_{un}^{*}{A}_{u\left(n+1\right)}{e}^{j\left(2n+1\right)\varphi }\right\}}^2$$

(28)

where

$$\varphi =\frac{\pi DL{\lambda }_c^2{f}_m^2}{c},$$

$$A_{ln}^{*}=\sqrt{2P_{in}}.\frac{r}{2}.\left(-j^n\right).J_n\left(m\right).\left(e^{-j\pi \gamma }+e^{jn\theta }\right)\mathrm{and}$$

Equation (28) shows that the recovered RF signal is obtained by multiplying the nth order lower sideband with the (n + 1)th order conjugated lower sideband plus the multiplication of the nth order conjugated upper sideband with the (n + 1)th order upper sideband, where n is an integer. It can be seen from Equation (28) that P_rec(L) is dependent on γ and θ. The C/N penalty is obtained by comparing P_rec(L) with P_rec(L = 0) and is given by [2]

$$\frac{C}{N}penalty=10\log \left|\frac{P_{rec}\left(L\right)}{P_{rec}\left(L=0\right)}\right|$$

(29)

The DPF level in this paper is measured by using the DF given by [32]:

$$DF=\sqrt{{\displaystyle \sum }_{i=0}^N\frac{{\left(\frac{C}{N} penalt{y}_i - \overline{\frac{C}{N} penalty}\right)}^2}{N}}$$

(30)

where $\frac{C}{N} penalt{y}_i$ is the i-sample of the C/N penalty, $\overline{\frac{C}{N} penalty}$ is the average sample of the C/N penalty, and N is the number of samples. The lower the DF is, the smaller the effect of dispersion on P_rec(L) or the better the system performance.

3.1. C/N Penalty of RoF Link with ODSB Modulation

The calculation of the C/N penalty aims to observe the DPF on the RoF link that uses DD-MZM as the E/O converter with ODSB modulation. This is done because IM on the RoF link generally produces modulated optical signals with a double sideband spectrum. Based on Equation (14), DD-MZM will generate a modulated optical signal with a double sideband spectrum only if it is set with parameters γ = ½ and θ = 180°. The following steps are completed to calculate the C/N penalty of the RoF link with the modulated ODSB. This study focused on the effect of dispersion so that attenuation was eliminated. In addition, the attenuation at optical fiber is minimal.

(a)

Calculate P_rec(L) using Equation (28) with r = 1 (without CA), P_in = 1 mw (0 dBm), γ = ½, θ = 180°, m = 0.5, λ_c = 1550 nm (D = 17 ps/(nm.km)), and f_m = 60 GHz with L = 0, 0.1, 0.2, … 5 km.

(b)

From the obtained P_rec(L) in (a), calculate the C/N penalty using Equation (29).

(c)

Repeat steps (a) and (b) for m = 1, 1.5, 2, 2.5, 3, 3.5, and 4.

(d)

The result of the calculation is shown in Figure 3a,b.

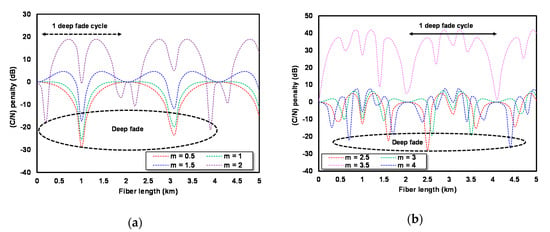Figure 3. C/N penalty of the RoF link with ODSB modulation for (a) m ≤ 2 and (b) m > 2.

The vertical axis in Figure 3 shows the C/N penalty in dB, whereas the horizontal axis depicts the fiber length in km. The C/N penalty of the RoF link curve with ODSB modulation at m ≤ 2 is shown in Figure 3a, while Figure 3b shows the C/N penalty at m > 2. Observed from the physical meaning side, the C/N value was influenced by constructive/destructive sideband interference. Therefore, the received power followed the cosine function, and it did not strictly increase/decrease. The RoF link with ODSB modulation at m = 0.5, 1, and 1.5 experiences deep fade (a massive power decline) at L = 1 and 3.1 km; at m = 2, deep fade occurs at L = 0.2 and 3.9 km. By using Equation (30), the DF value of the RoF link is obtained with ODSB modulation at m = 0.5, 1, 1.5 and 2 as much as 6.5, 5.5, 4.2 and 10.5, respectively. The RoF link at m = 2.5, 3, 3.5 and 4 undergoes deep fade at different L and has an irregular pattern. The DFs from the RoF link with ODSB modulation at m = 2.5, 3, 3.5 and 4 are 6.9, 5.5, 10.9, and 7.4, respectively. This shows that the level of the chromatic dispersion effect or the DPF value on the RoF link with ODSB modulation is very high.

It should be noted that several values of C/N have high positive values. This does not mean that the power of the signal was amplified. The C/N value is the ratio of the power of P_rec(L) with P_rec(L = 0). The C/N is positive when P_rec(L) is higher than P_rec(L = 0). This condition can be found when P_rec(L = 0) has low power due to destructive interference and P_rec(L) has high power due to constructive interference. Therefore, the C/N can be a positive or negative value.

This condition does not only apply to the irregular phase method but also to the ODSB (conventional) method. The value of θ will affect the spectrum shape of the optic signal. Moreover, the index modulation (m) will affect the value of n, and the value of n will affect the number of side bands. For instance, if we apply this equation to the ODSB (θ = 180°) system with parameter i.e., r = 1, P_in = 1 mw (0 dBm), γ = ½, θ = 180°, λ_c = 1550 nm (D = 17 ps/(nm.km)), and f_m = 60 GHz, as shown in Table 1,the value of $P_{rec}\left(L=0\right)$ is different for different values of m, and it was close to zero (very small). By this calculation, we use the different values of $P_{rec}\left(L=0\right)$. Therefore, the role of θ is clear for the irregular phase as well as for ODSB.

Table 1. Calculation of P_rec(L = 0) for ODSB modulation (θ = 180°).

Amplitude	Modulation Index (m)
	m = 0.1	m = 1	m = 2
Al3	0	0	0.0029 + 0.0029i
Al2	0	−0.0026−0.0026i	−0.0079−0.0079i
Al1	−0.0011−0.0011i	−0.0099−0.0099i	−0.013−0.013i
AC	0.0224 + 0.0224i	0.0172 + 0.0172i	0.005 + 0.005i
Au1	−0.0011−0.0011i	−0.0099−0.0099i	−0.013−0.013i
Au2	0	−0.0026−0.0026i	−0.0079−0.0079i
Au3	0	0	0.0029 + 0.009i
$P_{rec}\left(L=0\right)$ dBm	1.015 × 10−8	3.41 × 10−7	4.47 × 10−9

3.2. C/N Penalty of RoF Link with OSSB Modulation

One of the methods used to overcome DPF is OSSB modulation. Based on Equation (14), DD-MZM can generate OSSB modulation by setting the parameters γ = ½ and θ = 90°. The effectiveness of OSSB modulation in overcoming DPF can be seen through the C/N penalty curve of the link. The calculation of the C/N penalty of the RoF link with OSSB modulation can be completed using steps similar to ODSB modulation but using θ = 90°. The results of the calculation are shown in Figure 4a,b.

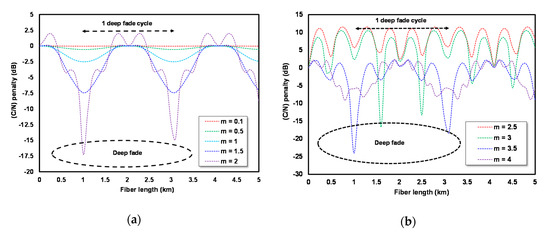
Figure 4. C/N penalty of the RoF link with OSSB modulation for (a) m ≤ 2 and (b) m > 2.

Figure 4a illustrates the curve of the C/N penalty of the RoF link with OSSB modulation at m ≤ 2. Figure 4b shows the curve of the C/N penalty at m > 2. There was no deep fade on the RoF link with OSSB modulation. There was almost no difference between the C/N penalty max and C/N penalty min (∆ C/N penalty) at m = 0.1 (only 0.029 dB). The ∆ C/N penalty at m = 0.5 is 0.560 dB, and it increased to 2.507 at m = 1. This shows that OSSB modulation could overcome DPF effectively at m = 0.1, and its effectiveness was reduced by increasing m.

A comparison of the value of the ∆ C/N penalty and DF between ODSB and OSSB modulation is shown in Table 2.

Table 2. Comparison value of the ∆ C/N Penalty and DF between the ODSB and OSSB Modulation.

m	ODSB Modulation		OSSB Modulation
	∆ C/N Penalty (dB)	DF	∆ C/N Penalty (dB)	DF
0.1	30.111	6.8	0.022	0.008
0.5	29.046	6.5	0.560	0.202
1	25.455	5.5	2.507	0.930
1.5	21.935	4.2	7.566	2.764
2	40.013	10.5	19.264	4.383
2.5	32.922	6.9	11.517	3.064
3	25.762	5.6	27.229	5.629
3.5	41.870	10.8	26.272	5.207
4	34.368	7.4	11.525	3.773

3.3. C/N Penalty of RoF Link with Irregular θ

The laser diode (LD) power distribution scheme in this paper is accomplished in 4 states, i.e.,

• The whole optical signal power of the LD output is used as the DD-MZM input (basic configuration),
• 75% of the optical signal power generated by LD is used as the DD-MZM input,
• 50% of the optical signal power generated by LD is used as the DD-MZM input, and
• 25% of the optical signal power generated by LD is used as the DD-MZM input,

While the bias point variation (γ) of DD-MZM is performed at 3 points, i.e., γ = ¼, ½, and ¾. Thus, all irregular θ schemes analyzed in this paper can be seen in detail in Table 3.

Table 3. Irregular θ scheme based on LD power distribution and variation in DD-MZM bias point.

Bias Point	Power Ratio of PDD-MZM/PIN
	4:4	3:4	2:4	1:4
¼	Scheme A1	A2	A3	A4
½	Scheme B1	B2	B3	B4
¾	Scheme C1	C2	C3	C4

3.3.1. Irregular θ Values for Scheme A1, A2, A3 and A4

Irregular θ is the value chosen from 0° to 360° so that the RoF link produces the smallest DF. Irregular θ values are different for different schemes. Irregular θ values for scheme A1 are sought with the following stages:

(a)

Calculate P_rec(L) using Equation (28) with r = 1 (4:4), γ = ¼, m = 0.1, θ = 0°, P_in = 1 mw (0 dBm), λ_c = 1550 nm (D = 17 ps/(nm.km)), and f_m = 60 GHz at L = 0, 0.1, 0.2, …, 5 km.

(b)

Calculate the C/N penalty from the calculation results (a) using Equation (29).

(c)

Calculate DF of all calculation results of (b) using Equation (30).

(d)

Repeat steps (a) to (c) for θ = 1°, 2°, 3°, …, 360°.

(e)

Find the θ value in step d), which produces the smallest DF (DF_min); this θ is called irregular θ.

(f)

Repeat steps (a) to (e) for m = 0.2, 0.3, …, 4.

(g)

The result of the calculation is shown in Figure 5a–d.

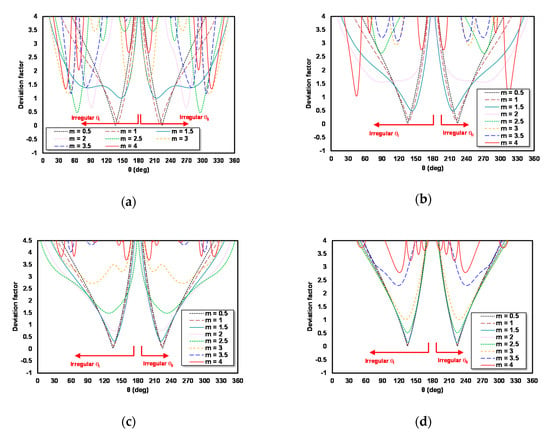Figure 5. Deviation factor as the θ function for (a) scheme A1; (b) A2, (c) A3; and (d) A4.

The examination result curve of irregular θ for scheme A1 is shown in Figure 5a. The irregular θ value on scheme A2 is searched by repeating steps (a) to (f) using r = ¾, r = ½ for scheme A3 and r = ¼ for scheme A4. The examination result curve of irregular θ for schemes A2, A3, and A4 can be seen in Figure 5b–d.

Figure 5 reveals that for each m used, there are two values of irregular θ: irregular θ I (θ_I) and irregular θ II (θ_II). The different m value and different schemes produce different irregular θ. The minimum DF for irregular θ I (θ_I) and irregular θ II (θ_II) is shown in Table 4.

Table 4. Irregular θ_I and θ_II for all schemes.

m	Scheme A1		Scheme A2		Scheme A3		Scheme A4
	θI (deg)	θII (deg)	θI (deg)	θII (deg)	θI (deg)	θII (deg)	θI (deg)	θII (deg)
0.5	136	224	136	224	135	225	135	225
1	141	219	139	221	137	223	136	224
1.5	147	213	144	216	138	222	136	224
2	91	269	88	272	138	222	136	224
2.5	64	296	89	271	128	232	135	225
3	47	313	116	244	98	262	132	228
3.5	53	307	117	243	60	300	119	241
4	43	317	45	315	160	200	121	239
m	Scheme B1		Scheme B2		Scheme B3		Scheme B4
	θI (deg)	θII (deg)	θI (deg)	θII (deg)	θI (deg)	θII (deg)	θI (deg)	θII (deg)
0.5	86	274	88	272	90	270	90	270
1	69	291	83	277	90	270	91	269
1.5	38	322	90	270	96	264	93	267
2	86	274	115	245	105	255	96	264
2.5	68	292	123	237	111	249	98	262
3	58	302	67	293	122	238	99	261
3.5	108	252	107	253	68	292	84	276
4	45	315	46	314	152	208	149	211
m	Scheme C1		Scheme C2		Scheme C3		Scheme C4
	θI (deg)	θII (deg)	θI (deg)	θII (deg)	θI (deg)	θII (deg)	θI (deg)	θII (deg)
0.5	39	321	315	45	47	313	46	314
1	26	334	50	310	53	307	48	312
1.5	12	348	86	274	64	296	51	309
2	71	289	103	257	77	283	55	305
2.5	154	206	103	257	83	277	58	302
3	156	204	123	237	78	282	65	295
3.5	103	257	102	258	69	291	69	291
4	101	259	101	259	89	271	78	282

The values of DF for each irregular θ at 0.1 ≤ m ≤ 4 of schemes A1, A2, A3 and A4 are depicted in Figure 6. The DF values of the RoF link with an irregular θ at m = 1 of schemes A1, A2, A3 and A4 are 0.089, 0.119, 0.113, and 0.070, respectively, which shows that at m = 1, irregular θ with scheme A4 and overcome DPF most effectively on the RoF link using DD-MZM with CA, which is biased at γ = ¼.

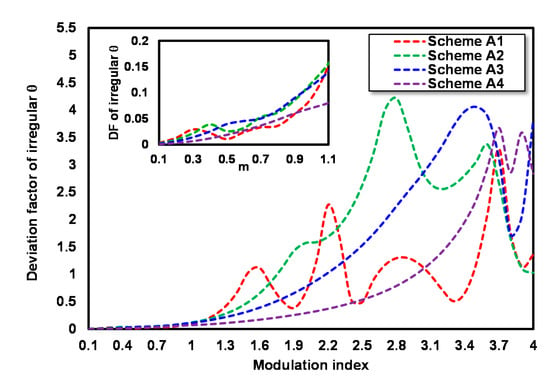
Figure 6. DF value for each irregular θ at 0.1 ≤ m ≤ 4 of scheme A1, A2, A3 and A4.

3.3.2. Irregular θ Values for Scheme B1, B2, B3 and B4

An irregular θ value for schemes B1, B2, B3 and B4 is attained by repeating the steps in finding irregular θ values for schemes A1, A2, A3 and A4 but using γ = ½. The curve of irregular θ searching results for schemes B1, B2, B3 and B4, respectively, can be seen in Figure 7a–d.

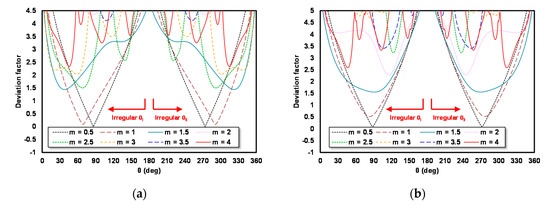
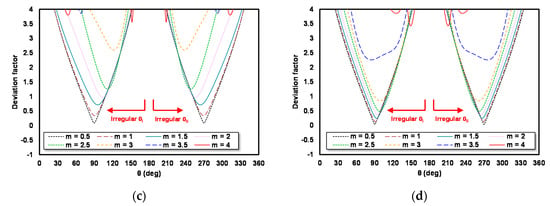
Figure 7. Deviation factor as the θ function for (a) scheme B1; (b) B2; (c) B3; and (d) B4.

Figure 7 reveals that for each m used, there are two values of irregular θ: irregular θ I (θ_I) and irregular θ II (θ_II). The different m value and different schemes produce different irregular θ. The minimum DF for irregular θ I (θ_I) and irregular θ II (θ_II) is shown in Table 4.

The DF values for each irregular θ at 0.1 ≤ m ≤ 4 of schemes B1, B2, B3 and B4 are illustrated in Figure 8. The DF values for the RoF link with an irregular θ at m = 1 for schemes B1, B2, B3 and B4 are 0.093, 0.524, 0.348, and 0.131, respectively, which shows that at m = 1, irregular θ with scheme B1 could overcome DPF most effectively on the RoF link that uses DD-MZM with CA that is biased at γ = ½.

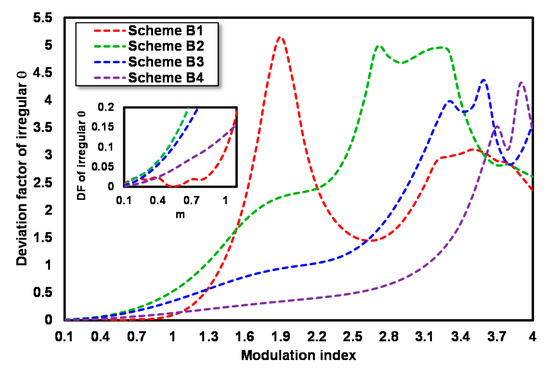
Figure 8. DF value for each irregular θ at 0.1 ≤ m ≤ 4 of schemes B1, B2, B3 and B4.

3.3.3. Irregular θ Values for Scheme C1, C2, C3 and C4

An irregular θ value for schemes C1, C2, C3 and C4 is obtained by repeating the steps in finding the irregular θ value for schemes A1, A2, A3 and A4 but using γ = ¾. The irregular θ search result curve for schemes C1, C2, C3 and C4 is shown in Figure 9a–d.

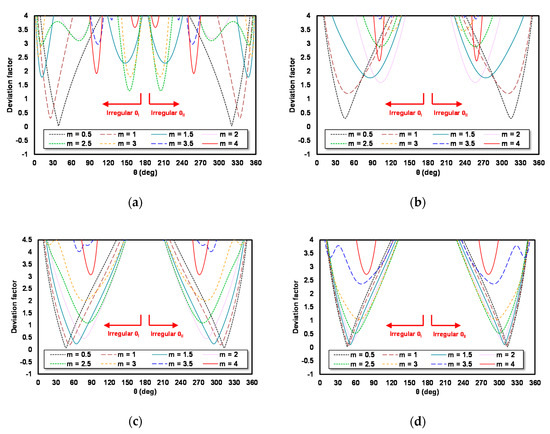
Figure 9. Deviation factor as the θ function for (a) scheme C1; (b) C2; (c) C3; and (d) C4.

Figure 9 shows that for each m used, there are two values of irregular θ: irregular θ I (θ_I) and irregular θ II (θ_II). The different m value and different schemes produce different irregular θ. The minimum DF for irregular θ I (θ_I) and irregular θ II (θ_II) is shown in Table 4.

The DF values for every irregular θ at 0.1 ≤ m ≤ 4 from schemes C1, C2, C3 and C4 are portrayed in Figure 10. The DF values of the RoF link with an irregular θ at m = 1 for schemes C1, C2, C3 and C4 are 0.304, 1.196, 0.194, and 0.030, respectively. It clarifies that at m = 1, irregular θ with scheme C4 is able to overcome DPF most effectively at the RoF link that uses DD-MZM with CA biased at γ = ¾.

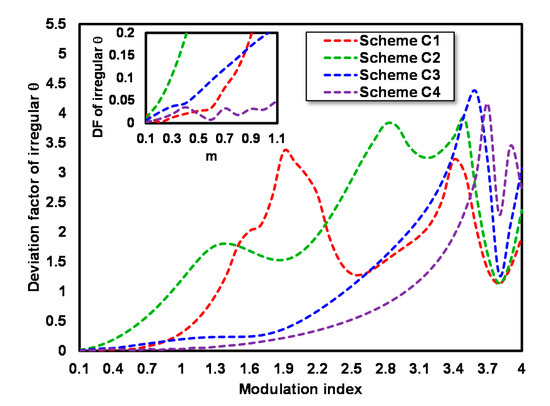
Figure 10. DF value for each irregular θ at 0.1 ≤ m ≤ 4 of schemes C1, C2, C3 and C4.

3.3.4. C/N Penalty of the RoF Link with an Irregular θ for All Schemes

The performance of irregular θ from all schemes in overcoming DPF can be observed through the DF value curve of irregular θ in all schemes, as depicted in Figure 11. The performance sequence of all schemes in overcoming DPF at m = 1 from the best to the worst is scheme C4, A4, A1, B1, A3, A2, B4, C3, C1, B3, B2 and C2. DF values of schemes C4, A4, A1, B1, A3, A2, B4, C3, C1, B3, B2 and C2 is 0.030, 0.070, 0.089, 0.093, 0.113, 0.119, 0.131, 0.197, 0.309, 0.348, 0.524, and 1.196 in order. This shows that only scheme C2 has worse performance than OSSB modulation.

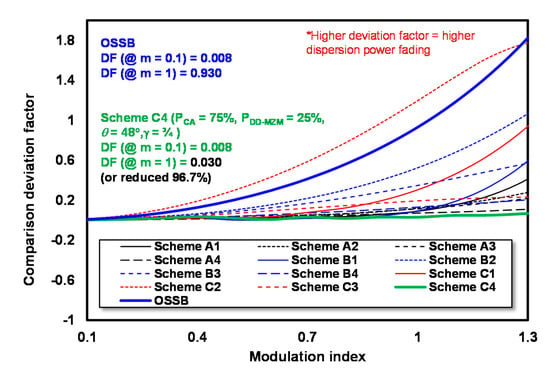
Figure 11. DF value of irregular θ for all schemes.

To observe the effectiveness of irregular θ of all schemes to overcome DPF, the C/N penalty is calculated for all schemes at m = 1. The calculation is performed with P_in = 1 mw (0 dBm), λ_c = 1550 nm (D = 17 ps/(nm.km)), and f_m = 60 GHz at L = 0, 0.1, 0.2, …, 5 km. For scheme C4, r = ¼ and γ = ¾ are used. θ_I for scheme C4 at m = 1 was 48°. For scheme A4, r = ¼ and γ = ¼ values are employed. θ_I for scheme A4 at m = 1 is 136°. r = 1 and γ = ¼ are used for scheme A1, and θ_I for scheme A1 at m = 1 is 141°. Furthermore, scheme B1 uses r = 1 and γ = ½ values. θ_I for scheme B1 at m = 1 is 69°. Next, scheme A3 uses r = ½ and γ = ¼ values. θ_I of scheme A3 at m = 1 s 137°. A2 uses r = ¾ and γ = ¼, and it is found that θ_I for the scheme at m = 1 is 139°. Scheme B4 uses r = ¼ and γ = ½. θ_I for scheme B4 at m = 1 is 91°. For scheme C3, the values r = ½ and γ = ¾ are used. θ_I for scheme C3 at m = 1 is 53°. Then, the values r = 1 and γ = ¾ are used for C1. θ_I for scheme C1 at m = 1 is 26°. For scheme B3, the values r = ½ and γ = ½ are used. θ_I for scheme B3 at m = 1 was 90°. Scheme B2 uses the values r = ¾ and γ = ½, and the θ_I at m = 1 is 83°. For scheme C2, the values r = ¾ and γ = ¾ are used. θ_I for scheme C2 at m = 1 is 50°. The calculation result of this C/N penalty is illustrated in Figure 12.

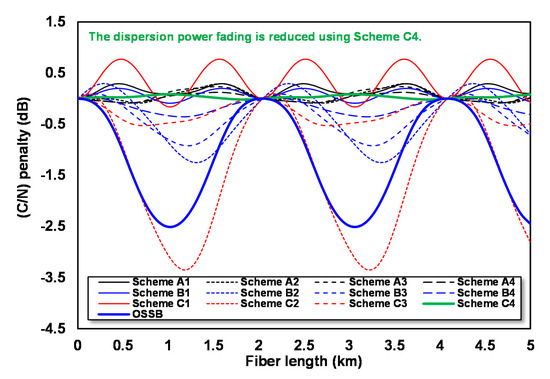
Figure 12. RoF links the C/N penalty with an irregular θ for all schemes at modulation index m = 1.

At m = 1, the power fluctuation that occurs on scheme C4 (a scheme with the smallest DF) is very small, where the difference between the maximum and minimum C/N penalties (∆ C/N penalty) is only 0.104 dB. The ∆ C/N penalty on scheme C2 (a scheme with the largest DF) reaches 3.444 dB.

4. Numerical Simulation

To evaluate the performance of irregular θ in overcoming DPF, a comparison of the C/N penalty curve from the RoF link with ODSB modulation, OSSB, scheme C4 (best performing scheme) irregular θ and scheme C2 (worst performing scheme) irregular θ is carried out using OptiSystem software. An evaluation is carried out at m = 1 with λ_c = 1550 nm (D = 17 ps/nm.km) and f_m = 60 GHz. This simulation circuit is shown in Figure 13, and the parameter setting of LiNb-MZM is shown in Table 5.

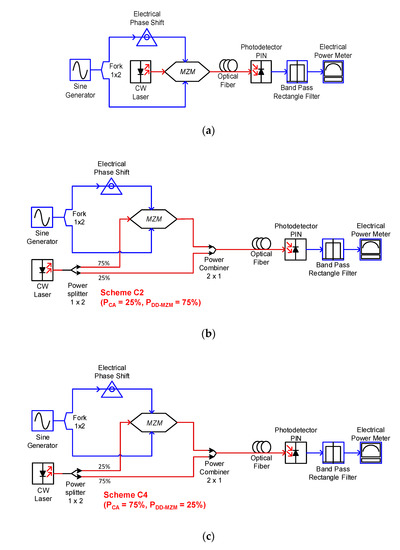
Figure 13. OptiSystem simulation system to validate irregular θ performance in overcoming DPF, (a) RoF link with ODSB and OSSB modulations; (b) RoF system with an irregular θ for scheme C2; and (c) scheme C4.

Table 5. Setting parameter of LiNb-MZM.

Parameter	Value	Units
Extinction ratio	60	dB
Switching bias voltage	4	V
Switching RF voltage	4	V
Insertion loss	0	dB
Normalize electrical signal	Unchecked	-
Bias voltage1	0	V
Bias voltage2	2	V

Figure 13a is a simulation system used to measure the C/N penalty of the RoF link with ODSB and OSSB modulation. The circuit consists of a sine generator, fork 1 × 2, electrical phase shift, continuous wave (CW) laser, MZM, optical fiber, photodetector PIN, bandpass rectangle filter and electrical power meter. The sine generator functions to generate the pure RF signal. The frequency of the sine generator is set to 60 GHz. Because the switching voltage V_π used in the simulation is 4 V, the sine generator voltage V_m is regulated at 1.274 V to obtain m = 1. The sine generator output is then duplicated using fork 1 × 2. The first fork output is forwarded to the EPS and is used as an input of the MZM upper arm. The second fork output is directly used as the input of the MZM lower arm. EPS is used to shift the RF signal phase by θ. To generate ODSB modulation, the phase shift value of EPS is regulated at 180 deg and 90 deg to produce OSSB modulation. The type MZM used is LiNb-MZM. The MZM is set with parameters as depicted in Table 2. The MZM optical input is obtained from the CW laser. The frequency of the CW laser is set to 1550 nm, the power is set at 0 dBm, and the linewidth is set to 10 MHz. The output of the MZM is therefore transmitted through a single-mode optical fiber. The optical fiber is thus configured using the parameters shown in Table 6.

Table 6. Setting parameter of Optical Fiber.

Parameter	Value	Units
User defined reference wavelength	Checked	-
Reference wavelength	1550	nm
Length	0–5	km
Attenuation effect	Unchecked	-
Group velocity dispersion	Checked	-
Third-order dispersion	Unchecked	-
Frequency domain parameter	Unchecked	-
Dispersion	17	ps/nm/km

In this simulation, the fiber attenuation effect is ignored. At the receiver, the optical signal is detected using photodetector PIN under the parameter of responsivity = 1 A/W and dark current = 10 nA. Because the output of the photodetector consists of an electrical signal with frequencies of 0, 60, 120 GHz, etc., it is filtered by means of a bandpass rectangle filter. To obtain an RF signal at 60 GHz, the parameter filter is used with a frequency of 60 GHz, bandwidth of 10 MHz, insertion loss of 0 dB and depth of 100 dB. The power of the recovered RF signal is measured using an electrical power meter. The power measurement is performed for fiber lengths of 0 to 5 km with a step of 0.1 km. The power value in the simulation is gauged in dBm. The C/N penalty value from the simulation result is obtained by subtracting P_rec(L) at length L from P_rec(L) at length 0.

Figure 13b is a circuit of simulations to measure the C/N penalty of the RoF link with an irregular θ on scheme C4. The components used in this circuit are approximately similar to the simulation circuit used to measure the C/N penalty of the RoF link with ODSB and OSSB modulations. Given that the DD-MZM optical input on scheme C4 is only 25% of the LD total power, the LD power in this circuit is first divided into 4 parts using a 1 × 4 optical splitter (OS). Therefore, 1 OS output is used as the MZM optical input, and 3 OS outputs are combined using the 3 × 1 optical combiner (OC). The output of 3 × 1 OC is then recombined with the output of MZM by means of 2 × 1 OC. For scheme C4, the bias voltage 2 of DD-MZM is regulated at 3 volts, and the value of the phase shift of EPS is set at 48°. The power measurement in this simulation is identical to the measurement on links with ODSB and OSSB modulations.

Figure 13c illustrates a simulation circuit to measure the C/N penalty of the RoF link with an irregular θ for scheme C4. The components used in this circuit are no different from the simulation circuit employed for measuring the C/N penalty of the RoF link with an irregular θ for scheme C2. However, this simulation uses MZM optical input by 25% from the LD total power; hence, MZM is given an input of 3 × 1 OC output. An OS output is then recombined with the output of MZM using 2 × 1 OC. For scheme C2, bias voltage 2 of MZM is also set at 3 V. The comparison result between the mathematical model and simulation model has very good agreement, which shows the validity of the proposed method, as shown in Figure 14.

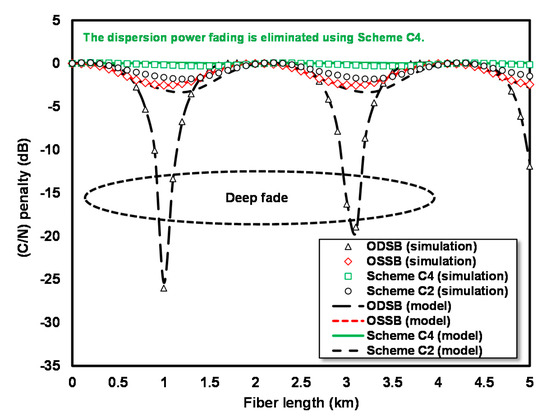
Figure 14. C/N penalty for the RoF link with ODSB and OSSB modulations, scheme C4 irregular θ and scheme C2 irregular θ at m = 1.

The C/N penalty of the RoF is linked with ODSB modulation, and both the calculation result and simulation show a deep fade at L = 1 and 3.1 km. However, deep fade does not occur in the C/N penalty of the RoF link with OSSB modulation, although there is still a ∆ C/N penalty of 2.5 dB. The ∆ C/N penalty in the C/N penalty of the RoF link curve with an irregular θ for scheme C4 was very small.

5. Conclusions

The dispersion power fading in RoF communication is successfully reduced using an asymmetric carrier divider with an irregular RF phase on the DD-MZ modulator. The minimum DF is obtained when the P_IN is separated as 75% for P_CA and 25% for P_DD-MZM with an irregular RF signal of θ = 48° and bias point value of γ = ¾. As the result, with the same power as OSSB, this proposed structure produces DF at m = 0.1 and m = 1 value are 0.008 and 0.03, or it can decrease the DF of 96.7% at m = 1. The mathematical model and simulation model have very good agreement, which validates the proposed method. The proposed scheme is more suitable for external modulation. It can be applied for applications such as supporting 5G communications or supporting IEEE 802.11 wireless network. It should be noted that the limitation at the implementation, such as the use of single-mode fiber optics, power splitter, power combiner, and polarization controller to make the polarization is constant. There are several suggestions for future research. First, the validation can be improved in future studies through measurements. Moreover, information signal analysis and bit error rate (BER) calculations can be potentially included. Lastly, iterations on power divider can be made more detailed and general.