Properties of Bilayer Graphene Quantum Dots for Integrated Optics: An Ab Initio Study
Abstract
1. Introduction
2. Computational Methods
3. Results and Discussion
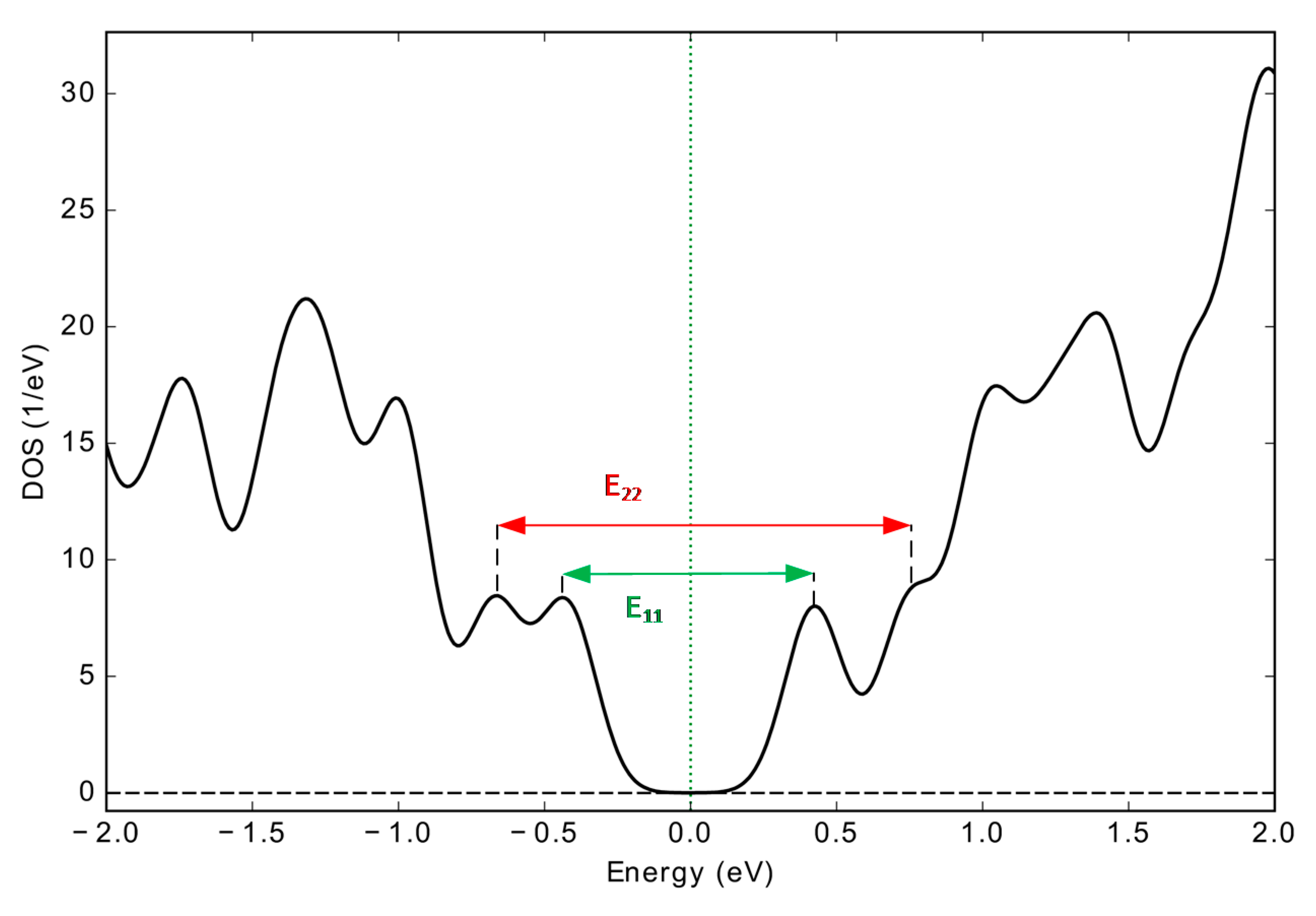
3.1. Electronic Properties
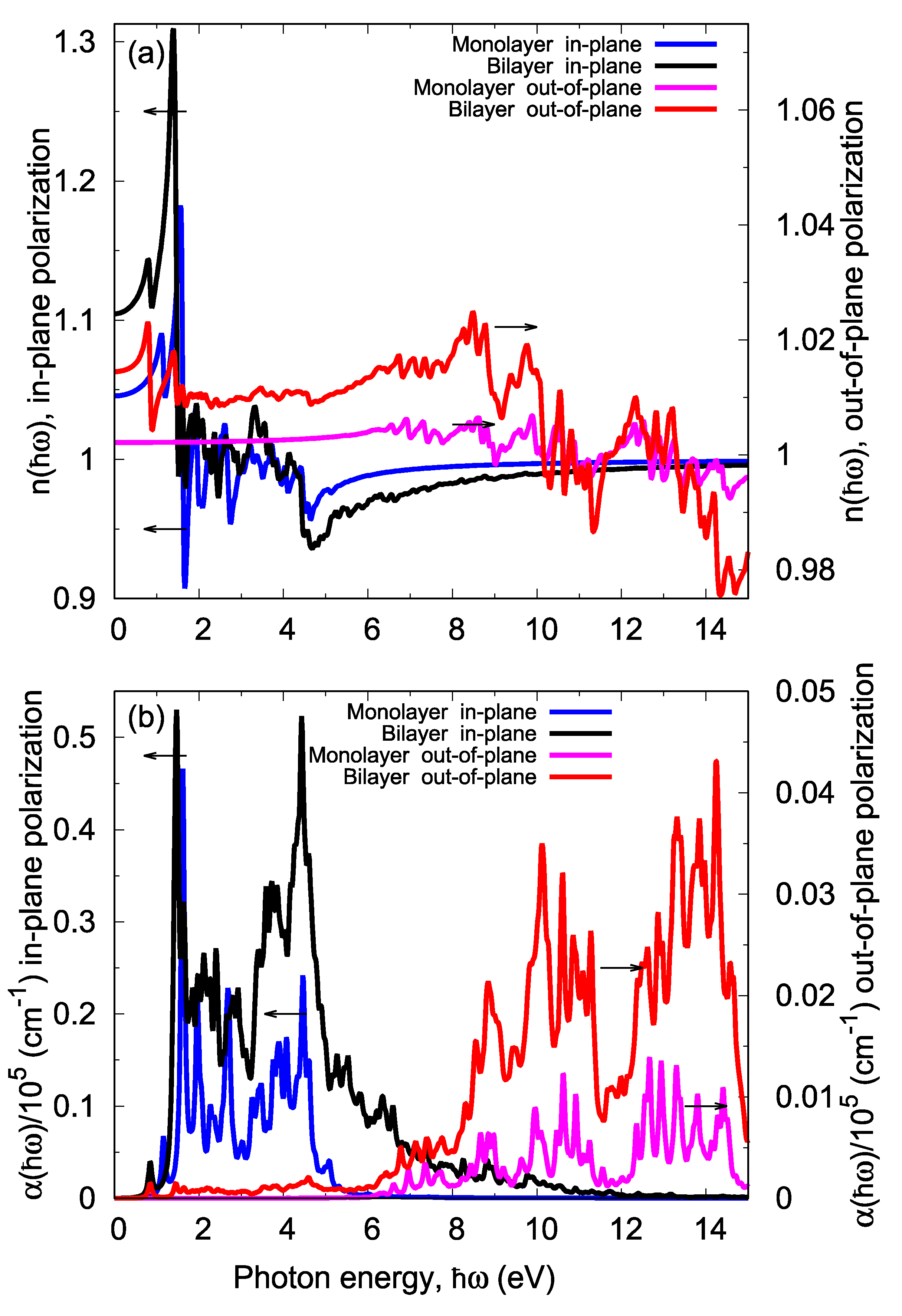
3.2. Optical Properties
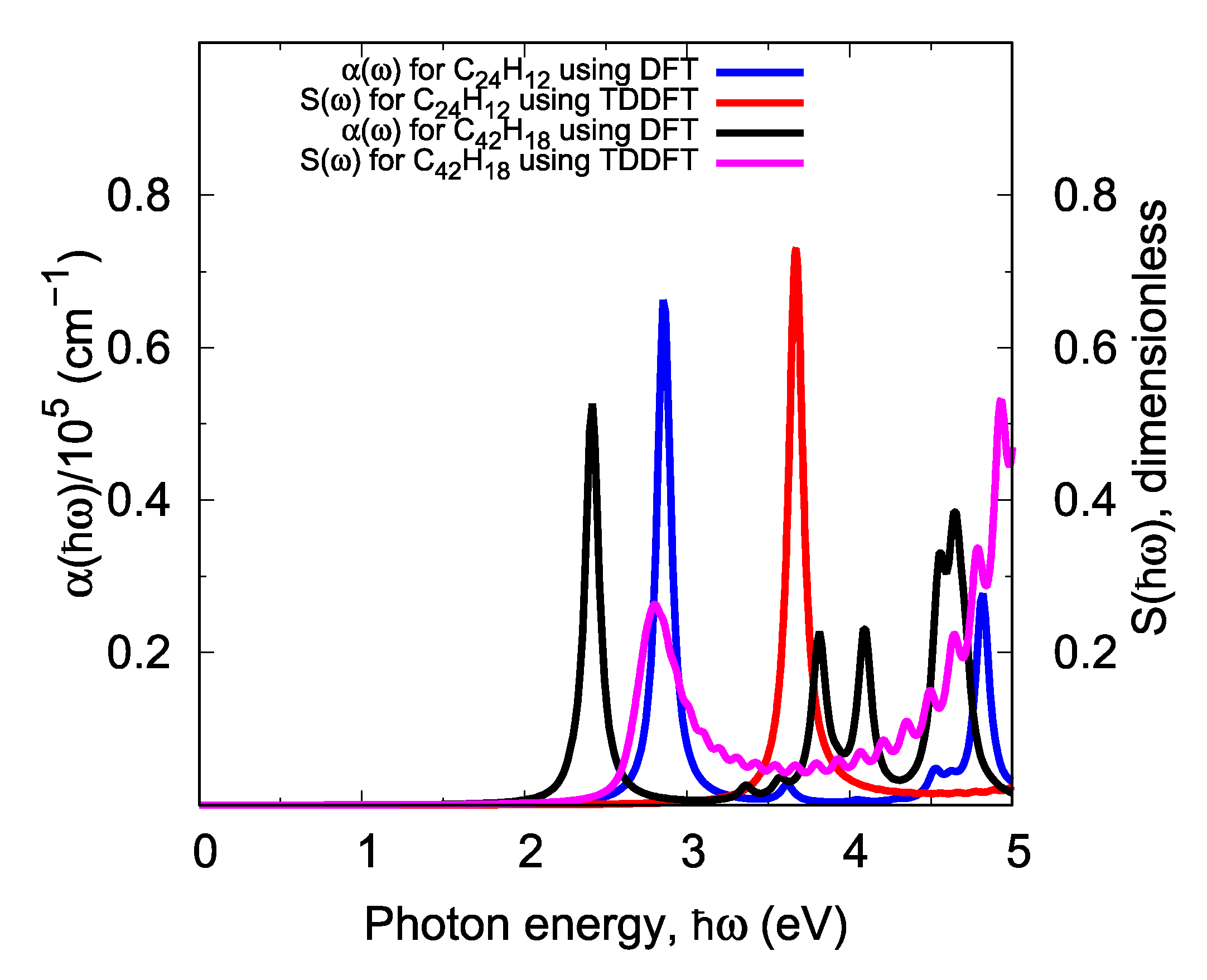
3.3. DFT vs. TDDFT for Calculating Optical Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Dragoman, M.; Dinescu, A.; Dragoman, D. 2D Materials Nanoelectronics: New Concepts, Fabrication, Characterization From Microwaves up to Optical Spectrum. Phys. Status Solidi A 2019, 216, 1800724. [Google Scholar] [CrossRef]
- Marinopoulos, A.G.; Reining, L.; Rubio, A.; Olevano, V. Ab initio study of the optical absorption and wave-vector-dependent dielectric response of graphite. Phys. Rev. B 2004, 69, 245419. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres NM, R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef]
- Mak, K.F.; Sfeir, M.Y.; Wu, Y.; Lui, C.H.; Misewich, J.A.; Heinz, T.F. Measurement of the Optical Conductivity of Graphene. Phys. Rev. Lett. 2008, 101, 196405. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Zhang, Y.; Tian, C.; Girit, C.; Zettl, A.; Crommie, M.; Shen, Y.R. Gate-Variable Optical Transitions in Graphene. Science 2008, 320, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Marini, A.; Cox, J.D.; García de Abajo, F.J. Theory of graphene saturable absorption. Phys. Rev. B 2017, 95, 125408. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, J.; Wang, J.; Huo, S.; Zhang, B.; Tang, Y. Microwave absorption properties of lightweight absorber based on Fe50Ni50-coated poly(acrylonitrile) microspheres and reduced graphene oxide composites. J. Magn. Magn. Mater. 2016, 413, 81–88. [Google Scholar] [CrossRef]
- Li, H.; Anugrah, Y.; Koester, S.J.; Li, M. Optical absorption in graphene integrated on silicon waveguides. Appl. Phys. Lett. 2012, 101, 111110. [Google Scholar] [CrossRef]
- Sedelnikova, O.V.; Bulusheva, L.G.; Okotrub, A.V. Ab initio study of dielectric response of rippled graphene. J. Chem. Phys. 2011, 134, 244707. [Google Scholar] [CrossRef]
- Sedelnikova, O.V.; Stolyarova, S.G.; Chuvilin, A.L.; Okotrub, A.V.; Bulusheva, L.G. Holey graphene with enhanced near-infrared absorption: Experimental and DFT study. Appl. Phys. Lett. 2019, 114, 091901. [Google Scholar] [CrossRef]
- Son, Y.-W.; Cohen, M.L.; Louie, S.G. Energy Gaps in Graphene Nanoribbons. Phys. Rev. Lett. 2006, 97, 216803–216811. [Google Scholar] [CrossRef] [PubMed]
- Ponomarenko, L.A.; Schedin, F.; Katsnelson, M.I.; Yang, R.; Hill, E.W.; Novoselov, K.S.; Geim, A.K. Chaotic Dirac Billiard in Graphene Quantum Dots. Science 2008, 320, 356. [Google Scholar] [CrossRef] [PubMed]
- Bhatnagar, D.; Singh, S.; Yadav, S.; Kumar, A.; Kaur, I. Experimental and theoretical investigation of relative optical band gaps in graphene generations. Mater. Res. Express 2017, 4, 015101. [Google Scholar] [CrossRef]
- Dreyer, D.R.; Park, S.; Bielawski, C.W.; Ruoff, R.S. The chemistry of graphene oxide. Chem. Soc. Rev. 2010, 39, 228–240. [Google Scholar] [CrossRef]
- Eda, G.; Lin, Y.-Y.; Mattevi, C.; Yamaguchi, H.; Chen, H.-A.; Chen, I.-S.; Chen, C.-W.; Chhowalla, M. Blue Photoluminescence from Chemically Derived Graphene Oxide. Adv. Mater. 2010, 22, 505–509. [Google Scholar] [CrossRef]
- Hunt, A.; Kurmaev, E.Z.; Moewes, A. Band gap engineering of graphene oxide by chemical modification. Carbon 2014, 75, 366–371. [Google Scholar] [CrossRef]
- Loh, K.P.; Bao, Q.; Eda, G.; Chhowalla, M. Graphene oxide as a chemically tunable platform for optical applications. Nat. Chem. 2010, 2, 1015–1024. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Chang, K.; Peeters, F.M. Tuning of energy levels and optical properties of graphene quantum dots. Phys. Rev. B 2008, 77, 235411. [Google Scholar] [CrossRef]
- Grujić, M.; Zarenia, M.; Chaves, A.; Tadić, M.; Farias, G.A.; Peeters, F.M. Electronic and optical properties of a circular graphene quantum dot in a magnetic field: Influence of the boundary conditions. Phys. Rev. B 2011, 84, 205441. [Google Scholar] [CrossRef]
- Li, Y.; Shu, H.; Wang, S.; Wang, J. Electronic and Optical Properties of Graphene Quantum Dots: The Role of Many-Body Effects. J. Phys. Chem. C 2015, 119, 4983–4989. [Google Scholar] [CrossRef]
- Zhao, M.; Yang, F.; Xue, Y.; Xiao, D.; Guo, Y. A Time-Dependent DFT Study of the Absorption and Fluorescence Properties of Graphene Quantum Dots. ChemPhysChem 2014, 15, 950–957. [Google Scholar] [CrossRef]
- Riesen, H.; Wiebeler, C.; Schumacher, S. Optical Spectroscopy of Graphene Quantum Dots: The Case of C132. J. Phys. Chem. A 2014, 118, 5189–5195. [Google Scholar] [CrossRef] [PubMed]
- Wettstein, C.M.; Bonafé, F.P.; Oviedo, M.B.; Sánchez, C.G. Optical properties of graphene nanoflakes: Shape matters. J. Chem. Phys. 2016, 144, 224305. [Google Scholar] [CrossRef] [PubMed]
- Dai, Y.; Li, Z.; Yang, J. A Density Functional Study of the Nonlinear Optical Properties of Edge-Functionalized Nonplanar Nanographenes. ChemPhysChem 2015, 16, 2783–2788. [Google Scholar] [CrossRef] [PubMed]
- Ozfidan, I.; Güçlü, A.D.; Korkusinski, M.; Hawrylak, P. Theory of optical properties of graphene quantum dots. Phys. Status Solidi RRL 2016, 10, 102–110. [Google Scholar] [CrossRef]
- Sun, C.; Figge, F.; Ozfidan, I.; Korkusinski, M.; Yan, X.; Li, L.-S.; Hawrylak, P.; McGuire, J.A. Biexciton Binding of Dirac fermions Confined in Colloidal Graphene Quantum Dots. Nano Lett. 2015, 15, 5472–5476. [Google Scholar] [CrossRef]
- Mokkath, J.H. Optical response tuning in graphene nanoflakes: A computational study. Chem. Phys. Lett. 2018, 692, 102–105. [Google Scholar] [CrossRef]
- Yamijala, S.S.; Mukhopadhyay, M.; Pati, S.K. Linear and Nonlinear Optical Properties of Graphene Quantum Dots: A Computational Study. J. Phys. Chem. C 2015, 119, 12079–12087. [Google Scholar] [CrossRef]
- Zhang, Y.; Sheng, W.; Li, Y. Dark excitons and tunable optical gap in graphene nanodots. Phys. Chem. Chem. Phys. 2017, 19, 23131–23137. [Google Scholar] [CrossRef]
- Ozfidan, I.; Korkusinski, M.; Güçlü, A.D.; McGuire, J.A.; Hawrylak, P. Microscopic theory of the optical properties of colloidal graphene quantum dots. Phys. Rev. B 2014, 89, 085310. [Google Scholar] [CrossRef]
- Trickey, S.B.; Müller-Plathe, F.; Diercksen, G.H.F.; Boettger, J.C. Interplanar binding and lattice relaxation in a graphite dilayer. Phys. Rev. B 1992, 45, 4460–4468. [Google Scholar] [CrossRef]
- Lam, K.-T.; Liang, G. An ab initio study on energy gap of bilayer graphene nanoribbons with armchair edges. Appl. Phys. Lett. 2008, 92, 223106. [Google Scholar] [CrossRef]
- Kuzmenko, A.B.; Crassee, I.; van der Marel, D.; Blake, P.; Novoselov, K.S. Determination of the gate-tunable band gap and tight-binding parameters in bilayer graphene using infrared spectroscopy. Phys. Rev. B 2009, 80, 165406. [Google Scholar] [CrossRef]
- da Costa, D.R.; Zarenia, M.; Chaves, A.; Farias, G.A.; Peeters, F.M. Energy levels of bilayer graphene quantum dots. Phys. Rev. B 2015, 92, 115437. [Google Scholar] [CrossRef]
- Tiutiunnyk, A.; Duque, C.A.; Caro-Lopera, F.J.; Mora-Ramos, M.E.; Correa, J.D. Opto-electronic properties of twisted bilayer graphene quantum dots. Physica E 2019, 112, 36–48. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502–395514. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901–465917. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Hamann, D.R. Generalized norm-conserving pseudopotentials. Phys. Rev. B 1989, 40, 2980–2987. [Google Scholar] [CrossRef]
- Hamann, D.R.; Schlüter, M.; Chiang, C. Norm-Conserving Pseudopotentials. Phys. Rev. Lett. 1979, 43, 1494–1497. [Google Scholar] [CrossRef]
- Dal Corso, A.; Baroni, S.; Resta, R.; de Gironcoli, S. Ab initio calculation of phonon dispersions in II-VI semiconductors. Phys. Rev. B 1993, 47, 3588–3592. [Google Scholar] [CrossRef] [PubMed]
- Mandal, B.; Sarkar, S.; Sarkar, P. Exploring the electronic structure of graphene quantum dots. J. Nanopart. Res. 2012, 14, 1317. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Taylor, J.; Guo, H.; Wang, J. Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 2001, 63, 24540701–24540713. [Google Scholar] [CrossRef]
- Smith, J.C.; Sagredo, F.; Burke, K. Warming Up Density Functional Theory. In Frontiers of Quantum Chemistry; Wójcik, M.J., Nakatsuji, H., Kirtman, B., Ozaki, Y., Eds.; Springer: Singapore, 2018; pp. 249–271. [Google Scholar]
- Adler, S.L. Quantum Theory of the Dielectric Constant in Real Solids. Phys. Rev. 1962, 126, 413–420. [Google Scholar] [CrossRef]
- Aspnes, D.E.; Studna, A.A. Dielectric functions and optical parameters of Si, Ge, GaP, GaAs, GaSb, InP, InAs, and InSb from 1.5 to 6.0 eV. Phys. Rev. B 1983, 27, 985–1009. [Google Scholar] [CrossRef]
- Wooten, F. Optical Properties of Solids; Academic Press: New York, NY, USA, 1972; pp. 173–185. [Google Scholar]
- Ehrenreich, H.; Cohen, M.H. Self-Consistent Field Approach to the Many-Electron Problem. Phys. Rev. 1959, 115, 786–790. [Google Scholar] [CrossRef]
- Alouani, M.; Wills, J.M. Calculated optical properties of Si, Ge, and GaAs under hydrostatic pressure. Phys. Rev. B 1996, 54, 2480–2490. [Google Scholar] [CrossRef]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- O’Boyle, N.M. Book Review of Gnuplot in Action. J. Chem. Inf. Model 2008, 48, 2095. [Google Scholar] [CrossRef]
- Ozfidan, I.; Korkusinski, M.; Hawrylak, P. Electronic properties and electron–electron interactions in graphene quantum dots. Phys. Status Solidi RRL Rapid Res. Lett. 2016, 10, 13–23. [Google Scholar] [CrossRef]
- Potasz, P.; Güçlü, A.D.; Wójs, A.; Hawrylak, P. Electronic properties of gated triangular graphene quantum dots: Magnetism, correlations, and geometrical effects. Phys. Rev. B 2012, 85, 075431. [Google Scholar] [CrossRef]
- Malcıoğlu, O.B.; Gebauer, R.; Rocca, D.; Baroni, S. turboTDDFT—A code for the simulation of molecular spectra using the Liouville–Lanczos approach to time-dependent density-functional perturbation theory. Comput. Phys. Commun. 2011, 182, 1744–1754. [Google Scholar] [CrossRef]
- Ge, X.; Binnie, S.J.; Rocca, D.; Gebauer, R.; Baroni, S. turboTDDFT 2.0—Hybrid functionals and new algorithms within time-dependent density-functional perturbation theory. Comput. Phys. Commun. 2014, 185, 2080–2089. [Google Scholar] [CrossRef]
- Rocca, D.; Gebauer, R.; Saad, Y.; Baroni, S. Turbo charging time-dependent density-functional theory with Lanczos chains. J. Chem. Phys. 2008, 128, 154105. [Google Scholar] [CrossRef]
- Ghazaryan, A.V.; Djotyan, A.P.; Moulopoulos, K.; Kirakosyan, A.A. Linear dynamic polarizability and the absorption spectrum of an exciton in a quantum ring in a magnetic field. Phys. Scr. 2011, 83, 035703. [Google Scholar] [CrossRef]
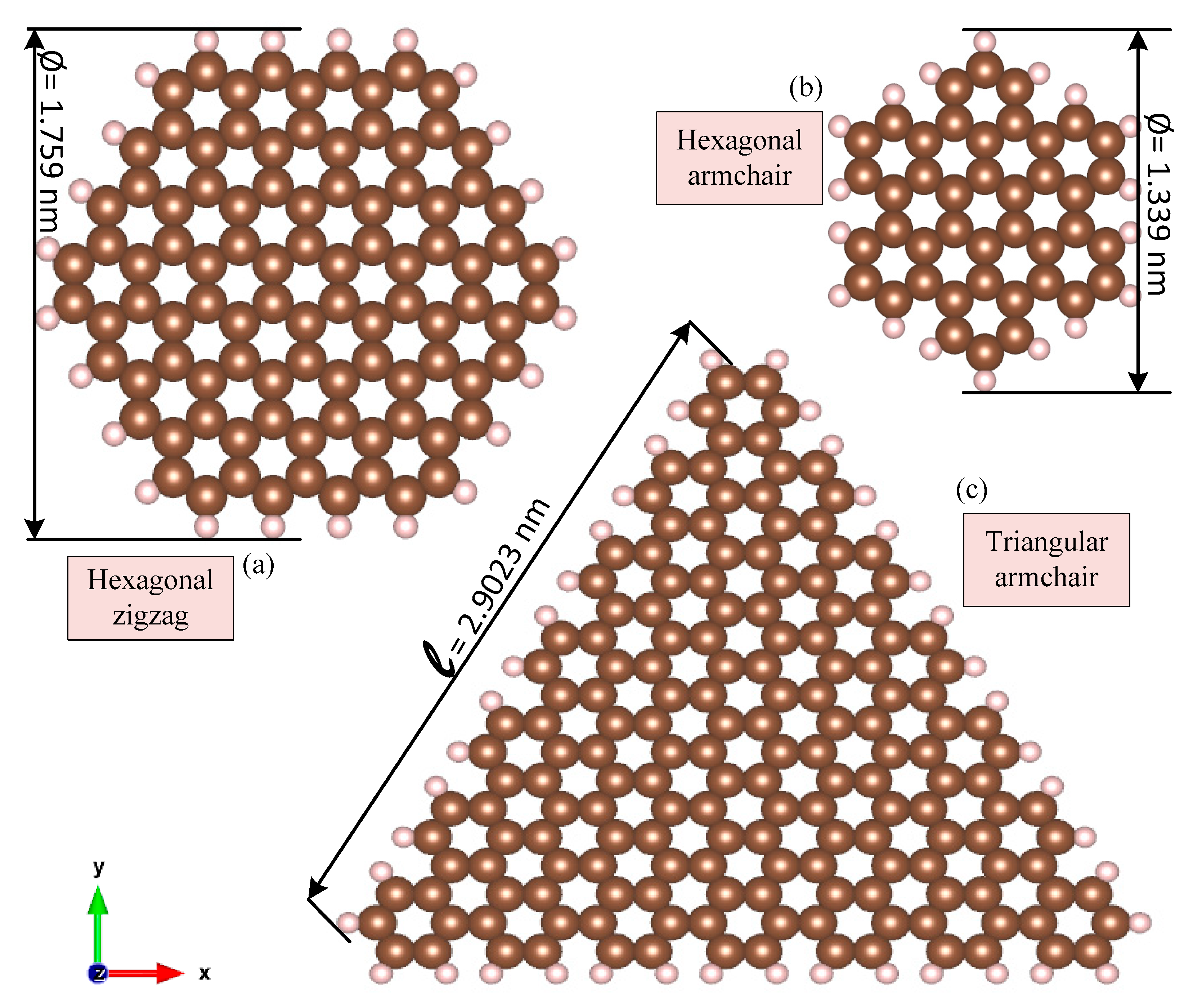
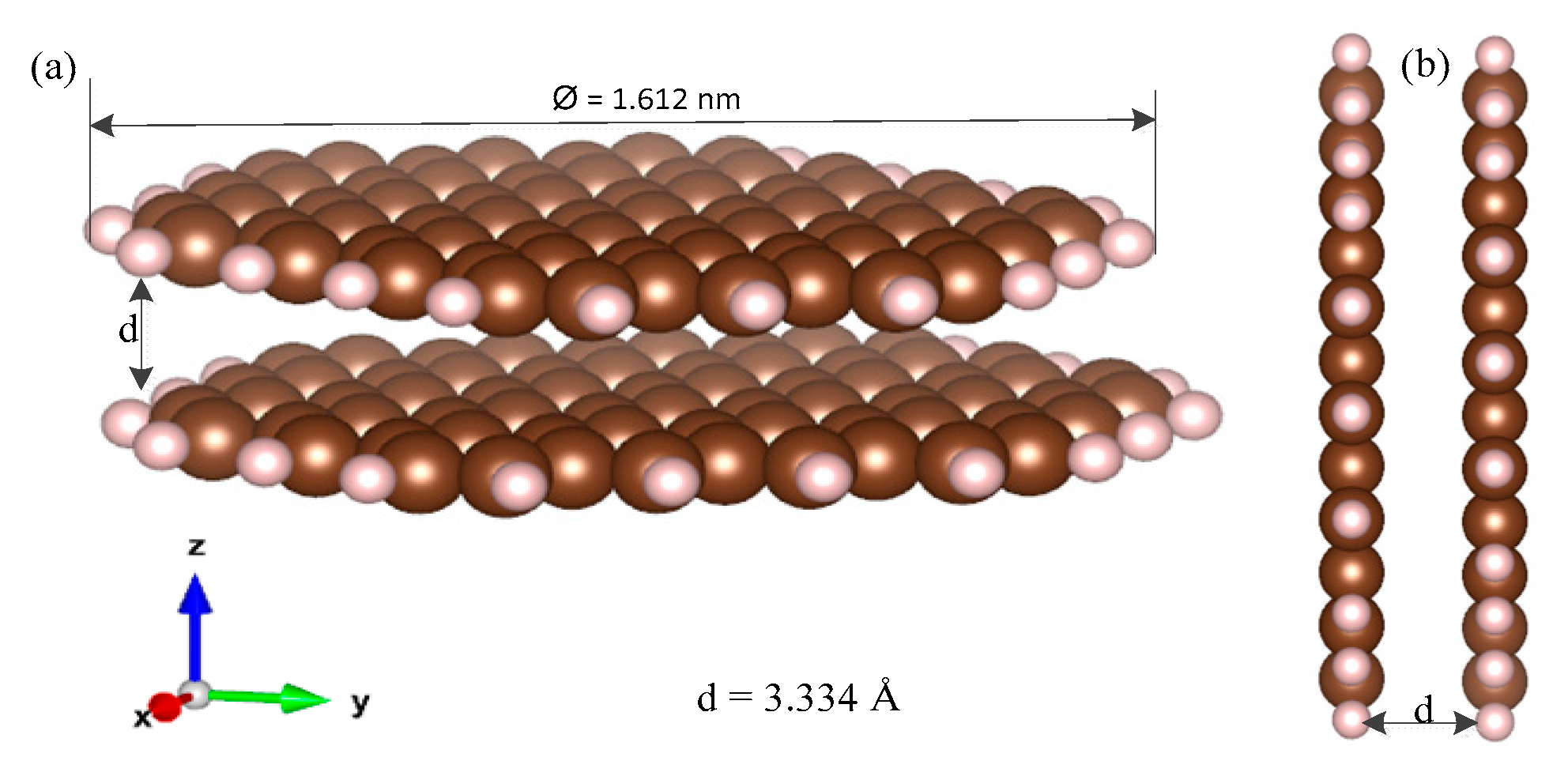

| System | Size (Å) | Layering | Atoms per Layer | Total Energy (Ry) | Bandgap (eV) | ||
|---|---|---|---|---|---|---|---|
| Standard DFT | Thermal DFT @ T = 300 K | Standard DFT | Thermal DFT @ T = 300 K | ||||
| Graphene | Sheet | Mono | Periodic | −2.265 × 101 | −2.224 × 101 | Semi-metal | |
| HexC24zzH12 | 9.51 | Mono | 36 | −2.871 × 102 | −2.871 × 102 | 2.852 | 2.845 |
| HexC42acH18 | 13.39 | Mono | 60 | −4.990 × 102 | −4.980 × 102 | 2.300 | 2.328 |
| TriC60acH24 | 17.59 | Mono | 84 | −7.109 × 102 | −7.108 × 102 | 2.174 | 2.174 |
| HexC96zzH24 | 19.04 | Mono | 120 | −1.121 × 103 | −1.121 × 103 | 1.290 | 1.275 |
| TriC168acH42 | 30.19 | Mono | 210 | −1.962 × 103 | −1.962 × 103 | 1.378 | 1.373 |
| Bilayer graphene | Sheet | Double | Periodic | −4.524 × 101 | −4.450 × 101 | Semi-metal | |
| ABhexC132zzH40 | 17.083 | Double | 86 | −1.550 × 103 | −1.549 × 103 | 0.844 | 0.855 |
| ABhexC78zzH34 | 14.709 | Double | 56 | −9.273 × 102 | −9.273 × 102 | 2.081 | 2.083 |
| ABhexC38zzH22 | 10.624 | Double | 30 | −4.579 × 102 | −4.580 × 102 | 3.063 | 3.077 |
| Bandgap (eV) | |||||||
|---|---|---|---|---|---|---|---|
| System | Shape | Edge | This work | Ref-a [29] | Ref-b [30] | Ref-c [55] | Ref-d [21] |
| C24H12 | Hexagonal | zig-zag | 2.852 | 2.850 | 2.90 | ||
| C42H18 | Hexagonal | arm-chair | 2.300 | 2.482 | 2.346 | 2.47 | |
| C60H24 | Triangle | arm-chair | 2.174 | 2.202 | 2.230 | ||
| C96H24 | Hexagonal | zig-zag | 1.290 | 1.310 | 1.147 | 1.36 | |
| C168H42 | Triangle | arm-chair | 1.378 | 1.239 | |||
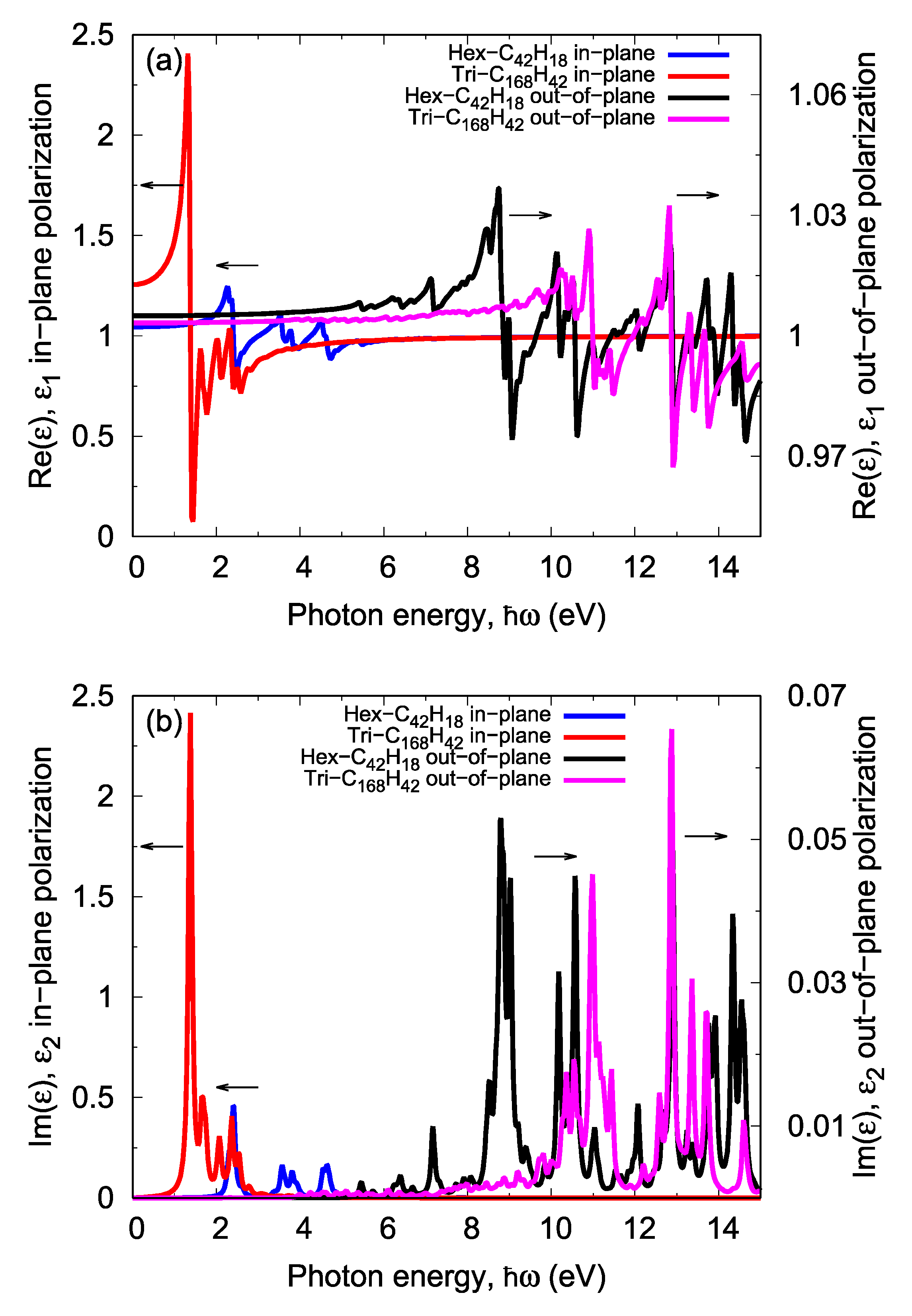
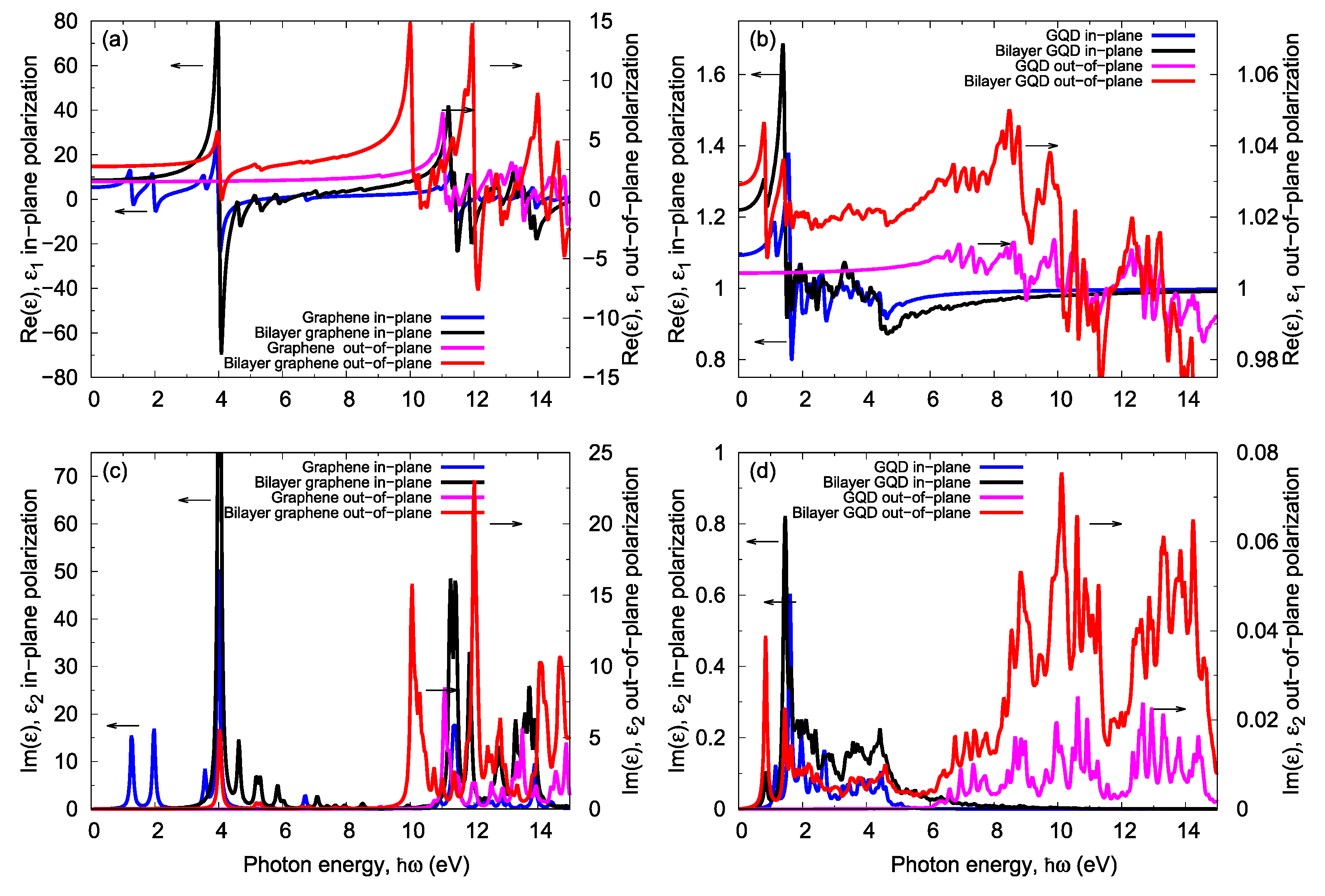
| System | Layering | Photon Energy (eV) | |||
|---|---|---|---|---|---|
| In-Plane Polarization | Out-of-Plane Polarization | ||||
| 1st Peak | 2nd Peak | 1st Peak | 2nd Peak | ||
| Graphene | Mono | 0.000 | 0.000 | 11.081 | 11.952 |
| HexC24zzH12 | Mono | 2.929 | 3.619 | 6.817 | 7.478 |
| HexC42acH18 | Mono | 2.402 | 3.574 | 7.177 | 8.799 |
| TriC60acH24 | Mono | 2.162 | 3.273 | 6.727 | 8.078 |
| HexC96zzH24 | Mono | 1.291 | 1.832 | 6.757 | 7.117 |
| TriC168acH42 | Mono | 1.381 | 1.652 | 10.360 | 10.991 |
| Bilayer graphene | Double | 0.000 | 0.000 | 4.024 | 10.060 |
| ABhexC132zzH40 | Double | 0.8408 | 1.456 | 0.841 | 1.456 |
| ABhexC78zzH34 | Double | 0.030 | 1.081 | 0.030 | 1.081 |
| ABhexC38zzH22 | Double | 0.600 | 1.532 | 0.600 | 1.562 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghandchi, M.; Darvish, G.; Moravvej-Farshi, M.K. Properties of Bilayer Graphene Quantum Dots for Integrated Optics: An Ab Initio Study. Photonics 2020, 7, 78. https://doi.org/10.3390/photonics7030078
Ghandchi M, Darvish G, Moravvej-Farshi MK. Properties of Bilayer Graphene Quantum Dots for Integrated Optics: An Ab Initio Study. Photonics. 2020; 7(3):78. https://doi.org/10.3390/photonics7030078
Chicago/Turabian StyleGhandchi, Majid, Ghafar Darvish, and Mohammad Kazem Moravvej-Farshi. 2020. "Properties of Bilayer Graphene Quantum Dots for Integrated Optics: An Ab Initio Study" Photonics 7, no. 3: 78. https://doi.org/10.3390/photonics7030078
APA StyleGhandchi, M., Darvish, G., & Moravvej-Farshi, M. K. (2020). Properties of Bilayer Graphene Quantum Dots for Integrated Optics: An Ab Initio Study. Photonics, 7(3), 78. https://doi.org/10.3390/photonics7030078






