Terahertz Emission Spectroscopy and Microscopy on Ultrawide Bandgap Semiconductor β-Ga2O3
Abstract
1. Introduction
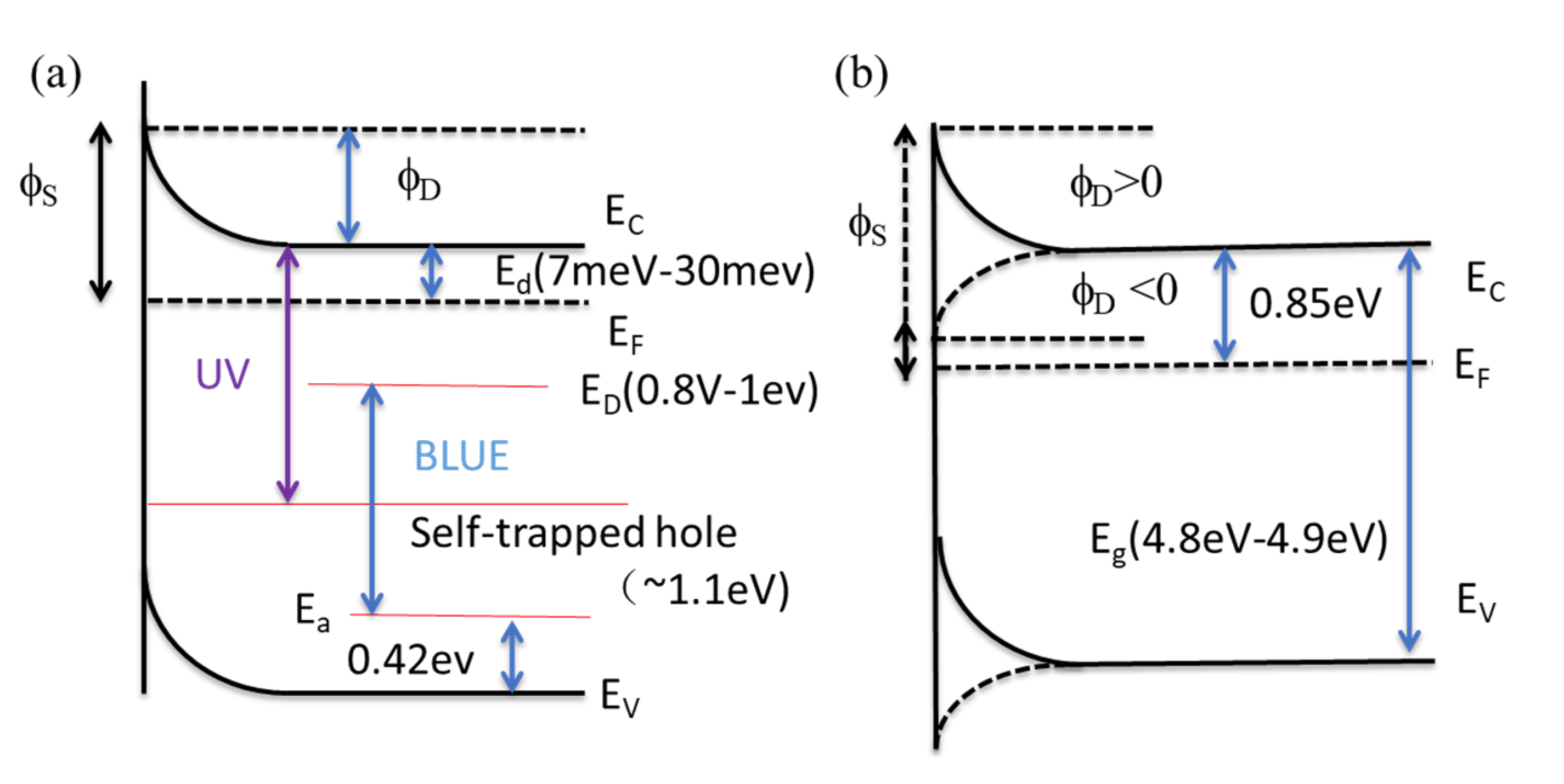
2. Terahertz Emission from Semiconductor Surfaces
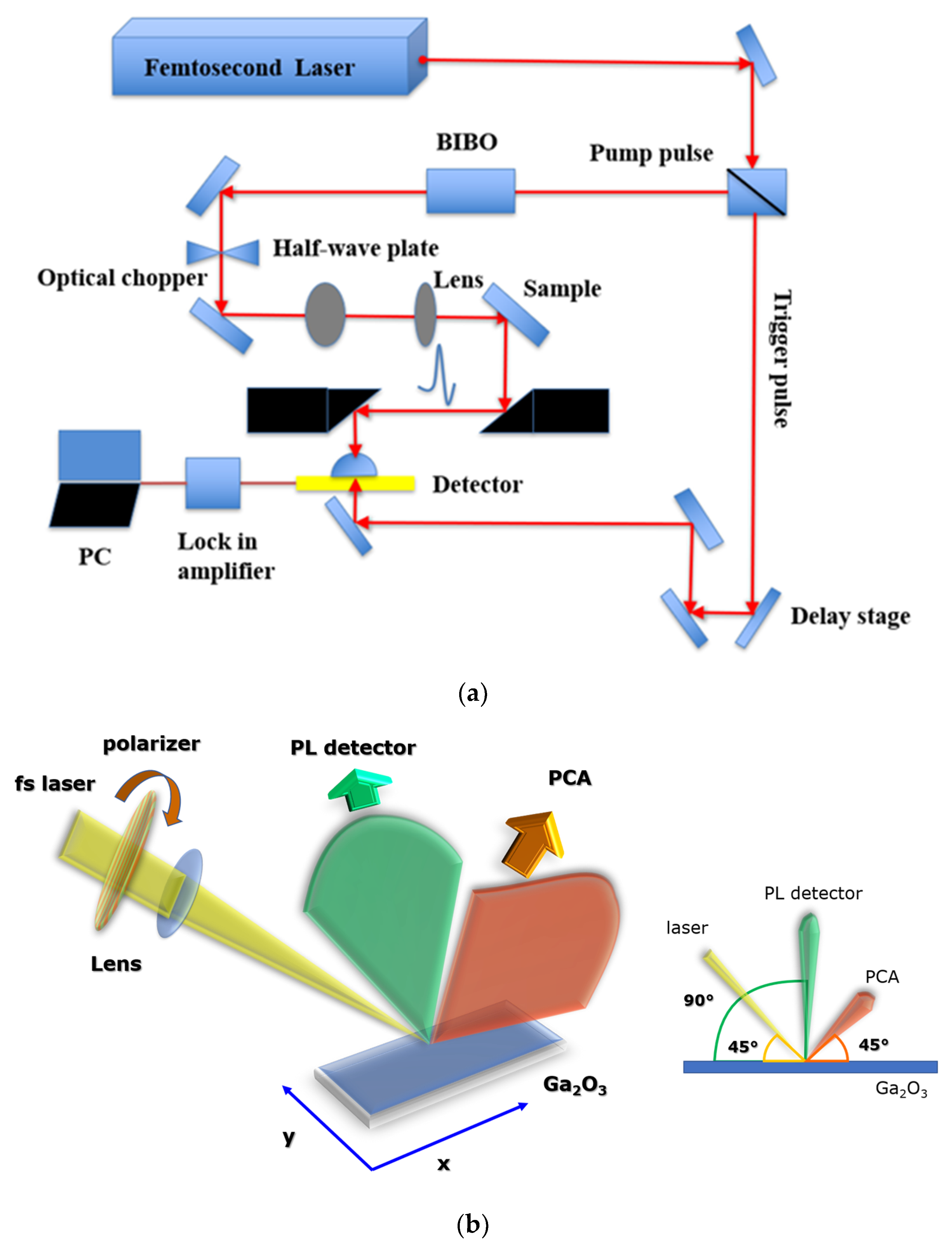
3. Samples and Experiments
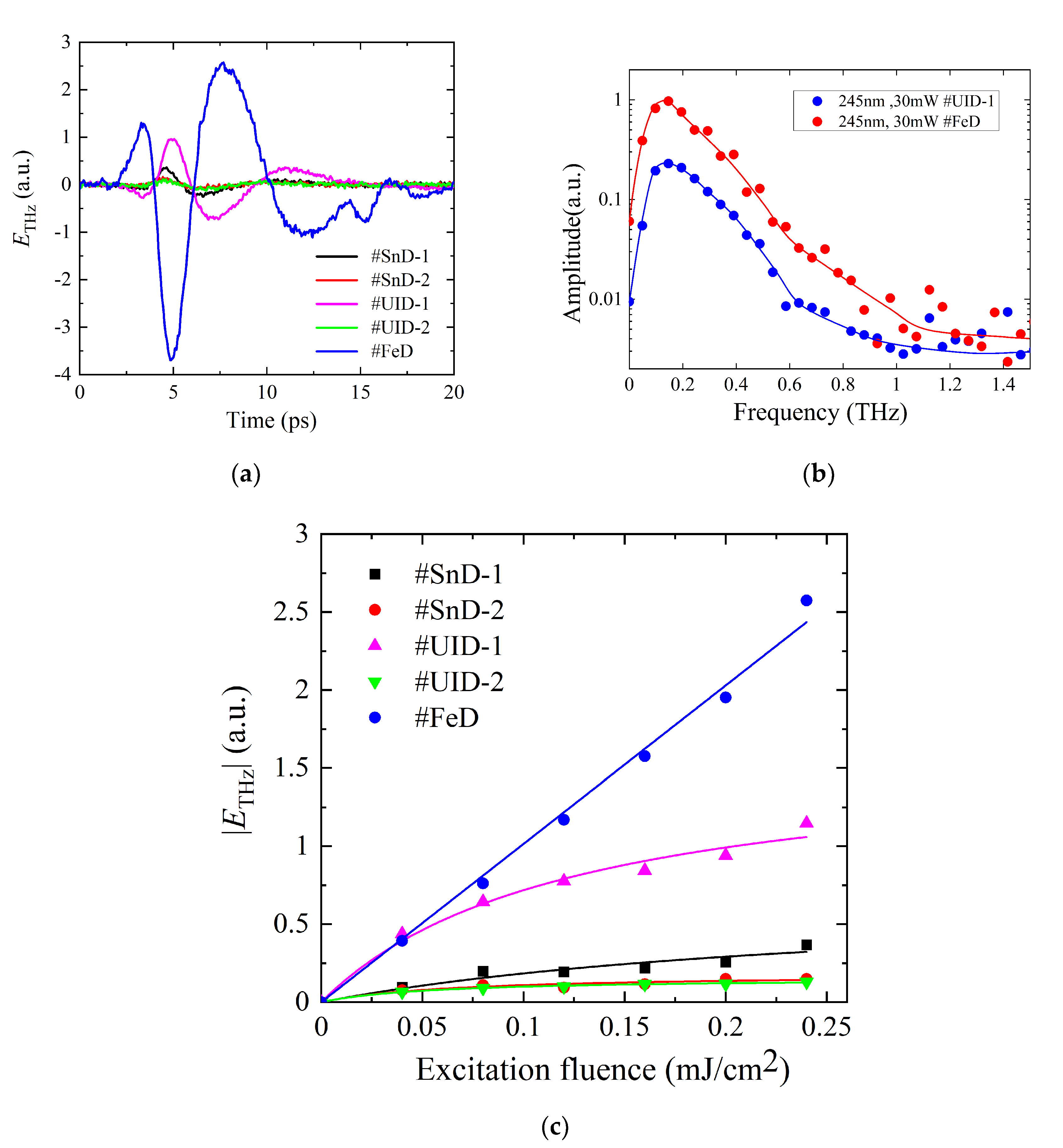
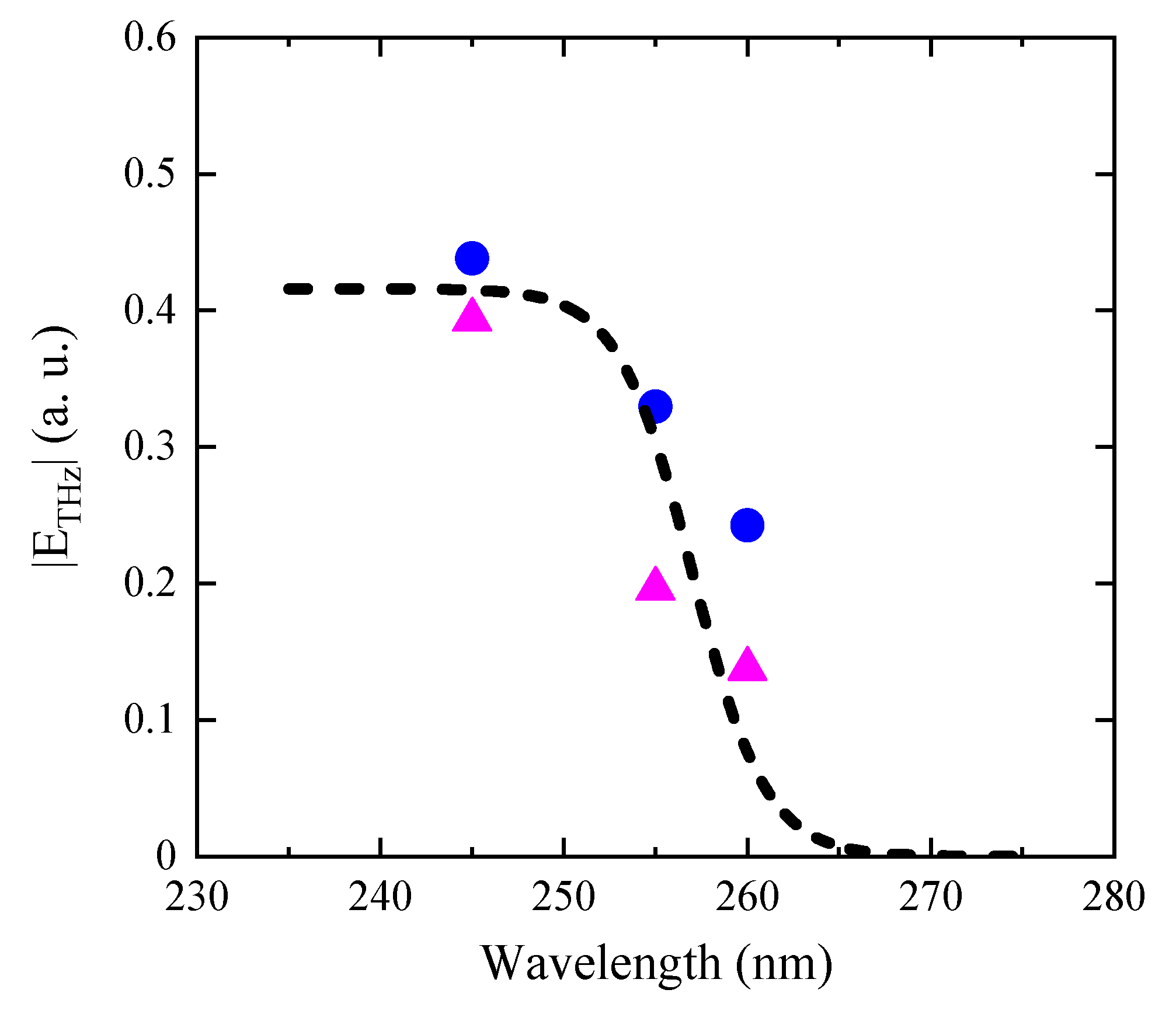
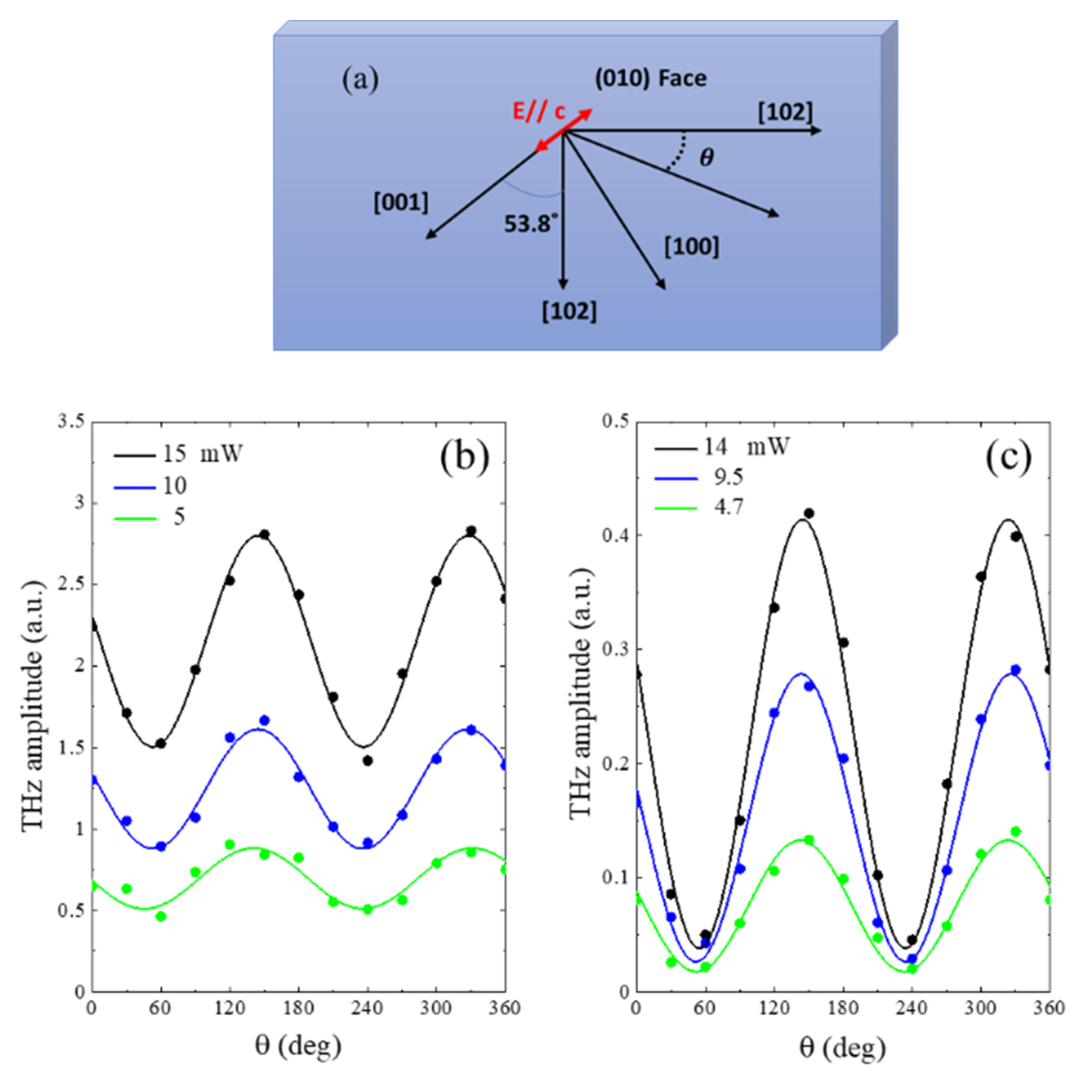
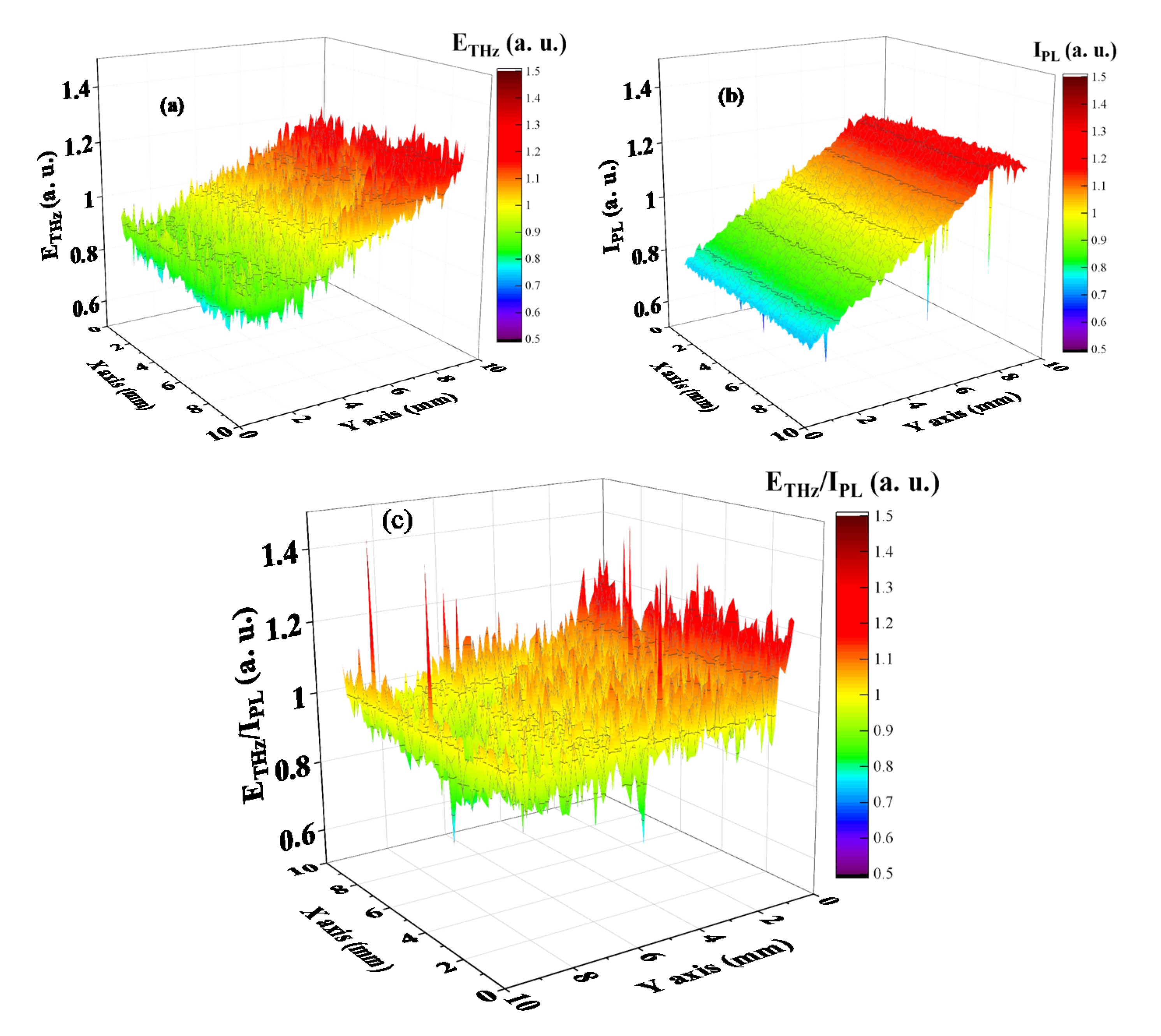
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Ahmadi, S.E.; Oshima, Y. Materials issues and devices of α-and β-Ga2O3. J. Appl. Phys. 2019, 126, 160901. [Google Scholar] [CrossRef]
- Pearton, S.J.; Ren, F.; Tadjer, M.; Kim, J. Perspective: Ga2O3 for ultra-high power rectifiers and MOSFETS. J. Appl. Phys. 2018, 124, 220901. [Google Scholar] [CrossRef]
- Higashiwaki, M.; Sasaki, K.; Murakami, H.; Kumagai, Y.; Koukitu, A.; Kuramata, A.; Masui, T.; Yamakoshi, S. Recent progress in Ga2O3 power devices. Semicond. Sci. Technol. 2016, 31, 034001. [Google Scholar] [CrossRef]
- Rana, D.S.; Tonouchi, M. Terahertz Emission Functionality of High-Temperature Superconductors and Similar Complex Systems. Adv. Opt. Mater. 2020, 8, 1900892. [Google Scholar] [CrossRef]
- Huang, Y.; Yao, Z.; He, C.; Zhu, L.; Zhang, L.; Bai, J.; Xu, X. Terahertz surface and interface emission spectroscopy for advanced materials. J. Phys. Condens. Matter. 2019, 31, 153001. [Google Scholar] [CrossRef]
- Nakanishi, H.; Ito, A.; Takayama, K.; Kawayama, I.; Murakami, H.; Tonouchi, M. Comparison between laser terahertz emission microscope and conventional methods for analysis of polycrystalline silicon solar cell. AIP Adv. 2015, 5, 117129. [Google Scholar] [CrossRef]
- Sakai, Y.; Kawayama, I.; Nakanishi, H.; Tonouchi, M. Polarization imaging of imperfect m-plane GaN surfaces. APL Photonics 2017, 2, 041304. [Google Scholar] [CrossRef]
- Mochizuki, T.; Ito, A.; Mitchell, J.; Nakanishi, H.; Tanahashi, K.; Kawayama, I.; Tonouchi, M.; Shirasawa, K.; Takato, H. Probing the surface potential of oxidized silicon by assessing terahertz emission. Appl. Phys. Lett. 2017, 110, 163502. [Google Scholar] [CrossRef]
- Mochizuki, T.; Ito, A.; Nakanishi, H.; Tanahashi, K.; Kawayama, I.; Tonouchi, M.; Shirasawa, K.; Takato, H. Noncontact evaluation of electrical passivation of oxidized silicon using laser terahertz emission microscope and corona charging. J. Appl. Phys. 2019, 125, 151615. [Google Scholar] [CrossRef]
- Nakanishi, H.; Fujiwara, S.; Takayama, K.; Kawayama, I.; Murakami, H.; Tonouchi, M. Imaging of a polycrystalline silicon solar cell using a Laser Terahertz Emission Microscope. Appl. Phys. Express. 2012, 5, 112301. [Google Scholar] [CrossRef]
- Orita, M.; Ohta, H.; Hirano, M. Deep-untravioletteansparent conductive β-Ga2O3 thin films. Appl. Phys. Lett. 2000, 77, 4166. [Google Scholar] [CrossRef]
- Tippins, H.H. Optical Absorption and Photoconductivity in the Band Edge of β-Ga2O3. Phys. Rev. 1965, 140, A316. [Google Scholar] [CrossRef]
- He, H.; Orlando, R.; Blanco, M.A.; Pandey, R. First-principles study of the structural, electronic, and optical properties of Ga2O3 in its monoclinic and hexagonal phases. Phys. Rev. B 2006, 74, 195123. [Google Scholar] [CrossRef]
- Ziaziulia, P.A.; Malevichb, V.L.; Manaka, I.S.; Krotkus, A. Generation of Terahertz Radiation by a Surface Ballistic Photocurrent in Semiconductors under Subpicosecond Laser Excitation. Semiconductors 2012, 46, 143. [Google Scholar] [CrossRef]
- Alfaro-Gomez, M.; Castro-Camus, E. The role of bandgap energy excess in surface emission of terahertz radiation from semiconductors. Appl. Phys. Lett. 2017, 110, 042101. [Google Scholar]
- Tonouchi, M. Simplified formulas for the generation of terahertz waves from semiconductor surfaces excited with a femtosecond laser. J. Appl. Phys. 2020, 127, 245703. [Google Scholar] [CrossRef]
- Ricci, F.; Boschi, F.; Baraldi, A.; Filippetti, A.; Higashiwaki, M.; Kuramata, A.; Fiorentini, V.; Fornari, R. Theoretical and experimental investigation of optical absorption anisotropy in β-Ga2O3. J. Phys. Cond. Matter 2016, 28, 224005. [Google Scholar] [CrossRef]
- Blumenschein, N.; Kadlec, C.; Romanyuk, O.; Paskova, T.; Muth, J.F.; Kadlec, F. Dielectric and conducting properties of unintentionally and Sn-doped β-Ga2O3 studied by terahertz spectroscopy. J. Appl. Phys. 2020, 127, 165702. [Google Scholar] [CrossRef]
- Harwig, T.; Kellendonk, F. Some observations on the photoluminescence of doped β-galliumsesquioxide. J. Solid State Chem. 1978, 24, 255. [Google Scholar] [CrossRef]
- Binet, L.; Gourier, D. Origin of photoluminescence in β−Ga2O3. J. Phys. Chem. Solids 1998, 59, 1241. [Google Scholar] [CrossRef]
- Huynh, T.T.; Lem, L.L.C.; Kuramata, A.; Phillips, M.R.; Ton-That, C. Kinetics of charge carrier recombination in β−Ga2O3 crystals. Phys. Rev. Mater. 2018, 2, 105203. [Google Scholar] [CrossRef]
- Tadjer, M.J.; Lyons, J.L.; Nepal, N.; Freitas, J.A., Jr.; Koehler, A.D.; Foster, G.M. Theory and Characterization of Doping and Defects in β-Ga2O3. ECS J. Solid State Sci. Tech. 2019, 8, Q3187. [Google Scholar] [CrossRef]
- Saleh, M.; Variey, J.B.; Jesenovec, J.; Bhattacharyya, A.; Krishnamoorthy, S.; Swain, S.; Lynn, K. Degenerate doping in β-Ga2O3 single crystals through Hf-doping. Semicond. Sci. Tech. 2020, 35. [Google Scholar] [CrossRef]
- Neal, A.T.; Mou, S.; Rafique, S.; Zhao, H.; Ahmadi, E.; Speck, J.S.; Stevens, K.T.; Blevins, J.D.; Thomson, D.B.; Moser, N.; et al. Donors and deep acceptors in β-Ga2O3. Appl. Phys. Lett. 2018, 113, 062101. [Google Scholar] [CrossRef]
- Ho, Q.D.; Fraunheim, T.; Deak, P. Origin of photoluminescence in β-Ga2O3. Phys. Rev. B 2018, 97, 115163. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Smirnov, N.B.; Shchemerov, I.V.; Pearton, S.J.; Ren, F.; Chernykh, A.V.; Kochkova, A.I. Electrical properties of bulk semi-insulating β-Ga2O3 (Fe). Appl. Phys. Lett. 2018, 113, 142102. [Google Scholar] [CrossRef]
- Islam, M.M.; Rana, D.; Hernandez, A.; Haseman, M.; Selim, F.A. Study of trap levels in β-Ga2O3 by thermoluminescence spectroscopy. J. Appl. Phys. 2019, 125, 055701. [Google Scholar] [CrossRef]
- Chabak, K.D.; Leedy, K.D.; Green, A.J.; Mou, S.; Neal, A.T.; Asel, T.; Heller, E.R.; Hendricks, N.S.; Liddy, K.; Crespo, A.; et al. Lateral β-Ga2O3 field effect transistors. Semicond. Sci. Technol. 2020, 35, 013002. [Google Scholar] [CrossRef]
- Fu, H.; Chen, H.; Huang, X.-Q.; Baranowski, I.; Montes, J.; Yang, T.-H.; Zhao, Y. A Comparative Study on the Electrical Properties of Vertical (-201) and (010)-Ga2O3Schottky Barrier Diodes on EFG Single-Crystal Substrates. IEEE Electron. Dev. 2018, 65, 3507. [Google Scholar] [CrossRef]
- Kim, S.; Murakami, H.; Tonouchi, M. Transmission-Type Laser THz emission microscope using a solid immersion lens. IEEE J. Select. Topic Quant. Electron. 2008, 14, 498. [Google Scholar] [CrossRef]
- Sakai, Y.; Kawayama, I.; Nakanishi, H.; Tonouchi, M. Visualization of GaN surface potential using terahertz emission enhanced by local defects. Sci. Rep. 2015, 5, 13860. [Google Scholar] [CrossRef] [PubMed]
- Yamahara, K.; Mannan, A.; Kawayama, I.; Nakanishi, H.; Tonouchi, M. Ultrafast Spatiotemporal Photocarrier Dynamics near GaN Surfaces Studied by Terahertz Emission Spectroscopy. Sci. Rep. 2020, 10, 14633. [Google Scholar] [CrossRef]
- Tani, M.; Tonouchi, M.; Wang, Z.; Sakai, K.; Hangyo, M. Enhanced Sub-Picosecond Electromagnetic Radiation from YBa2Cu3O7-d thin-Film Bow-Tie Antennas Excited with Femtoseconds Laser Pulses. Jpn. J. Appl. Phy. Part 2 1996, 9B, L1184. [Google Scholar] [CrossRef]
- Tonouchi, M.; Saijo, H. Terahertz Radiation from YBCO Thin Film Log-periodic Antennas. J. Supercond. Novel Magn. 2003, 16, 867–871. [Google Scholar] [CrossRef]
- Taylor, A.J.; Rodriguez, G.; Some, D. Ultrafast field dynamics in large-aperture photoconductors. Opt. Lett. 1997, 22, 715. [Google Scholar] [CrossRef]
- Gu, P.; Tani, M.; Kono, S.; Sakai, K.; Zhang, X.-C. Study of terahertz radiation from InAs and InSb. J. Appl. Phys. 2002, 91, 5533. [Google Scholar] [CrossRef]
- Dimitrov, V.; Sakka, S. Linear and nonlinear optical properties of simple oxides. II. J. Appl. Phys. 1996, 79, 1741. [Google Scholar] [CrossRef]
- Li, W.; Saraswat, D.; Long, Y.; Nomoto, K.; Jena, D.; Xing, H.G. Near-ideal reverse leakage current and practical maximum electronc field in β-Ga2O3 Schpttky barrier diodes. Appl. Phys. Lett. 2020, 116, 192101. [Google Scholar] [CrossRef]
- Wang, Y.; Dickens, R.T.; Varley, J.B.; Ni, X.; Lotubai, E.; Sprawls, S.; Liu, F.; Lordi, F.; Krishnamoorthy, S.; Blair, S.; et al. Incident wavelength and polarization dependence of spectral shifts in β-Ga2O3 UV photoluminescence. Sci. Rep. 2018, 8, 18075. [Google Scholar] [CrossRef]
- Mengle, K.A.; Shi, G.; Bayerl, D.; Kioupakis, E. First-principles calculations of the near-edge optical properties of β-Ga2O3. Appl. Phys. Lett. 2016, 109, 212104. [Google Scholar] [CrossRef]
- Guo, D.; Wu, Z.; Li, P.; An, Y.; Liu, H.; Guo, X.; Yan, H.; Wang, G.; Sun, C.; Li, L.; et al. Fabrication of β-Ga2O3 thin films and solar-blind photodetectors by laser MBE technology. Opt. Mat. Express 2014, 4, 1067. [Google Scholar] [CrossRef]
- Tonouchi, M.; Kawasaki, N.; Yoshimura, T.; Wald, H.; Seidel, P. Pump and Probe Terahertz Generation Study of Ultrafast Carrier Dynamics in Low-Temperature Grown-GaAs. Jpn. J. Appl. Phys. 2002, 41, L706. [Google Scholar] [CrossRef]
- Ma, N.; Tanen, N.; Verma, A.; Guo, Z.; Luo, T.; Xing, H.; Jena, D. Intrinsic electron mobility limits in β-Ga2O3. Appl. Phys. Lett. 2016, 109, 212101. [Google Scholar] [CrossRef]

| Samples | Orientation | Dopant | Thickness (mm) | n (cm−3) | μe (cm2/Vs) | (eV) | w (nm) | EMax (MV/cm) | (a.u) |
|---|---|---|---|---|---|---|---|---|---|
| #SnD-1 | (010) | Sn | 0.65 | 6.81018 | 45 a | 1.63 b | 16 | 1.9 | 13.66 |
| #SnD-2 | () | Sn | 0.65 | 1.81018 | 50 a | 1.14 b | 26 | 0.85 | 10.61 |
| #UID-1 | (010) | UID | 0.5 | 1.41017 | 80 a | 1.63 b | 113 | 0.28 | 24.38 |
| #UID-2 | () | UID | 0.5 | 3.81017 | 60 a | 1.14 b | 57 | 0.39 | 12.74 |
| #FeD | (010) | Fe | 0.5 | - | - | - | - | - | - |
| Samples | #SnD-1 | #SnD-2 | #UID-1 | #UID-2 | #FeD |
|---|---|---|---|---|---|
| E0 | 0.69 | 0.18 | 1.60 | 0.16 | 36.0 |
| Fsat | 0.28 | 0.07 | 0.12 | 0.06 | 3.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Gong, C.; Nishimura, T.; Murakami, H.; Kawayama, I.; Nakanishi, H.; Tonouchi, M. Terahertz Emission Spectroscopy and Microscopy on Ultrawide Bandgap Semiconductor β-Ga2O3. Photonics 2020, 7, 73. https://doi.org/10.3390/photonics7030073
Jiang H, Gong C, Nishimura T, Murakami H, Kawayama I, Nakanishi H, Tonouchi M. Terahertz Emission Spectroscopy and Microscopy on Ultrawide Bandgap Semiconductor β-Ga2O3. Photonics. 2020; 7(3):73. https://doi.org/10.3390/photonics7030073
Chicago/Turabian StyleJiang, Hao, Chen Gong, Tatsuhiko Nishimura, Hironaru Murakami, Iwao Kawayama, Hidetoshi Nakanishi, and Masayoshi Tonouchi. 2020. "Terahertz Emission Spectroscopy and Microscopy on Ultrawide Bandgap Semiconductor β-Ga2O3" Photonics 7, no. 3: 73. https://doi.org/10.3390/photonics7030073
APA StyleJiang, H., Gong, C., Nishimura, T., Murakami, H., Kawayama, I., Nakanishi, H., & Tonouchi, M. (2020). Terahertz Emission Spectroscopy and Microscopy on Ultrawide Bandgap Semiconductor β-Ga2O3. Photonics, 7(3), 73. https://doi.org/10.3390/photonics7030073







