The Significance of Carrier Leakage for Stable Lasing in Split-Well Direct Phonon Terahertz Quantum Cascade Lasers

Abstract

We studied the temperature performance of split-well direct phonon terahertz quantum cascade lasers and found that it is limited by a lasing instability that becomes significant as the temperature increases. When the hot electrons of the upper laser level cannot scatter effectively to excited states due to the high radiative barriers of the structures, a lasing instability occurs, which limits the temperature performance.

1. Introduction

The maximum operating temperature (T_max) reported so far for terahertz-quantum cascade lasers (THz-QCLs) is ~210 K [1]. For THz-QCLs based on spatially vertical transitions, the major physical mechanism that limits T_max was identified as thermally activated LO-phonon scattering from the upper to the lower laser level [2]. A strategy for counteracting the temperature degradation of THz-QCLs is to reduce the thermally activated LO-phonon scattering by using diagonal structures [3]. In previous studies, we investigated potential mechanisms that limit the temperature performance of diagonal THz-QCLs and identified that thermally activated leakage of charge carriers into the continuum [4] or into excited bound states [5,6] reduces the upper laser level lifetime. Structures with widely separated higher-laying excited states enabled by using high barriers were implemented to reduce the adverse effects of these mechanisms. The suppression of those leakage channels in a resonant-phonon [5] and two-well [7] schemes was demonstrated—as indicated by the observation of negative differential resistance (NDR) at room temperature. To improve the temperature performance of these lasers, a new THz-QCL structure, named split-well direct phonon (SWDP), has been suggested as an ideal platform for studying the carrier dynamics [8]. As a result of this scheme, the lasers benefit from flexible design and the efficient isolation of laser levels from excited and continuum states [4,5,6]. A clean three-level system, in which most of the electrons reside in the three lowest subbands even at elevated temperatures, is achieved in the SWDP design, as indicated by the NDR behavior at room temperature. Due to the enhanced flexibility in the design, these schemes serve as a good platform for studying the mechanisms that govern the temperature degradation. Here, we studied different realizations of the SWDP scheme using different barrier compositions than the original contribution and analyzed their performance. We found that the lasers are limited by a lasing instability [9,10] that becomes significant as the temperature increases.

In this paper, diagonal [3], (f ~0.22) SWDP THz-QCLs with Al_0.30Ga_0.70As potential barriers and carrier density per cascade of ~3 × 10¹⁰ cm⁻², (Figure 1) are investigated. The molecular beam epitaxy (MBE) wafer is labeled VB0843. The device is called Device 1 for simplicity. Further information about this design is presented in

Table 1. Main nominal design parameters and device data.

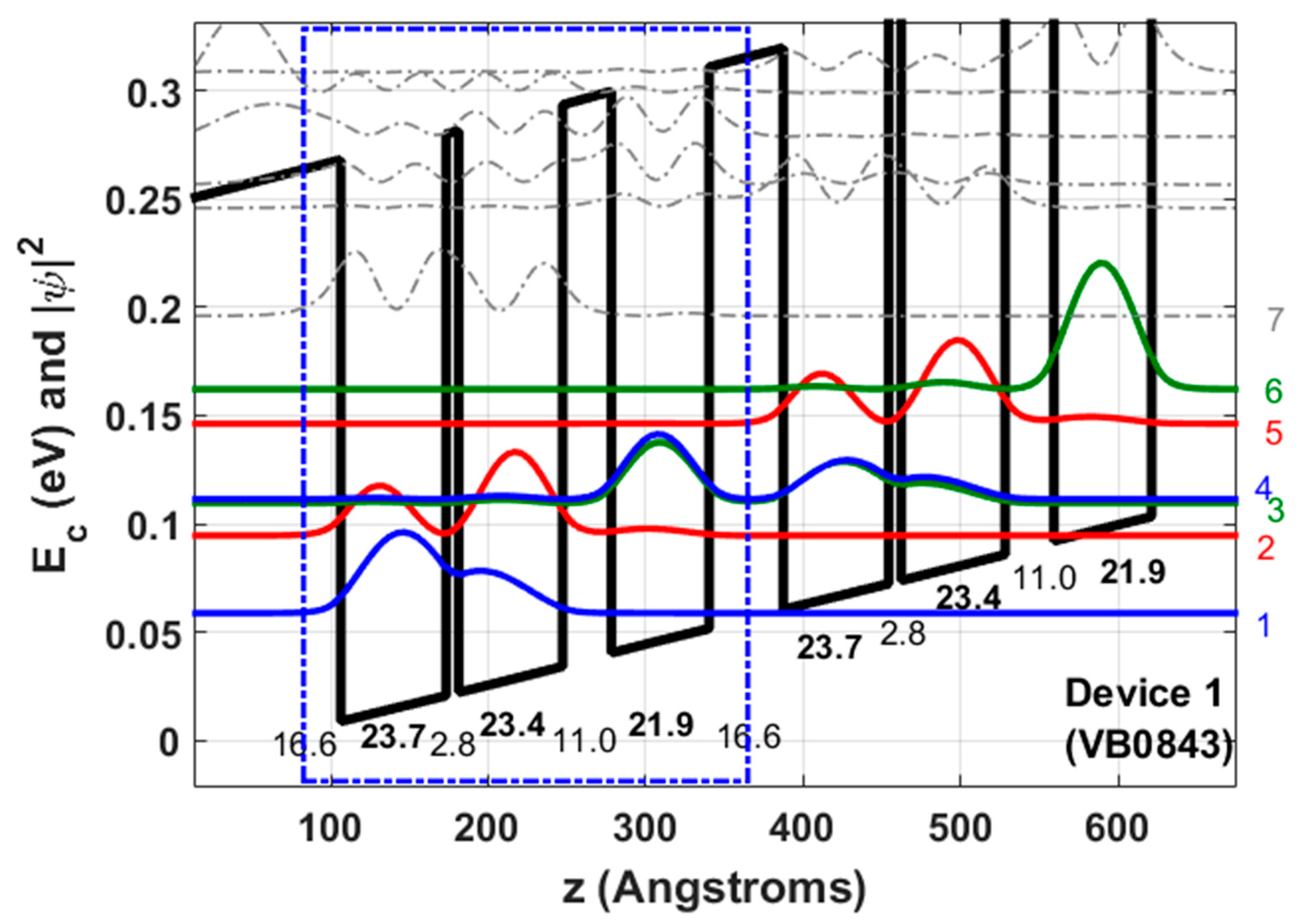
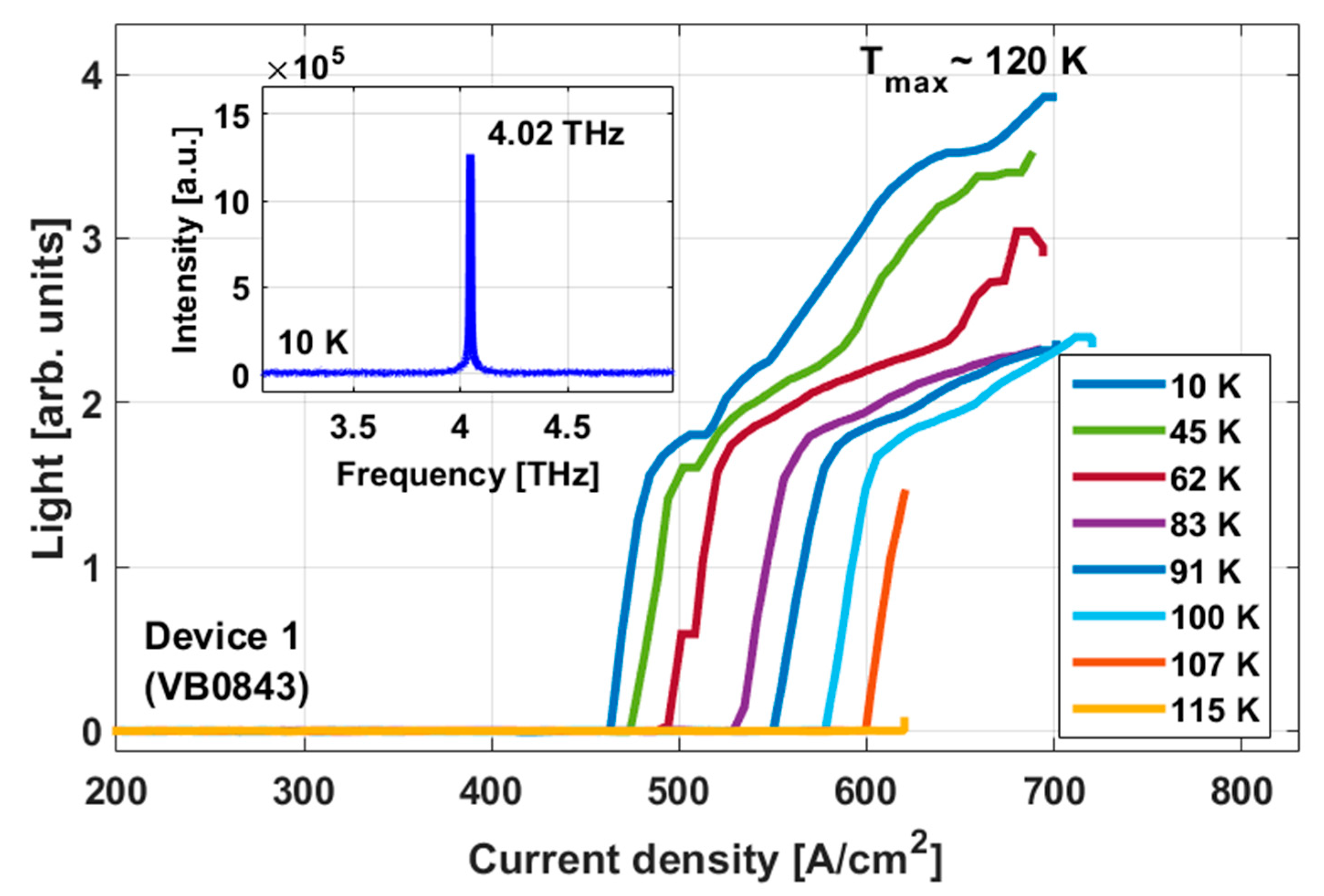
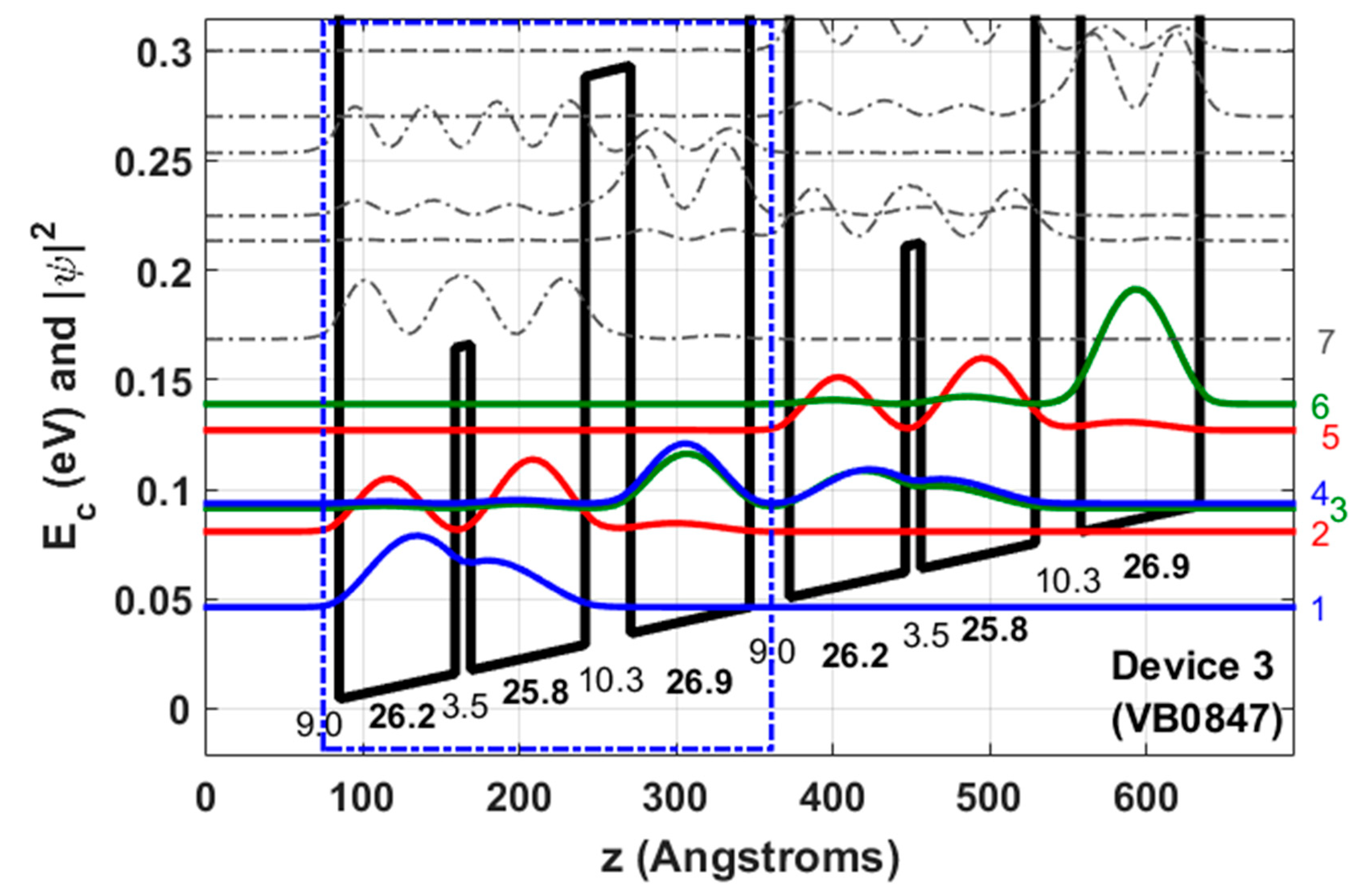
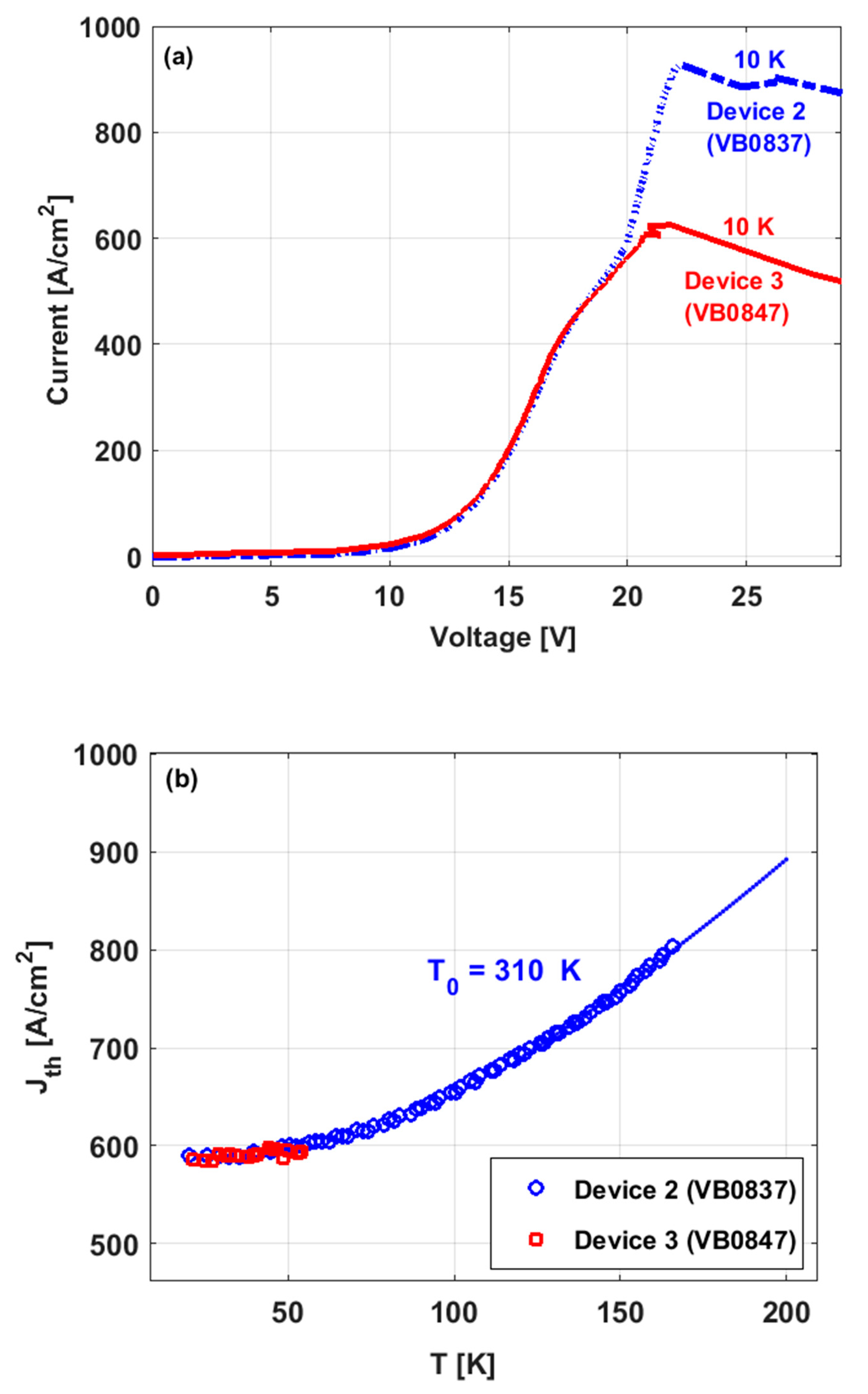
Device	Lasing Energy [meV]	E21 [meV]	Oscillator Strength	Nom. Expected Activation Energy [meV]	E47 [meV]	Layer Sequence [#ML*], Barrier Composition and Doping Level	Process Details
Device 1 (VB0843), (Figure 1)	14.9	36	0.22	21.1	84.6	16.6/23.7/2.8/23.4/11.0/21.9 355 periods GaAs/Al0.30Ga0.70As 2.24 × 1016 cm−3 in the 23.7 and 23.4 ML wells (2.98 × 1010 cm−2).	Metal–metal (100 Å Ta/2500 Å) Top contact n+ layer was removed Dry etched Mesa size 150 μm × 1.8 mm
Device 2 (VB0837) ([8])	11.1	34.5	0.26	24.9	72.5	9.0/24.8/3.5/24.8/17.3/24.8 353 periods GaAs/mixed barriers Al0.55Ga0.45As (Injector) and Al0.15Ga0.85As (Radiative, Intrawell) 2.13 × 1016 cm−3 in the 24.8 ML wells (2.98 × 1010 cm−2).	Metal-metal (100 Å Ta/2500 Å Au) Top contact n+ layer was removed Dry etched Mesa size 150 μm × 1.8 mm
Device 3 (VB0847) (Figure 5)	10.7	34.5	0.25	25.3	75.1	9.0/26.2/3.5/25.8/10.3/26.9 362 periods GaAs/mixed barriers: Al0.55Ga0.45As (Injector), Al0.30Ga0.70As (Radiative) and Al0.15Ga0.85As (Intrawell) 2.03 × 1016 cm−3 in the 26.2 and 25.8 ML wells (2.98 × 1010 cm−2).	Metal-metal (100 Å Ta/2500 Å) Top contact n+ layer was removed Dry etched Mesa size 150 μm × 1.8 mm

* #ML is the number of monolayers, AlGaAs barriers are in bold and GaAs wells are italicized. the barriers’ composition and doping data are given in detail, the doped layer in the sequence is underscored.

and

Table 2. Device parameters and performance.

Device	Injection Coupling $\left(2\mathit{\hslash }{\mathsf{\Omega }}_{\mathit{i}\mathit{j}}\right)$ [meV]	Design Electric Field [kV/cm]	τ0ul [ps] *	τ021 [ps] **	IFR Gain Broadening [meV] ***	Exp. Lasing Energy [meV]	Expected Activation Energy [meV]	Jth (10 K) [A/cm2]	Jmax (10 K)[A/cm2]	Dynamic Range (10 K) [A/cm2]	Jmax (290 K) [A/cm2]	Tmax [K]
Device 1 (VB0843), (Figure 1)	1.87	18.4	1.23	0.17	4.19	16.6	19.4	463	708	245	657	120
Device 2 (VB0837) ([8])	2.08	16.5	1.21	0.18	4.37	10.05	25.5	578	928	350	750	170
Device 3 (VB0847) (Figure 5)	2.12	16.8	1.08	0.19	4.10	10.8	25.2	578	625	47	646	57

* ULL to LLL raw LO-phonon scattering time. ** LLL (level 2) to Injector (level 1) LO–phonon scattering time. *** Calculated according to Flores and Albo [25].

.

In Figure 1, a structure with three fundamental subbands in each module is shown. All other levels seen in the figure are considered parasitic. A direct-phonon scattering scheme is formed by aligning the upper laser level (ULL, level 3 in the scheme) and the injector level (level 4 in the scheme), a scheme that resembles the one of a two-well (TW) structure [11,12,13]. Direct-phonon structures proved to be superior to resonant-phonon (RP) ones, hence the motivation to keep this design for SWDP. One of the main advantages of the scheme is the very fast depopulation of the lower laser level (LLL), reached by longitudinal-optical (LO)-phonon scattering only, with no resonance coupling involved in the process. Furthermore, its sensitiveness to misalignment of the laser levels (due to the Poisson effect that causes band bending [7,14,15]) is lower. Another advantage is that the added barrier of the SWDP reduces carrier leakage channels to a larger extent, including intermodule leakage.

The energy splitting between levels 1 and 2 (see Figure 1) is controlled by using an intra-well thin barrier. The energy gap can be changed to be the exact LO-phonon energy (E₂₁ = 36 meV) by adjusting the thickness of the intra-well barrier. Reaching this exact energy level enables the fastest LO-phonon scattering rate depopulating the LLL. Additionally, in the SWDP design, the resonant LO-phonon scattering condition of E₂₁ = 36 meV is kept even when pushing the excited levels to higher energies, thanks to the thickness adjustability of the intra-well barrier [8]. It is essential to keep the fastest possible LLL depopulation rate, as demonstrated by several works that establish the disadvantages of slow LLL depopulation on the laser performance for THz-QCLs [5,7,16,17,18]. Nevertheless, high laser performance can also be achieved with E₂₁ > 36 meV [19,20].

2. Discussion

The maximum temperature reached in Device 1 (fabricated from wafer VB0843) was of about 120 K. In Figure 1, we can appreciate the fact that the excited states (levels ≥ 7) are well separated from the three active subbands (levels 1–3) [8]. We can see that the first excited state (level 7) is not only located ~85 meV above the ULL, but it is also spatially located in the next neighboring quantum well. As the scheme in Figure 1 indicates, this excited state and the ULL hardly overlap. Moreover, the ULL of the second module (level 6) in the higher energy side of the scheme (module i+1), is also energetically positioned bellow the first excited state (level 7). We infer from these facts that there is a decrease of intermodule leakage as compared to TW structures [7]. The lasing frequency observed was of ~4.02 THz (~17 meV, Figure 2 inset and Table 2) in comparison to the designed lasing value of ~3.60 THz (Table 1).

The L–I curves of Device 1 in Figure 2 show a two-slope behavior of the power output (P_out). According to the energy schemes in Figure 1, the second reduced slope cannot be explained by intermodule leakage. An alternative explanation for the slope reduction might be the heating of the ULL electrons upon lasing [21,22,23]. Furthermore, the I–V curves in Figure 3 demonstrate that the device has NDR at room temperature. This is indication for an effective isolation of the three active laser states from the excited and continuum states, i.e., a clean three laser-level system was obtained in this device. At temperatures close to T_max, we observe fluctuations in the I–V curves (Figure 3) indicating lasing instability [9,24]. The occurrence of fluctuations in the I–V curves is correlated with the disappearance of the second slope from the L–I curves in the vicinity of T_max and to fast deterioration of the laser intensity (Figure 2).

The laser instability behavior is indicated by the faster drop in power versus temperature as observed in the L–I curves in Figure 2 and the fluctuations in the I–V curves in Figure 3 that become very significant as the temperature approaches T_max. In fact, it seems that the temperature performance as indicated by T_max is limited by the lasing instability rather than the population inversion drop.

The change in light (P_out) as a function of temperature was analyzed. Arrhenius plots according to Albo and Hu’s method [2] using $\ln \left(1-\frac{P_{out}\left(T\right)}{P_{out}{}_{max}}\right)\approx \ln \left(a\right)-\frac{E_a}{kT}$ (where $a$ is a constant), were used to extract the activation energies ($E_a$). Data close to T_max was ignored, and reasonable activation energy values were obtained for Device 1 (Figure 4). Our procedure is validated, as can be seen, by the smooth curves in the temperature range used for extraction. The dependence on temperature of the current dynamic range $\mathsf{\Delta }{J}_d=$($J_{max}-J_{th})$ was also analyzed, implying the dependence of the output lasing power on temperature. The best fit to the data using Arrhenius plots according to $\ln \left(1-\frac{\mathsf{\Delta }{J}_d\left(T\right)}{\mathsf{\Delta }{J}_d{}_{max}}\right)\approx \ln \left(b\right)-\frac{E_a}{kT}$, where $b$ is a constant, was utilized to extract the activation energies for the current dynamic range, as done before for P_out. No contribution from parallel leakage current exists, leading to the fact that the maximum current J_max results only from the transport through the active laser states. Thus, the use of the dynamic range for the analysis was reasonable. Therefore, the stimulated emission rate and generated radiation power, with much lower data fluctuations, are directly reflected by the dynamic range. The main assumption is that $\mathsf{\Delta }{J}_d=$($J_{max}-J_{th})\approx \left(J_{max}-J_{nl}\right) \propto P_{out}$, i.e., the threshold current $J_{th}$ approximates the nonlasing current $J_{nl}$ (the current that will be measured on nonlasing device). Consequently, the fit of the current dynamic range can be affected by underestimation of the electron excess temperature because the electron temperature may increase at the nonlasing maximum current biasing conditions with respect to the threshold biasing conditions [21,22,23].

Given the current dynamic range of Device 1, we extracted an experimental activation energy of ~19 meV (see Figure 4), as expected for thermally activated LO-phonon scattering, i.e., $E_{LO}-h\nu$ [2,12]. Thermally activated leakage channels through excited states were effectively suppressed as indicated by this result. A different result was observed from the analysis of the P_out data. We extracted a lower activation energy value from P_out, i.e., ~5 meV. We attribute the lower slope to the electrons’ nonzero excess temperature at the ULL [7]. We observed in former THz-QCL designs that the ULL temperature converges to the lattice temperature at lattice temperatures above ~100 K [2], for which case we probed an activation energy value that corresponds to the ULL to LLL thermally activated LO-phonon scattering. In Device 1 the leakage channels were strongly suppressed also for hot electrons, and electrons have fewer scattering paths to cool down, so they are kept above the lattice temperature and also at temperatures higher than 100 K. The small activation energy that we observed here is not the real physical activation energy because the electrons at the ULL are much hotter than the lattice. Inclusion of a characteristic excess temperature of ~60 K in an Arrhenius plot presented as a function of the total electron temperature rather than the lattice temperature (Figure 4 inset) would result in an activation barrier of ~19 meV, which is similar to that extracted from the current dynamic range data with zero excess electron temperature.

We consider that the lower slope observed for the P_out data analysis allows us to probe a characteristic excess electron temperature through a comparison with the slope of the current dynamic range, i.e., a characteristic excess temperature of ~60 K. This excess temperature indicates that the electrons remain hot above 100 K.

From this analysis of Device 1, we obtained an indication for the physical mechanism behind the lasing instability. We identified that in the ULL in Device 1 electrons did not cool down at temperatures above ~100 K due to a reduced capability for hot electrons to leak into scattering paths through excited states. We interpret that inability for hot electrons to relax through leakage to excited states is behind the intense lasing instability in this device. In devices with more tendency for intramodule leakage due to lower radiative barriers such as Device 2 (wafer VB0837 in Albo et al. [8], Table 1 and Table 2), hot electrons could relax more easily through leakage paths (as scattering from the ULL to level 7 in Figure 1 in [8]) and the instability was much more moderate. The main reason for the laser instability may be the formation of electric field domains [9,10] in the NDR region in the absence of parallel leakage channels.

The tendency for lasing instability is more pronounced as the barriers of the laser get higher. For example, when the radiative barriers of Device 2 described by Albo et al. [8] with 15% aluminum (Al_0.15Ga_0.85As) are replaced with radiative barriers containing 30% Al (Al_0.30Ga_0.70As) in Device 3 (wafer VB0847) (Figure 5, Table 1 and Table 2), T_max drops from ~170 to ~57 K (Table 2). The intense lasing instability behavior in Device 3 is indicated by the comparison of the low temperature I–V curves of the two devices (Figure 6a). The lasing instability in Device 3 is indicated by the fluctuation in the I–V curve in Figure 6a following by an early NDR already at low temperatures. Device 2 presents relatively stable lasing up to temperatures close to its T_max as indicated by its I–V and L–I curves in [8]. The threshold current in both devices was the same (Table 2, Figure 6b), which indicates that gain broadening or additional loss do not constitute the detrimental effect. The intermediate case between the two devices is that of Device 1, where all of the barriers contain 30% Al (Al_0.30Ga_0.70As). In this case, T_max drops only to ~120 K due to the lasing instability. The calculated interface roughness (IFR) contribution to the gain broadening is large and was about the same for all these three devices (Table 2) and cannot explain the deviation in behavior between these devices. Similar to our structures in this work, one of the first reports on THz-QCLs with variable barrier height can be found in [26].

Following observation of the entire experimental data, i.e., of the L–I measurements in Figure 2 and I–V measurements in Figure 3 and their analysis in Figure 4, we consider that the two-slope behavior of the L–I of Device 1 is a characteristic of the increase in excess electron temperature at the ULL as lasing begins, i.e., the second reduced slope of the L–I curves is due to electron heating. The second reduced slope becomes more significant and the L–I curves become flatter as the temperature increases, indicating an increase in electron heat at the ULL as the temperature increases (Figure 2). The second slope eventually disappears (Figure 2), and laser instability begins (Figure 3) and terminates the lasing. The reduced slope and the tendency for lasing instability are both caused by the lack of parasitic leakage from the ULL.

In conclusion, we studied the temperature performance of SWDP THz-QCLs and found that it is limited by lasing instability that becomes significant with increasing temperature. When hot electrons of the ULL cannot leak through scattering to excited states due to the high radiative barriers of the structures, lasing instability occurs and limits the temperature performance. These results indicate that in the SWDP THz-QCLs design, the carrier leakage through excited states must be considered for maintaining stable lasing. More specifically, assuming the temperature performance of Device 2 is limited also by lasing instability, then allowing more leakage from the ULL into the excited state should improve the maximum operating temperature beyond 170 K. For this purpose, the effectiveness of designing thermally-activated IFR leakage paths should be explored.