Cloaking Using the Anisotropic Multilayer Sphere
Abstract
1. Introduction
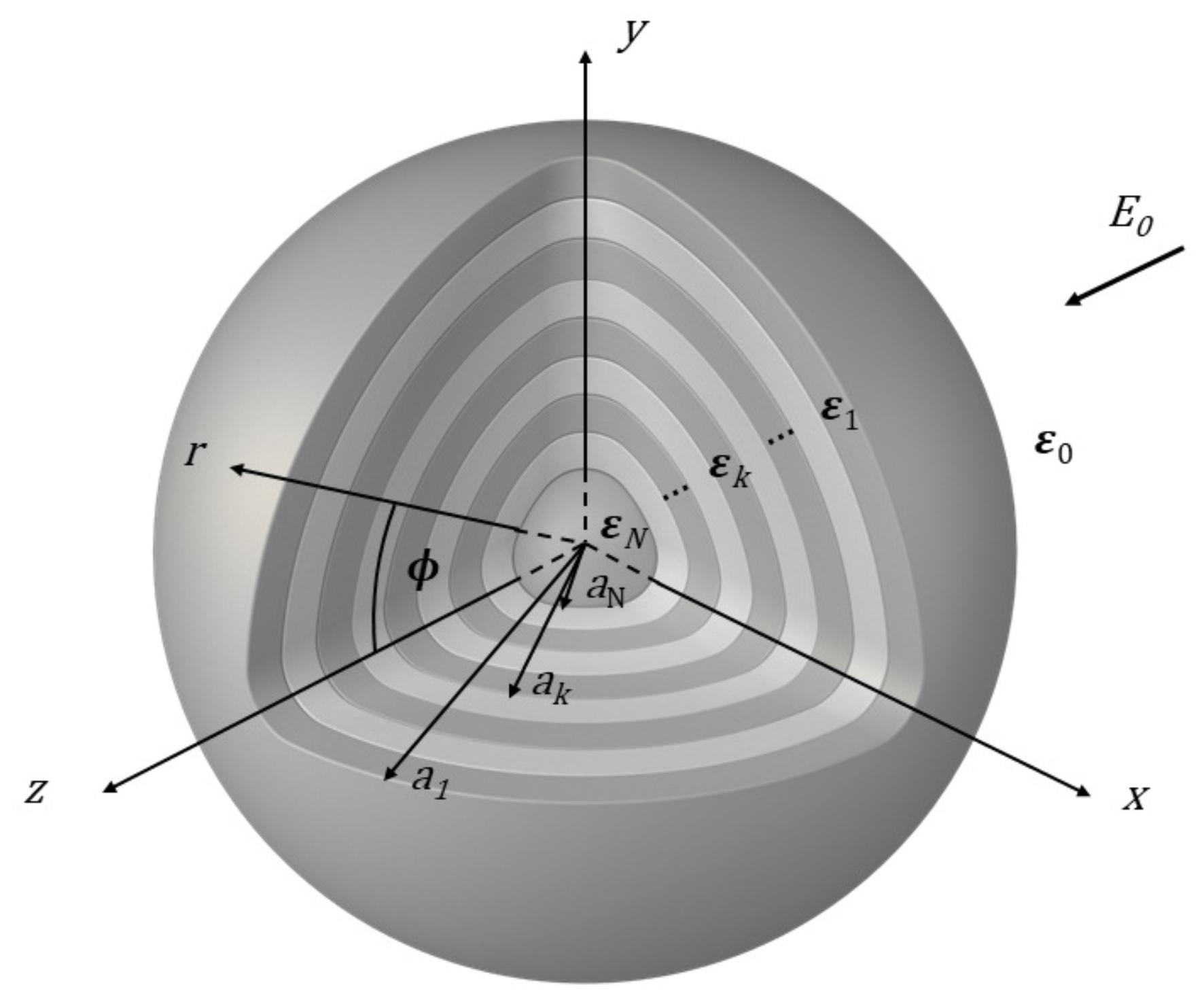
2. Formation
3. Special Cases
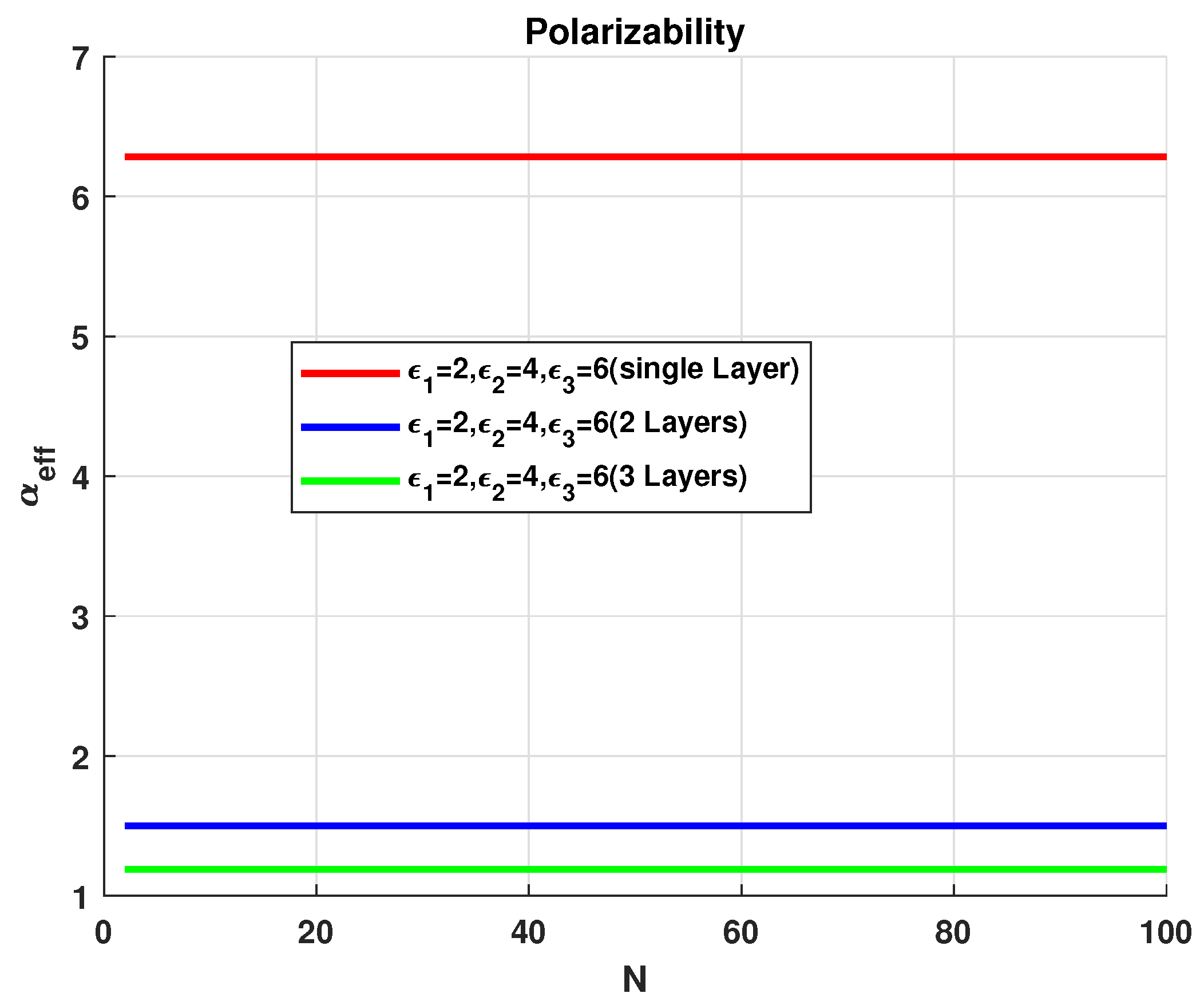
3.1. Case-1 : For Number of Layers (N) = 1
3.2. Case-2 : For Number of Layers (N) = 2
3.3. Case-3 : For Number of Layers (N) = 3
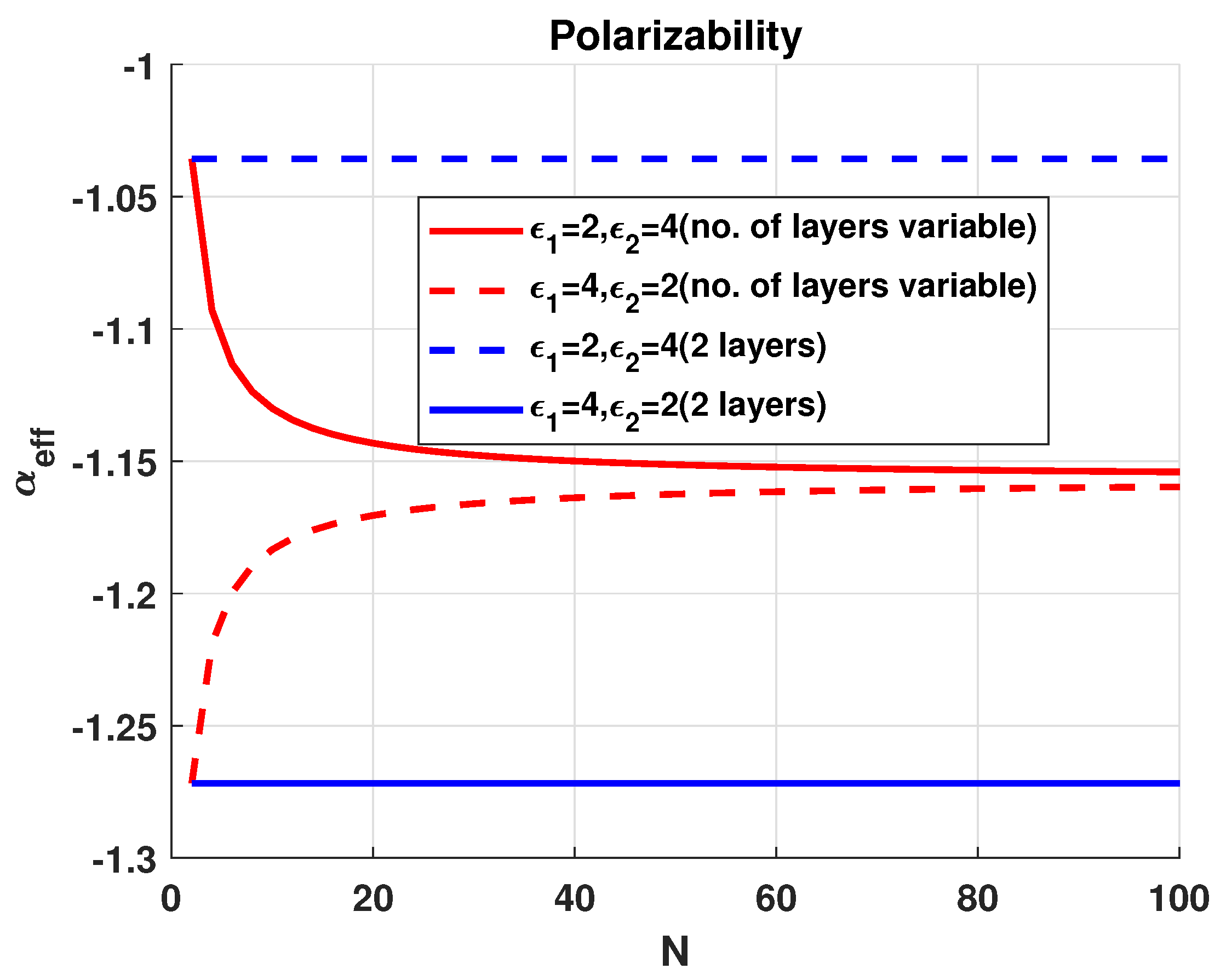
4. Multilayer Sphere as a Cloak
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 23, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Leonhardt, U. Optical conformal mapping. Science 2006, 23, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 10, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Alu, A.; Engheta, N. Theory and potentials of multi-layered plasmonic covers for multi-frequency cloaking. New J. Phys. 2008, 27, 115–146. [Google Scholar]
- Qiu, C.W.; Hu, L.; Xu, X.; Feng, Y. Spherical cloaking with homogeneous isotropic multilayered structures. New J. Phys. 2009, 23, 602–620. [Google Scholar] [CrossRef]
- Alu, A.; Engheta, N. Achieving transparency with plasmonic and metamaterial coatings. Phys. Rev. E 2005, 72, 623–636. [Google Scholar] [CrossRef]
- Alu, A. Mantle cloak: Invisibility induced by a surface. Phys. Rev. B 2009, 21, 115–124. [Google Scholar]
- Batool, S.; Frezza, F.; Mangini, F.; Xu, Y.L. Scattering from multiple PEC sphere using Translation Addition Theorems for Spherical Vector Wave Function. J. Quant. Spectrosc. Radiat. Transf. 2020, 248, 106905. [Google Scholar] [CrossRef]
- Batool, S.; Naqvi, Q.A.; Fiaz, M.A. Scattering from a cylindrical obstacle deeply buried beneath a planar non-integer dimensional dielectric slab using Kobayashi potential method. Optik 2018, 21, 95–108. [Google Scholar] [CrossRef]
- Batool, S.; Frezza, F.; Mangini, F.; Simeoni, P. Introduction to Radar Scattering Application in Remote Sensing and Diagnostics: Review. Atmosphere 2020, 11, 517. [Google Scholar] [CrossRef]
- Ni, Y.; Gao, L.; Qiu, C.W. Achieving invisibility of homogeneous cylindrically anisotropic cylinders. Plasmonics 2010, 5, 251–258. [Google Scholar] [CrossRef]
- Yu, X.; Gao, L. Nonlinear dielectric response in partially resonant composites with radial dielectric anisotropy. Phys. Lett. A 2006, 4, 516–522. [Google Scholar] [CrossRef]
- Chen, H.L.; Gao, L. Anomalous electromagnetic scattering from radially anisotropic nanowires. Phys. Lett. A 2012, 19, 825–845. [Google Scholar] [CrossRef]
- Chen, H.; Wu, B.I.; Zhang, B.; Kong, J.A. Electromagnetic wave interactions with a metamaterial cloak. Phys. Rev. Lett. 2007, 6, 903–920. [Google Scholar] [CrossRef] [PubMed]
- Cohoon, D.K. An exact solution of Mie type for scattering by a multilayer anisotropic sphere. J. Electromagnetic Wave 1989, 1, 421–448. [Google Scholar] [CrossRef]
- Geng, Y.L.; Guo, S.X.; Li, L.W. EM scattering by radially multilayered uniaxial anisotropic spheres. In Proceedings of the 2009 Asia Pacific Microwave Conference, Singapore, 7–10 December 2009; pp. 669–672. [Google Scholar]
- Gao, L.; Fung, T.H.; Yu, K.W.; Qiu, C.W. Electromagnetic transparency by coated spheres with radial anisotropy. Phys. Rev. E 2008, 78, 046–609. [Google Scholar] [CrossRef]
- Qiu, C.W.; Li, L.W.; Yeo, T.S.; Zouhdi, S. Scattering by rotationally symmetric anisotropic spheres: Potential formulation and parametric studies. Phys. Rev. E 2007, 13, 209–299. [Google Scholar] [CrossRef]
- Kettunen, H.; Wallen, H.; Sihvola, A. Cloaking and magnifying using radial anisotropy. J. Appl. Phys. 2013, 28, 110–124. [Google Scholar] [CrossRef]
- Nisar, M.; Naqvi, Q.A. Cloaking and magnifying using radial anisotropy in non-integer dimensional space. Phys. Lett. A 2018, 10, 2055–2060. [Google Scholar] [CrossRef]
- Chen, P.Y.; Alu, A. Mantle cloaking using thin patterned metasurfaces. Phys. Rev. B 2011, 84, 205110. [Google Scholar] [CrossRef]
- Chen, P.Y.; Argyropoulos, C.; Alu, A. Broadening the cloaking bandwidth with non-Foster metasurfaces. Phys. Rev. Lett. 2013, 111, 233001. [Google Scholar] [CrossRef] [PubMed]
- Mangini, F.; Tedeschi, N.; Frezza, F.; Sihvola, A. Homogenization of a multilayer sphere as a radial uniaxial sphere: Features and limits. J. Electromagn. Wave 2014, 28, 916–931. [Google Scholar] [CrossRef]
- Mangini, F.; Tedeschi, N.; Frezza, F.; Sihvola, A. Realization of a Radial Uniaxial sphere with a multilayer sphere. In Proceedings of the XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014; pp. 1–4. [Google Scholar]
- Wallen, H.; Kettunen, H.; Sihvola, A. Singularities or emergent losses in radially uniaxial spheres. In Proceedings of the International Symposium on Electromagnetic Theory, Hiroshima, Japan, 20–24 May 2013. [Google Scholar]
- Sihvola, A. Electromagnetic Mixing Formulas and Applications; The Institution of Electrical Engineers: London, UK, 1999. [Google Scholar]
- Mangini, F.; Tedeschi, N.; Frezza, F.; Sihvola, A. Analysis of the polarizability of an array of spherical metallic inclusions in a dielectric host sphere. J. Opt. Soc. Am. A 2014, 31, 2409–2414. [Google Scholar] [CrossRef]
- Mangini, F.; Tedeschi, N.; Frezza, F.; Sihvola, A. Electromagnetic interaction with two eccentric spheres. J. Opt. Soc. Am. A 2014, 31, 783–789. [Google Scholar] [CrossRef] [PubMed]
- Sihvola, A.; Lindell, I.V. Transmission line analogy for calculating the effective permittivity of mixtures with spherical multilayer scatterers. J. Electromagn. Wave 1988, 2, 741–756. [Google Scholar]
- Frezza, F.; Mangini, F. Electromagnetic scattering of an inhomogeneous elliptically polarized plane wave by a multilayered sphere. J. Electromagn. Wave 2016, 30, 492–504. [Google Scholar] [CrossRef]
- Cheng, Y.; Liu, X.J. Three dimensional multilayered acoustic cloak with homogeneous isotropic materials. J. Appl. Phys. A 2009, 94, 25–30. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batool, S.; Nisar, M.; Frezza, F.; Mangini, F. Cloaking Using the Anisotropic Multilayer Sphere. Photonics 2020, 7, 52. https://doi.org/10.3390/photonics7030052
Batool S, Nisar M, Frezza F, Mangini F. Cloaking Using the Anisotropic Multilayer Sphere. Photonics. 2020; 7(3):52. https://doi.org/10.3390/photonics7030052
Chicago/Turabian StyleBatool, Sidra, Mehwish Nisar, Fabrizio Frezza, and Fabio Mangini. 2020. "Cloaking Using the Anisotropic Multilayer Sphere" Photonics 7, no. 3: 52. https://doi.org/10.3390/photonics7030052
APA StyleBatool, S., Nisar, M., Frezza, F., & Mangini, F. (2020). Cloaking Using the Anisotropic Multilayer Sphere. Photonics, 7(3), 52. https://doi.org/10.3390/photonics7030052






