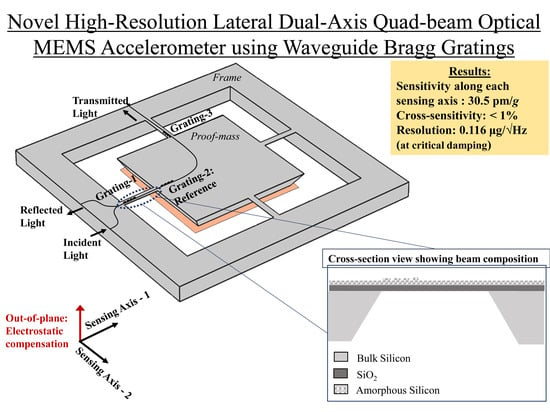
Novel High-Resolution Lateral Dual-Axis Quad-Beam Optical MEMS Accelerometer Using Waveguide Bragg Gratings
Abstract
1. Introduction
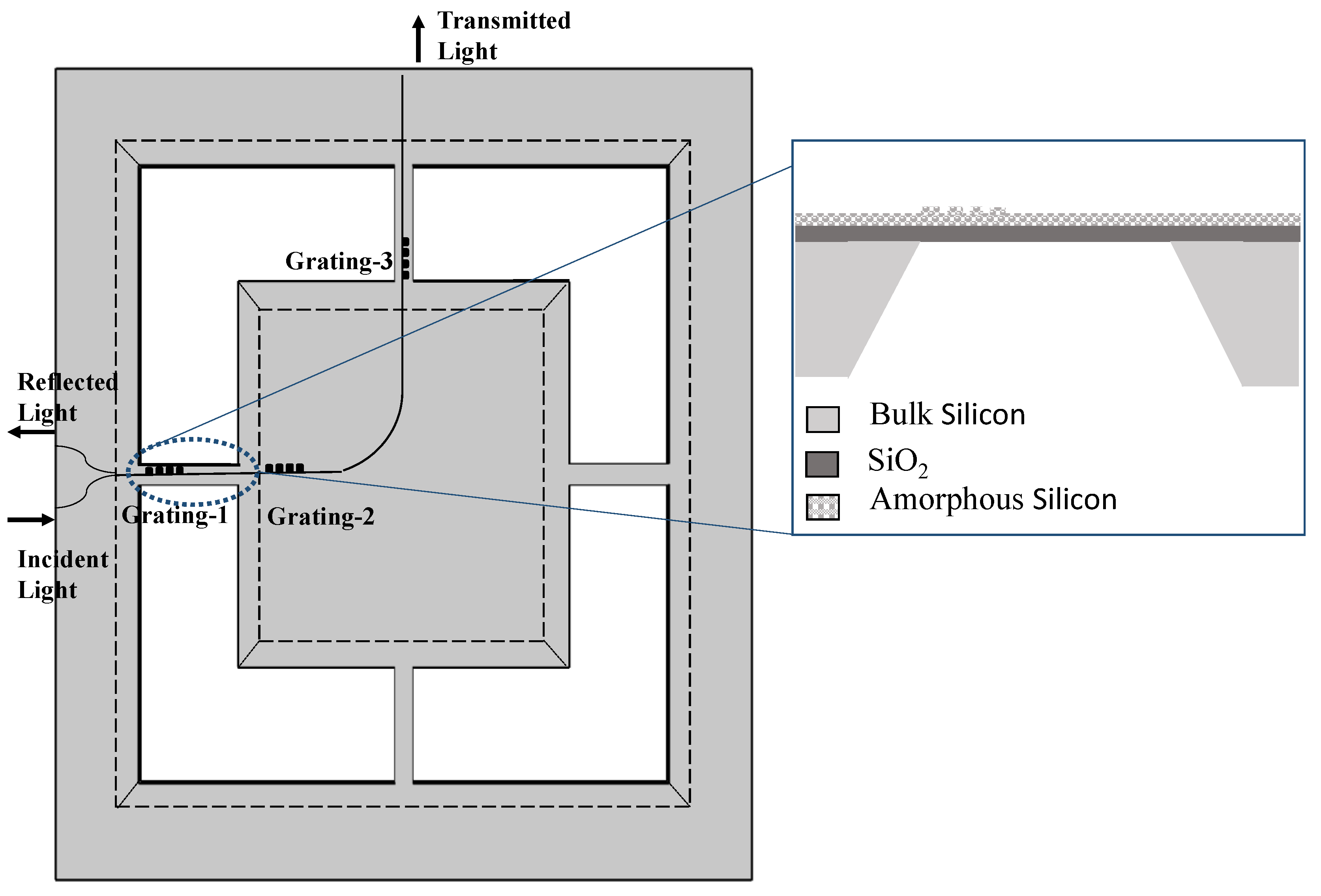
2. Sensor Configuration
3. Sensor Design and Mathematical Modelling
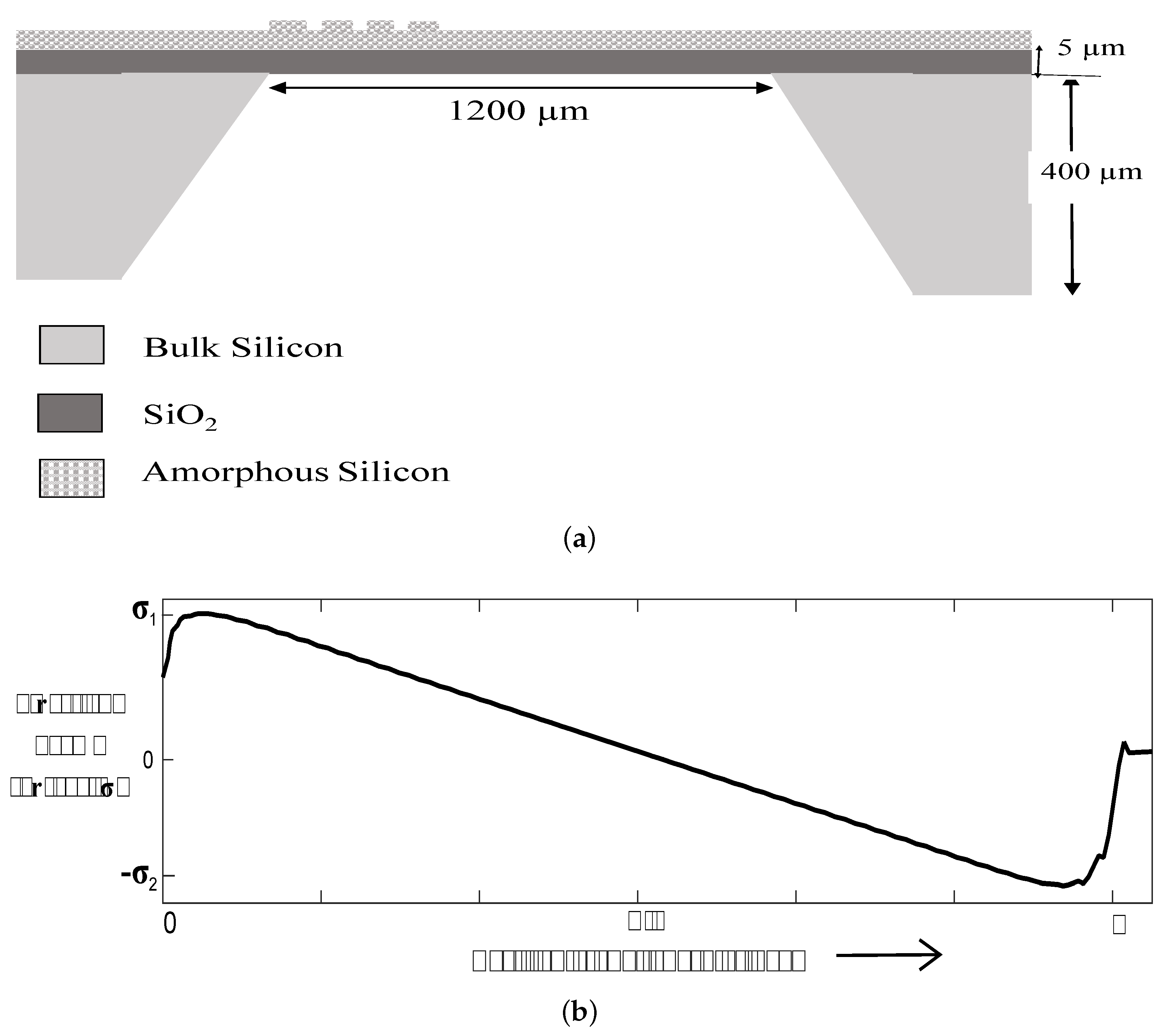
3.1. Mechanical Design of Quad-Beam Accelerometer
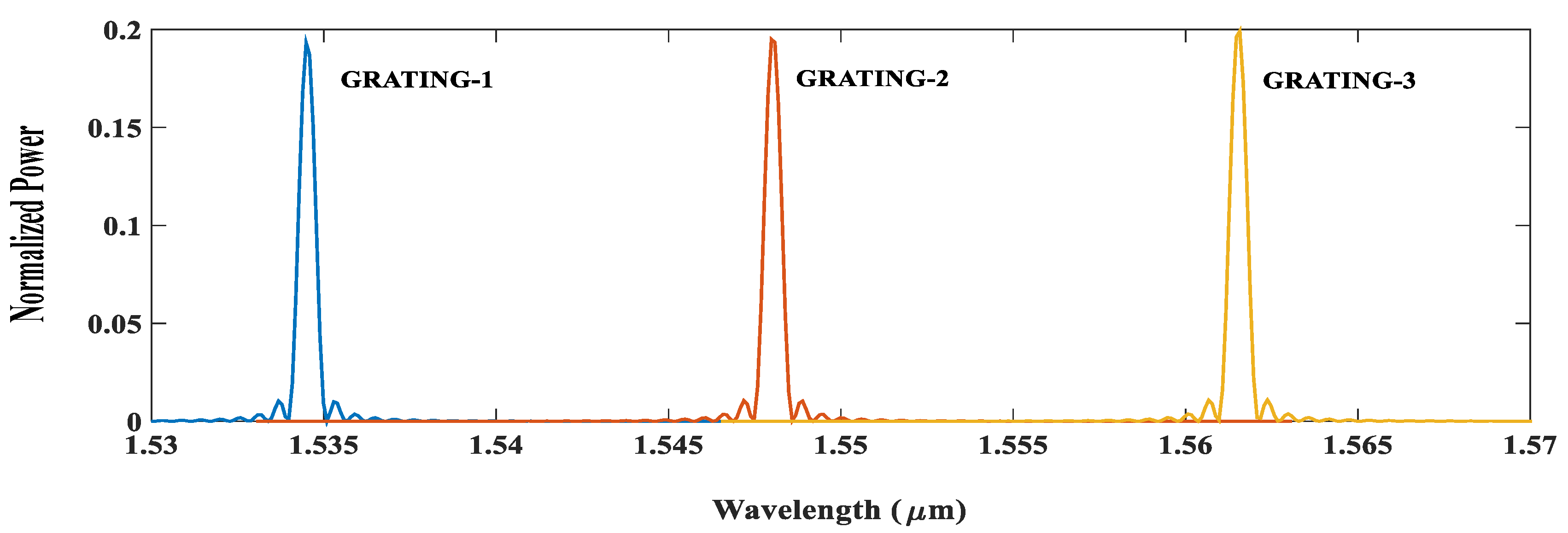
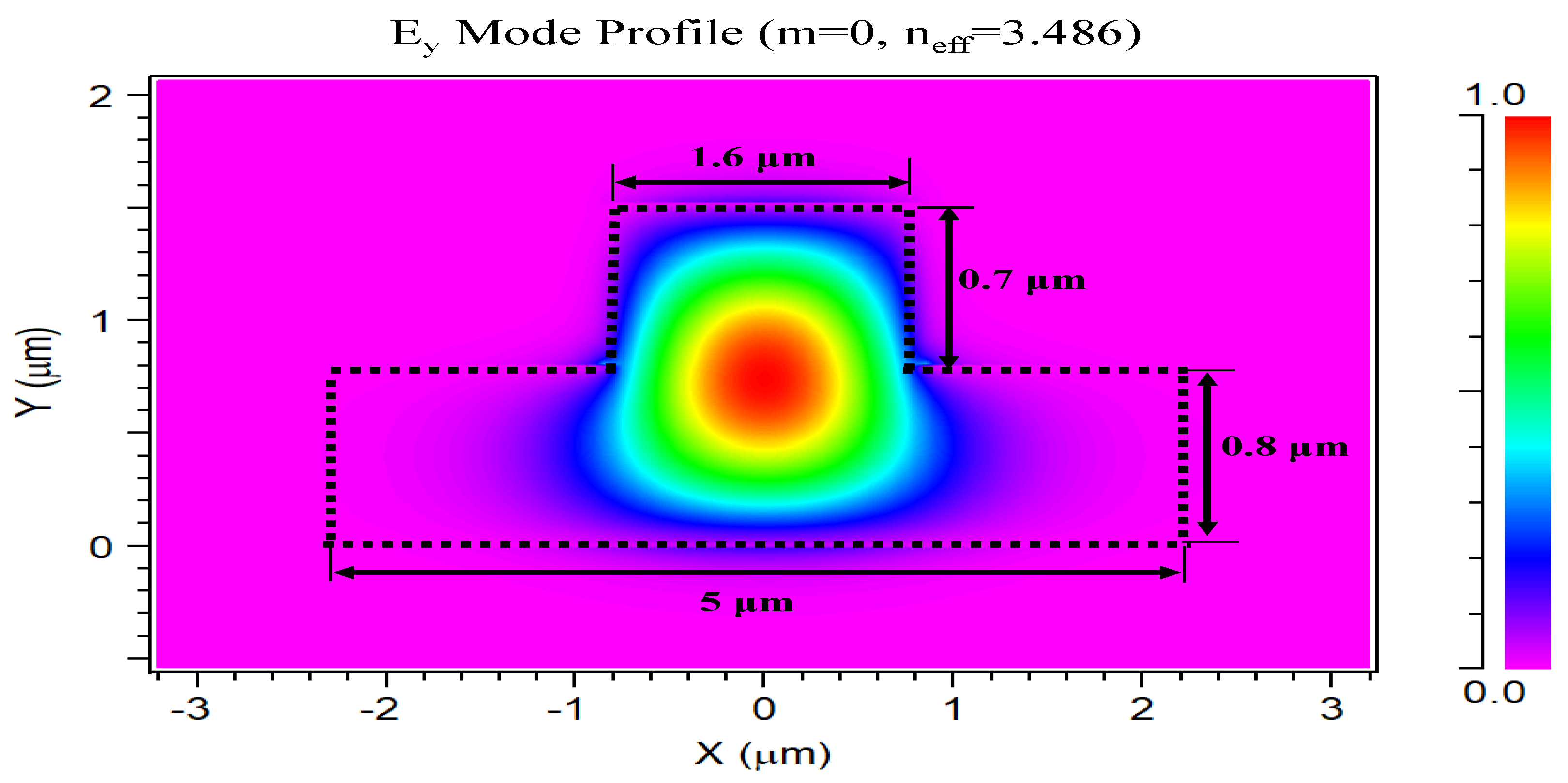
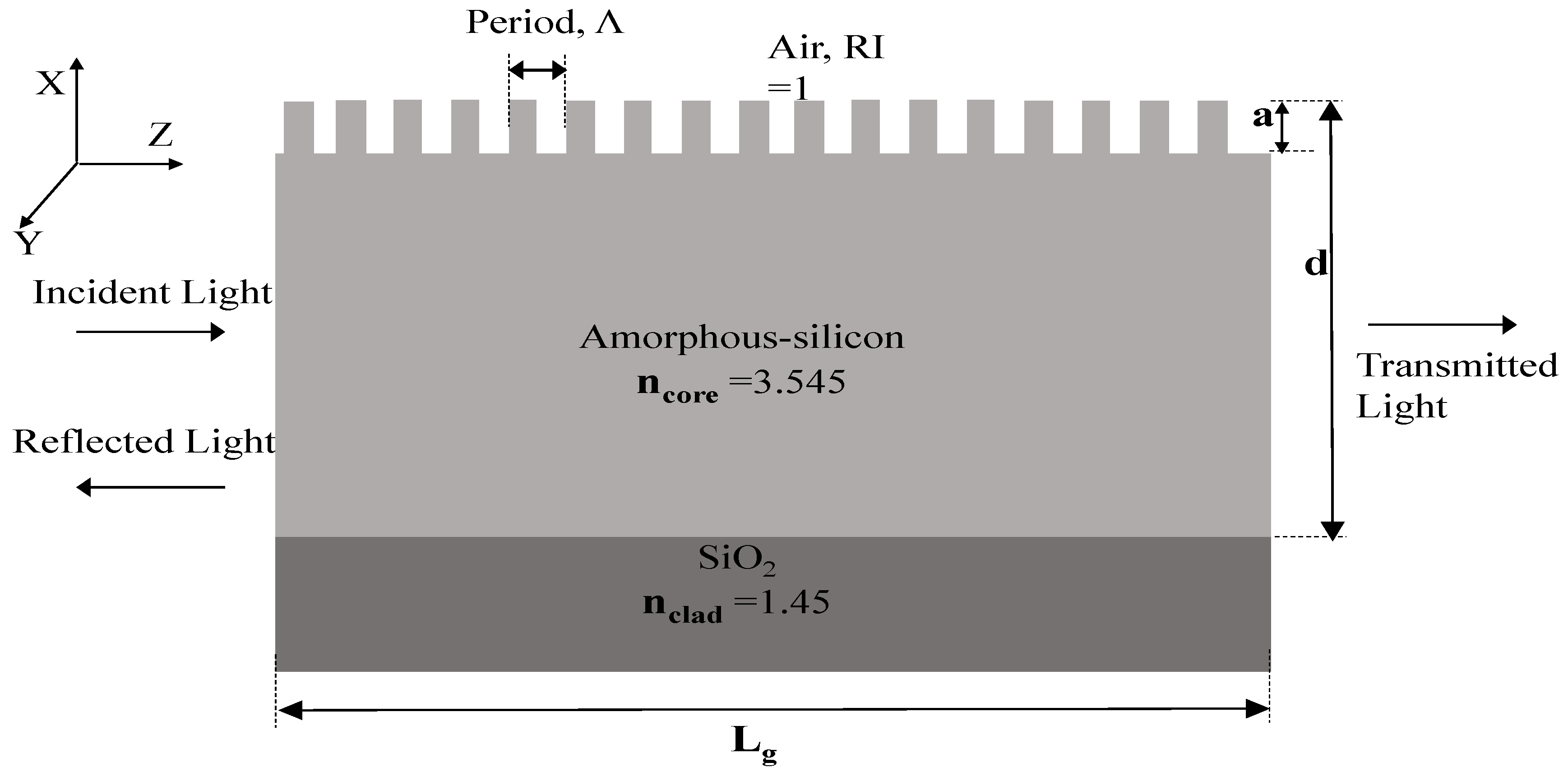
3.2. Waveguide Bragg Grating
3.3. Opto-Mechanical Coupling
3.4. Sensitivity and Resolution
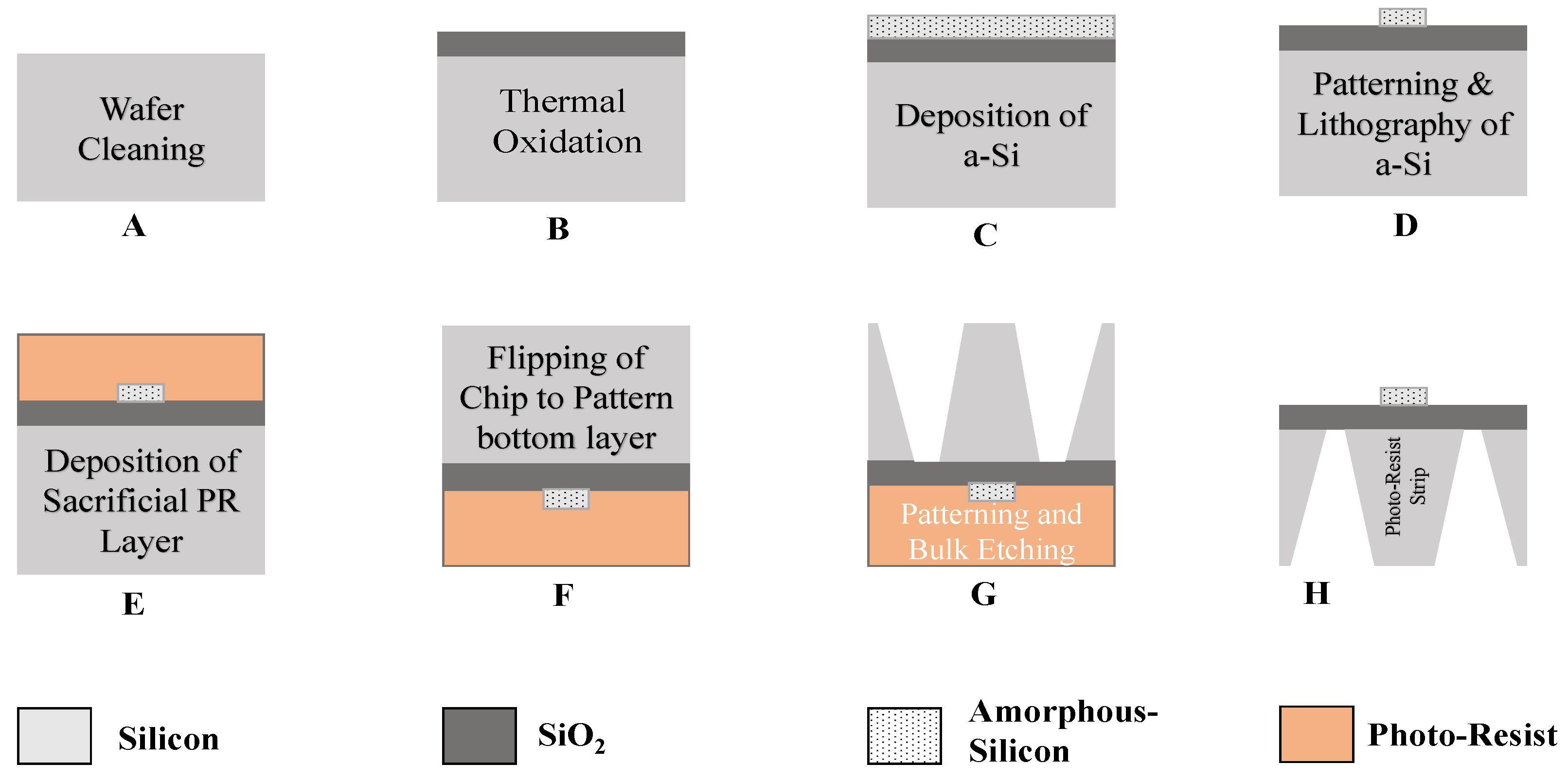
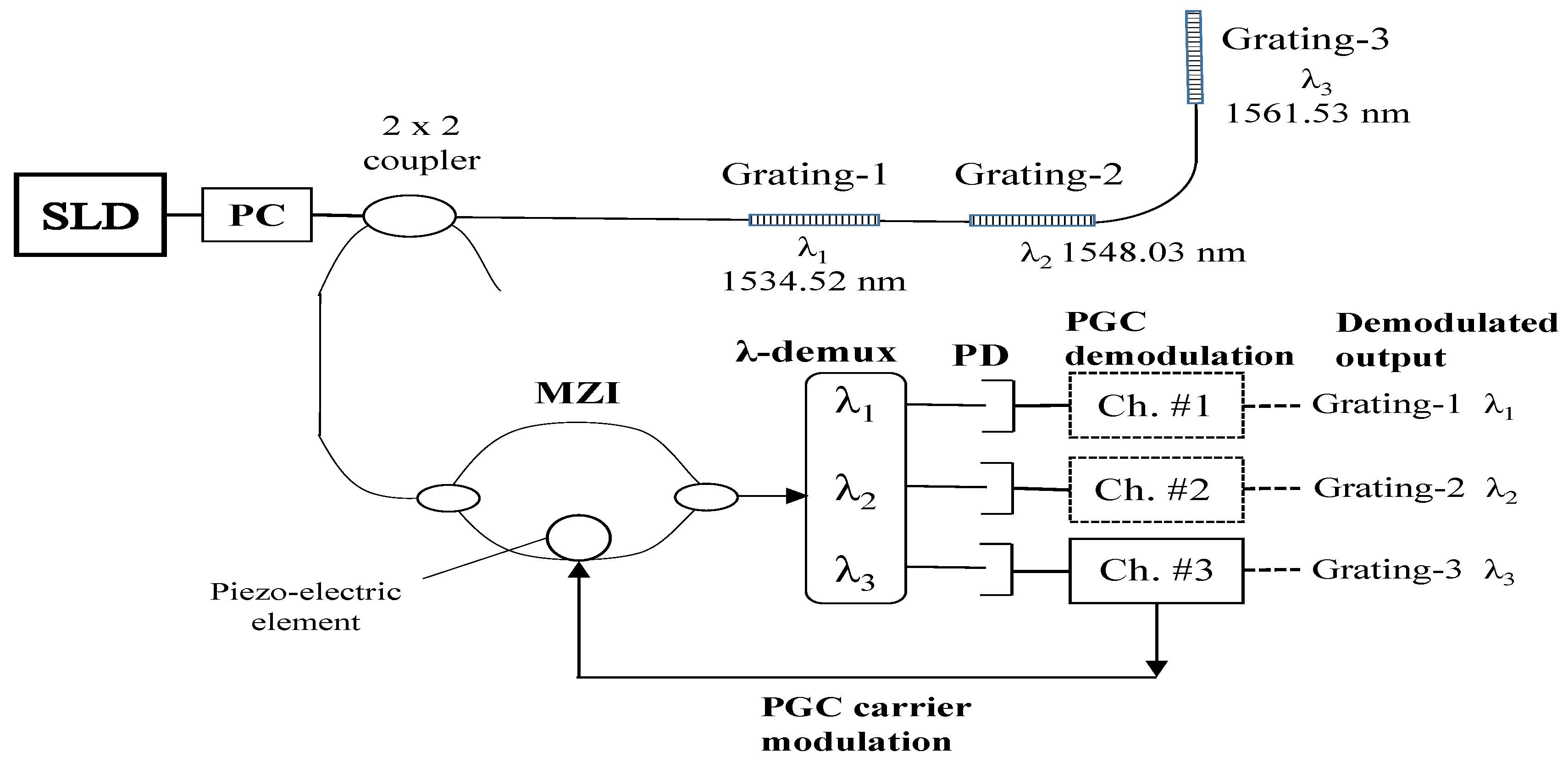
4. Proposed Fabrication Procedure and Testing Set-up
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Solgaard, O.; Godil, A.A.; Howe, R.T.; Lee, L.P.; Peter, Y.A.; Zappe, H. Optical MEMS: From Micromirrors to Complex Systems. J. Microelectromech. Syst. 2014, 23, 517–538. [Google Scholar] [CrossRef]
- Pattnaik, P.K.; Vijayaaditya, B.; Srinivas, T.; Selvarajan, A. Optical MEMS pressure and vibration sensors using integrated optical ring resonators. In Proceedings of the SENSORS, 2005 IEEE, Irvine, CA, USA, 30 October–3 November 2005; pp. 636–639. [Google Scholar]
- Perez, M.A.; Shkel, A.M. Design and demonstration of a bulk micromachined Fabry–Pérot μg-resolution accelerometer. IEEE Sens. J. 2007, 7, 1653–1662. [Google Scholar] [CrossRef]
- Yang, J.; Jia, S.; Du, Y. Novel optical accelerometer based on Fresnel diffractive micro lens. Sens. Actuators A Phys. 2009, 151, 133–140. [Google Scholar] [CrossRef]
- Zandi, K.; Wong, B.; Zou, J.; Kruzelecky, R.V.; Jamroz, W.; Peter, Y.A. In-plane silicon-on-insulator optical MEMS accelerometer using waveguide fabry-perot microcavity with silicon/air bragg mirrors. In Proceedings of the 23rd IEEE International Conference Micro Electro Mechanical Systems (EMS), Wanchai, Hong Kong, China, 24–28 January 2010; pp. 839–842. [Google Scholar]
- Rogers, A. Distributed optical-fibre sensing. Meas. Sci. Technol. 1999, 10, R75. [Google Scholar] [CrossRef]
- Sreekumar, K.; Asokan, S. Compact fiber Bragg grating dynamic strain sensor cum broadband thermometer for thermally unstable ambience. J. Opt. 2009, 12, 015502. [Google Scholar] [CrossRef]
- Wu, H.; Lin, Q.; Jiang, Z.; Zhang, F.; Li, L.; Zhao, L. A temperature and strain sensor based on a cascade of double fiber Bragg grating. Meas. Sci. Technol. 2019, 30, 065104. [Google Scholar] [CrossRef]
- Lim, A.E.; Song, J.; Fang, Q.; Li, C.; Tu, X.; Duan, N.; Chen, K.K.; Tern, R.P.; Liow, T. Review of Silicon Photonics Foundry Efforts. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 405–416. [Google Scholar] [CrossRef]
- Errando-Herranz, C.; Takabayashi, A.Y.; Edinger, P.; Sattari, H.; Gylfason, K.B.; Quack, N. MEMS for Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–16. [Google Scholar] [CrossRef]
- Bao, M.H. Micro Mechanical Transducers: Pressure Sensors, Accelerometers and Gyroscopes; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Guldimann, B.; Dubois, P.; Clerc, P.A.; de Rooij, N. Fiber Optic—MEMS Accelerometer with high mass displacement resolution. In Transducers’ 01 Eurosensors XV; Springer: Berlin, Heidelberg, 2001; pp. 438–441. [Google Scholar]
- Plaza, J.A.; Llobera, A.; Dominguez, C.; Esteve, J.; Salinas, I.; Garcia, J.; Berganzo, J. BESOI-based integrated optical silicon accelerometer. J. Microelectromech. Syst. 2004, 13, 355–364. [Google Scholar] [CrossRef]
- Zhang, B.; Li, W.F. Development of a micro accelerometer based MOEMS. In Proceedings of the 2012 International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Shaanxi, China, 29 August–1 September 2012; pp. 250–253. [Google Scholar]
- Zandi, K.; Zou, J.; Wong, B.; Kruzelecky, R.V.; Peter, Y.A. VOA-based optical MEMS accelerometer. In Proceedings of the 16th International Conference on Optical MEMS and Nanophotonics, Istanbul, Turkey, 8–11 August 2011; pp. 15–16. [Google Scholar]
- Hortschitz, W.; Steiner, H.; Sachse, M.; Stifter, M.; Kohl, F.; Schalko, J.; Jachimowicz, A.; Keplinger, F.; Sauter, T. Robust Precision Position Detection With an Optical MEMS Hybrid Device. IEEE Trans. Ind. Electron. 2012, 59, 4855–4862. [Google Scholar] [CrossRef]
- Mo, W.; Wu, H.; Gao, D.; Zhou, Z. A novel accelerometer based on microring resonator. Chin. Opt. Lett. 2009, 7, 798–801. [Google Scholar]
- Mo, W.; Zhou, Z.; Wu, H.; Gao, D. Silicon-based stress-coupled optical racetrack resonators for seismic prospecting. IEEE Sens. J. 2011, 11, 1035–1039. [Google Scholar] [CrossRef]
- Bramhavar, S.; Kharas, D.; Juodawlkis, P. Integrated Photonic Inertial Sensors. In OSA Advanced Photonics Congress (AP) 2019 (IPR, Networks, NOMA, SPPCom, PVLED); OSA Technical Digest (Optical Society of America: Burlingame, CA, USA, 2019; p. ITh3A.2. [Google Scholar]
- Wu, Y.; Zeng, X.; Rao, Y.; Gong, Y.; Hou, C.; Yang, G. MOEMS Accelerometer Based on Microfiber Knot Resonator. IEEE Photonics Technol. Lett. 2009, 21, 1547–1549. [Google Scholar] [CrossRef]
- Hou, C.L.; Wu, Y.; Zeng, X.; Zhao, S.; Zhou, Q.; Yang, G. Novel high sensitivity accelerometer based on a microfiber loop resonator. Opt. Eng. 2010, 49, 014402. [Google Scholar]
- Krause, A.G.; Winger, M.; Blasius, T.D.; Lin, Q.; Painter, O. A high-resolution microchip optomechanical accelerometer. Nat. Photonics 2012, 6, 768. [Google Scholar] [CrossRef]
- Sheikhaleh, A.; Abedi, K.; Jafari, K. An optical MEMS accelerometer based on a two-dimensional photonic crystal add-drop filter. J. Lightwave Technol. 2017, 35, 3029–3034. [Google Scholar] [CrossRef]
- Krishnamoorthy, U.; Olsson Iii, R.; Bogart, G.R.; Baker, M.; Carr, D.; Swiler, T.; Clews, P. In-plane MEMS-based nano-g accelerometer with sub-wavelength optical resonant sensor. Sens. Actuators A Phys. 2008, 145, 283–290. [Google Scholar] [CrossRef]
- Schröpfer, G.; Elflein, W.; de Labachelerie, M.; Porte, H.; Ballandras, S. Lateral optical accelerometer micromachined in (100) silicon with remote readout based on coherence modulation. Sens. Actuators A Phys. 1998, 68, 344–349. [Google Scholar] [CrossRef]
- Lin, Q.; Chen, L.; Li, S.; Wu, X. A high-resolution fiber optic accelerometer based on intracavity phase-generated carrier (PGC) modulation. Meas. Sci. Technol. 2010, 22, 015303. [Google Scholar] [CrossRef]
- Trigona, C.; Andò, B.; Baglio, S. Design, fabrication, and characterization of BESOI-accelerometer exploiting photonic bandgap materials. IEEE Trans. Instrum. Meas. 2014, 63, 702–710. [Google Scholar] [CrossRef]
- Davies, E.; George, D.S.; Gower, M.C.; Holmes, A.S. MEMS Fabry–Pérot optical accelerometer employing mechanical amplification via a V-beam structure. Sens. Actuators A Phys. 2014, 215, 22–29. [Google Scholar] [CrossRef]
- Zhao, M.; Jiang, K.; Bai, H.; Wang, H.; Wei, X. A MEMS based Fabry–Pérot accelerometer with high resolution. Microsys. Technol. 2020, 26, 1961–1969. [Google Scholar] [CrossRef]
- Berkoff, T.; Kersey, A. Experimental demonstration of a fiber Bragg grating accelerometer. IEEE Photonics Technol. Lett. 1996, 8, 1677–1679. [Google Scholar] [CrossRef]
- Storgaard-Larsen, T.; Bouwstra, S.; Leistiko, O. Opto-mechanical accelerometer based on strain sensing by a Bragg grating in a planar waveguide. Sens. Actuators A Phys. 1996, 52, 25–32. [Google Scholar] [CrossRef]
- Kersey, A.; Berkoff, T.; Morey, W. High-resolution fibre-grating based strain sensor with interferometric wavelength-shift detection. Electron. Lett. 1992, 28, 236–238. [Google Scholar] [CrossRef]
- Rao, Y.J. In-fibre Bragg grating sensors. Meas. Sci. Technol. 1997, 8, 355. [Google Scholar] [CrossRef]
- Gagliardi, G.; Salza, M.; Ferraro, P.; De Natale, P.; Di Maio, A.; Carlino, S.; De Natale, G.; Boschi, E. Design and test of a laser-based optical-fiber Bragg-grating accelerometer for seismic applications. Meas. Sci. Technol. 2008, 19, 085306. [Google Scholar] [CrossRef]
- Lam, T.T.; Gagliardi, G.; Salza, M.; Chow, J.H.; De Natale, P. Optical fiber three-axis accelerometer based on lasers locked to π phase-shifted Bragg gratings. Meas. Sci. Technol. 2010, 21, 094010. [Google Scholar] [CrossRef]
- Rosenberger, M.; Eisenbeil, W.; Schmauss, B.; Hellmann, R. Simultaneous 2D strain sensing using polymer planar Bragg gratings. Sensors 2015, 15, 4264–4272. [Google Scholar] [CrossRef]
- Malara, P.; Campanella, C.; Giorgini, A.; Avino, S.; Zullo, R.; Gagliardi, G.; De Natale, P. Sensitive strain measurements with a fiber Bragg-grating ring resonator. In Proceedings of the 23rd International Conference on Optical Fibre Sensors, International Society for Optics and Photonics, Santander, Spain, 2–6 June 2014; Volume 9157, p. 915706. [Google Scholar]
- Gagliardi, G.; De Nicola, S.; Ferraro, P.; De Natale, P. Interrogation of fiber Bragg-grating resonators by polarization-spectroscopy laser-frequency locking. Opt. Express 2007, 15, 3715–3728. [Google Scholar] [CrossRef]
- Gagliardi, G.; Salza, M.; Ferraro, P.; De Natale, P. Interrogation of FBG-based strain sensors by means of laser radio-frequency modulation techniques. J. Opt. A Pure Appl. Opt. 2006, 8, S507. [Google Scholar] [CrossRef]
- Gagliardi, G.; Salza, M.; Lam, T.T.Y.; Chow, J.H.; De Natale, P. 3-axis accelerometer based on lasers locked to π-shifted fibre Bragg gratings. In Proceedings of the 20th International Conference on Optical Fibre Sensors, International Society for Optics and Photonics, Edinburgh, UK, 5–9 October 2009; Volume 7503, p. 75033X. [Google Scholar]
- Neeharika, V.; Pattnaik, P.K. Optical MEMS pressure sensors incorporating dual waveguide Bragg gratings on diaphragms. IEEE Sens. J. 2015, 16, 681–687. [Google Scholar] [CrossRef]
- Thondagere, C.; Kaushalram, A.; Srinivas, T.; Hegde, G. Mathematical modeling of optical MEMS differential pressure sensor using waveguide Bragg gratings embedded in Mach Zehnder interferometer. J. Opt. 2018, 20, 085802. [Google Scholar] [CrossRef]
- Rosenberger, M.; Hessler, S.; Belle, S.; Schmauss, B.; Hellmann, R. Compressive and tensile strain sensing using a polymer planar Bragg grating. Opt. Express 2014, 22, 5483–5490. [Google Scholar] [CrossRef]
- Rosenberger, M.; Hessler, S.; Belle, S.; Schmauss, B.; Hellmann, R. TOPAS-based humidity insensitive polymer planar Bragg gratings for temperature and multi-axial strain sensing. Proc. SPIE 9444. In Proceedings of the International Seminar on Photonics, Optics, and Its Applications (ISPhOA 2014), Sanur, Bali, Indonesia, 14–15 October 2014; pp. 43–48. [Google Scholar]
- Balasubramanian, M.; Poornalakshmi, U.; Agarwal, S.; Pattnaik, P.K. Waveguide grating based SOI MOEMS accelerometer. In Proceedings of the 2015 International Conference on Optical MEMS and Nanophotonics (OMN), Jerusalem, Israel, 2–5 August 2015; pp. 1–2. [Google Scholar]
- Malayappan, B.; Poornalakshmi, U.; Pattnaik, P.K. Temperature insensitive waveguide grating based SOI MOEMS accelerometer. In Proceedings of the 2015 Workshop on Recent Advances in Photonics (WRAP), Bangalore, India, 16–17 December 2015; pp. 1–3. [Google Scholar]
- Tsao, S.L.; Lee, S.G. Characteristics analysis of SOI waveguide Michelson interferometers for developing biomedical fiber temperature-sensing head. In Proceedings of the Photonics Taiwan, International Society for Optics and Photonics, Taipei, Taiwan, 26–28 July 2000; pp. 278–285. [Google Scholar]
- Christensen, R. Mechanics of Composite Materials; A Wiley-Interscience Publication: New York, NY, USA, 1979. [Google Scholar]
- Aalto, T. Microphotonic Silicon Waveguide Components; VTT Technical Research Centre of Finland: Aalto, Finland, 2004. [Google Scholar]
- Uppalapati, P.L.; Malayappan, B.; Krishnaswamy, N.; Pattnaik, P.K. Electrostatically tunable MOEMS waveguide Bragg grating-based DWDM optical filter. J. Micro/Nanolithography MEMS MOEMS 2019, 18, 015503. [Google Scholar] [CrossRef]
- Lakshmi, U.P.; Balasubramanian, M.; Narayan, K.; Pattnaik, P.K. MEMS tunable SOI waveguide Bragg grating filter with 1.3 THz tuning range for C-band 100 GHz DWDM optical network. Photonic Netw. Commun. 2019, 38, 280–288. [Google Scholar] [CrossRef]
- Pollock, C.; Lipson, M. Integrated Photonics; Springer: Boston, MA, USA, 2003. [Google Scholar]
- Yariv, A. Coupled-mode theory for guided-wave optics. IEEE J. Quantum Electron. 1973, 9, 919–933. [Google Scholar] [CrossRef]
- Erdogan, T. Fiber grating spectra. J. Lightwave Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef]
- Tosi, D. Review and analysis of peak tracking techniques for fiber Bragg grating sensors. Sensors 2017, 17, 2368. [Google Scholar] [CrossRef]
- Cooper, D.J.; Smith, P.W. Limits in wavelength measurement of optical signals. JOSA B 2004, 21, 908–913. [Google Scholar] [CrossRef]
- Kogelnik, H. Filter response of nonuniform almost-periodic structures. Bell Syst. Tech. J. 1976, 55, 109–126. [Google Scholar] [CrossRef]
- Schriever, C.; Bohley, C.; Schilling, J.; Wehrspohn, R.B. Strained silicon photonics. Materials 2012, 5, 889–908. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Almeida, V.R.; Panepucci, R.R.; Lipson, M. Experimental demonstration of guiding and confining light in nanometer-size low-refractive-index material. Opt. Lett. 2004, 29, 1626–1628. [Google Scholar] [CrossRef]
- Frey, B.J.; Leviton, D.; Madison, T. Temperature-dependent refractive index of silicon and germanium. Proc. SPIE 6273. In Proceedings of the Optomechanical Technologies for Astronomy 2006, Orlando, FL, USA, 24–31 May 2006; pp. 790–799. [Google Scholar]
- Gabrielson, T.B. Mechanical-thermal noise in micromachined acoustic and vibration sensors. IEEE Trans. Electron. Devices 1993, 40, 903–909. [Google Scholar] [CrossRef]
- Krishnan, G.; Kshirsagar, C.U.; Ananthasuresh, G.; Bhat, N. Micromachined high-resolution accelerometers. J. Indian Inst. Sci. 2007, 87, 333. [Google Scholar]
- Motamedi, M.E. MOEMS: Micro-Opto-Electro-Mechanical Systems; SPIE Press: Bellingham, WA, USA, 2005; Volume 126. [Google Scholar]
- Gagliardi, G.; Salza, M.; Ferraro, P.; Chehura, E.; Tatam, R.P.; Gangopadhyay, T.K.; Ballard, N.; Paz-Soldan, D.; Barnes, J.A.; Loock, H.P.; et al. Optical fiber sensing based on reflection laser spectroscopy. Sensors 2010, 10, 1823–1845. [Google Scholar] [CrossRef]
- Kersey, A.; Berkoff, T.; Morey, W. Fiber-optic Bragg grating strain sensor with drift-compensated high-resolution interferometric wavelength-shift detection. Opt. Lett. 1993, 18, 72–74. [Google Scholar] [CrossRef]
- Berkoff, T.; Kersey, A. Fiber Bragg grating array sensor system using a bandpass wavelength division multiplexer and interferometric detection. IEEE Photonics Technol. Lett. 1996, 8, 1522–1524. [Google Scholar] [CrossRef]
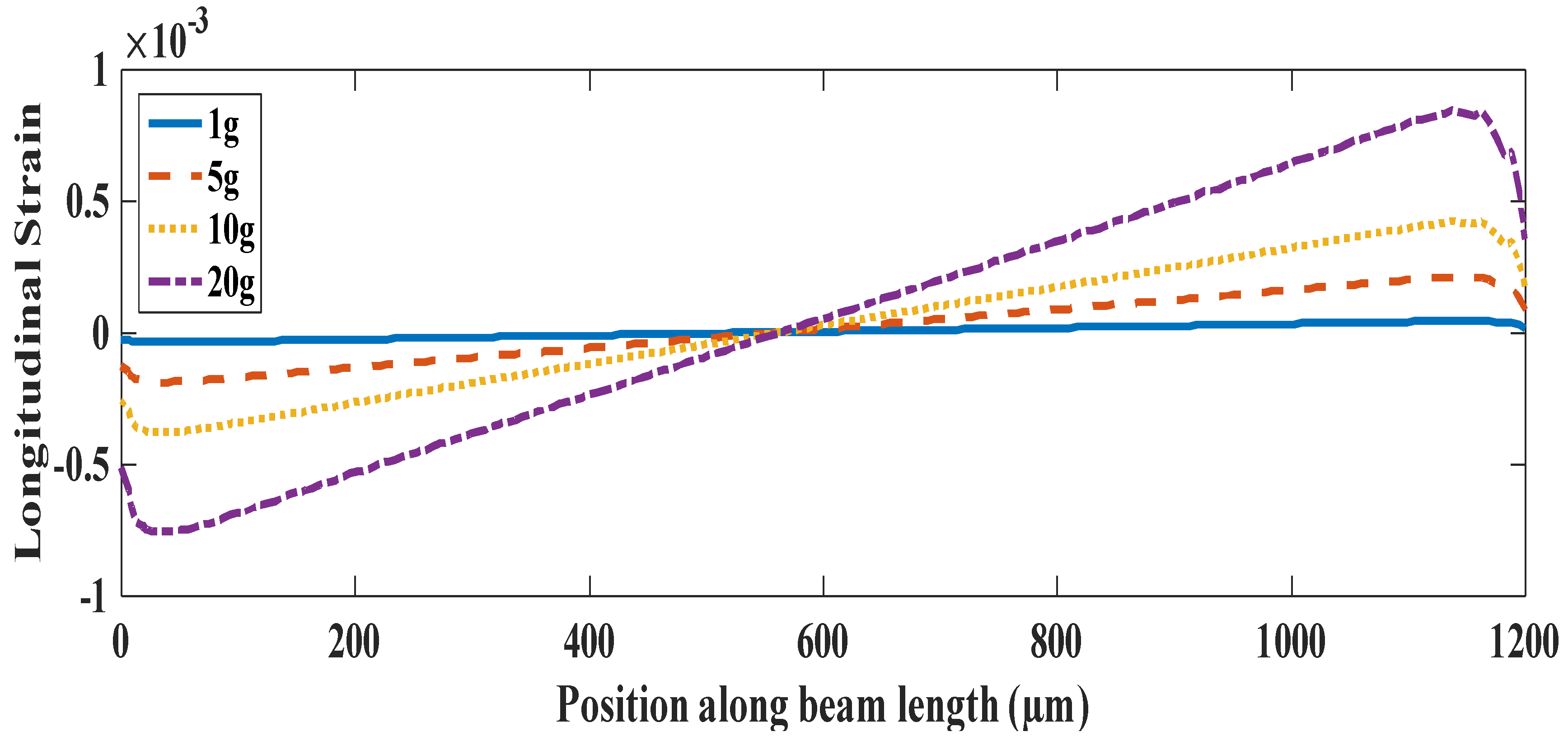

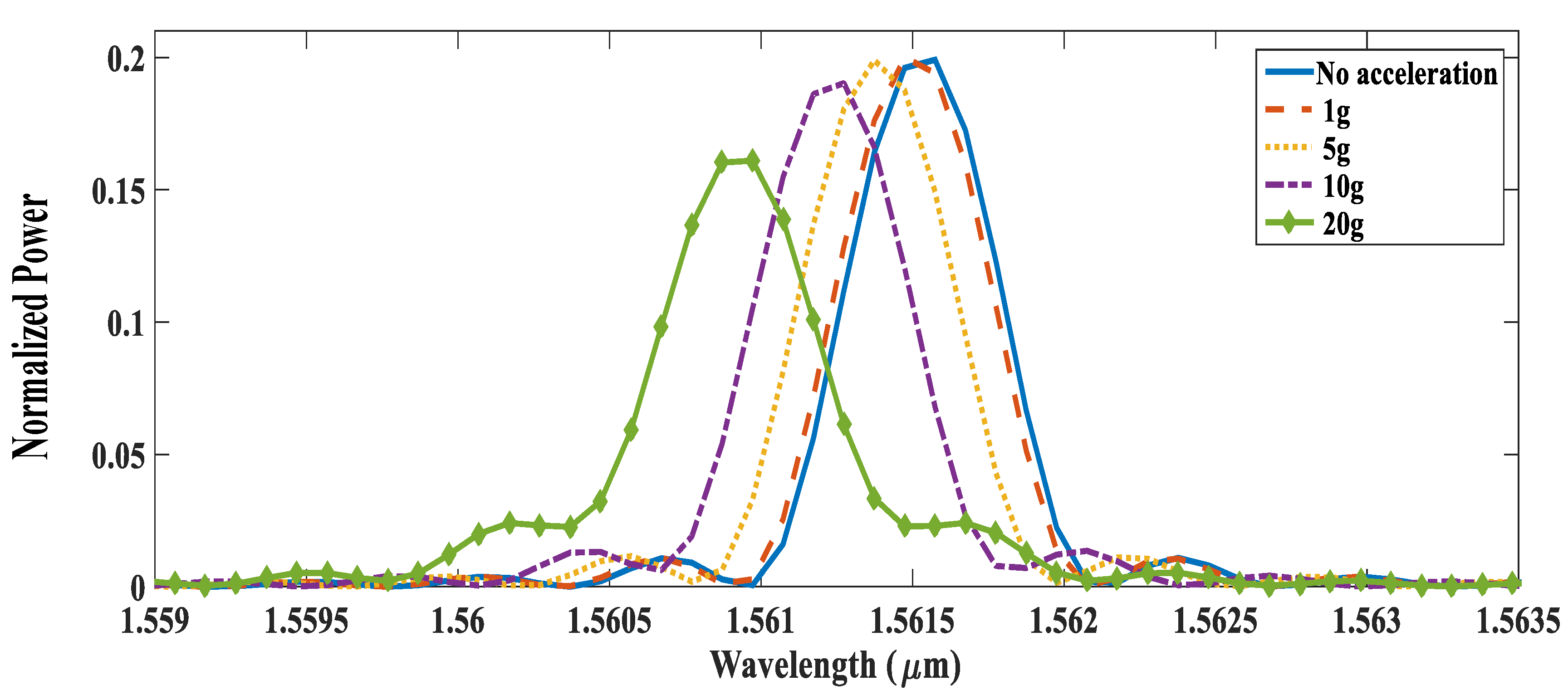
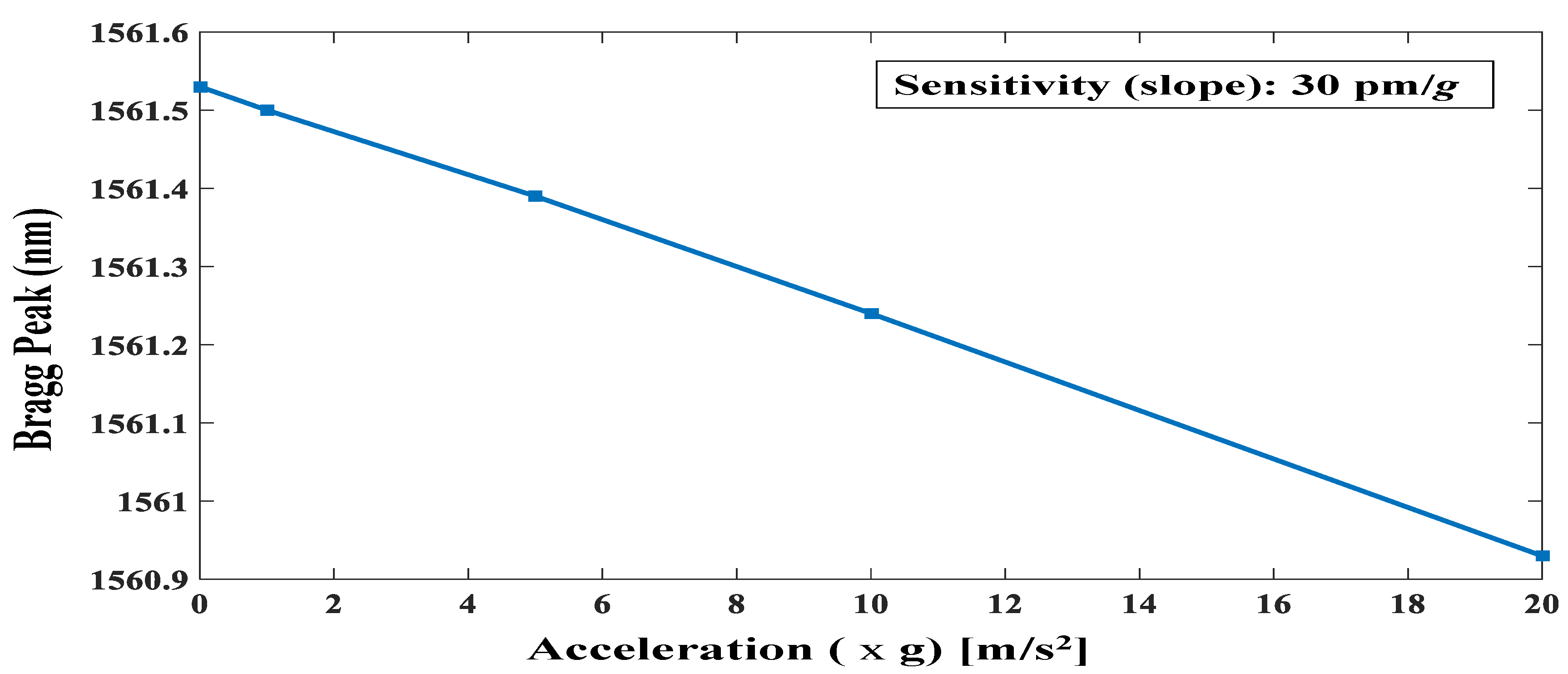
| Sensing Technique | Sensitivity | Range | Bandwidth | Remarks |
|---|---|---|---|---|
| Intensity Modulation [12,13,14,15,16] | Low | Low | Medium | Amenable to integration; free-space light propagation; source noise is crucial |
| Ring resonators [17,18,19,20,21] | High | Low | High | Small footprint; non-linear sensor output; guided-wave propagation; wavelength shift due to acceleration |
| Photonic Crystals [22,23] | High | Low | High | Coupling light into and out of sensor is challenging; guided-wave propagation; photonic bandgap is modified |
| Diffraction Gratings [24] | High | Low | Low to High | Free-space light propagation; complex packaging; high sensitivity requires complex detection mechanism |
| Interferometers [3,25,26,27,28,29] | Low to High | High | Low to High | Free-space light propagation; precise positioning and alignment needed |
| Bragg gratings [30,31,32,33,34,35,36] | Medium | High | Low | Guided-wave propagation; wavelength-encoded acceleration; advanced interrogation schemes allow sub-pico strain detection |
| Parameter | Value |
|---|---|
| Top side length of square proof-mass () | 4 mm |
| Thickness of proof-mass () | 400 m |
| Length of each beam (l) | 1200 m |
| Width of each beam (b) | 210 m |
| Thickness of each beam (h) | 5 m |
| Length of each Bragg grating () | 600 m |
| Etch depth of Bragg grating (a) | 50 nm |
| Refractive index of core in operating wavelength range () | 3.545 |
| Refractive index of cladding in operating wavelength range () | 1.45 |
| Thermo-optic coefficient at room temperature () | 1.5 × 10/K |
| Thermal expansion coefficient () | 2.62 × 10/K |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malayappan, B.; Krishnaswamy, N.; Pattnaik, P.K. Novel High-Resolution Lateral Dual-Axis Quad-Beam Optical MEMS Accelerometer Using Waveguide Bragg Gratings. Photonics 2020, 7, 49. https://doi.org/10.3390/photonics7030049
Malayappan B, Krishnaswamy N, Pattnaik PK. Novel High-Resolution Lateral Dual-Axis Quad-Beam Optical MEMS Accelerometer Using Waveguide Bragg Gratings. Photonics. 2020; 7(3):49. https://doi.org/10.3390/photonics7030049
Chicago/Turabian StyleMalayappan, Balasubramanian, Narayan Krishnaswamy, and Prasant Kumar Pattnaik. 2020. "Novel High-Resolution Lateral Dual-Axis Quad-Beam Optical MEMS Accelerometer Using Waveguide Bragg Gratings" Photonics 7, no. 3: 49. https://doi.org/10.3390/photonics7030049
APA StyleMalayappan, B., Krishnaswamy, N., & Pattnaik, P. K. (2020). Novel High-Resolution Lateral Dual-Axis Quad-Beam Optical MEMS Accelerometer Using Waveguide Bragg Gratings. Photonics, 7(3), 49. https://doi.org/10.3390/photonics7030049