Abstract
This article presents the results of a computer simulation of whispering gallery modes in the structure of a silicon disk resonator with a wedge-shaped profile made on a silicon-on-isolator base (SOI). The rationale for the choice of silicon as a material for its manufacturing is given. The results of the study of the influence of the wedge angle on the whispering gallery mode parameters (WGM) are presented. The optimum wedge angle of a silicon disk resonator is determined, which ensures the minimum loss and maximum mode stability. The technological aspects of plasma-chemical etching processes for forming a wedge-shaped profile of the edge of a silicon disk resonator are studied.
1. Introduction
The possibility of creating high-quality optical dielectric resonators using the phenomenon of total internal reflection of a wave in axisymmetric bodies to localize light beams, called the whispering gallery modes, was expressed in 1939 by R.D. Richtmyer r [1]. The modes got this name by analogy with the phenomenon of the propagation of acoustic waves in St. Paul’s cathedral described by Lord Rayleigh.
Whispering gallery modes (WGM) are electromagnetic waves that are circulating in a very limited structure, which from geometric optics’ point of view are considered as optical rays that are completely reflected and focused by the surface itself. A circulating ray of light, returning to the same point with the same phase, structurally interferes with itself, forming resonant standing waves [2,3,4]
The increasing interest in WGM resonators is associated with a unique combination of such characteristics as:
- small size;
- small mode volumes;
- high quality factor (Q-factor);
- possibility of application in optical and telecommunication systems.
The scope of WGM resonators in photonics is extremely extensive. On their basis, it is possible to create a number of functional devices: modulators, switches, resonators for pumping lasers, bio- and chemical sensors. They also find application in unique quantum nonperturbing experiments and measurements with cold atoms, proposed in 1982 by V. B. Braginsky [5].
Recent studies have demonstrated the possibility of generating a coherent frequency comb in optical microresonators [6,7], which opens up new prospects in the development of low-noise radio frequency sources [8], optical frequency synthesizers [9] and compact spectrometers [10,11].
In [12], the generation of a coherent frequency comb by means of soliton mode locking in the middle infrared band on silicon resonators with anomalous group velocity dispersion was clearly demonstrated.
2. Materials and Methods
2.1. Description of the Investigated Constructions of the Silicon Disk WGM Resonator
Currently, there are a number of constructions of WGM resonators. Naturally, each of them has its pros and cons. One of the main parameters of an optical resonator is the Q-factor. The Q-factor of a resonator is the total energy of the circulating modes inside the resonator divided by the amount of energy that is introduced into the resonator during one full oscillation of the field to maintain equilibrium [13]. The use of ultra-high-Q WGM resonators makes it possible to achieve extremely high values of the mode circulation intensity even at relatively low pump powers. This allows the implementation of non-linear optical effects to be simplified [14].
The Q-factor of the resonator (Qint) is determined by losses arising for various reasons, and can be represented as follows: [14]
where Qmat is the intrinsic absorption in the material (wave attenuation in the material); Qsurf are losses owing to absorption on the surface; Qscatt is scattering loss, mainly owing to defects such as roughness; Qbend are losses due to bending.
Qint-1 = Qmat-1 + Qsurf-1 + Qscatt-1 + Qbend-1
In creating optical resonators, it is extremely important to use materials with low optical losses in order to achieve a long photon lifetime (high Q-factor) [15]. To maintain the mode inside the waveguide structure, it is necessary to choose the materials of the core and the cladding so that the refractive index of the core exceeds the refractive index of the cladding. The higher the difference between the refractive indices of the adjacent media, the higher the mode localization in the waveguide medium is.
Waveguide structures and WGM structures of resonators that are made on the basis of dielectric films are widely studied. In particular, silicon oxide is one of the suitable materials for the manufacture of WGM resonators owing to the low absorption inside the material, the high difference in refractive indices (nSiO2 = 1.46; nAir = 1), as well as the possibility of manufacturing and, therefore, integration with devices made using silicon technology as the most common in microelectronics.
One of the promising structures is a toroidal WGM resonator made of silicon oxide using a CO2 laser, which is used to fuse a quartz disk in order to reduce the roughness of the surface of the microdisk edge [16,17]. However, this technology is very complex and expensive and also requires the use of unique, expensive equipment.
In [18], a method for manufacturing a spiral WGM waveguide made of a silicon oxide film 8 μm thick etched to form a wedge-shaped profile on both sides was described. According to the results of measurements made on an optical backscatter reflectometer (LunaOBR 4400), researchers at the University of California chose an optimal wedge angle of 27°, which, in their opinion, can optimally hold the mode inside the resonator.
Silicon is the main material used in modern microelectronics and photonics. The use of silicon as a material for the manufacture of various elements is advisable for several reasons: the processing technology is well developed, and it is possible to create elements and devices on a single crystal, which simplifies the integration of elements in the product as much as possible, increases the reproducibility of manufacturing processes and reduces the cost of the final product.
In addition, owing to its high nonlinear refractive index n2 = 4.5 · 10–18 m2/W [19], which makes it possible to observe nonlinear effects at fairly low power levels, silicon is an extremely promising material for the manufacture of nonlinear devices in the near and mid-IR range, which opens up prospects for the development of nonlinear elements based on WGMs.
It is important to note that owing to the greater difference in the refractive indices at the interfaces (air–silicon–air compared with air–silicon oxide–air), it should be expected that the mode formed in the silicon disk resonator (refractive index of silicon n = 3.46) should be more sustainable. This makes it possible to fabricate a high-quality WGM resonator of a smaller size, thereby leveling the effect of optical linear losses in silicon. This assumption is also confirmed by studies proving the possibility of achieving a Q-factor of 1.2 · 109 in silicon optical resonators at a wavelength of 1550 μm [20].
Silicon has a significant material light wave attenuation coefficient owing to its crystal lattice structural features. Let us consider the light wave transmitted to the resonator in terms of wave-particle duality theory (the concept in quantum mechanics that every particle or quantum entity may be described as either a particle or a wave).
Attenuation occurs as a result of photon interaction (collision) with nodes of the crystal lattice. Such interactions lead to individual photon energy loss and consequently decreasing intensity of the whole luminous flux. The attenuation value is directly dependent on the quantity of such interactions.
Therefore we have chosen a wedge-shaped silicon disk resonator profile for further research, since such profile notably reduces the repeatedly reflected wave optical path length.
Given the structure of the silicon crystal lattice it is critical to determine the optimal wedge angle, namely the optical path length of the input radiation.
Based on the above results obtained by researchers from California [18], and also minding the prospects of using silicon as a material for manufacturing high-quality WGM resonators with the possibility of obtaining nonlinear effects, we proposed a construction of the resonator, which is shown in Figure 1.
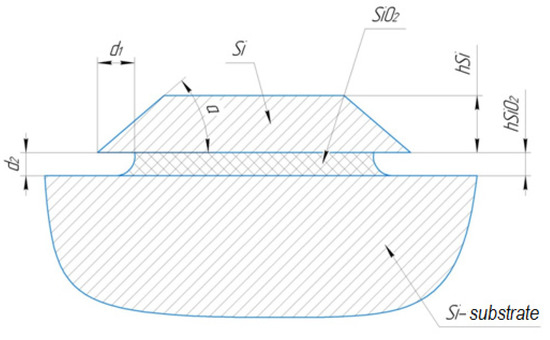
Figure 1.
Sketch of the cross-section of the structure of the silicon WGM waveguide, environment is air: hSi—the thickness (height) of the wedge-shaped waveguide; hSiO2—thickness (height) of the dielectric layer; d1—distance from the edge of the wedge to the beginning of the oxide beam (support); d2—the gap between the edge of the wedge-shaped waveguide and the Si substrate; a—wedge angle.
We have modeled the structure of the WGM using the finite element method in order to select the optimal resonator design for further manufacture. A sketch of the studied structure of a silicon WGM waveguide is shown in Figure 1.
2.2. Modeling of WGM Formation in a Silicon Disk Resonator with a Wedge-Shaped Profile
To evaluate the parameters of WGM resonator, a 3D model was developed. For the practical implementation of this construction, it was proposed to use the silicon-on-insulator (SOI) structure. The main parameters of the SOI structure are the working (upper) silicon layer and the separating dielectric (hidden layer).
The working layer of silicon had a thickness hSi = 5 μm and the hidden layer of silicon oxide had a thickness hSiO2 = 2 μm (Figure 1). The height of the silicon disk was chosen to be 5 μm. The diameter of the simulated resonator was 100 μm. These values were taken as the basis for building the model.
When designing the construction of a silicon disk resonator with a wedge-shaped profile, it is important to determine one of the key parameters, namely, the value of the wedge angle. This parameter is necessary to ensure the conditions under which a standing wave in the resonator can appear. It is also necessary to ensure conditions under which the mode spot magnitude and mode field intensity will be optimal for greater mode localization in the resonator. The possibility of achieving small (as compared with dielectric counterparts) dimensions of the resonator minimizes the effect of optical attenuation in silicon. We believe that the most optimal way the mode is formed is in the corner of the wedge, since the condition of the minimum distance between the materials is ensured. When a light wave propagates in a wedge-shaped profile, minimal optical losses are achieved owing to attenuation of the optical signal because of absorption and scattering by inhomogeneities in the waveguide layer.
In order to optimize the construction of the resonator by the finite element method, calculations were performed for the values of the wedge angles: 20°, 27°, 30°, and 70°. Figure 2 shows the results of modeling the WGM resonator at different angles of inclination of the sidewall. To simplify and reduce the calculation time, the developed model was transformed into 2D-axisymmetric. The scale on the right displays the distribution of the mode field’s strength.
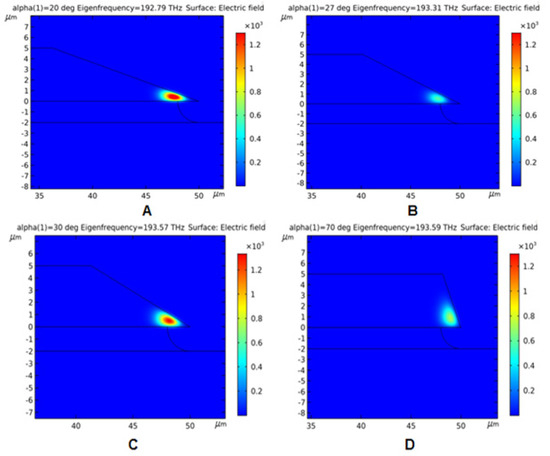
Figure 2.
Finite Element Modeling Results at a wavelength of λ0 = 1.55 μm, natural resonator frequency F0 ~ 193 THz;: (A)—wedge angle of 20°, the maximum value of the field is 1498 V/m; (B)—wedge angle 27°, maximum field value −580 V/m; (C)—wedge angle 30°, maximum field value −1398 V/m; (D)—wedge angle 70°, maximum field value −725 V/m. The scale on the right displays the distribution of the mode field strength.
The simulation results show that as the angle value changes, the maximum value of the mode field strength in it changes too. This means that when choosing the value of the angle of the wedge-shaped profile it is necessary to take into account the non-linearity of the dependence of the electric field strength on its value. So, based on the calculated data, when the wedge angle is 27° (the angle chosen as optimal for the silicon oxide material, as in [18]), the maximum field value is even lower than at. Therefore, the obtained dependence of electric field intensity versus the wedge angle, shown in Figure 3, is nonlinear.
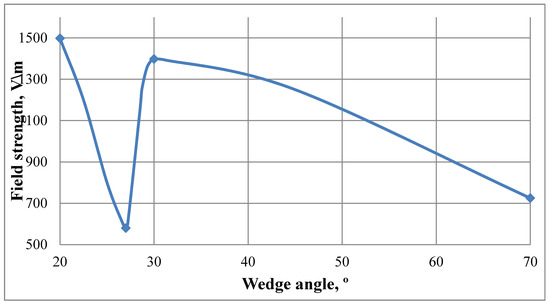
Figure 3.
The dependence of the electric field on the angle of the wedge-shaped profile.
It is also necessary to take into account that when performing calculations, the model under study is considered ideal, without roughness and defects that to one degree or another are formed during the manufacturing process. Therefore, when choosing the optimal angle of the projected wedge-shaped profile, it is necessary to give preference to the profile with the angle that makes a stable mode formation most likely when calculating the ideal model.
2.3. A Method of Obtaining a Wedge-Shaped Profile of Etching Silicon
We have studied the technological aspects of manufacturing the silicon disk resonators with optimal angles of the wedge-shaped profile.
A structural feature of the investigated disk WGM resonator is the wedge-shaped shape of its lateral face. In this case, the edge of the resonator should have a minimum roughness to minimize optical loss due to scattering.
In order to obtain the optimum angle of the lateral face, an experimental study of the technological regimes of plasma-chemical etching (PCT) of the wedge-shaped silicon profile was carried out.
One of the main conditions for the formation of an inclined etching profile is the preparation of a masking coating. In the process of testing, a photoresist mask with thicknesses of 2, 4.5, and 9 μm was used. In order to stabilize the photoresist mask before silicon PCT, the photoresist was heat treated in three consecutive modes at temperatures of 120, 140 and 160 ° C in a Binder electrical cabinet. The duration of each cycle was 10 min.
Another important criterion is the selection of the etching mode, which has an increased degree of anisotropy. High anisotropy in the process of dry etching of silicon, as a rule, is achieved by using a working gas or a combination of gases with a high chemical activity, for example, CF4 or a mixture of CF4 and O2.
Based on the results of testing the process of plasma-chemical etching of the wedge-shaped profile of a silicon disk WGM resonator, the optimal mode was selected that allows a minimum roughness of the side surface to be achieved. Figure 4 shows scanning electron microscope (SEM) images of etching profiles obtained with silicon PCT in a Cl4 + SF6 medium through a 4.5 μm thick photoresist mask.

Figure 4.
SEM images of the wedge-shaped profile of silicon etching.
3. Results
We have presented the results of modeling the wedge-shaped profile of a silicon disk WGM resonator. Silicon was chosen as the material for its manufacture, as an extremely promising material, especially from the point of view of studying and further applying its nonlinear properties (to create various kinds of optical elements). The results of computer simulation by the finite element method clearly demonstrated that when the angle of the wedge-shaped profile of the resonator model under consideration changes, the degree of localization of the mode formed in it gets changed.
Thanks to the studies, the optimal configuration of the silicon resonator with the angle of the wedge-shaped profile was selected for subsequent implementation. As can be seen from the result of modeling the formation of the mode with the wedge angle selected according to the results of the studies, the mode is localized and reliably held in the wedge corner even taking into account that the gap between the substrate and the “undercut” in silicon is only hSiO2 = 2 μm. This is possible because of the large difference in refractive indices. We can say that the mode is “reliably formed” in the corner of a silicon disk WGM resonator with a wedge-shaped profile as considered in the article.
During the development of the plasma-chemical etching process of silicon, the optimal mode was selected, which allowed us to obtain an etching profile with a selected angle of inclination of the sidewalls. This PCT mode allowed us to obtain the necessary etching profile during the formation of the WGM resonator structure. The studies presented in this article are a step for further research, the search for technological solutions and testing the manufacturing technology of WGM resonators of this construction.
Author Contributions
Conceptualization, A.Y. and S.G.; methodology, A.Y. and A.K.; software, A.K.; validation, V.A. and S.G.; formal analysis, A.Y. and A.K.; investigation, A.Y.; resources, V.A. and S.G.; data curation, V.A. and S.G.; writing—original draft preparation, A.Y.; writing—review and editing, D.G.; visualization, A.Y. and D.G.; supervision, V.A. and S.G.; project administration, V.A. and S.G.; funding acquisition, V.A. All authors have read and agreed to the published version of the manuscript.
Funding
This article was prepared with the financial support of the Ministry of Education and Science of the Russian Federation as part of the State Assignment for 2019 (project No. 0N59-2019-0020) “Theoretical and experimental studies of structural and technological methods for creating integrated optics elements compatible with silicon technology.” The etching process was carried out using equipment “Functional control and diagnostics of micro- and nanosystem technology” on the basis of SMC “Technological centre”. The authors are grateful to F.A. Egorov for useful discussions of the results of the work.
Acknowledgments
Theoretical and experimental studies of structural and technological methods for creating integrated optics elements compatible with silicon technology. The etching process was carried out using equipment “Functional control and diagnostics of micro- and nanosystem technology” on the basis of SMC “Technological centre”. The authors are grateful to F.A. Egorov for useful discussions of the results of the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Richtmyer, R.D. Dielectric resonators. J. Appl. Phys 1939, 10, 391–398. [Google Scholar] [CrossRef]
- Rayleigh, L. The problem of the whispering gallery. Philos. Mag. 1910, 20, 1001. [Google Scholar] [CrossRef]
- Rayleigh, L. Trapped whispering-gallery optical modes in white light-emitting diode lamps with remote phosphor. Sci. Pap. 1912, 5, 617. [Google Scholar]
- Little, B.E.; Laine, J.P.; Haus, H.A. Analytic theory of coupling from tapered fibers and half-blocksinto microsphere resonators. J. Lightwave Technol. 1999, 17, 704–715. [Google Scholar] [CrossRef]
- Braginsky, V.B.; Gorodetsky, M.L.; Ilchenko, V.S. Quality-factor and nonlinear properties of optical whispering gallery modes. Phys. Lett. A 1989, 137, 393–397. [Google Scholar] [CrossRef]
- Herr, T.; Brasch, V.; Jost, J.D.; Wang, C.Y.; Kondratiev, N.M.; Gorodetsky, M.L.; Kippenberg, T.J. Temporal solitons in optical microresonators. Nat. Photonics 2014, 8, 145. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Gaeta, A.L.; Lipson, M.; Gorodetsky, M.L. Dissipative Kerr solitons in optical microresonators. Science 2018, 361, eaan8083. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Eliyahu, D.; Ilchenko, V.S.; Savchenkov, A.A.; Matsko, A.B.; Seidel, D.; Maleki, L. High spectral purity Kerr frequency comb radio frequency photonic oscillator. Nat. Commun. 2015, 6, 7957. [Google Scholar] [CrossRef] [PubMed]
- Spencer, D.T.; Drake, T.; Briles, T.C.; Stone, J.; Sinclair, L.C.; Fredrick, C.; Li, Q.; Westly, D.; Ilic, B.R.; Bluestone, A.; et al. An optical-frequency synthesizer using integrated photonics. Nature 2018, 557, 81. [Google Scholar] [CrossRef] [PubMed]
- Suh, M.G.; Yang, Q.F.; Yang, K.Y.; Yi, X.; Vahala, K.J. Microresonator soliton dual-comb spectroscopy. Science 2016, 354, 600. [Google Scholar] [CrossRef] [PubMed]
- Pavlov, N.G.; Lihachev, G.; Koptyaev, S.; Lucas, E.; Karpov, M.; Kondratiev, N.M.; Bilenko, I.A.; Kippenberg, T.J.; Gorodetsky, M.L. Soliton dual frequency combs in crystalline microresonators. Opt. Lett. 2017, 42, 514. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Okawachi, Y.; Griffith, A.G.; Lipson, M.; Gaeta, A.L. Mode-locked mid-infrared frequency combs in a silicon microresonator. Optica 2016, 3, 854. [Google Scholar] [CrossRef]
- Gorodetsky, M.L. Optical Microresonators with Giant Q-Factor; Fizmatlit: Moscow, Russia, 2011; pp. 18–112. [Google Scholar]
- Gomilšek, M.; Ravnik, M. “Whispering Gallery Modes”. November 2011, University of Ljubljana, Faculty of Mathematics and Physics, Department of Physics, In Ljubljana Seminar. Available online: http://mafija.fmf.uni-lj.si/seminar/files/2011_2012/wgm.pdf (accessed on 30 November 2011).
- Tobing, L.; Dumon, P. Fundamental Principles of Operation and Notes on Fabrication of Photonic Microresonators. In Photonic Microresonator Research and Applications; Springer: Boston, MA, USA, 2010; Volume 156, pp. 1–27. [Google Scholar]
- Armani, D.K.; Kippenberg, T.J.; Spillane, S.M.; Vahala, K.J. Ultra-high-Q toroid microcavity on a chip. Nature 2003, 421, 925. [Google Scholar] [CrossRef] [PubMed]
- Armani, D.K. Ultra-High-Q Planar Microcavities and Appications. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2005. [Google Scholar]
- Chen, T.; Lee, H.; Watson, T.J.; Vahala, K.J. Design and characterization of whispering-gallery spiral waveguides. Opt. Express 2014, 22, 5196–5208. [Google Scholar] [CrossRef] [PubMed]
- Bristow, A.D.; Rotenberg, N.; Van Driel, H.M. Two-photon absorption and Kerr coefficients of silicon for 850–2200 nm. Appl. Phys. Lett. 2007, 90, 191104. [Google Scholar] [CrossRef]
- Shitikov, A.E.; Bilenko, I.A.; Kondratev, N.M.; Lobanov, V.E.; Markosyan, A.; Gorodetsky, M.L. Billion Q-factor in silicon WGM resonators. Opt. Lett. 2018, 5, 1525. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).