1. Introduction
In accordance with increasing traffic on optical communication networks, a spatial mode division multiplexing scheme based on orbital angular momentum (OAM) modes have attracted great attention in recent years [
1,
2,
3,
4]. By taking advantage of its unique property, that is, a helical phase front expressed as exp(-
ilϕ), where
l is a topological charge number, and
ϕ is an azimuthal angle, an OAM beam can have numerous modes distinguished by the topological charge number
l. To exploit this characteristic, there have been various theoretical and experimental studies on the generation, coupling, and multiplexing of OAM modes in fiber-optic communication [
5,
6,
7,
8,
9]. In spite of the fact that the fiber bending is inevitably involved in practical uses of the optical fibers, the effect of the fiber bending on OAM mode propagation has not been studied sufficiently with theoretical and numerical bases. There have only been a few investigations on the additional propagation loss or OAM mode deformation caused by the bending [
10,
11,
12]. More serious impairments on OAM modes due to the fiber bending have not been investigated in depth. For example, since the OAM mode is basically composed of two degenerate eigenmodes of opposite spatial symmetry which are excited with a relative phase difference of 90°, the additional phase difference caused by the effective index variation of the eigenmodes in the bent fiber will impair the OAM mode. In addition, the mode profile deformation in the bent optical fibers will cause intermodal crosstalk and coupling loss at the intersection between the bent and the straight parts of fibers. All these impairments should be investigated quantitatively for the practical use of OAM fibers.
In this paper, we theoretically investigated the bending-induced impairments on a OAM
l = −1 mode in three types of optical fibers: Vortex fiber (VF) [
13], ring core fiber (RCF) [
11], and photonic crystal fiber (PCF) [
10,
14]. The bending effects were investigated in terms of the bending loss, topological charge number degradation, and intermodal crosstalk.
2. Methods
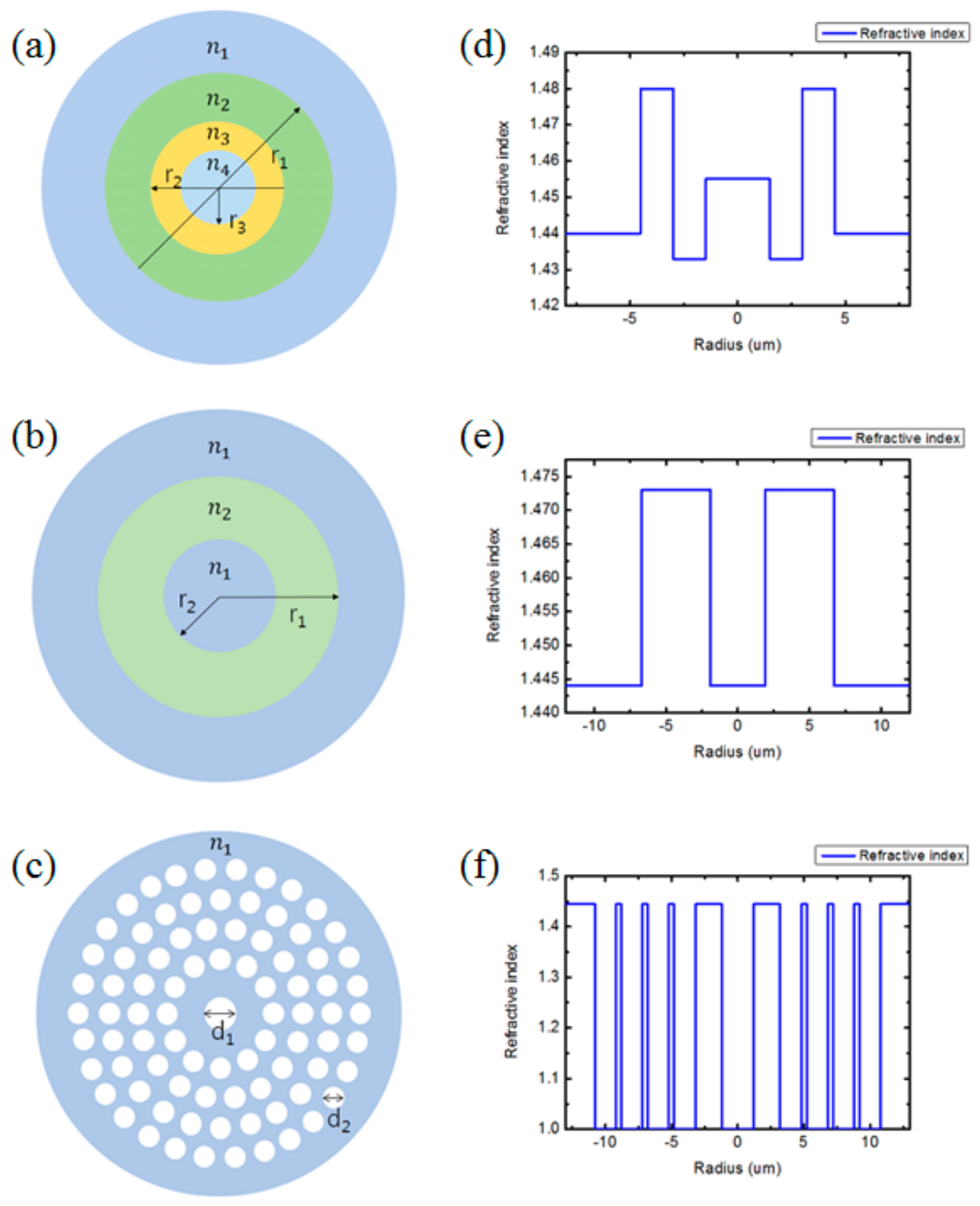
Figure 1 shows the cross-sections and the refractive index profiles (along the radial direction) of the three types of optical fibers that were investigated in this work. Those three types of fibers (VF, RCF, and PCF) were chosen as the representative types of OAM mode fibers that have been designed or experimentally demonstrated in the recent literature. The specific structures of the chosen fiber types were also adopted from the literature [
10,
11,
13,
14]. The PCF structure considered in reference [
10], where its bending loss was investigated numerically, was first chosen, and then, the structures of VF and RCF of about the same mode sizes as the PCF were chosen for a fair comparison. In the VF, depicted in
Figure 1a,d, there are three different core regions whose radii and refractive indices are r
1 = 4 µm, r
2 = 3 µm, r
3 = 1.5 µm, n
1 = 1.44, n
2 = 1.48, n
3 = 1.433, and n
4 = 1.455, respectively [
13]. As presented in
Figure 1b,e, the RCF has only two separate regions composed of the ring-shaped core and the clad. In this work, we considered one of the previously demonstrated RCF structures [
11], whose structural parameters are r
1 = 6.7 µm, r
2 = 1.9 µm, n
1 = 1.444, and n
2 = 1.473 at 1.55 µm. The PCF, depicted in
Figure 1c,f, consists of the central point defect (enlarged air hole) of d
1 = 2.4 µm and the ring-shaped defect (absence of air holes) in the concentrically arranged air holes of d
2 = 1.6 µm embedded in the matrix of n = 1.444 [
10,
14]. In all the fiber structures, step index profiles were assumed for simplicity.
To investigate bending effects in each fiber, we used a commercial finite difference method (FDM)-based software (Lumerical Bent Waveguide Solver). Furthermore, to quantify the OAM mode quality, the purity of the OAM modes was assessed by the direct numerical calculation of topological charge numbers from the field profiles. All calculations were conducted at the wavelength of 1.55 µm.
3. Results
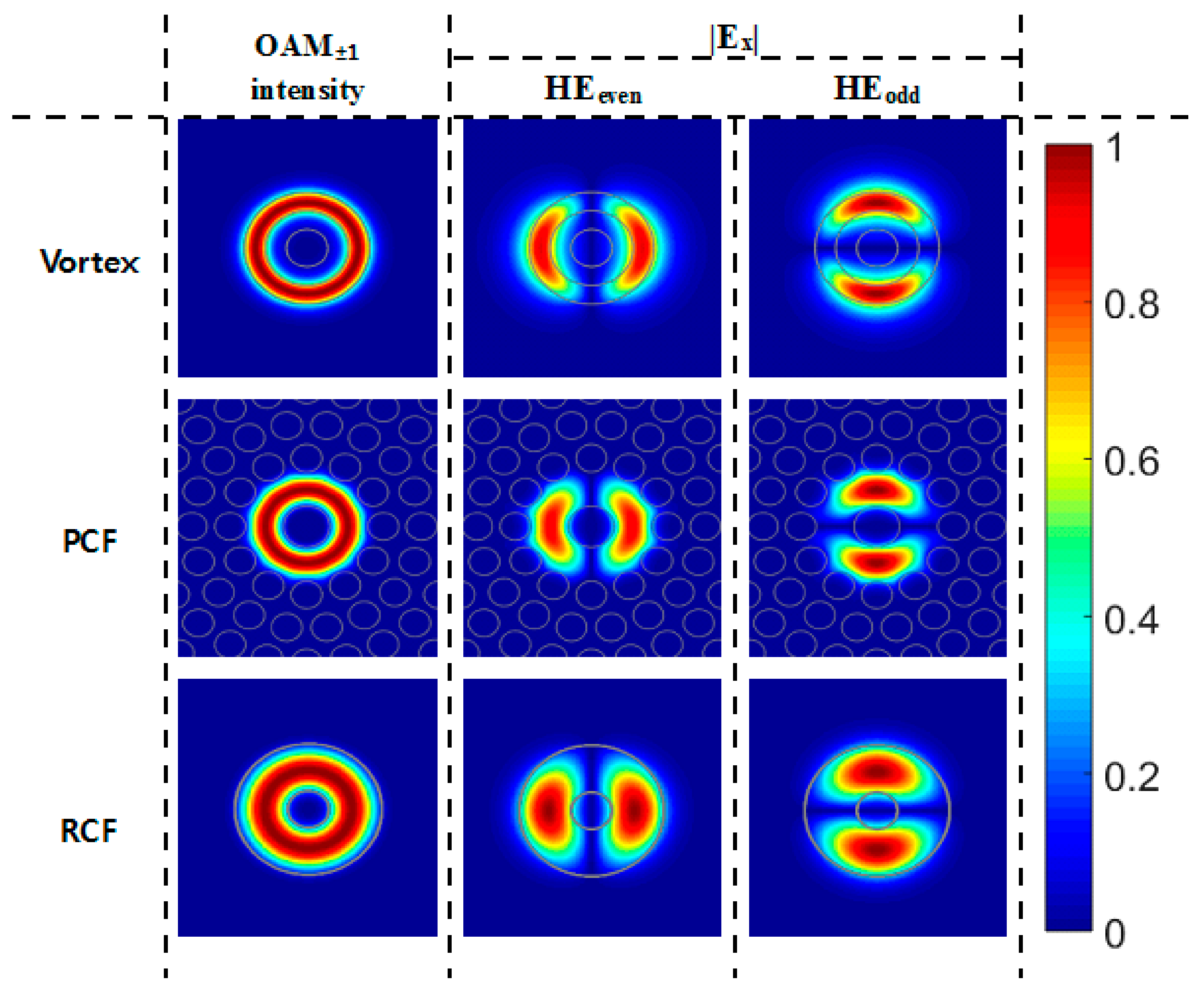
Each OAM mode guided in an optical fiber is formed by combining two degenerate eigenmodes (HE
21-even and HE
21-odd) with a 90° relative phase difference.
Figure 2 shows the field (E
x) and the phase profiles of OAM
l = −1 mode and the field profiles of its compositional eigenmodes (HE
21-even and HE
21-odd) in the three types of optical fibers considered in this work.
To examine the bending effects of OAM mode, we first analyzed two compositional eigenmodes (HE
21-even and HE
21-odd) of OAM
l = −1 mode in bent optical fibers.
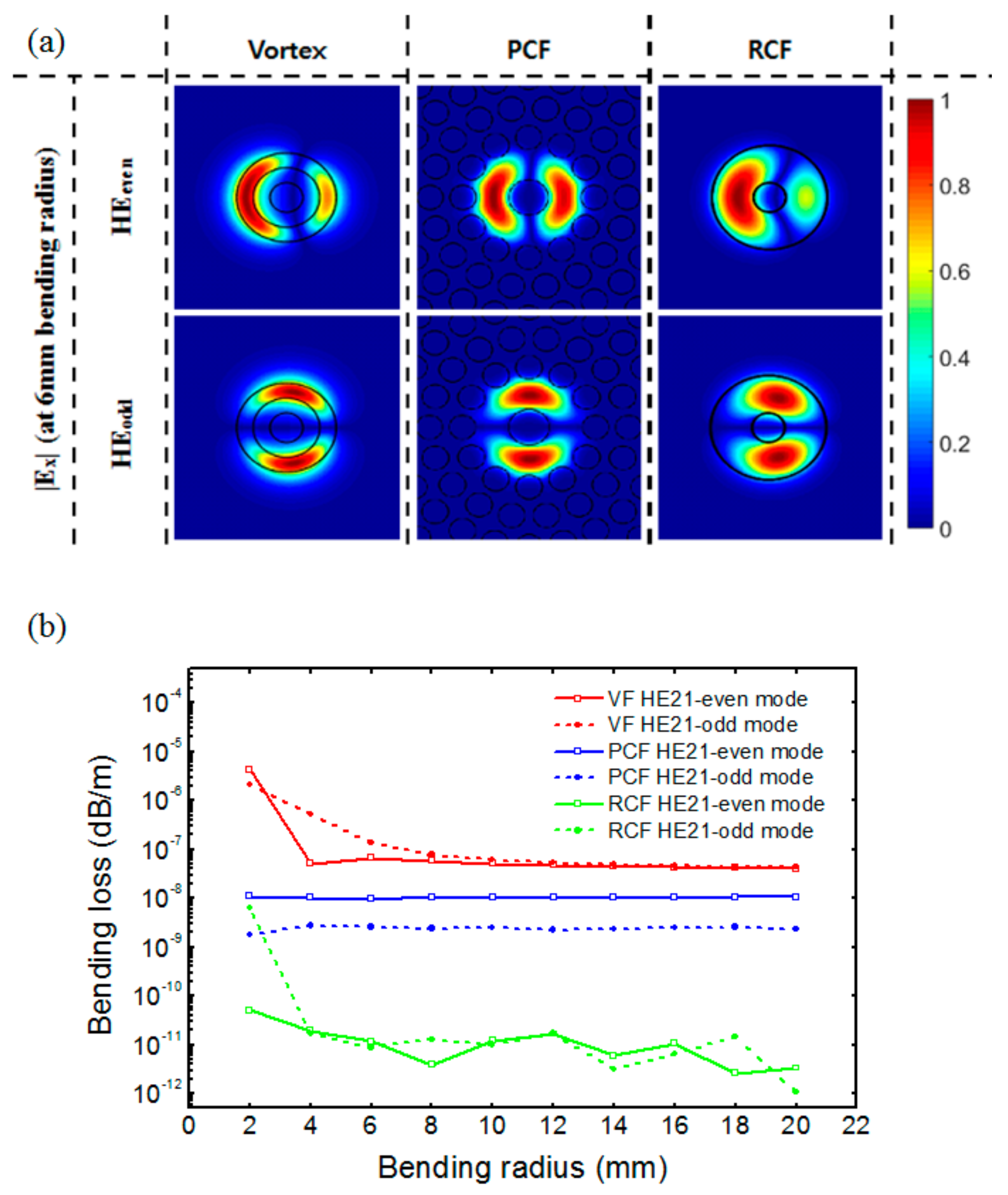
Figure 3a shows the field (E
x) amplitude distributions of HE
21-even and HE
21-odd modes in those three types optical fibers, where the bending occurs in the horizontal direction and the radius of the bending is 6 mm. One can see that in all the optical fibers, the eigenmodes become asymmetric in the horizontal direction, as previously discussed in reference [
11], which results in a mode mismatch and a coupling loss at the interface to a straight optical fiber. The bending of the fibers also causes propagation losses due to the radiation in the radial direction and makes the propagation constants of the eigenmodes complex.
Figure 3b shows the propagation losses of the compositional eigenmodes due to the bending as a function of a bending radius, which were calculated from the imaginary part of the propagation constants of the eigenmodes, which is given by
As one can see, all the compositional eigenmodes show very low loss even for a tight bending with a bending radius down to 2 mm. Since OAMl = −1 and OAMl = +1 modes share the same compositional eigenmode (only the sign of the relative phase difference between HE21-even and HE21-odd modes are different), so we can conclude that the bending losses of OAMl = ±1 modes are quite small and negligible in practical use. This contrasts sharply with a conventional single mode fiber (SMF), which suffers from a huge bending loss at 2 mm bending radius. It is surmised that the low bending losses of the OAM fibers stem from their larger core sizes.
In contrast to the negligible bending losses, the horizontally asymmetric profiles of the compositional eigenmodes bring about serious impairments, which has not been investigated in depth in the previous studies. As seen in
Figure 3a, HE
21-even and HE
21-odd modes of the bent OAM fibers do not match the ones of the straight fibers. So, the coupling loss occurs at the interface between the bent and the straight fibers.
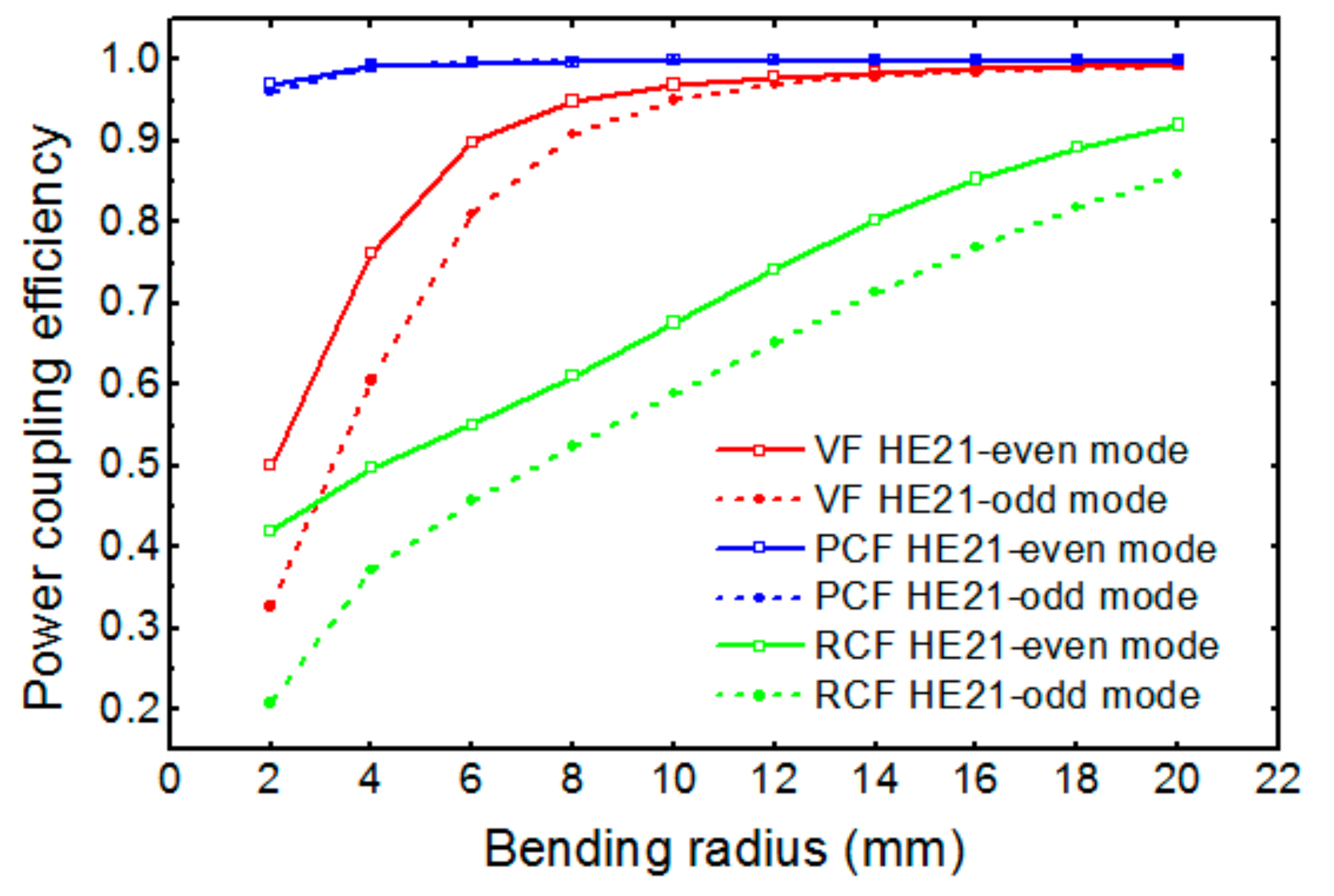
Figure 4 shows the power coupling efficiency between the straight and bent OAM fibers as a function of a bending radius, which were calculated from the mode overlap integral [
15]:
where the subscripts 1 and 2 represent the straight and the bent fibers, respectively. While the PCF shows almost no degradation in the coupling efficiency, the VF and the RCF show serious coupling efficiency degradation for the bending radius smaller than 10 mm. The broken horizontal symmetry of the eigenmodes in the bent fiber also raises crosstalks to other guided modes such as HE
11-even, HE
11-odd, TE, and TM modes when coupled to the straight fibers.
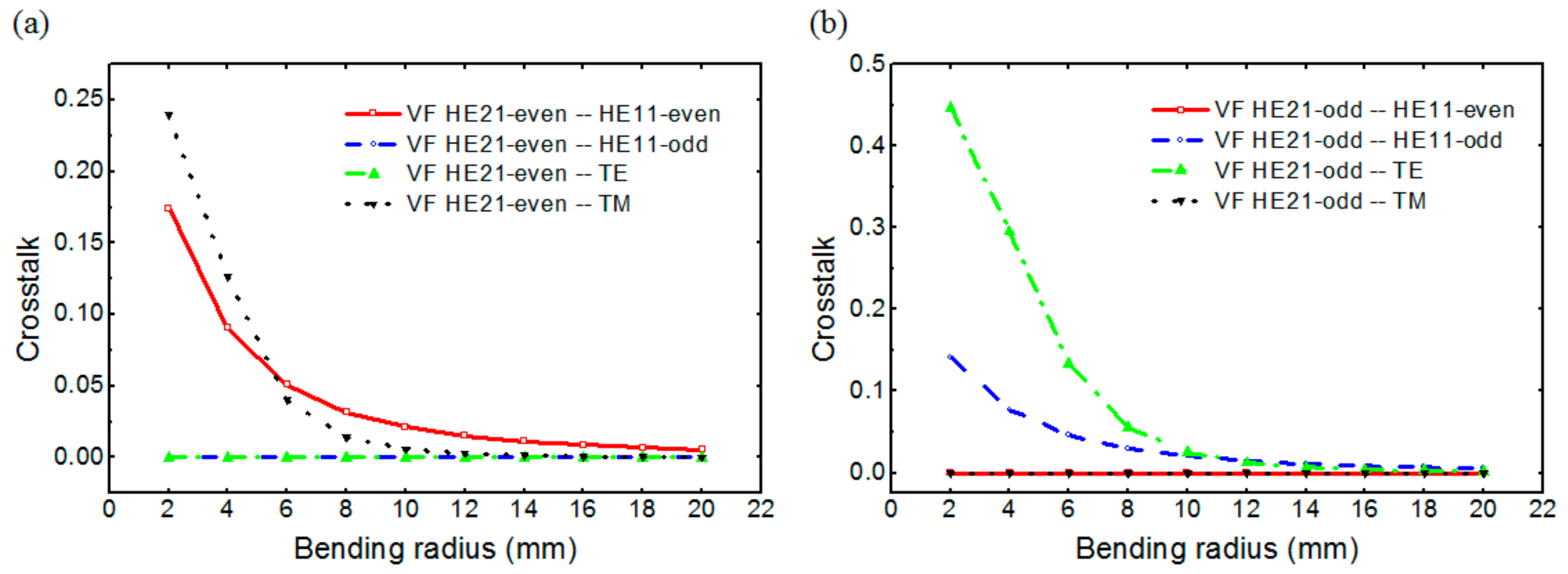
Figure 5a,b show, respectively, the crosstalks from HE
21-even and HE
21-odd modes to the other lower-order modes in the straight VF. For both the eigenmodes, considerable crosstalks occur for the bending radius smaller than 10 mm. Obviously, the bending radius range of the serious crosstalk increase is almost the same as that of the coupling efficiency drop. For the RCF, considerable crosstalk increases are observed for the bending radius smaller than 20 mm, which are not shown here. In this work, the VF and the RCF structures supporting only OAM
l = ±1 modes have been considered. If the dimensions of those fibers are increased, higher-order OAM modes will be supported. In this case, it is straightforward that bending will cause crosstalks among the OAM modes, which will be a serious problem in spatial mode division multiplexing communications. Whereas, for the PCF, the crosstalks are negligible even for a bending radius down to 2 mm, as expected from the coupling efficiency dependence on a bending radius, which is not shown here.
The fiber bending also induces birefringence in addition to the horizontal symmetry breaking of the eigenmodes, that is, the effective indices of HE
21-even and HE
21-odd modes become different in the bending region. The birefringence affects the relative phase difference between HE
21-even and HE
21-odd modes as the OAM mode propagates through the bending region and consequently, OAM mode will be ruined or become impure. The field after passing through a 90° bending is expressed as
where E
even/odd represents a field profile of HE
21-even/odd, C
e/o represent a power coupling ratio of HE
21-even/odd from a straight to a bend fibers, n
bend,even/odd is an effective index of HE
21-even/odd in the bending region, and r
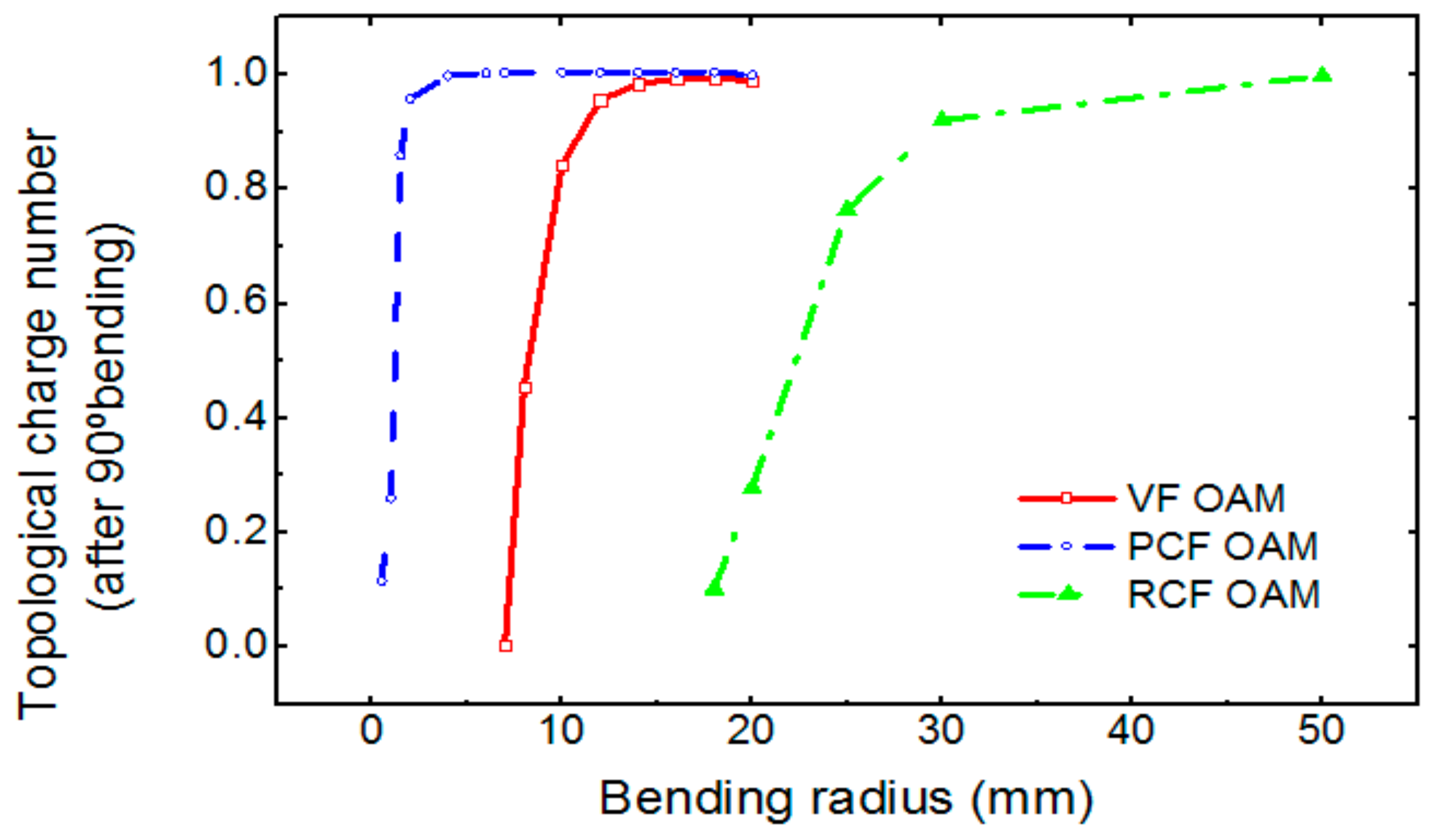
b is a bending radius. To investigate the purity of the OAM mode after passing through a 90° bending, we calculated a topological charge number from the field distribution of Equation 3 [
16,
17], which is plotted as a function of a bending radius in
Figure 6. The VF and the RCF show serious OAM mode purity degradation for bending radii smaller than ~15 and ~45 mm, respectively. Compared to the cases of the coupling loss and the crosstalk, the OAM mode purity degradation occurs at the larger bending radius and more rapidly as a bending radius decreases which is because both the broken horizontal symmetry of the eigenmode and the birefringence affect OAM mode purity. However, the PCF shows high OAM mode purity even for a bending radius down to 4 mm.
From our investigation, the OAM mode purity degradation and the crosstalk appear to limit the minimum bending radius in the practical use of the OAM fibers, not the bending loss. It also appears that the bandgap-guiding mechanism in the PCF is more robust to bending than the index guiding in the VF and the RCF.