The Optical Effective Attenuation Coefficient as an Informative Measure of Brain Health in Aging
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.1.1. Estimation of Cardiorespiratory Fitness
2.1.2. Neuropsychological Testing
2.2. Collection and Processing of sMRI Data
2.3. Optical Data Collection
2.4. EAC Computation
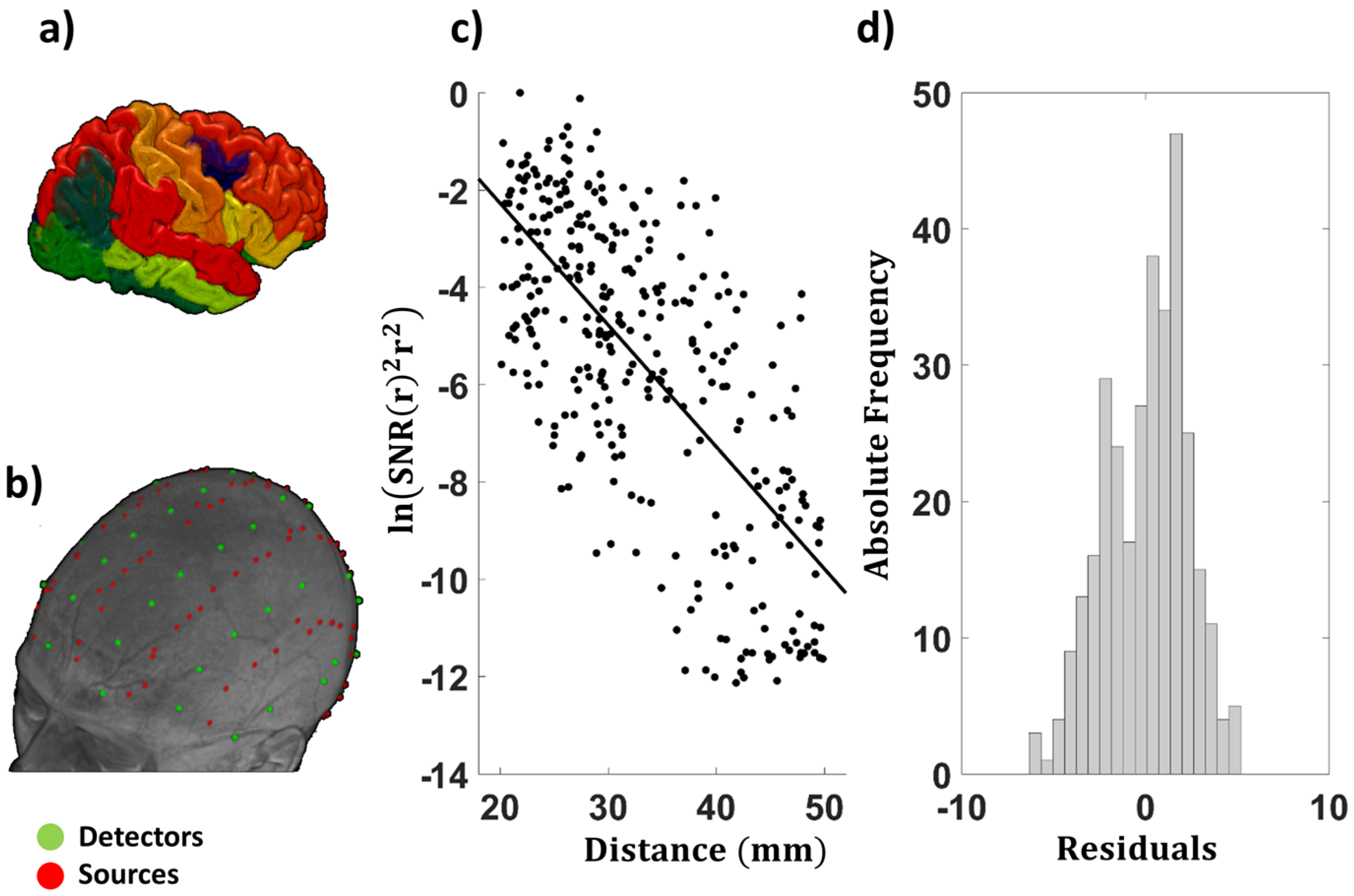
2.5. Examination of the EAC as a Function of Source–Detector Distance
2.6. Computation of the Tissue Oxygenation Index
2.7. Computation of the Cerebral Arterial Pulse Relaxation Function Obtained with Pulse-DOT
2.8. Heart Rate and Heart Rate Variability
2.9. Post-Processing and Statistical Analyses
3. Results
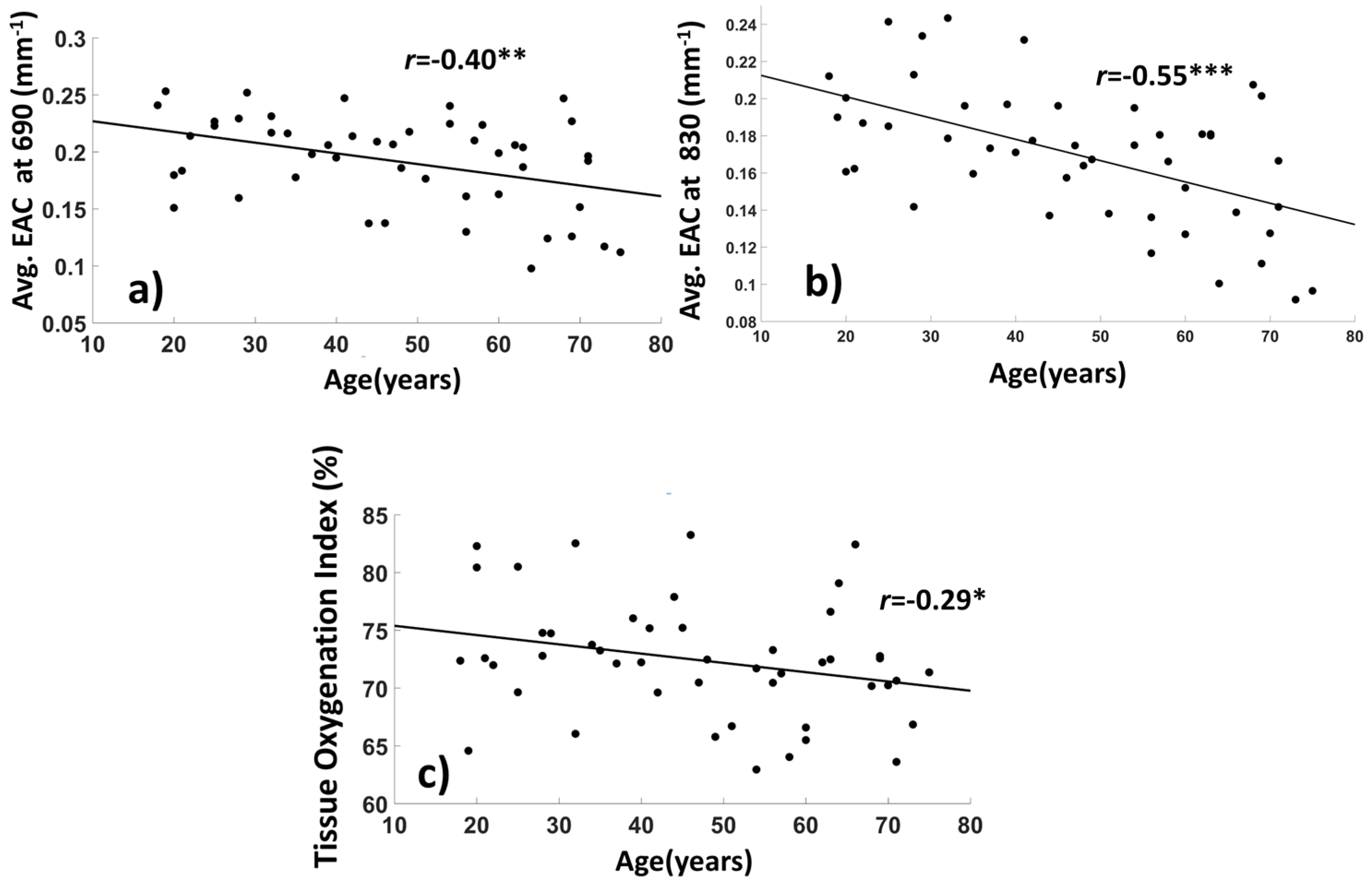
3.1. Basic Statistics and Interpretation of the EAC
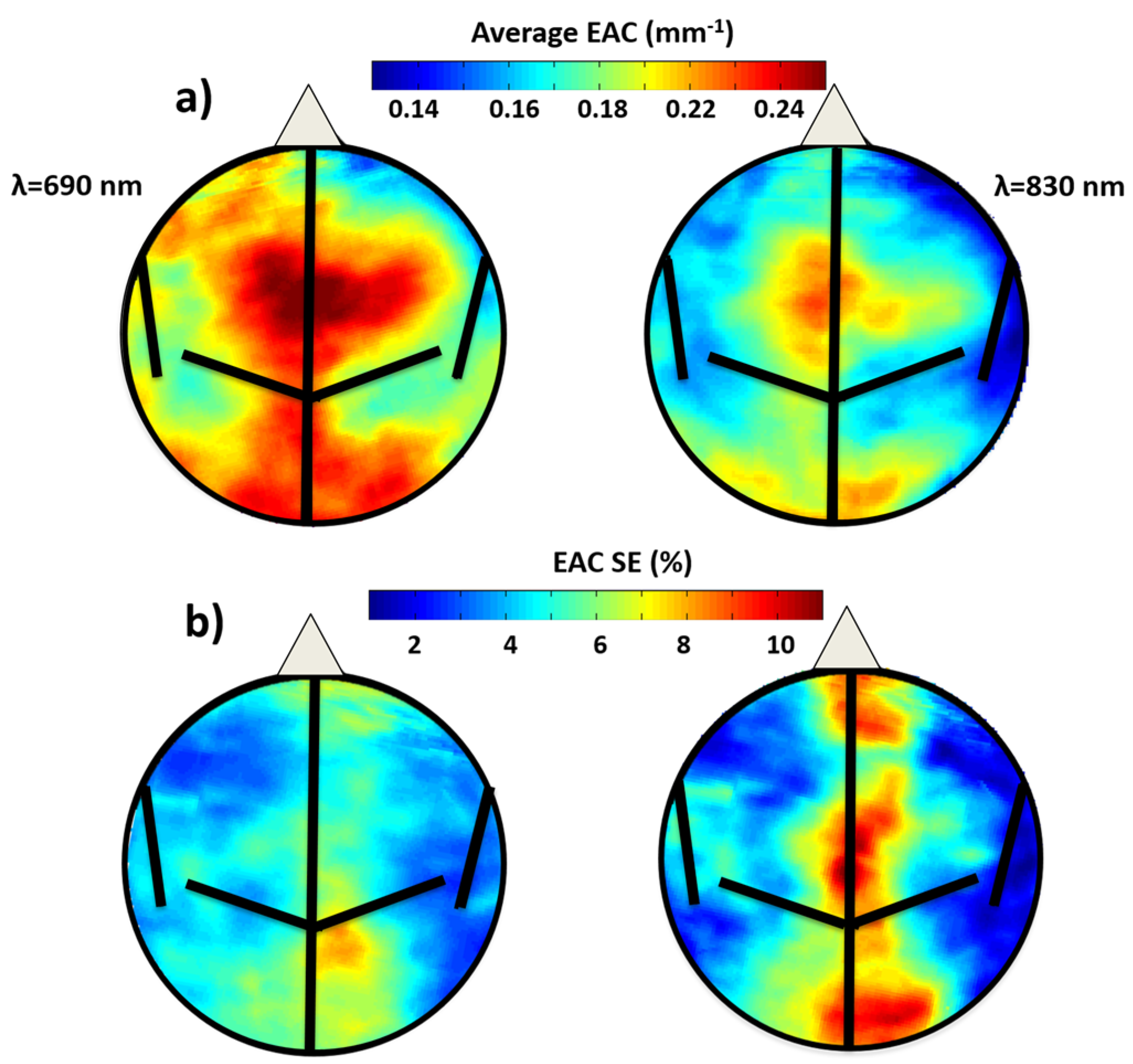
3.1.1. EAC Maps Characteristics
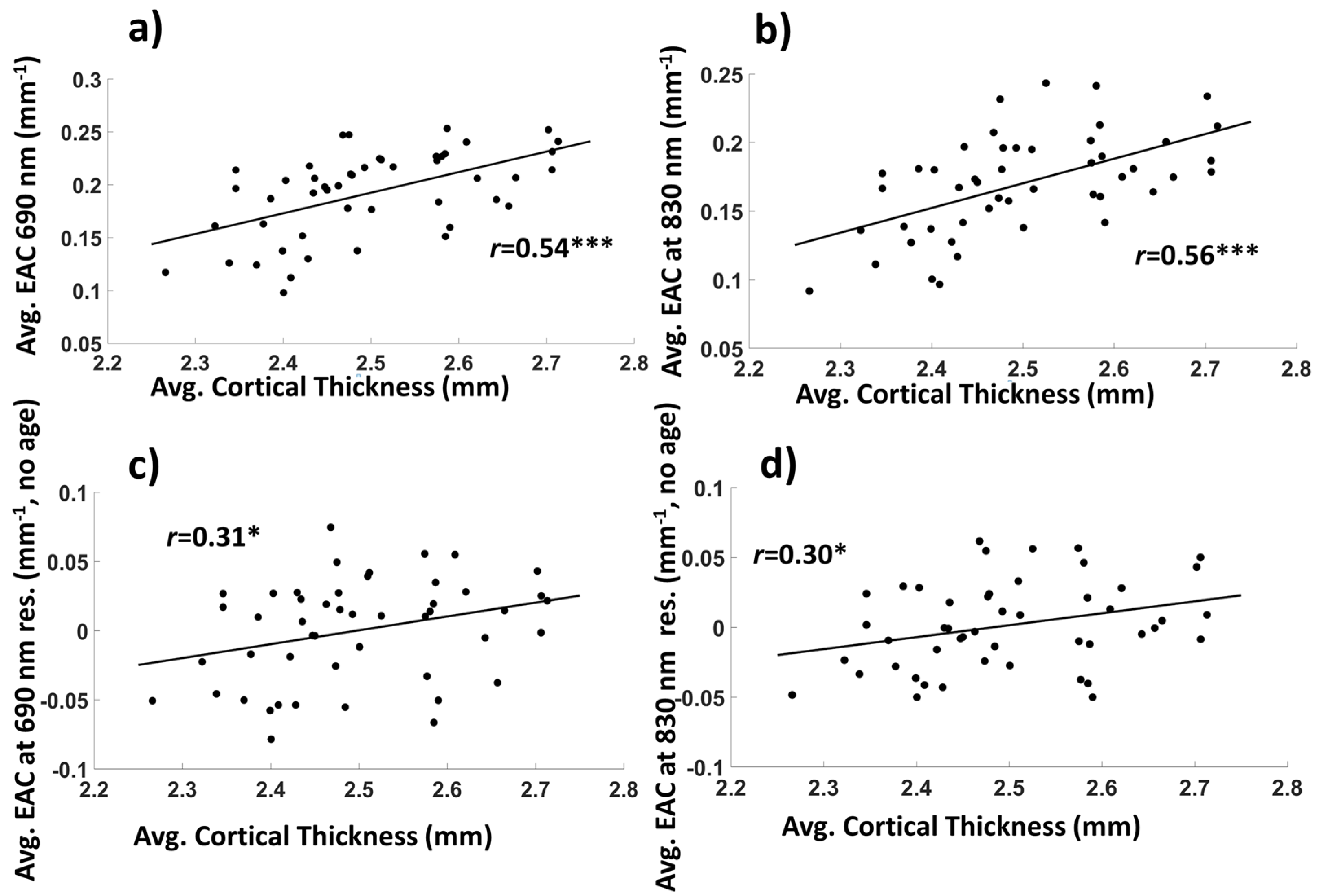
3.1.2. Average EAC Characteristics
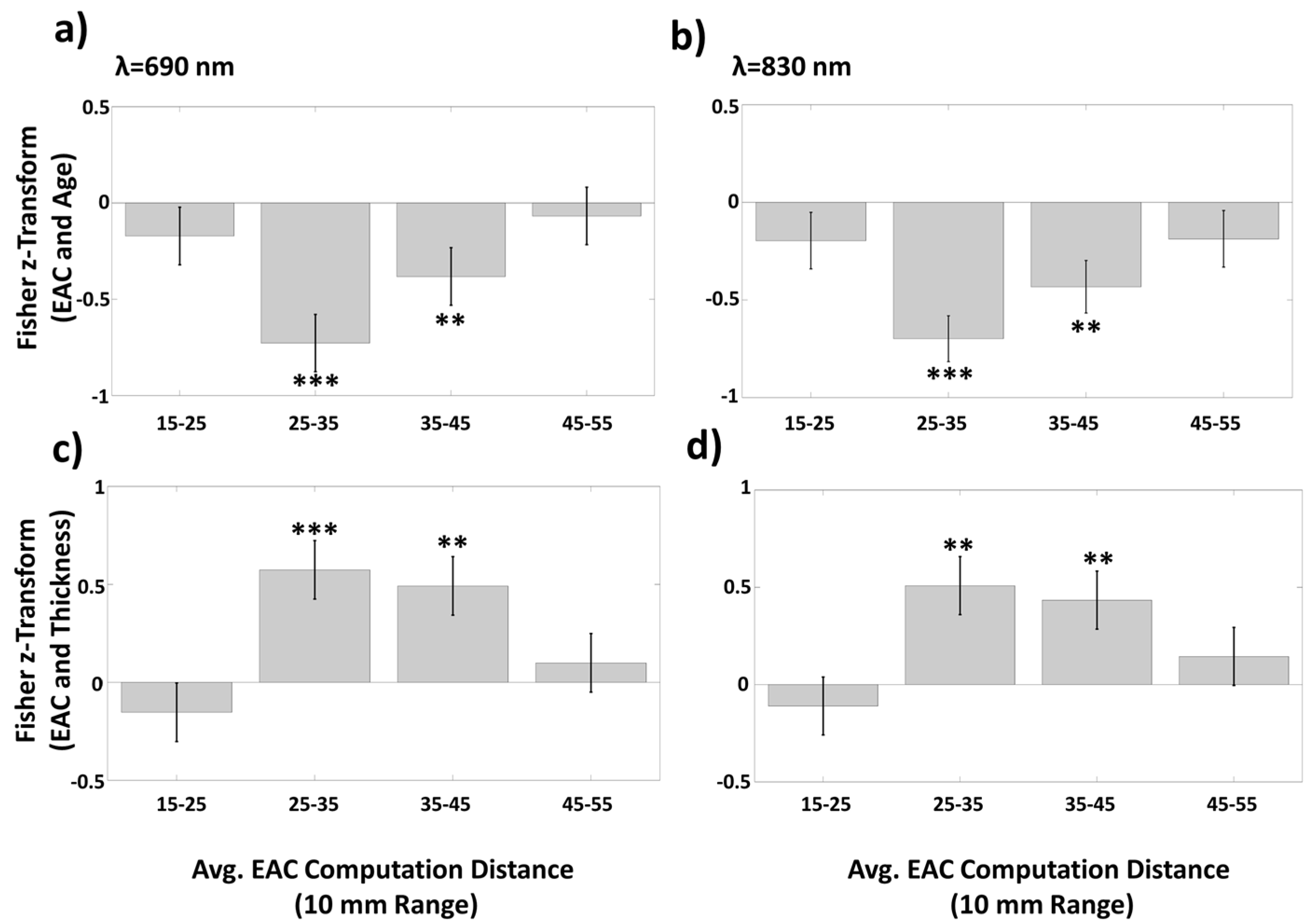
3.1.3. Average EAC as a Function of Source–Detector Distance
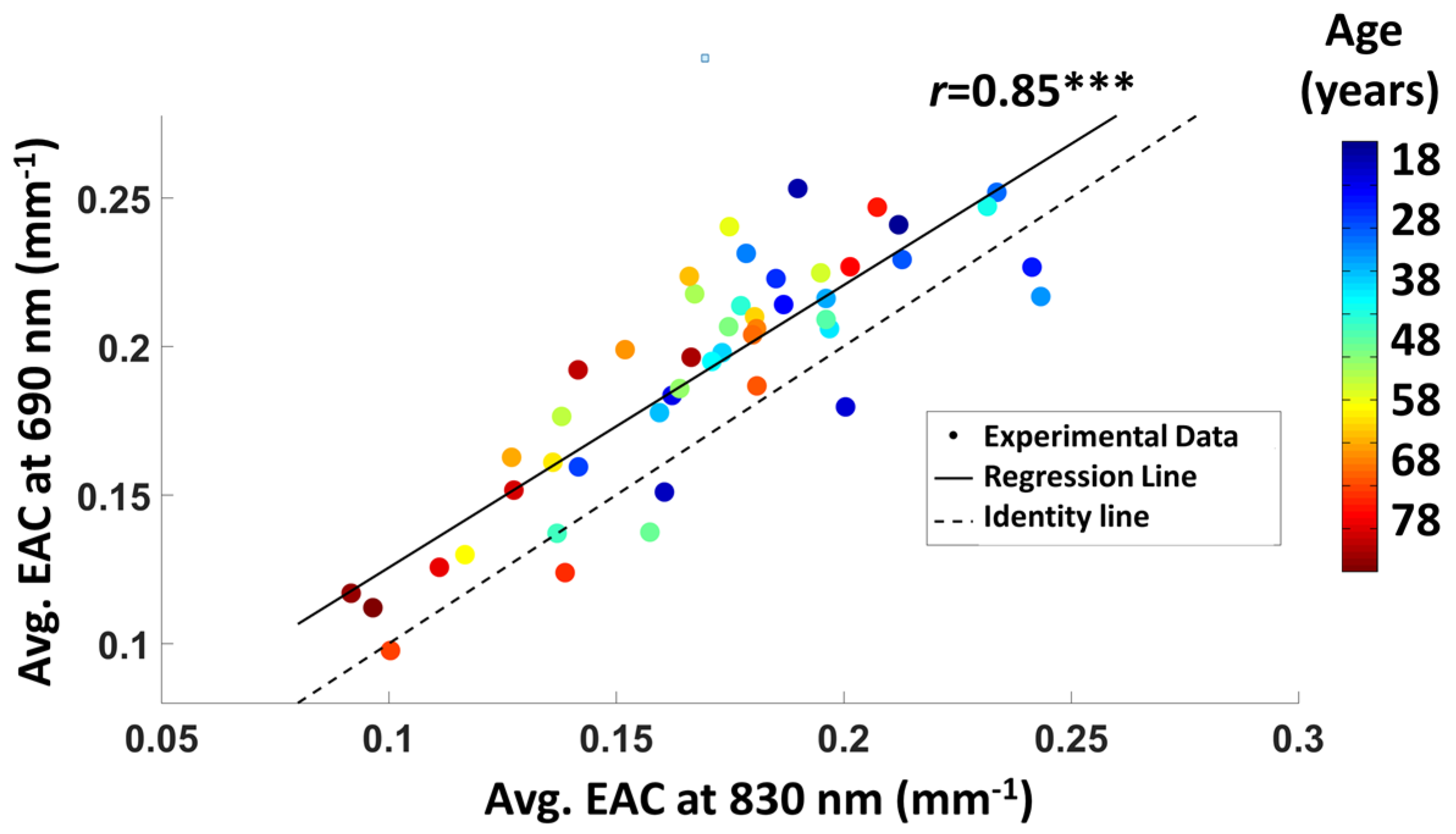
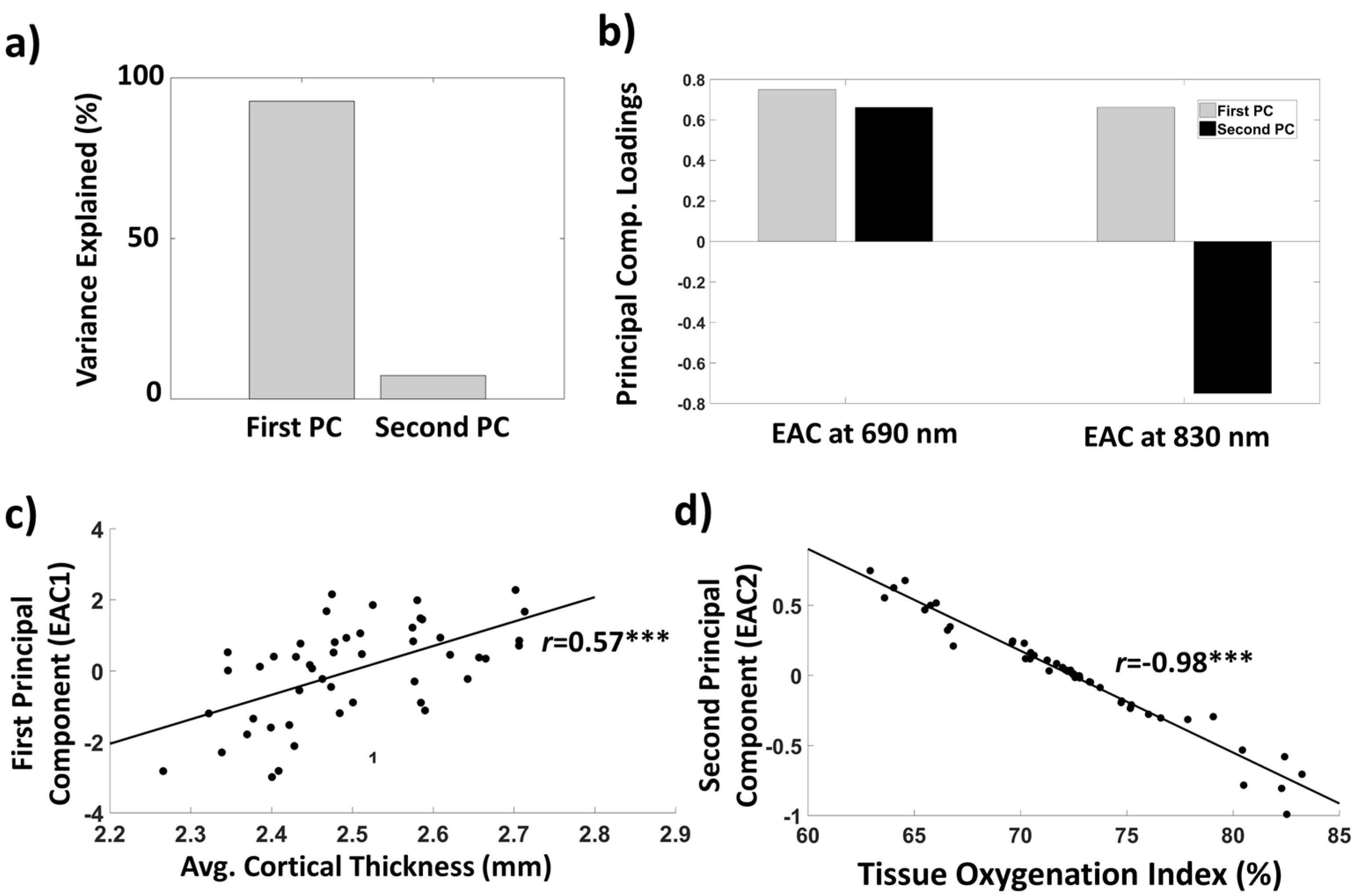
3.1.4. EAC Orthogonalization in Wavelength Space
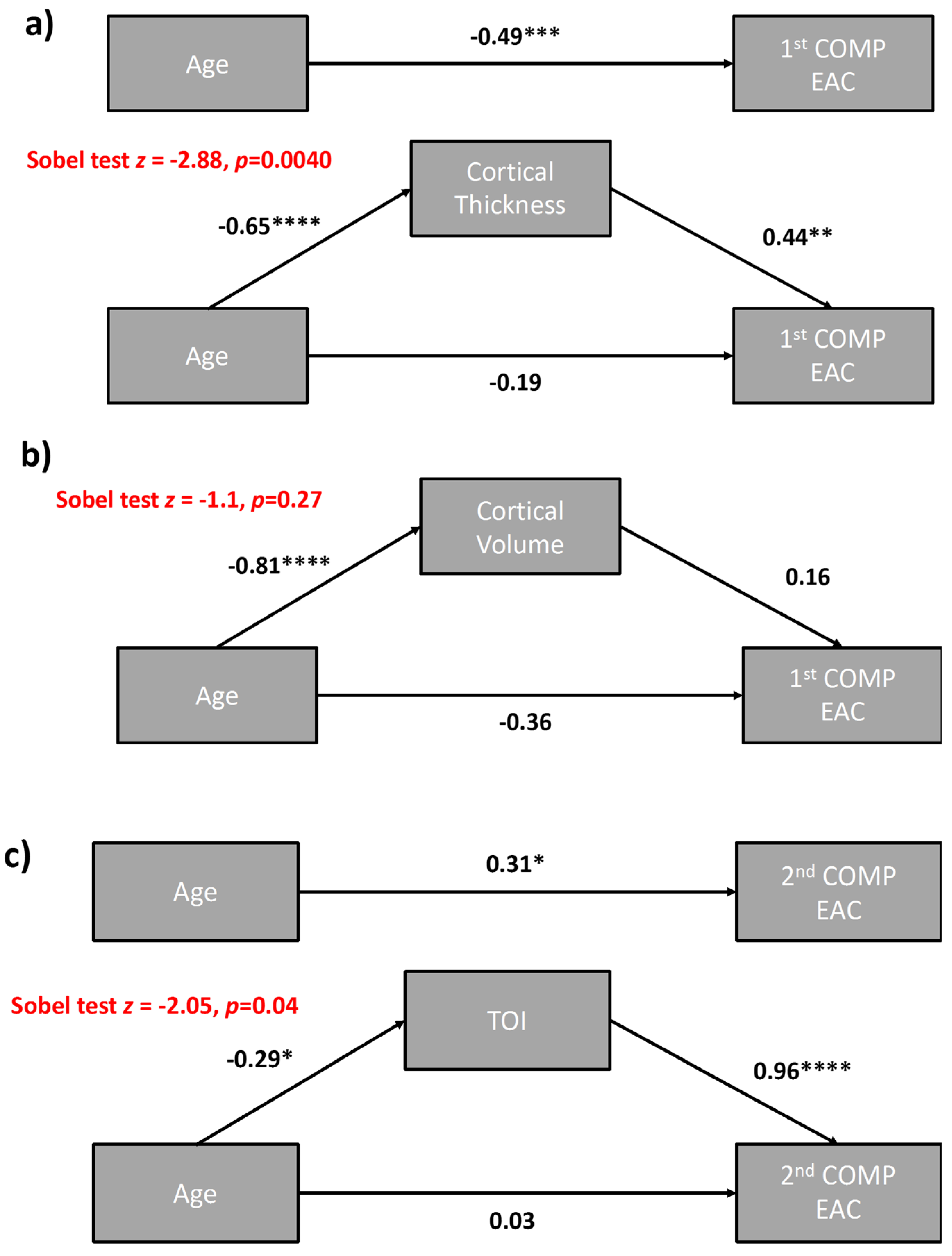
3.1.5. Mediation Analyses
3.2. Relationships between EAC Eigen-Solutions and Brain Anatomy, Cardiorespiratory Fitness, and Cognitive Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dickerson, B.C.; Bakkour, A.; Salat, D.H.; Feczko, E.; Pacheco, J.; Greve, D.N.; Grodstein, F.; Wright, C.I.; Blacker, D.; Rosas, H.D.; et al. The Cortical Signature of Alzheimer’s Disease: Regionally Specific Cortical Thinning Relates to Symptom Severity in Very Mild to Mild AD Dementia and is Detectable in Asymptomatic Amyloid-Positive Individuals. Cereb Cortex 2009, 19, 497–510. [Google Scholar] [CrossRef] [PubMed]
- Putcha, D.; Brickhouse, M.; O’Keefe, K.; Sullivan, C.; Rentz, D.; Marshall, G.; Dickerson, B.; Sperling, R. Hippocampal Hyperactivation Associated with Cortical Thinning in Alzheimer’s Disease Signature Regions in Non-Demented Elderly Adults. J. Neurosci. 2011, 31, 17680–17688. [Google Scholar] [CrossRef] [PubMed]
- Xia, C.; Makaretz, S.J.; Caso, C.; McGinnis, S.; Gomperts, S.N.; Sepulcre, J.; Gomez-Isla, T.; Hyman, B.T.; Schultz, A.; Vasdev, N.; et al. Association of In Vivo [18F] AV-1451 Tau PET Imaging Results With Cortical Atrophy and Symptoms in Typical and Atypical Alzheimer Disease. JAMA Neurol. 2017, 74, 427–510. [Google Scholar] [CrossRef] [PubMed]
- Becker, J.A.; Hedden, T.; Carmasin, J.; Maye, J.; Rentz, D.M.; Putcha, D.; Fischl, B.; Greve, D.N.; Marshall, G.A.; Salloway, S.; et al. Amyloid-β Associated Cortical Thinning in Clinically Normal Elderly. Ann. Neurol. 2011, 69, 1032–1042. [Google Scholar] [CrossRef] [PubMed]
- Fabiani, M. It was the best of times, it was the worst of times: A psychophysiologist’s view of cognitive aging. Psychophysiology 2012, 49, 283–304. [Google Scholar] [CrossRef] [PubMed]
- Bishop, N.A.; Lu, T.; Yankner, B.A. Neural mechanisms of ageing and cognitive decline. Nature 2010, 464, 529–535. [Google Scholar] [CrossRef] [PubMed]
- Hedden, T.; Gabrieli, J.D.E. Insights into the ageing mind: A view from cognitive neuroscience. Nat. Rev. Neurosci. 2004, 5, 87–96. [Google Scholar] [CrossRef]
- Deary, I.J.; Corley, J.; Gow, A.J.; Harris, S.E.; Houlihan, L.M.; Marioni, R.E.; Penke, L.; Rafnsson, S.B.; Starr, J.M. Age-associated cognitive decline. Br. Med. Bull. 2009, 92, 135–152. [Google Scholar] [CrossRef]
- Fischl, B. FreeSurfer. Neuroimage 2012, 62, 774–781. [Google Scholar] [CrossRef]
- Villringer, A.; Chance, B. Non-invasive optical spectroscopy and imaging of human brain function. Trends Neurosci. 1997, 20, 435–442. [Google Scholar] [CrossRef]
- Croce, P.; Zappasodi, F.; Merla, A.; Chiarelli, A.M. Exploiting neurovascular coupling: A Bayesian sequential Monte Carlo approach applied to simulated EEG fNIRS data. J. Neural Eng. 2017, 14, 046029. [Google Scholar] [CrossRef] [PubMed]
- Gratton, G.; Corballis, P.M.; Cho, E.; Fabiani, M.; Hood, D.C. Shades of gray matter: Noninvasive optical images of human brain reponses during visual stimulation. Psychophysiology 1995, 32, 505–509. [Google Scholar] [CrossRef] [PubMed]
- Fabiani, M.; Low, K.A.; Tan, C.H.; Zimmerman, B.; Fletcher, M.A.; Schneider-Garces, N.; Maclin, E.L.; Chiarelli, A.M.; Sutton, B.P.; Gratton, G. Taking the pulse of aging: Mapping pulse pressure and elasticity in cerebral arteries with optical methods. Psychophysiology 2014, 51, 1072–1088. [Google Scholar] [CrossRef] [PubMed]
- Chiarelli, A.M.; Fletcher, M.A.; Tan, C.H.; Low, K.A.; Maclin, E.L.; Zimmerman, B.; Kong, T.; Gorsuch, A.; Gratton, G.; Fabiani, M. Individual differences in regional cortical volumes across the life span are associated with regional optical measures of arterial elasticity. Neuroimage 2017, 162, 199–213. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.H.; Low, K.A.; Kong, T.; Fletcher, M.A.; Zimmerman, B.; Maclin, E.L.; Chiarelli, A.M.; Gratton, G.; Fabiani, M. Mapping cerebral pulse pressure and arterial compliance over the adult lifespan with optical imaging. PLoS ONE 2017, 12, e0171305. [Google Scholar] [CrossRef] [PubMed]
- Chiarelli, A.M.; Mahmoudzadeh, M.; Low, K.A.; Maclin, E.L.; Kongolo, G.; Goudjil, S.; Fabiani, M.; Wallois, F.; Gratton, G. Assessment of cerebrovascular development and intraventricular hemorrhages in preterm infants with optical measures of the brain arterial pulse wave. J. Cereb. Blood Flow Metab. 2019, 39, 466–480. [Google Scholar] [CrossRef] [PubMed]
- Pifferi, A.; Contini, D.; Mora, A.D.; Farina, A.; Spinelli, L.; Torricelli, A. New frontiers in time-domain diffuse optics, a review. J. Biomed. Opt. 2016, 21, 091310. [Google Scholar] [CrossRef]
- Pogue, B.W.; Patterson, M.S. Frequency-domain optical absorption spectroscopy of finite tissue volumes using diffusion theory. Phys. Med. Biol. 1994, 39, 1157–1180. [Google Scholar] [CrossRef]
- Fishkin, J.B.; Gratton, E. Propagation of photon-density waves in strongly scattering media containing an absorbing semi-infinite plane bounded by a straight edge. J. Opt. Soc. Am. A 1993, 10, 127–140. [Google Scholar] [CrossRef]
- Chiarelli, A.M.; Maclin, E.L.; Low, K.A.; Fantini, S.; Fabiani, M.; Gratton, G. Low-resolution mapping of the effective attenuation coefficient of the human head: A multidistance approach applied to high-density optical recordings. Neurophotonics 2017, 4, 021103. [Google Scholar] [CrossRef]
- Fletcher, M.A.; Low, K.A.; Boyd, R.; Zimmerman, B.; Gordon, B.A.; Tan, C.H.; Schneider-Garces, N.; Sutton, B.P.; Gratton, G.; Fabiani, M. Comparing Aging and Fitness Effects on Brain Anatomy. Front. Hum. Neurosci. 2016, 10. [Google Scholar] [CrossRef] [PubMed]
- Gordon, B.A.; Rykhlevskaia, E.I.; Brumback, C.R.; Lee, Y.; Elavsky, S.; Konopack, J.F.; McAuley, E.; Kramer, A.F.; Colcombe, S.; Gratton, G.; et al. Neuroanatomical correlates of aging, cardiopulmonary fitness level, and education. Psychophysiology 2008, 45, 825–838. [Google Scholar] [CrossRef] [PubMed]
- Raz, N.; Lindenberger, U.; Rodrigue, K.M.; Kennedy, K.M.; Head, D.; Williamson, A.; Dahle, C.; Gerstorf, D.; Acker, J.D. Regional Brain Changes in Aging Healthy Adults: General Trends, Individual Differences and Modifiers. Cereb. Cortex 2005, 15, 1676–1689. [Google Scholar] [CrossRef]
- Grégoire, J.; Linden, M.V.D. Effect of age on forward and backward digit spans. Aging Neuropsychol. Cogn. 1997, 4, 140–149. [Google Scholar] [CrossRef]
- Rusinek, H.; De Santi, S.; Frid, D.; Tsui, W.-H.; Tarshish, C.Y.; Convit, A.; de Leon, M.J. Regional Brain Atrophy Rate Predicts Future Cognitive Decline: 6-year Longitudinal MR Imaging Study of Normal Aging. Radiology 2003, 229, 691–696. [Google Scholar] [CrossRef]
- Suzuki, S.; Takasaki, S.; Ozaki, T.; Kobayashi, Y. Tissue oxygenation monitor using NIR spatially resolved spectroscopy. Proc. SPIE 1999, 3597, 582–593. [Google Scholar]
- Jurca, R.; Jackson, A.S.; LaMonte, M.J.; Morrow, J.R.; Blair, S.N.; Wareham, N.J.; Haskell, W.L.; van Mechelen, W.; Church, T.S.; Jakicic, J.M.; et al. Assessing cardiorespiratory fitness without performing exercise testing. Am. J. Prev. Med. 2005, 29, 185–193. [Google Scholar] [CrossRef]
- Oldfield, R.C. The assessment and analysis of handedness: The Edinburgh inventory. Neuropsychologia 1971, 9, 97–113. [Google Scholar] [CrossRef]
- Mayeux, R.; Stern, Y.; Rosen, J.; Leventhal, J. Depression, intellectual impairment, and Parkinson disease. Neurology 1981, 31, 645–650. [Google Scholar] [CrossRef]
- Beck, A.T.; Steer, R.A.; Brown, G.K. Manual for the Beck Depression Inventory, 2nd ed.; The Psychological Corporation: San Antonio, TX, USA, 1996. [Google Scholar]
- Mailey, E.L.; White, S.M.; Wójcicki, T.R.; Szabo, A.N.; Kramer, A.F.; McAuley, E. Construct validation of a non-exercise measure of cardiorespiratory fitness in older adults. BMC Public Health 2010, 10, 59. [Google Scholar] [CrossRef]
- McAuley, E.; Szabo, A.N.; Mailey, E.L.; Erickson, K.I.; Voss, M.; White, S.M.; Wójcicki, T.R.; Gothe, N.; Olson, E.A.; Mullen, S.P.; et al. Non-exercise estimated cardiorespiratory fitness: Associations with brain structure, cognition, and memory complaints in older adults. Ment. Health Phys. Act. 2011, 4, 5–11. [Google Scholar] [CrossRef] [PubMed]
- Jetté, M.; Sidney, K.; Blümchen, G. Metabolic equivalents (METS) in exercise testing, exercise prescription, and evaluation of functional capacity. Clin. Cardiol. 1990, 13, 555–565. [Google Scholar] [CrossRef] [PubMed]
- Corrigan, J.D.; Hinkeldey, N.S. Relationships between parts A and B of the Trail Making Test. J. Clin. Psychol. 1987, 43, 402–409. [Google Scholar] [CrossRef]
- Benton, A.L.; Hamsher, K. Multilingual Aphasia Examination Manual; University of Iowa: Iowa City, IA, USA, 1989. [Google Scholar]
- Unsworth, N.; Heitz, R.P.; Schrock, J.C.; Engle, R.W. An automated version of the operation span task. Behav. Res. Methods 2005, 37, 498–505. [Google Scholar] [CrossRef] [PubMed]
- Raven, J.; Raven, J.C.; Court, J.H. Manual for Raven’s Progressive Matrices and Vocabulary Scales; Harcourt Assessment: San Antonio, TX, USA, 2003. [Google Scholar]
- Kaufman, A.S.; Kaufman, N.L. Kaufman Brief Intelligence Test, 2nd ed.; The Psychological Corporation: San Antonio, TX, USA, 2004. [Google Scholar]
- Shipley, W.C. A self-administering scale for measuring intellectual impairment and deterioration. J. Psychol. 1940, 9, 371–377. [Google Scholar] [CrossRef]
- Chan, M.Y.; Park, D.C.; Savalia, N.K.; Petersen, S.E.; Wig, G.S. Decreased segregation of brain systems across the healthy adult lifespan. Proc. Natl. Acad. Sci. USA 2014, 111, E4997–E5006. [Google Scholar] [CrossRef]
- Desikan, R.S.; Ségonne, F.; Fischl, B.; Quinn, B.T.; Dickerson, B.C.; Blacker, D.; Buckner, R.L.; Dale, A.M.; Maguire, R.P.; Hyman, B.T.; et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 2006, 31, 968–980. [Google Scholar] [CrossRef]
- Dale, A.M.; Fischl, B.; Sereno, M.I. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage 1999, 9, 179–194. [Google Scholar] [CrossRef]
- Fischl, B.; Liu, A.; Dale, A.M. Automated manifold surgery: Constructing geometrically accurate and topologically correct models of the human cerebral cortex. IEEE Trans. Med. Imaging 2001, 20, 70–80. [Google Scholar] [CrossRef]
- Fischl, B.; Sereno, M.I.; Dale, A.M. Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. Neuroimage 1999, 9, 195–207. [Google Scholar] [CrossRef]
- Fischl, B.; Sereno, M.I.; Tootell, R.B.; Dale, A.M. High-resolution intersubject averaging and a coordinate system for the cortical surface. Hum. Brain Mapp. 1999, 8, 272–284. [Google Scholar] [CrossRef]
- Jack, C.R.; Twomey, C.K.; Zinsmeister, A.R.; Sharbrough, F.W.; Petersen, R.C.; Cascino, G.D. Anterior temporal lobes and hippocampal formations: Normative volumetric measurements from MR images in young adults. Radiology 1989, 172, 549–554. [Google Scholar] [CrossRef] [PubMed]
- Barkhof, F.; Scheltens, P. Imaging of White Matter Lesions. Cerebrovasc. Dis. 2002, 13, 21–30. [Google Scholar] [CrossRef] [PubMed]
- Schiffmann, R.; van der Knaap, M.S. Invited article: An MRI-based approach to the diagnosis of white matter disorders. Neurology 2009, 72, 750–759. [Google Scholar] [CrossRef] [PubMed]
- Fazekas, F.; Niederkorn, K.; Schmidt, R.; Offenbacher, H.; Horner, S.; Bertha, G.; Lechner, H. White matter signal abnormalities in normal individuals: Correlation with carotid ultrasonography, cerebral blood flow measurements, and cerebrovascular risk factors. Stroke 1988, 19, 1285–1288. [Google Scholar] [CrossRef] [PubMed]
- Chiarelli, A.M.; Maclin, E.L.; Low, K.A.; Fabiani, M.; Gratton, G. Comparison of procedures for co-registering scalp-recording locations to anatomical magnetic resonance images. J. Biomed. Opt. 2015, 20, 016009. [Google Scholar] [CrossRef] [PubMed]
- Eggebrecht, A.T.; Ferradal, S.L.; Robichaux-Viehoever, A.; Hassanpour, M.S.; Dehghani, H.; Snyder, A.Z.; Hershey, T.; Culver, J.P. Mapping distributed brain function and networks with diffuse optical tomography. Nat. Photonics 2014, 8, 448–454. [Google Scholar] [CrossRef] [PubMed]
- Chiarelli, A.M.; Maclin, E.L.; Fabiani, M.; Gratton, G. A kurtosis-based wavelet algorithm for motion artifact correction of fNIRS data. Neuroimage 2015, 112, 128–137. [Google Scholar] [CrossRef] [PubMed]
- Delorme, A.; Makeig, S. EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Gratton, G.; Fabiani, M. Fast optical imaging of human brain function. Front. Hum. Neurosci. 2010, 4, 52. [Google Scholar] [CrossRef]
- Oliver James, J.; Webb David, J. Noninvasive Assessment of Arterial Stiffness and Risk of Atherosclerotic Events. Arterioscler. Thromb. Vasc. Biol. 2003, 23, 554–566. [Google Scholar] [CrossRef] [PubMed]
- Ishimaru, A. Diffusion of light in turbid material. Appl. Opt. 1989, 28, 2210–2215. [Google Scholar] [CrossRef] [PubMed]
- Paulsen, K.D.; Jiang, H. Spatially varying optical property reconstruction using a finite element diffusion equation approximation. Med. Phys. 1995, 22, 691–701. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, H.; Eames, M.E.; Yalavarthy, P.K.; Davis, S.C.; Srinivasan, S.; Carpenter, C.M.; Pogue, B.W.; Paulsen, K.D. Near infrared optical tomography using NIRFAST: Algorithm for numerical model and image reconstruction. Commun. Numer. Methods Eng. 2008, 25, 711–732. [Google Scholar] [CrossRef] [PubMed]
- Chiarelli, A.M.; Maclin, E.L.; Low, K.A.; Mathewson, K.E.; Fabiani, M.; Gratton, G. Combining energy and Laplacian regularization to accurately retrieve the depth of brain activity of diffuse optical tomographic data. J. Biomed. Opt. 2016, 21, 36008. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Mallinckrodt, B.; Abraham, W.T.; Wei, M.; Russell, D.W. Advances in testing the statistical significance of mediation effects. J. Couns. Psychol. 2006, 53, 372–378. [Google Scholar] [CrossRef]
- Strangman, G.E.; Li, Z.; Zhang, Q. Depth Sensitivity and Source-Detector Separations for Near Infrared Spectroscopy Based on the Colin27 Brain Template. PLoS ONE 2013, 8, e66319. [Google Scholar] [CrossRef]
- Horn, J.L.; Cattell, R.B. Age differences in fluid and crystallized intelligence. Acta Psychol. 1967, 26, 107–129. [Google Scholar] [CrossRef]
- Baltes, P.B.; Dittmann-Kohli, F.; Kliegl, R. Reserve capacity of the elderly in aging-sensitive tests of fluid intelligence: Replication and extension. Psychol. Aging 1986, 1, 172–177. [Google Scholar] [CrossRef][Green Version]
- Farina, A.; Torricelli, A.; Bargigia, I.; Spinelli, L.; Cubeddu, R.; Foschum, F.; Jäger, M.; Simon, E.; Fugger, O.; Kienle, A.; et al. In-vivo multilaboratory investigation of the optical properties of the human head. Biomed. Opt. Express 2015, 6, 2609–2623. [Google Scholar] [CrossRef] [PubMed]
- Giacalone, G.; Zanoletti, M.; Contini, D.; Re, R.; Spinelli, L.; Roveri, L.; Torricelli, A. Cerebral time domain-NIRS: Reproducibility analysis, optical properties, hemoglobin species and tissue oxygen saturation in a cohort of adult subjects. Biomed. Opt. Express 2017, 8, 4987–5000. [Google Scholar] [CrossRef] [PubMed]
- Haeussinger, F.B.; Heinzel, S.; Hahn, T.; Schecklmann, M.; Ehlis, A.-C.; Fallgatter, A.J. Simulation of Near-Infrared Light Absorption Considering Individual Head and Prefrontal Cortex Anatomy: Implications for Optical Neuroimaging. PLoS ONE 2011, 6, e26377. [Google Scholar] [CrossRef] [PubMed]
- Byrne, J.V. Cranial Venous Anatomy. In Tutorials in Endovascular Neurosurgery and Interventional Neuroradiology; Springer: Cham, Switzerland, 2017; pp. 57–75. ISBN 978-3-319-54833-3. [Google Scholar]
- Uludag, K.; Kohl-Bareis, M.; Steinbrink, J.; Obrig, H.; Villringer, A. Crosstalk in the Lambert-Beer calculation for near-infrared wavelengths estimated by Monte simulations. J. Biomed. Opt. 2002, 7, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Caeyenberghs, K.; Metzler-Baddeley, C.; Foley, S.; Jones, D.K. Dynamics of the Human Structural Connectome Underlying Working Memory Training. J. Neurosci. 2016, 36, 4056–4066. [Google Scholar] [CrossRef] [PubMed]
- Auger, H.; Bherer, L.; Boucher, É.; Hoge, R.; Lesage, F.; Dehaes, M. Quantification of extra-cerebral and cerebral hemoglobin concentrations during physical exercise using time-domain near infrared spectroscopy. Biomed. Opt. Express 2016, 7, 3826–3842. [Google Scholar] [CrossRef] [PubMed]
- Forcione, M.; Colonnese, C.; Belli, A. Cerebral Hemodynamic Influences in Task-Related Functional Magnetic Resonance Imaging and Near-Infrared Spectroscopy in Acute Sport-Related Concussion: A Review. J. Imaging 2018, 4, 59. [Google Scholar] [CrossRef]
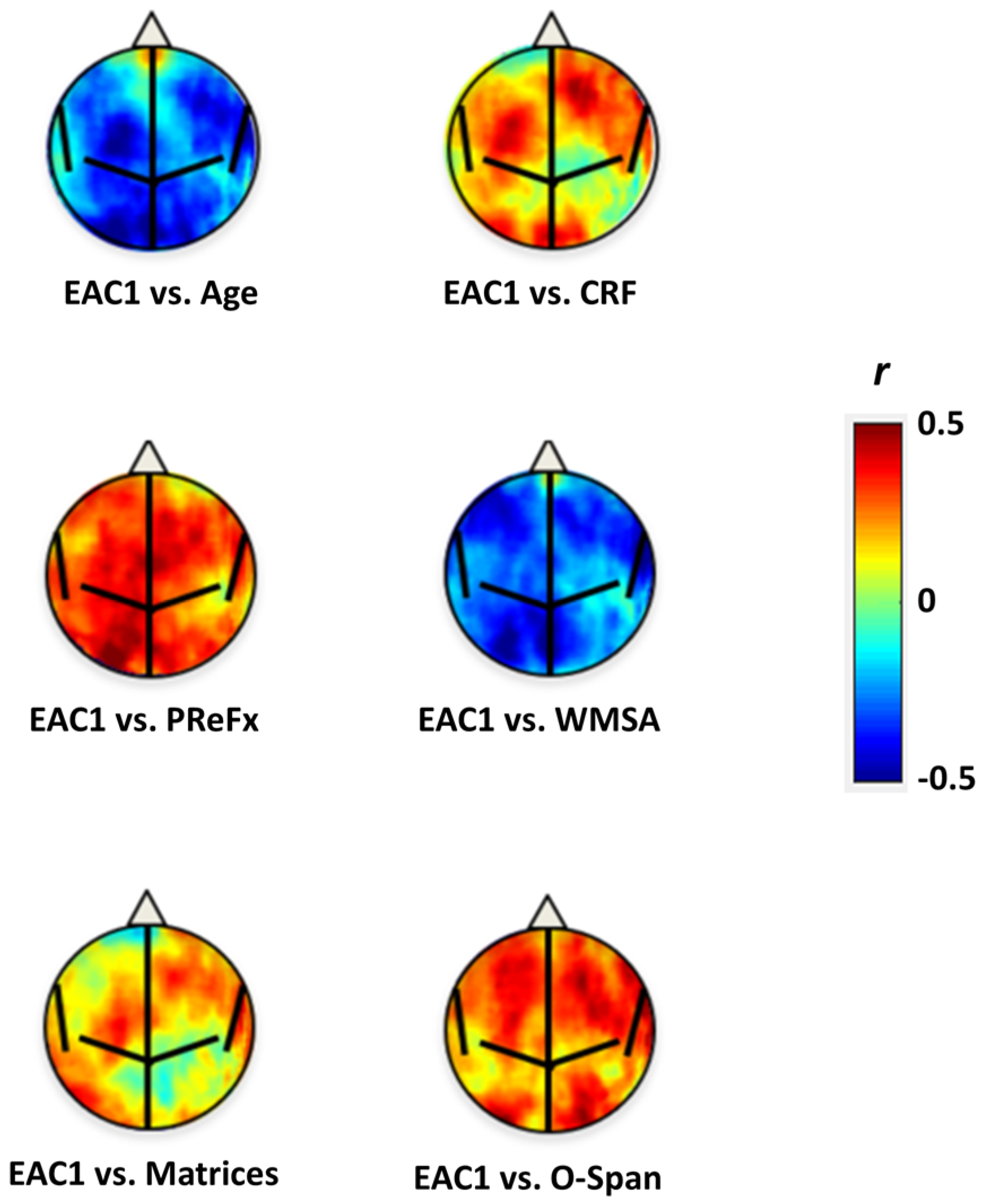
| Variable | EAC1 | EAC2 | Age | EAC1.Age | EAC2.Age |
|---|---|---|---|---|---|
| Age | −0.496 | 0.275 | |||
| CRF | 0.332 | −0.247 | −0.741 | −0.062 | −0.067 |
| Sex (1 = M, 2 = F) | 0.230 | 0.183 | 0.034 | 0.284 | 0.180 |
| Education (Yrs) | −0.155 | 0.027 | 0.492 | 0.119 | −0.129 |
| Heart Rate (bpm) | −0.042 | 0.068 | −0.144 | −0.132 | 0.113 |
| Heart Rate Var. (ms) | 0.172 | −0.334 | −0.635 | −0.213 | −0.215 |
| PReFx (overall) | 0.423 | −0.049 | −0.409 | 0.278 | 0.072 |
| PReFx (L Hem) | 0.438 | −0.010 | −0.392 | 0.305 | 0.110 |
| PReFx (R Hem) | 0.388 | −0.085 | −0.407 | 0.235 | 0.030 |
| Cortical Thickness (mm) | 0.575 | −0.034 | −0.658 | 0.380 | 0.204 |
| WMSA (log voxels) | −0.534 | 0.014 | 0.552 | −0.359 | −0.172 |
| Performance Score | 0.457 | −0.150 | −0.471 | 0.291 | −0.024 |
| Verbal Score | −0.194 | 0.006 | 0.430 | 0.025 | −0.129 |
| Perf.-Verb. Score | 0.433 | −0.099 | −0.617 | 0.185 | 0.093 |
| mMMS | −0.161 | −0.058 | 0.168 | −0.091 | −0.110 |
| KBIT | −0.186 | 0.112 | 0.172 | −0.118 | 0.069 |
| Raven’s Matrices | 0.293 | −0.102 | −0.387 | 0.126 | 0.005 |
| Shipley Vocabulary | −0.186 | 0.245 | 0.457 | 0.052 | 0.139 |
| Forward Digit Span | −0.078 | 0.011 | 0.351 | 0.117 | −0.095 |
| Backward Digit Span | −0.192 | −0.016 | 0.270 | −0.069 | −0.098 |
| Verbal Fluency | −0.069 | −0.297 | 0.127 | −0.007 | −0.348 |
| O-Span | 0.417 | −0.089 | −0.454 | 0.248 | 0.042 |
| Trail A (sec.) | −0.260 | 0.226 | 0.271 | −0.150 | 0.164 |
| Trial B (sec.) | −0.364 | 0.165 | 0.290 | −0.265 | 0.092 |
| Trail B-A (sec.) | −0.293 | 0.085 | 0.206 | −0.225 | 0.031 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiarelli, A.M.; Low, K.A.; Maclin, E.L.; Fletcher, M.A.; Kong, T.S.; Zimmerman, B.; Tan, C.H.; Sutton, B.P.; Fabiani, M.; Gratton, G. The Optical Effective Attenuation Coefficient as an Informative Measure of Brain Health in Aging. Photonics 2019, 6, 79. https://doi.org/10.3390/photonics6030079
Chiarelli AM, Low KA, Maclin EL, Fletcher MA, Kong TS, Zimmerman B, Tan CH, Sutton BP, Fabiani M, Gratton G. The Optical Effective Attenuation Coefficient as an Informative Measure of Brain Health in Aging. Photonics. 2019; 6(3):79. https://doi.org/10.3390/photonics6030079
Chicago/Turabian StyleChiarelli, Antonio M., Kathy A. Low, Edward L. Maclin, Mark A. Fletcher, Tania S. Kong, Benjamin Zimmerman, Chin Hong Tan, Bradley P. Sutton, Monica Fabiani, and Gabriele Gratton. 2019. "The Optical Effective Attenuation Coefficient as an Informative Measure of Brain Health in Aging" Photonics 6, no. 3: 79. https://doi.org/10.3390/photonics6030079
APA StyleChiarelli, A. M., Low, K. A., Maclin, E. L., Fletcher, M. A., Kong, T. S., Zimmerman, B., Tan, C. H., Sutton, B. P., Fabiani, M., & Gratton, G. (2019). The Optical Effective Attenuation Coefficient as an Informative Measure of Brain Health in Aging. Photonics, 6(3), 79. https://doi.org/10.3390/photonics6030079






