Stability Boundaries in Laterally-Coupled Pairs of Semiconductor Lasers
Abstract
1. Introduction
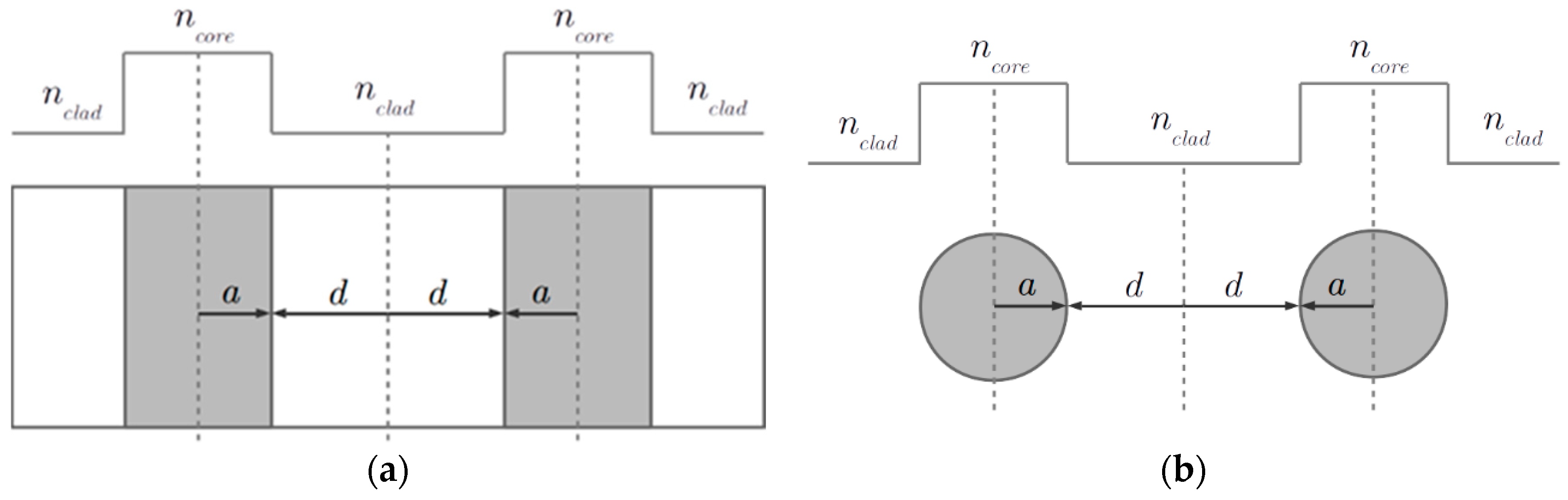
2. Model
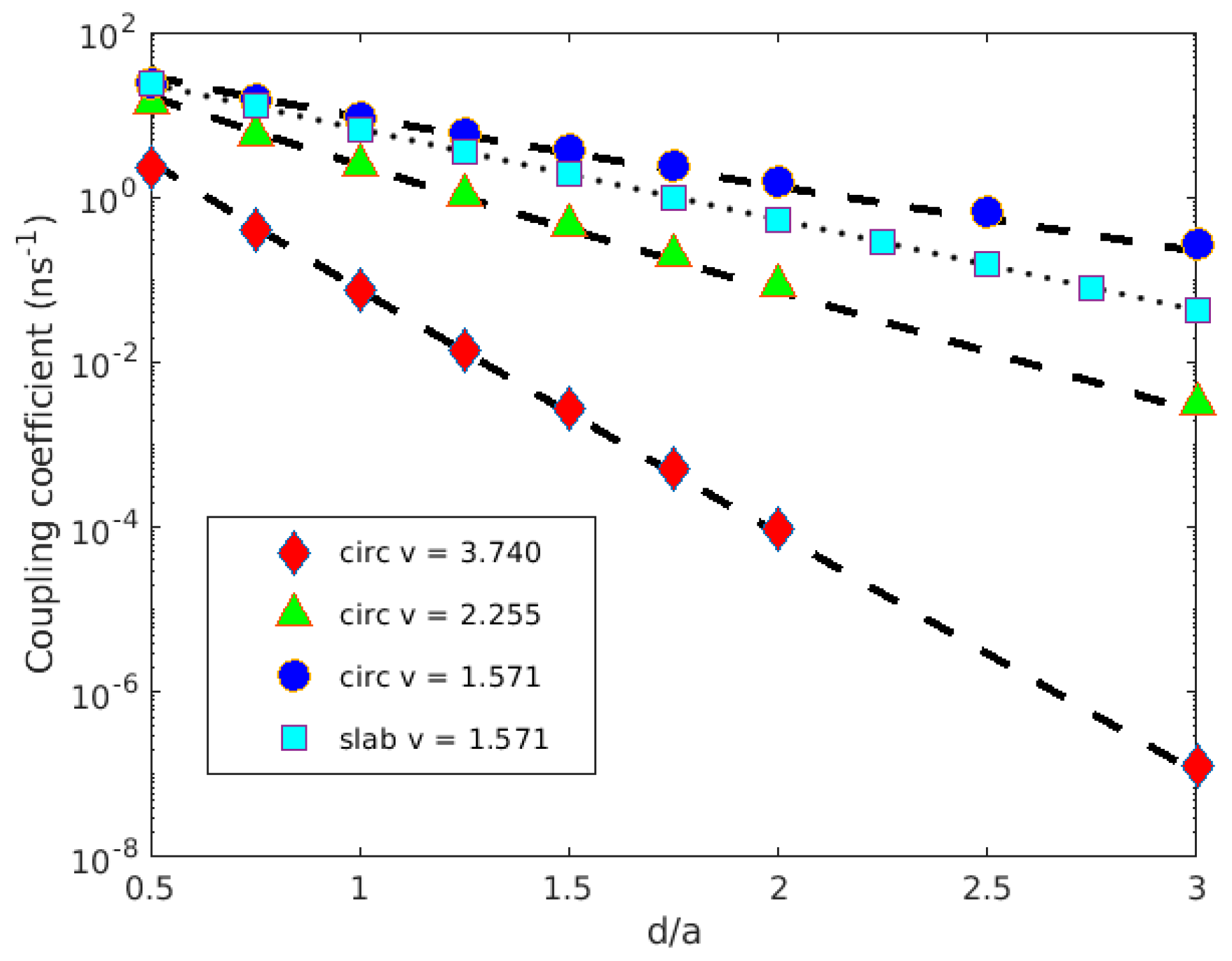
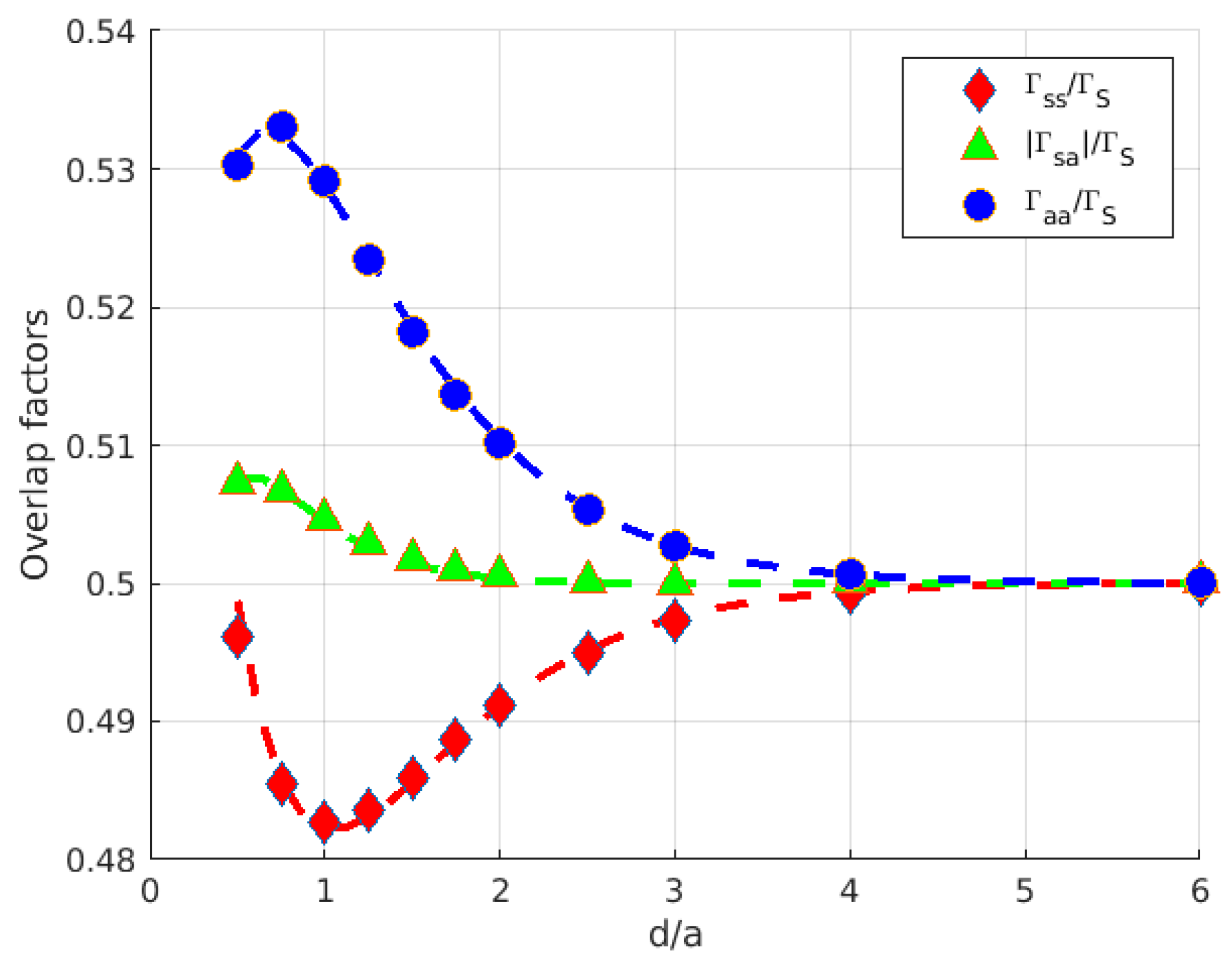
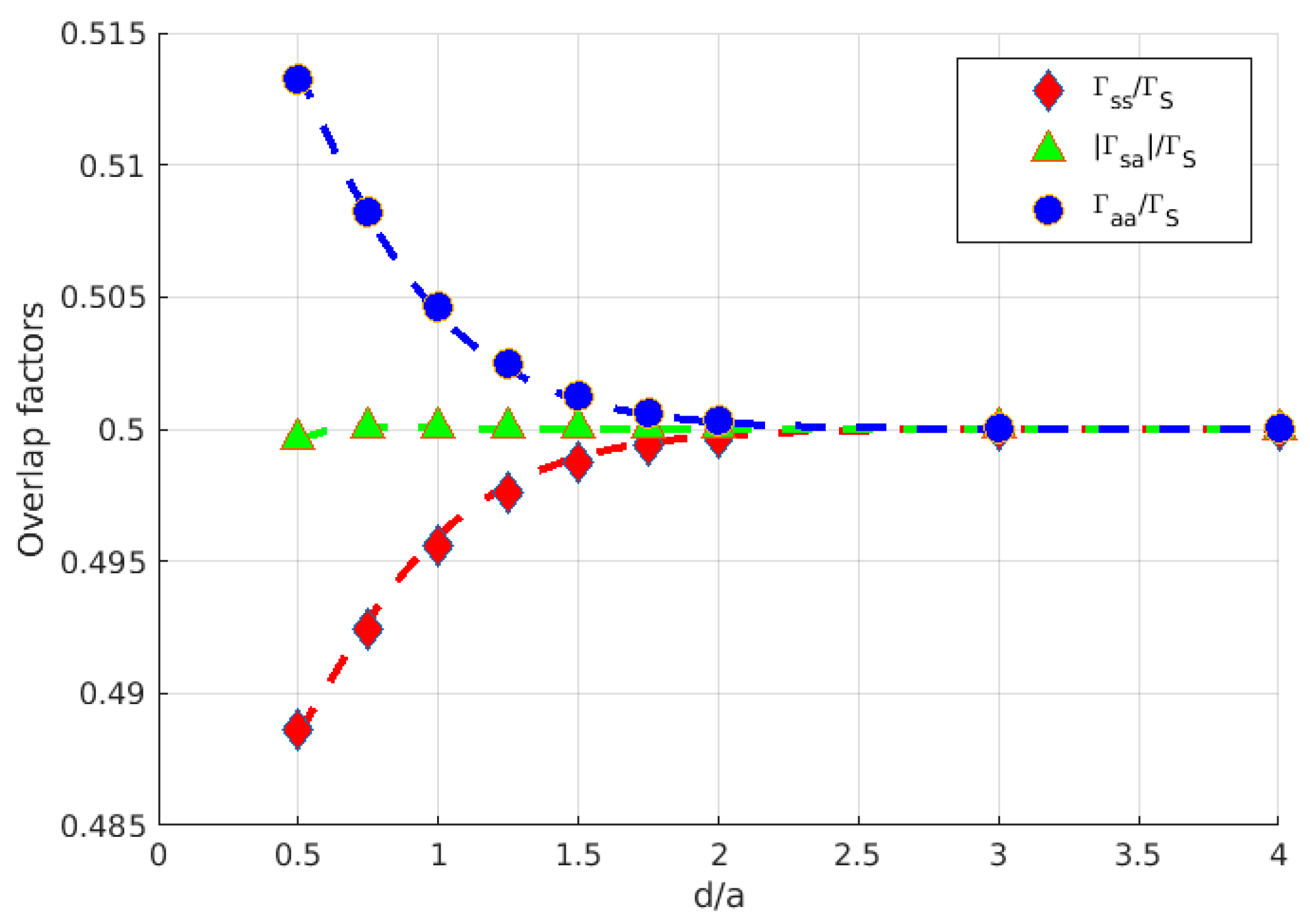
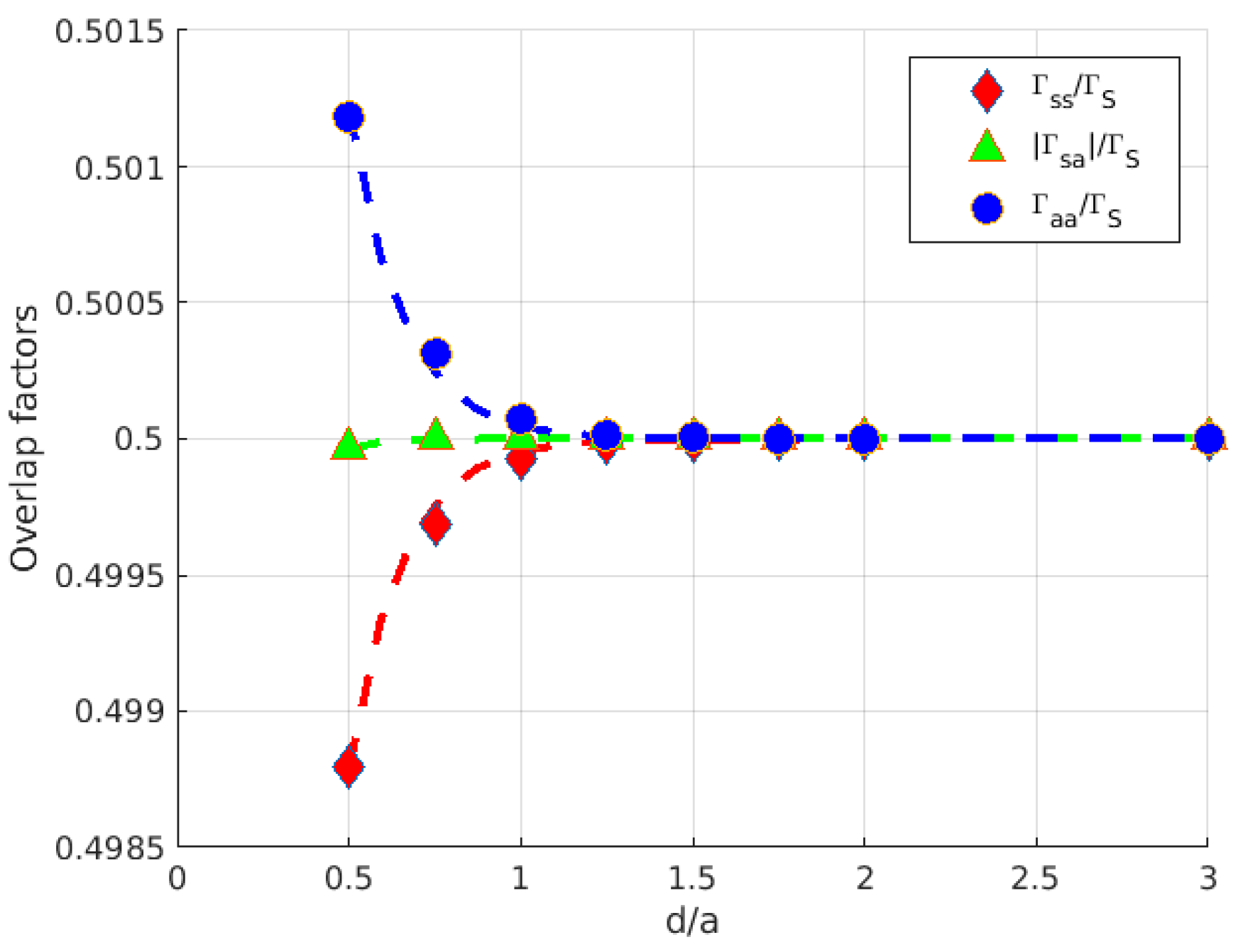
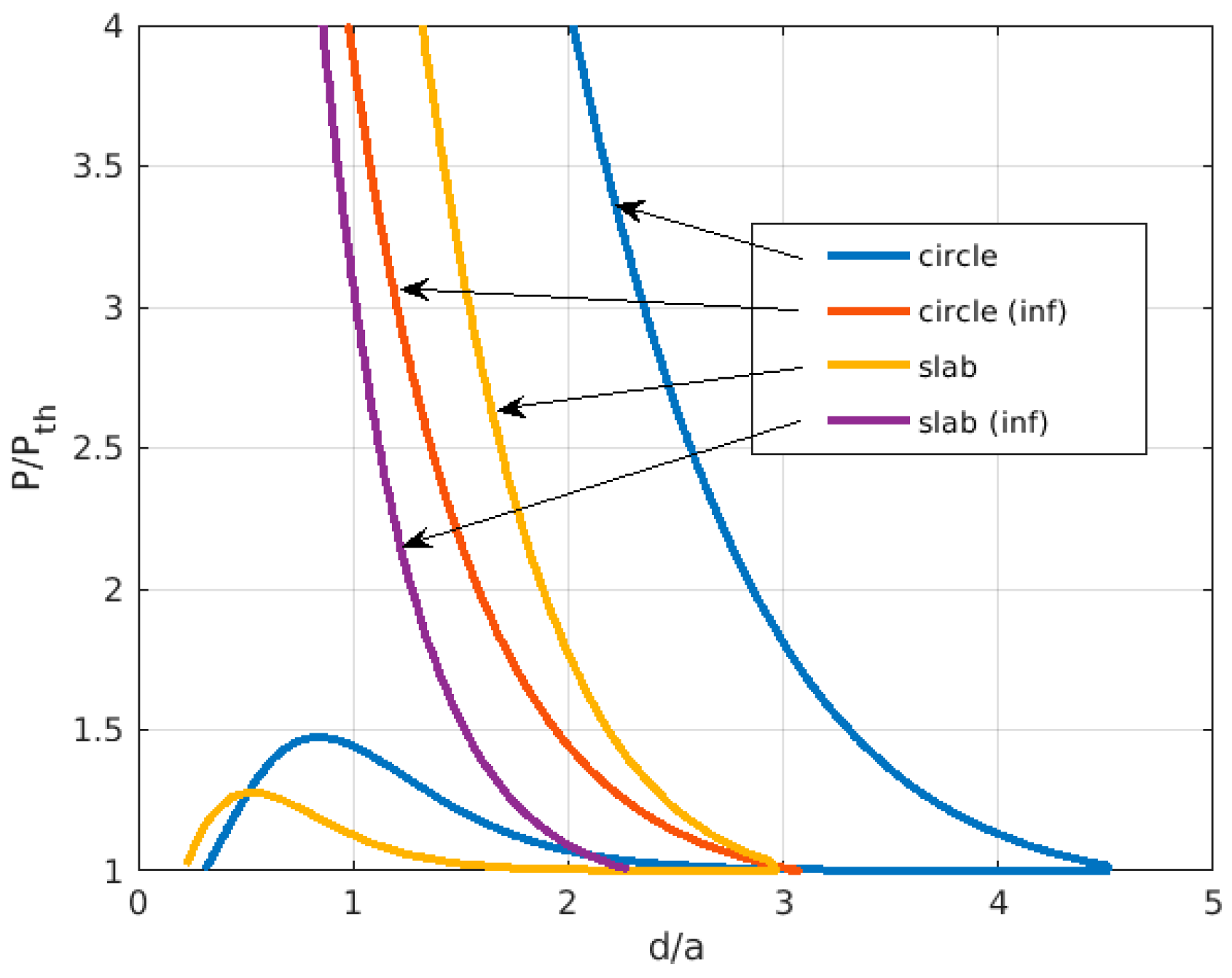
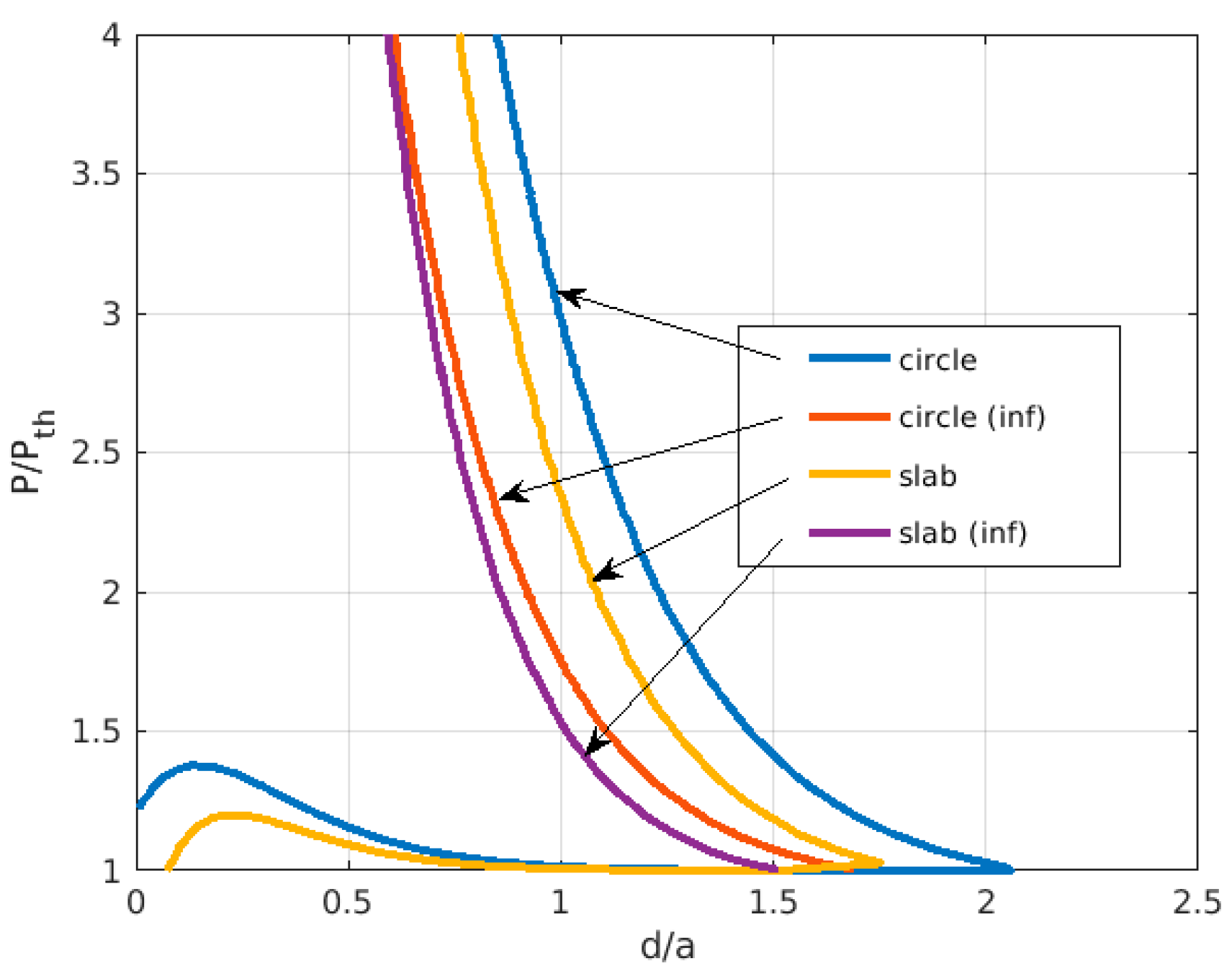
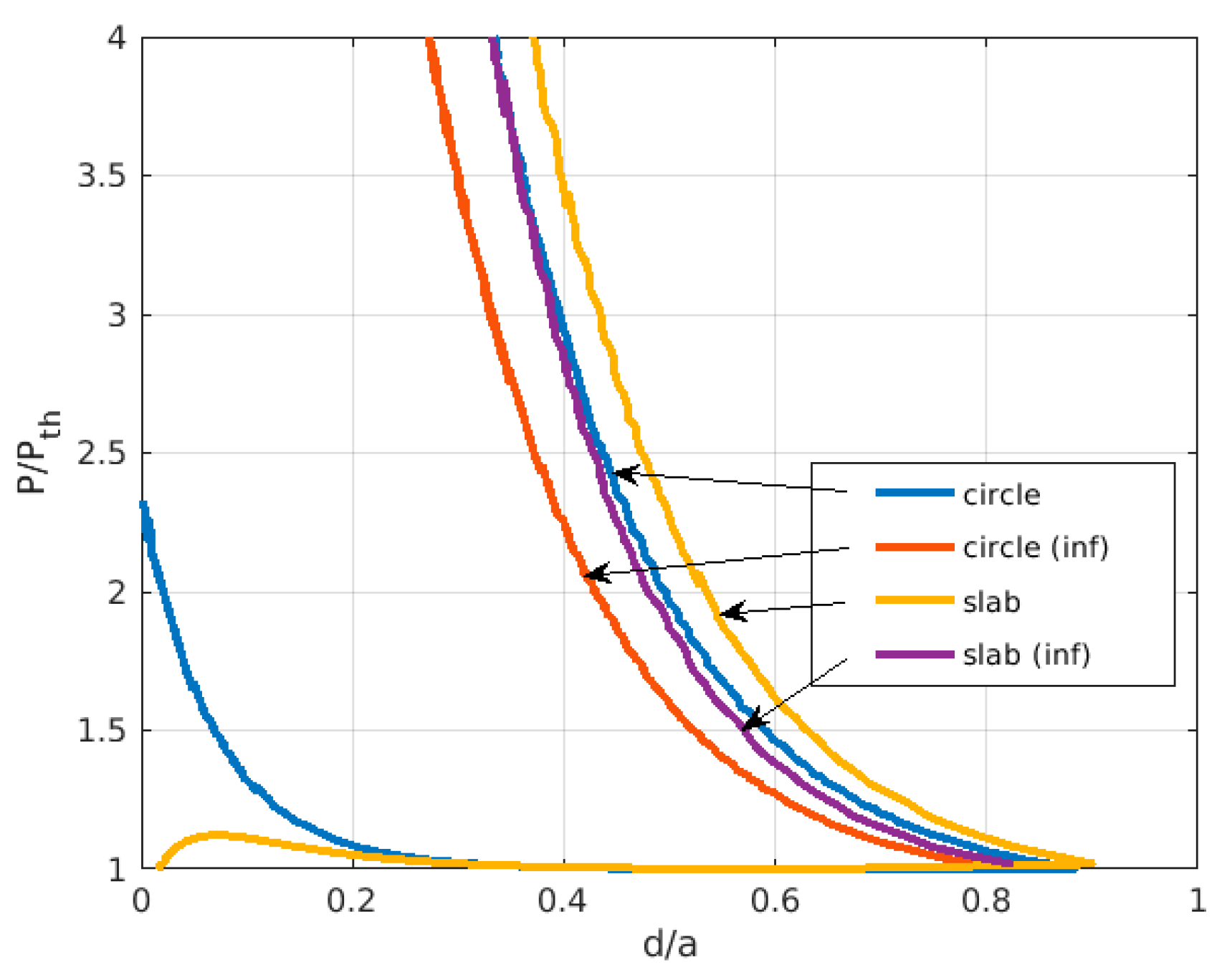
3. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Botez, D.; Scifres, D.R. (Eds.) Diode Laser Arrays; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Seurin, J.F.P. High-Power VCSEL Arrays. In VCSELs Fundamentals, Technology and Applications of Vertical-Cavity Surface-Emitting Lasers; Michalzik, R., Ed.; Springer: Berlin, Germany, 2013. [Google Scholar]
- Wilson, G.A.; DeFreez, R.K.; Winful, H.G. Modulation of phased-array semiconductor lasers at K-band frequencies. IEEE J. Quantum Electron. 1991, 27, 1696–1704. [Google Scholar] [CrossRef]
- Fryslie, S.T.M.; Gao, Z.; Dave, H.; Thompson, B.J.; Lakomy, K.; Lin, S.; Decker, P.; McElfresh, D.; Schutt-Aine, J.E.; Choquette, K.D. Modulation of coherently-coupled phased photonic crystal vertical cavity laser arrays. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1700409. [Google Scholar] [CrossRef]
- Hill, D.E. Phased array tracking of semiconductor laser arrays with complex coupling coefficients. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1501209. [Google Scholar] [CrossRef]
- Gao, Z.; Fryslie, S.T.M.; Thompson, B.J.; Scott Carney, P.; Choquette, K.D. Parity-time symmetry in coherently coupled vertical cavity laser arrays. Optica 2017, 4, 323–329. [Google Scholar] [CrossRef]
- Hardy, A.; Streifer, W. Coupled mode theory of parallel waveguides. J. Lightwave Technol. 1985, 3, 1135–1146. [Google Scholar] [CrossRef]
- Botez, D.; Mawst, L.J. Phase-locked laser arrays revisited. IEEE Circuits Devices Mag. 1996, 12, 25–32. [Google Scholar] [CrossRef]
- Gao, Z.; Siriani, D.; Choquette, K.D. Coupling coefficient in antiguided coupling: magnitude and sign control. J. Opt. Soc. Am. B 2018, 35, 417–422. [Google Scholar] [CrossRef]
- Wang, S.S.; Winful, H.G. Dynamics of phase-locked semiconductor laser arrays. Appl. Phys. Lett. 1988, 52, 1774–1776. [Google Scholar] [CrossRef]
- Winful, H.G.; Wang, S.S. Stability of phase-locking in coupled semiconductor laser arrays. Appl. Phys. Lett. 1988, 53, 1894–1896. [Google Scholar] [CrossRef]
- Yoo, H.J.; Hayes, J.R.; Paek, E.G.; Scherer, A.; Kwon, Y.S. Array mode analysis of two-dimensional phased arrays of vertical cavity surface emitting lasers. IEEE J. Quantum Electron. 1990, 26, 1039–1051. [Google Scholar] [CrossRef][Green Version]
- Ru, P.; Jakobsen, P.K.; Moloney, J.V.; Indik, R. Generalized coupled-mode model for the multistripe index-guided laser arrays. J. Opt. Soc. Am. B 1993, 10, 507–515. [Google Scholar] [CrossRef]
- Silber, M.; Fabiny, L.; Wiesenfeld, K. Stability results for in-phase and splay-phase states of solid-state laser arrays. J. Opt. Soc. Am. B 1993, 10, 1121–1129. [Google Scholar] [CrossRef]
- Leonés, M.; Lamela, H.; Carpintero, G. Coupling effects in the dynamic behavior of two laterally coupled semiconductor lasers. Proc. SPIE. 1999, 3625, 707–714. [Google Scholar]
- Lamela, H.; Leonés, M.; Carpintero, G.; Simmendinger, C.; Hess, O. Analysis of the dynamic behavior and short-pulse modulation scheme for laterally coupled diode lasers. IEEE J. Sel. Top. Quantum Electron. 2001, 7, 192–200. [Google Scholar] [CrossRef]
- Erzgräber, H.; Wieczorek, S.; Krauskopf, B. Dynamics of two laterally coupled semiconductor lasers: Strong- and weak-coupling theory. Phys. Rev. E 2008, 78, 066201. [Google Scholar] [CrossRef] [PubMed]
- Erzgräber, H.; Wieczorek, S.; Krauskopf, B. Locking behaviour of three coupled laser oscillators. Phys. Rev. E 2009, 80, 026212. [Google Scholar] [CrossRef] [PubMed]
- Blackbeard, N.; Erzgräber, H.; Wieczorek, S. Shear-induced bifurcations and chaos in models of three coupled lasers. SIAM J. Appl. Dyn. Syst. 2011, 10, 469–509. [Google Scholar] [CrossRef][Green Version]
- Blackbeard, N.; Wieczorek, S.; Erzgräber, H.; Dutta, P.S. From synchronisation to persistent optical turbulence in laser arrays. Phys. D 2014, 286–287, 43–58. [Google Scholar] [CrossRef]
- Adams, M.J.; Li, N.Q.; Cemlyn, B.R.; Susanto, H.; Henning, I.D. Effects of detuning, gain-guiding and index antiguiding on the dynamics of two laterally-coupled semiconductor lasers. Phys. Rev. A 2017, 95, 053869. [Google Scholar] [CrossRef]
- Li, N.Q.; Susanto, H.; Cemlyn, B.R.; Henning, I.D.; Adams, M.J. Nonlinear dynamics of solitary and optically injected two-element laser arrays with four different waveguide structures: A numerical study. Opt. Express 2018, 26, 4751–4765. [Google Scholar] [CrossRef]
- Ning, C.Z.; Goorjian, P.M. Ultrafast directional beam switching in coupled vertical-cavity surface-emitting lasers. J. Appl. Phys. 2001, 90, 497–499. [Google Scholar] [CrossRef]
- Ning, C.Z. Self-sustained ultrafast pulsation in coupled vertical-cavity surface-emitting lasers. Opt. Lett. 2002, 27, 912–914. [Google Scholar] [CrossRef]
- Goorjian, P.M.; Ning, C.Z. Ultrafast beam self-switching by using coupled vertical cavity surface-emitting lasers. J. Mod. Opt. 2002, 49, 707–718. [Google Scholar] [CrossRef]
- Marom, E.; Ramer, O.G.; Ruschin, S. Relation between normal-mode and coupled-mode analyses of parallel waveguides. IEEE J. Quantum Electron. 1984, 20, 1311–1319. [Google Scholar] [CrossRef]
- Yariv, A. Optical Electronics in Modern Communications, 5th ed.; Oxford University Press: New York, NY, USA, 1997; Section 13.8. [Google Scholar]
- Snyder, A.W. Coupled-mode theory for optical fibers. J. Opt. Soc. Am. 1972, 62, 1267–1277. [Google Scholar] [CrossRef]
- Ogawa, K. Simplified theory of the multimode fiber coupler. Bell Syst. Tech. J. 1977, 56, 729–745. [Google Scholar] [CrossRef]
- Yoo, H.J.; Hayes, J.U.; Kwon, Y.S. Analysis of coupling coefficient between two vertical cavity surface emitting lasers for two-dimensional phase-locked array. Electron. Lett. 1990, 26, 896–897. [Google Scholar] [CrossRef]
- Hendriks, R.F.M.; van Exter, M.P.; Woerdman, J.P.; van der Poel, C.J. Phase coupling of two optically pumped vertical-cavity surface-emitting lasers. Appl. Phys. Lett. 1996, 69, 869–871. [Google Scholar] [CrossRef]
- Gloge, D. Weakly guiding fibers. Appl. Opt. 1971, 10, 2252–2258. [Google Scholar] [CrossRef]
- Alexeyev, C.N.; Boklag, N.A.; Yavorsky, M.A. Higher order modes of coupled optical fibres. J. Opt. 2010, 12, 115704. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaughan, M.; Susanto, H.; Li, N.; Henning, I.; Adams, M. Stability Boundaries in Laterally-Coupled Pairs of Semiconductor Lasers. Photonics 2019, 6, 74. https://doi.org/10.3390/photonics6020074
Vaughan M, Susanto H, Li N, Henning I, Adams M. Stability Boundaries in Laterally-Coupled Pairs of Semiconductor Lasers. Photonics. 2019; 6(2):74. https://doi.org/10.3390/photonics6020074
Chicago/Turabian StyleVaughan, Martin, Hadi Susanto, Nianqiang Li, Ian Henning, and Mike Adams. 2019. "Stability Boundaries in Laterally-Coupled Pairs of Semiconductor Lasers" Photonics 6, no. 2: 74. https://doi.org/10.3390/photonics6020074
APA StyleVaughan, M., Susanto, H., Li, N., Henning, I., & Adams, M. (2019). Stability Boundaries in Laterally-Coupled Pairs of Semiconductor Lasers. Photonics, 6(2), 74. https://doi.org/10.3390/photonics6020074






