THz Mixing with High-TC Hot Electron Bolometers: A Performance Modeling Assessment for Y-Ba-Cu-O Devices
Abstract
:1. Introduction
2. Models and Methods
2.1. Describing the Superconducting Transition at THz Frequencies
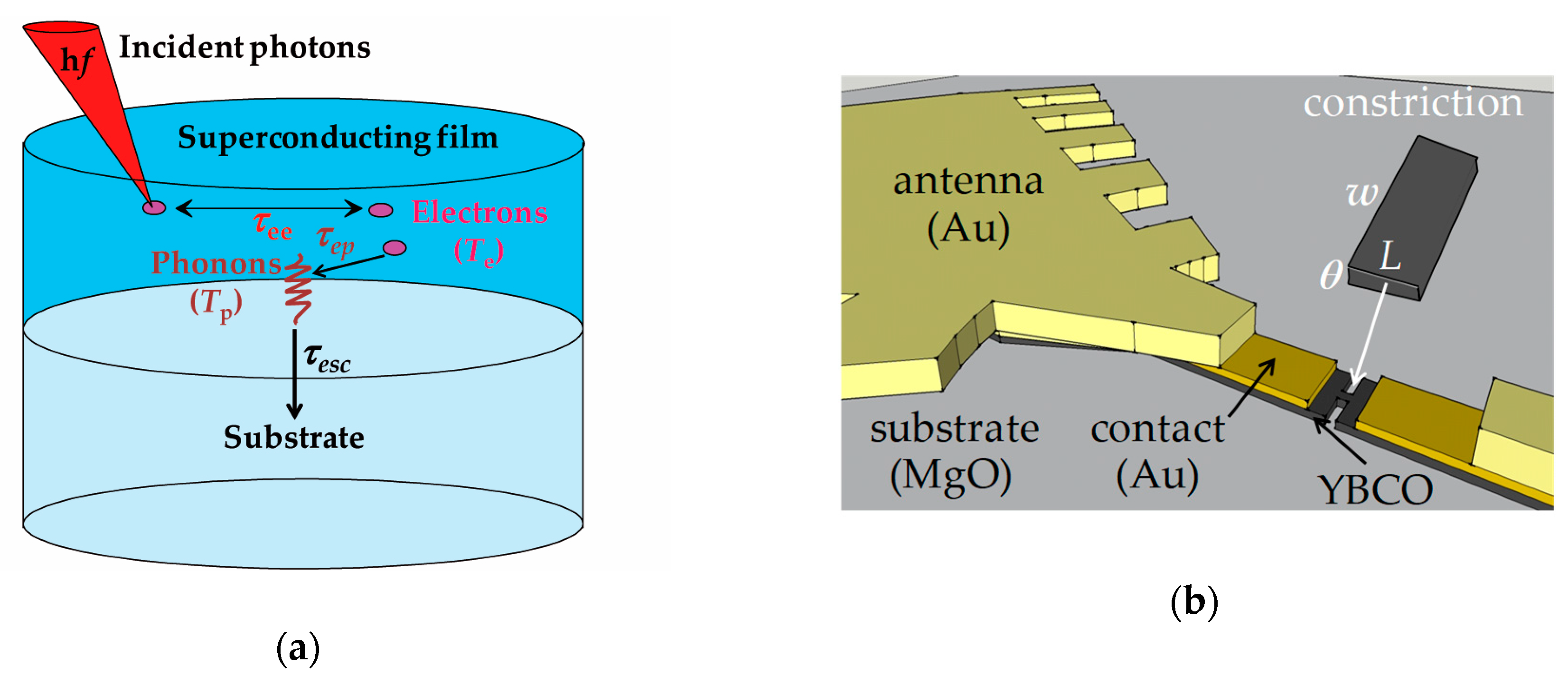
2.2. HEB Master Equations
- These equations obviously describe a phonon cooling mechanism for the electrons in YBCO, as opposed to Nb HEBs, where cooling by electron diffusion to the metal contacts is the dominant process [3,31]. In fact, using YBCO data (cf. Section 3.2, Table 1), we evaluate the electron diffusion length le ≈ π(τepκe/Ce)1/2 ≅ 25 nm, a significantly smaller value than the constriction length (100 to 400 nm) considered here, so that phonon cooling will prevail [22].
- It also appears from Equation (5) that the DC and THz current densities are assumed to be constant across the area SC, a point discussed at length in Reference [32]. Due to the resistivity vs. Te(x) dependence, DC and THz powers are non-uniformly absorbed along the constriction, as noticed in Reference [33].
- The constriction ends (at coordinates x = 0 and x = L) are at reference temperature T0, which is the cryostat/cryogenerator cold finger temperature (gold antenna contacts). So that: Te(0) = Tp(0) = Te(L) = Tp(L) = T0.
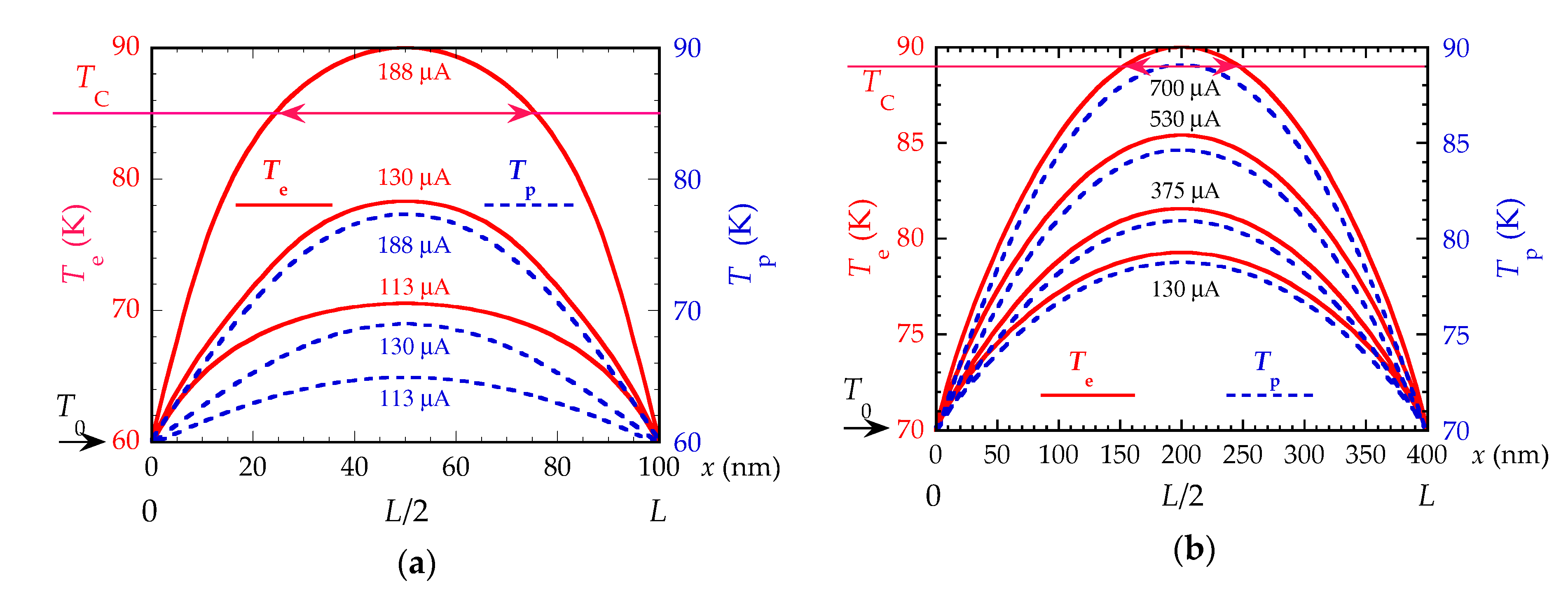
- The solutions Te(x) and Tp(x) follow the geometrical symmetry of the constriction with respect to its center: Te(x) = Te(L − x) and Tp(x) = Tp(L − x). Consequently, the equation solving will be performed in a half-constriction, e.g., x ∈ [L/2, L].
- The dissipated power in the constriction tends to raise Te(x) and Tp(x), which will reach their maximum values at the constriction center, so that: Temax = Te(L/2), and Tpmax = Tp(L/2), with dTe(L/2)/dx = dTp(L/2)/dx = 0.
- The energy exchange exponent n = 3 was taken for YBCO, as extracted from electron-phonon interaction time measurements (see, e.g., Reference [1]). The YBCO to substrate phonon mismatch index m = 3 resulted from the number of available phonon modes, proportional to T3 (Debye’s model).
- For numerical computation convenience, the resistive superconductive transition has been approximated by a Fermi-Dirac function of the form ρ = ρ0 [1 + exp((TC − Te)/ΔT)]−1, to fit the variation given by Equation (3).
- Due to thermal effects, TC is sensitive to the constriction DC bias current IDC; this effect has been taken into account by writing TC(IDC) = TC(0)[1 − (IDC/(JrefSC))2/3], where Jref is a reference current density. This point is mentioned in Reference [25] and discussed in Reference [34], in the context of YBCO thin film electrical transport vs. microstructure relationship.
- Because we can have access to the constriction RF impedance, it was possible to handle the effective power dissipated in the constriction as α × PLO, with α = αimp × α’, where αimp is the impedance matching factor between the constriction and the antenna, and α’ represents all the losses from other origins (focusing optics, diplexer, etc.).
2.3. Solving HEB Master Equations
2.4. HEB Mixer Performance
2.4.1. General Considerations and Conversion Gain
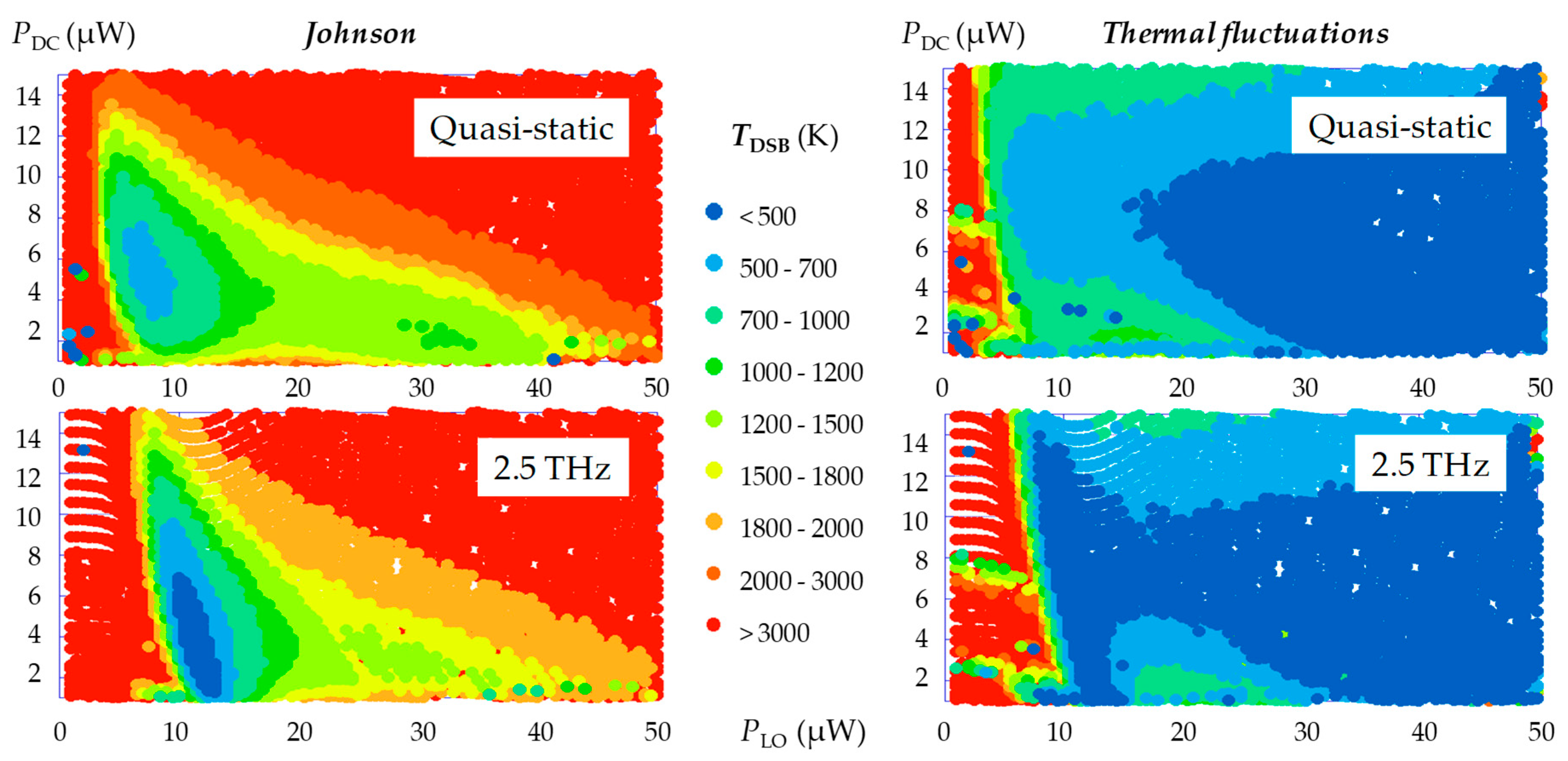
2.4.2. Noise Temperature Contributions
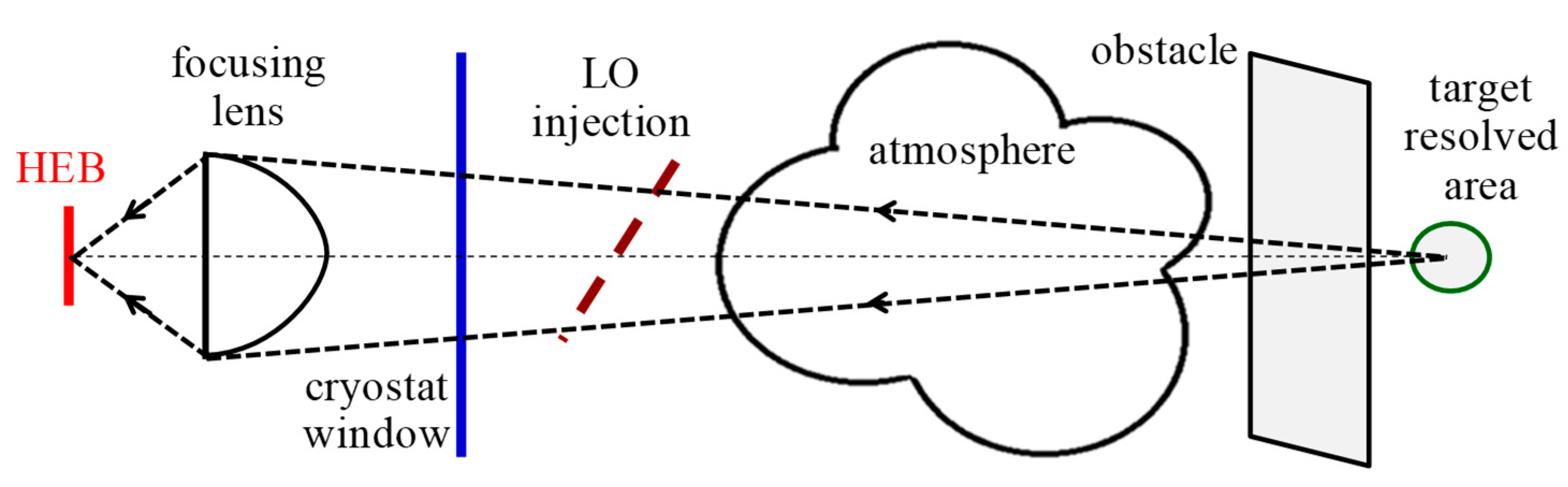
2.5. Standoff Detection Implementation with an HEB Heterodyne Detector
- topt includes the HEB planar antenna main lobe efficiency, the focusing lens and the detector cryostat window losses, and the LO injection losses (diplexer or beam splitter).
- tobs represents the transmission through some obstacle existing in front of the target (cloth, cardboard, etc.).
3. Simulation Results
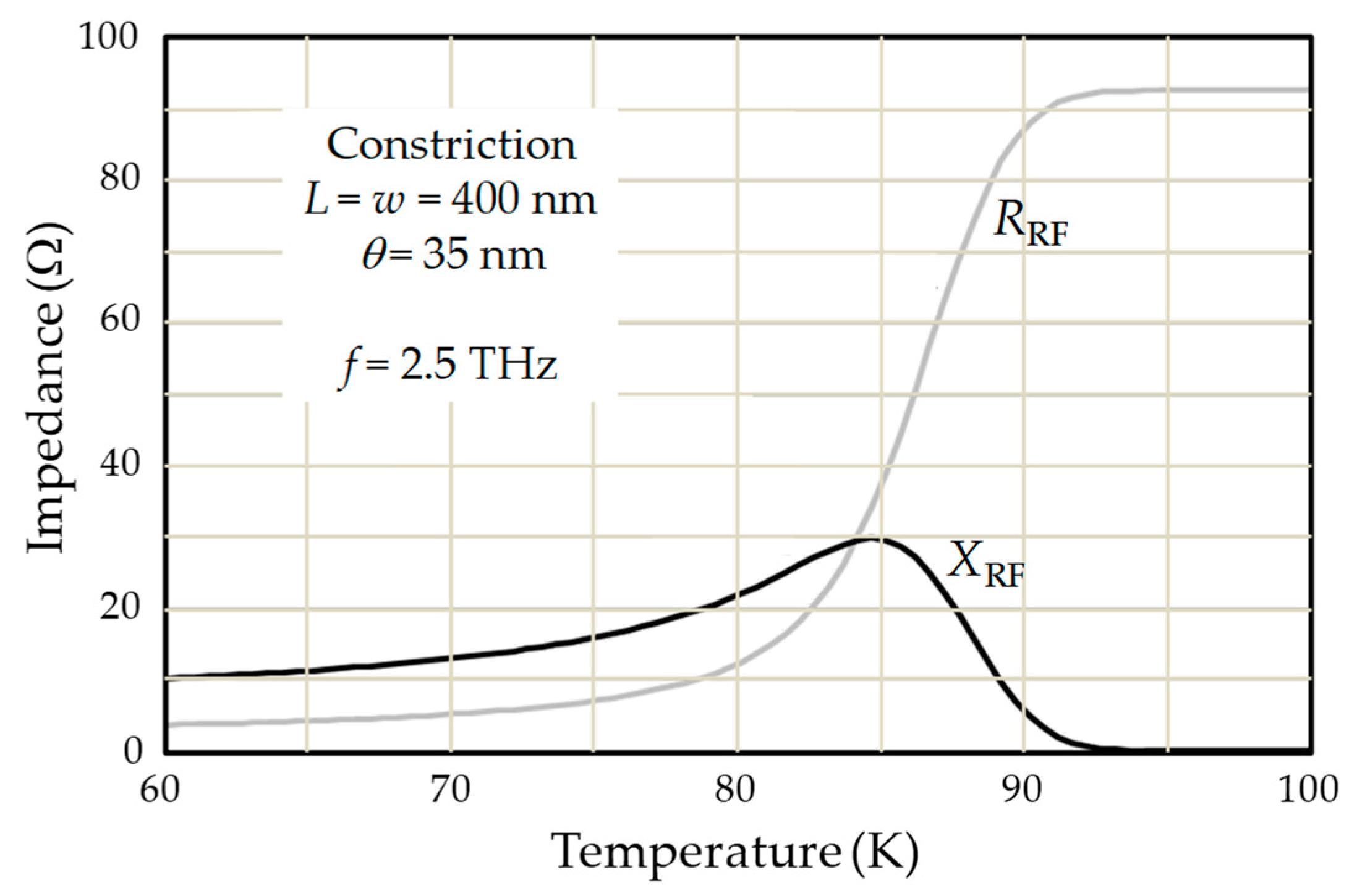
3.1. YBCO Superconducting Transition in the THz Range
3.2. DC Characteristics
3.2.1. Temperature Profiles
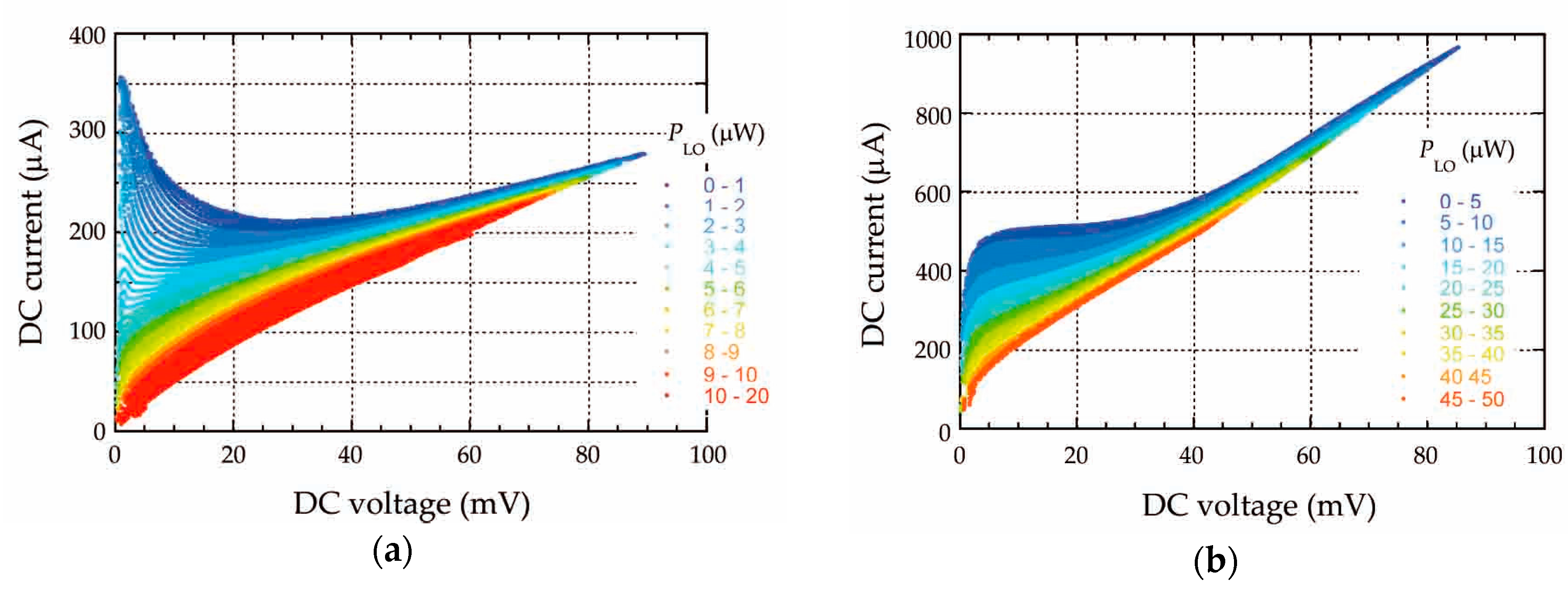
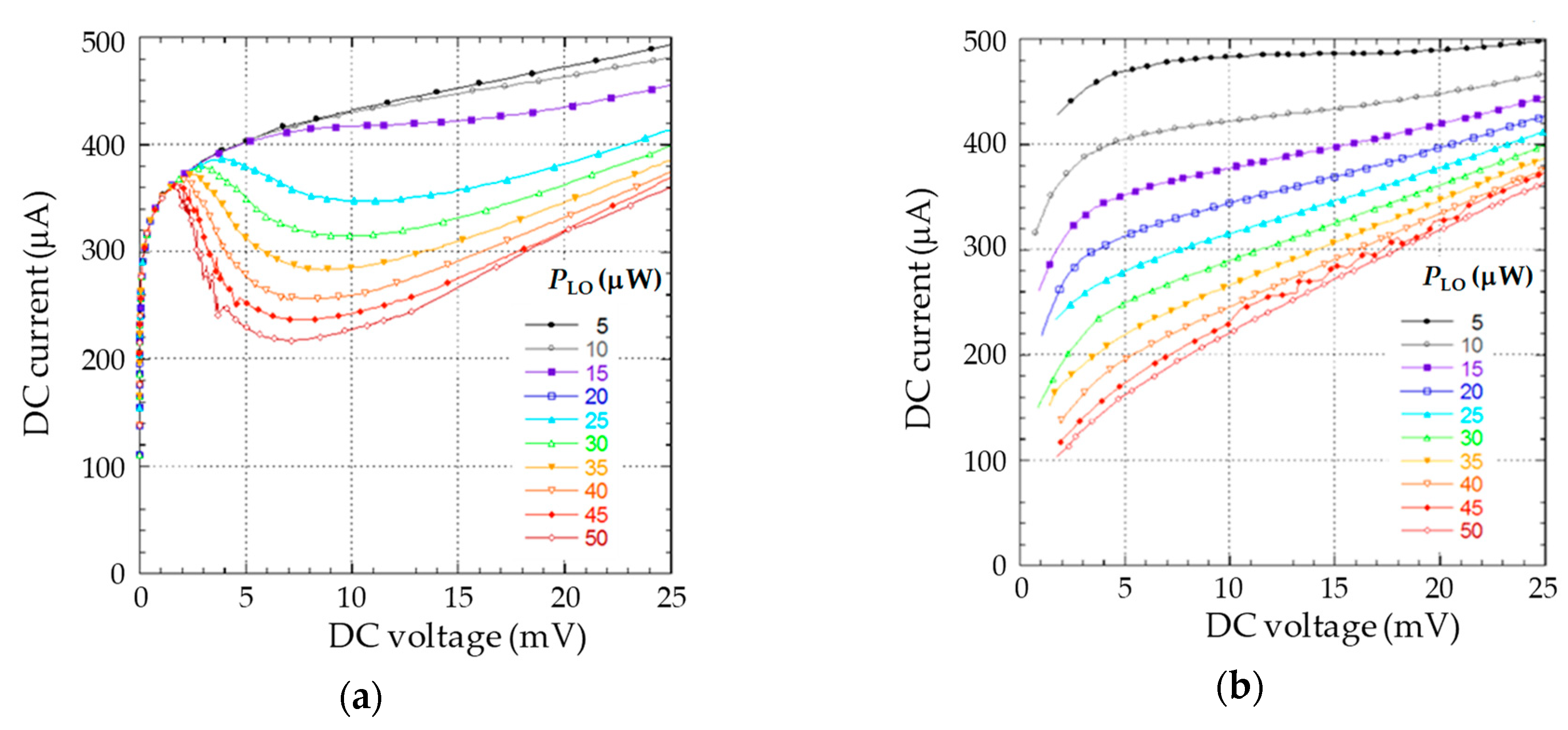
3.2.2. Current-Voltage Plots
3.3. Mixer Performance
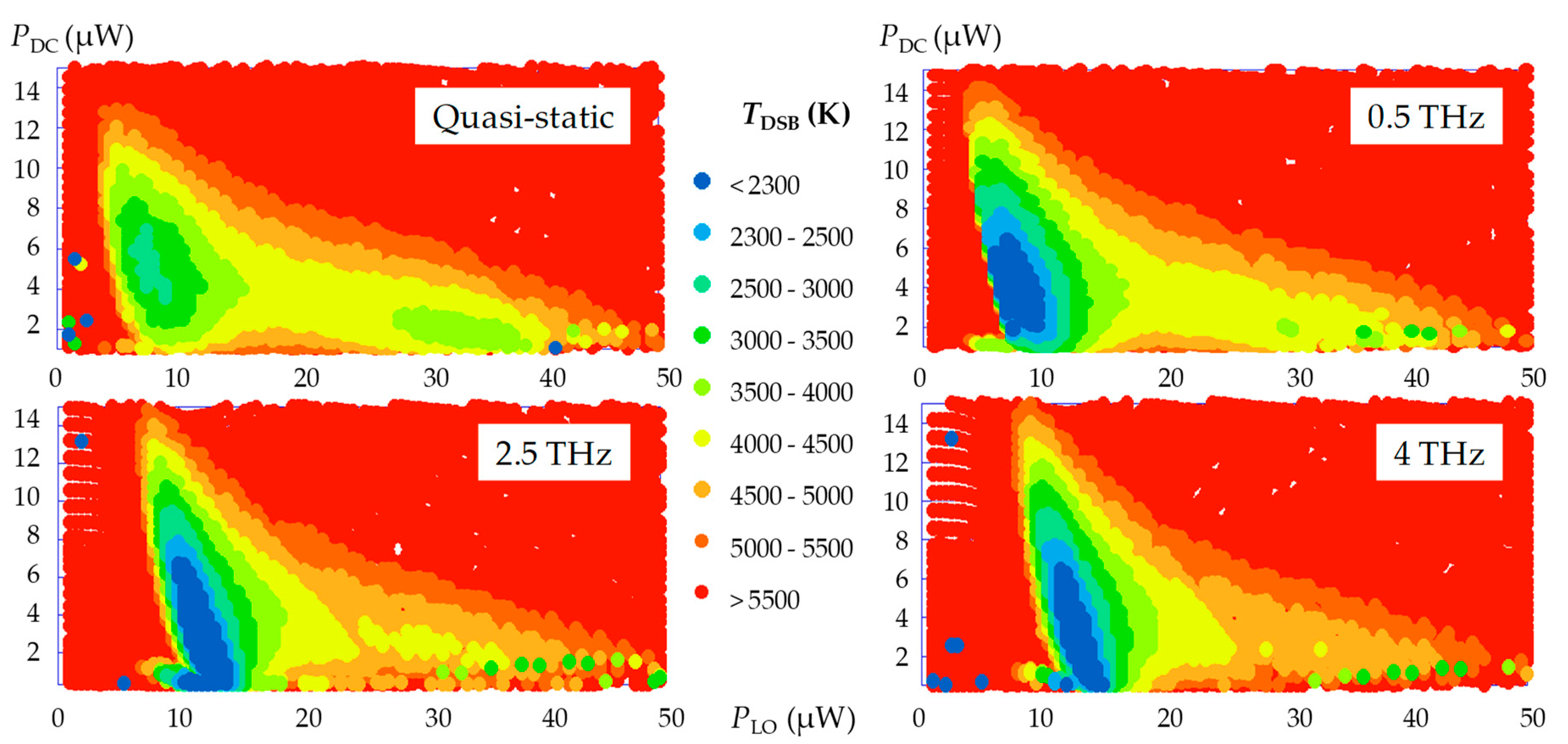
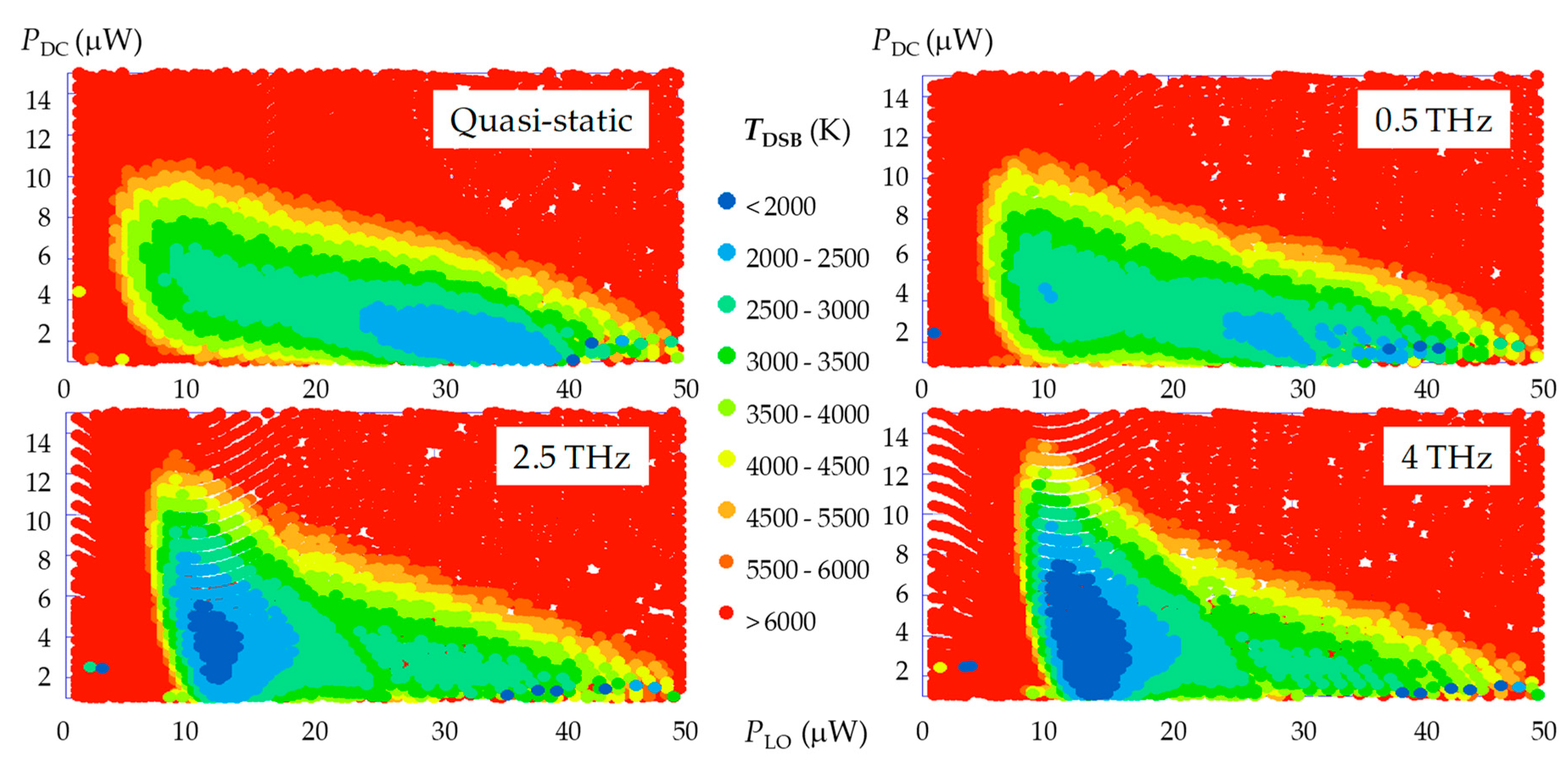
3.3.1. Noise Temperature
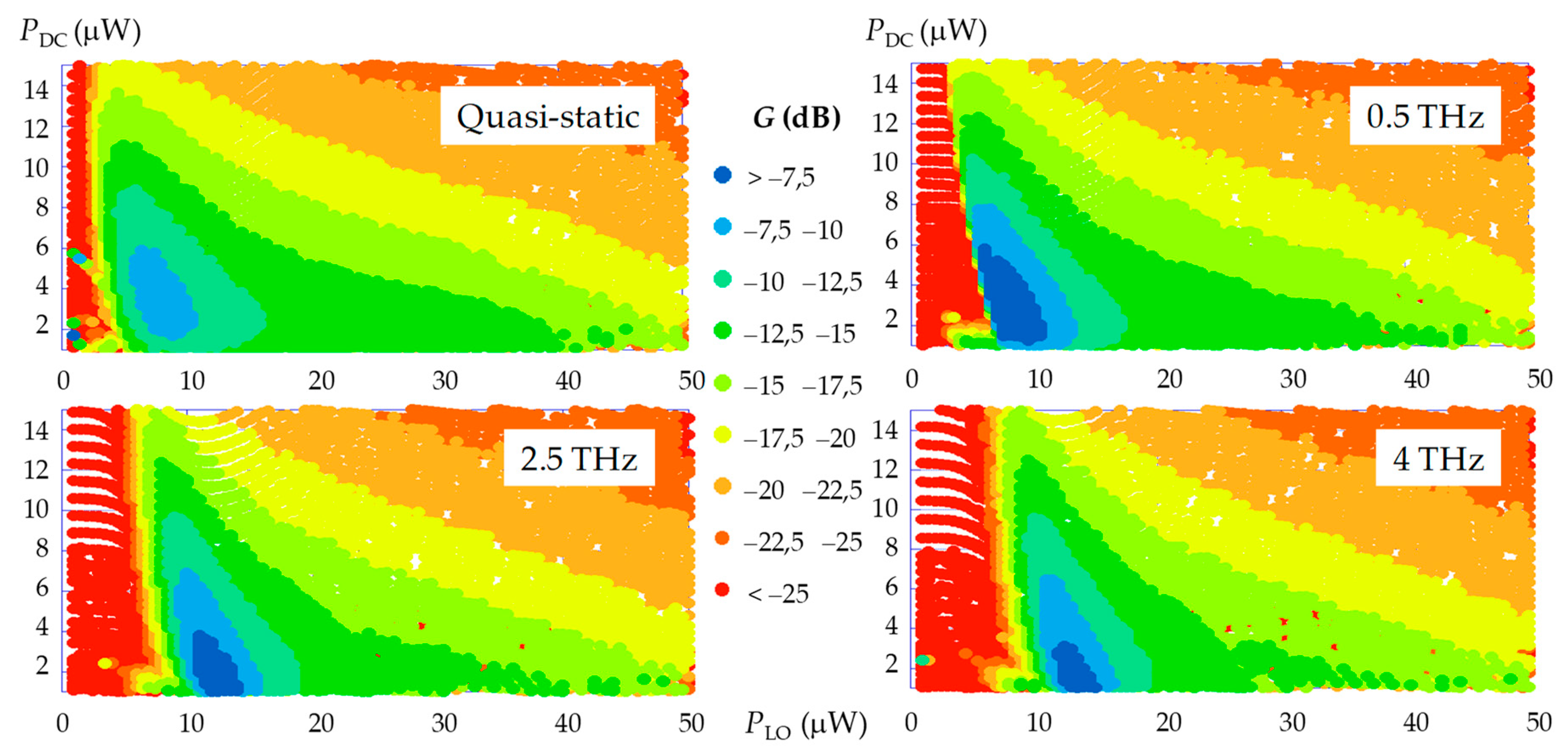
3.3.2. Conversion Gain and Summary of Mixer Results
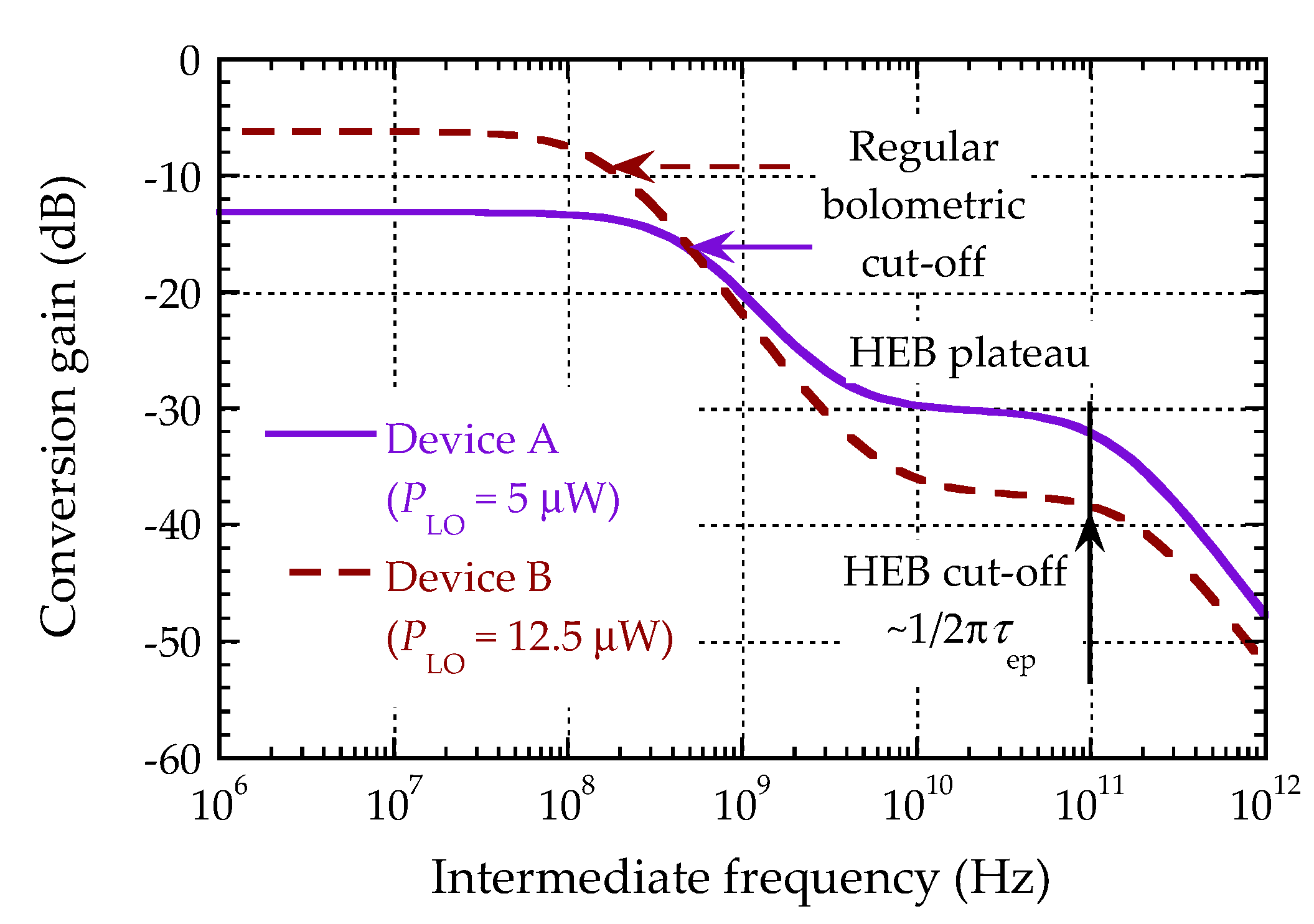
3.3.3. IF Bandwidth
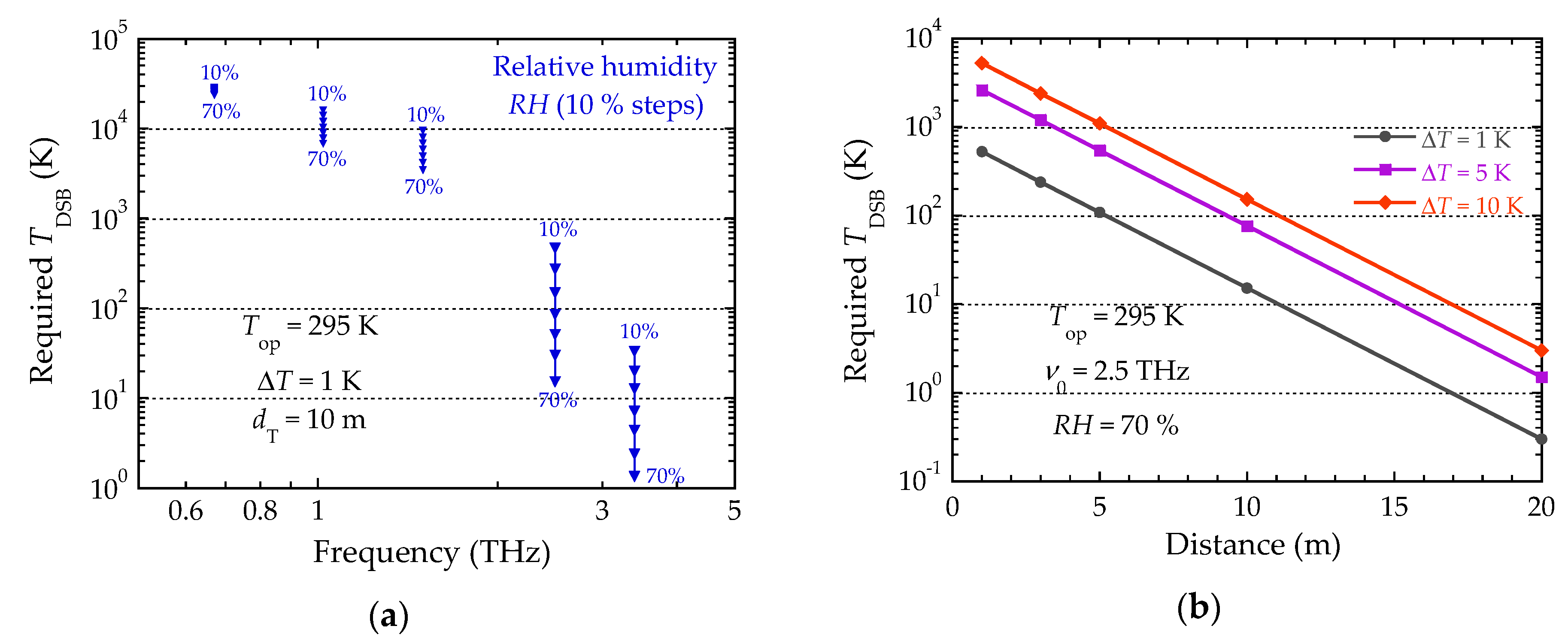
3.4. Standoff Detection Performances Requirements
- Target emissivity εT = 1.
- Optical losses were evaluated according to the antenna main lobe efficiency (−2 dB), the focusing lens and the detector cryostat window losses (−1 dB), and the LO injection losses (beam splitter: −3 dB), amounting to topt ≅ 24%.
- tatm was determined for various relative humidity values (RH, in the 10% to 70% range) at operating temperature Top = 295 K, at sea level and with clear atmospheric conditions (e.g., no dust).
4. Discussion
4.1. Inhomogeneous PLO Hypothesis Effect on I-V Plots at Low DC Voltage
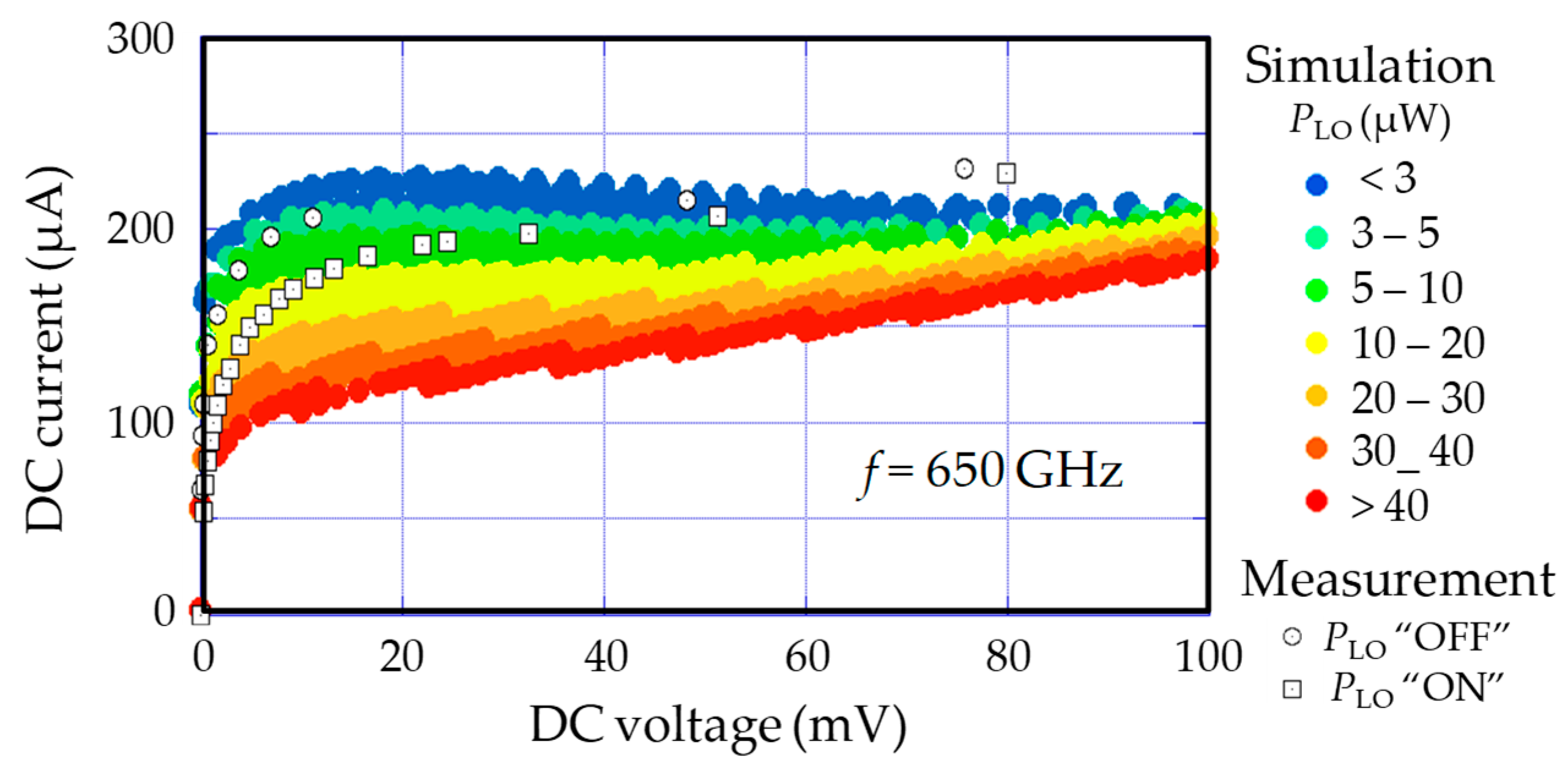
- In the conventional hot spot method (homogeneous PLO dissipation), the LO power expression, including impedance matching, is written as:where R is the constriction resistance, Ra is the antenna resistance, PLO is the power actually applied prior to losses, and is deduced from αPLO which is the power used for the hot spot calculation. When R → 0, αPLO → 0 at all PLO values (Figure 12a).
- In the hot spot method with RF current (inhomogeneous PLO dissipation), the terahertz power is determined from the intensity of the terahertz current, as outlined in Section 2.3 (Equations (6)–(10)). After some manipulations, still with the constriction low impedance value hypothesis, the following ILO vs. PLO relationship can be worked out [27]:Even at low PDC and PLO levels, we observe there is a non-zero ILO ∝ PLO1/2 along the constriction in the superconducting state. If PLO is strong enough, the critical temperature TC(ILO) < T0 and RRF is no longer negligible. Consequently, the PLO dissipation causes the increase of the electron temperature and therefore a non-zero resistance even at low current (Figure 12b).
4.2. Taking the Resistivity Limit in the Superconducting Transition into Account
4.3. Mixer Noise: Effect of Taking the Impedance Matching Factor into Account
4.4. Comparing Simulated Mixer Noise with Experimental Results
4.5. Standoff Detection Limits with YBCO HEB Mixers
5. Conclusions and Future Plans
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gershenzon, E.M.; Gol’tsman, G.N.; Gousev, Y.P.; Elant’ev, A.I.; Semenov, A.D. Electromagnetic radiation mixer based on electron heating in resistive state of superconductive Nb and YBCO films. IEEE Trans. Magn. 1991, 27, 1317–1320. [Google Scholar] [CrossRef]
- Shukarov, A.; Lobanov, Y.; Gol’tsman, G. Superconducting hot-electron bolometer: From the discovery of hot-electron phenomena to practical applications. Supercond. Sci. Technol. 2016, 29, 023001. [Google Scholar] [CrossRef]
- Karasik, B.S.; McGrath, W.R.; Wyss, R.A. Optimal Choice of Material for HEB Superconducting Mixers. IEEE Trans. Appl. Supercond. 1999, 9, 4213–4216. [Google Scholar] [CrossRef]
- Karasik, B.S.; Sergeev, A.V.; Prober, D.E. Nanobolometers for THz Photon Detection. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 97–111. [Google Scholar] [CrossRef]
- Maezawa, H. Application of Superconducting Hot-Electron Bolometer Mixers for Terahertz-Band Astronomy. IEICE Trans. Electron. 2015, E98-C, 196–206. [Google Scholar] [CrossRef]
- Lindgren, M.; Currie, M.; Williams, C.; Hsiang, T.Y.; Fauchet, P.M.; Sobolewski, R. Intrinsic picosecond response time of Y-Ba-Cu-O superconducting photodetectors. Appl. Phys. Lett. 1999, 74, 853–855. [Google Scholar] [CrossRef]
- Garcés-Chávez, V.; De Luca, A.; Gaugue, A.; Georges, P.; Kreisler, A.; Brun, A. Temporal response of high-temperature superconductor thin-film using femtosecond pulses. In Proceedings of the 4th European Conference on Applied Superconductivity, Sitges, Spain, 14–17 September 1999; Obradors, X., Ed.; Institute of Physics: Bristol, UK, 2000; pp. 93–96. [Google Scholar]
- Thoma, P.; Raasch, J.; Scheuring, A.; Hofherr, M.; Il’in, K.; Wünsch, S.; Semenov, A.; Hübers, H.-W.; Judin, V.; Müller, A.-S.; et al. Highly responsive Y-Ba-Cu-O Thin Film THz Detectors With Picosecond Time Resolution. IEEE. Trans. Appl. Supercond. 2013, 23, 2400206. [Google Scholar] [CrossRef]
- Li, C.T.; Deaver, B.S., Jr.; Lee, M.; Weikle, R.M., II; Rao, R.A.; Eom, C.B. Gain bandwidth and noise characteristics of millimeter-wave YBa2Cu3O7 hot-electron bolometer mixers. Appl. Phys. Lett. 1998, 73, 1727–1929. [Google Scholar] [CrossRef]
- Harnack, O.; Beuven, S.; Darula, M.; Kohlstedt, H.; Tarasov, M.; Stephanson, E.; Ivanov, Z. HTS mixers based on the Josephson effect and on the hot-electron bolometric effect. IEEE Trans. Appl. Supercond. 1999, 9, 3765–3768. [Google Scholar] [CrossRef]
- Uchida, T.; Yazaki, H.; Yasuoka, Y.; Suzuki, K. Slot antenna coupled YBa2Cu3O7−δ hot-electron bolometers for millimeter-wave radiation. Phys. C 2001, 357–360, 1596–1599. [Google Scholar] [CrossRef]
- Il’in, K.S.; Siegel, M. Microwave mixing in microbridges made from YBCO thin films. J. Appl. Phys. 2002, 92, 361–369. [Google Scholar] [CrossRef]
- Gousev, Y.P.; Semenov, A.D.; Nebosis, R.S.; Pechen, E.V.; Varlashkin, A.V.; Renk, K.F. Broad-band coupling of THz radiation to YBa2Cu3O7−δ hot-electron bolometer mixer. Supercond. Sci. Technol. 1996, 9, 779–787. [Google Scholar] [CrossRef]
- Cherednichenko, S.; Rönnung, F.; Gol’tsman, G.; Kollberg, E.; Winkler, D. YBa2Cu3O7−δ hot-electron bolometer mixer at 0.6 THz. Proc. Int. Symp. Space Terahertz Technol. 2000, 526–531. [Google Scholar]
- Lee, M.; Li, R.C.-T. Wide bandwidth far-infrared mixing using a high-Tc superconducting bolometer. In Proceedings of the 8th International Conference on Terahertz Electronics, Darmstadt, Germany, 28–29 September 2000; pp. 99–101. [Google Scholar]
- Kreisler, A.J.; Dégardin, A.F.; Aurino, M.; Péroz, C.; Villegier, J.-C.; Beaudin, G.; Delorme, Y.; Redon, M.; Sentz, A. New trend in terahertz detection: High-Tc superconducting hot electron bolometer technology may exhibit advantages vs. low-Tc devices. In Proceedings of the 2007 IEEE/MTT-S International Microwave Symposium, Honolulu, HI, USA, 3–8 June 2007; pp. 345–348. [Google Scholar] [CrossRef]
- Harrabi, K.; Cheenne, N.; Chibane, F.; Boyer, F.; Delord, P.; Ladan, F.-R.; Maneval, J.-P. Thermal boundary resistance of YBa2Cu3O7 on MgO films deduced from the transient V(I) response. Supercond. Sci. Technol. 2000, 13, 1222–1226. [Google Scholar] [CrossRef]
- Ladan, F.-R.; Harrabi, K.; Rosticher, M.; Mathieu, P.; Maneval, J.-P.; Villard, C. Current-temperature diagram of resistive states in long superconducting niobium filaments. J. Low Temp. Phys. 2008, 153, 103–122. [Google Scholar] [CrossRef]
- Harnack, O.; Il’in, K.S.; Siegel, M.; Karasik, B.S.; McGrath, W.R.; de Lange, G. Dynamics of the response to microwave radiation in YBa2Cu3O7−x hot-electron bolometer mixers. Appl. Phys. Lett. 2001, 79, 1906–1908. [Google Scholar] [CrossRef]
- Cunnane, D.; Kawamura, J.H.; Wolak, M.A.; Acharya, N.; Xi, X.X.; Karasik, B.S. Optimization of Parameters of MgB2 Hot-Electron Bolometers. IEEE Trans. Appl. Supercond. 2017, 27, 2300405. [Google Scholar] [CrossRef]
- Novoselov, E.; Cherednichenko, S. Broadband MgB2 Hot-Electron Bolometer Mixers Operating up to 20 K. IEEE Trans. Appl. Supercond. 2017, 27, 2300504. [Google Scholar] [CrossRef]
- Karasik, B.S.; McGrath, W.R.; Gaidis, M.C. Analysis of a high-Tc hot-electron superconducting mixer for terahertz applications. J. Appl. Phys. 1997, 81, 1581–1589. [Google Scholar] [CrossRef]
- Adam, A.; Gaugue, A.; Ulysse, C.; Kreisler, A.; Boulanger, C. Three-temperature model for hot electron superconducting bolometers based on high-Tc superconductor for terahertz applications. IEEE Trans. Appl. Supercond. 2003, 13, 155–159. [Google Scholar] [CrossRef]
- Khosropanah, P.; Merkel, H.; Yngvesson, S.; Adam, A.; Cherednichenko, S.; Kollberg, E. A distributed device model for phonon-cooled HEB mixers predicting IV characteristics, gain, noise and IF bandwidth. In Proceedings of the 11th International Symposium on Space Terahertz Technology, University of Michigan, Ann Arbor, MI, USA, 1–3 May 2000; pp. 474–488. [Google Scholar]
- Ladret, R.G.; Dégardin, A.F.; Kreisler, A.J. Nanopatterning and hot spot modeling of YBCO ultrathin film constrictions for THz mixers. IEEE Trans. Appl. Supercond. 2013, 23, 2300305. [Google Scholar] [CrossRef]
- Ladret, R.G.; Kreisler, A.J.; Dégardin, A.F. High-TC micro and nano-constrictions modeling: Hot spot approach for DC characteristics and HEB THz mixer performance. J. Phys. Conf. Ser. 2014, 507, 042020. [Google Scholar] [CrossRef]
- Ladret, R.G.; Kreisler, A.J.; Dégardin, A.F. YBCO-Constriction Hot Spot Modeling: DC and RF Descriptions for HEB THz Mixer Noise Temperature and Conversion Gain. IEEE Trans. Appl. Supercond. 2015, 25, 2300505. [Google Scholar] [CrossRef]
- Ma, J.-G.; Wolff, I. Modeling the microwave properties of superconductors. IEEE Trans. Microw. Theory Technol. 1995, 43, 1053–1059. [Google Scholar] [CrossRef]
- Ma, J.-G.; Wolff, I. Electromagnetics in high-Tc superconductors. IEEE Trans. Microw. Theory Technol. 1996, 44, 537–542. [Google Scholar] [CrossRef]
- Péroz, C.; Villégier, J.-C.; Dégardin, A.F.; Guillet, B.; Kreisler, A.J. High critical current densities observed in PrBa2Cu3O7−δ/YBa2Cu3O7−δ/PrBa2Cu3O7−δ ultrathin film constrictions. Appl. Phys. Lett. 2006, 89, 142502. [Google Scholar] [CrossRef]
- Gao, J.-R.; Yagoubov, P.A.; Klapwijk, T.M.; de Korte, P.A.J.; Ganzevles, W.F.; Floet, D.W. Development of THz Nb diffusion-cooled hot electron bolometer mixers. Proc. SPIE Conf. 2003, 4855, 371–382. [Google Scholar] [CrossRef]
- Kollberg, E.L.; Yngvesson, K.S.; Ren, Y.; Zhang, W.; Gao, J.-R. Impedance of hot-electron bolometer mixers at terahertz frequencies. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 383–389. [Google Scholar] [CrossRef]
- Miao, W.; Zhang, W.; Zhong, J.Q.; Shi, S.C.; Delorme, Y.; Lefevre, R.; Feret, A.; Vacelet, T. Non-uniform absorption of terahertz radiation on superconducting hot electron bolometer microbridges. Appl. Phys. Lett. 2014, 104, 052605. [Google Scholar] [CrossRef]
- Abbott, F.; Dégardin, A.F.; Kreisler, A.J. YBCO thin film sputtering: An efficient way to promote microwave properties. IEEE Trans. Appl. Supercond. 2005, 15, 2907–2910. [Google Scholar] [CrossRef]
- Grossman, E.-N. Lithographic antennas for submillimeter and infrared frequencies. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Atlanta, GA, USA, 14–18 August 1995; Volume 14–18, pp. 102–107. [Google Scholar]
- Türer, I.; Dégardin, A.F.; Kreisler, A.J. UWB Antennas for CW Terahertz Imaging: Geometry Choice Criteria. In Ultra-Wideband, Short-Pulse Electromagnetics 10; Sabath, F., Mokole, E.L., Eds.; Springer: New York, NY, USA, 2014; pp. 463–472. ISBN 978-1-4614-9499-7. [Google Scholar]
- Karasik, B.S.; Elantiev, A.I. Noise temperature limit of a superconducting hot-electron bolometer mixer. Appl. Phys. Lett. 1996, 68, 853–855. [Google Scholar] [CrossRef]
- Semenov, A.D.; Hubers, H.-W. Bandwidth of a hot-electron bolometer mixer according to the hot spot model. IEEE Trans. Appl. Supercond. 2001, 11, 196–199. [Google Scholar] [CrossRef]
- Rieke, G.H. Visible and infrared coherent receivers. In Detection of Light: From the Ultraviolet to the Submillimeter, 2nd ed.; Cambridge University Press: New York, NY, USA, 2003; pp. 275–301, ISBN-13: 978-0-511-06518-7. [Google Scholar]
- Wallace, B. Analysis of RF imaging applications at frequencies over 100 GHz. Appl. Opt. 2010, 49, E38–E47. [Google Scholar] [CrossRef] [PubMed]
- Slocum, D.M.; Goyette, T.M.; Slingerland, E.J.; Giles, R.H.; Nixon, W.E. Terahertz atmospheric attenuation and continuum effects. Proc. SPIE Conf. 2013, 8716, 871607. [Google Scholar] [CrossRef]
- Beno, M.A.; Soderholm, L.; Capone, D.W., II; Hinks, D.G.; Jorgensen, J.D.; Grace, J.D.; Schuller, I.K.; Segre, C.U.; Zhang, K. Structure of the single-phase high-temperature superconductor YBa2Cu3O7−δ. Appl. Phys. Lett. 1987, 51, 57–59. [Google Scholar] [CrossRef]
- Streiffer, S.K.; Zielinski, E.M.; Lairson, B.M.; Bravman, J.C. Thickness dependence of the twin density in YBa2Cu3O7−δ thin films sputtered onto MgO substrates. Appl. Phys. Lett. 1991, 58, 2171–2173. [Google Scholar] [CrossRef]
- Kreisler, A.; Dégardin, A.; Guillet, B.; Villégier, J-C.; Chaubet, M. High-Tc Superconducting Hot Electron Bolometers for Terahertz Mixer Applications. In Proceedings of the 9th World Multi-Conference on Systemics, Cybernetics and Informatics, Orlando, FL, USA, 10–13 July 2005; pp. 165–217. [Google Scholar]
- Ladret, R.G.; Kreisler, A.J.; Dégardin, A.F. Terahertz superconducting hot electron bolometers: Technological issues and predicted mixer performance for Y-Ba-Cu-O devices. Proc. SPIE Conf. 2014, 9252, 92520R. [Google Scholar] [CrossRef]
- Goyette, T.M.; Dickinson, J.C.; Linden, K.J.; Neal, W.R.; Joseph, C.S.; Gorveatt, W.J.; Waldman, J.; Giles, R.; Nixon, W.E. 1.56 Terahertz 2-frames per second standoff imaging. Proc. SPIE Conf. 2008, 6893, 68930J. [Google Scholar] [CrossRef]
- Puc, U.; Abina, A.; Rutar, M.; Zidansek, A.; Jeglic, A.; Valusis, G. Terahertz spectroscopic identification of explosive and drug simulants concealed by various hiding techniques. Appl. Opt. 2015, 54, 4495–4502. [Google Scholar] [CrossRef] [PubMed]
- Raash, J. Electrical-Field Sensitive YBa2Cu3O7−x Detectors for Real-Time Monitoring of Picosecond THz Pulses. Doktor-Ingenieur Thesis, Karlsruhe Institut für Technologie (KIT), Karlsruhe, Germany, August 2017. Available online: https://publikationen.bibliothek.kit.edu/1000073798 (accessed on 24 January 2019).
- Ladret, R. Nano-Mélangeurs Bolométriques Supraconducteurs à Electrons Chauds en Y-Ba-Cu-O Pour Récepteur Térahertz en Mode Passif. PhD Thesis, Université Pierre et Marie Curie, Paris, France, July 2016. Available online: https://tel.archives-ouvertes.fr/tel-01832519/document (accessed on 15 Ianuary 2019). (In French).
- Schmid, A.; Raasch, J.; Kuzmin, A.; Steinmann, J.L.; Wuensch, S.; Arndt, M.; Siegel, M.; Müller, A.-S.; Cinque, G.; Frogley, M.D. An Integrated Planar Array of Ultrafast THz Y–Ba–Cu–O Detectors for Spectroscopic Measurements. IEEE Trans. Appl. Supercond. 2017, 27, 2200105. [Google Scholar] [CrossRef]
- Tretyakov, I.; Ryabchun, S.; Finkel, M.; Maslennikova, A.; Kaurova, N.; Lobastova, A.; Voronov, B.; Gol’tsman, G. Low noise and wide bandwidth of NbN hot-electron bolometer mixers. Appl. Phys. Lett. 2011, 98, 033507. [Google Scholar] [CrossRef]
- Kloosterman, J.L.; Hayton, D.J.; Ren, Y.; Kao, T.-Y.; Hovenier, N.; Gao, J.-R.; Klapwijk, T.M.; Hu, Q.; Walker, C.K.; Reno, J.L. Hot electron bolometer heterodyne receiver with a 4.7-THz quantum cascade laser as a local oscillator. Appl. Phys. Lett. 2013, 102, 011123. [Google Scholar] [CrossRef]
- Wolak, M.A.; Acharya, N.; Tan, T.; Cunnane, D.; Karasik, B.S.; Xi, X. Fabrication and Characterization of Ultrathin MgB2 Films for Hot-Electron Bolometer Applications. IEEE Trans. Appl. Supercond. 2015, 25, 7500905. [Google Scholar] [CrossRef]
- Arpaia, R.; Ejrnaes, M.; Parlato, L.; Tafuri, F.; Cristiano, R.; Golubev, D.; Sobolewski, R.; Bauch, T.; Lombardi, F.; Pepe, G.P. High-temperature superconducting nanowires for photon detection. Phys. C 2015, 509, 16–21. [Google Scholar] [CrossRef]
- Lyatti, M.; Savenko, A.; Poppe, U. Ultra-thin YBa2Cu3O7−x films with high critical current density. Supercond. Sci. Technol. 2016, 29, 065017. [Google Scholar] [CrossRef]
- Kreisler, A.; Gaugue, A. Recent progress in HTSC bolometric detectors: From the mid-infrared to the far-infrared (THz) range. Supercond. Sci. Technol. 2000, 13, 1235–1245. [Google Scholar] [CrossRef]
- Vadiodes. Available online: http://www.vadiodes.com/en/frequency-multipliers (accessed on 14 January 2019).
- Microtech Inst. Available online: http://mtinstruments.com/THz_Generators.html (accessed on 14 January 2019).
- Ravarro, M.; Jagtap, V.; Santarelli, G.; Sirtori, C.; Li, L.; Khanna, S.P.; Linfield, E.; Barbieri, S. Continuous- wave coherent imaging with terahertz quantum cascade lasers using electro-optic harmonic sampling. Appl. Phys. Lett. 2013, 102, 091107. [Google Scholar] [CrossRef]
- Wang, T.; Liu, J.; Liu, F.; Wang, L.; Zhang, J.; Wang, Z. High-Power Single-Mode Tapered Terahertz Quantum Cascade Lasers. IEEE Photonics Technol. Lett. 2015, 27, 1492–1494. [Google Scholar] [CrossRef]
- Masther Research Project Funded by the French National Research Agency under Grant # 2011-BS03-008-01. Information. Available online: http://www.agence-nationale-recherche.fr/suivi-bilan/editions-2013-et-anterieures/recherches-exploratoires-et-emergentes/blanc-generalite-et-contacts/blanc-presentation-synthetique-du-projet/?tx_lwmsuivibilan_pi2%5BCODE%5D=ANR-11-BS03-0008 (accessed on 14 January 2019). (In French).




| Device | L, w (nm) | θ (nm) | Ce (J·m−3·K−1) | Cp (J·m−3·K−1) | κe (W·m−1·K−1) | κp(W·m−1·K−1) | |
| A | 100 | 10 | 2.5×104 | 6.5×105 | 1 | 10 | |
| B | 400 | 35 | 2.5×104 | 6.5×105 | 1 | 10 | |
| Device | τep (ps) | τesc (ns) | σN1 (Ω–1·m–1) | JC2 (A·cm–2) | TC3 (K) | ΔT (K) | T0 (K) |
| A | 1.0 | 0.75 | 3.15×105 | 2.2×106 | 85 | 1.2 | 60 |
| B | 1.7 | 2.6 | 3.15×105 | 2.2×106 | 89 | 1.2 | 70 |
| Frequency | IDC (μA) | R (Ω) 1 | PDC (µW) | PLO (μW) | G (dB) | TDSB (K) |
|---|---|---|---|---|---|---|
| QS | 454 | 21.3 | 4.4 | 7.5 | −9.0 | 1781 |
| 500 GHz | 464 | 21.4 | 4.6 | 7.5 | −7.1 | 1208 |
| 2.5 THz | 394 | 14.6 | 2.3 | 12.5 | −6.1 | 1013 |
| 4 THz | 379 | 13.0 | 1.9 | 13.5 | −6.5 | 1093 |
| Frequency (THz) | 0.67 | 1.02 | 1.49 | 2.52 | 3.44 |
| tobs (%) | 75 | 47 | 21 | 2 | 0.1 |
| Frequency | IDC (μA) | R (Ω) 1 | PDC (µW) | PLO (μW) | G (dB) | TDSB (K) |
|---|---|---|---|---|---|---|
| QS | 241 | 27.9 | 1.6 | 35 | −13.8 | 2607 |
| 500 GHz | 271 | 26.4 | 1.9 | 30 | −13.6 | 2704 |
| 2.5 THz | 392 | 19.2 | 3.0 | 12 | −10.8 | 2332 |
| 4 THz | 389 | 18.2 | 2.7 | 12.5 | −10.1 | 2021 |
| Frequency (THz) | TDSB-MIN (K) [27] | Obstacle | ΔT (K) | RH (%) | DT (m) | NEP (fW/Hz1/2) | TDSB (K) |
|---|---|---|---|---|---|---|---|
| 0.67 | 2480 1 | Yes | 0.5 | 70 | 78 | 3.1 | 2495 |
| 0.67 | 2480 1 | No | 0.5 | 70 | 90.8 | 3.1 | 2485 |
| 1.02 | 2730 | Yes | 1.0 | 70 | 19.0 | 3.4 | 2760 |
| 1.02 | 2730 | No | 1.0 | 70 | 26.5 | 3.4 | 2775 |
| 2.52 | 4150 | Yes | 10 | 30 | 3.8 | 5.1 | 4160 |
| 2.52 | 4150 | Yes | 10 | 70 | 1.6 | 5.1 | 4150 |
| 2.52 | 4150 | No | 10 | 70 | 11.5 | 5.2 | 4245 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ladret, R.; Dégardin, A.; Jagtap, V.; Kreisler, A. THz Mixing with High-TC Hot Electron Bolometers: A Performance Modeling Assessment for Y-Ba-Cu-O Devices. Photonics 2019, 6, 7. https://doi.org/10.3390/photonics6010007
Ladret R, Dégardin A, Jagtap V, Kreisler A. THz Mixing with High-TC Hot Electron Bolometers: A Performance Modeling Assessment for Y-Ba-Cu-O Devices. Photonics. 2019; 6(1):7. https://doi.org/10.3390/photonics6010007
Chicago/Turabian StyleLadret, Romain, Annick Dégardin, Vishal Jagtap, and Alain Kreisler. 2019. "THz Mixing with High-TC Hot Electron Bolometers: A Performance Modeling Assessment for Y-Ba-Cu-O Devices" Photonics 6, no. 1: 7. https://doi.org/10.3390/photonics6010007
APA StyleLadret, R., Dégardin, A., Jagtap, V., & Kreisler, A. (2019). THz Mixing with High-TC Hot Electron Bolometers: A Performance Modeling Assessment for Y-Ba-Cu-O Devices. Photonics, 6(1), 7. https://doi.org/10.3390/photonics6010007







