1. Introduction
Spectroscopic optical coherence tomography (SOCT) [
1] extends the function of optical coherence tomography (OCT) to obtain the depth resolved spectra of samples [
2]. The spectra could provide invaluable information such as the health condition of the cells or tissues [
3,
4], authenticity of Chinese freshwater pearls [
5], and mapping of microvascular hemoglobin [
6]. The heart of SOCT is the time–frequency analysis of the SOCT measurements. Various time–frequency analysis approaches such as the short-time Fourier transform method [
4], the Wigner transform method [
7], and the Dual window Fourier transform method [
8] have been developed successfully and demonstrated capable of obtaining depth resolved spectra. In application of the time–frequency analysis, it is assumed that the SOCT measurement consists of fields scattered directly by the sample features of interest. However, SOCT measurement also consists of those fields that are scattered multiple times from the features [
9]. The multiple scattered fields reduce image contrast and make it more difficult to localize features or estimate scattered spectra, particularly at increased imaging depth [
10]. Hence, SOCT could gain benefits from combining the time–frequency analysis with some pre- or post-processing methods to mitigate the multiple scattering artifacts.
Post-processing methods such as spatial averaging or angular averaging have been proposed to mitigate the multiple scattering effect. Each of these methods have advantages and disadvantages. For example, the method proposed in [
9] is able to distinguish multiple scattering from single scattering, but it is limited to the samples that are accessible from both sides. More recently, pre-processing methods based on signal correlation [
11] or on a mixture of adaptive and computational optics [
12] have also been developed, but these methods requires additional apparatus and they are not scalable to existing OCT setups. In this paper, we propose to model the light fields in the sample by a multiple multipole expansion (MMP) approach [
13]. The SOCT measurements are characterized by the positions and parameters of the multipoles. It is found that the MMP terms of higher orders are sensitive to the multiple scatterings. Thus, the multiple scattering artifacts can be removed if time–frequency analysis is applied only on those SOCT measurements that are fitted by the MMP terms of lower orders. Simulation and experimental studies show that the pre-processing is effective for any time–frequency based SOCT methods.
The rest of this paper is organized into the following sections.
Section 2 formulates the proposed pre-processing method of using a multiple multipole expansion.
Section 3 illustrates a simulation study where multiple scatterings are simulated and their effects on high order MMP terms are disclosed. In
Section 4, the performance of the proposed method is demonstrated experimentally on a home-made phantom.
2. Spectroscopic OCT Using MMP Model
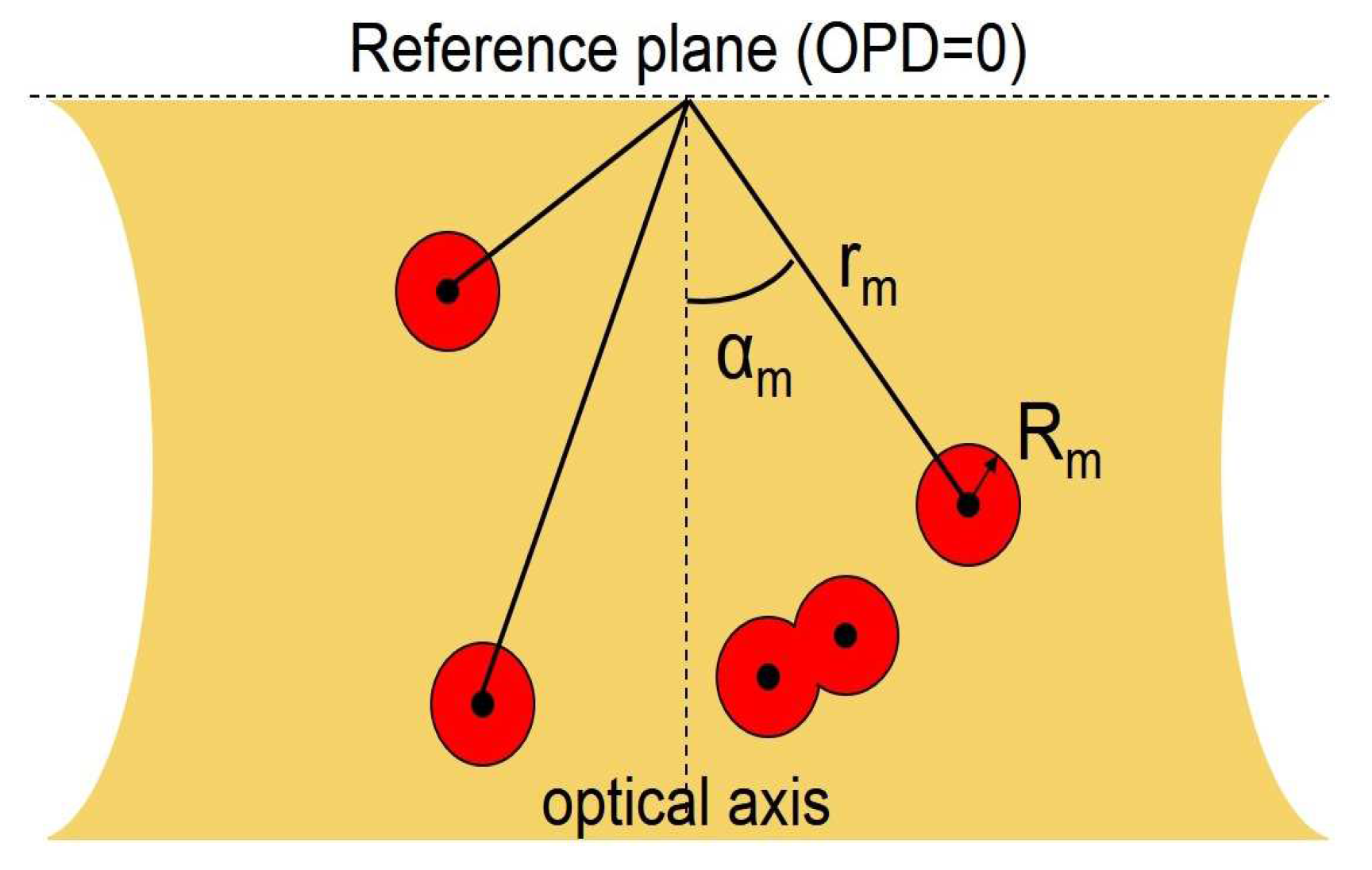
In the proposed method, each scatterer also representing a sub-surface feature of interest in SOCT is modeled as a multipole with boundaries formed by circles, semi-circles, connected circular arcs, or combinations of them, as shown in
Figure 1. Specifically, we consider using
M multipoles, each individual position is marked by, respectively, the radial distance
and the azimuthal angle
with reference to the center of the focusing lens in an OCT system. The light field detected at the focusing center can be expressed as the sum of scattered fields from the
M multipoles as follows [
13]:
where
is the Bessel function of order
n,
and
are unknown expansion coefficients, and
is
times the reciprocal of the wavelength.
Ignoring the self-correlation terms and DC terms due to the sample scattered spectrum and the mirror scattered spectrum, the depth resolved spectrum at the depth given by
can be obtained by
where
is the spectrum of the broadband light source used in the SOCT system.
The SOCT measurement can be expressed in the following compact format
where
is a vector with elements of
and
for
, and
=
.
It is noted that the model has factored into multiple scatterings. As shown in
Section 3, multiple scatterings are contained only in the MMP terms of higher order. Hence, by removing the fields characterized by the high order terms from the SOCT measurement, the multiple scattering artifacts is removed from the SOCT results. Now, the problem of the proposed pre-processing method can be stated as the one of solving unknown parameters
,
,
, and
from the available
. Once these unknowns are obtained, the pre-processed SOCT measurements are obtained by the summation in Equation (
3) over those multipoles of pre-set orders.
For easy calculation, we take spectral measurements at different
for
and
.
L equations of
unknowns are obtained as
where
,
, and
. Equation (
4) can be solved by the following optimization:
Considering noises in measurement, Equation (
4) can be solved by the following mixed
-optimization.
where
denotes the noise level. The pre-processed SOCT measurements can be computed using the solution of Equation (
5) with MMP terms of higher order removed.
3. Effect of Multiple Scattering on MMP Expansion
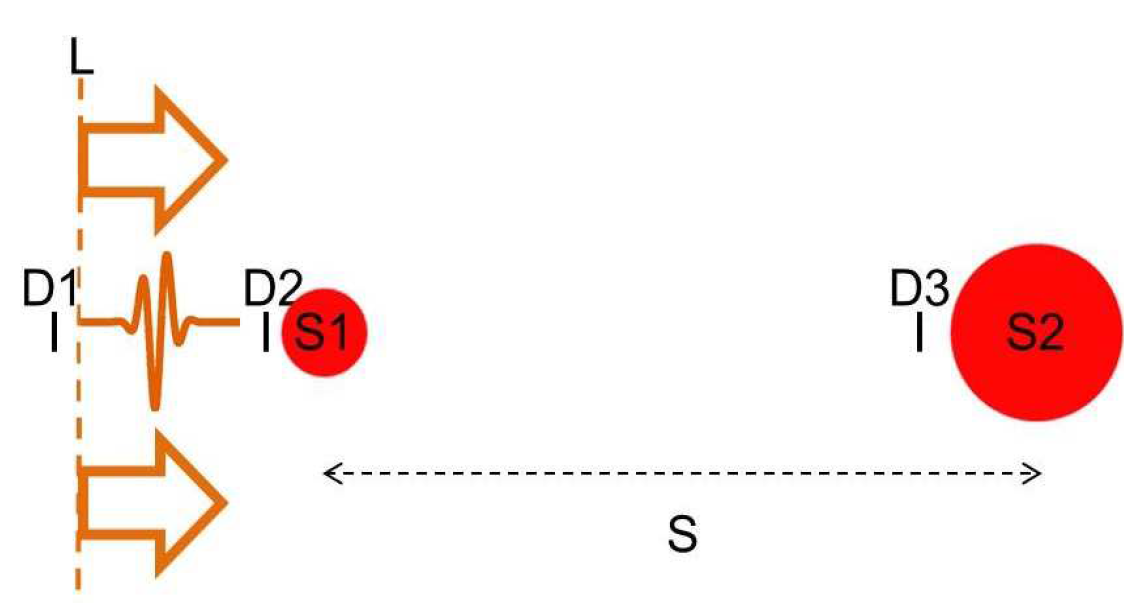
In this section, simulation studies are carried out to evaluate the contributions of multiple scatterings to the MMP expansion of SOCT measurements. We consider a sample with two spherical scatterers with diameters of 1
m and 4.5
m, respectively. The two scatterers are 10
m apart in space, as shown in
Figure 2. The multiple scattering process is simulated in the following way. Assume a single light pulse of 6 fs starts from
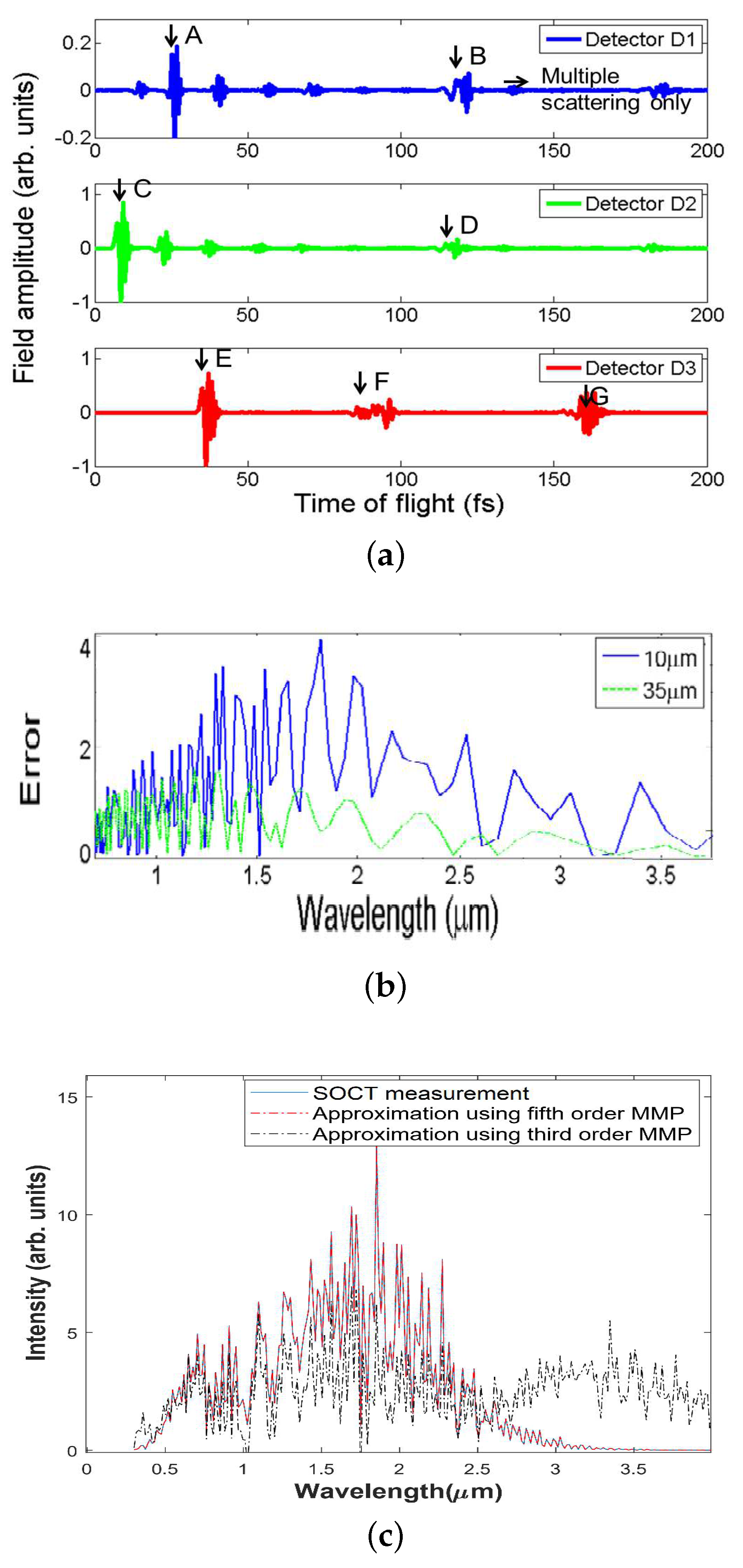
L and travels through the scatterers sequentially, we calculate the amplitudes of light fields at various positions and time using finite-difference time-domain (FDTD) method. This method is used to simulate the field distribution as it neither needs to assume the geometry of the scatterers nor the extent of multiple scattering. Thus, the method is able to consider the contributions of multiple scattering effectively in the calculated field distribution. We used commercial FDTD software (Lumerical) working in temporal mode to simulate the light fields over a time duration of 300 fs. Other simulation parameters included setting the maximum mesh size to 50 nm to ensure that the mesh size is smaller than the smallest wavelength used, and using perfectly matched layer (PML) boundary condition to terminate the field. Then, the simulation was run and the amplitudes at locations marked by D1, D2, and D3 are recorded at different time, as shown in
Figure 3a.
First, we considered the scattering events that contribute to the single scattered electric field received by D1. The light pulse first passes D2 and gives the response marked by C in
Figure 3a, and then it encounters S1. One portion of the light is backscattered by S1 towards D1 and gives the response marked by A in
Figure 3a. The other portion continues travelling towards D3 and gives a response marked by E in
Figure 3a. After the light encounters S2, a portion of it carries on its forward propagation and does not return, whereas a backscattered portion travels towards D2. The backscattered portion propagates towards detector D2 and D1 and produces responses marked by D and B in
Figure 3a, respectively. Beyond this instance, the scatterings that take place are multiple scattering fields and when the light pulse returns to D1, it generates the multiple scattering fields in SOCT measurement. Earlier when S1 is first illuminated by the light pulse, S1 scatters a portion of the field towards D3 to give the response F in
Figure 3a. Likewise, the field described above that generates the response marked by D in
Figure 3a is backscattered by S1 towards S2 to generate the response G in
Figure 3a.
This process of scattering to and fro between spheres S1 and S2 goes on several times and gives the total field received at D1 containing both single and multiple scatterings. Thus, by filtering the response at D1 at different time durations, we can calculate, respectively, the spectrum due to electric field from single scattering and the spectrum due to the total received field including the multiple scattering portion. Furthermore, we can obtain the corresponding spectra. The difference between the two spectra is plotted in
Figure 3b. For comparison, we repeated the simulation for the case when two scatterers are separated further by S = 35
m. The corresponding spectrum difference is included in the figure. The comparison clearly shows that the spectrum difference due to multiple scatterings becomes more significant when the two scatterers are closer. It is the spectrum difference that contributes the multiple scattering artifacts in SOCT.
Next, we show that MMP terms of higher order fit well the multiple scattering fields in SOCT measurements. We solve the optimization problem in Equation (
5) on the SOCT measurements consisting of multiple scatterings using
and
, respectively. We take
m,
m,
m …
m] and
. The resultant SOCT measurements are shown in
Figure 3c. It is evident that the MMP terms of higher order can be used to characterize effectively the multiple scattering artifacts in the SOCT measurements. Hence, it is possible to filter the multiple scattering fields in SOCT measurements by limiting the order of the multiple multipole expansion. The filtered SOCT measurements from Equation (
5) can then be used to calculate the depth resolved spectroscopy of SOCT.
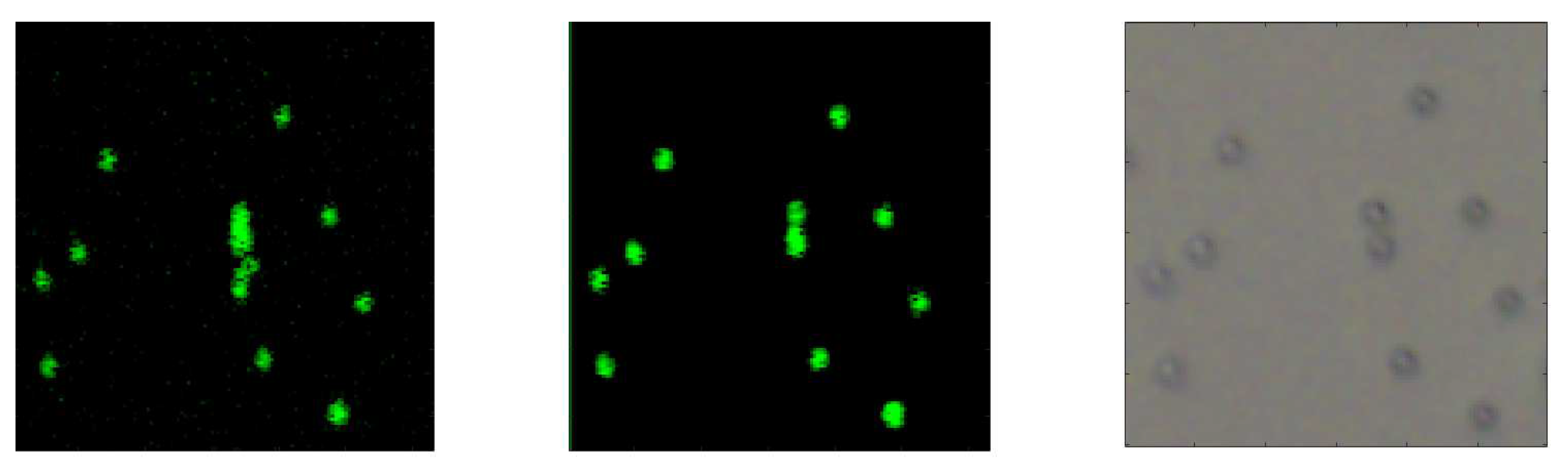
5. Conclusions
In summary, this paper uses a multiple multipole expansion method to model the light fields in a sample under SOCT imaging. Since OCT and SOCT setup uses the same set of measurement, the pre-processing method is also applicable to OCT. Using the proposed method, multiple scatterings from features in the sample can be effectively modeled by a parameterized optimization problem. With the parameters obtained, multiple scattering fields can be filtered out from the SOCT measurements before applying routine time–frequency analysis of SOCT. The multiple scattering artifacts are removed in the SOCT imaging results. Experiments on a calibrated phantom has exemplified that the proposed method can improve the image quality. The challenges to integrate this method to existing time–frequency analysis methods are with obtaining a suitable scattering model of the features and minimizing the spectral distortion that could arise from dispersion. In the case of industrial samples, suitable scattering models would be determined by characterizing the scattered spectra and dispersion of the different materials used to manufacture the samples.