Resonant self-injection locking of a laser relies on optical feedback resulting from resonant back reflection of laser light from a resonant optical structure. Emission frequency of a laser self-injection locked by means of a high-Q resonator depends on the frequency of the resonator used for the optical feedback as well as on the optical path length between the resonator and the laser. To create a stable self-injection locked laser both these factors should be taken into account. While stability limitations of the resonators were studied in detail, the importance of the stabilization of the optical phase accumulated between the laser and the resonator was not investigated as deep. We study it in this work using a resonator with low environmental sensitivity. In this case, the resonator-related variations of the laser frequency are excluded and the instability due to variations of the optical path is revealed.
2.1. Principles of Thermal Compensation of a WGMR
There were multiple attempts to fabricate a monolithic resonator with reduced thermal sensitivity. For example, thermal refraction effect can be eliminated in a silica microtoroid resonator by a thin layer of polydimethylsiloxane (PDMS) evanescently interacting with the light confined in the resonator [
19]. The polymer has a negative thermal refraction effect. The resonator spectrum experiences red frequency shift due to optical attenuation and blue frequency shift due to PDMS. The effects can cancel each other. Fluctuations of the ambient temperature still impact the frequency of the composite structure.
Thermal expansion reduction in MgF
[
20] and CaF
[
17] WGMRs was reported. The MgF
resonators were attached to a Zerodur substrate resulting in seven times reduction of the thermal sensitivity of the resonator frequency spectrum associated with thermal expansion. Laminating a CaF
resonator between two Zerodur layers leaded to reduction of the thermal sensitivity by a factor of three. Significantly better thermal compensation can be achieved in a CaF
WGMR integrated with ceramic layers characterized with negative thermal expansion coefficient. Resultant zero sensitivity of the WGM frequency to the ambient temperature change can be realized [
18]. In this study, we created a WGMR using this recipe, locked a laser to it, and have shown that the stability of the laser is still limited. We attributed the limitation to the instability of the optical path and shown experimentally that a modification of the path allows tuning the laser emission frequency by more than a FWHM of the WGMR.
2.2. Laser Stabilization Using a Thermally Compensated WGMR
Creating two identical experimental setups described in
Section 4 of this paper we stabilized two semiconductor lasers using compensated CaF
WGMRs. The temperature of the WGMRs was tuned to the position when the frequency of the resonators spectra weakly depends on the ambient temperature variations. The reduction of the thermal sensitivity was two orders of magnitude. If the thermal sensitivity of a standard CaF
WGMR is approximately 10 parts per million (ppm) per
C, the compensated resonators had the sensitivity of 0.1 ppm/
C.
The thermal sensitivity of the standard resonator allows us to roughly evaluate the temperature variations of the resonator mode measuring the frequency variations of the laser locked to the mode. The mode frequency changes by approximately 2 GHz per C. The accuracy of the measurement is given by the mode bandwidth and the lock tightness and agility. The self-injection locking mechanism is very fast. In another experiment, we have observed fast modulation of a self-injection locked laser frequency with response time approaching a s by modulating the frequency of the resonator using a piezo actuator. Therefore, the laser frequency is tracking the resonator mode at 1 s time scale. If the laser frequency moves less than 20 kHz per 1 s (regularly observed in our experiments), we can say that the temperature variations of the resonator are at the level of 10C or less. The accuracy of the measurement is limited because of the long term drift of the laser frequency with respect to the mode center, so the measurement shows the maximum possible temperature variations.
We created two nearly identical self-injection locked lasers involving the thermally compensated resonators. The emission of the lasers was combined in a single optical fiber and sent to a fast photodiode. The frequencies of the lasers were tuned in a way that the radio frequency (RF) signal escaping the photodiode had frequency 30 MHz. We studied stability of the signal using a frequency counter as well as a signal analyzer stabilized to an external Rubidium clocks. The signal analyzer was used to perform short term measurements, while the frequency counter was used to record the long term stability. The RF beat note of the lasers has stability defined by the least stable laser out of two.
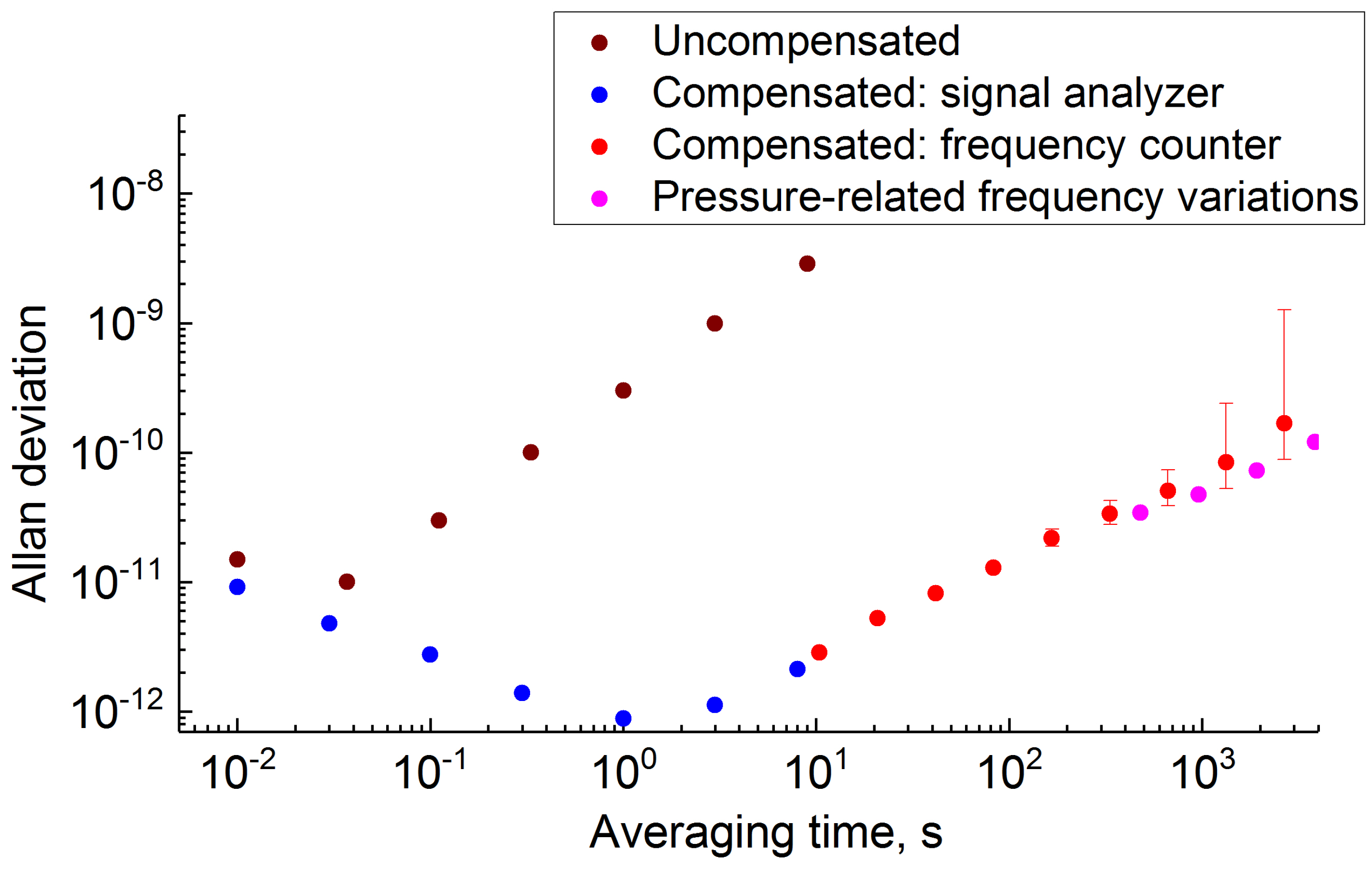
The resonator platform was stabilized using a thermo-electric cooler. The short term thermal stability of the resonator platform was on the order 10
C. As the result, the resonator without thermal compensation had relative frequency stability approaching
at 1 s integration time. The long term stability of the resonator temperature was on the order of 0.01
C, so that the corresponding relative frequency variations were on the order of
. The compensated resonator resulted in a two orders of magnitude better performance. The measurement results are illustrated in
Figure 1. One can see that Allan deviation of
can be achieved at 1 s integration time with a compensated resonator. A frequency drift is observed at longer integration times. Up to our knowledge, this is the best 1 s stability reported for a thermally stabilized self-injection locked semiconductor laser involving a WGMR and operating under normal atmospheric conditions.
The short term Allan deviation was limited because of optical shot noise averaging due to the optical locking. Contribution of this noise was relatively large since the resonator was intentionally overloaded to 20 MHz bandwidth. The frequency bandwidth of the resonator mode defines the short term stability of the self-injection locked laser in a similar way as the bandwidth of a laser cavity defines the linewidth of the laser (see Discussion for details). The large bandwidth was necessary to measure the variation of the laser frequency with modification of the optical path between the laser and the resonator.
Another reason for the short term frequency instability is associated with the low stiffness of the locking point of the self-injection locking system. Variations of the optical path as well as the current driving the laser result in the frequency shift of the laser emission with respect to the WGM frequency studied in this paper.
We attribute the long term frequency drift to both the variation of the atmospheric pressure and the compensated resonator temperature. The resonator was not hermetically sealed and, as was shown earlier, variations of the atmospheric pressure deform the resonator, change its refractive index because of the associated stress, and modify the refractive index of the surrounding air that can be sensed by the evanescent field of the WGMs.
The variation of the WGMR temperature also could have a sizable contribution the frequency drift. Long term temperature related relative frequency instability of the resonator on the order of (associated with 0.01 C long term thermal stabilization magnitude) can lead to 1 s instability on the order of if the Allan deviation averaging time dependence is expected.
Our current study does not allow a reliable separation of the pressure and temperature associated long term frequency drifts. The resonator should be placed into an evacuated package to remove the pressure variation impact. However, even if the thermal stabilization of the resonator is improved and both these effects are removed, the long term stability of the self-injection locked laser, similarly to the short-term stability, still can be compromised due to low tightness of the self-injection locking. As shown below, the entire platform, not only the WGMR, has to be thermally stabilized to improve the stabilization quality. The thermal instability of the platform also can explain the observed relative frequency stability.
2.3. Tightness of Self-Injection Lock
Self-injection locking is a frequency pulling phenomenon. The emission of the laser is determined by the frequency of the laser cavity, frequency of the WGMR, and phase delay associated with the optical path. By creating a stable WGMR we can reduce the impact of the WGMR on the frequency of the laser and figure out the impact of the other two factors on the laser frequency.
2.3.1. Laser Current Change
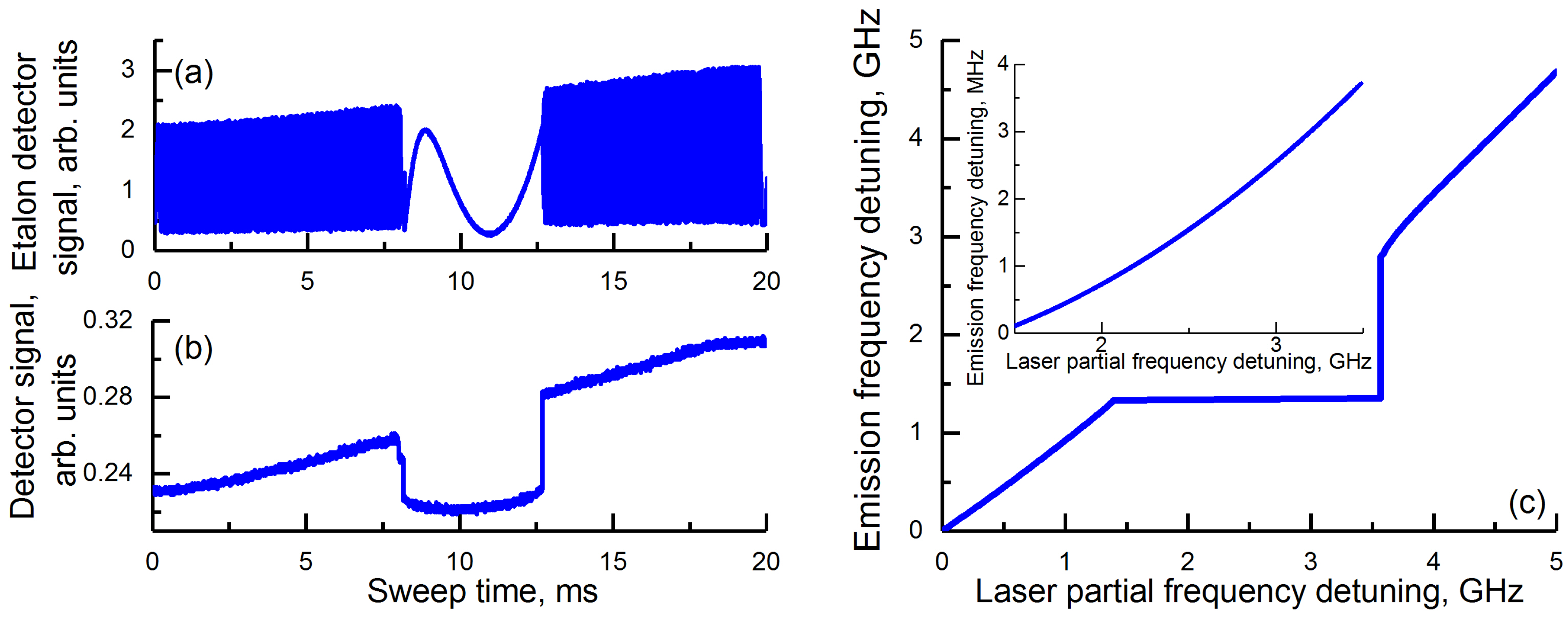
Change of the laser current modifies both the frequency and the power of the laser emission. In the self-injection locked system it changes partial frequency of the laser. By “partial frequency” here we understand the frequency of the laser emission observed in a free running, not self-injection locked, laser. The actual laser frequency changes much slower because of the self-injection locking. We demonstrated this effect experimentally (
Figure 2). We measured frequency tuning of the laser using a frequency etalon as a discriminator,
Figure 2a. The self-injection locking range was monitored using the LI-curve (dependence of the power of the laser on the laser current),
Figure 2b. The classical curve for the self-injection locked laser emission frequency versus partial frequency of the laser chip was created using the data,
Figure 2c.
We modulated the laser current using a saw tooth signal. The center of the modulation was selected in a way that the laser emission hits a WGM and the laser locks to it. The locking can be visualized with a slow photodiode. The photocurrent linearly increases with the driving current increase. At this point the light from the laser has relatively large linewidth and it does not enter the resonator. The photocurrent drops suddenly when the laser locks to the mode since a part of the light is reflected (scattered) back to the laser. This process is illustrated in
Figure 2b.
The power change is associated with the frequency change. To characterize the laser locking frequency we used a Fabry-Perot etalon with 5 MHz free spectral range (FSR) followed by another slow photodiode. When the laser frequency is scanned through the etalon, the photocurrent is modulated with a fast rate associated with the frequency change with respect to the etalon modes. Locking of the laser results in reduction of the frequency tuning so the modulation frequency suddenly decreases. When the laser unlocks the frequency start changing again. In the vicinity of the locking point the frequency change can be too fast to be measured. The process is illustrated in
Figure 2a.
Knowledge of the etalon FSR allows us to find dependence of the laser frequency on the current magnitude and the current ramp speed and calibrate the measurement results in the frequency units. The result of the calibration of the measurement data with respect to the laser partial frequency is shown in
Figure 2c. One can see that the laser frequency tuning reduces by 1000 times when the laser is locked to the mode of the resonator. The overall tuning range is approximately 20% of the resonator FWMH.
The locking range of the laser exceeds the bandwidth of the mode significantly. Ultimately, the locking range is limited by the bandwidth of the laser chip gain and the laser emission frequency can be tuned continuously by tuning the WGM frequency within the bandwidth of the laser chip gain. The observed locking range value is much narrower in our experiment since we do not adjust the other parameters of the system during the measurement. To achieve a much broader tuning one needs to modify the phase delay between the laser and the resonator while changing the resonator frequency.
The measurement shows that if the frequency tuning of the free running laser is GHz/mA, the tuning of the self-injection locked laser is MHz/mA. To achieve relative stability of the laser at the level of , the associated driving current variation should be A at 1 s. This is a rather small value for a commercial current driver, however we apparently achieved it in our experiment.
The locking can be made tighter if the frequency bandwidth of the WGM is reduced. A calcium fluoride WGMR can have bandwidth of 10 kHz [
21]. The laser locked to the narrow mode should be tunable by a few kHz while locked. However, measurement of the frequency shift is not simple at this level. We had to overload the resonator to measure the effect using a standard etalon. That is why the Q-factor of the resonator used in the current experiment was relatively low.
2.3.2. Optical Path Change
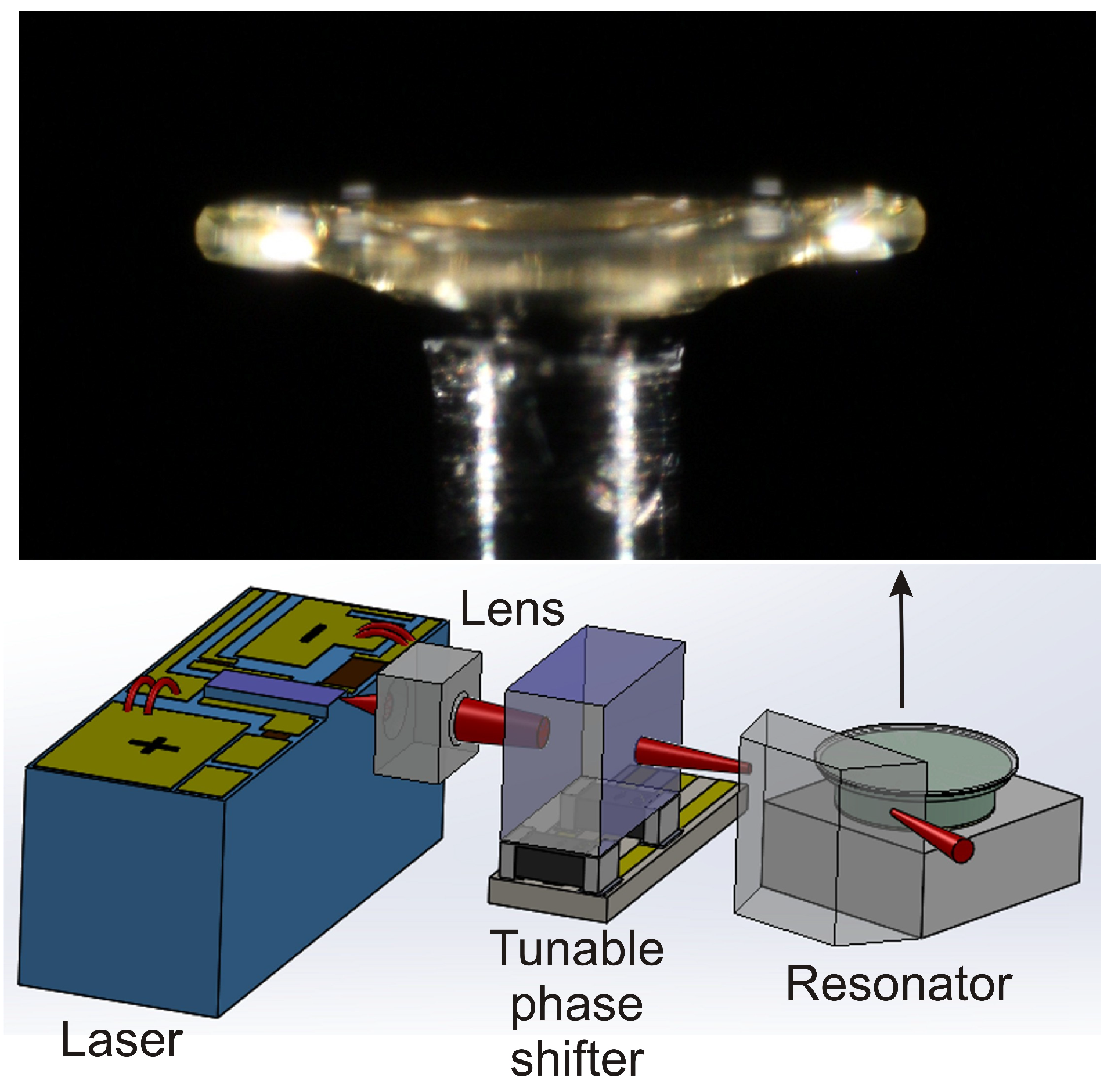
To understand how the optical path length change impacts the frequency shift of the self-injection locked laser we introduced a tunable phase delay in between of the laser and the resonator, as described in
Section 4 of the paper. By changing the optical path length we were able to tune the frequency of the laser through injection locked region. This tuning emulates the otherwise uncontrollable optical path variations in self-injection locked lasers.
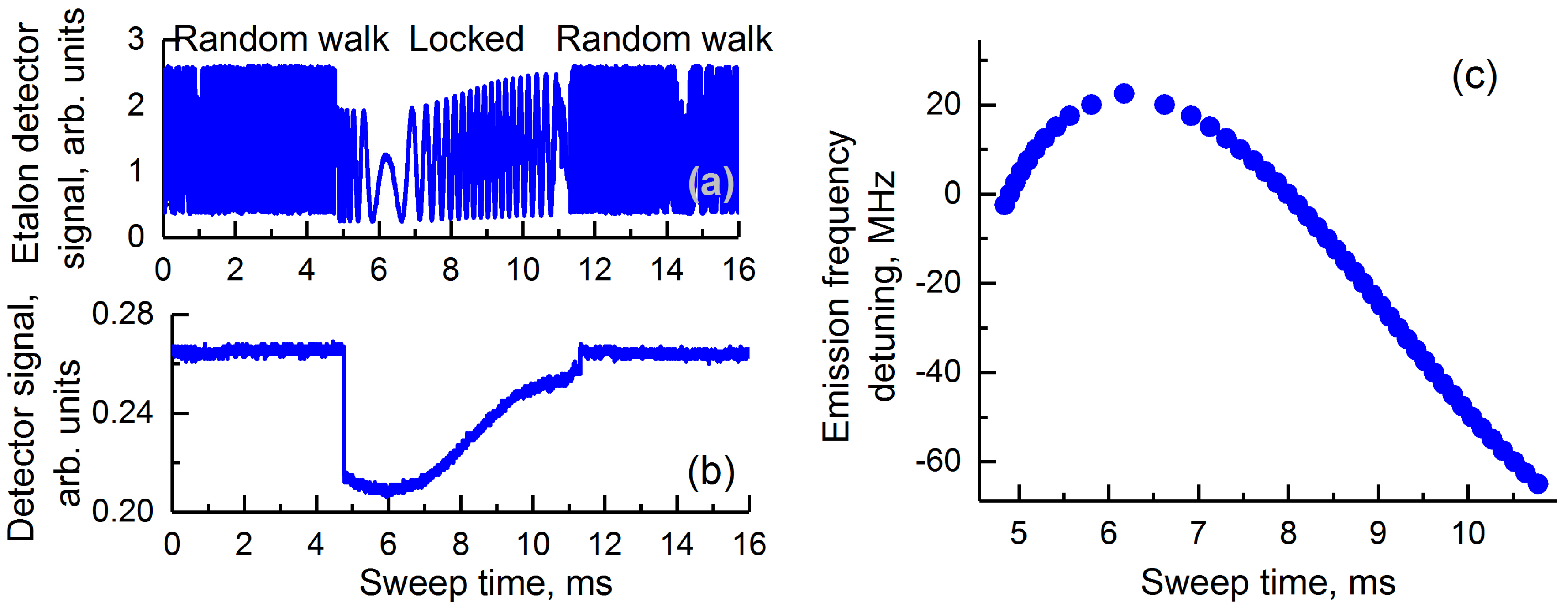
The experiment was performed as follows. Keeping the temperature of the phase section as well as the laser current constant we tuned the temperature of the resonator to observe the locking. The locking was observed when the partial temperature of the laser coincided with the resonator mode frequency and the phase delay between the laser and the resonator was optimal. Then we fixed the temperature of the resonator and ramped the temperature of the phase shifter. The experiment shown that there is a limited range of the phase shifter temperatures for which self-injection locking was conserved.
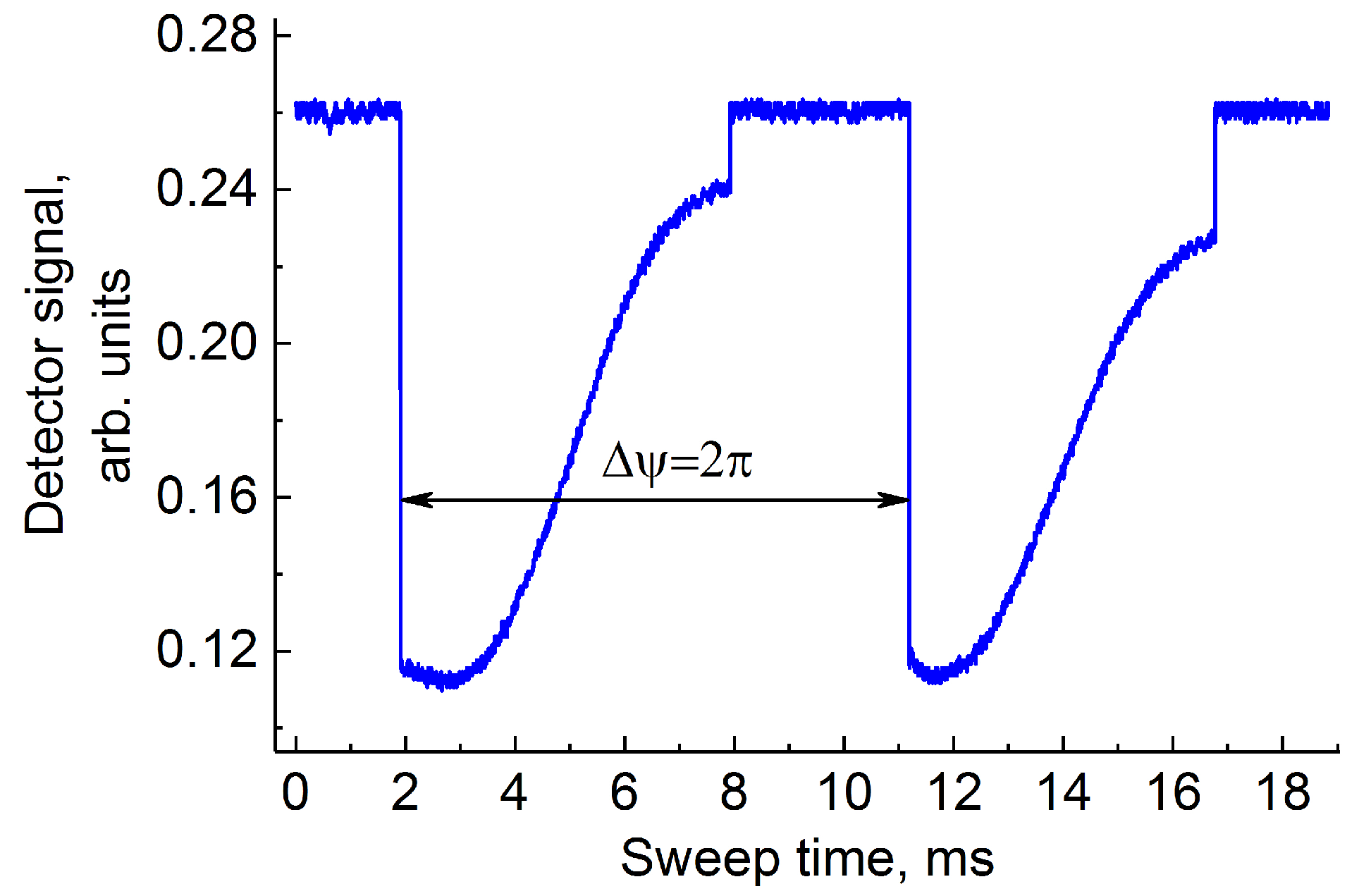
Unlike the case of the laser frequency tuning described in the previous section, the phase shifter did not influence the laser frequency and power when the laser was not locked to the resonator mode,
Figure 3. When the locking occurred, the phase shifter impacted the emission frequency of the system. Measuring the frequency shift using the Fabry-Perot etalon we observed that the absolute value of the emission frequency was shifted by approximately 80 MHz, or more than four FWHMa of the WGM. This is a very large number.
In the worst case scenario the shift rate was 10 MHzC. To estimate it we have noticed that the optical frequency shifts 80 MHz per approximately optical path change. The wavelength is m, the optical path length is cm. Assuming thermal expansion of C, we find that the temperature change needed for the change of the path by is 8 C. This results in the frequency rate change with temperature variations of the build.
The observation means that the temperature of the entire system should be stabilized to approximately C level to achieve relative frequency stability of . This level of thermal stabilization of the entire platform is hard to maintain for a long time. On the other hand, it is clear from the measurement that there is a certain length of the optical path that corresponds to the turning point at which the variations of the setup temperature do not impact the laser frequency. In addition, improving Q-factor of the resonator by several orders of magnitude results in softening the requirements to the temperature stabilization of the optical path.
In our experiment intended for achieving the highest possible stabilization of the laser we selected the phase in such a way that the turning point was reached. The system did not have an active stabilization of the optical path and due to thermal drift the moved from the desirable point approximately in an hour. This feature limited the stability measurements (
Figure 1) by approximately 1000 s.
Interestingly, the nonlinear dependence of the frequency shift of the self-injection locked laser on the phase delay between the WGM resonator and the laser chip complicate the stabilization of the resonator frequency using external optical clock transition. The temperature of the resonator can vary in a frequency range determined by the stiffness of the lock even if we stabilize the laser to the atomic cell. To avoid this discrepancy, one has to stabilize actively the optical path between the laser and the resonator and also use a high-Q resonator.