Label-Free Saturated Structured Excitation Microscopy
Abstract
:1. Introduction
2. Methods
2.1. Imaging Theory
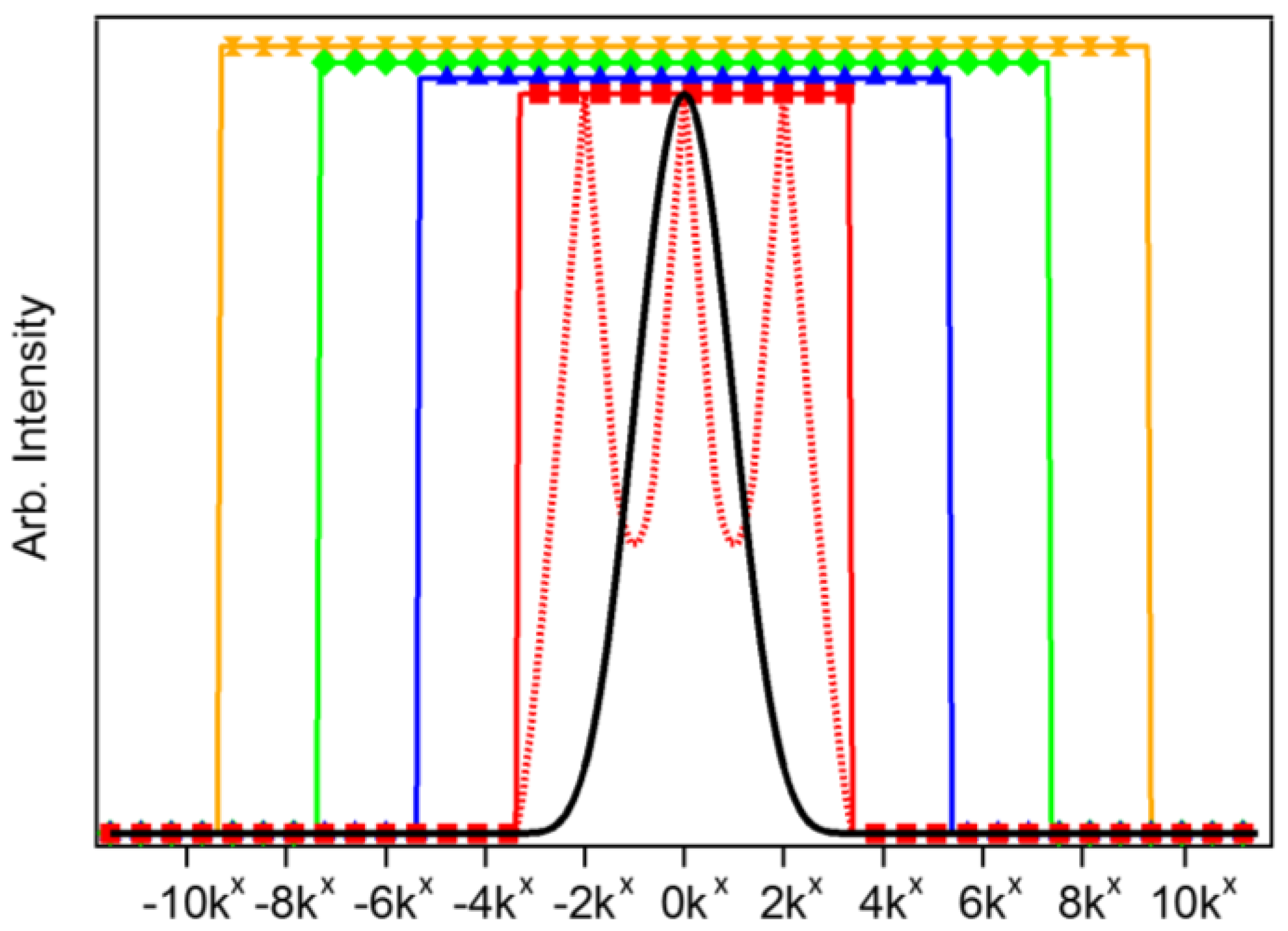
2.2. Structured Excitation
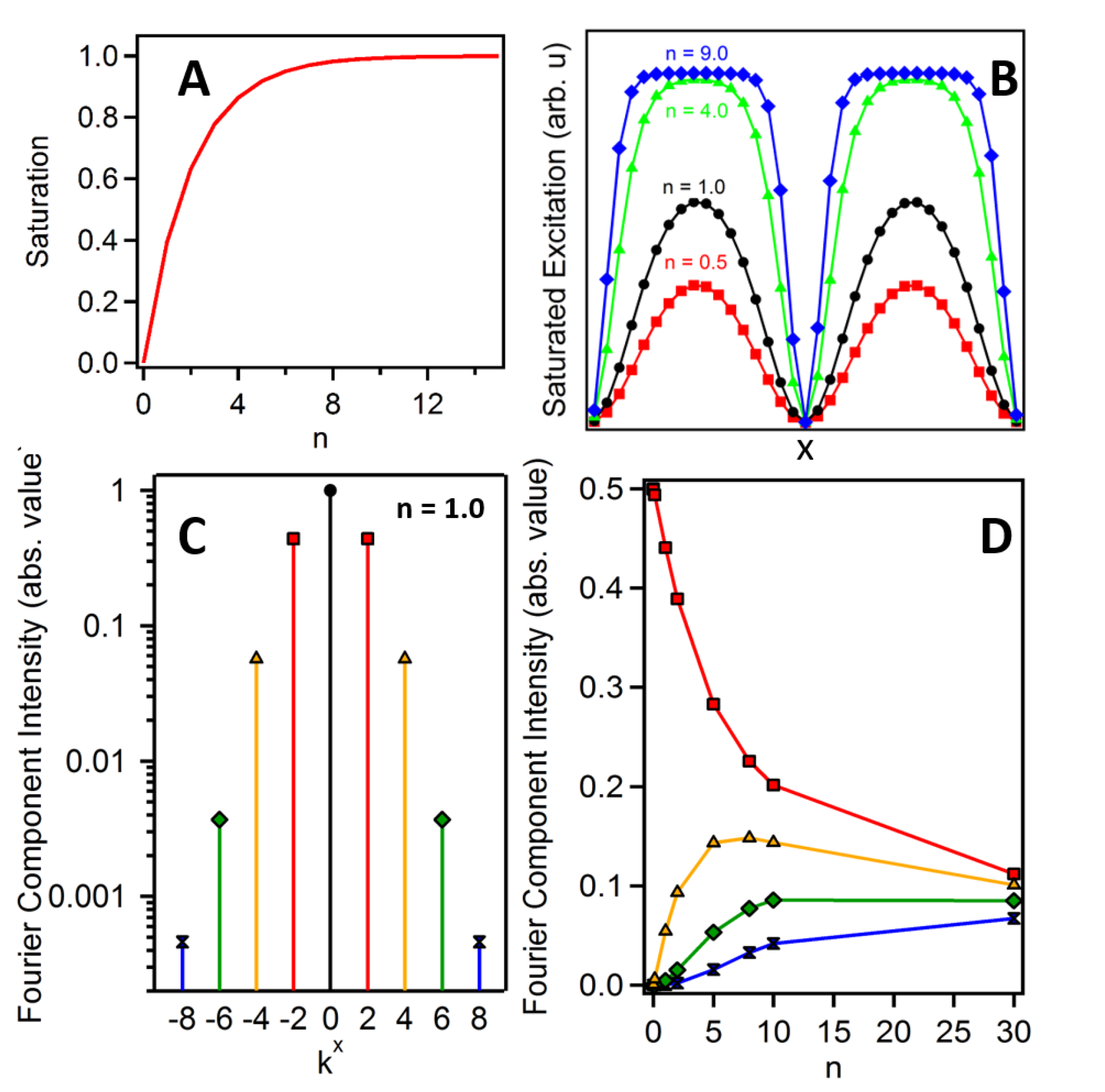
2.3. Saturated Excitation
2.4. Image Reconstruction
3. Results
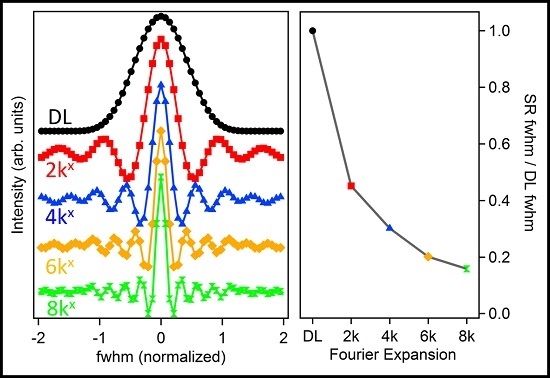
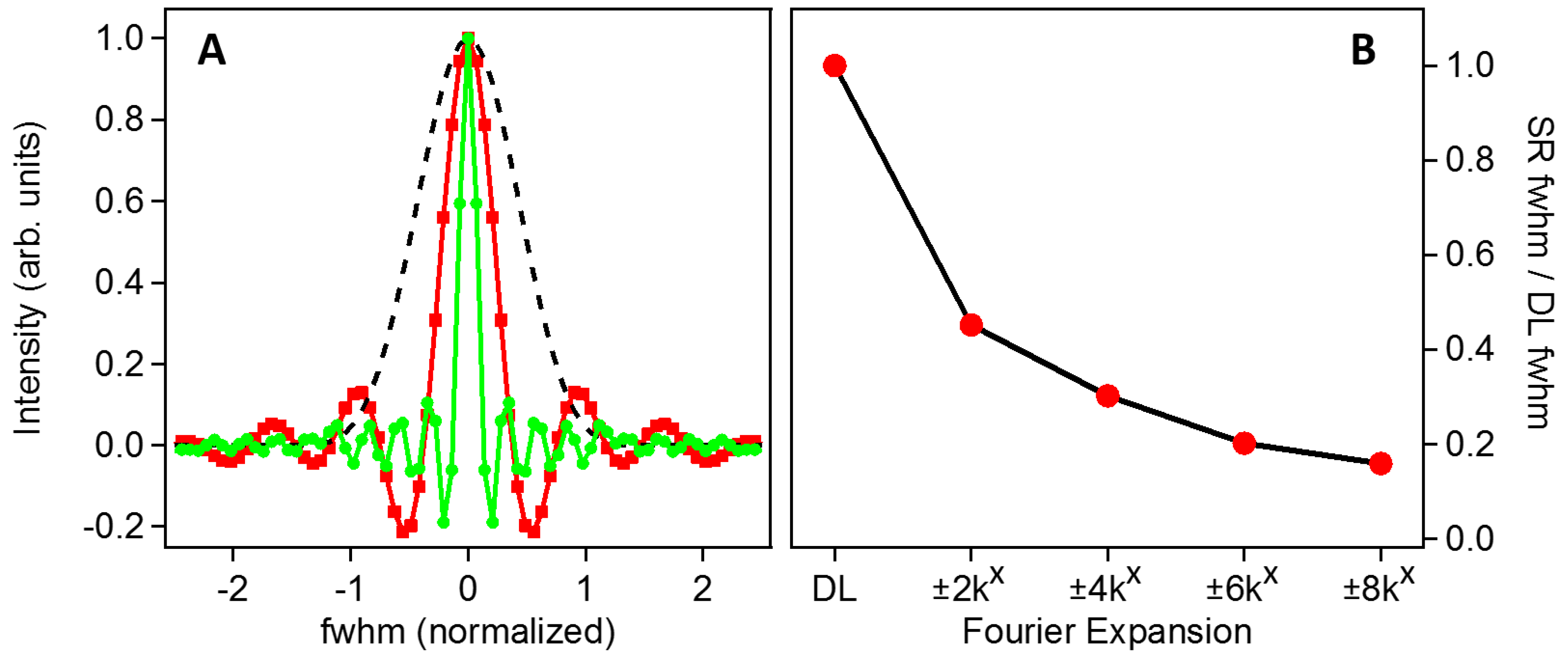
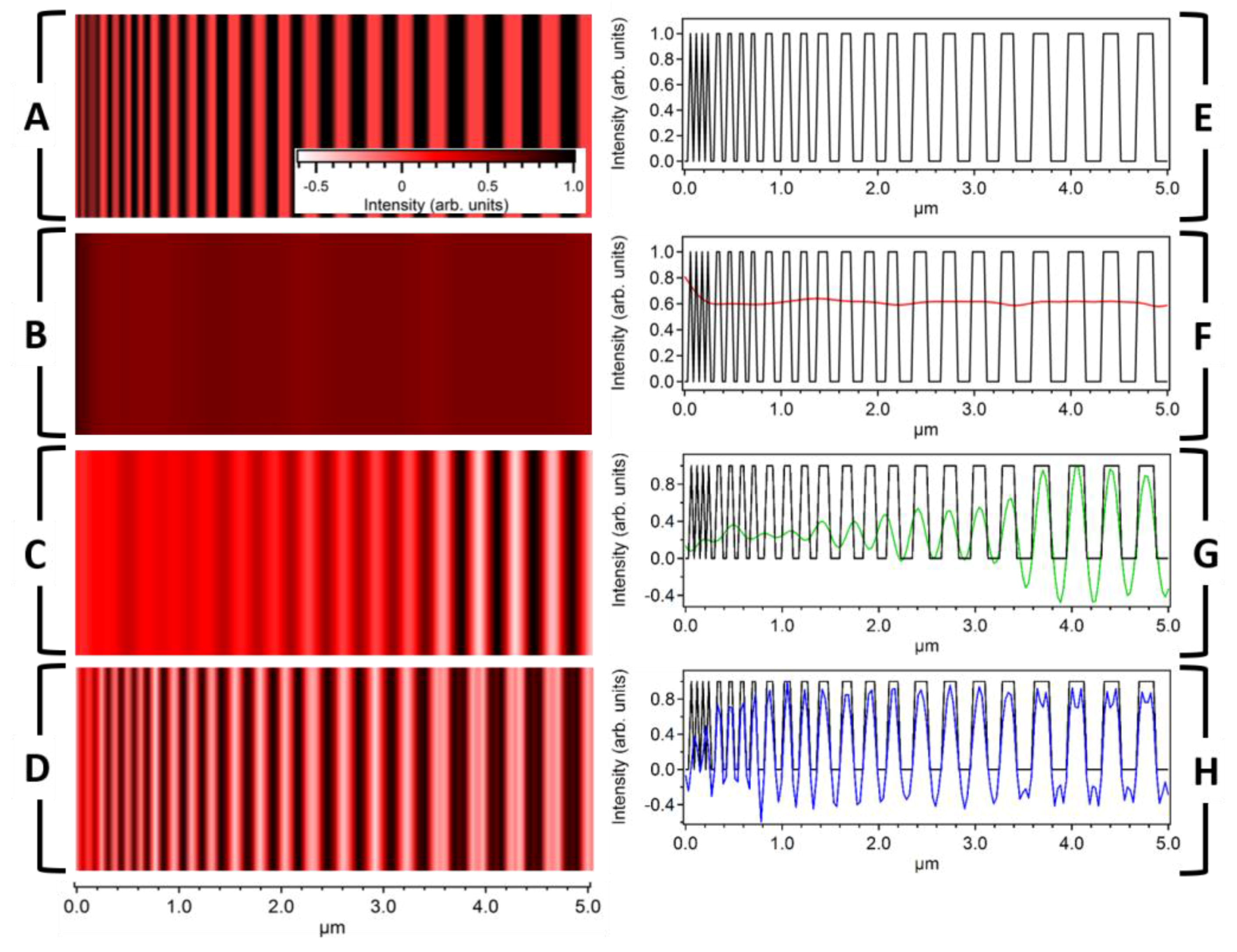
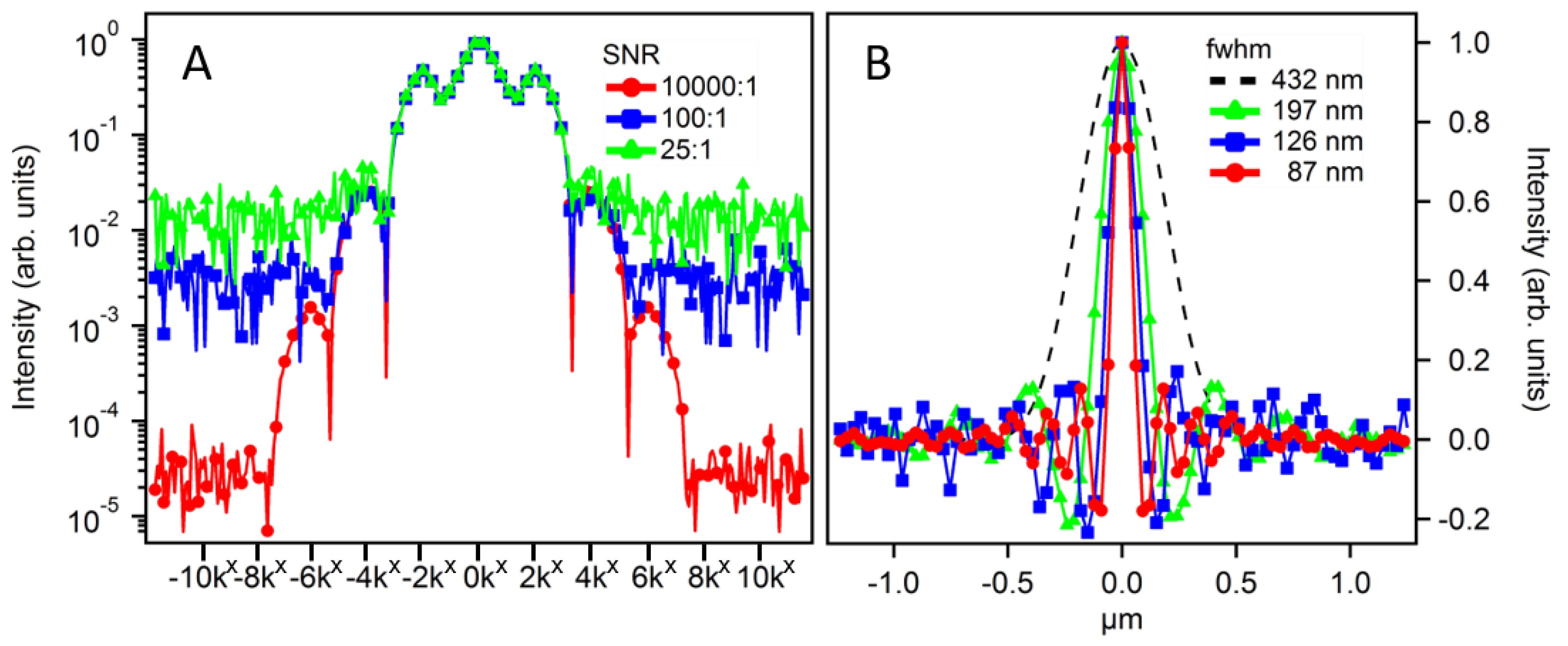
3.1. PSF Comparison
3.2. Imaging Capabilities
3.3. Signal-to-Noise Ratio Dependence
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Köhler, H. On abbe’s theory of image formation in the microscope. Opt. Acta Int. J. Opt. 1981, 28, 1691–1701. [Google Scholar] [CrossRef]
- Schermelleh, L.; Heintzmann, R.; Leonhardt, H. A guide to super-resolution fluorescence microscopy. J. Cell Biol. 2010, 190, 165–175. [Google Scholar] [CrossRef] [PubMed]
- Rust, M.J.; Bates, M.; Zhuang, X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (storm). Nat. Methods 2006, 3, 793–795. [Google Scholar] [CrossRef] [PubMed]
- Betzig, E.; Patterson, G.H.; Sougrat, R.; Lindwasser, O.W.; Olenych, S.; Bonifacino, J.S.; Michael, W.; Davidson, J.L.-S.; Hess, H.F. Imaging intracellular fluorescent proteins at nanometer resolution. Science 2006, 313, 1642–1645. [Google Scholar] [CrossRef] [PubMed]
- Hell, S.W.; Wichmann, J. Breaking the diffraction resolution limit by stimulated emission- stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. [Google Scholar] [CrossRef] [PubMed]
- Heintzmann, R.; Cremer, C. Laterally modulated excitation microscopy—Improvement of resolution by using a diffraction grating. Proc. SPIE 1999, 3568, 185–196. [Google Scholar]
- Silva, W.R.; Graefe, C.T.; Frontiera, R.R. Toward label-free super-resolution microscopy. ACS Photonics 2016, 3, 79–86. [Google Scholar] [CrossRef]
- Wang, P.; Slipchenko, M.N.; Mitchell, J.; Yang, C.; Potma, E.O.; Xu, X.; Cheng, J.X. Far-field imaging of non-fluorescent species with sub-diffraction resolution. Nat. Photonics 2013, 7, 449–453. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Kumbham, M.; Pita, I.; Guo, Y.; Bianchini, P.; Diaspro, A.; Tofail, S.A.M.; Peremans, A.; Silien, C. Far-field subdiffraction imaging of semiconductors using nonlinear transient absorption differential microscopy. ACS Photonics 2016, 3, 478–485. [Google Scholar] [CrossRef]
- Hajek, K.M.; Littleton, B.; Turk, D.; McIntyre, T.J.; Rubinsztein-Dunlop, H. A method for achieving super-resolved widefield cars microscopy. Opt. Express 2010, 18, 19263–19272. [Google Scholar] [CrossRef] [PubMed]
- Massaro, E.S.; Hill, A.H.; Grumstrup, E.M. Super-resolution structured pump–probe microscopy. ACS Photonics 2016, 3, 501–506. [Google Scholar] [CrossRef]
- Massaro, E.S.; Hill, A.H.; Kennedy, C.L.; Grumstrup, E.M. Imaging theory of structured pump-probe microscopy. Opt. Express 2016, 24, 20868–20880. [Google Scholar] [CrossRef] [PubMed]
- Heintzmann, R. Saturated patterned excitation microscopy with two-dimensional excitation patterns. Micron 2003, 34, 283–291. [Google Scholar] [CrossRef]
- Gustafsson, M.G. Nonlinear structured-illumination microscopy: Wide-field fluorescence imaging with theoretically unlimited resolution. Proc. Nat. Acad. Sci. USA 2005, 102, 13081–13086. [Google Scholar] [CrossRef] [PubMed]
- Frolov, S.V.; Vardeny, Z.V. Double-modulation electro-optic sampling for pump-and-probe ultrafast correlation measurements. Rev. Sci. Instrum. 1998, 69, 1257–1260. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massaro, E.S.; Grumstrup, E.M. Label-Free Saturated Structured Excitation Microscopy. Photonics 2017, 4, 36. https://doi.org/10.3390/photonics4020036
Massaro ES, Grumstrup EM. Label-Free Saturated Structured Excitation Microscopy. Photonics. 2017; 4(2):36. https://doi.org/10.3390/photonics4020036
Chicago/Turabian StyleMassaro, Eric S., and Erik M. Grumstrup. 2017. "Label-Free Saturated Structured Excitation Microscopy" Photonics 4, no. 2: 36. https://doi.org/10.3390/photonics4020036
APA StyleMassaro, E. S., & Grumstrup, E. M. (2017). Label-Free Saturated Structured Excitation Microscopy. Photonics, 4(2), 36. https://doi.org/10.3390/photonics4020036