Optimization and Characterization of High-Harmonic Generation for Probing Solid Density Plasmas
Abstract
:1. Introduction
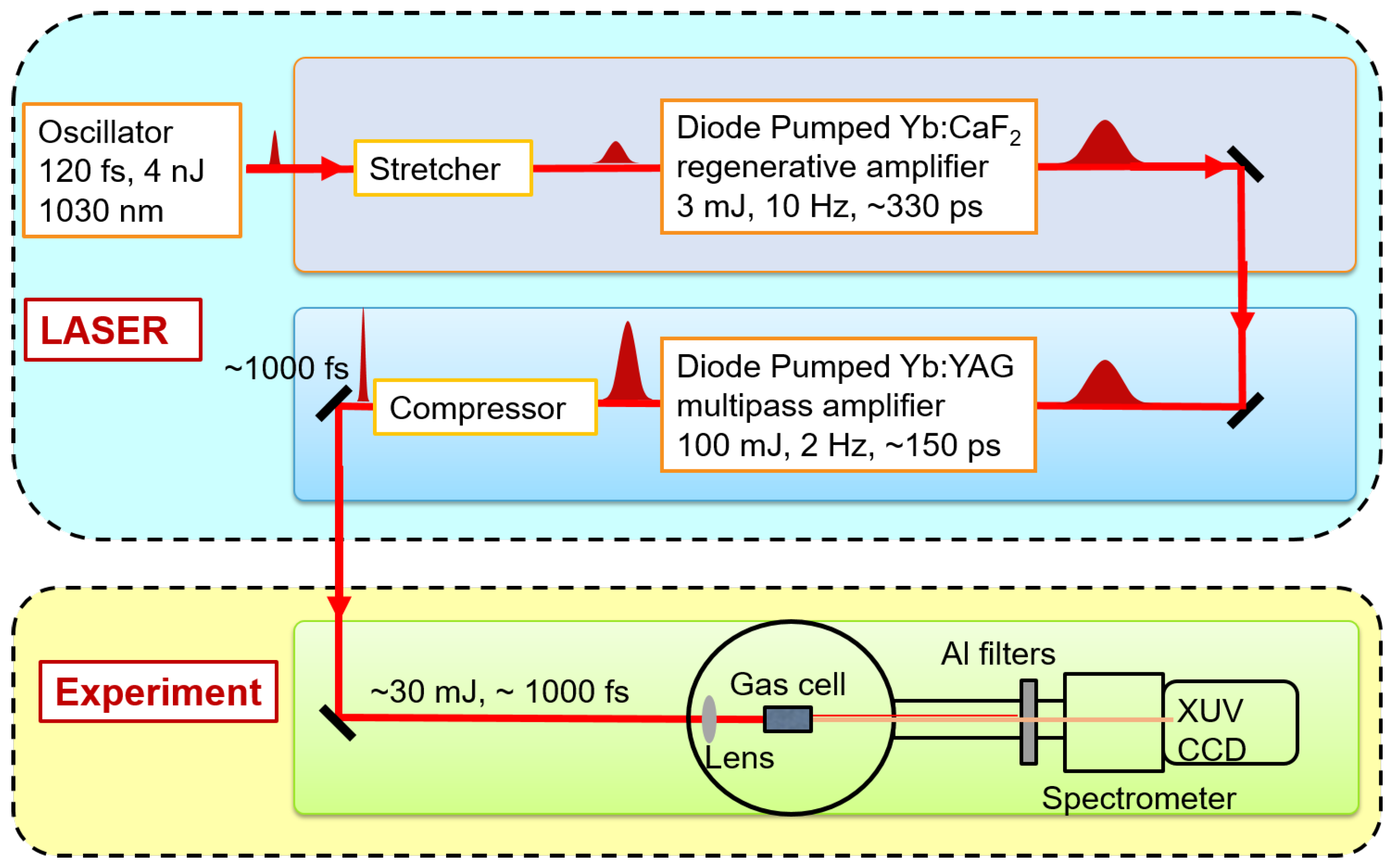
2. Experimental Setup
3. Results
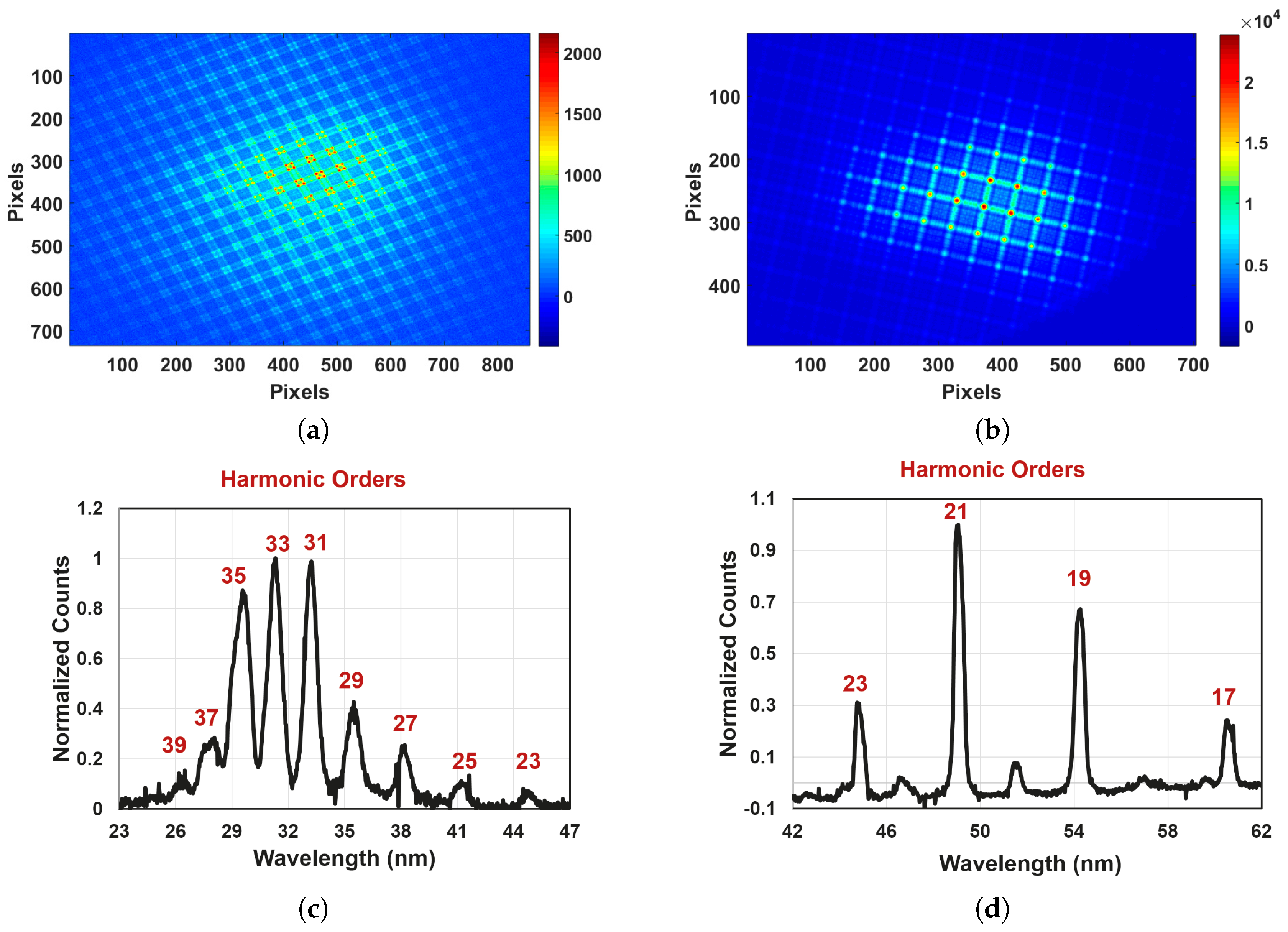
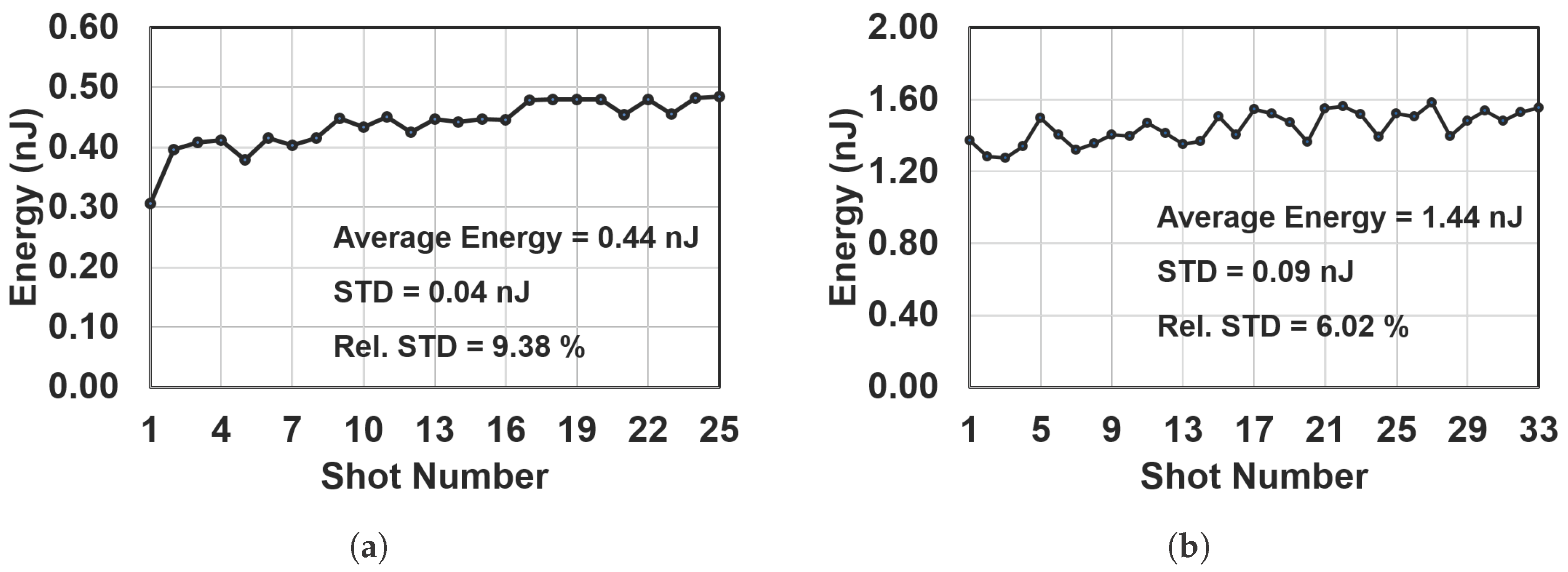
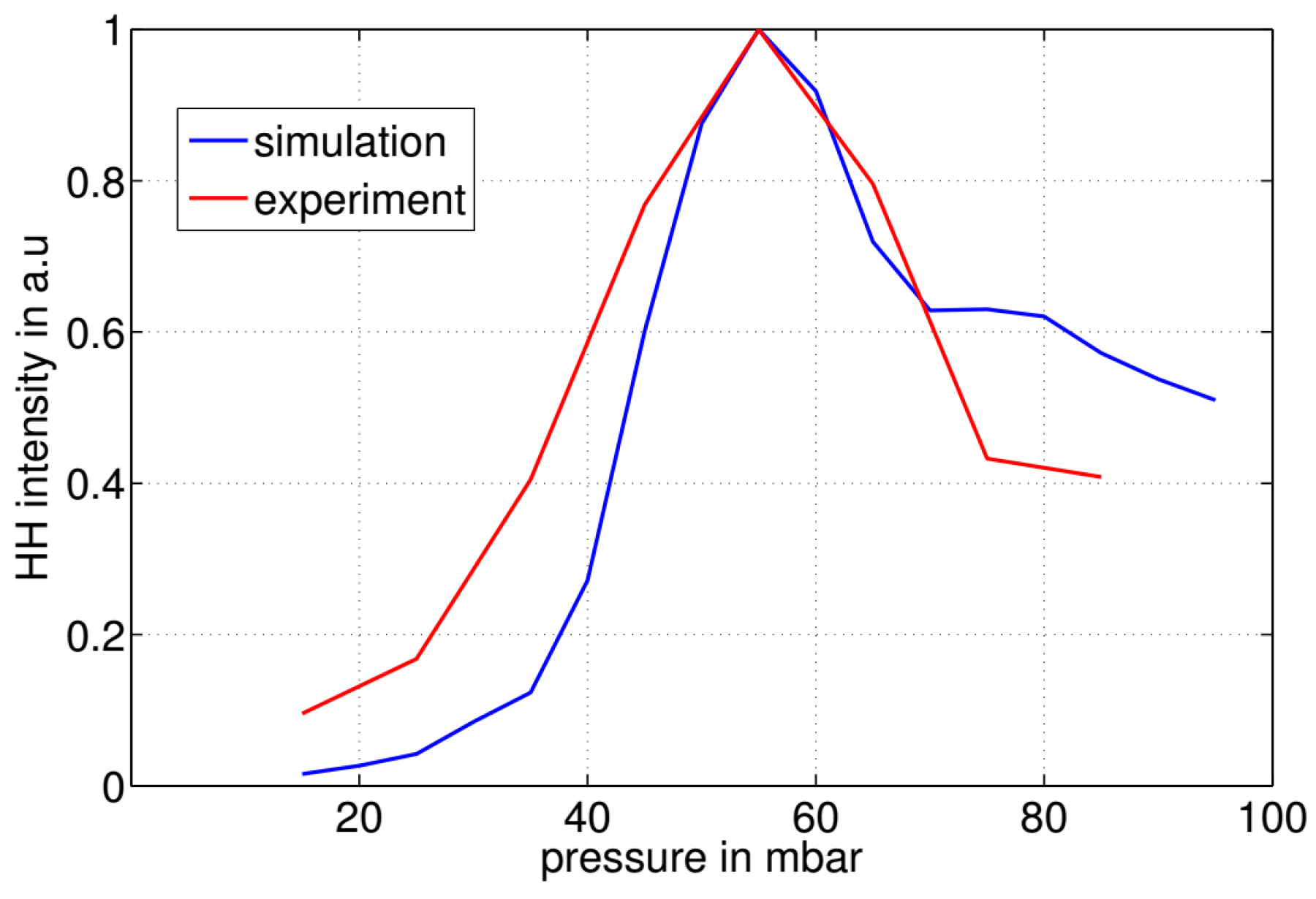
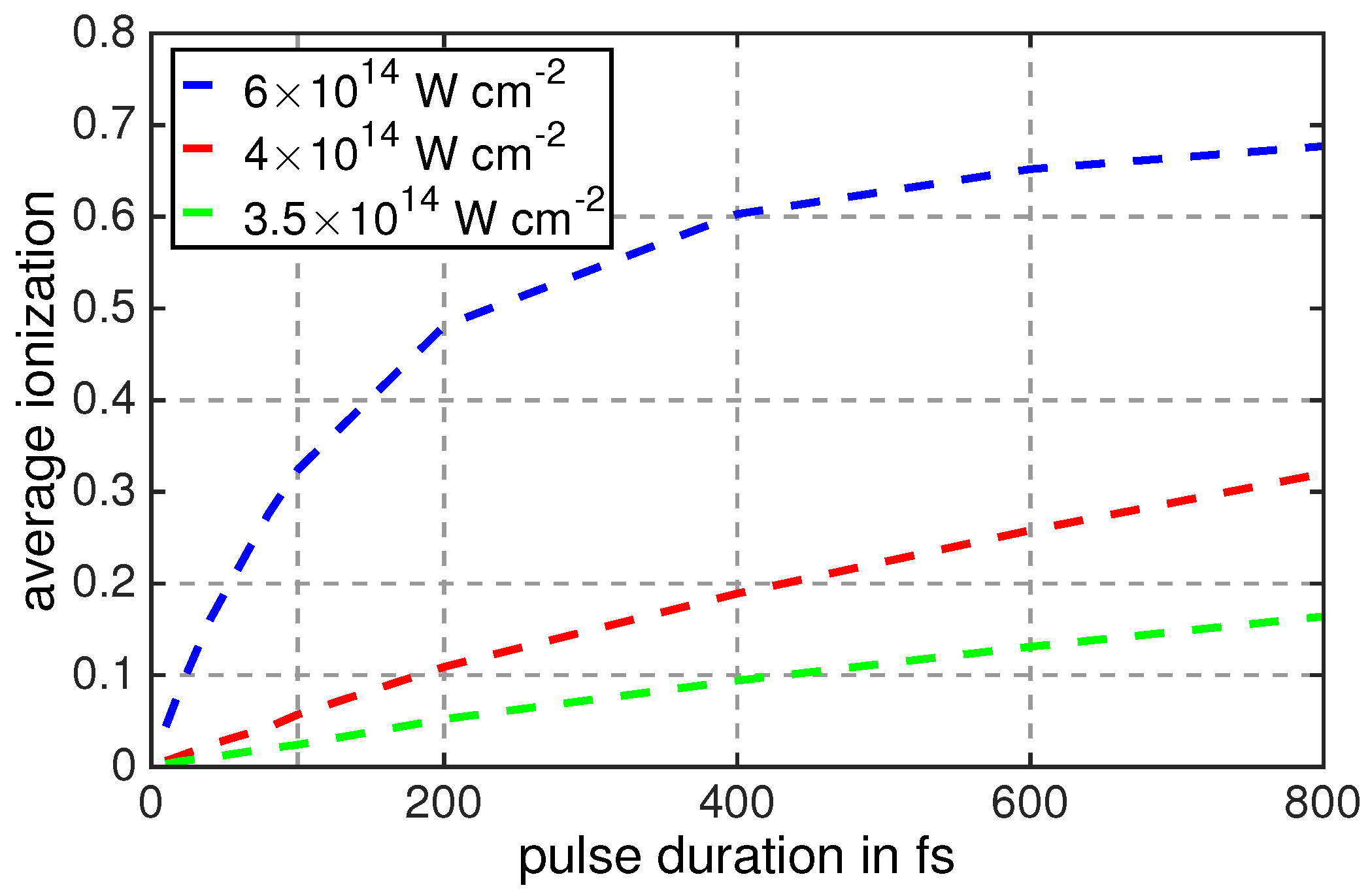
3.1. HHG and Optimization
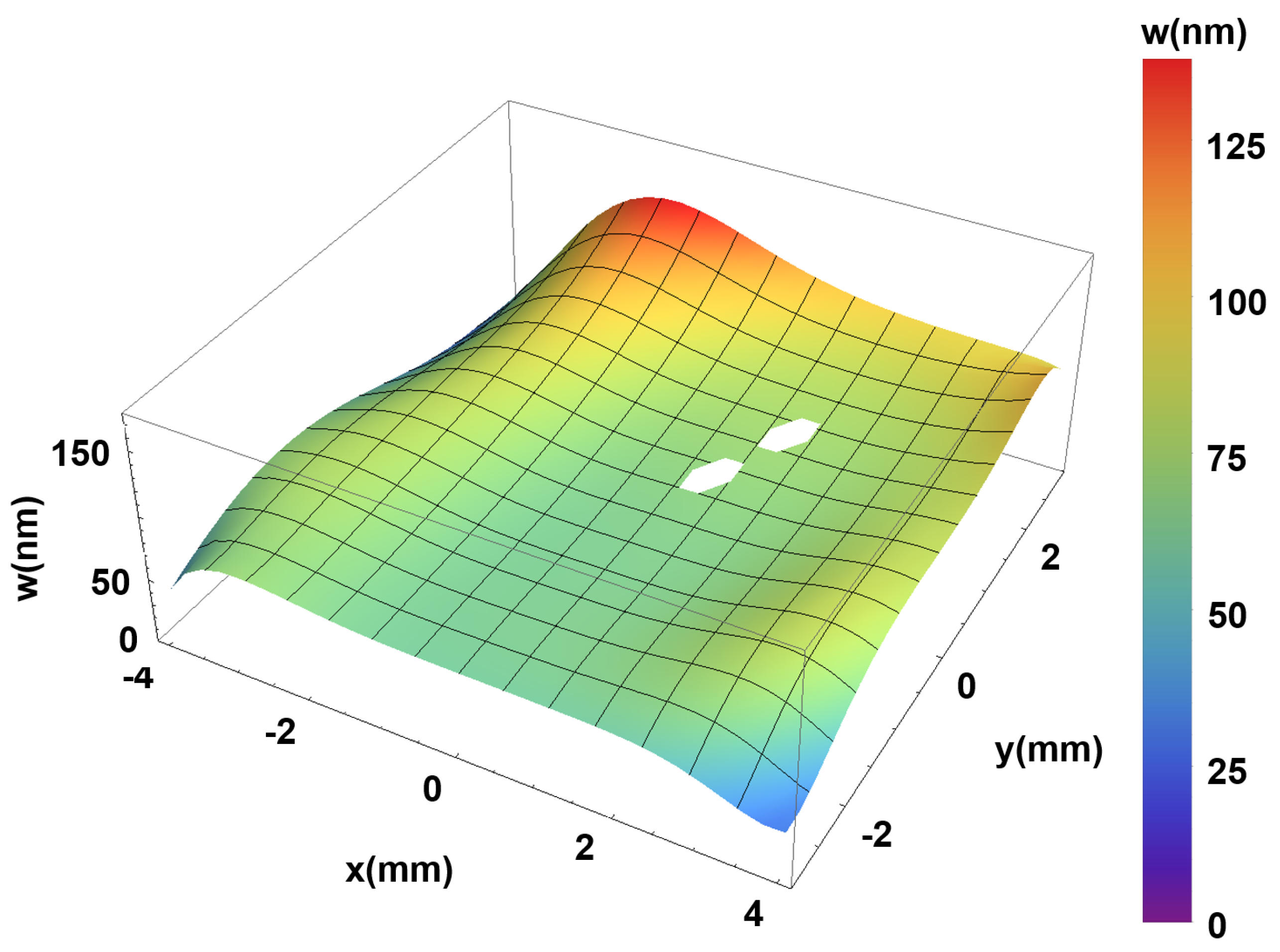
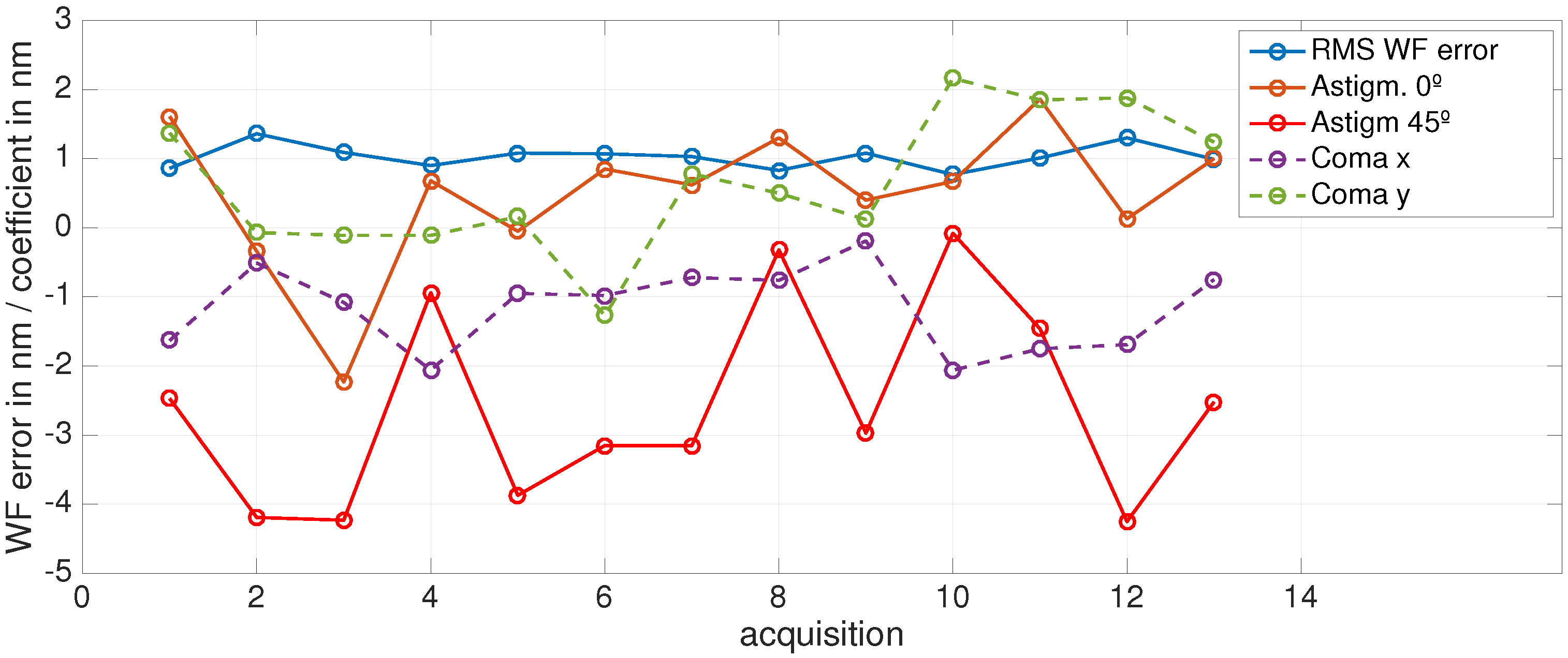
3.2. Wavefront Measurement
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lee, R.W.; Baldis, H.A.; Cauble, R.C.; Landen, O.L.; Wark, J.S.; Ng, A.; Rose, S.J.; Lewis, C.; Riley, D.; Gauthier, J.C.; et al. Plasma-based studies with intense X-ray and particle beam sources. Laser Part. Beams 2002, 20, 527–536. [Google Scholar] [CrossRef]
- Zastrau, U. Innovative XUV and X-ray Plasma Spectroscopy to Explore Warm Dense Matter. Ph.D. Thesis, Friedrich-Schiller-Universität Jena, Jena, Germany, 2002. [Google Scholar]
- Lindl, J.D.; Amendt, P.; Berger, R.L.; Glendinning, S.G.; Glenzer, S.H.; Haan, S.W.; Kauffman, R.L.; Landen, O.L.; Suter, L.J. The physics basis for ignition using indirect-drive targets on the National Ignition Facility. Phys. Plasmas 2004, 11, 339–491. [Google Scholar] [CrossRef]
- Saumon, D.; Chabrier, G.; Wagner, D.J.; Xie, X. Modelling pressure-ionization of hydrogen in the context of astrophysics. High Pressure Res. 2000, 16, 331–343. [Google Scholar] [CrossRef]
- Kluge, T.; Gutt, C.; Huang, L.G.; Metzkes, J.; Schramm, U.; Bussmann, M.; Cowan, T.E. Using X-ray free-electron lasers for probing of complex interaction dynamics of ultra-intense lasers with solid matter. Phys. Plasmas 2014, 21, 033110. [Google Scholar] [CrossRef]
- Attwood, D.T. The Soft X-Ray And Extreme Ultraviolet Regions of the Electromagnetic Spectrum. In Soft X-rays and Extreme Ultraviolet Radiation: Principles and Applications; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Dobosz, S.; Doumy, G.; Stabile, H.; D’Oliveira, P.; Monot, P.; Réau, F.; Hüller, S.; Martin, P. Probing Hot and Dense Laser-Induced Plasmas with Ultrafast XUV Pulses. Phys. Rev. Lett. 2005, 95, 025001. [Google Scholar] [CrossRef] [PubMed]
- Hergott, J.F. XUV interferometry using high-order harmonics: Application to plasma diagnostics. In Atoms, Solids, and Plasmas in Super-Intense Laser Fields; Springer: New York, NY, USA, 2001. [Google Scholar]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.-J.; et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Young, L.; Kanter, E.P.; Krässig, B.; Li, Y.; March, A.M.; Pratt, S.T.; Santra, R.; Southworth, S.H.; Rohringer, N.; DiMauro, L.F.; et al. Femtosecond electronic response of atoms to ultra-in tense X-rays. Nature 2010, 466, 56–61. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Zhang, Q.; Chini, M.; Wu, Y.; Wang, X.; Chang, Z. Tailoring a 67 attosecond pulse through advantageous phase-mismatch. Opt. Lett. 2012, 37, 3891–3893. [Google Scholar] [CrossRef] [PubMed]
- Ravasio, A.; Gauthier, D.; Maia, F.R.N.C.; Billon, M.; Caumes, J.-P.; Garzella, D.; Géléoc, M.; Gobert, O.; Hergott, J.-F.; Pena, A.-M.; et al. Single shot diffractive imaging with a table top femtosecond soft X-ray laser harmonics source. Phys. Rev. Lett. 2009, 103, 028104. [Google Scholar] [CrossRef] [PubMed]
- Williams, G.O.; Chung, H.-K.; Vinko, S.M.; Künzel, S.; Sardinha, A.B.; Zeitoun, Ph.; Fajardo, M. Method of time resolved refractive index measurements of X-ray laser heated solids. Phys. Plasmas 2013, 20, 042701. [Google Scholar] [CrossRef]
- Morlens, A.-S.; Gautier, J.; Rey, G.; Zeitoun, Ph.; Caumes, J.-P.; Kos-Rosset, M.; Merdji, M.; Kazamias, S.; Cassou, K.; Fajardo, M. Submicrometer digital in-line holographic microscopy at 32 nm with high-order harmonics. Opt. Lett. 2006, 31, 3095–3097. [Google Scholar] [CrossRef] [PubMed]
- Zeitoun, P.; Faivre, G.; Sebban, S.; Mocek, T.; Hallou, A.; Fajardo, M.; Aubert, D.; Balcou, P.; Burgy, F.; Douillet, D.; et al. A high-intensity highly coherent soft X-ray femtosecond laser seeded by a high harmonic beam. Nature 2004, 431, 426–429. [Google Scholar] [CrossRef] [PubMed]
- Constant, E.; Garzella, D.; Breger, P.; Mével, E.; Dorrer, Ch.; Le Blanc, C.; Salin, F.; Agostini, P. Optimizing High Harmonic Generation in Absorbing Gases: Model and Experiment. Phys. Rev. Lett. 1999, 82, 1668. [Google Scholar] [CrossRef]
- Vuong, C.V.; Khuong, B.D.; Peter, H.; Dao, V. Lap Influence of absorption in phase-matched high-order harmonic generation in a semi-infinite gas cell. J. Nonlinear Opt. Phys. Mater. 2015, 24, 1550031. [Google Scholar] [CrossRef]
- Gautier, J.; Zeitoun, P.; Hauri, C.; Morlens, A.-S.; Rey, G.; Valentin, C.; Papalarazou, E.; Goddet, J.-P.; Sebban, S.; Burgy, F.; et al. Optimization of the wave front of high order harmonics. Eur. Phys. J. D 2008, 48, 459–463. [Google Scholar] [CrossRef]
- Künzel, S.; Williams, G.O.; Boutu, W.; Galtier, E.; Barbrel, B.; Lee, H.J.; Nagler, B.; Zastrau, U.; Dovillaire, G.; Lee, R.W.; et al. Shot-to-shot intensity and wavefront stability of high-harmonic generation. Appl. Opt. 2015, 54, 4745–4749. [Google Scholar] [CrossRef] [PubMed]
- Morrissey, F.X.; Fan, T.Y.; Miller, D.E.; Rand, D. Picosecond kilohertz-class cryogenically cooled multistage Yb-doped chirped pulse amplifier. Opt. Lett. 2017, 42, 707–710. [Google Scholar] [CrossRef] [PubMed]
- Baumgarten, C.; Pedicone, M; Bravo, H.; Wang, H.; Yin, L; Menoni, C.S.; Rocca, J.J.; Reagan, B.A. 1 J, 0.5 kHz repetition rate picosecond laser. Opt. Lett. 2016, 41, 3339–3342. [Google Scholar] [CrossRef] [PubMed]
- Kazamias, S.; Douillet, D.; Weihe, F.; Valentin, C.; Rousse, A.; Sebban, S.; Grillon, G.; Augé, F.; Hulin, D.; Balcou, P. Global optimization of high harmonic generation. Phys. Rev. Lett. 2003, 90, 193901. [Google Scholar] [CrossRef] [PubMed]
- João, C.P.; Pires, H.; Figueira, G. Hybrid diode-pumped Yb:CaF2/YAG laser system delivers 20 mJ pulses at 1050 nm for Nd:glass amplifier seeding. OSA Tech. Dig. 2014. [Google Scholar] [CrossRef]
- Flöter, B.; Juranić, P.; Kapitzki, S.; Keitel, B.; Mann, K.; Plönjes, E.; Schäfer, B.; Tiedtke, K. EUV Hartmann sensor for wavefront measurements at the Free-electron Laser in Hamburg. New J. Phys. 2010, 12, 083015. [Google Scholar] [CrossRef]
- Keitel, B.; Plönjes, E.; Kreis, S.; Kuhlmann, M.; Tiedtke, K.; Mey, T.; Schäfer, B.; Mann, K. Hartmann wavefront sensors and their application at FLASH. J. Synchrotron Radiat. 2016, 23, 43–49. [Google Scholar] [CrossRef] [PubMed]
- Ammoso, M.V.; Delone, N.B.; Krainov, V.P. Tunnel ionization of complex atoms and of atomic ions in an alternating electromagnetic field. Sov. Phys. JETP 1986, 64, 1191–1194. [Google Scholar]
- Henke, B.L.; Gullikson, E.M.; Davis, J.C. X-ray interactions: Photoabsorption, scattering, transmission, and reflection at E = 50–30,000 eV, Z = 1–92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Gartside, L.M.R.; Tallents, G.J.; Rossall, A.K.; Wagenaars, E.; Whittaker, D.S.; Kozlová, M.; Nejdl, J.; Sawicka, M.; Polan, J.; Kalal, M.; et al. Extreme ultraviolet interferometry of warm dense matter in laser plasmas. Opt. Lett. 2010, 35, 3820–3822. [Google Scholar] [CrossRef] [PubMed]
- Ping, Y.; Correa, A.A.; Ogitsu, T.; Draeger, E.; Schwegler, E.; Ao, T.; Widmann, K.; Price, D.F.; Lee, E.; Tam, H.; et al. Warm dense matter created by isochoric laser heating. High Energy Density Phys. 2009, 6, 246–257. [Google Scholar] [CrossRef]
- Kettle, B.; Dzelzainis, T.; White, S.; Li, L.; Dromey, B.; Zepf, M.; Lewis, C.L.S.; Williams, G.; Künzel, S.; Fajardo, M.; et al. Experimental measurements of the collisional absorption of XUV radiation in warm dense aluminium. Phys. Rev. E 2016, 94, 023203. [Google Scholar] [CrossRef] [PubMed]
- Hornung, M.; Liebetrau, H.; Keppler, S.; Kessler, A.; Hellwing, M.; Schorcht, F.; Becker, A.; Reuter, M.; Polz, J.; Körner, J.; et al. 54 J pulses with 18 nm bandwidth from a diode pumped chirped-pulse amplification laser system. Opt. Lett. 2016, 41, 5413–5416. [Google Scholar] [CrossRef] [PubMed]
- Siebold, M.; Roeser, F.; Loeser, M.; Albach, D.; Schramm, U. PEnELOPE: A high peak-power diode-pumped laser system for laser-plasma experiments. Proc. SPIE 2013, 8780. [Google Scholar] [CrossRef]
| Gas | Rayleigh Length | Focal Length | Pressure | HH Photon Number | HH Energy |
|---|---|---|---|---|---|
| Units | mm | mm | mbar | Photons per Shot | nJ |
| Argon | 3.3 | 500 | 55 | 7 × | 0.44 ± 0.05 |
| Xenon | 6.4 | 700 | 15 | 3.6 × | 1.44 ± 0.16 |
| Gas | Divergence Horizontal | Divergence Vertical | Energy Stability |
|---|---|---|---|
| Units | mrad | mrad | % |
| Argon | 2.48 | 2.18 | 9.4 |
| Xenon | 1.89 | 1.25 | 6.0 |
| Parameter | Mean | Standard Deviation |
|---|---|---|
| RMS Wavefront Error | 4.90 nm | 1.14 nm |
| Astigmatism | −41.50 nm | 18.48 nm |
| Astigmatism | 5.12 nm | 9.55 nm |
| Coma X | 9.37 nm | 6.86 nm |
| Coma Y | −21.85 nm | 35.03 nm |
| RMS Slope | 0.60 mrad | 0.01 mrad |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koliyadu, J.C.P.; Künzel, S.; Wodzinski, T.; Keitel, B.; Duarte, J.; Williams, G.O.; João, C.P.; Pires, H.; Hariton, V.; Galletti, M.; et al. Optimization and Characterization of High-Harmonic Generation for Probing Solid Density Plasmas. Photonics 2017, 4, 25. https://doi.org/10.3390/photonics4020025
Koliyadu JCP, Künzel S, Wodzinski T, Keitel B, Duarte J, Williams GO, João CP, Pires H, Hariton V, Galletti M, et al. Optimization and Characterization of High-Harmonic Generation for Probing Solid Density Plasmas. Photonics. 2017; 4(2):25. https://doi.org/10.3390/photonics4020025
Chicago/Turabian StyleKoliyadu, Jayanath C. P., Swen Künzel, Thomas Wodzinski, Barbara Keitel, Joana Duarte, Gareth O. Williams, Celso P. João, Hugo Pires, Victor Hariton, Mario Galletti, and et al. 2017. "Optimization and Characterization of High-Harmonic Generation for Probing Solid Density Plasmas" Photonics 4, no. 2: 25. https://doi.org/10.3390/photonics4020025
APA StyleKoliyadu, J. C. P., Künzel, S., Wodzinski, T., Keitel, B., Duarte, J., Williams, G. O., João, C. P., Pires, H., Hariton, V., Galletti, M., Gomes, N., Figueira, G., Dias, J. M., Lopes, N., Zeitoun, P., Plönjes, E., & Fajardo, M. (2017). Optimization and Characterization of High-Harmonic Generation for Probing Solid Density Plasmas. Photonics, 4(2), 25. https://doi.org/10.3390/photonics4020025




