Generation of Attosecond Light Pulses from Gas and Solid State Media
Abstract
:1. Introduction
2. Theoretical Description of the XUV Emission from Gases and Solids
2.1. XUV Emission from Gases
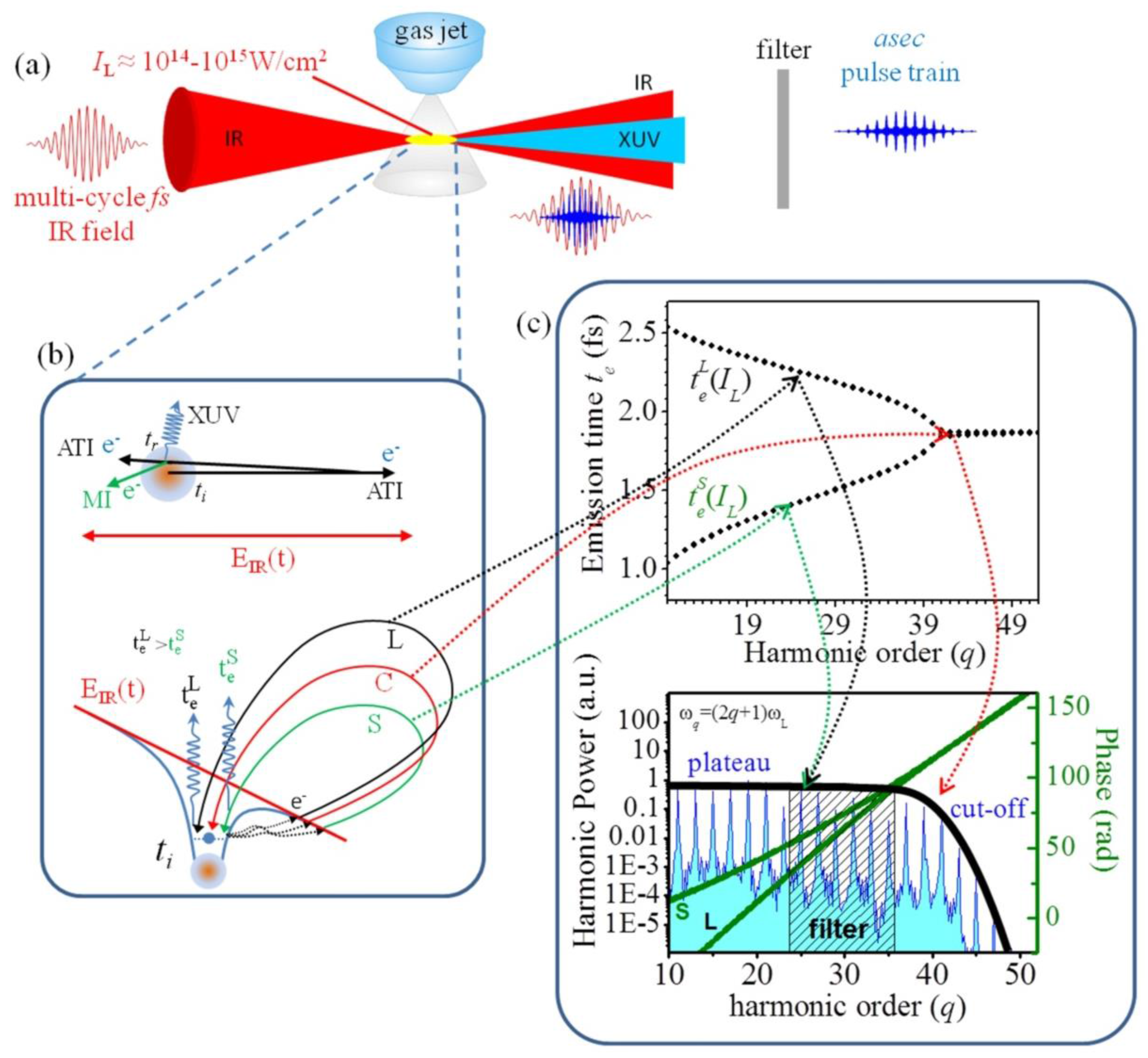
2.1.1. Single Atom Response
2.1.2. Generation of Asec Pulse Trains
2.1.3. Generation of Isolated Asec Pulses
2.1.4. Macroscopic Effects in HHG
- Linear effects: during propagation even linear dispersion causes a temporal stretch of the broad bandwidth laser pulse. Due to diffraction/focusing (and HHG is usually achieved in a focusing arrangement) the intensity distribution changes both along propagation, and in the transverse plane, affecting both the amplitude and the phase of the generated radiation.
- The high intensity laser beam evokes the Kerr-type non-linear refractive index of the generating medium, leading to self-focusing of the beam, and a blue-(red) shift on the rising (falling) slope due to self-phase modulation.
- Due to the ionization of the medium by the driving field, the presence of free electrons modifies both the linear and non-linear properties of the medium. This can even result in defocusing of the beam.
- Neutral dispersion—for XUV spectral domain negative, for IR components it is positive.
- Plasma dispersion—it is always negative, and scales as λ2, so IR is effected more. Since ionization fraction varies in space and time, this contribution is also varying.
- Gouy phase shift—affects the focused IR beam, there is a negative contribution as we go from before focus to after focus.
- Dipole/atomic phase—proportional to the intensity of the IR field, and depends on whether the generation occurs via the short or long trajectory. As the driving field intensity is space and time dependent, this component also varies spatiotemporally.
- (a)
- Long (few tens of cm scale), low pressure (few mbar) target: Scaling up high order harmonic generation by increasing driving laser powers in the low density target regime has been investigated thoroughly in [99,112]. Phase matching conditions by balancing the effects of Gouy phase shift, neutral and plasma dispersion provides scaling principles. It has been found, that for this low ionization regime increasing laser powers requires the up-scaling of the geometric parameters (focal length, target length) and downscaling the target pressure. In this phase matching regime today’s state of the art laser pulses will require focusing of several tens (to a hundred) meters and gas target lengths of tens of centimeters (to meters).
- (b)
- Short (mm scale), high pressure (tens to thousands of mbar) target: Generating intense XUV radiation by intense laser pulses can also be achieved in a different phase matching regime, using high density short gas targets (jets) [113]. In this case the required focal lengths are somewhat shorter (few to ten meters), leading to higher intensity in the target. This means that the target will be ionized stronger than in the previous case, but due to the shorter medium length the distortion of the laser pulse can be reduced. The high number of interacting atoms, required to achieve a high XUV flux, in this case is confined in a small volume.
- (c)
- Quasi phase matching: Various quasi phase matching techniques have been applied for gas HHG to reduce the phase mismatch naturally accompanying the nonlinear process see [114,115] and references therein. In these arrangements either the target or the propagating laser beam is periodically modulated (by means of successive gas targets, propagation of the beam in a modulated waveguide or superposing a secondary modulating laser beam counter- or perpendicularly propagating with the generating laser pulse).
2.2. XUV Emission from Solid Surfaces
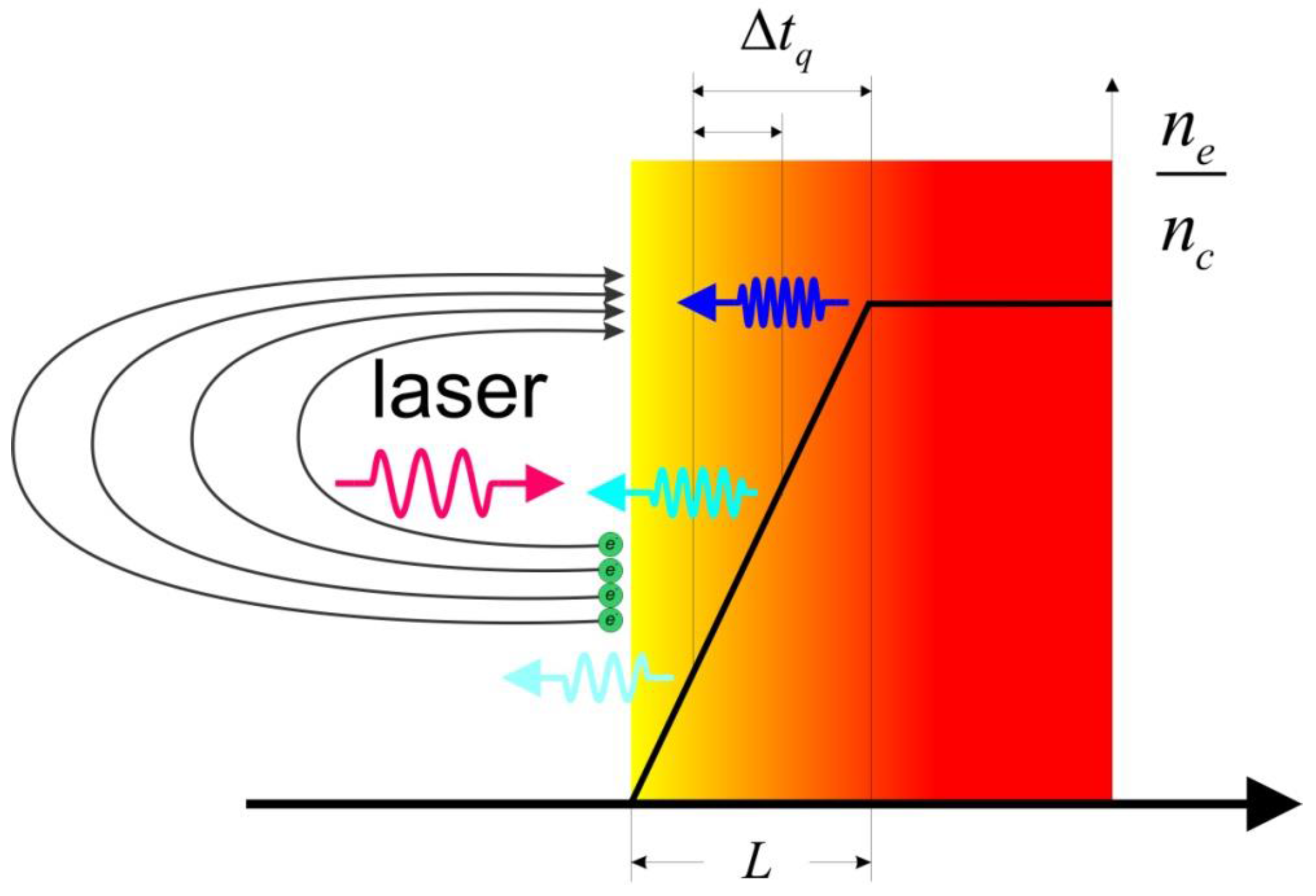
2.2.1. The Coherent Wake Emission (CWE) Mechanism
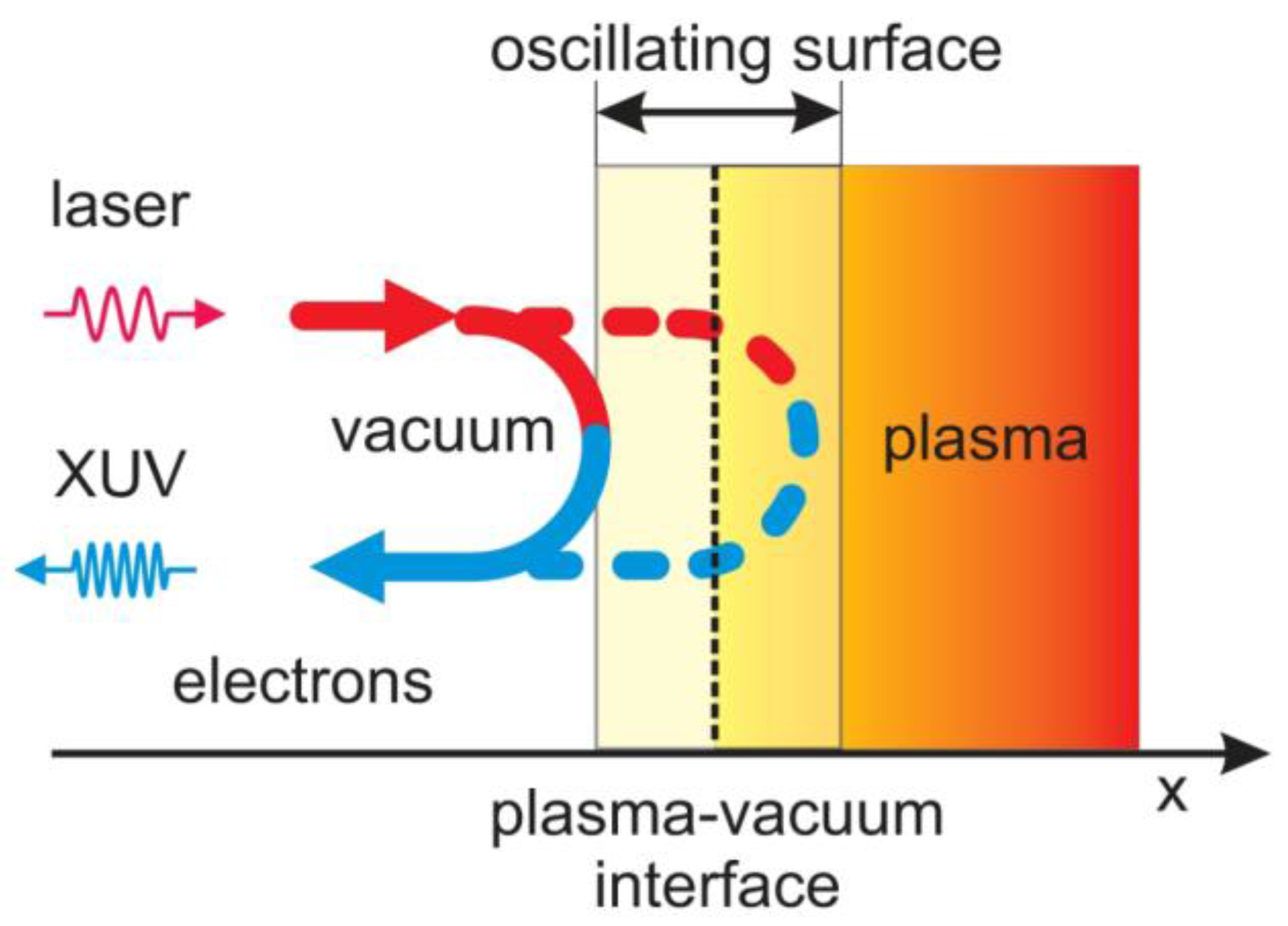
2.2.2. The Relativistic Oscillating Mirror (ROM) Mechanism
2.2.3. Particle-in-Cell (PIC) Simulations
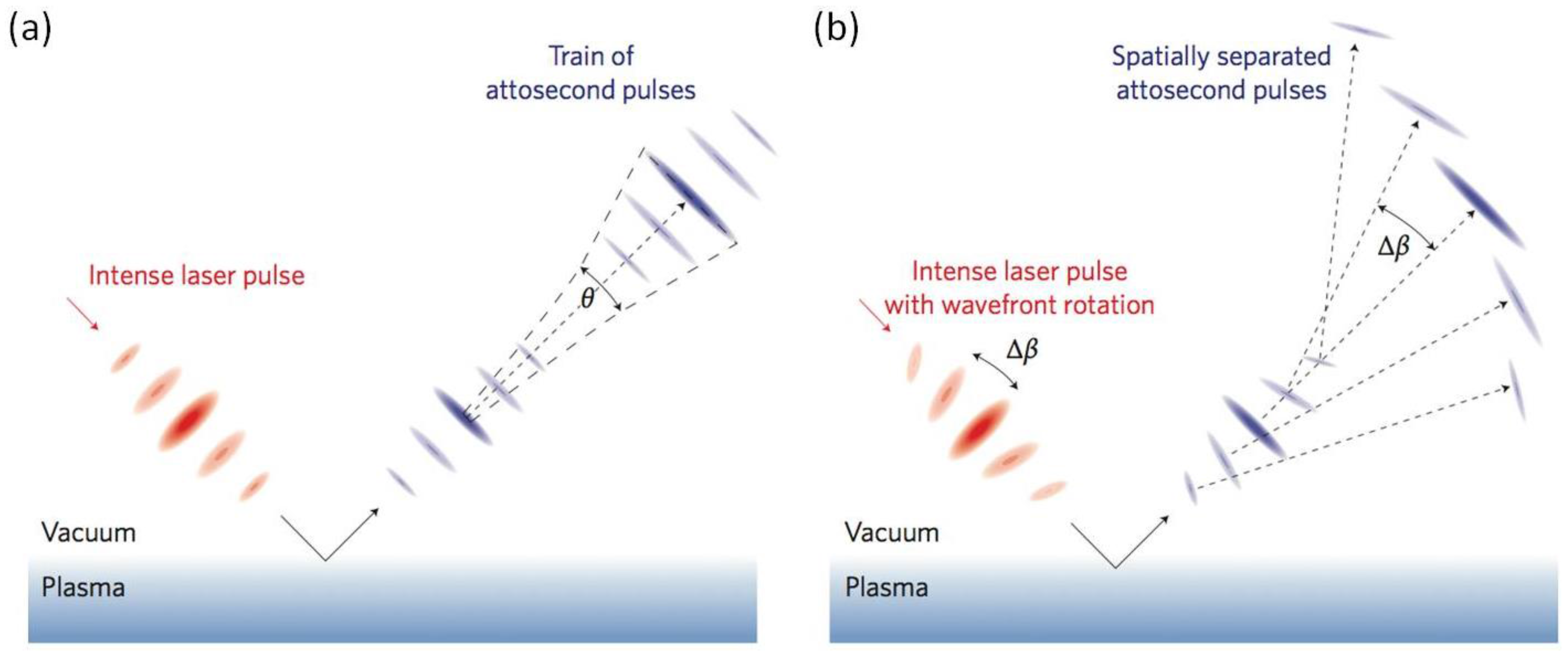
2.2.4. Asec Lighthouse Effect
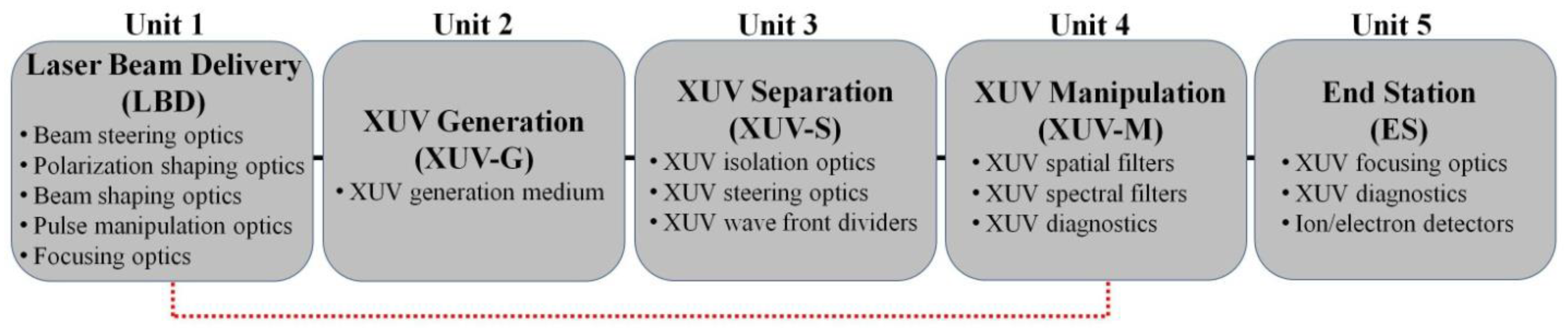
3. Asec Beam Lines
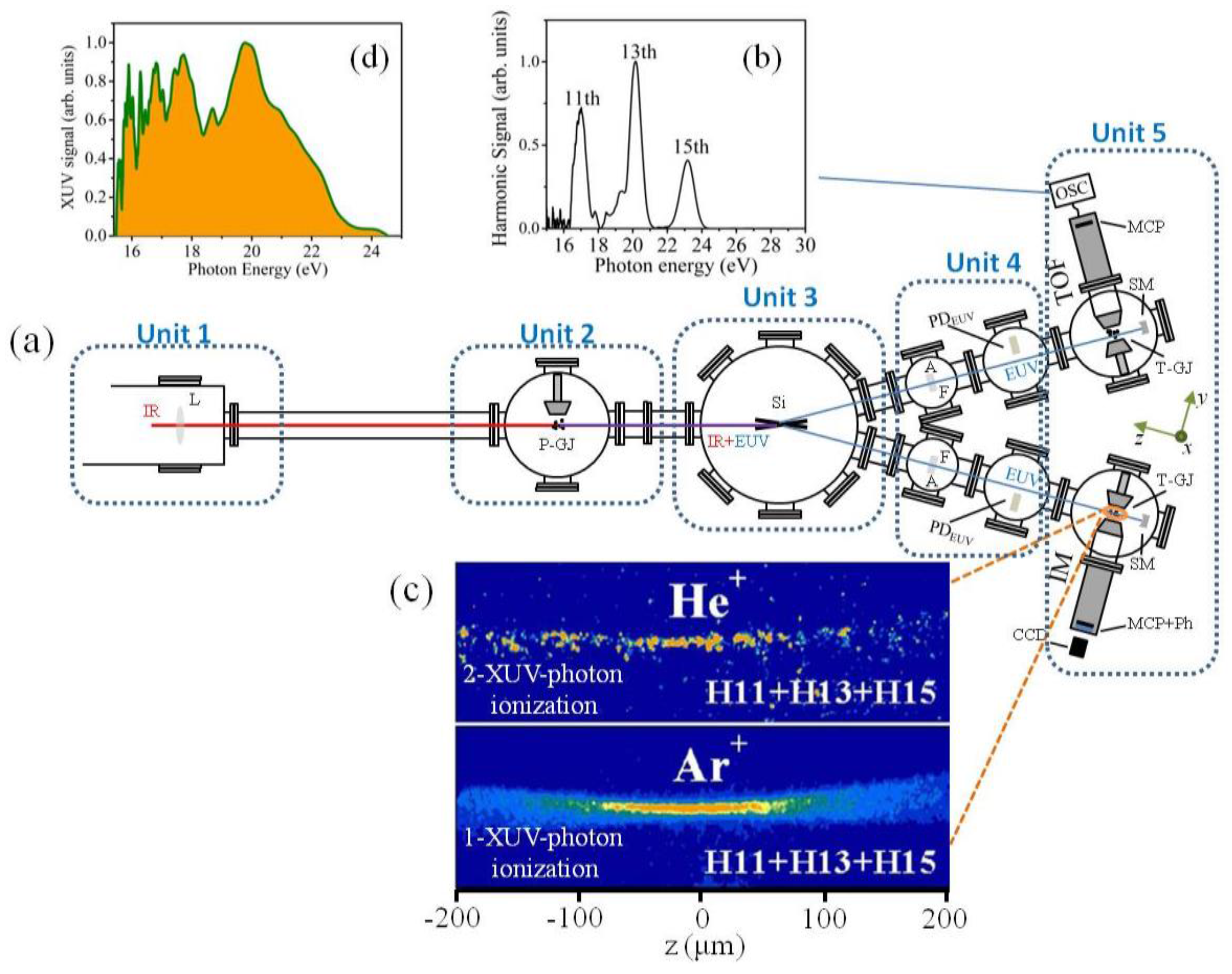
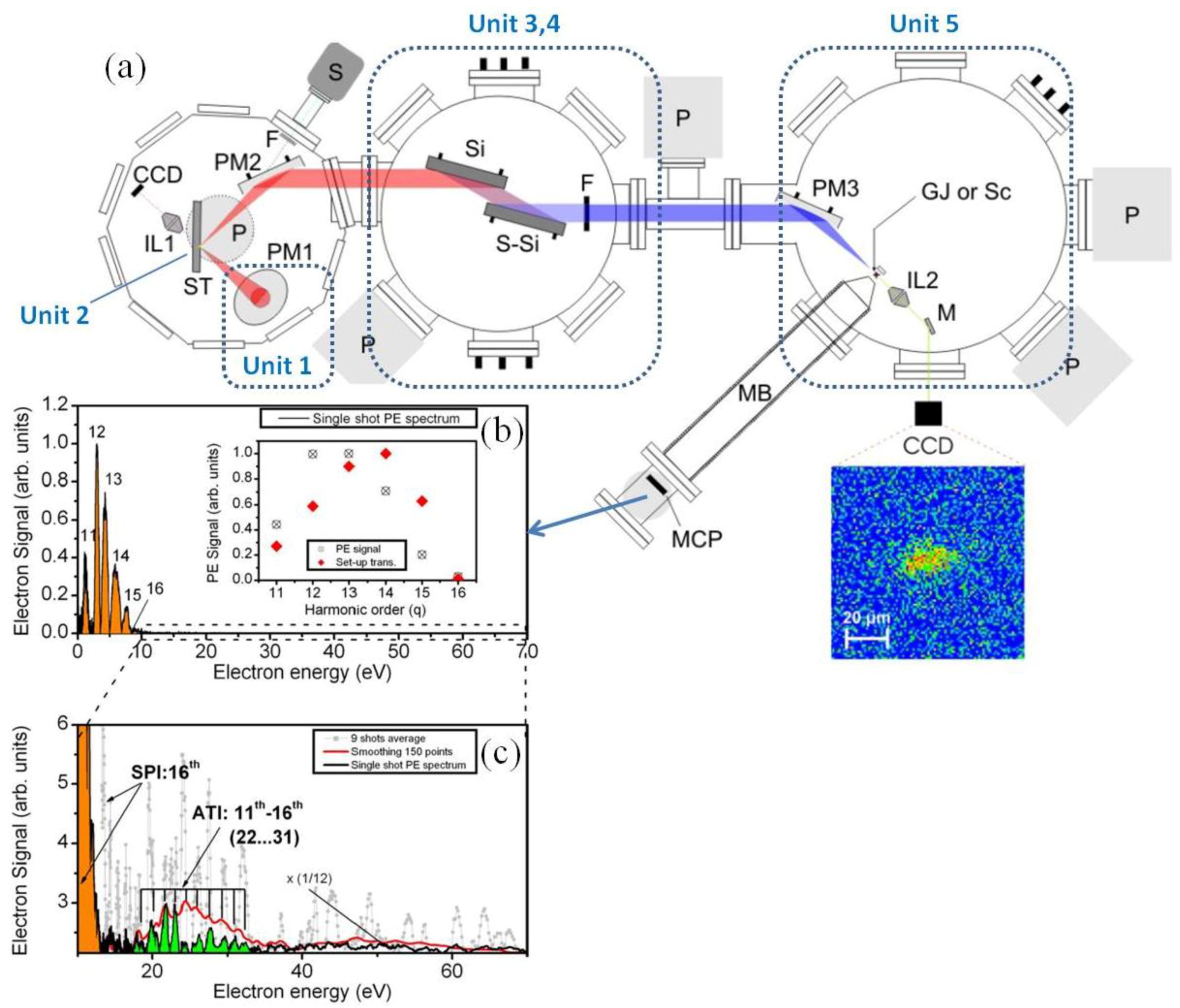
3.1. Asec Beam Lines for Gas Phase Media
3.2. Asec Beam Lines for Solid Surface Media
4. Characterization of XUV Sources
4.1. Temporal Characterization of Asec Pulses Generated in Gases
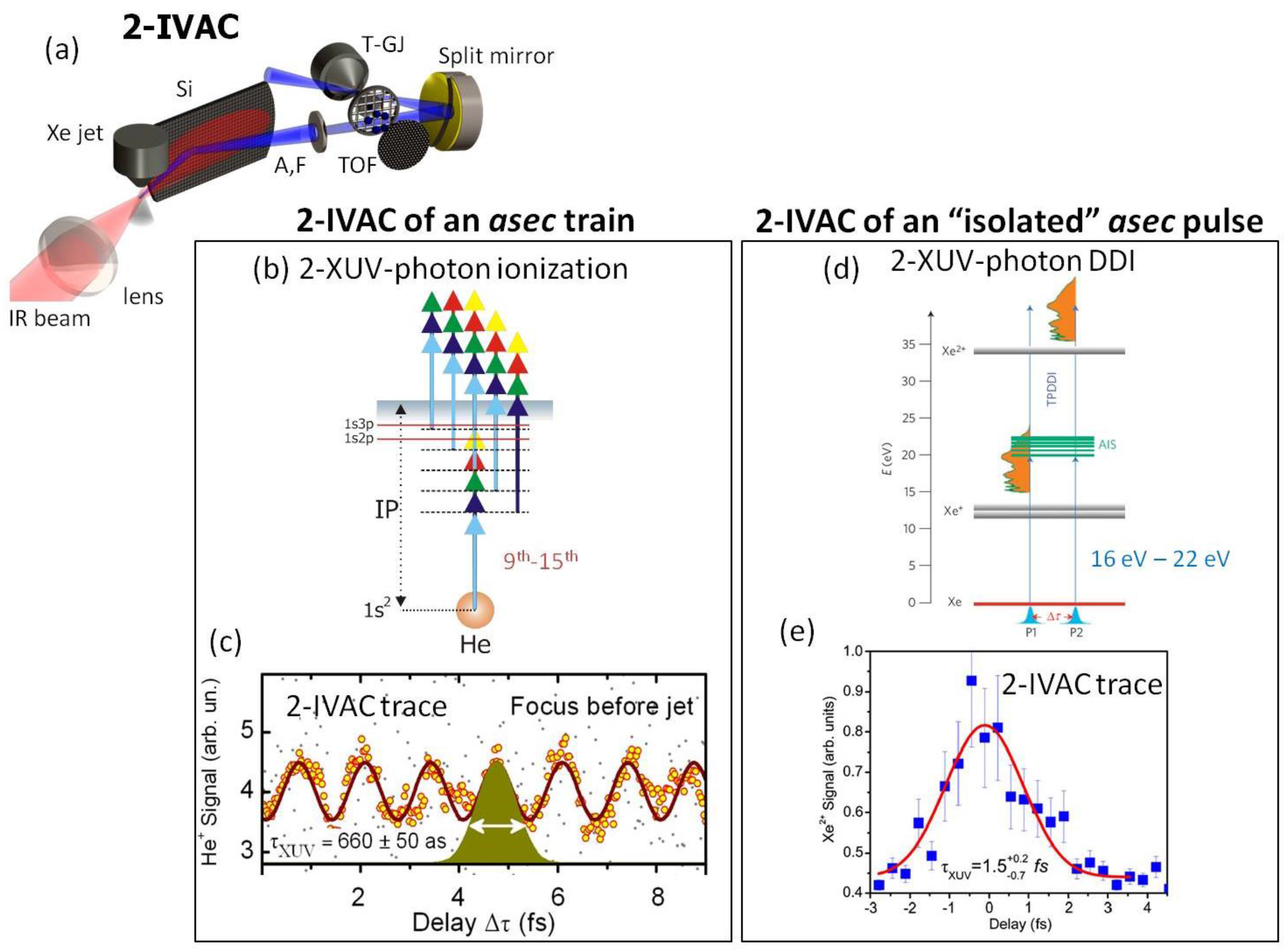
4.1.1. The 2-IVAC Method in Gas-Phase Harmonics
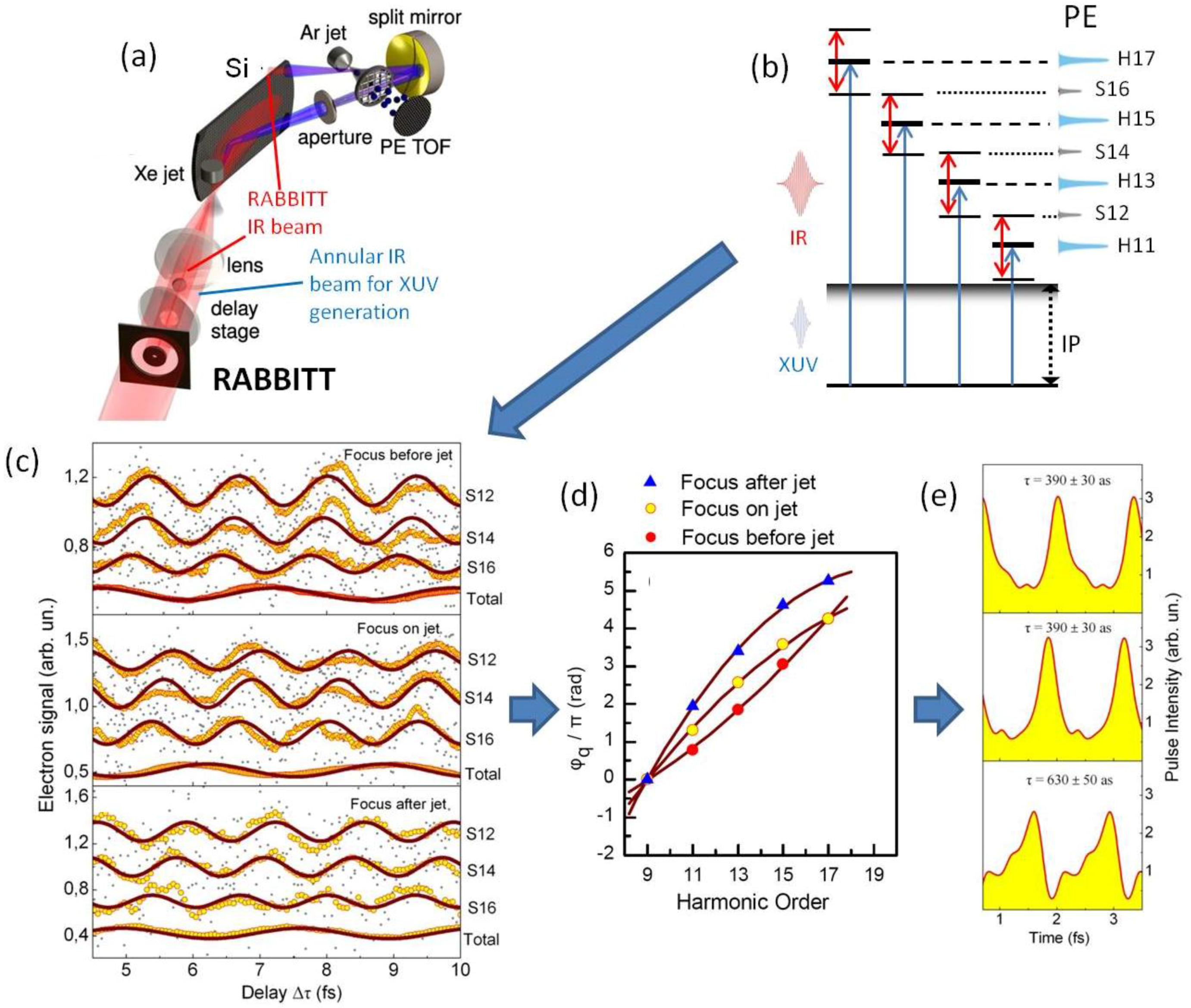
4.1.2. The RABBITT Method in Gas-Phase Harmonics
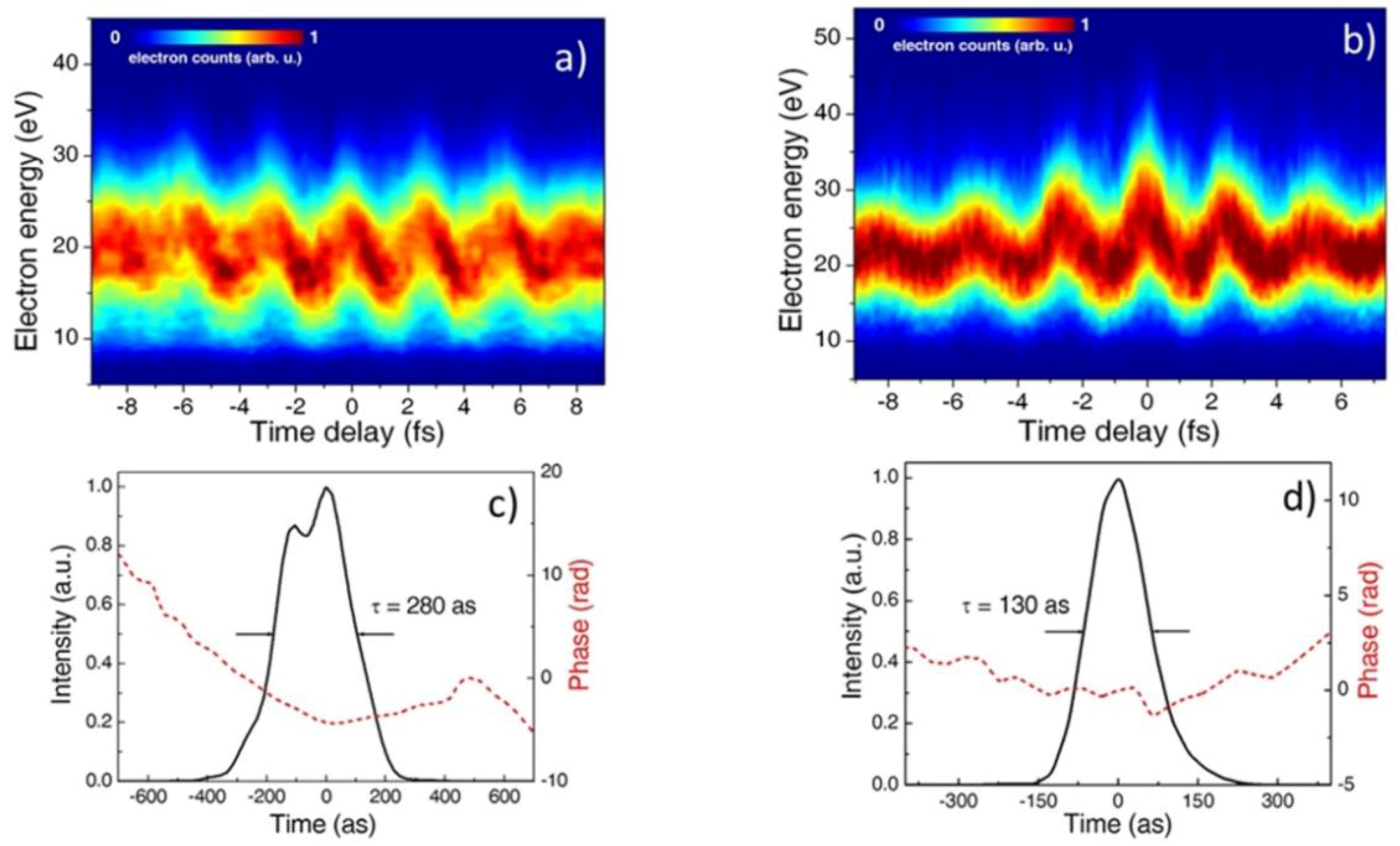
4.1.3. Temporal Characterization of Asec Pulses Using FROG-CRAB
4.2. Characterization of Asec Pulses Generated in Solid-Surfaces
4.2.1. Temporal Characterization of Asec Pulses Using the 2-IVAC Method
4.2.2. Spectrally Resolved Spatial Phase and Amplitude Retrieval of Solid-Surface Harmonics
5. Conclusions and Ongoing Development on Gas-Phase and Solid-Surface Asec Sources
Acknowledgments
Conflicts of Interest
References
- Steinmeyer, G.; Sutter, D.H.; Galmann, L.; Matuschek, N.; Keller, U. Frontiers in Ultrashort Pulse Generation: Pushing the Limits in Linear and non linear optics. Science 1999, 286, 1507–1512. [Google Scholar] [CrossRef] [PubMed]
- Brabec, T.; Krausz, F. Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 2010, 72, 545. [Google Scholar] [CrossRef]
- Keller, U. Recent developments in compact ultrafast lasers. Nature 2003, 424, 831–838. [Google Scholar] [CrossRef] [PubMed]
- Witte, S.; Zinkstok, R.T.; Hogervorst, W.; Ubachs, W.; Eikema, K.S.E. A source of 2 terawatt, 2.7 cycle laser pulses based on noncollinear optical parametric chirped pulse amplification. Opt. Express 2006, 14, 8168–8177. [Google Scholar] [CrossRef] [PubMed]
- Hermann, D.; Veisz, L.; Tautz, R.; Tavella, F.; Schmid, K.; Pervak, V.; Krausz, F. Generation of sub-three-cycle, 16 TW16 TW light pulses by using noncollinear optical parametric chirped-pulse amplification. Opt. Lett. 2009, 34, 2459–2461. [Google Scholar] [CrossRef]
- Major, Z.; Trushin, S.A.; Ahmad, I.; Siebold, M.; Wandt, C.; Klingebiel, S.; Wang, T.J.; FÜ Lop, J.A.; Henig, A.; Kruber, S.; et al. Basic concepts and current status of the petawatt field synthesizer-a new approach to ultrahigh field generation. Rev. Laser Eng. 2009, 37, 431–436. [Google Scholar] [CrossRef]
- Gavrila, M. Atoms in Intense Fields; Academic Press: Boston, MA, USA, 1992. [Google Scholar]
- Protopappas, M.; Keitel, C.H.; Knight, P.L. Atomic physics with super-high intensity lasers. Rep. Prog. Phys. 1997, 60, 389. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994. [Google Scholar] [CrossRef] [PubMed]
- Lewenstein, M.; Balcou, Ph.; Ivanov, M.Y.; L’Huiller, A.; Corkum, P.B. Theory of high harmonic generation by low frequency fields. Phys. Rev. A 1994, 49, 2117. [Google Scholar] [CrossRef] [PubMed]
- Krause, J.L.; Schafer, K.J.; Kulander, K.C. High-order harmonic generation from atoms and ions in the high intensity regime. Phys. Rev. Lett. 1992, 68, 3535. [Google Scholar] [CrossRef] [PubMed]
- Schafer, K.J.; Yang, B.; DiMauro, L.F.; Kulander, K.C. Above threshold ionization beyond the high harmonic cutoff. Phys. Rev. Lett. 1993, 70, 1599. [Google Scholar] [CrossRef] [PubMed]
- Becker, W.; Long, S.; and Melver, J.K. Modeling harmonic generation by a zero-range potential. Phys. Rev. A 1994, 50, 1540. [Google Scholar] [CrossRef] [PubMed]
- Salières, P.; Carre, B.; Le Deroff, L.; Grasbon, F.; Paulus, G.G.; Walther, H.; Kopold, R.; Becker, W.; Milosevic, D.B.; Sanpera, A.; et al. Feynman’s path-integral approach for intense-laser-atom interactions. Science 2001, 292, 902–905. [Google Scholar] [CrossRef] [PubMed]
- Gonoskov, I.A.; Tsatrafyllis, N.; Kominis, I.K.; Tzallas, P. Quantum optical signatures in strong-field laser physics: Infrared photon counting in high-order-harmonic generation. Sci. Rep. 2016, 6, 32821. [Google Scholar] [CrossRef] [PubMed]
- Tsatrafyllis, N.; Kominis, I.K.; Gonoskov, I.A.; Tzallas, P. High-order harmonics measured by the photon statistics of the infrared driving-field exiting the atomic medium. Nat. Commun. 2017, 8, 15170. [Google Scholar]
- Bezzerides, B.; Jones, R.D.; Forslund, D.W. Plasma Mechanism for Ultraviolet Harmonic Radiation Due to Intense CO2 Light. Phys. Rev. Lett. 1982, 49, 202. [Google Scholar] [CrossRef]
- Grebogi, C.; Tripathi, V.K.; Chen, H.H. Harmonic generation of radiation in a steep density profile. Phys. Fluids 1983, 26, 1904–1908. [Google Scholar] [CrossRef]
- Von Der Linde, D.; Rzazewski, K. High-order optical harmonic generation from solid surfaces. Appl. Phys. B 1996, 63, 499–506. [Google Scholar] [CrossRef]
- Teubner, U.; Gibbon, P. High-order harmonics from laser irradiated plasma surfaces. Rev. Mod. Phys. 2009, 81, 445. [Google Scholar] [CrossRef]
- Baeva, T.; Gordienko, S.; Pukhov, A. Theory of high-order harmonic generation in relativistic laser interaction with overdense plasma. Phys. Rev. E 2006, 74, 046404. [Google Scholar] [CrossRef] [PubMed]
- Quéré, F.; Thaury, C.; Monot, P.; Dobosz, S.; Martin, P.; Geindre, J.-P.; Audebert, P. Coherent wake emission of high-order harmonics from overdense plasmas. Phys. Rev. Lett. 2006, 96, 125004. [Google Scholar] [CrossRef] [PubMed]
- Blaga, C.I.; Catoire, F.; Colosimo, P.; Paulus, G.G.; Muller, H.G.; Agostini, P.; DiMauro, L.F. Strong-field photoionization revisited. Nat. Phys. 2009, 5, 335–338. [Google Scholar] [CrossRef]
- Gohle, C.; Udem, T.; Hermann, M.; Rauschenberger, J.; Holzwarth, R.; Shuessler, H.A.; Krausz, F.; Hansch, T.W. A frequency comb in the extreme ultraviolet. Nature 2005, 436, 234–237. [Google Scholar] [CrossRef] [PubMed]
- Cingöz, A.; Yost, D.C.; Allison, T.K.; Ruehl, A.; Fermann, M.E.; Hartl, I.; Ye, J. Direct frequency comb spectroscopy in the extreme ultraviolet. Nature 2012, 482, 68–71. [Google Scholar] [CrossRef] [PubMed]
- Träger, F. Springer Handbook of Lasers and Optics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 219–236. [Google Scholar]
- Reduzzi, M.; Carpeggiani, P.; Kühn, S.; Calegari, F.; Nisoli, M.; Stagira, S.; Vozzi, C.; Dombi, P.; Kahaly, S.; Tzallas, P.; et al. Advances in high-order harmonic generation sources for time-resolved investigations. J. Electron Spectrosc. Relat. Phenom. 2015, 204, 257–268. [Google Scholar] [CrossRef]
- Corkum, P.B.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381–387. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163. [Google Scholar] [CrossRef]
- Gallman, L.; Cirelli, C.; Keller, U. Attosecond Science: Recent Highlights and Future Trends. Annu. Rev. Phys. Chem. 2012, 63, 447–469. [Google Scholar] [CrossRef] [PubMed]
- Burnett, N.H.; Baldis, H.A.; Richardson, M.C.; Enright, G.D. Harmonic generation in CO2 laser target interaction. Appl. Phys. Lett. 1977, 31, 172–174. [Google Scholar] [CrossRef]
- Carman, R.L.; Forslund, D.W.; Kindel, J.M. Visible Harmonic Emission as a Way of Measuring Profile Steepening. Phys. Rev. Lett. 1981, 46, 29. [Google Scholar] [CrossRef]
- Ferray, M.; L’Huillier, A.; Li, X.F.; Lompré, L.A.; Mainfray, G.; Manus, C. Multiple-harmonic conversion of 1064 nm radiation in rare gases. J. Phys. B At. Mol. Opt. Phys. 1988, 21, L31. [Google Scholar] [CrossRef]
- L’Huillier, A.; Balcou, P. High-order harmonic generation in rare gases with a 1-ps 1053-nm laser. Phys. Rev. Lett. 1993, 70, 774. [Google Scholar] [CrossRef] [PubMed]
- Heissler, P.; Lugovoy, E.; Hörlein, R.; Waldecker, L.; Wens, J.; Heigoldt, M.; Khrennikov, K.; Karsch, S.; Krausz, F.; Abel, B.; et al. Using the third state of matter: High harmonic generation from liquid targets. New J. Phys. 2014, 16, 113045. [Google Scholar] [CrossRef]
- Poole, P.L.; Willis, C.; Cochran, G.E.; Hanna, R.T.; Andereck, C.D.; Schumacher, D.W. Moderate repetition rate ultra-intense laser targets and optics using variable thickness liquid crystal films. Appl. Phys. Lett. 2016, 109, 151109. [Google Scholar] [CrossRef]
- Poole, P.L.; Andereck, C.D.; Schumacher, D.W.; Daskalova, R.L.; Feister, S.; George, K.M.; Willis, C.; Akli, K.U.; Chodhury, E.A. Liquid crystal films as on-demand, variable thickness (50–5000 nm) targets for intense lasers. Phys. Plasmas 2014, 21, 063109. [Google Scholar] [CrossRef]
- Bierbach, J.; Yeung, M.; Eckner, E.; Roedel, C.; Kuschel, S.; Zepf, M.; Paulus, G.G. Long-term operation of surface high-harmonic generation from relativistic oscillating mirrors using a spooling tape. Opt. Express 2015, 23, 12321–12327. [Google Scholar] [CrossRef] [PubMed]
- Ghimire, E.; DiChiara, A.D.; Sistrunk, E.; Agostini, P.; DiMauro, L.F.; Reis, D.A. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 2011, 7, 138–141. [Google Scholar] [CrossRef]
- Luu, T.T.; Wörner, H.J. High-order harmonic generation in solids: A unifying approach. Phys. Rev. B 2016, 94, 115164. [Google Scholar] [CrossRef]
- Han, S.; Kim, H.; Kim, Y.W.; Kim, Y.J.; Kim, S.; Park, I.Y.; Kim, S.W. High-harmonic generation by field enhanced femtosecond pulses in metal-sapphire nanostructure. Nat. Commun. 2016, 7, 13105. [Google Scholar] [CrossRef] [PubMed]
- Constant, E.; Garzella, D.; Breger, P.; Mével, E.; Dorrer, Ch.; Le Blanc, C.; Salin, F.; Agostini, P. Optimizing High Harmonic Generation in Absorbing Gases: Model and Experiment. Phys. Rev. Lett. 1999, 82, 1668. [Google Scholar] [CrossRef]
- Papadogiannis, N.A.; Nikolopoulos, L.A.A.; Charalambidis, D.; Tzallas, P.; Tsakiris, G.; Witte, K. Two-photon ionization of He through a superposition of higher harmonics. Phys. Rev. Lett. 2003, 90, 133902. [Google Scholar] [CrossRef] [PubMed]
- Hergott, J.F.; Kovacev, M.; Merdji, H.; Hubert, C.; Jean, E.; Breger, P.; Agostini, P.; Carré, B.; Salières, P. Extreme-ultraviolet high-order harmonic pulses in the microjoule range. Phys. Rev. A 2002, 66, 021821. [Google Scholar] [CrossRef]
- Tzallas, P.; Charalambidis, D.; Papadogiannis, N.A.; Witte, K.; Tsakiris, G.D. Direct observation of attosecond light bunching. Nature 2003, 426, 267–271. [Google Scholar] [CrossRef] [PubMed]
- Skantzakis, E.; Tzallas, P.; Kruse, J.; Kalpouzos, C.; Charalambidis, D. Coherent continuum extreme ultraviolet radiation in the sub-100-nJ range generated by a high-power many-cycle laser field. Opt. Lett. 2009, 34, 1732–1734. [Google Scholar] [CrossRef] [PubMed]
- Midorikawa, K.; Nabekawa, Y.; Suda, A. XUV multiphoton processes with intense high-order harmonics. Prog. Quant. Electron. 2008, 32, 43–88. [Google Scholar] [CrossRef]
- Tzallas, P.; Skantzakis, E.; Nikolopoulos, L.A.A.; Tsakiris, G.D.; Charalambidis, D. Extreme-ultraviolet pump–probe studies of one-femtosecond-scale electron dynamics. Nat. Phys. 2011, 7, 781–784. [Google Scholar] [CrossRef]
- Sansone, G.; Poletto, L.; Nisoli, M. High-energy attosecond light sources. Nat. Photonics 2011, 5, 655–663. [Google Scholar] [CrossRef]
- Takahashi, E.J.; Lan, P.; Mücke, O.D.; Nabekawa, Y.; Midorikawa, K. Attosecond nonlinear optics using gigawatt-scale isolated attosecond pulses. Nat. Commun. 2013, 4, 2691. [Google Scholar] [CrossRef] [PubMed]
- Brizuela, F.; Heyl, C.M.; Rudawski, P.; Kroon, D.; Rading, L.; Dalhström, J.M.; Mauritsson, J.; Johnsson, P.; Arnold, C.L.; L’Huillier, A. Efficient high-order harmonic generation boosted by below-threshold harmonics. Sci. Rep. 2013, 3, 1410. [Google Scholar] [CrossRef] [PubMed]
- Manschwetus, B.; Rading, L.; Campi, F.; Maclot, S.; Coudert-Alteirac, H.; Lahl, J.; Wikmark, H.; Rudawski, P.; Heyl, C.M.; Farkas, B.; et al. Two-photon double ionization of neon using an intense attosecond pulse train. Phys. Rev. A 2016, 93, 061402. [Google Scholar] [CrossRef]
- Wu, Y.; Cunninghmam, E.; Zang, H.; Li, J.; Chini, M. Generation of high-flux attosecond extreme ultraviolet continuum with a 10 TW laser. Appl. Phys. Lett. 2013, 102, 201104. [Google Scholar] [CrossRef]
- Nomura, Y.; Hörlein, R.; Tzallas, P.; Dromey, B.; Rykovanov, S.; Major, Z.S.; Osterhoff, J.; Karsch, S.; Veisz, L.; Zepf, M.; et al. Attosecond phase locking of harmonics emitted from laser-produced plasmas. Nat. Phys. 2009, 5, 124–128. [Google Scholar] [CrossRef]
- Heissler, P.; BarnaJ, A.; Mikhailova, J.M.; Ma, G.; Khrennikov, K.; KarschL, S.; Veisz, L.; Földes, I.B.; Tsakiri, G.D. Multi-μJ harmonic emission energy from laser-driven plasma. Appl. Phys. B 2015, 118, 195–201. [Google Scholar] [CrossRef]
- Bierbach, J.; Rödel, C.; Yeung, M.; Dromey, B.; Hahn, T.; Pour, A.G.; Fuchs, S.; Paz, A.E.; Herzer, S.; Kuschel, S.; et al. Generation of 10 μW relativistic surface high-harmonic radiation at a repetition rate of 10 Hz. New J. Phys. 2012, 14, 065005. [Google Scholar] [CrossRef]
- Thaury, C.; Quéré, F.; Geindre, J.P.; Levy, A.; Ceccotti, T.; Monot, P.; Bougeard, M.; Réau, F.; d’Oliveira, P.; Audebert, P.; et al. Plasma mirrors for ultrahigh-intensity optics. Nat. Phys. 2007, 3, 424–429. [Google Scholar] [CrossRef]
- Heissler, P.; Hörlein, R.; Stafe, M.; Mikhailova, J.M.; Nomura, Y.; Hermann, D.; Tautz, R.; Rykovanov, S.G.; Földes, I.B.; Varju, K.; et al. Toward single attosecond pulses using harmonic emission from solid-density plasmas. Appl. Phys. B 2010, 101, 511–521. [Google Scholar] [CrossRef]
- Gibbon, P. Harmonic Generation by Femtosecond Laser-Solid Interaction: A Coherent “Water-Window” Light Source? Phys. Rev. Lett. 1996, 76, 50. [Google Scholar] [CrossRef] [PubMed]
- Lichters, E.; Meyer-Teh-Vehn, J.; Pukhov, A. Short-pulse laser harmonics from oscillating plasma surfaces driven at relativistic intensity. Phys. Plasmas 1996, 3, 3425–3437. [Google Scholar] [CrossRef]
- Dromey, B.; Adams, D.; Hörlein, R.; Nomura, Y.; Rykovanov, S.G.; Carroll, D.C.; Foster, P.S.; Kar, S.; Markey, K.; McKenna, P.; et al. Diffraction-limited performance and focusing of high harmonics from relativistic plasmas. Nat. Phys. 2009, 5, 146–152. [Google Scholar] [CrossRef]
- Sola, I.J.; Mével, E.; Elouga, L.; Constant, E.; Strelkov, V.; Poletto, L.; Villoresi, P.; Benedetti, E.; Caumes, J.P.; Stagira, S.; et al. Controlling attosecond electron dynamics by phase-stabilized polarization gating. Nat. Phys. 2006, 2, 319–322. [Google Scholar] [CrossRef]
- Sansone, G.; Benedetti, E.; Calegari, F.; Vozzi, C.; Avaldi, L.; Flammini, R.; Poletto, L.; Villoresi, P.; Altucci, C.; Velotta, R.; et al. Isolated Single-Cycle Attosecond Pulses. Science 2006, 314, 443–446. [Google Scholar] [CrossRef] [PubMed]
- Tzallas, P.; Skantzakis, E.; Kalpouzos, C.; Benis, E.P.; Tsakiris, G.D.; Charalambidis, D. Generation of intense continuum extreme-ultraviolet radiation by many-cycle laser fields. Nat. Phys. 2007, 3, 846–850. [Google Scholar] [CrossRef]
- Abel, M.J.; Pfeifer, T.; Nagel, P.M.; Boutu, W.; Bell, M.J.; Steiner, C.P.; Neumark, D.M.; Leone, S.R. Isolated attosecond pulses from ionization gating of high-harmonic emission. Chem. Phys. 2009, 366, 9–14. [Google Scholar] [CrossRef]
- Ferrari, F.; Calegari, F.; Lucchini, M.; Vozzi, C.; Stagira, S.; Sansone, G.; Nisoli, M. High-energy isolated attosecond pulses generated by above-saturation few-cycle fields. Nat. Photonics 2010, 4, 875–879. [Google Scholar] [CrossRef]
- Wheeler, J.A.; Borot, A.; Monchocé, S.; Vincenti, H.; Ricci, A.; Malvache, A.; Lopez-Martens, R.; Quéré, F. Attosecond lighthouses from plasma mirrors. Nat. Photonics 2012, 6, 829–833. [Google Scholar] [CrossRef]
- Kim, K.T.; Zhang, C.; Ruchon, T.; Hergott, J.F.; Auguste, T.; Villeneuve, D.M.; Corkum, P.B.; Quéré, F. Photonic streaking of attosecond pulse trains. Nat. Photonics 2013, 7, 651–656. [Google Scholar] [CrossRef]
- Quéré, F.; Vincenti, H.; Borot, A.; Monchocé, S.; Hammond, T.J.; Kim, K.T.; Wheeler, J.A.; Zhang, C.; Ruchon, T.; Auguste, T. Applications of ultrafast wavefront rotation in highly nonlinear optics. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 124004. [Google Scholar] [CrossRef]
- Feng, X.; Gilbertson, S.; Mashiko, H.; Wang, H.; Khan, S.D.; Chini, M.; Wu, Y.; Zhao, K.; Chang, Z. Generation of Isolated Attosecond Pulses with 20 to 28 Femtosecond Lasers. Phys. Rev. Lett. 2009, 103, 183901. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, E.J.; Lan, P.; Mücke, O.D.; Nabekawa, Y.; Midorikawa, K. Infrared Two-Color Multicycle Laser Field Synthesis for Generating an Intense Attosecond Pulse. Phys. Rev. Lett. 2010, 104, 233901. [Google Scholar] [CrossRef] [PubMed]
- Kolliopoulos, G.; Carpeggiani, P.A.; Rompotis, D.; Charalambidis, D.; Tzallas, P. A compact collinear polarization gating scheme for many cycle laser pulses. Rev. Sci. Instr. 2012, 83, 063102. [Google Scholar] [CrossRef] [PubMed]
- Haessler, S.; Balciunas, T.; Fan, G.; Chipperfield, L.E.; Baltuska, A. Enhanced multi-colour gating for the generation of high-power isolated attosecond pulses. Sci. Rep. 2015, 5, 10084. [Google Scholar] [CrossRef] [PubMed]
- Shiner, A.D.; Trallero-Herrero, C.; Kajumba, N.; Bandulet, H.-C.; Comtois, D.; Légaré, F.; Giguère, M.; Kieffer, J.C.; Corkum, P.B.; Villeneuve, D.M. Wavelength Scaling of High Harmonic Generation Efficiency. Phys. Rev. Lett. 2009, 103, 073902. [Google Scholar] [CrossRef] [PubMed]
- L’Huillier, A.; Li, X.F.; Lompré, L.A. Propagation effects in high-order harmonic gene-ration in rare gases. J. Opt. Soc. Am. B 1990, 7, 527–536. [Google Scholar] [CrossRef]
- Priori, E.; Cerullo, G.; Nisoli, M.; Stagira, S.; De Silvestri, S.; Villoresi, P.; Poletto, L.; Ceccherini, P.; Altucci, C.; Bruzzese, R.; et al. Nonadiabatic three-dimensional model of high-order harmonic generation in the few-optical-cycle regime. Phys. Rev. A 2000, 61, 063801. [Google Scholar] [CrossRef]
- Jin, C.; Le, A.T.; Lin, C.D. Medium propagation effects in high-order harmonic generation of Ar and N2. Phys. Rev. A 2011, 83, 023411. [Google Scholar] [CrossRef]
- Seres, J.; Yakovlev, V.S.; Seres, E.; Streli, C.; Wobrauschek, P.; Spielmann, C.; Krausz, F. Coherent superposition of laser-driven soft-X-ray harmonics from successive sources. Nat. Phys. 2007, 3, 878–883. [Google Scholar] [CrossRef]
- Popmintchev, T.; Chen, M.-C.; Popmintchev, D.; Arpin, P.; Brown, S.; Ališauskas, S.; Andriukaitis, G.; Balčiunas, T.; Mücke, O.D.; Pugzlys, A.; et al. Bright Coherent Ultrahigh Harmonicsin the keV X-ray Regime from Mid-Infrared Femtosecond Lasers. Science 2012, 336, 1287–1291. [Google Scholar] [CrossRef] [PubMed]
- Teichmann, S.M.; Silva, F.; Cousin, S.L.; Hemmer, M.; Biegert, J. 0.5-keV Soft X-ray attosecond continua. Nat. Commun. 2016, 7, 11493. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Zhang, Q.; Chini, M.; Wu, Y.; Wang, X.; Chang, Z. Tailoring a 67 attosecond pulse through advantageous phase-mismatch. Opt. Lett. 2012, 37, 3891–3893. [Google Scholar] [CrossRef] [PubMed]
- Leblanc, A.; Denoeud, A.; Chopineau, L.; Mennerat, G.; Martin, P.; Quéré, F. Plasma holograms for ultrahigh-intensity optics. Nat. Phys. 2017. [Google Scholar] [CrossRef]
- Goulielmakis, E.; Schultze, M.; Hofstetter, M.; Yakovlev, V.S.; Gagnon, J.; Uiberacker, M.; Aquila, A.L.; Gullikson, E.M.; Attwood, D.T.; Kienberger, R.; et al. Single-Cycle Nonlinear Optics. Science 2008, 320, 1614–1617. [Google Scholar] [CrossRef] [PubMed]
- Vincenti, H.; Monchocé, S.; Kahaly, S.; Bonnaud, G.; Martin, P.; Quéré, F. Optical properties of relativistic plasma mirrors. Nat. Commun. 2014, 5, 3403. [Google Scholar] [CrossRef] [PubMed]
- Monchocé, S.; Kahaly, S.; Leblanc, A.; Videau, L.; Combis, P.; Réau, F.; Garzella, D.; D’Oliveira, P.; Martin, P.; Quéré, F. Optically Controlled Solid-Density Transient Plasma Gratings. Phys. Rev. Lett. 2014, 112, 145008. [Google Scholar] [CrossRef] [PubMed]
- Leblanc, A.; Monchocé, S.; Bourassin-Bouchet, C.; Kahaly, S.; Quéré, F. Ptychographic measurements of ultrahigh-intensity laser–plasma interactions. Nat. Phys. 2016, 12, 301. [Google Scholar] [CrossRef]
- Tsakiris, G.D.; Eidmann, K.; Meyer-ter-Vehn, J.; Krausz, F. Route to intense single attosecond pulses. New J. Phys. 2006, 8, 19. [Google Scholar] [CrossRef]
- Heissler, P.; Hörlein, R.; Mikhailova, J.M.; Waldecker, L.; Tzallas, P.; Buck, A.; Schmid, K.; Sears, C.M.S.; Krausz, F.; Veisz, L.; et al. Few-Cycle Driven Relativistically Oscillating Plasma Mirrors: A Source of Intense Isolated Attosecond Pulses. Phys. Rev. Lett. 2012, 108, 235003. [Google Scholar] [CrossRef] [PubMed]
- Dromey, B.; Zepf, M.; Gopal, A.; Lancaster, K.; Wei, M.S.; Krushelnick, K.; Tatarakis, M.; Vakakis, N.; Moustaizis, S.; Kodama, R.; et al. High harmonic generation in the relativistic limit. Nat. Phys. 2006, 2, 456–459. [Google Scholar] [CrossRef]
- Danson, C.N.; Brummitt, P.A.; Clarke, R.J.; Collier, J.L.; Fell, B.; Frackiewicz, A.J.; Hancock, S.; Hawkes, S.; Hernandez-Gomez, C.; Holligan, P.; et al. Vulcan Petawatt—An ultra-high-intensity interaction facility. Nucl. Fusion 2004, 44, S239. [Google Scholar] [CrossRef]
- Borot, A.; Malvache, A.; Chen, X.; Jullien, A.; Geindre, J.-P.; Audebert, P.; Mourou, G.; Quéré, F.; Lopez-Martens, R. Attosecond control of collective electron motion in plasmas. Nat. Phys. 2012, 8, 416–421. [Google Scholar] [CrossRef]
- Heissler, P.; Tzallas, P.; Mikhailova, J.M.; Khrennikov, K.; Waldecker, L.; Krausz, F.; Karsch, S.; Charalambidis, D.; Tsakiris, G.D. Two-photon above-threshold ionization using extreme-ultraviolet harmonic emission from relativistic laser–plasma interaction. New J. Phys. 2012, 14, 043025. [Google Scholar] [CrossRef]
- Ammosov, M.V.; Delone, N.B.; Krainov, V.P. Tunnel ionization of complex atoms and of atomic ions in an alternating electromagnetic field. Sov. Phys. JETP 1986, 64, 1191. [Google Scholar]
- Perelomov, A.M.; Popov, V.S.; Terent’ev, M.V. Ionization of atoms in an alternating electric field. Sov. Phys. JETP 1966, 23, 924. [Google Scholar]
- Zaïr, A.; Holler, M.; Guandalini, A.; Schapper, F.; Biegert, J.; Gallmann, L.; Keller, U.; Wyatt, A.S.; Monmayrant, A.; Walmsley, I.A.; et al. Quantum Path Interferences in High-Order Harmonic Generation. Phys. Rev. Lett. 2008, 100, 143902. [Google Scholar] [CrossRef] [PubMed]
- Corsi, C.; Pirri, A.; Sali, E.; Tortora, A.; Bellini, M. Direct interferometric measurement of the atomic dipole phase in high-order harmonic generation. Phys. Rev. Lett. 2006, 97, 023901. [Google Scholar] [CrossRef] [PubMed]
- Kruse, J.E.; Tzallas, P.; Skantzakis, E.; Kalpouzos, C.; Tsakiris, G.D.; Charalambidis, D. Inconsistencies between two attosecond pulse metrology methods: A comparative study. Phys. Rev. A 2010, 82, 021402. [Google Scholar] [CrossRef]
- Kolliopoulos, G.; Bergues, B.; Schröder, H.; Carpeggiani, P.A.; Veisz, L.; Tsakiris, G.D.; Charalambidis, D.; Tzallas, P. Revealing quantum path details in high-field physics. Phys. Rev. A 2014, 90, 013822. [Google Scholar] [CrossRef]
- Heyl, C.M.; Coudert-Alteirac, H.; Miranda, M.; Louisy, M.; Kovacs, K.; Tosa, V.; Balogh, E.; Varjú, K.; L’Huillier, A.; Couairon, A.; et al. Scale-invariant nonlinear optics in gases. Optica 2016, 3, 75–81. [Google Scholar] [CrossRef]
- Varjú, K.; Mairesse, Y.; Carré, B.; Gaarde, B.M.; Johnsson, P.; Kazamias, S.; López-Martens, R.; Mauritsson, J.; Schafer, K.J.; Balcou, P.; et al. Frequency chirp of harmonic and attosecond pulses. J. Mod. Opt. 2004, 52, 379–394. [Google Scholar] [CrossRef]
- Antoine, P.; L’huillier, A.; Lewenstein, M. Attosecond pulse trains using high–order harmonics. Phys. Rev. Lett. 1996, 77, 1234. [Google Scholar] [CrossRef] [PubMed]
- Balcou, P.; Salieres, P.; L’Huillier, A.; Lewenstein, M. Generalized phase-matching conditions for high harmonics: The role of field-gradient forces. Phys. Rev. A 1997, 55, 3204. [Google Scholar] [CrossRef]
- Bellini, M.; Lyngå, C.; Tozzi, A.; Gaarde, M.B.; Hänsch, T.W.; L’Huillier, A.; Wahlström, C.G. Temporal coherence of ultrashort high-order harmonic pulses. Phys. Rev. Lett. 1998, 81, 297. [Google Scholar] [CrossRef]
- Gaarde, M.B.; Schafer, K.J. Space-time considerations in the phase locking of high harmonics. Phys. Rev. Lett. 2002, 89, 213901. [Google Scholar] [CrossRef] [PubMed]
- Brugnera, L.; Hoffmann, D.J.; Siegel, T.; Frank, F.; Zaïr, A.; Tisch, J.W.; Marangos, J.P. Trajectory selection in high harmonic generation by controlling the phase between orthogonal two-color fields. Phys. Rev. Lett. 2011, 107, 153902. [Google Scholar] [CrossRef] [PubMed]
- Hutchison, C.; Houver, S.; Lin, N.; Hoffmann, D.J.; McGrath, F.; Siegel, T.; Marangos, J.P. Electron trajectory control of odd and even order harmonics in high harmonic generation using an orthogonally polarised second harmonic field. J. Mod. Opt. 2014, 61, 608. [Google Scholar] [CrossRef]
- Mashiko, H.; Gilbertson, S.; Li, C.; Khan, S.D.; Shakya, M.M.; Moon, E.; Chang, Z. Double Optical Gating of High-Order Harmonic Generation with Carrier-Envelope Phase Stabilized Lasers. Phys. Rev. Lett. 2008, 100, 103906. [Google Scholar] [CrossRef] [PubMed]
- Tzallas, P.; Skantzakis, E.; Charalambidis, D. Measuring the absolute carrier-envelope phase of many-cycle laser fields. Phys. Rev. A 2010, 82, 061401. [Google Scholar] [CrossRef]
- Tosa, V.; Kovacs, K.; Major, B.; Balogh, E.; Varju, K. Propagation effects in highly ionised gas media. Quantum Electron. 2016, 46, 321. [Google Scholar] [CrossRef]
- Tosa, V.; Kim, K.; Nam, C.H. Macroscopic generation of attosecond-pulse trains in strongly ionized media. Phys. Rev. A 2009, 79, 043828. [Google Scholar] [CrossRef]
- Schütte, B.; Weber, P.; Kovács, K.; Balogh, E.; Major, B.; Tosa, V.; Han, S.; Vrakking, M.J.J.; Varjú, K.; Rouzée, A. Bright attosecond soft X-ray pulse trains by transient phase-matching in two-color high-order harmonic generation. Opt. Express 2015, 23, 33947–33955. [Google Scholar] [CrossRef] [PubMed]
- Rudawski, P.; Heyl, C.M.; Brizuela, F.; Schwenke, J.; Persson, A.; Mansten, E.; Rakowski, R.; Rading, L.; Campi, F.; Kim, B.; et al. A high-flux high-order harmonic source. Rev. Sci. Instr. 2013, 84, 073103. [Google Scholar] [CrossRef] [PubMed]
- Dubrouil, A.; Hort, O.; Catoire, F.; Descamps, D.; Petit, S.; Mével, E.; Constant, E. Spatio–spectral structures in high-order harmonic beams generated with Terawatt 10-fs pulses. Nat. Commun. 2014, 5, 4637. [Google Scholar] [CrossRef] [PubMed]
- Popmintchev, T.; Chen, M.-C.; Arpin, P.; Murnane, M.M.; Kapteyn, H.C. The attosecond nonlinear optics of bright coherent X-ray generation. Nat. Photonics 2010, 4, 822–832. [Google Scholar] [CrossRef]
- Balogh, E.; Varjú, K. Field strength scaling in quasi-phase-matching of high-order harmonic generation by low-intensity assisting fields. J. Opt. Soc. Am. B 2016, 33, 230–238. [Google Scholar] [CrossRef]
- Hörlein, R.; Nomura, Y.; Tzallas, P.; Rykovanov, S.G.; Dromey, B.; Osterhoff, J.; Major, Z.; Karsch, S.; Veisz, L.; Zepf, M.; et al. Temporal characterization of attosecond pulses emitted from solid-density plasmas. New J. Phys. 2010, 12, 043020. [Google Scholar] [CrossRef]
- Tarasevitch, A.; Orisch, A.; von der Linde, D.; Balcou, P.; Rey, G.; Chambaret, J.P.; Teubner, U.; Klöpfel, D.; Theobald, W. Generation of high-order spatially coherent harmonics from solid targets by femtosecond laser pulses. Phys. Rev. A 2000, 62, 023816. [Google Scholar] [CrossRef]
- Kahaly, S.; Monchocé, S.; Vincenti, H.; Dzelzainis, T.; Dromey, B.; Zepf, M.; Martin, P.; Quéré, F. Direct Observation of Density-Gradient Effects in Harmonic Generation from Plasma Mirrors. Phys. Rev. Lett. 2013, 110, 175001. [Google Scholar] [CrossRef] [PubMed]
- Ma, G.; Dallari, W.; Borot, A.; Krausz, F.; Yu, W.; Tsakiris, G.D.; Veisz, L. Intense isolated attosecond pulse generation from relativistic laser plasmas using few-cycle laser pulses. Phys. Plasmas 2016, 22, 033105. [Google Scholar] [CrossRef]
- An der Brügge, D.; Kumar, N.; Pukhov, A.; Rödel, C. Influence of Surface Waves on Plasma High-Order Harmonic Generation. Phys. Rev. Lett. 2012, 108, 125002. [Google Scholar] [CrossRef] [PubMed]
- Dromey, B.; Rykovanov, S.; Yeung, M.; Hörlein, R.; Jung, D.; Gautier, D.C.; Dzelzainis, T.; Kiefer, D.; Palaniyppan, S.; Shah, R.; et al. Coherent synchrotron emission from electron nanobunches formed in relativistic laser–plasma interactions. Nat. Phys. 2012, 8, 804–808. [Google Scholar] [CrossRef]
- Mikhailova, J.M.; Fedorov, M.V.; Karpowicz, N.; Gibbon, P.; Platonenko, V.T.; Zheltikov, A.M.; Krausz, F. Isolated Attosecond Pulses from Laser-Driven Synchrotron Radiation. Phys. Rev. Lett. 2012, 109, 245005. [Google Scholar] [CrossRef] [PubMed]
- Dromey, B.; Cousens, S.; Rykovanov, S.; Yeung, M.; Jung, D.; Gautier, D.C.; Dzelzainis, T.; Kiefer, D.; Palaniyppan, S.; Shah, R.; et al. Coherent synchrotron emission in transmission from ultrathin relativistic laser plasmas. New J. Phys. 2013, 15, 015025. [Google Scholar] [CrossRef]
- Cousens, S.; Reville, B.; Dromey, B.; Zepf, M. Temporal Structure of Attosecond Pulses from Laser-Driven Coherent Synchrotron Emission. Phys. Rev. Lett. 2016, 116, 083901. [Google Scholar] [CrossRef] [PubMed]
- Yeung, M.; Rykovanov, S.; Bierbach, J.; Li, L.; Eckner, E.; Kuschel, S.; Woldegeorgis, A.; Rödel, C.; Sävert, A.; Paulus, G.G.; et al. Experimental observation of attosecond control over relativistic electron bunches with two-colour fields. Nat. Photonics 2017, 11, 32–35. [Google Scholar] [CrossRef]
- Teubner, U.; Eidmann, K.; Wagner, U.; Andiel, U.; Pisani, F.; Tsakiris, G.D.; Witte, K.; Meyer-ter-Vehn, J.; Schlegel, T.; Förster, E. Harmonic Emission from the Rear Side of Thin Overdense Foils Irradiated with Intense Ultrashort Laser Pulses. Phys. Rev. Lett. 2004, 92, 185001. [Google Scholar] [CrossRef] [PubMed]
- Brunel, F. Not-so-resonant, resonant absorption. Phys. Rev. Lett. 1987, 59, 52. [Google Scholar] [CrossRef] [PubMed]
- Hinkel-Lipsker, D.E.; Fried, B.D.; Morales, G.J. Analytic expression for mode conversion of Langmuir and electromagnetic waves. Phys. Rev. Lett. 1989, 62, 2680. [Google Scholar] [CrossRef] [PubMed]
- Bulanov, S.V.; Naumova, N.M.; Pegoraro, F. Interaction of an ultrashort, relativistically strong laser pulse with an overdense plasma. Phys. Plasmas 1994, 1, 745–757. [Google Scholar] [CrossRef]
- Gordienko, S.; Pukhov, A.; Shorokhov, O.; Baeva, T. Relativistic Doppler Effect: Universal Spectra and Zeptosecond Pulses. Phys. Rev. Lett. 2004, 93, 115002. [Google Scholar] [CrossRef] [PubMed]
- Baeva, T.; Gordienko, S.; Pukhov, A. Relativistic plasma control for single attosecond x-ray burst generation. Phys. Rev. E 2006, 74, 065401. [Google Scholar] [CrossRef] [PubMed]
- Baeva, T.; Gordienko, S.; Pukhov, A. Relativistic plasma control for single attosecond pulse generation: Theory, simulations, and structure of the pulse. Laser Part. Beams 2007, 25, 339. [Google Scholar] [CrossRef]
- Dromey, B.; Kar, S.; Bellei, C.; Carroll, D.C.; Clarke, R.J.; Green, J.S.; Kneip, S.; Markey, K.; Nagel, S.R.; Simpson, P.T.; et al. Bright Multi-keV Harmonic Generation from Relativistically Oscillating Plasma Surfaces. Phys. Rev. Lett. 2007, 99, 085001. [Google Scholar] [CrossRef] [PubMed]
- Gonoskov, A.A.; Korzhimanov, A.V.; Kim, A.V.; Marklund, M.; Sergeev, A.M. Ultrarelativistic nanoplasmonics as a route towards extreme-intensity attosecond pulses. Phys. Rev. E 2011, 84, 046403. [Google Scholar] [CrossRef] [PubMed]
- Debayle, A.; Sanz, J.; Gremillet, L. Self-consistent theory of high-order harmonic generation by relativistic plasma mirror. Phys. Rev. E 2015, 92, 053108. [Google Scholar] [CrossRef] [PubMed]
- Zepf, M.; Tsakiris, G.D.; Pretzler, G.; Watts, I.; Chambers, D.M.; Norreys, P.A.; Andiel, U.; Dangor, A.E.; Eidmann, K.; Gahn, C.; et al. Role of the plasma scale length in the harmonic generation from solid targets. Phys. Rev. E 1998, 58, 5253. [Google Scholar] [CrossRef]
- Watts, I.; Zepf, M.; Clark, E.L.; Tatarakis, M.; Krushelnick, K.; Dangor, A.E.; Allott, R.M.; Clarke, R.J.; Neely, D.; Norreys, P.A. Dynamics of the Critical Surface in High-Intensity Laser-Solid Interactions: Modulation of the XUV Harmonic Spectra. Phys. Rev. Lett. 2002, 88, 155001. [Google Scholar] [CrossRef] [PubMed]
- Teubner, U.; Pretzler, G.; Schlegel, T.; Eidmann, K.; Förster, E.; Witte, K. Anomalies in high-order harmonic generation at relativistic intensities. Phys. Rev. A 2003, 67, 013816. [Google Scholar] [CrossRef]
- Rykovanov, S.G.; Geissler, M.; Meyer-ter-Vehn, J.; Tsakiris, G.D. Intense single attosecond pulses from surface harmonics using the polarization gating technique. New J. Phys. 2008, 10, 025025. [Google Scholar] [CrossRef]
- Rykovanov, S.G.; Ruhl, H.; Meyer-ter-Vehn, J.; Hörlein, R.; Dromey, B.; Zepf, M.; Tsakiris, G.D. Plasma surface dynamics and smoothing in the relativistic few-cycle regime. New J. Phys. 2011, 13, 023008. [Google Scholar] [CrossRef]
- Vincenti, H.; Quéré, F. Attosecond lighthouses: How to use spatiotemporally coupled light fields to generate isolated attosecond pulses. Phys. Rev. Lett. 2012, 108, 113904. [Google Scholar] [CrossRef] [PubMed]
- Akturk, S.; Gu, X.; Gabolde, P.; Trebino, R. The general theory of first-order spatio-temporal distortions of Gaussian pulses and beams. Opt. Express 2005, 13, 8642–8661. [Google Scholar] [CrossRef] [PubMed]
- Hammond, T.J.; Brown, G.G.; Kim, K.T.; Villeneuve, D.M.; Corkum, P.B. Attosecond pulses measured from the attosecond lighthouse. Nat. Photonics 2016, 10, 171. [Google Scholar] [CrossRef]
- Mairesse, Y.; de Bohan, A.; Frasinski, L.J.; Merdji, H.; Dinu, L.C.; Monchicourt, P.; Breger, P.; Kovacev, M.; Taïeb, R.; Carré, B.; et al. Attosecond synchronization of high-harmonic soft x-rays. Science 2003, 302, 1540–1543. [Google Scholar] [CrossRef] [PubMed]
- Paulus, G.G.; Grasbon, F.; Walther, H.; Villoresi, P.; Nisoli, M.; Stagira, S.; Priori, E.; De Silvestri, S. Absolute-phase phenomena in photoionization with few-cycle laser pulses. Nature 2001, 414, 182–184. [Google Scholar] [CrossRef] [PubMed]
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Auge, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a train of attosecond pulses from high harmonic generation. Science 2001, 292, 1689–1692. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, E.J.; Hasegawa, H.; Nabekawa, Y.; Midorikawa, K. High-throughput, high-damage-threshold broadband beam splitter for high-order harmonics in the extreme-ultraviolet region. Opt. Lett. 2004, 29, 507–509. [Google Scholar] [CrossRef] [PubMed]
- Nagata, Y.; Nabekawa, Y.; Midorikawa, K. Development of High-Throughput, High-Damage-Threshold Beam Separator for 13 nm High-Order Harmonics. Opt. Lett. 2006, 31, 1316–1318. [Google Scholar] [CrossRef] [PubMed]
- Wolter, H. Spiegelsysteme streifenden Einfalls als abbildende Optiken für Röntgenstrahlen. Ann. Phys. 1952, 445, 94–114. [Google Scholar] [CrossRef]
- Tsatrafyllis, N.; Bergues, B.; Schröder, H.; Veisz, L.; Skantzakis, E.; Gray, D.; Bodi, B.; Kuhn, S.; Tsakiris, G.D.; Charalambidis, D.; et al. The ion microscope as a tool for quantitative measurements in the extreme ultraviolet. Sci. Rep. 2016, 6, 21556. [Google Scholar] [CrossRef] [PubMed]
- Goulielmakis, E.; Yakovlev, V.S.; Cavalieri, A.L.; Uiberacker, M.; Pervak, V.; Apolonski, A.; Kienberger, R.; Kleineberg, U.; Krausz, F. Attosecond Control and Measurement: Lightwave Electronics. Science 2007, 317, 769–775. [Google Scholar] [CrossRef] [PubMed]
- Frank, F.; Arrell, C.; Witting, T.; Okell, W.A.; McKenna, J.; Robinson, J.S.; Haworth, C.A.; Austin, D.; Teng, H.; Walmsley, I.A.; et al. Invited Review Article: Technology for Attosecond Science. Rev. Sci. Instrum. 2012, 83, 071101. [Google Scholar] [CrossRef] [PubMed]
- Frassetto, F.; Trabattoni, A.; Anumula, S.; Sansone, G.; Calegari, F.; Nisoli, M.; Poletto, L. High-throughput beamline for attosecond pulses based on toroidal mirrors with microfocusing capabilities. Rev. Sci. Instrum. 2014, 85, 103115. [Google Scholar] [CrossRef] [PubMed]
- Locher, R.; Lucchini, M.; Herrmann, J.; Sabbar, M.; Weger, M.; Ludwig, A.; Castiglioni, L.; Greif, M.; Hengsberger, M.; Gallmann, L.; et al. Versatile attosecond beamline in a two-foci configuration for simultaneous time-resolved measurements. Rev. Sci. Instrum. 2014, 85, 013113. [Google Scholar] [CrossRef] [PubMed]
- Schultze, M.; Bergues, B.; Schröder, H.; Krausz, F.; Kompa, K.L. Spatially resolved measurement of ionization yields in the focus of an intense laser pulse. New J. Phys. 2011, 13, 033001. [Google Scholar] [CrossRef]
- Tzallas, P.; Skantzakis, E.; Charalambidis, D. Direct two-XUV-photon double ionization in xenon. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 074007. [Google Scholar] [CrossRef]
- Skantzakis, E.; Tzallas, P.; Kruse, j.E.; Kalpouzos, C.; Faucher, O.; Tsakiris, G.D.; Charalambidis, D. Tracking Autoionizing-Wave-Packet Dynamics at the 1-fs Temporal Scale. Phys. Rev. Lett. 2010, 105, 043902. [Google Scholar] [CrossRef] [PubMed]
- Carpeggiani, P.A.; Tzallas, P.; Palacios, A.; Gray, D.; Martín, F.; Charalambidis, D. Disclosing intrinsic molecular dynamics on the 1-fs scale through extreme-ultraviolet pump-probe measurements. Phys. Rev. A 2014, 89, 023420. [Google Scholar] [CrossRef]
- Nabekawa, Y.; Shimizu, T.; Okino, T.; Furusawa, K.; Hasegawa, H.; Yamanouchi, K.; Midorikawa, K. Conclusive Evidence of an Attosecond Pulse Train Observed with the Mode-Resolved Autocorrelation Technique. Phys. Rev. Lett. 2006, 96, 083901. [Google Scholar] [CrossRef] [PubMed]
- Drescher, M.; Hentschel, M.; Kienberger, R.; Tempea, G.; Spielmann, C.; Reider, G.A.; Corkum, P.B.; Krausz, F. X-ray Pulses Approaching the Attosecond Frontier. Science 2001, 291, 1923–1927. [Google Scholar] [CrossRef] [PubMed]
- Mairesse, Y.; Quéré, F. Frequency-resolved optical gating for complete reconstruction of attosecond bursts. Phys. Rev. A 2005, 71, 011401. [Google Scholar] [CrossRef]
- Chini, M.; Gilbertson, S.; Khan, S.D.; Chang, Z. Characterizing ultrabroadband attosecond lasers. Opt. Express 2010, 18, 13006–13016. [Google Scholar] [CrossRef] [PubMed]
- Keathley, P.D.; Bhardwaj, S.; Mose, J.; Kärtner, F.X. Volkov transform generalized projection algorithm for attosecond pulse characterization. New J. Phys. 2016, 18, 073009. [Google Scholar] [CrossRef]
- Grguraš, I.; Maier, A.R.; Behrens, C.; Mazza, T.; Kelly, T.J.; Radcliffe, P.; Düsterer, S.; Kazansky, A.K.; Kabachnik, N.M.; Tschentscher, T.; et al. Ultrafast X-ray pulse characterization at free-electron lasers. Nat. Photonics 2012, 6, 852–857. [Google Scholar] [CrossRef]
- Mairesse, Y.; Gobert, O.; Breger, P.; Merdji, H.; Meynadier, P.; Monchicourt, P.; Perdrix, M.; Salières, P.; Carré, B. High harmonic XUV spectral phase interferometry for direct electric-field reconstruction. Phys. Rev. Lett. 2005, 94, 173903. [Google Scholar] [CrossRef] [PubMed]
- Cormier, E.; Walmsley, I.A.; Kosik, E.M.; Wyatt, A.S.; Corner, L.; DiMauro, L.F. Self-Referencing, Spectrally, or Spatially Encoded Spectral Interferometry for the Complete Characterization of Attosecond Electromagnetic Pulses. Phys. Rev. Lett. 2005, 94, 033905. [Google Scholar] [CrossRef] [PubMed]
- Dudovich, N.; Smirnova, O.; Levesque, J.; Mairesse, Y.; Ivanov, M.Y.; Villeneuve, D.M.; Corkum, P.B. Measuring and controlling the birth of attosecond XUV pulses. Nat. Phys. 2006, 2, 781–786. [Google Scholar] [CrossRef]
- Cattaneo, L.; Vos, J.; Lucchini, M.; Gallmann, L.; Cirelli, C.; Keller, U. Comparison of attosecond streaking and RABBITT. Opt. Express 2016, 24, 29060–29076. [Google Scholar] [CrossRef] [PubMed]
- Tzallas, P.; Charalambidis, D.; Papadogiannis, N.A.; Witte, K.; Tsakiris, G.D. Second-order autocorrelation measurements of attosecond XUV pulse trains. J. Mod. Opt. 2005, 52, 321–338. [Google Scholar] [CrossRef]
- Nikolopoulos, L.A.A.; Benis, E.P.; Tzallas, P.; Charalambidis, D.; Witte, K.; Tsakiris, G.D. Second order autocorrelation of an XUV attosecond pulse train. Phys. Rev. Lett. 2005, 94, 113905. [Google Scholar] [CrossRef] [PubMed]
- Trebino, R.; Kane, D.J. Using phase retrieval to measure the intensity and phase of ultrashort pulses: Frequency-resolved optical gating. J. Opt. Soc. Am. A 1993, 10, 1101–1111. [Google Scholar] [CrossRef]
- Itatani, J.; Quéré, F.; Yudin, G.L.; Ivanov, M.Y.; Krausz, F.; Corkum, P.B. Attosecond streak camera. Phys. Rev. Lett. 2002, 88, 173903. [Google Scholar] [CrossRef] [PubMed]
- Kitzler, M.; Milosevic, N.; Scrinzi, A.; Krausz, F.; Brabec, T. Quantum theory of attosecond XUV pulse measurement by laser dressed photoionization. Phys. Rev. Lett. 2002, 88, 173904. [Google Scholar] [CrossRef] [PubMed]
- Kienberger, R.; Goulielmakis, E.; Uiberacker, M.; Baltuska, A.; Yakovlev, V.; Bammer, F.; Scrinzi, A.; Westerwalbesloh, T.; Kleinberg, U.; Heinzmann, U.; et al. Atomic transient recorder. Nature 2004, 427, 817–821. [Google Scholar] [CrossRef] [PubMed]
- Thaury, C.; Quéré, F. High-order harmonic and attosecond pulse generation on plasma mirrors: Basic mechanisms. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 213001. [Google Scholar] [CrossRef]
- Thévenet, M.; Leblanc, A.; Kahaly, S.; Vincenti, H.; Vernier, A.; Quéré, F.; Faure, J. Vacuum laser acceleration of relativistic electrons using plasma mirror injectors. Nat. Phys. 2016, 12, 355. [Google Scholar] [CrossRef]
- Bocoum, M.; Thévenet, M.; Böhle, F.; Beaurepaire, B.; Vernier, A.; Jullien, A.; Faure, J.; Lopez-Martens, R. Anticorrelated Emission of High Harmonics and Fast Electron Beams From Plasma Mirrors. Phys. Rev. Lett. 2016, 116, 185001. [Google Scholar] [CrossRef] [PubMed]
- Quéré, F.; Thaury, C.; George, H.; Geindre, J.-P.; Lefebvre, E.; Bonnaud, G.; Monot, P.; Martin, P. High-order harmonic generation using plasma mirrors. Plasma Phys. Control. Fusion 2008, 50, 124007. [Google Scholar] [CrossRef]
- Silva, F.; Teichmann, S.M.; Cousin, S.L.; Hemmer, M.; Biegert, J. Spatiotemporal isolation of attosecond soft X-ray pulses in the water window. Nat. Commun. 2015, 6, 6611. [Google Scholar] [CrossRef] [PubMed]
- Nabekawa, Y.; Furukawa, Y.; Okino, T.; Eilanlou, A.A.; Takahashi, E.J.; Yamanouchi, K.; Midorikawa, K. Sub-10-fs control of dissociation pathways in the hydrogen molecular ion with a few-pulse attosecond pulse train. Nat. Commun. 2016, 7, 12835. [Google Scholar] [CrossRef] [PubMed]
- Palacios, A.; González-Castrillo, A.; Martín, F. Molecular interferometer to decode attosecond electron–nuclear dynamics. PNAS 2014, 111, 3973–3978. [Google Scholar] [CrossRef] [PubMed]
- Kühn, S.; Dumergue, M.; Kahaly, S.; Mondal, S.; Füle, M.; Csizmadia, T.; Farkas, B.; Major, B.; Calegari, F.; Devetta, M.; et al. The ELI-ALPS facility: The next generation of attosecond sources. J. Phys. B At. Mol. Opt. Phys. 2017, in press. [Google Scholar]
- Dinu, L.C.; Muller, H.G.; Kazamias, S.; Mullot, G.; Augé, F.; Balcou, P.; Kovačev, M.; Breger, P.; Agostini, P. Measurement of the subcycle timing of attosecond XUV bursts in high-harmonic generation. Phys. Rev. Lett. 2003, 91, 063901. [Google Scholar] [CrossRef] [PubMed]
- Aseyev, S.A.; Ni, Y.; Frasinski, L.J.; Muller, H.G.; Vrakking, M.J.J. Attosecond angle-resolved photoelectron spectroscopy. Phys. Rev. Lett. 2003, 91, 223902. [Google Scholar] [CrossRef] [PubMed]
- Faucher, O.; Tzallas, P.; Benis, E.P.; Kruse, J.; Peralta Conde, A.; Kalpouzos, C.; Charalambidis, D. Four-dimensional investigation of the 2nd order volume autocorrelation technique. Appl. Phys. B 2009, 97, 505–510. [Google Scholar] [CrossRef]
- Nabekawa, Y.; Shimizu, T.; Okino, T.; Furusawa, K.; Hasegawa, H.; Yamanouchi, K.; Midorikawa, K. Interferometric autocorrelation of an attosecond pulse train in the single-cycle regime. Phys. Rev. Lett. 2006, 97, 153904. [Google Scholar] [CrossRef] [PubMed]
- Benis, E.P.; Tzallas, P.; Nikolopoulos, L.A.A.; Kovacev, M.; Kalpouzos, C.; Charalambidis, D.; Tsakiris, G.D. Frequency-resolved photoelectron spectra of two-photon ionization of He by an attosecond pulse train. New J. Phys. 2006, 9, 92. [Google Scholar] [CrossRef]
- Kolliopoulos, G.; Tzallas, P.; Bergues, B.; Carpeggiani, P.A.; Heissler, P.; Schröder, H.; Veisz, L.; Charalambidis, D.; Tsakiris, G.D. Single-shot autocorrelator for extreme-ultraviolet radiation. J. Opt. Soc. Am. B 2014, 31, 926–938. [Google Scholar] [CrossRef]
- Skantzakis, E.; Chatziathanasiou, S.; Carpeggiani, P.A.; Sansone, G.; Nayak, A.; Gray, D.; Tzallas, P.; Charalambidis, D.; Hertz, E.; Faucher, O. Polarization shaping of high order harmonics in laser-aligned molecules. Sci. Rep. 2016, 6, 39325. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatziathanasiou, S.; Kahaly, S.; Skantzakis, E.; Sansone, G.; Lopez-Martens, R.; Haessler, S.; Varju, K.; Tsakiris, G.D.; Charalambidis, D.; Tzallas, P. Generation of Attosecond Light Pulses from Gas and Solid State Media. Photonics 2017, 4, 26. https://doi.org/10.3390/photonics4020026
Chatziathanasiou S, Kahaly S, Skantzakis E, Sansone G, Lopez-Martens R, Haessler S, Varju K, Tsakiris GD, Charalambidis D, Tzallas P. Generation of Attosecond Light Pulses from Gas and Solid State Media. Photonics. 2017; 4(2):26. https://doi.org/10.3390/photonics4020026
Chicago/Turabian StyleChatziathanasiou, Stefanos, Subhendu Kahaly, Emmanouil Skantzakis, Giuseppe Sansone, Rodrigo Lopez-Martens, Stefan Haessler, Katalin Varju, George D. Tsakiris, Dimitris Charalambidis, and Paraskevas Tzallas. 2017. "Generation of Attosecond Light Pulses from Gas and Solid State Media" Photonics 4, no. 2: 26. https://doi.org/10.3390/photonics4020026
APA StyleChatziathanasiou, S., Kahaly, S., Skantzakis, E., Sansone, G., Lopez-Martens, R., Haessler, S., Varju, K., Tsakiris, G. D., Charalambidis, D., & Tzallas, P. (2017). Generation of Attosecond Light Pulses from Gas and Solid State Media. Photonics, 4(2), 26. https://doi.org/10.3390/photonics4020026




