1. Introduction
In recent years, there has been an increasing interest in the processing of quantum information (QIP) with continuous variables (CV-QIP) [
1]. CV-QIP protocols are based on Gaussian states as resources of entanglement. However, the use of non-Gaussian states has been shown to be essential in certain quantum protocols, like the entanglement distillation [
2,
3,
4,
5]. These states are obtained from Gaussian states through non-Gaussian operations, like the subtraction and addition of photons [
6]. This area of research has led to table-top ground-breaking demonstrations like the transition from classical to quantum states by photon addition [
7,
8], the generation of Schrödinger cat-like states via photon absorption [
9,
10], and the opening of new roads in quantum computation and communications [
11,
12].
However, it is unlikely that any eventual quantum-light-based mainstream technology will be built upon the current bulk optics-based optical circuits. Instead, this technology will be based on practical, low cost, interlinked and tunable components, as those which constitute fiber and integrated optics (IO) [
13]. In this regard, IO shows unique features for QIP as sub-wavelength stability, essential for quantum interference [
14]; great miniaturization, indispensable as the level of complexity of the circuit increases [
15]; and the optical properties of the waveguide substrates, which enable the generation of quantum states on-chip by means of their enhanced nonlinear features [
16,
17,
18], its manipulation by means of their thermo-, electro- and strain-optic properties [
19,
20,
21], and the integration of detectors in the circuit [
22,
23]. In this regard, the implementation of CV-QIP in IO is taking its first steps. Demonstrations of on-chip squeezing up to
dB in the pulsed wave (PW) regime and
dB in the continuous wave (CW) regime have been reported [
24,
25], as well as the first demonstration of CV entanglement on-chip has been recently presented [
26].
Likewise, the bits of quantum information can be encoded in many different degrees of freedom such as polarization, spatial mode, path, time, orbital angular momentum (OAM), and so on. Due to the continuous nature of the OAM, which gives access to an infinite dimensional Hilbert space, and its easy tailoring with light, the use of single-photon optical vortices for QIP have attracted great attention over the past decades [
27,
28]. These quantum states have an analog in the optical field-strength space: the quantum vortex states, originally proposed in [
29]. These are entangled, non-Gaussian and non-classical quantum states, as well as eigenstates of the
z component of the abstract angular momentum operator
, analogous with the quantum eigenstates of the spatial OAM operator, showing order and handedness, therefore with possibilities in DV- and CV-QIP [
30]. Other quantum vortices with different properties and symmetries have been also proposed, like the SU(2)-transformed Fock states [
31], the generalized quantum vortices [
32,
33,
34,
35], the Bessel-Gauss quantum vortex states [
36,
37] and the Hermite polynomial quantum vortices [
38].
Taking into account all of the above, our main motivation is to sketch a monolithic IO chip able to produce quantum vortex states of light by means of nonlinear waveguides, directional couplers (DC) and conditional measurement, as well as to introduce a measurement device which can detect their order and handedness. As we will show, a quantum vortex state would be heralded by the detection of a number of photons subtracted by a weakly coupled directional coupler from an entangled squeezed state propagating in a Mach-Zehnder interferometer. Furthermore, we present a realistic approach based on the Wigner function, where the propagation losses, the non-unity efficiency of the heralding detectors and the modal purity of the states are considered. In addition, a vorticity integrated detection system is introduced. We analyze the theoretical basis of this device and present a realistic model based on the inefficient operation of the number-resolving detectors. These devices together open the possibility of using the quantum optical vortices in QIP protocols.
The article is organized as follows:
Section 2 presents a scheme of the ideal generation of quantum vortices on-chip, studying their field-strength probability and phase distributions as well as their Wigner distribution on the phase space. A realistic model of the states produced with this scheme is presented in
Section 3. In
Section 4, a vortex–order and handedness measurement device is proposed, and its inefficient operation is studied. Finally, the main results of this article are summarized in
Section 5.
2. Device Operation
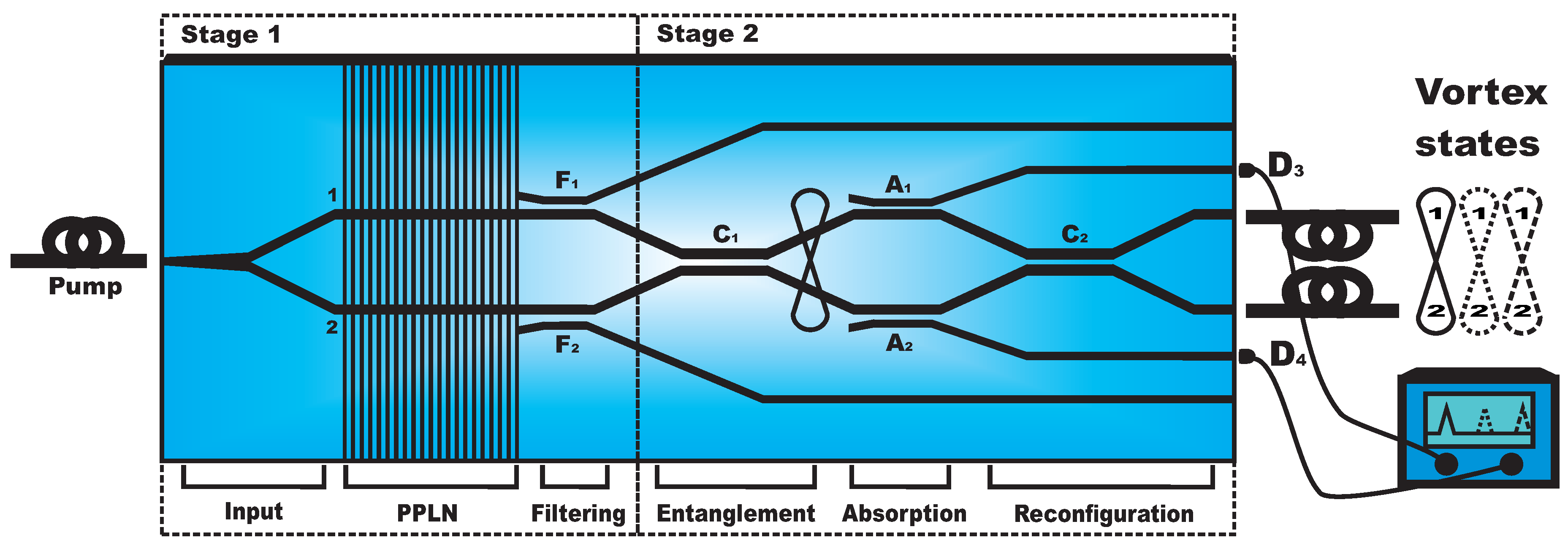
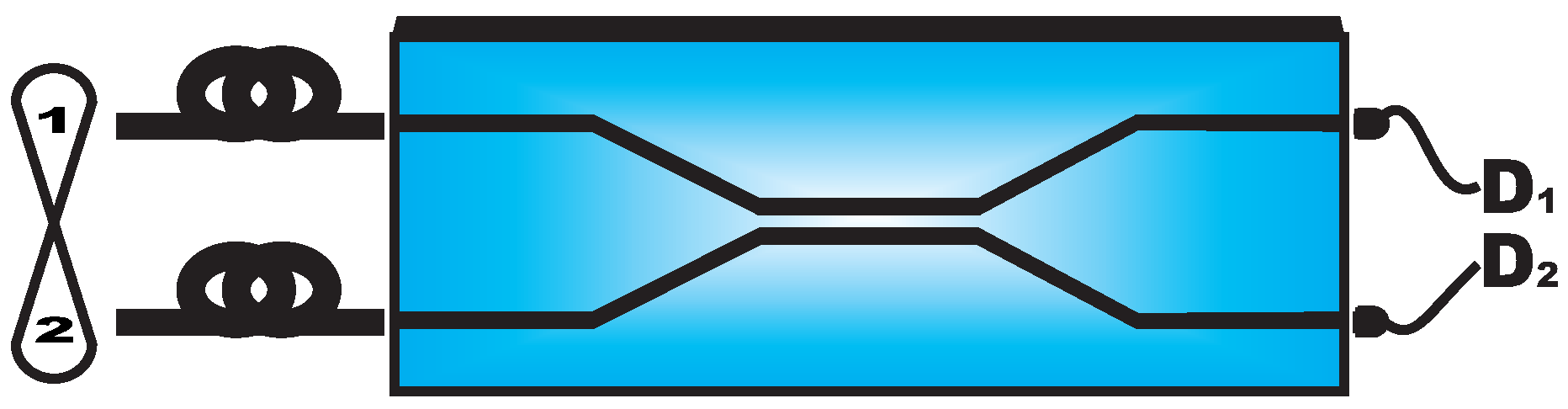
The proposed device is shown in
Figure 1. It is composed of two stages. The purpose of the first stage is to generate two single-mode squeezed states. Materials like lithium niobate (LN) or potassium titanyl phosphate (KTP) are suitable to be chosen as material substrate. We will focus on the first one due to its appealing properties related to the production of squeezed states on-chip, where large conversion efficiencies (≈10
photon pairs mW
·nm
·s
in the telecom C and L bands), broad bandwidths (BW) in the CW regime (≈10 THz), and transmission losses as low as
dB·cm
have been reported [
39].
The first stage is composed by an integrated taper, where a slow transition between single- and two-mode parts of the input waveguide is designed in order to maximize the coupling of an input coherent field to the following symmetric splitter. The power of the pump is halved, and these two pumps propagating within waveguides 1 and 2 cross two areas specially engineered in order to maximize the nonlinear effect of the substrate. A large conversion efficiency between the pump and the daughter fields is obtained by tailoring the nonlinearity of the material by periodically poling (PPLN), enabling quasi-phase matching of the propagation constants (QPM) [
40]. The period of the grating Λ is tailored such that
where
represents the propagation constants mismatch between a pump photon (p) and its daughter photons, labelled signal (s) and idler (i), caused by dispersion. Likewise, type-0 spontaneous parametric down conversion (SPDC) is chosen, coupling the interacting fields along the extraordinary axis of the crystal through the higher component of its second order nonlinear tensor,
[
39].
From the quantum field theory, it is known that the generator of the temporal evolution of the quantum states is the Hamiltonian operator
, while their spatial propagation is best described by the momentum operator
[
41,
42]. Therefore, the generation of quantum light in waveguides can be also described by this operator [
43,
44], which, in this case, is given by
with
and
;
is the vacuum permittivity;
the second order effective nonlinearity in the poling area, the integral is performed over the transverse area of the waveguide and the period of the waves, and
are the quantum optical fields given by
with
and
the absorption operators and the normalized transverse vector amplitudes related to each mode
, respectively. Setting the pump as a strong classical field and applying the above fields into Equation (
2), we obtain the following momentum corresponding to the waveguide
j
where we have considered QPM and conservation of energy, in such a way that the signal and idler waves are degenerated in frequency
), and where
κ is the nonlinear coupling constant, which depends on
, the pump intensity, the mode mismatch and the QPM. These momentum operators lead to two degenerated single-mode squeezed vacuum states given by
where
is the single-mode squeezing operator and
the squeezing parameter generated in a poling area of length
, which we have chosen to be real in order to simplify [
40].
Next, the pump is filtered by means of suitably designed wavelength dependent DCs (
and
in
Figure 1). Quantum-mechanically, a DC working at frequency
ω is given by
, or in matrix form by
with
,
the frequency-dependent coupling strength of a DC of length
, and
is the corresponding Pauli operator [
45].
stands for a DC with effective reflectivity
and transmittivity
. Since the DCs
and
are designed to filter the pumps, they fully reflect the pump (
) towards ancillary waveguides
l and transmit the squeezed vacua (
) through the signal waveguides
. These dispersive couplers have been experimentally demonstrated in SPDC on an LN chip showing a pump suppression of ≈30 dB [
17], and, recently, they have been proposed as new tools for quantum state control showing functionalities without equivalent in bulk optics [
46].
The second stage consists of a Mach-Zehnder interferometer made up of two 3 dB DCs at the signal frequency (
and
in
Figure 1) and two single-mode waveguides. These guides are also weakly coupled to two ancillary waveguides, in such a way that photons are leaked into them from the main modes.
The quantum state Equation (5) after the directional coupler
is transformed into the following Einstein-Podolsky-Rosen (EPR) state [
47]
where
stands for the two-mode squeezed operator. Then, the quantum state (
7) finds two weakly coupled DCs (
and
in
Figure 1), which couple the main waveguides with two ancillary ones (3 and 4). These directional couplers cause the following mixing of the modes
As input modes 3 and 4 are in the vacuum, using the disentangling theorem for the SU(2) group [
6], Equation (
8) can be written as
The measurement operator related to the subtraction of
n photons from the mode
j is given by [
48]
Considering high transmittivity (
or equally
) and moderate squeezing, the detection of
n photons in the mode 3 is given by
A similar result would be obtained detecting
n photons in the mode 4. It should be outlined that the measurement operator can be carried out by using photon number-resolving detectors (PNRDs) [
49]. In the case of using avalanche photodiodes (APDs), they do not distinguish between one or several photons impinging on it at the same time, so the "click" event projects the state into a statistical mixture. We will study that case in the following section. Moreover, bearing in mind that
, by using the two-mode squeezing Bogoliubov transformation
, Equation (
11) can be rewritten as
Finally, this quantum state finds the second 3 dB DC (
in
Figure 1) designed in such a way that it performs the unitary
. Hence, the detection of
n photons in the leaky modes would herald the following quantum state:
where we have used the similarity transformation
[
50] and the plus and minus signs appear after the detection of photons in the modes 3 and 4, respectively. This is a quantum vortex state
of order
n and ± handedness, or
[
29]. This family of states shows a high entanglement, as well as non-Gaussian and non-classical features as recently shown in [
30]. It should be noted that the probability of heralding a quantum vortex of order
n scales with
, so this scheme would be only practical in the production of low-order quantum vortices. On the other hand, the vorticity of these states is better visualized in the optical field-strength space, where
is the eigenvalue of the optical field-strength operator
, proportional to the first quadrature of the quantum optical field, and, analogously,
is related to the second quadrature [
51]. In this representation, the normalized wavefunction corresponding to the quantum state given by Equation (
13) is as follows:
where
are eigenstates of the optical field-strength fulfilling
.
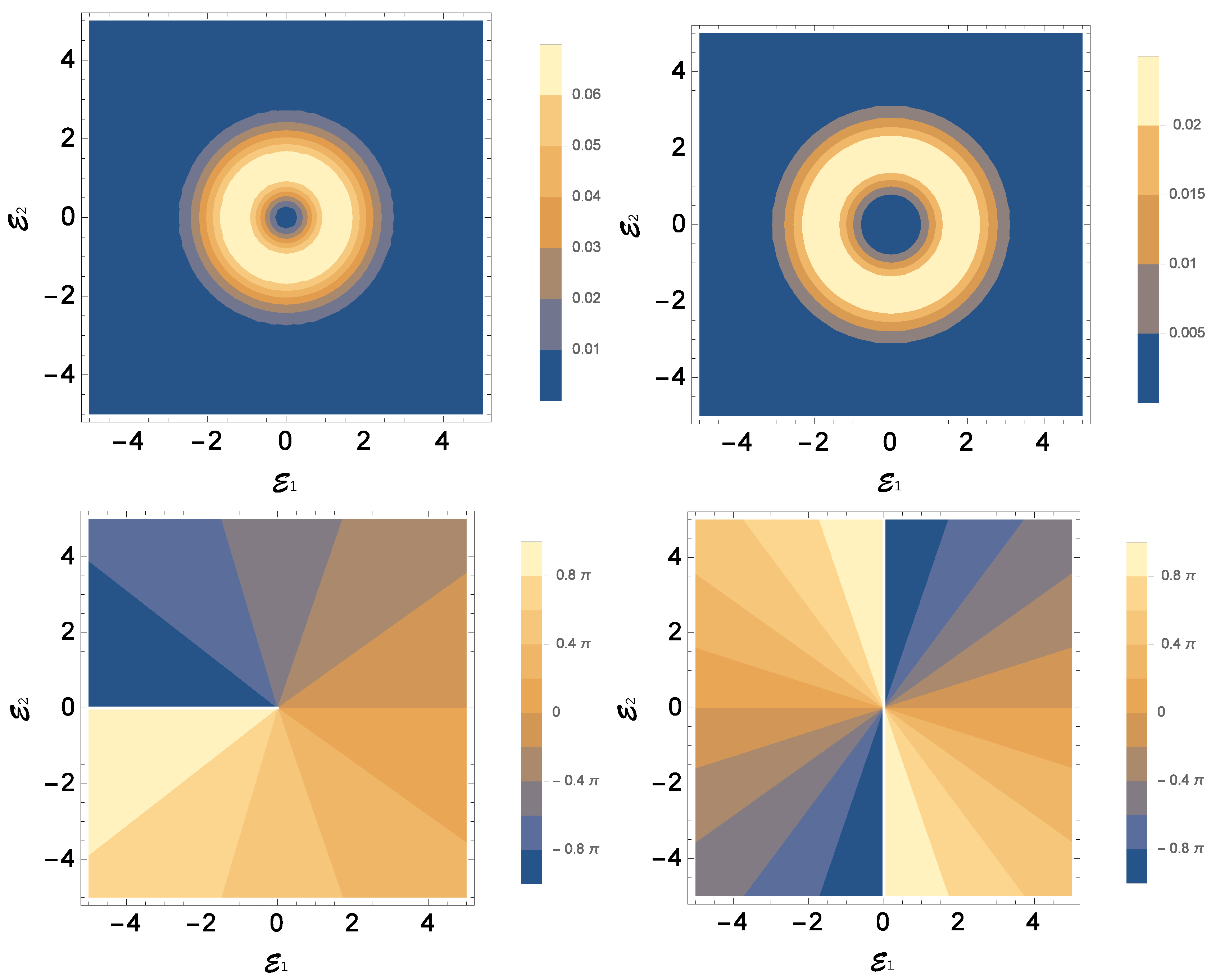
Figure 2 shows the probability
and phase
densities for a squeezing factor
, vortex orders 1 (
Figure 2 (left)) and 2 (
Figure 2 (right)) and minus handedness. We can observe the circular symmetry of the vortex with a growing radius with the number of photons (
Figure 2 (upper)) and the order of the vortex appearing in the phase as the number of complete cycles (
Figure 2 (lower)). If we had detected photons in mode 4, instead of mode 3, the only difference would be a change in handedness. Remarkably, both the probability and phase densities of the quantum state can be reconstructed by means of a weak values scheme [
52].
Likewise, the Wigner function associated with the quantum vortex
is easily worked out from the wavefunction Equation (
14) and the Wigner formula
obtaining [
53]
where
(x) is the Laguerre polynomial or order
n and argument
x.
Figure 3 shows the Wigner distributions related to the quantum vortices with vorticity order
and 2, for a squeezing factor
. In order to sketch the four-dimensional Wigner function given by Equation (
16) in two dimensions, we have set
. The presence of negative values around the origin of the phase space for the order 1 vortex, and far from the origin for the order 2 vortex is remarkable, which is a sign of the non-classicality of these quantum states.
Additionally, it should be noted that the simultaneous detection of photons in the leaky modes does not lead to a vortex state. In that case, the following expression is obtained:
with
C a constant factor. That is, the heralded quantum state after simultaneous measurement of
n photons by
and
m photons by
is not the vortex state of order
given in the right term of Equation (
17).
3. Realistic Scenario
This section is devoted to the study of the generation of quantum vortices in a realistic approach, that is, when propagation losses, non-unity efficiency of the heralding detectors and modal purity of the heralded quantum state are taken into account. There are two main approaches in this direction: the density matrix and the Wigner function [
54]. Since the quantum states involved are Gaussian until the de-Gaussification produced by the photon absorption, the Gaussian formalism related to the Wigner function will be less cumbersome and more transparent than that corresponding to the density matrix. This approach has been extensively used along the last decade in the study of the generation of quantum states under different experimental imperfections [
55,
56,
57].
Therefore, we start calculating the Wigner function related to Equation (5), given by [
58]
These modes are mixed on the first 3 dB DC (C1) turning out in the following expression:
corresponding to the EPR state Equation (
7). The quantum state finds the two weakly coupled DCs (
and
). Modes 1 and 2 are mixed with vacuum modes 3 and 4, respectively. The Wigner function of the vacuum is given by
. The output state can be then written as
Now, we analyze the detection of photons in the ancillary modes 3 and 4. We will choose as detectors a pair of APDs, since they are more commonly used. These can not distinguish the number of photons. They only give information on whether some photons were absorbed or not, in such a way that they project the state into a statistical mixture. This kind of detection, so-called on/off, can be modeled by the following operator:
where
stands for the identity operator and
a for the ancillary mode measured. Note the contrast with the PNRD operator given by Equation (
10), which measures a fixed number of photons. The quantum state obtained after this measurement is given by
with
the heralding probability and where
s stands for the signal mode,
is the trace operator and
the matrix density of the quantum state before measurement. In the Wigner representation, this operation is given by [
59]
where
is the Wigner function of the input quantum state and
the one related to the on/off operator Equation (
21). This expression is easily generalized to a higher number of modes, as in our case.
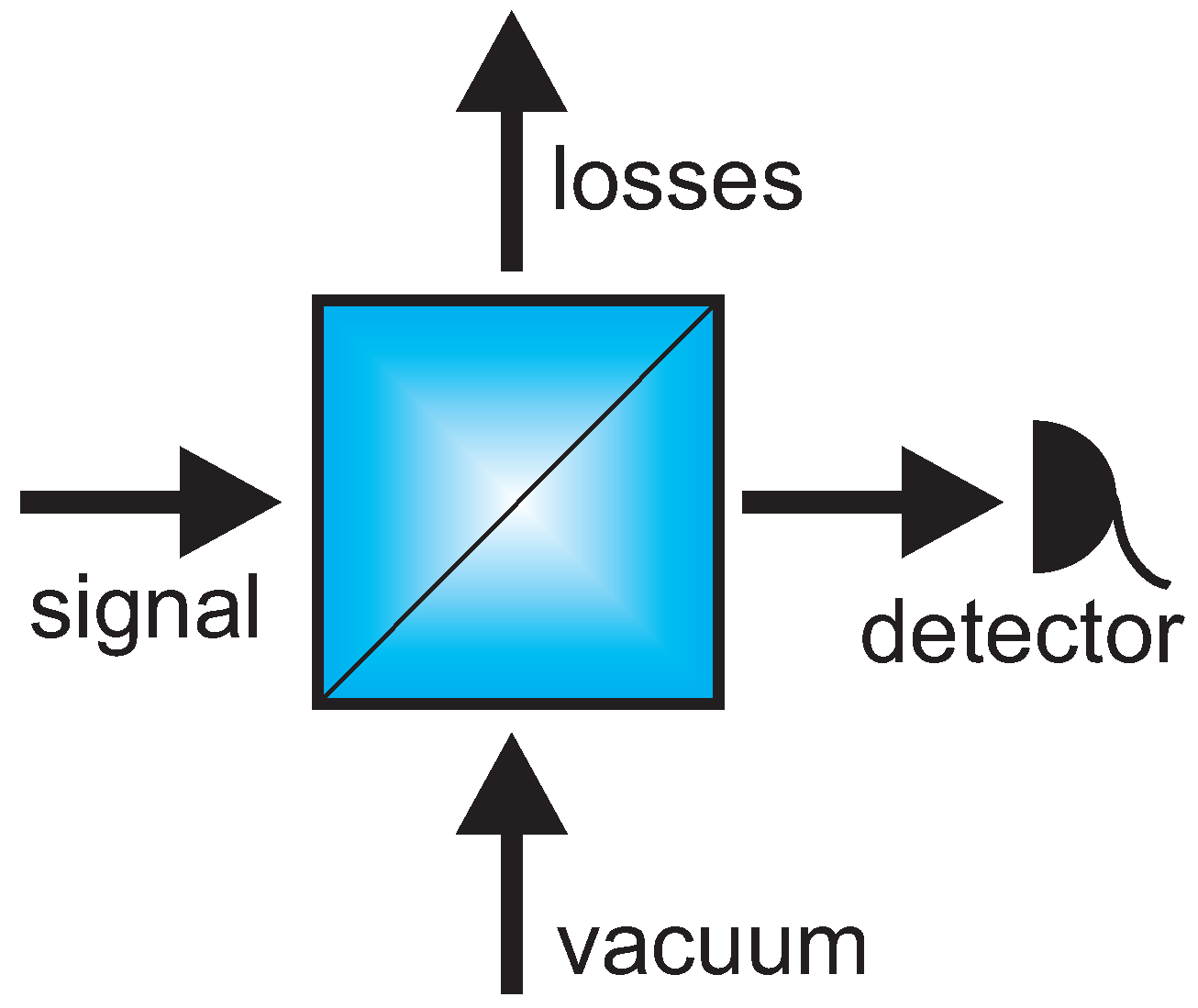
Moreover, the detector is characterized by a total efficiency
ν for the photons to be detected, given by its quantum efficiency and the losses in the ancillary channel. This non-unity efficiency can be included in the analysis by inserting a fictitious beamsplitter before the detector, mixing the state with a vacuum and tracing it out [
59] (
Figure 4). The Wigner function when these losses are taken into account is given by
where 5 and 6 are the auxiliary modes, which are mixed in the beamsplitter, and
and
are the total efficiencies of the APDs
and
. Then, a click event in mode 3 and no-click in mode 4 produces the following Wigner function:
where
is the heralding probability, with
and
. This expression is obtained after applying Equation (
24) on a generalization of Equation (
23) to this case. Additionally, the situation of a click in the detector
and no-click in
could be also studied by only exchanging the subindices 3 and 4 in Equation (
25).
Likewise, another question should be borne in mind in our analysis: the dark counts. In this case, a click will be recorded without any impinging photon due to thermal noise in the diode. Therefore, the detector does not differ between a genuine photon and a dark count. Since a dark count click gives no information about the conditional state, it mixes the desired quantum state with the unconditional one. The fraction of genuine photons is called modal purity
ζ, and its effect is included in the Wigner representation via the following expression [
60]
where
is the Wigner function of the unconditonal state. Moreover, the modal purity can incorporate others sources of false clicks like mode crosstalk and afterpulsing.
The quantum vortex state of light is obtained after crossing the second 3 dB DC (
), which performs the inverse operation of
. Following Equation (
19), the next Wigner function is obtained
Finally, propagation losses in modes 1 and 2 and the output coupling to fibers have to be taken into account. By using a fictitious beamsplitter such as in Equation (
24), the Wigner function of the output quantum vortex state is then
where
and
stand for the propagation losses in the modes 1 and 2, respectively, and 7 and 8 are vacuum auxiliary modes.
The realistic approach above introduced measures the consequences on the quality of the quantum states produced by the use of non-ideal detectors and losses. The Wigner function related to non-classical quantum states show negative values along the phase space. Particularly, single-photon subtracted quantum states show a large negativity in the center of the phase space, which is considered a strong signature of non-classicality. Due to this feature, an extensively used figure of merit in the generation of photon-subracted quantum states is the value of the Wigner function at the origin,
[
61]. In the case of ideal quantum vortices, a value
is obtained for a vortex order
, as shown in
Figure 3. However, experimental imperfections and mixing due to the absorption of higher number of photons will reduce this value. In the following lines we use this figure to show the effect of the inefficient operation on the quantum state. Likewise, the dependence of the heralding probability
on some parameters is also shown to complement the analysis of the system. In order to simplify, we have set identical values for the transmittivity of
and
,
, the total efficiencies of detectors
and
,
, and propagation and output coupling losses
. The transmittivity and input squeezing dependence of the normalized Wigner function related to the ideal value
and the heralding probability
are sketched in
Figure 5 (left and right), respectively, where no losses are considered. They show the inverse relationship between non-classicality and heralding probability. For a fixed transmittivity of the directional couplers
and
, a higher value of squeezing increases the rate of production of vortex states at the cost, however, of the subtraction of higher number of photons that are available in the state, decreasing accordingly the value of
due to the statistical mixture produced. This admixture is shown in
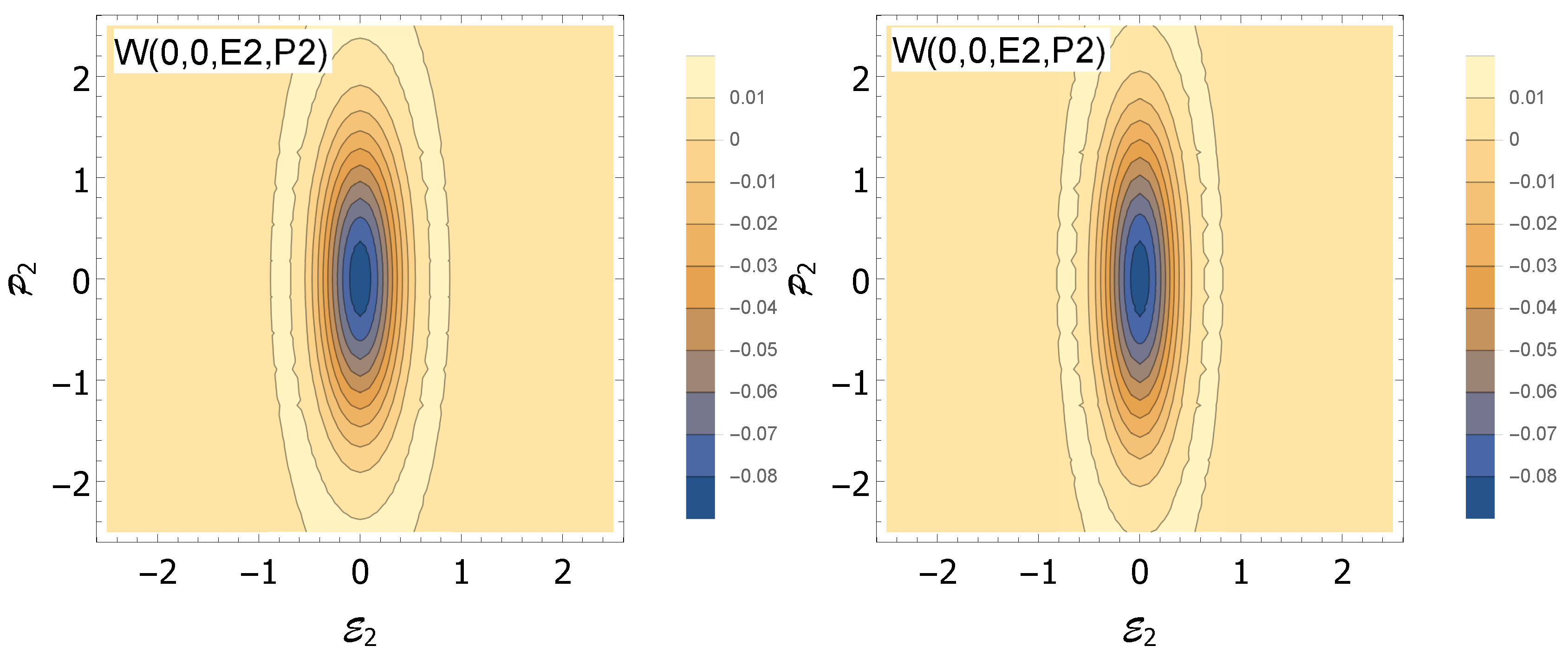
Figure 6, where we have compared the Wigner function
for a squeezing factor as high as
and a transmittivity
with a superposition of the Wigner functions associated with the first two ideal quantum vortices (
Figure 3) given by Equation (
16):
, where the coefficients are the calculated fidelities
between the quantum state
and the ideal vortices, given by [
59]
Figure 6 shows a good agreement between both Wigner functions in the area surrounding the origin of the phase space. However, higher order vortex terms should be added in order to get a better fit in the areas far from it.
Likewise,
Figure 7 (left) shows the effect of the total efficiency of the heralding detectors and imperfections in channels 1 and 2 on the non-classicality. A dramatic dependence with the losses in the main channels is shown, whereas the efficiency in the ancillary detectors is barely noticed, lowering, however, the heralding rate as it decreases. In
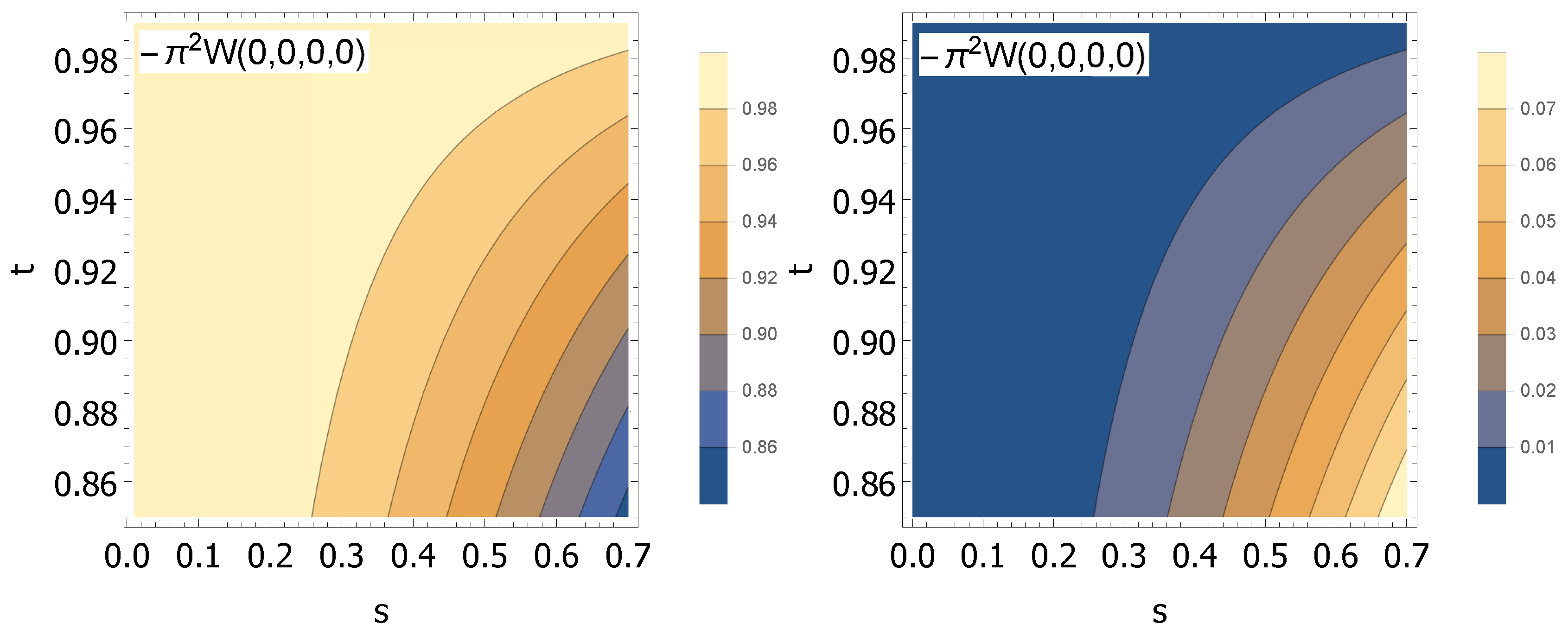
Figure 7 (right), the joint effect of the modal purity and the main losses are depicted. The mixing of the conditioned and unconditioned states weighted by the modal purity shows a severe impact on the quality of the generated state, sometimes even losing the non-classicality. Therefore, we can conclude that the main causes of degradation of the output quantum state are the losses due to propagation and coupling in the principal modes and the modal purity of the quantum state, mainly related to dark counts, and they are the key points to be improved for the optimal operation of this photonic device.
4. Order and Handedness Detection
The quantum vortices above presented show an hybrid nature: they are CV quantum states that carry DV quantum information. This can be shown by applying the abstract angular momentum operator
on Equation (
14) as follows [
29]:
Therefore, the quantum vortices
are eigenstates of the abstract angular momentum with eigenvalues (or vorticity)
, and they carry an orbital angular momentum of
. This feature can be used in the implementation of specific protocols in QIP. However, a measurement scheme is necessary in order to do so. To this end, the following simple detector of the order and handedness of the quantum vortex states is proposed: a 3 dB DC with two photon number-resolving detectors (PNRDs) [
62] connected at its outputs or integrated on-chip (
Figure 8). The operation of this device is easily shown by applying the 3 dB DC operator to Equation (
30) [
63]
This is an eigenvalue equation where
are eigenstates of the operator
with eigenvalues
, where the prime denotes the output modes related to the DC. Working out the value of the transformed abstract angular momentum operator we have
, with
the photon number operator related to each mode
j at the output. Hence, Equation (
31) is rewritten as follows:
The interpretation of this Equation is clear: measuring the difference of the number of photons at each output and , we can obtain the order and abstract handedness of the quantum vortex associated with the modes 1 and 2. This measurement device therefore enables the use of quantum vortices as a carrier of quantum information with possibilities in QIP.
However, as shown in
Section 2, the quality in the detection of the number of photons will be degraded by the propagation losses as well as by the non-unity efficiency and the dark counts of the detector [
62]. An input quantum state
given by a Wigner function
is transformed after crossing the 3 dB DC as given by Equation (
19). If the dark counts are not considered, the propagation losses, coupling efficiency and non-unity efficiency of the detectors can be introduced in our model as in the above section by means of Equation (
28), taking
and
as the total detection efficiencies at each output of the detection system. On the other hand, when the photodetectors show dark counts, the vacua in the auxiliary modes entering the free input ports of the fictitious beam splitters should be replaced by either thermal states
or phase-averaged coherent states
, depending on the origin of the noise, either thermal or Poissonian, which are admixed with the input signal state in the same way as in Equation (
28) [
64]. The Wigner distributions related to these two kinds of noise are given by
where
, with
k the Boltzmann’s constant,
T the temperature and
the
order modified Bessel function of the first kind with argument
x. The mean number of dark counts in the selected detection window is given by
in the case of thermal noise or by
if the noise is Poissonian. When the mean number of dark counts is zero, the vacuum state is recovered. It should be outlined that a different treatment of the dark counts problem has been carried out in
Section 3. The reason is that, in this case, we were not interested in the quantum state of the auxiliary channel, but in the heralded quantum state propagating in the signal waveguides, thus the introduction of the modal purity.
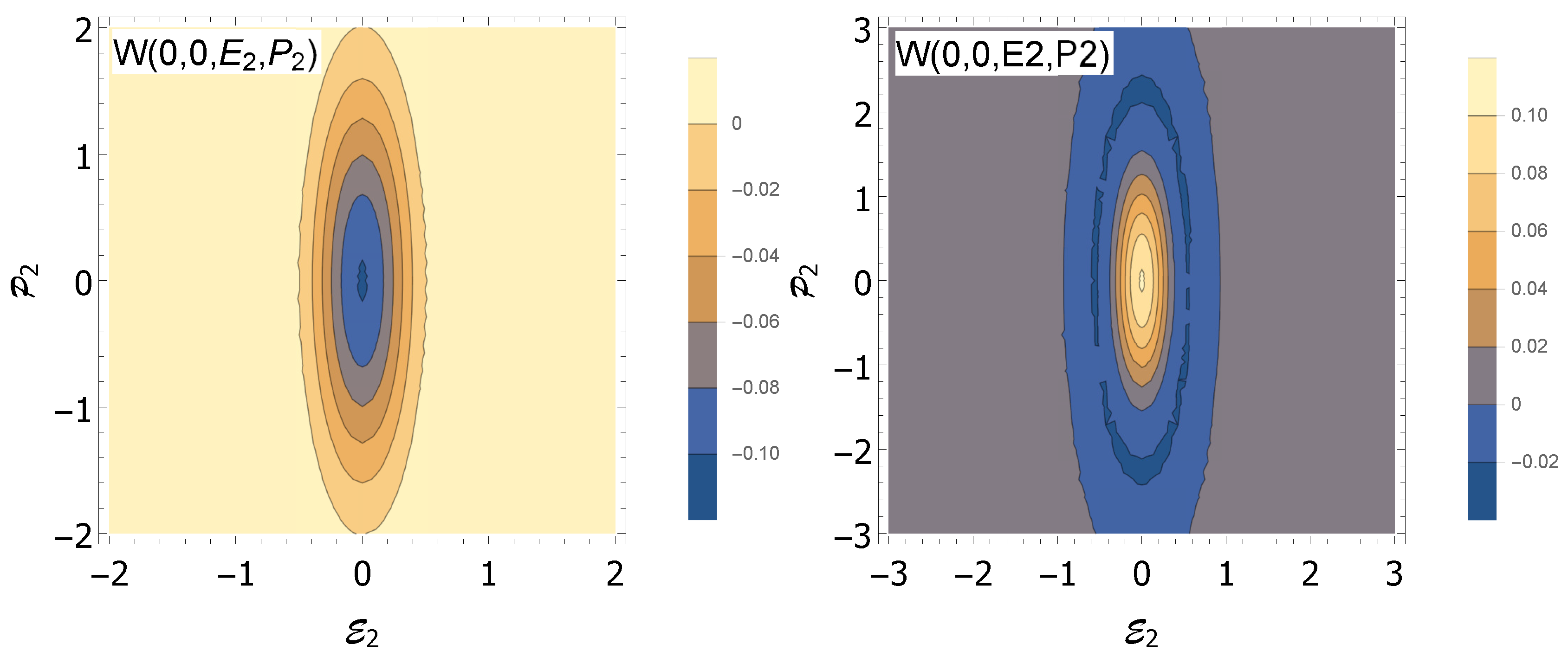
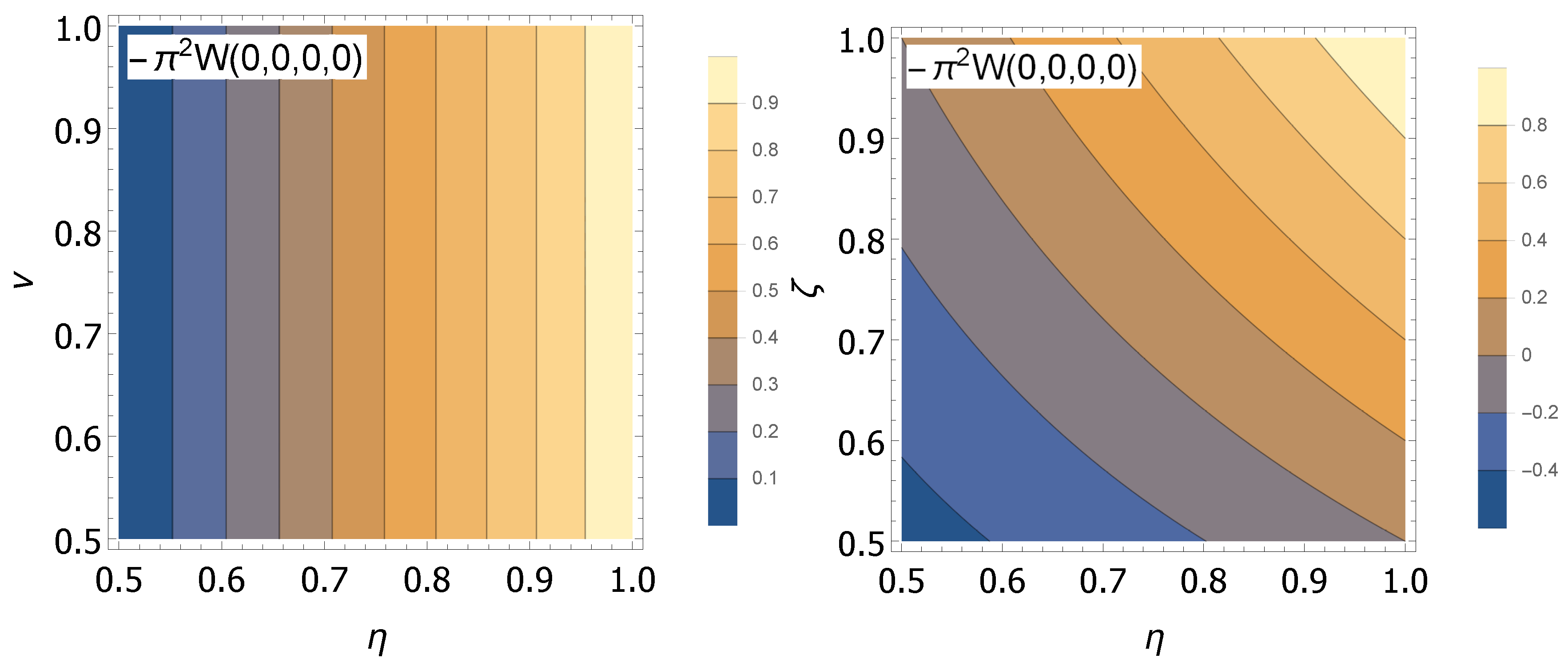
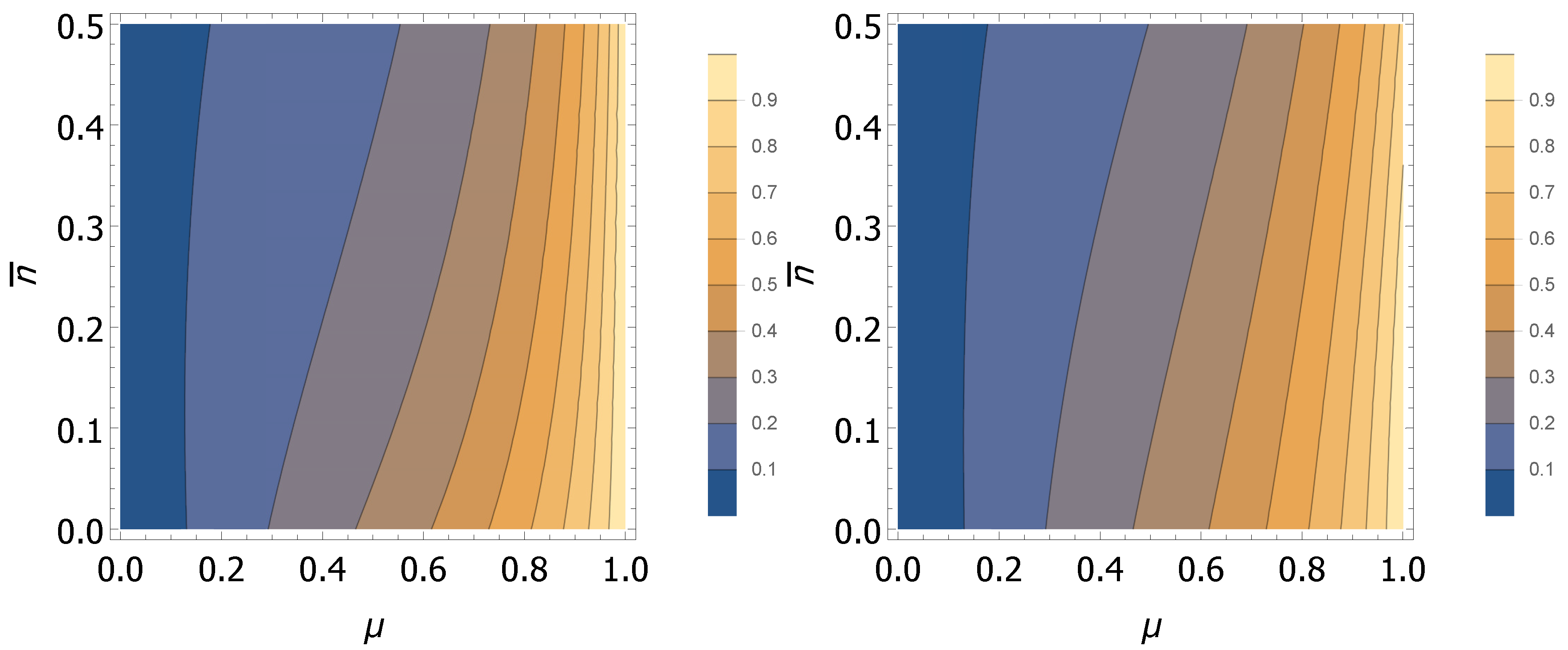
Figure 9 shows the fidelity
of the measured state
for an input quantum vortex
with squeezing factor
, where the effect of dark counts and total efficiencies of the detectors (
) is shown for thermal (
Figure 9 (left)) and Poissonian (
Figure 9 (right)) noise. These fidelities have been worked out applying the Wigner function
associated with the output quantum state
on Equation (
29). Likewise,
has been obtained applying Equations (19), (28) and (33) on
in the way pointed out in the previous paragraph. It is shown that, in both cases, the detection efficiency produces a stronger impact on the fidelity than the dark counts in the regime depicted. For instance, four-photon waveguide PNRDs based on superconducting niobium-nitride (NbN) nanowires present efficiencies of ≈24%, a dark count rate of ≈5 Hz and a timing resolution of ≈20 ns [
65]. Then, in this detection window, we would have ≈10
dark counts, which is a negligible value. However, the fidelity of the state for this detection efficiency would be highly degraded, with values of ≈15%. On the other hand, a tungsten transition edge sensor (TES) PNRD with an efficiency close to
and negligible dark counts has been recently shown on an integrated chip [
66]. However, TES devices show a poor temporal resolution, being three orders of magnitude slower than the superconducting NbN nanowires. In this case, we would obtain fidelities of about
.
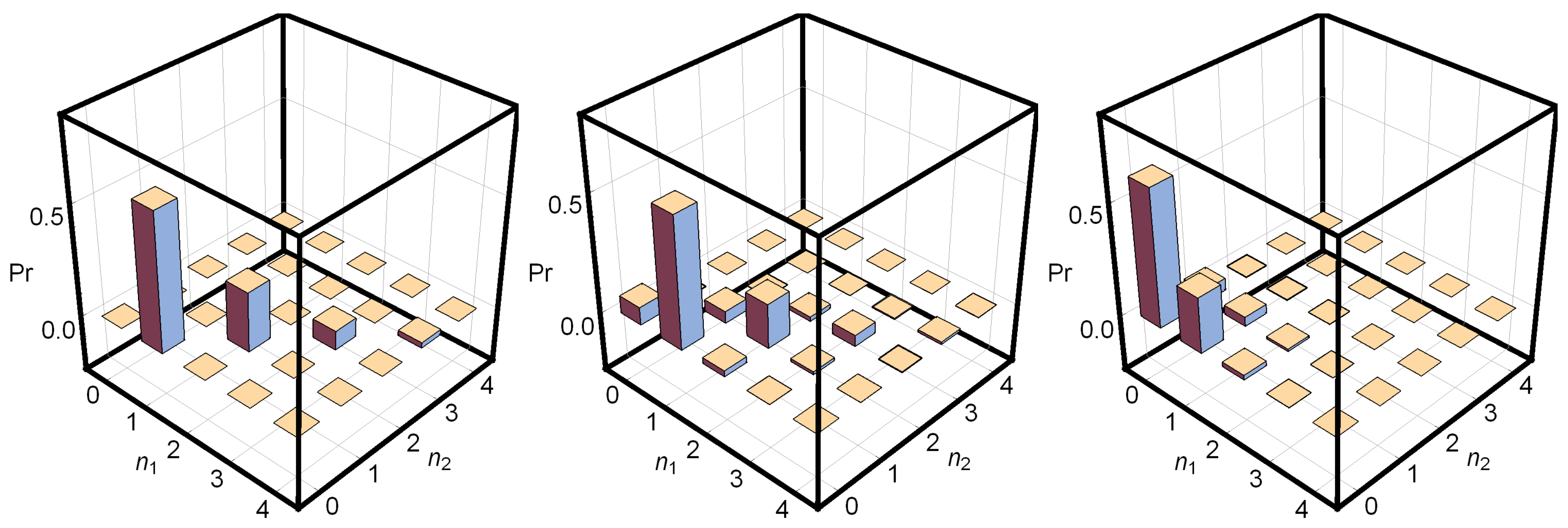
Finally, since the PNRDs placed at the outputs of the integrated detection system will measure the number of photons of the state, it would be interesting to calculate the joint probability distribution of the number of photons
and
measured at each detector under the experimental imperfections previously mentioned. This probability is equivalent to the fidelity between the measured state and the Fock states in each mode
, and it is calculated by means of
where
is the Wigner function corresponding to a Fock state
. In
Figure 10, the joint probability distribution of the number of photons
is depicted for an input vortex state
with squeezing factor
for the ideal (
Figure 10 (left)) and realistic cases (
Figure 10 (center and right)). In the ideal case (
Figure 10 (left)), the difference of one photon between the output modes is hold along the distribution, obtaining an order 1 and + abstract handedness by means of Equation (
32). In the case of the use of TES PNRDs with the detection system, where
and
, a contribution from the vacuum that decreases the overall probability of detection is shown (
Figure 10 (center)), as well as a number of spurious counts that slightly degrade the measurement of the vorticity. On the other hand,
Figure 10 (right) shows the outcome when superconducting NbN nanowires PNRDs are chosen, with parameters
and
. It is shown there that the contribution of the vacuum is so high that more than half of the input states would be lost without detection, and the number of spurious counts would be ≈40% of those really related to the input quantum vortex, heavily degrading the ability of the detection system to measure the abstract angular momentum of the quantum state. Therefore, highly efficient PNRDs are necessary in order to have order and handedness detection devices with high-fidelity.