Implementation of Traveling Odd Schrödinger Cat States in Circuit-QED
Abstract
:1. Introduction
2. Photon-Subtraction from an SVS
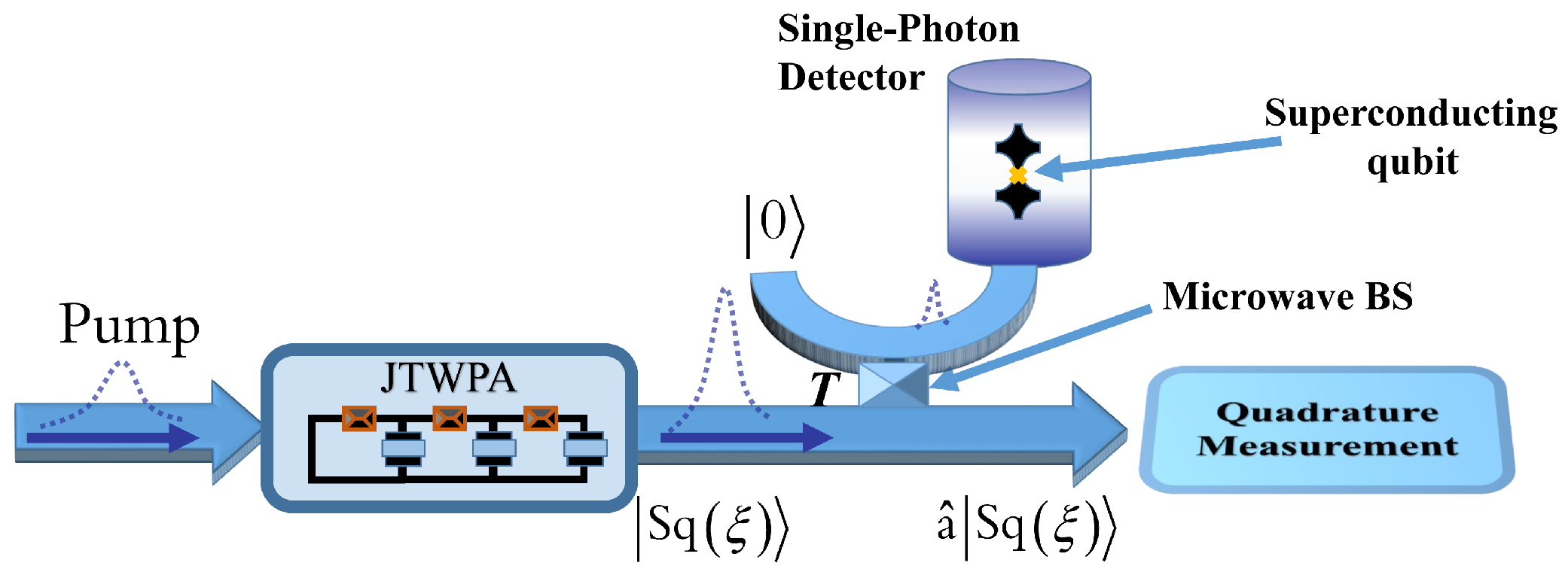
3. Implementation in Circuit-QED
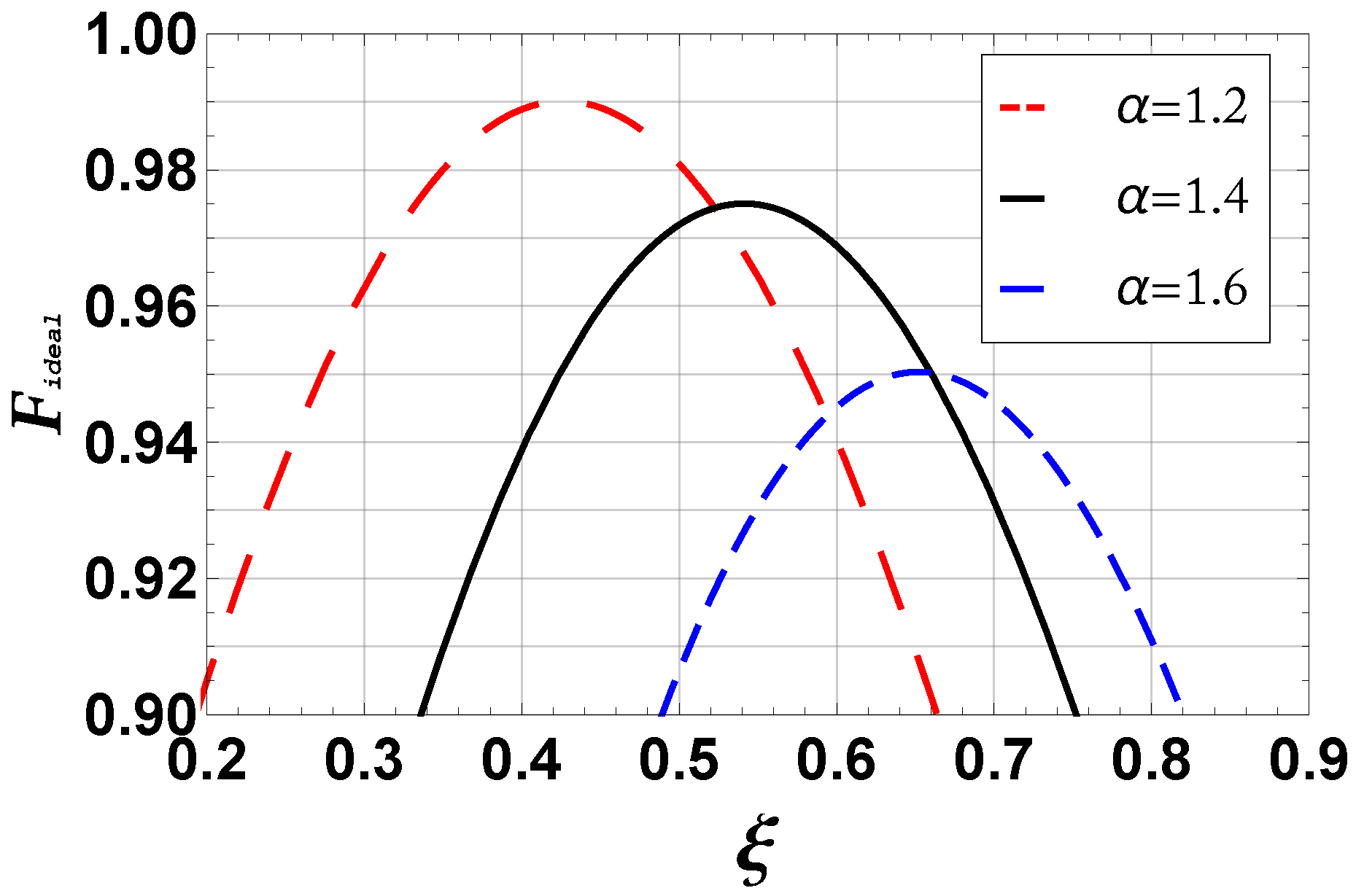
3.1. Protocol
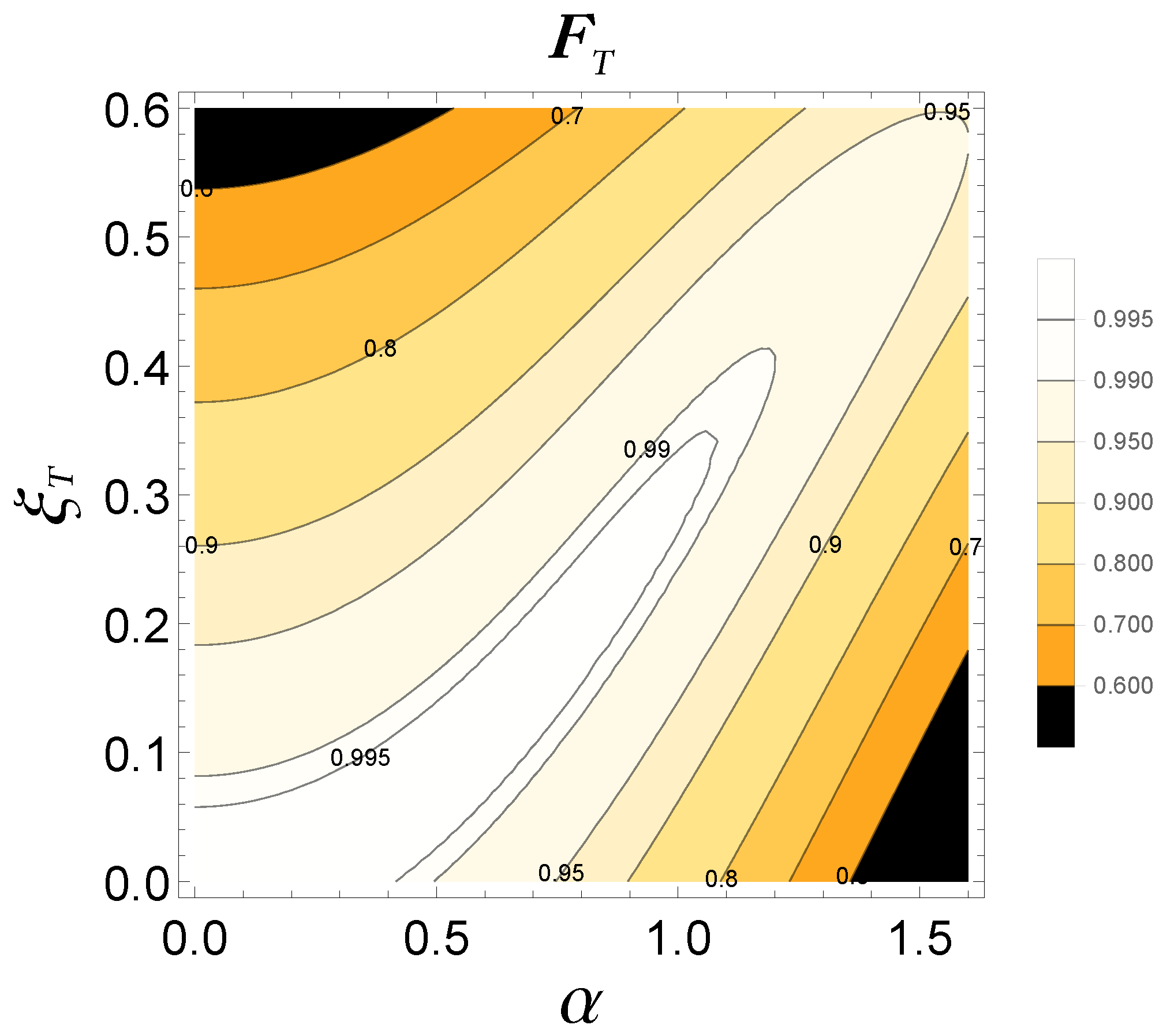
3.2. Single-Photon Detection with a
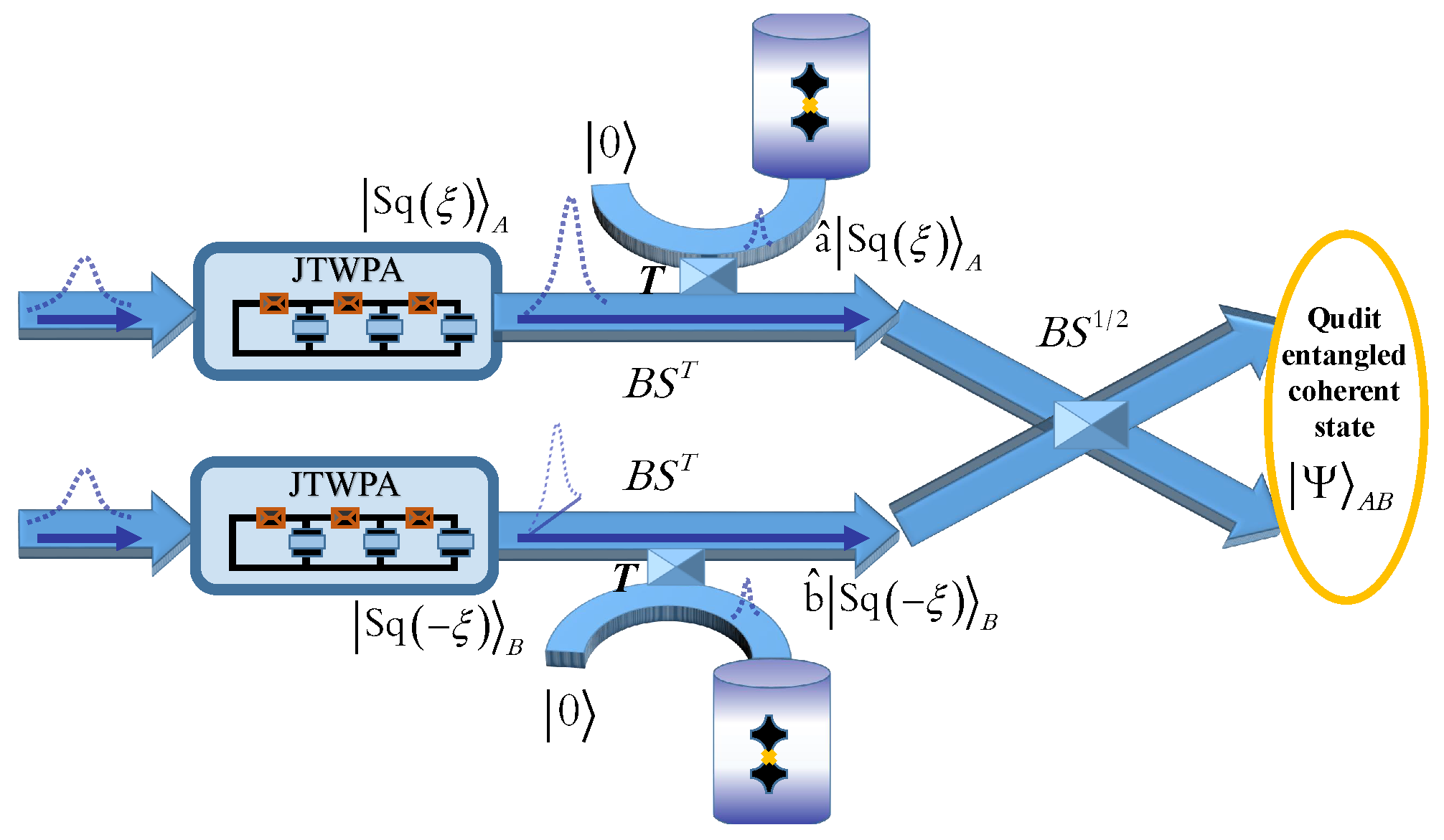
4. Traveling Qudit ECS
5. Conclusions and Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schrödinger, E. Die gegenwärtige Situation in der Quantenmechanik I-III. Naturwissenschaften 1935, 23, 823. [Google Scholar] [CrossRef]
- Yurke, B.; Stoler, D. Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion. Phys. Rev. Lett. 1986, 57, 13–16. [Google Scholar] [CrossRef] [PubMed]
- Milburn, G.J. Quantum and classical Liouville dynamics of the anharmonic oscillator. Phys. Rev. A 1986, 33, 674–685. [Google Scholar] [CrossRef]
- Myers, C.R.; Ralph, T.C. Coherent state topological cluster state production. New J. Phys. 2011, 13, 115015. [Google Scholar] [CrossRef]
- Ralph, T.C.; Gilchrist, A.; Milburn, G.J.; Munro, W.J.; Glancy, S. Quantum computation with optical coherent states. Phys. Rev. A 2003, 68, 042319. [Google Scholar] [CrossRef]
- Jeong, H.; Kim, M.S. Efficient Quantum Computation using Coherent States. Phys. Rev. A 2002, 65, 042305. [Google Scholar] [CrossRef]
- Joo, J.; Munro, W.J.; Spiller, T.P. Quantum metrology with entangled coherent states. Phys. Rev. Lett. 2011, 107, 083601. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.-Y.; Lee, C.-W.; Nha, H.; Kaszlikowski, D. Quantum phase estimation using a multi-headed cat state. J. Opt. Soc. Am. B 2015, 32, 1186–1192. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Lee, C.-W.; Lee, J.; Nha, H. Quantum phase estimation using path-symmetric entangled states. Sci. Rep. 2016, 6, 30306. [Google Scholar] [CrossRef] [PubMed]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. High-rate measurement-device-independent quantum cryptography. Nat. Photonics 2015, 9, 397–402. [Google Scholar] [CrossRef]
- Brune, M.; Hagley, E.; Dreyer, J.; Maitre, X.; Maali, A.; Wunderlich, C.; Raimond, J.M.; Haroche, S. Observing the Progressive Decoherence of the “Meter” in a Quantum Measurement. Phys. Rev. Lett. 1996, 77, 4887. [Google Scholar] [CrossRef] [PubMed]
- Brune, M.; Haroche, S.; Raimond, J.M.; Davidovich, L.; Zagury, N. Manipulation of photons in a cavity by dispersive atom-field coupling: Quantum-nondemolition measurements and generation of “Schrödinger cat” states. Phys. Rev. A 1992, 45, 5193. [Google Scholar] [CrossRef] [PubMed]
- Deléglise, S.; Dotsenko, I.; Sayrin, C.; Bernu, J.; Brune, M.; Raimond, J.M.; Haroche, S. Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 2008, 455, 510–514. [Google Scholar] [CrossRef] [PubMed]
- Lund, A.P.; Jeong, H.; Ralph, T.C.; Kim, M.S. Conditional production of superpositions of coherent states with inefficient photon detection. Phys. Rev. A 2004, 70, 020101. [Google Scholar] [CrossRef]
- Ourjoumtsev, A.; Tualle-Brouri, R.; Laurat, J.; Grangier, P. Generating optical Schrödinger kittens for quantum information processing. Science 2006, 312, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Ourjoumtsev, A.; Jeong, H.; Tualle-Brouri, R.; Grangier, P. Generation of optical ‘Schrödinger cats’ from photon number states. Nature 2007, 448, 784–786. [Google Scholar] [CrossRef] [PubMed]
- Neergaard-Nielsen, J.S.; Nielsen, B.M.; Hettich, C.; Mølmer, K.; Polzik, E.S. Generation of a superposition of odd photon number states for quantum information networks. Phys. Rev. Lett. 2006, 97, 083604. [Google Scholar] [CrossRef] [PubMed]
- Marek, P.; Jeong, H.; Kim, M.S. Generating “squeezed” superpositions of coherent states using photon addition and subtraction. Phys. Rev. A 2008, 78, 063811. [Google Scholar] [CrossRef]
- Takeoka, M.; Takahashi, H.; Sasaki, M. Large-amplitude coherent-state superposition generated by a time-separated two-photon subtraction from a continuous-wave squeezed vacuum. Phys. Rev. A 2008, 77, 062315. [Google Scholar] [CrossRef]
- Lee, C.-W.; Lee, J.; Nha, H.; Jeong, H. Generating a Schrödinger-cat-like state via a coherent superposition of photonic operations. Phys. Rev. A 2012, 85, 063815. [Google Scholar] [CrossRef]
- Takahashi, H.; Wakui, K.; Suzuki, S.; Takeoka, M.; Hayasaka, K.; Furusawa, A.; Sasaki, M. Generation of Large-Amplitude Coherent-State Superposition via Ancilla-Assisted Photon Subtraction. Phys. Rev. Lett. 2008, 101, 233605. [Google Scholar] [CrossRef] [PubMed]
- Namekata, N.; Takahashi, Y.; Fujii, G.; Fukuda, D.; Kurimura, S.; Inoue, S. Non-Gaussian operation based on photon subtraction using a photon-number-resolving detector at a telecommunications wavelength. Nat. Photonics 2010, 4, 655–660. [Google Scholar] [CrossRef]
- Gerrits, T.; Glancy, S.; Clement, T.S.; Calkins, B.; Lita, A.E.; Miller, A.J.; Migdall, A.L.; Nam, S.W.; Mirin, R.P.; Knill, E. Generation of optical coherent-state superpositions by number-resolved photon subtraction from the squeezed vacuum. Phys. Rev. A 2010, 82, 031802. [Google Scholar] [CrossRef]
- Lund, A.P.; Ralph, T.C.; Haselgrove, H.L. Fault-tolerant linear optical quantum computing with small-amplitude coherent States. Phys. Rev. Lett. 2008, 100, 030503. [Google Scholar] [CrossRef] [PubMed]
- Joo, J.; Elliott, M.; Oi, D.K.L.; Ginossar, E.; Spiller, T.P. Deterministic amplification of Schrödinger cat states in circuit quantum electrodynamics. New J. Phys. 2016, 18, 023028. [Google Scholar] [CrossRef]
- Park, J.; Joo, J.; Zavatta, A.; Bellini, M.; Jeong, H. Efficient noiseless linear amplification for light fields with larger amplitudes. Opt. Express 2016, 24, 1331–1346. [Google Scholar] [CrossRef] [PubMed]
- Mann, A.; Sanders, B.C.; Munro, W.J. Bell’s inequality for an entanglement of nonorthogonal states. Phys. Rev. A 1995, 51, 989–991. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H. Testing Bell inequalities with photon-subtracted Gaussian states. Phys. Rev. A 2008, 78, 042101. [Google Scholar] [CrossRef]
- Jeong, H.; Son, W.; Kim, M.S. Quantum nonlocality test for continuous-variable states with dichotomic observables. Phys. Rev. A 2003, 67, 012106. [Google Scholar] [CrossRef]
- Wilson, D.; Jeong, H.; Kim, M.S.J. Quantum Nonlocality for a Mixed Entangled Coherent State. J. Mod. Opt. 2002, 49, 851–864. [Google Scholar] [CrossRef]
- Stobińska, M.; Jeong, H.; Ralph, T.C. Violation of Bell’s inequality using classical measurements and nonlinear local operations. Phys. Rev. A 2007, 75, 052105. [Google Scholar] [CrossRef]
- Gerry, C.C.; Mimih, J.; Benmoussa, A. Maximally entangled coherent states and strong violations of Bell-type inequalities. Phys. Rev. A 2009, 80, 022111. [Google Scholar] [CrossRef]
- Lee, C.-W.; Jeong, H. Effects of squeezing on quantum nonlocality of superpositions of coherent states. Phys. Rev. A 2009, 80, 052105. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Lee, C.-W.; Kurzynśki, P.; Kaszlikowski, D.; Kim, J. Duality in entanglement of macroscopic states of light. Phys. Rev. A 2016, 94, 022314. [Google Scholar] [CrossRef]
- Vlastakis, B.; Kirchmair, G.; Leghtas, Z.; Nigg, S.E.; Frunzio, L.; Girvin, S.M.; Mirrahimi, M.; Devoret, M.H.; Schoelkopf, R.J. Deterministically encoding quantum information using 100-photon Schrödinger cat states. Science 2013, 342, 607–610. [Google Scholar] [CrossRef] [PubMed]
- Bretheau, L.; Campagne-Ibarcq, P.; Flurin, E.; Mallet, F.; Huard, B. Quantum optics. Quantum dynamics of an electromagnetic mode that cannot contain N photons. Science 2015, 348, 776–779. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Gao, Y.Y.; Reinhold, P.; Heeres, R.W.; Ofek, N.; Chou, K.; Axline, C.; Reagor, M.; Blumoff, J.; Sliwa, K.M.; et al. A Schrödinger cat living in two boxes. Science 2016, 352, 1087–1091. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, T.; Inomata, K.; Watanabe, M.; Matsuba, K.; Miyazaki, T.; Oliver, W.D.; Nakamura, Y.; Tsai, J.S. Flux-driven Josephson parametric amplifier. Appl. Phys. Lett. 2008, 93, 042510. [Google Scholar] [CrossRef]
- Castellanos-Beltran, M.A.; Lehnert, K.W. Widely tunable parametric amplifier based on a superconducting quantum interference device array resonator. Appl. Phys. Lett. 2007, 91, 083509. [Google Scholar] [CrossRef]
- Lähteenmäki, P.; Paraoanu, G.S.; Hassel, J.; Hakonen, P.J. Coherence and multimode correlations from vacuum fluctuations in a microwave superconducting cavity. Nat. Commun. 2016, 7, 12548. [Google Scholar] [CrossRef] [PubMed]
- Lähteenmäki, P.; Vesterinen, V.; Hassel, J.; Paraoanu, G.S.; Seppä, H.; Hakonen, P. Advanced concepts in Josephson junction reflection amplifiers. J. Low Temp. Phys. 2014, 175, 868–876. [Google Scholar] [CrossRef]
- Lähteenmäki, P.; Paraoanu, G.S.; Hassel, J.; Hakonen, P.J. Dynamical Casimir effect in a Josephson metamaterial. Proc. Natl. Acad. Sci. USA 2013, 110, 4234–4238. [Google Scholar] [CrossRef]
- Bergeal, N.; Vijay, R.; Manucharyan, V.E.; Siddiqi, I.; Schoelkopf, R.J.; Girvin, S.M.; Devoret, M.H. Analog information processing at the quantum limit with a Josephson ring modulator. Nat. Phys. 2010, 6, 296–302. [Google Scholar] [CrossRef]
- Macklin, C.; O’Brien, K.; Hover, D.; Schwartz, M.E.; Bolkhovsky, V.; Zhang, X.; Oliver, W.D.; Siddiqi, I. A near-quantum-limited Josephson traveling-wave parametric amplifier. Science 2015, 350, 307–310. [Google Scholar] [CrossRef] [PubMed]
- Grimsmo, A.L.; Blais, A. Squeezing and quantum state engineering with Josephson traveling wave amplifiers. arXiv, 2016; arXiv:1607.07908. [Google Scholar]
- Murch, K.W.; Weber, S.J.; Beck, K.M.; Ginossar, E.; Siddiqi, I. Reduction of the radiative decay of atomic coherence in squeezed vacuum. Nature 2013, 499, 62–65. [Google Scholar] [CrossRef] [PubMed]
- Toyli, D.M.; Eddins, A.W.; Boutin, S.; Puri, S.; Hover, D.; Bolkhovsky, V.; Oliver, W.D.; Blais, A.; Siddiqi, I. Resonance Fluorescence from an Artificial Atom in Squeezed Vacuum. Phys. Rev. X 2016, 6, 031004. [Google Scholar] [CrossRef]
- Fedorov, K.G.; Zhong, L.; Pogorzalek, S.; Eder, P.; Fischer, M.; Goetz, J.; Xie, E.; Wulschner, F.; Inomata, K.; Yamamoto, T.; et al. Displacement of Propagating Squeezed Microwave States. Phys. Rev. Lett. 2016, 117, 020502. [Google Scholar] [CrossRef] [PubMed]
- Ourjoumtsev, A.; Ferreyrol, F.; Tualle-Brouri, R.; Grangier, P. Preparation of non-local superpositions of quasi-classical light states. Nat. Phys. 2009, 5, 189–192. [Google Scholar] [CrossRef]
- Inomata, K.; Lin, Z.; Koshino, K.; Oliver, W.D.; Tsai, J.-S.; Yamamoto, T.; Nakamura, Y. Single microwave-photon detector using an artificial Lambda-type three-level system. Nat. Commun. 2016, 7, 12303. [Google Scholar] [CrossRef] [PubMed]
- Narla, A.; Shankar, S.; Hatridge, M.; Leghtas, Z.; Sliwa, K.M.; Zalys-Geller, E.; Mundhada, S.O.; Pfaff, W.; Frunzio, L.; Schoelkopf, R.J.; et al. Robust Concurrent Remote Entanglement between Two Superconducting Qubits. Phys. Rev. X 2006, 6, 031036. [Google Scholar] [CrossRef]
- Ofek, N.; Petrenko, A.; Heeres, R.; Reinhold, P.; Leghtas, Z.; Vlastakis, B.; Liu, Y.; Frunzio, L.; Girvin, S.M.; Jiang, L.; et al. Demonstrating quantum error correction that extends the lifetime of quantum information. arXiv, 2016; arXiv:1602.04768. [Google Scholar]
- Leghtas, Z.; Kirchmair, G.; Vlastakis, B.; Schoelkopf, R.J.; Devoret, M.H.; Mirrahimi, M. Hardware-efficient autonomous quantum memory protection. Phys. Rev. Lett. 2013, 111, 120501. [Google Scholar] [CrossRef] [PubMed]
- Heeres, R.W.; Reinhold, P.; Ofek, N.; Frunzio, L.; Devoret, M.H.; Schoelkopf, R.J. Implementing a Universal Gate Set on a Logical Qubit Encoded in an Oscillator. arXiv, 2016; arXiv:1608.02430. [Google Scholar]
- Jozsa, R. Fidelity for mixed quantum states. J. Mod. Opt. 1994, 41, 2315–2323. [Google Scholar] [CrossRef]
- Paraoanu, G.-S.; Scutaru, H. Fidelity for multimode thermal squeezed states. Phys. Rev. A 2000, 61, 022306. [Google Scholar] [CrossRef]
- Kim, M.S. Recent developments in photon-level operations on travelling light fields. J. Phys. B 2008, 41, 133001. [Google Scholar] [CrossRef]
- Mallet, F.; Castellanos-Beltran, M.A.; Ku, H.S.; Glancy, S.; Knill, E.; Irwin, K.D.; Hilton, G.C.; Vale, L.R.; Lehnert, K.W. Quantum State Tomography of an Itinerant Squeezed Microwave Field. Phys. Rev. Lett. 2011, 106, 220502. [Google Scholar] [CrossRef] [PubMed]
- Sanders, B.C. Entangled coherent states. Phys. Rev. A 1992, 45, 6811. [Google Scholar] [CrossRef] [PubMed]
- Sanders, B.C. Review of entangled coherent states. J. Phys. A 2012, 45, 244002. [Google Scholar] [CrossRef]
- Leghtas, Z.; Kirchmair, G.; Vlastakis, B.; Devoret, M.H.; Schoelkopf, R.J.; Mirrahimi, M. Deterministic protocol for mapping a qubit to coherent state superpositions in a cavity. Phys. Rev. A 2013, 87, 042315. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.; Ji, S.-W.; Nha, H.; Anisimov, P.M.; Dowling, J.P. Coherent-state optical qudit cluster state generation and teleportation via homodyne detection. Opt. Commun. 2015, 337, 79–82. [Google Scholar] [CrossRef]
- Michael, M.H.; Silveri, M.; Brierley, R.T.; Albert, V.V.; Salmilehto, J.; Jiang, L.; Girvin, S.M. New Class of Quantum Error-Correcting Codes for a Bosonic Mode. Phys. Rev. X 2016, 6, 031006. [Google Scholar] [CrossRef]
- Huver, S.; Wildfeuer, C.F.; Dowling, J.P. Entangled Fock states for robust quantum optical metrology, imaging, and sensing. Phys. Rev. A 2008, 78, 063828. [Google Scholar] [CrossRef]
- Dorner, U.; Demkowicz-Dobrzanski, R.; Smith, B.J.; Lundeen, J.S.; Wasilewski, W.; Banaszek, K.; Walmsley, I.A. Optimal Quantum Phase Estimation. Phys. Rev. Lett. 2009, 102, 040403. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joo, J.; Lee, S.-Y.; Kim, J. Implementation of Traveling Odd Schrödinger Cat States in Circuit-QED. Photonics 2016, 3, 57. https://doi.org/10.3390/photonics3040057
Joo J, Lee S-Y, Kim J. Implementation of Traveling Odd Schrödinger Cat States in Circuit-QED. Photonics. 2016; 3(4):57. https://doi.org/10.3390/photonics3040057
Chicago/Turabian StyleJoo, Jaewoo, Su-Yong Lee, and Jaewan Kim. 2016. "Implementation of Traveling Odd Schrödinger Cat States in Circuit-QED" Photonics 3, no. 4: 57. https://doi.org/10.3390/photonics3040057
APA StyleJoo, J., Lee, S.-Y., & Kim, J. (2016). Implementation of Traveling Odd Schrödinger Cat States in Circuit-QED. Photonics, 3(4), 57. https://doi.org/10.3390/photonics3040057



